Laser Polishing Die Steel Assisted by Steady Magnetic Field
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Materials
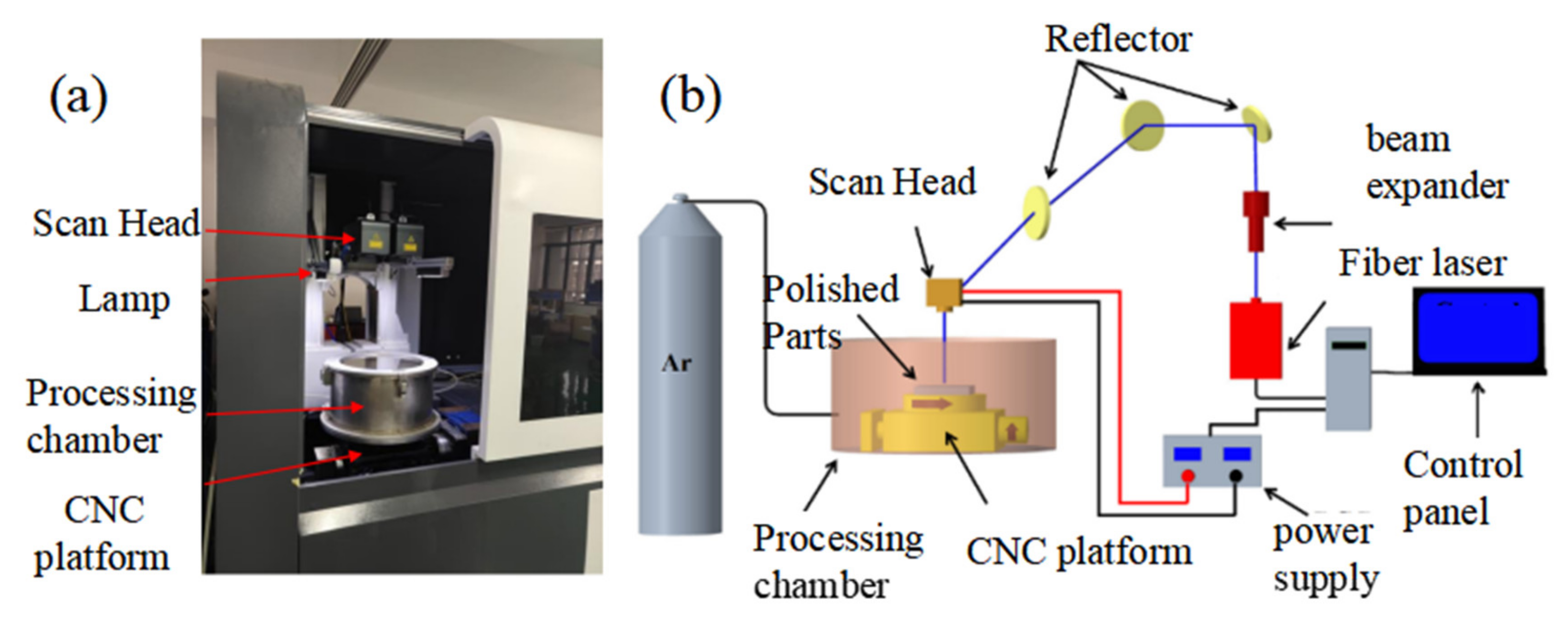
2.2. Experimental Equipment
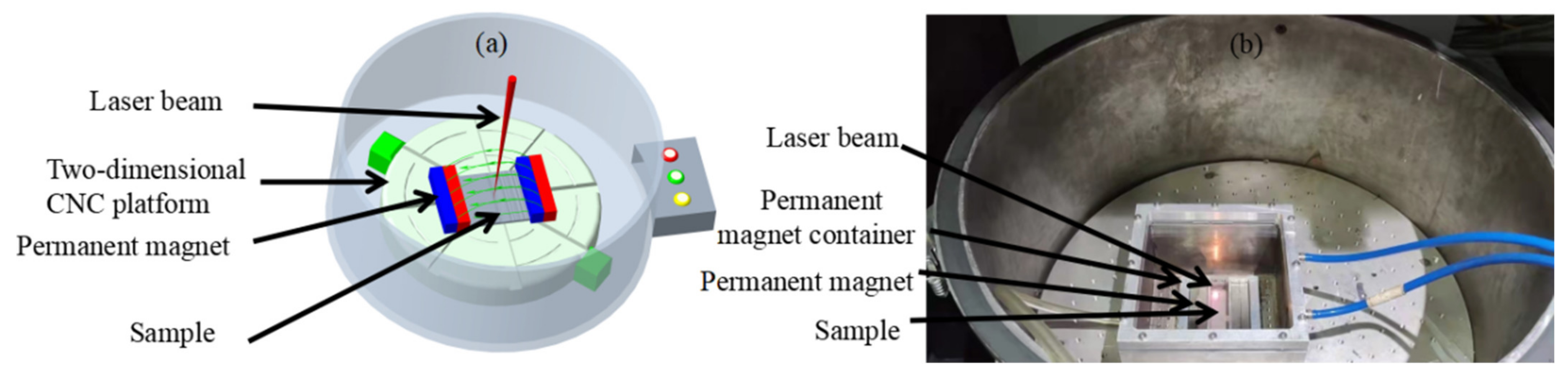
2.3. Experimental Method
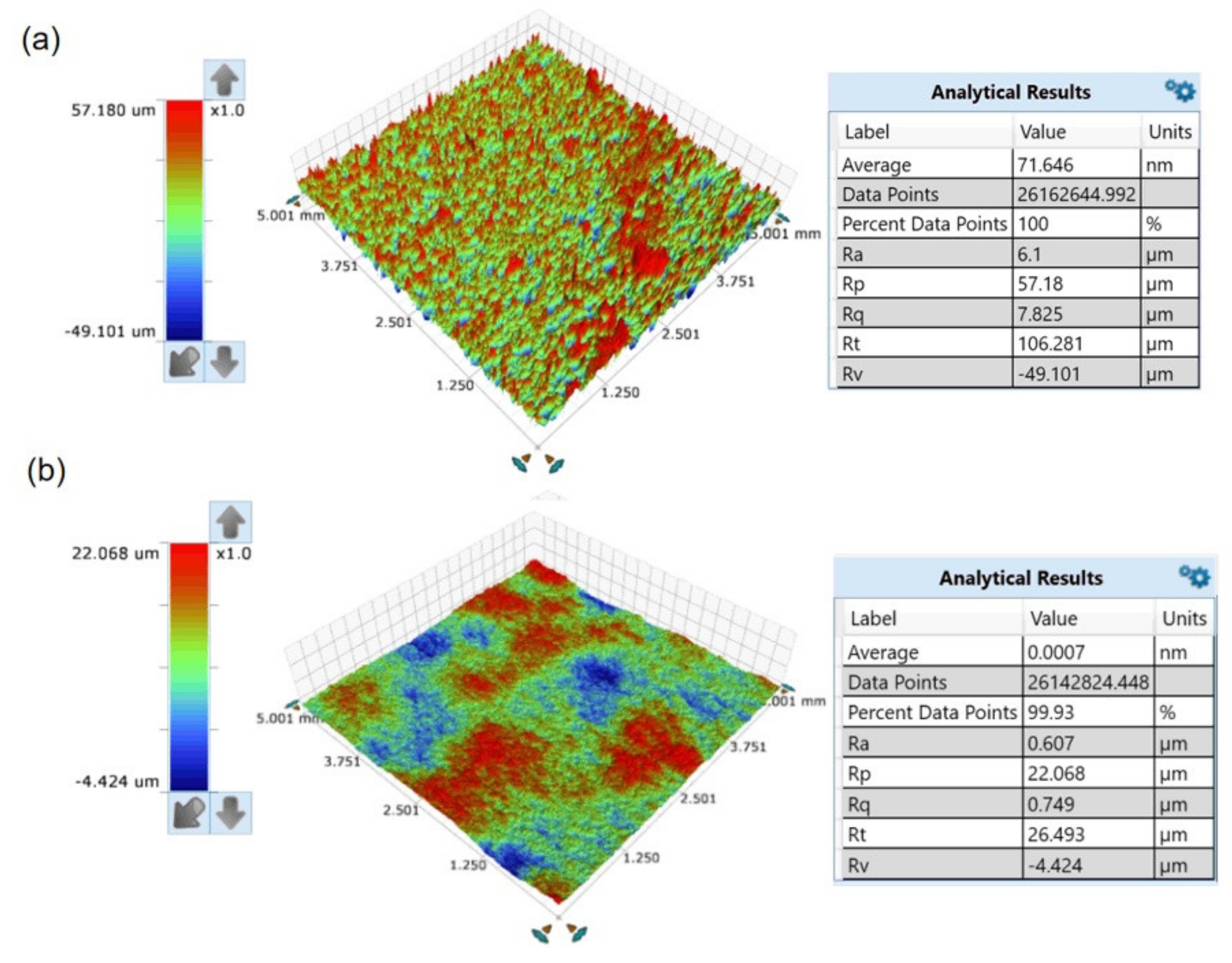
2.4. Results and Discussion
3. Model Building
3.1. Model Hypothesis
- The flow of molten metal is regarded as incompressible Newtonian laminar flow.
- The material has the characteristics of uniform distribution and is isotropic, and the thermal physical parameters of the material vary with temperature.
- The maximum temperature of laser polishing is lower than the boiling point of the material without considering the evaporation of the model.
- In the course of the experiment, because the sealing device is filled with argon protective gas, the chemical reaction between metal and air at high temperature is ignored.
- The gas domain is not considered in the modeling process. Due to the great differences in viscosity and density between the molten metal and the protective gas, the air domain can be ignored in order to reduce the calculation time.
- The flux density is uniformly distributed.
3.2. Control Equation
3.3. Computational Domain and Initial Model Establishment of the Model
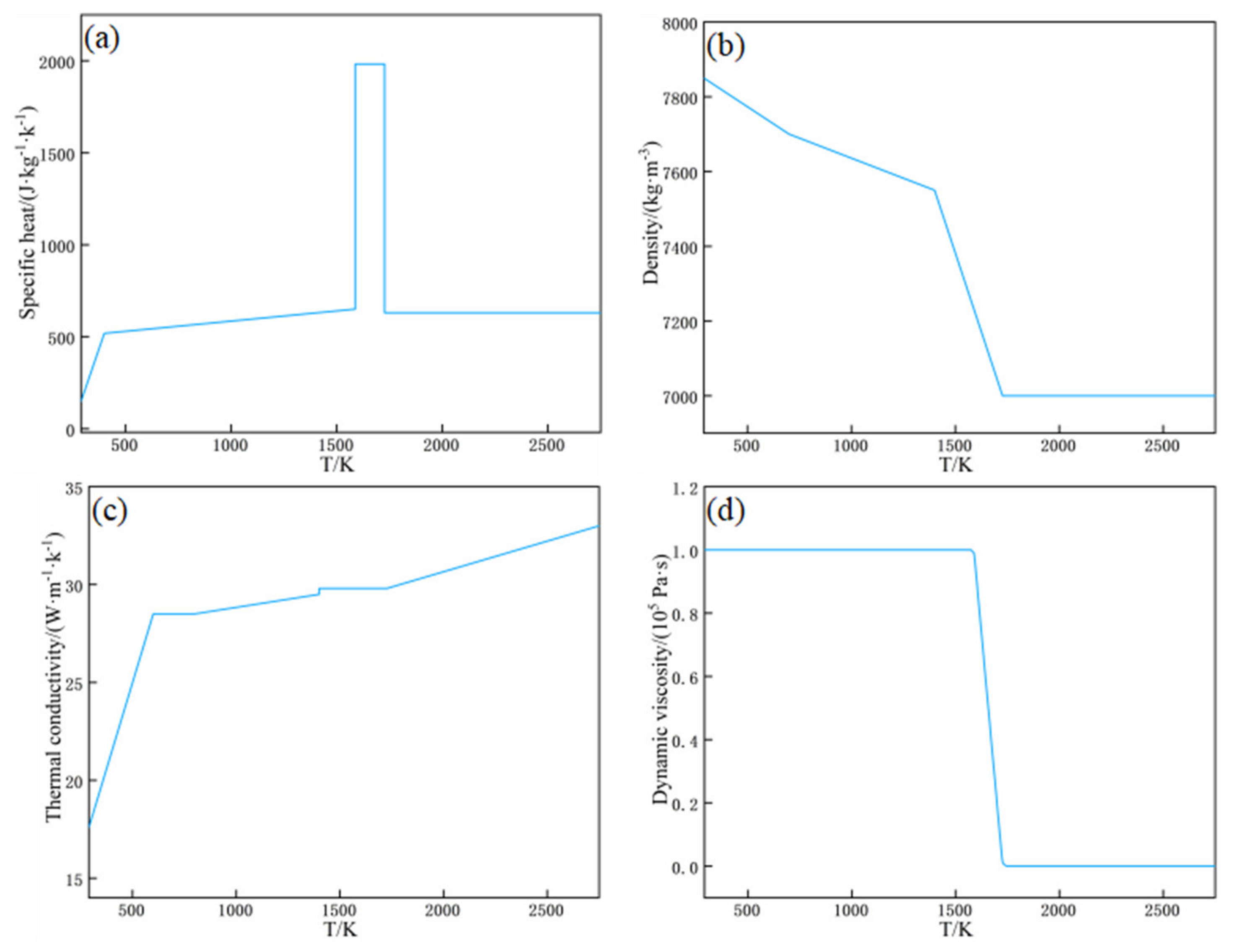
3.4. Material Properties
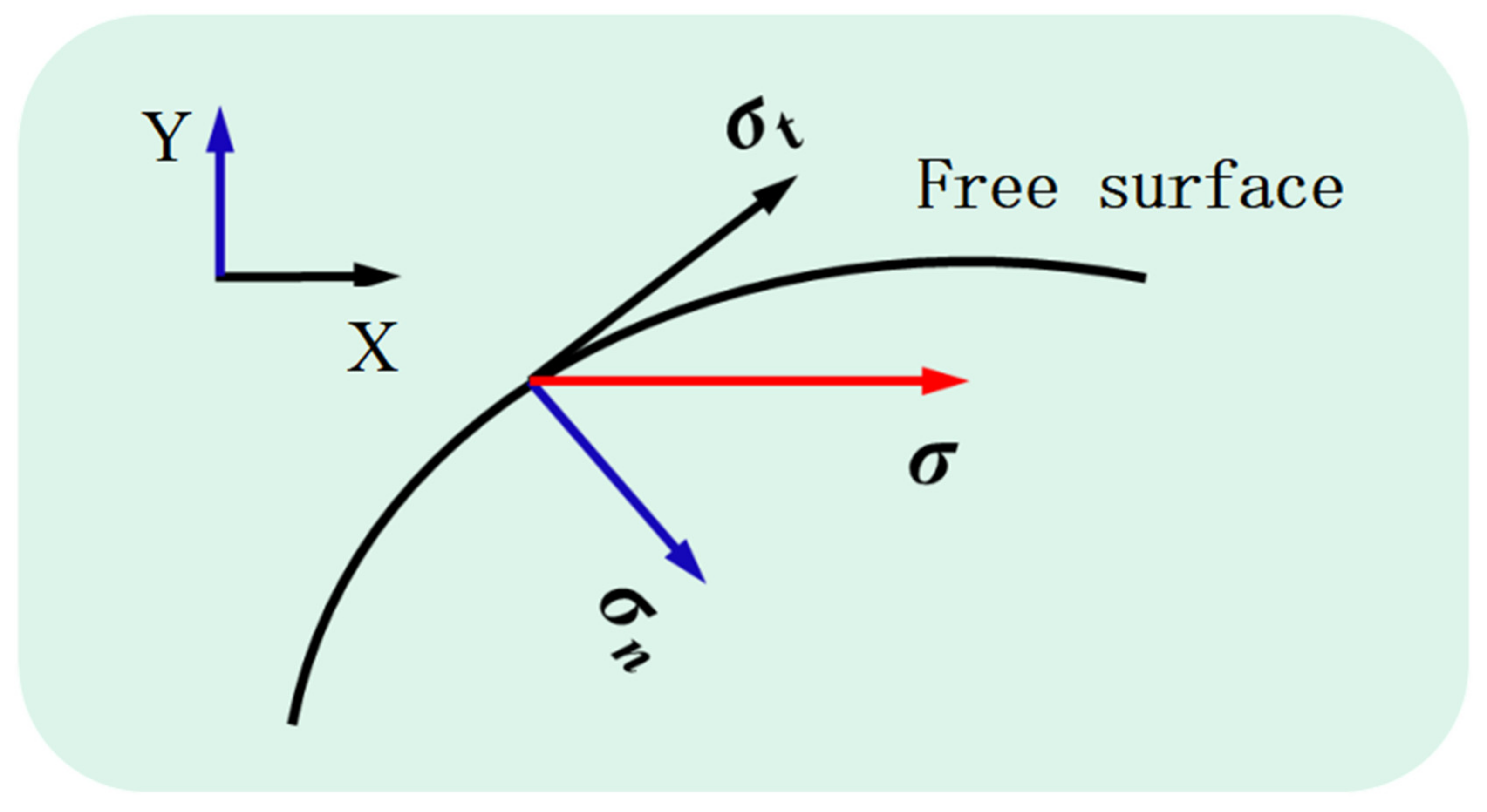
3.5. Boundary Conditions
3.6. Meshing
3.7. Solver Configuration
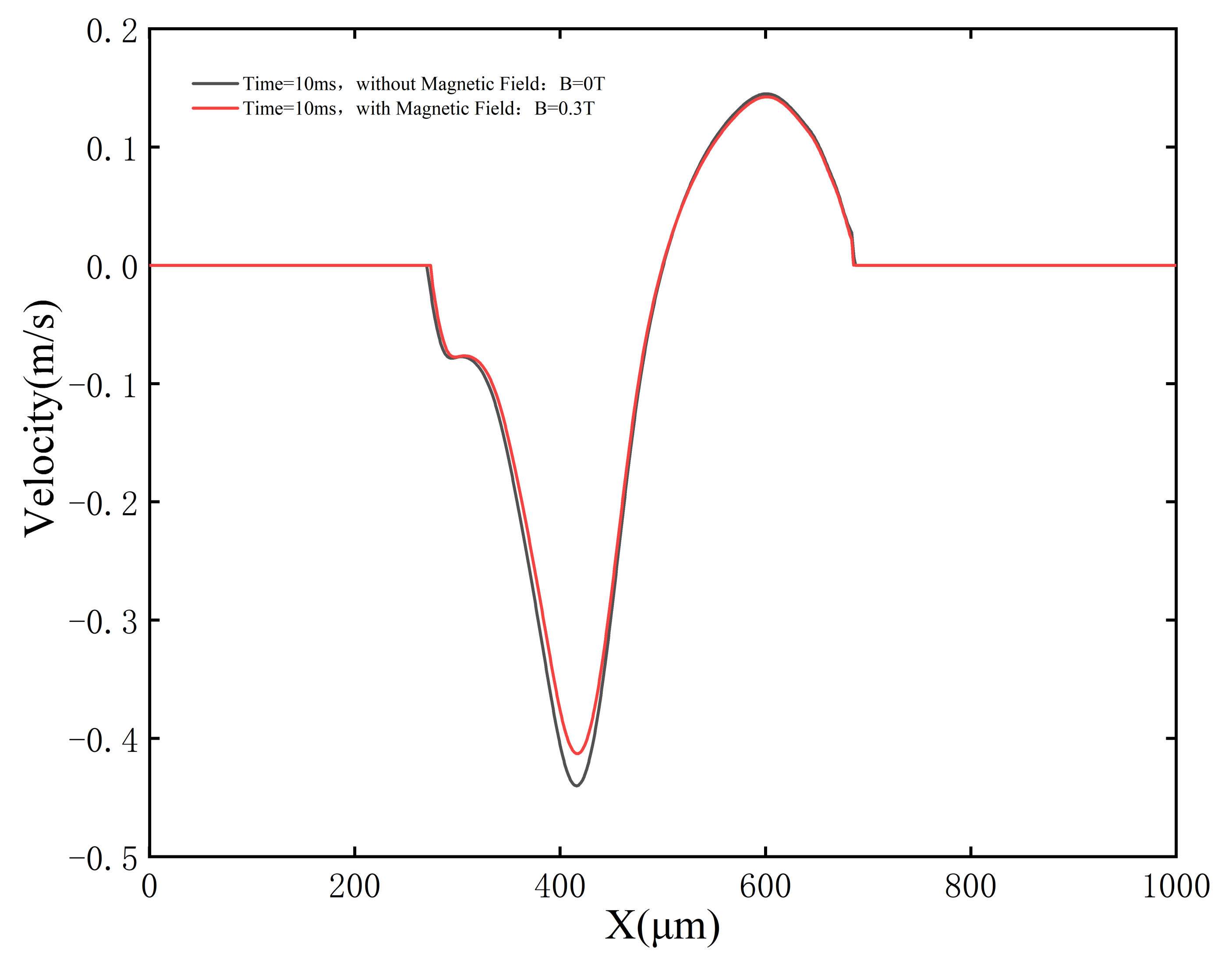
4. Simulation Results and Discussion
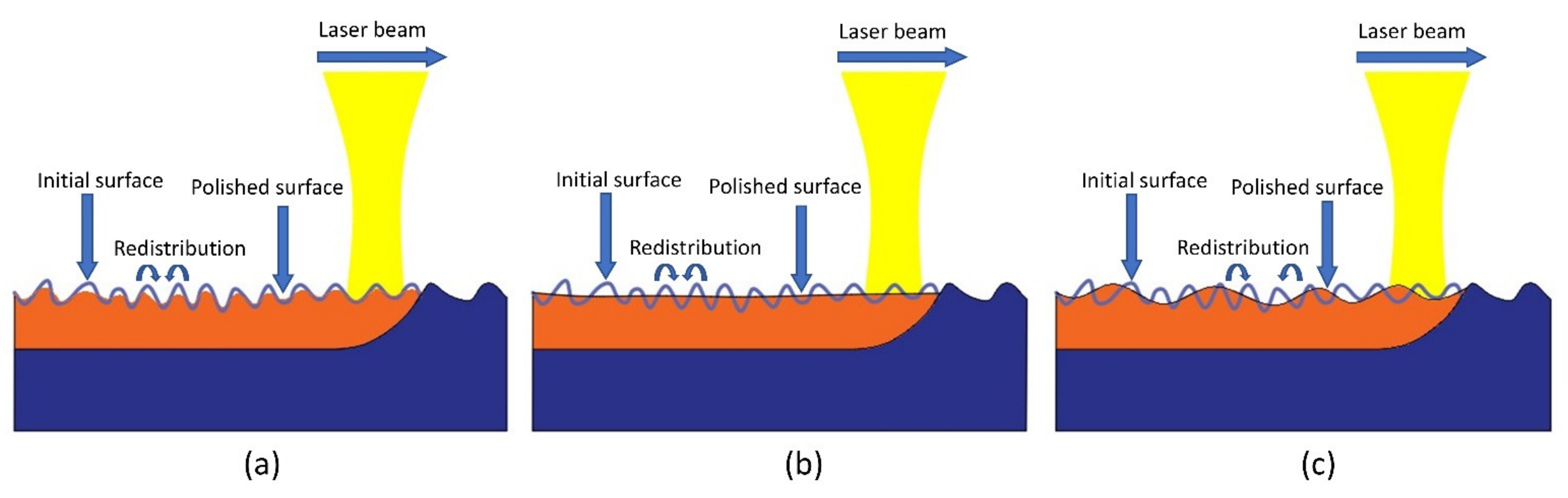
4.1. Evolution of Surface Profile of Molten Pool
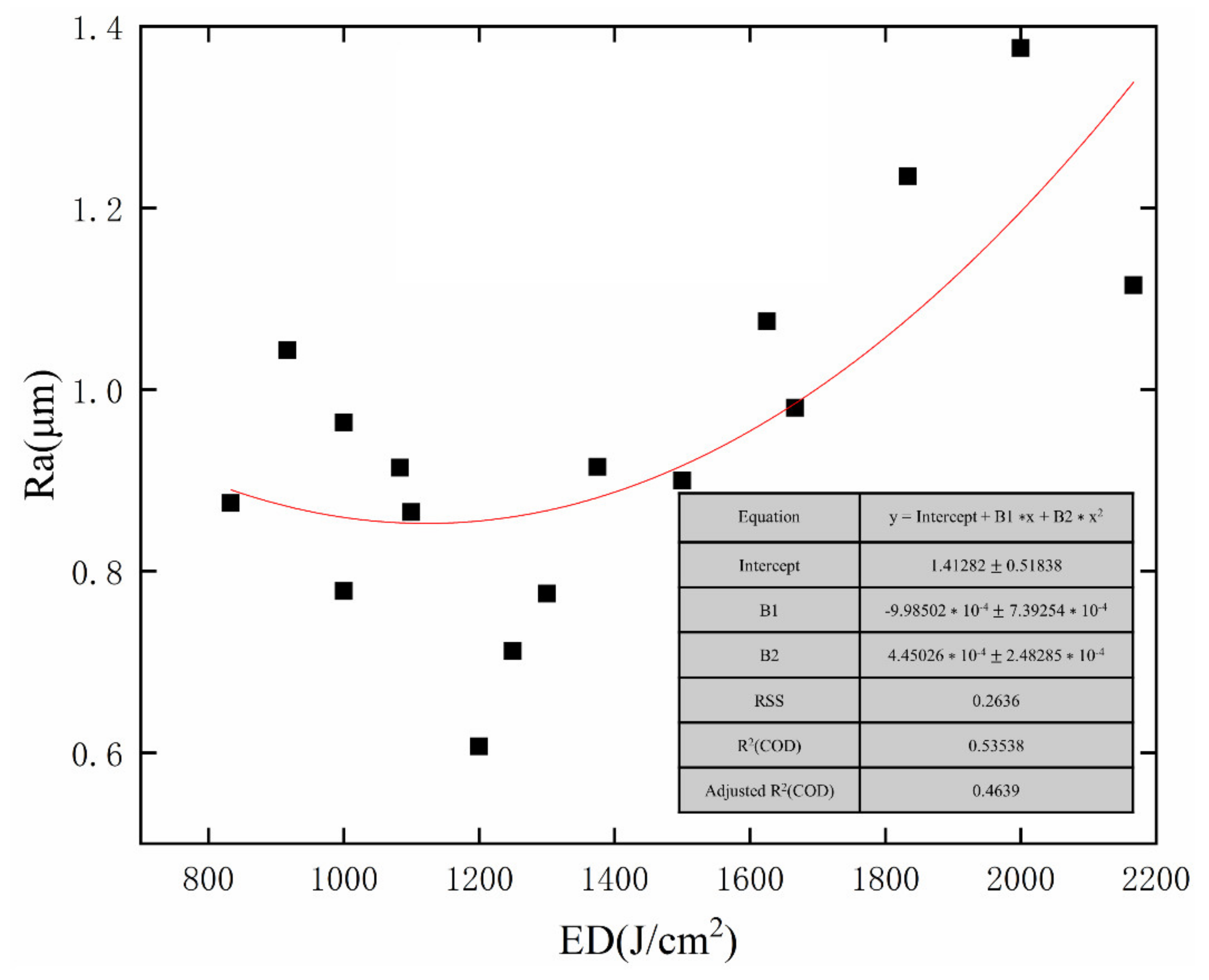
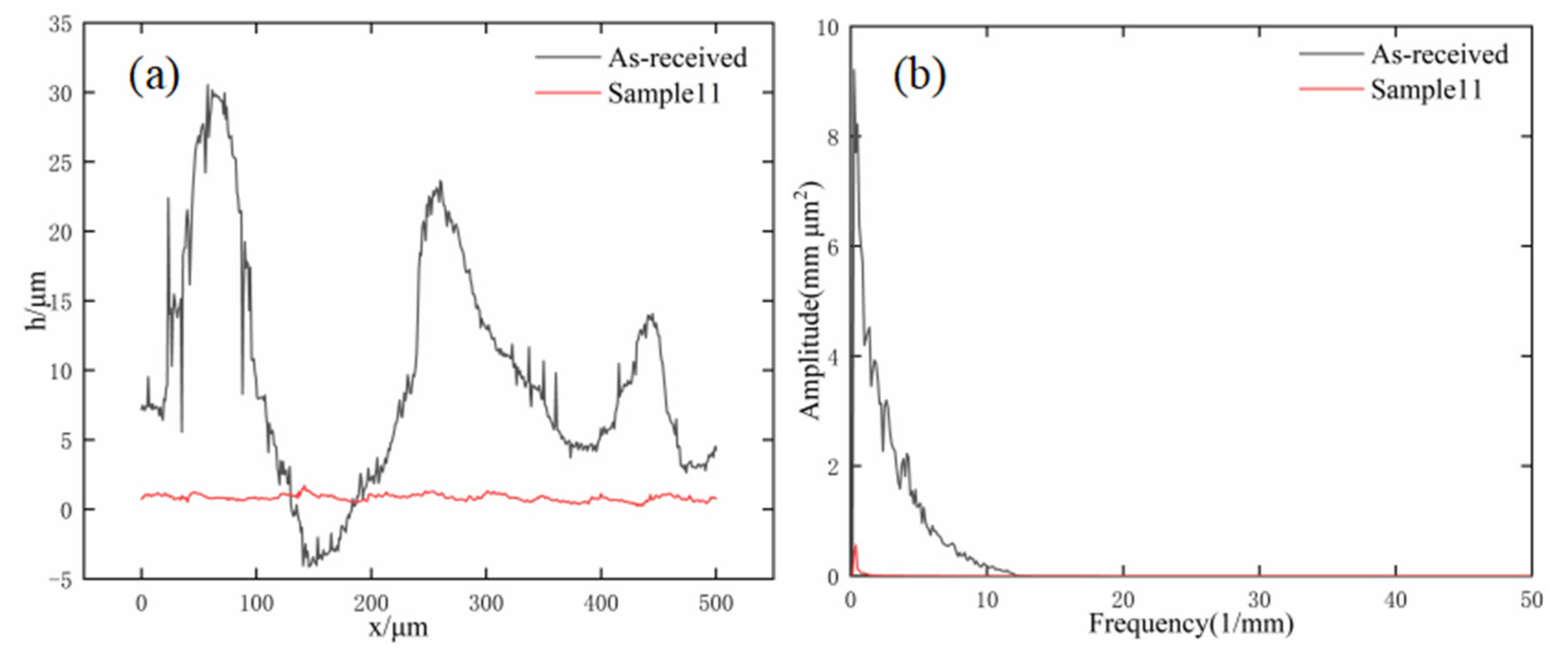
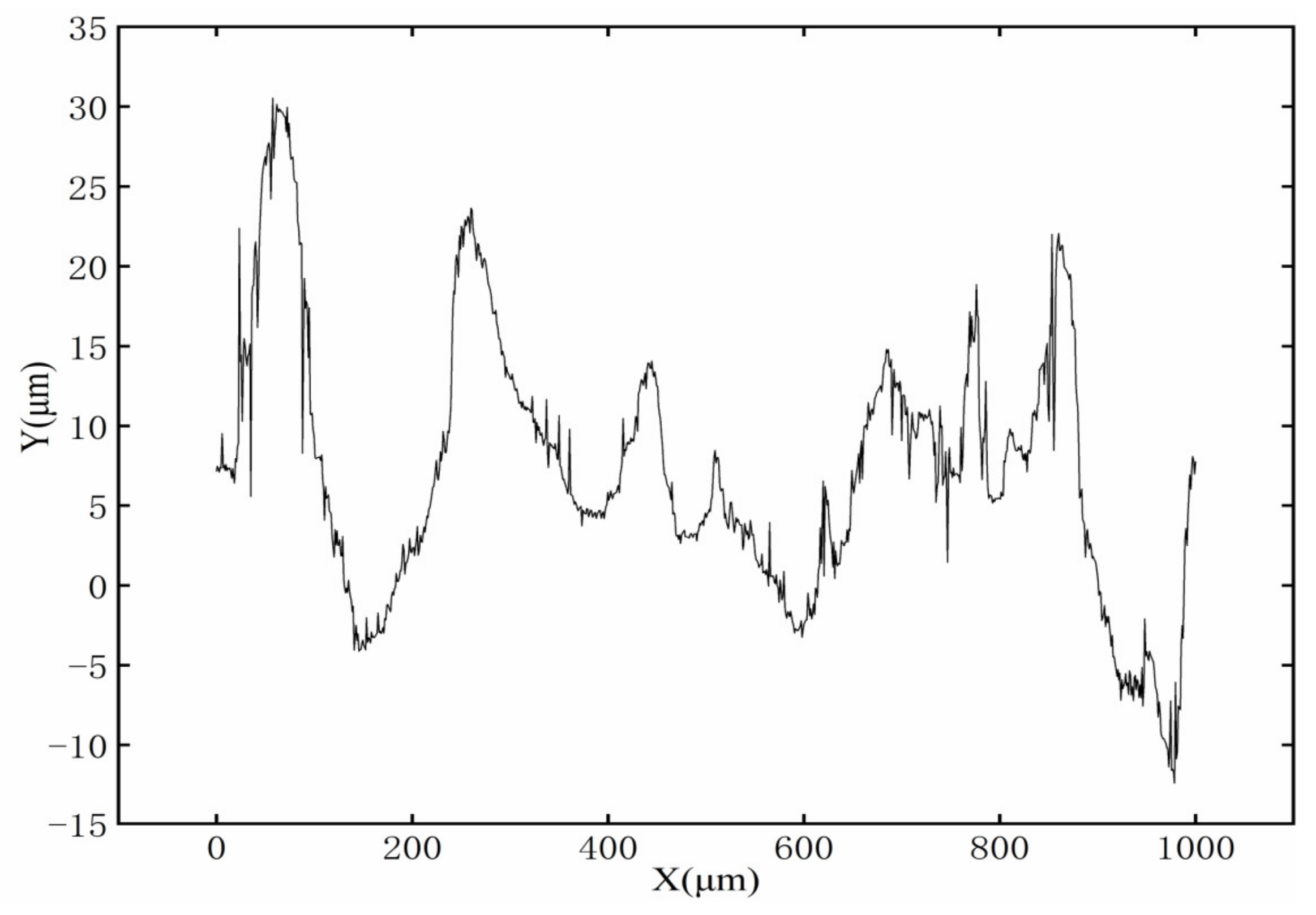
4.2. Experimental Verification
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yuan, Q.; Li, D.L.; Yuan, T.; Lv, F. Failure analysis of SKD61 steel die in its early stage. Ordnance Mater. Sci. Eng. 2004, 27, 58–61. [Google Scholar]
- Pan, X.F.; Zhou, X.Y. Heat Treatment Process and Performance of SKD61 Steel. Heat Treat. 2009, 26, 38–41. [Google Scholar]
- Si, H.L.; Li, J.Q.; Jia, Z.X. Microstructure and Properties of SKD61 Die Steel Strengthened by Biomimetic Laser-Remelting. Mater. Mech. Eng. 2014, 24, 39–43. [Google Scholar]
- Ma, X.Y.; Zhou, J.P. High Speed Milling Machining Processes of a SKD61 Hardened Steel. Mater. Mech. Eng. 2004, 28, 27–29. [Google Scholar]
- Chen, B.W.; Sun, S.F.; Wang, Q.; Zhang, F.Y.; Shao, Y.; Zhang, L.L.; Zhao, D.L.; Wang, P.P.; Chen, X.Z.; Liu, J.X.; et al. Research progress of laser polishing technology for material surface. China Surf. Eng. 2021, 34, 74–89. [Google Scholar]
- Xu, J.; Zou, P.; Wang, W.; Kang, D. Study on the mechanism of surface topography evolution in melting and transition regimes of laser polishing. Opt. Laser Technol. 2021, 139, 106947. [Google Scholar] [CrossRef]
- Li, K.; Zhao, Z.; Zhou, H.; Zhou, H.; Jin, J. Numerical analyses of molten pool evolution in laser polishing Ti6Al4V. J. Manuf. Process. 2020, 58, 574–584. [Google Scholar] [CrossRef]
- Na, R.; Chen, T. YAG laser polishing of 38CrMoAl surface. Laser Optoelectron. Prog. 2016, 53, 011402. [Google Scholar]
- Obeidi, M.; McCarthy, E.; O’Connell, B.; Ahad, I.U.; Brabazon, D. Laser polishing of additive manufactured 316L stainless steel synthesized by selective laser melting. Materials 2019, 12, 991. [Google Scholar] [CrossRef]
- Chik, N.; Wan Md Zain, W.S.; Mohamad, A.J.; Sidek, M.Z.; Ibrahim, W.W.; Reif, A.; Rakebrandt, J.H.; Pfleging, W.; Liu, X. Bacterial adhesion on the titanium and stainless-Steel surfaces undergone two different treatment methods: Polishing and ultrafast laser treatment. IOP Conf. Ser. Mater. Sci. Eng. 2018, 358, 012034. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Zhao, Z.Y.; Zhang, W.; Xiao, H.; Xu, X. Experiment study of rapid laser polishing of free form steel Surface by Dual-Beam. Coatings 2019, 9, 324. [Google Scholar] [CrossRef]
- Zhang, W.K.; Dai, W.; Zhen, Z.Z.; Li, J.J.; Deng, T.T. Numerical simulation and verification of free-surface evolution in laser polishing of H13 tool steel. Chin. J. Lasers 2019, 46, 75–85. [Google Scholar]
- Weingarten, C.; Heidrich, S.; Wu, Y.; Willenborg, E. Laser Polishing of Glass; Bentley, J.L., Stoebenau, S., Eds.; Rochester: New York, NY, USA, 2015; p. 963303. [Google Scholar]
- Ma, Z.; Wang, Q.; Dong, J.; Wang, Z.; Yu, T. Experimental investigation and numerical analysis for machinability of alumina ceramic by laser-assisted grinding. Precis. Eng. 2021, 72, 798–806. [Google Scholar] [CrossRef]
- Samant, A.N.; Du, B.; Dahotre, N.B. In-situ surface absorptivity prediction during 1.06 μm wavelength laser low aspect ratio machining of structural ceramics. Phys. Status Solidi (a) 2009, 206, 1433–1439. [Google Scholar] [CrossRef]
- Musaev, O.R.; Midgley, A.E.; Wrobel, J.M.; Kruger, M.B. Laser ablation of alumina in water. Chem. Phys. Lett. 2010, 487, 81–83. [Google Scholar] [CrossRef]
- Lü, K.; Han, X. Research on Numerical Simulation of Ultrafast Laser Polishing Brittle Optical Materials. Laser Optoelectron. Prog. 2021, 58, 0532001. [Google Scholar]
- Ukar, E.; Lamikiz, A.; López de Lacalle, L.N. Laser polishing of tool steel with CO(2) laser and high-power diode laser. Int. J. Mach. Tools Manuf. 2010, 50, 115–125. [Google Scholar] [CrossRef]
- Bhaduri, D.; Penchev, P.; Batal, A.; Dimov, S.; Soo, S.L.; Sten, S.; Harrysson, U.; Zhang, Z.; Dong, H. Laser polishing of 3D printed mesoscale components. Appl. Surf. Sci. 2017, 405, 29–46. [Google Scholar] [CrossRef]
- Ramos-Grez, J.A.; Bourell, D.L. Reducing surface roughness of metallic freeform-fabricated parts using non-tactile finishing methods. Int. J. Mater. Prod. Technol. 2004, 21, 297. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, J.; Shen, H. Role of Capillary and Thermocapillary Forces in Laser Polishing of Metals. J. Manuf. Sci. Eng. 2017, 139, 041019. [Google Scholar] [CrossRef]
- Wang, L.; Yao, J.; Hu, Y.; Song, S. Suppression effect of a steady magnetic field on molten pool during laser remelting. Appl. Surf. Sci. 2015, 351, 794–802. [Google Scholar] [CrossRef]
- Xiao, H.B.; Zhou, Y.Q.; Liu, M.J. Laser polishing of tool steel using a continuous-wave laser assisted by a steady magnetic field. AIP Adv. 2020, 10, 025319. [Google Scholar] [CrossRef]
- Li, K.; Zhao, Z.Y.; Zhou, H.M.; Zhou, H.; Yin, J.; Zhang, W.; Zhou, G. Numerical Simulation of effect of different initial morphologies on melt hydrodynamics in Laser polishing of Ti6Al4V. Micromachines 2021, 12, 581. [Google Scholar] [CrossRef]








| Chemical Element | C | Si | Mn | P | S | Cr | Mo | Ni | Cu | V | Fe |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass fraction (%) | 0.3–0.45 | 0.8–1.2 | 0.2–0.5 | 0.03 | 0.03 | 4.75–5.5 | 1.1–1.75 | 0.3 | 0.25 | 0.8–1.2 | ≥88 |
| Specimen Code | P (W) | V (mm/s) | D (mm) | MF (T) | ED (J/cm2) | Ra (μm) |
|---|---|---|---|---|---|---|
| As-received | – | – | – | – | – | 6.1 |
| 1 | 150 | 30 | 0.03 | 0 | 1666.667 | 0.980 |
| 2 | 150 | 40 | 0.05 | 0.3 | 1250.000 | 0.712 |
| 3 | 150 | 50 | 0.07 | 0.6 | 1000.000 | 0.778 |
| 4 | 150 | 60 | 0.09 | 0.9 | 833.333 | 0.875 |
| 5 | 165 | 30 | 0.05 | 0.6 | 1833.333 | 1.235 |
| 6 | 165 | 40 | 0.03 | 0.9 | 1375.000 | 0.915 |
| 7 | 165 | 50 | 0.09 | 0 | 1100.000 | 0.865 |
| 8 | 165 | 60 | 0.07 | 0.3 | 916.667 | 1.043 |
| 9 | 180 | 30 | 0.07 | 0.9 | 2000.000 | 1.376 |
| 10 | 180 | 40 | 0.09 | 0.6 | 1500.000 | 0.901 |
| 11 | 180 | 50 | 0.03 | 0.3 | 1200.000 | 0.607 |
| 12 | 180 | 60 | 0.05 | 0 | 1000.000 | 0.964 |
| 13 | 195 | 30 | 0.09 | 0.3 | 2166.667 | 1.115 |
| 14 | 195 | 40 | 0.07 | 0 | 1625.000 | 1.075 |
| 15 | 195 | 50 | 0.05 | 0.9 | 1300.000 | 0.775 |
| 16 | 195 | 60 | 0.03 | 0.6 | 1083.333 | 0.914 |
| Property (Units) | Symbol | Value |
|---|---|---|
| Liquidus temperature (K) | 1727 | |
| Solidus temperature (K) | 1588 | |
| Melting temperature (K) | 1657.5 | |
| Reference temperature (K) | 1727 | |
| Latent heat of fusion (J/kg) | 2.8 × 105 | |
| Surface tension of pure metal (N/m) | 1.909 | |
| Thermal expansion coefficient (1/K) | 1 × 10−4 | |
| Convective coefficient (W/(m2·K)) | 10 | |
| Emissivity | 0.5 | |
| Constant of surface tension gradient (N/(m·K)) | 5.2 × 10−4 |
| Physics | Physical Condition | Boundary | Boundary Condition |
|---|---|---|---|
| Heat transfer | Laser irradiation | 2 | Heat flux |
| Natural convection | 1,2,3 | Convection | |
| Radiation | 1,2,3 | Diffuse surface | |
| Insulation | 4 | Thermal insulation | |
| Fluid flow | Normal stress | 2 | Weak contribution |
| Tangential stress | 2 | Marangoni effect | |
| Wall | 1,3,4 | No-slip wall | |
| Magnetic field | Insulation | 1,2,3,4 | Electrical insulation |
| Insulation | 1,2,3,4 | Magnetic insulation | |
| Moving mesh | Fixed boundary | 1,3,4 | Prescribed displacement |
| Free deformation | 2 | Prescribed displacement |
| Parameter (Unit) | Top Layer | The Rest |
|---|---|---|
| Maximum element size (μm) | 2 | 14.3 |
| Minimum element size (μm) | 0.1 | 0.638 |
| Maximum element growth rate | 1.05 | 1.15 |
| Curvature factor | 0.2 | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Zeng, J.; Lai, Z.; Yin, J.; Guo, T. Laser Polishing Die Steel Assisted by Steady Magnetic Field. Micromachines 2022, 13, 1493. https://doi.org/10.3390/mi13091493
Zhao Z, Zeng J, Lai Z, Yin J, Guo T. Laser Polishing Die Steel Assisted by Steady Magnetic Field. Micromachines. 2022; 13(9):1493. https://doi.org/10.3390/mi13091493
Chicago/Turabian StyleZhao, Zhenyu, Junyong Zeng, Zhouyi Lai, Jie Yin, and Ting Guo. 2022. "Laser Polishing Die Steel Assisted by Steady Magnetic Field" Micromachines 13, no. 9: 1493. https://doi.org/10.3390/mi13091493
APA StyleZhao, Z., Zeng, J., Lai, Z., Yin, J., & Guo, T. (2022). Laser Polishing Die Steel Assisted by Steady Magnetic Field. Micromachines, 13(9), 1493. https://doi.org/10.3390/mi13091493









