DC-Dielectrophoretic Manipulation and Isolation of Microplastic Particle-Treated Microalgae Cells in Asymmetric-Orifice-Based Microfluidic Chip
Abstract
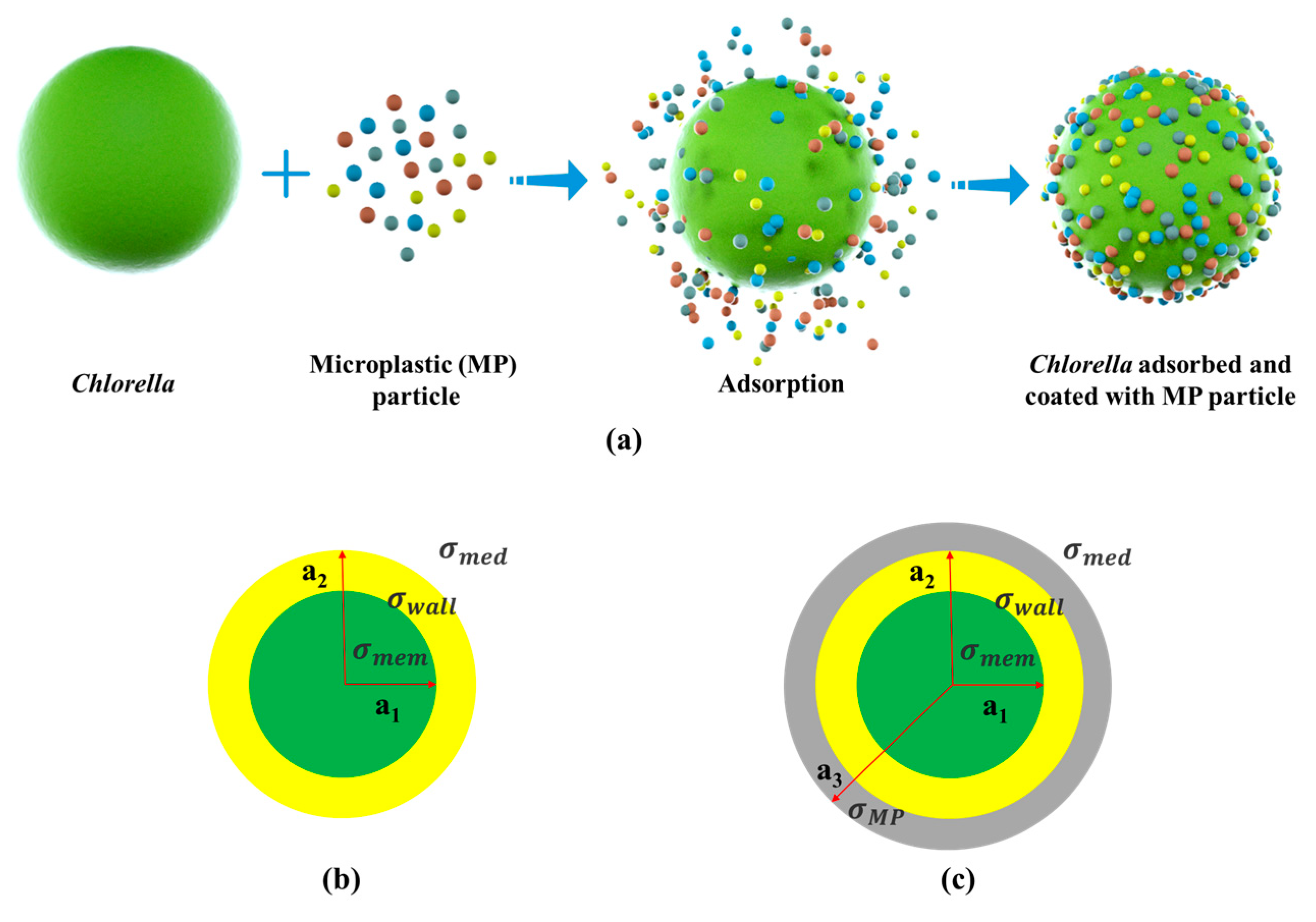
:1. Introduction
2. Dielectrophoresis
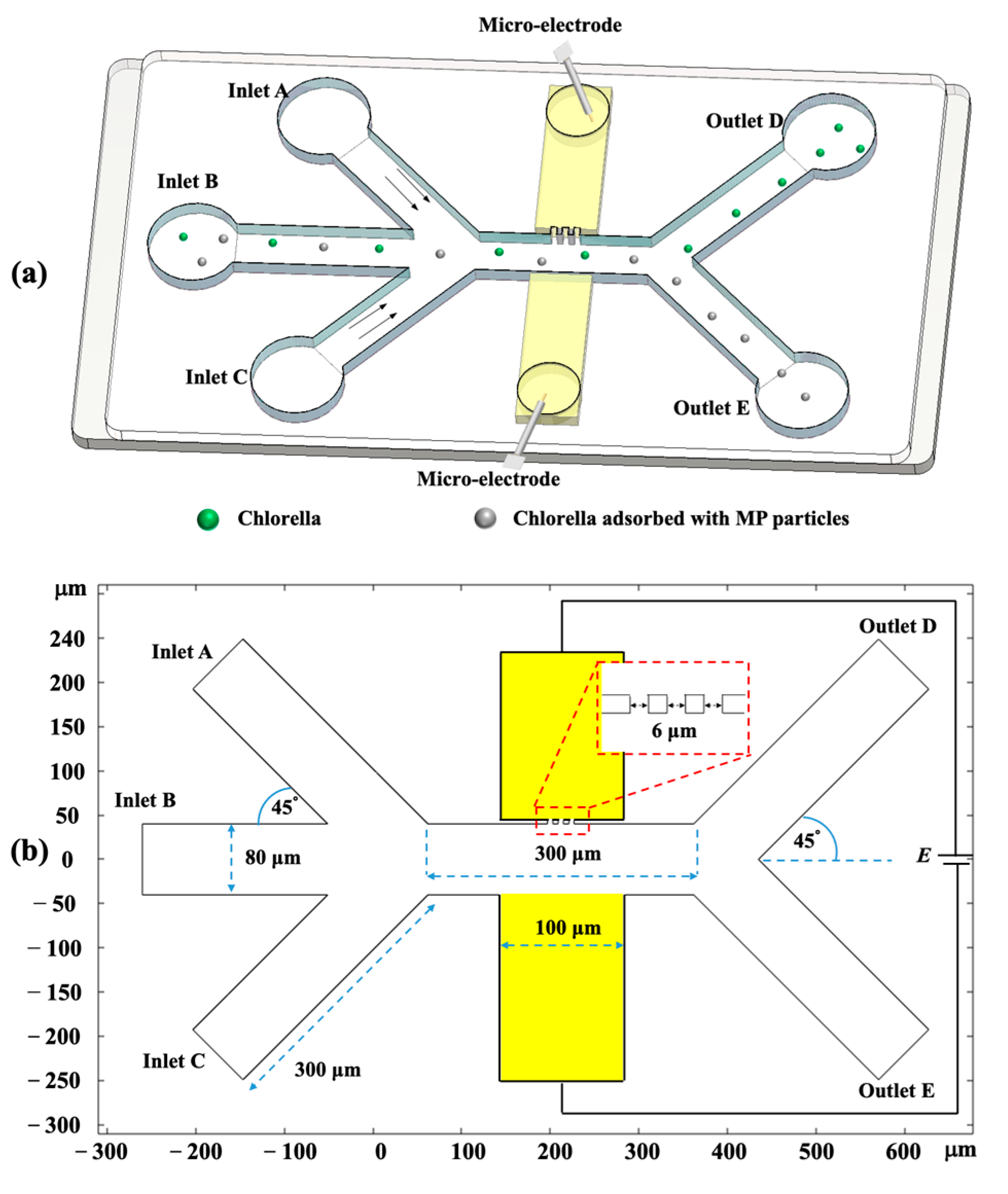
3. Numerical Methods
3.1. Electric Field
3.2. Flow Field
3.3. Particle Tracing
4. Discussion
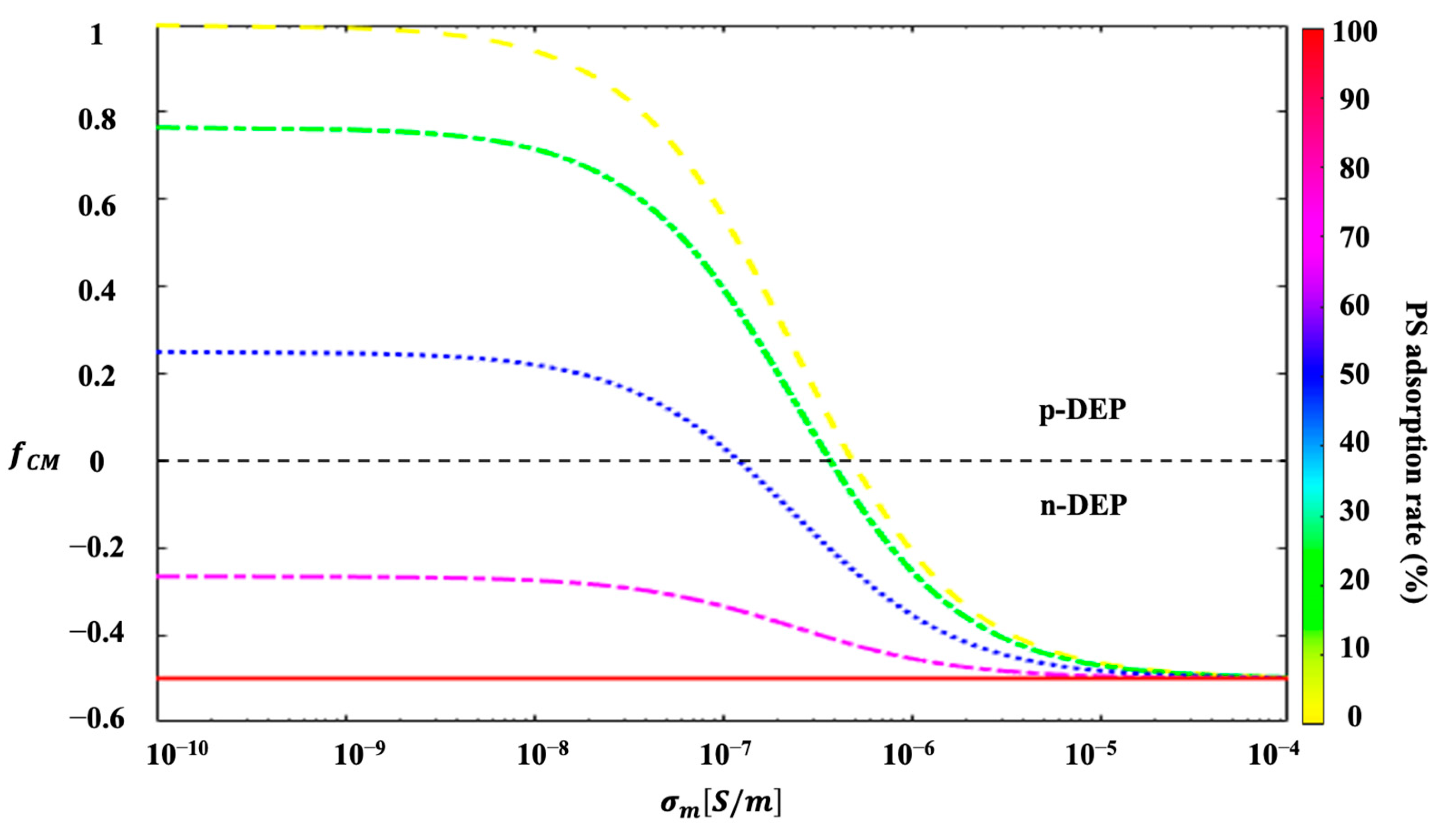
4.1. Simulation of the Electric Field
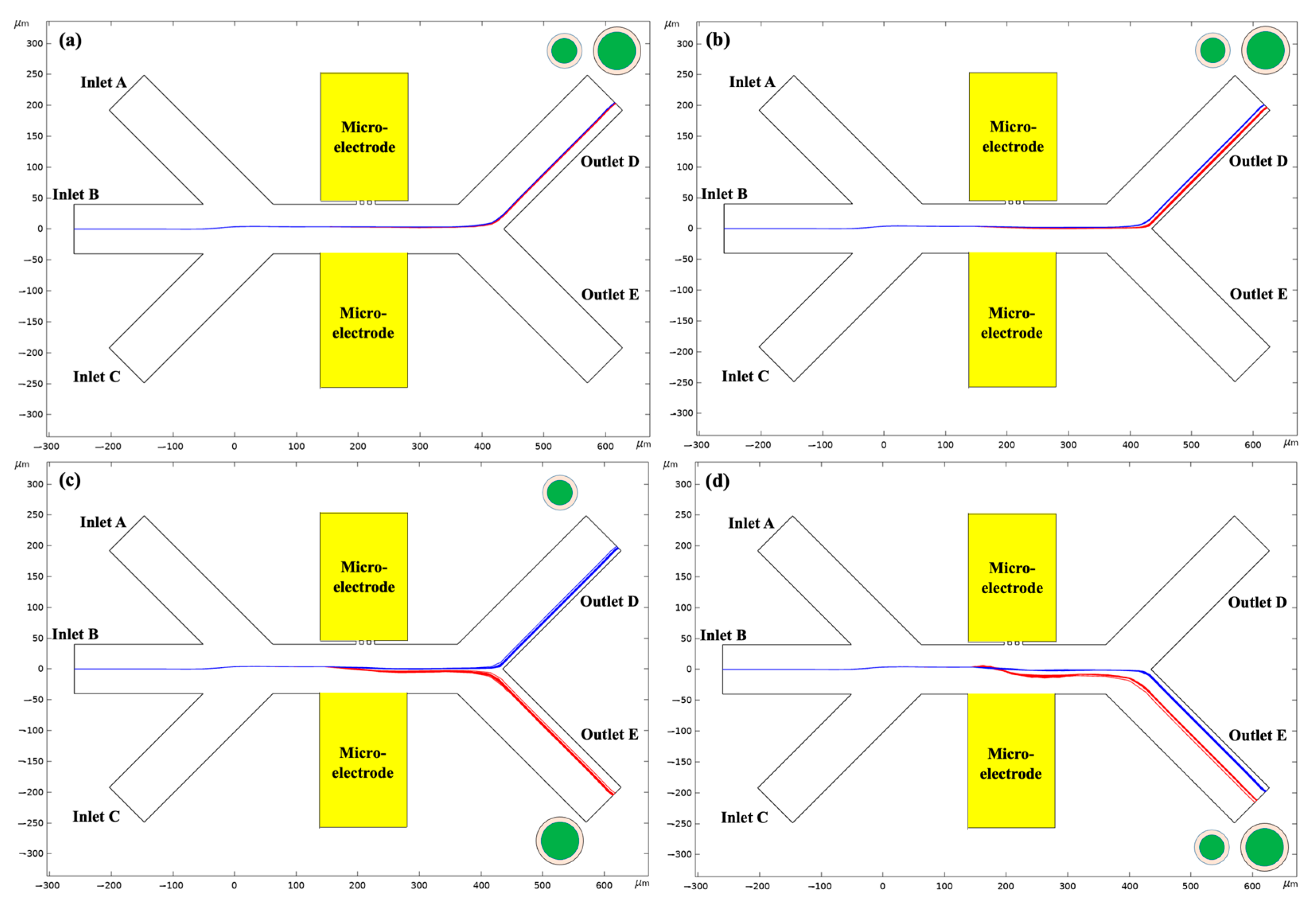
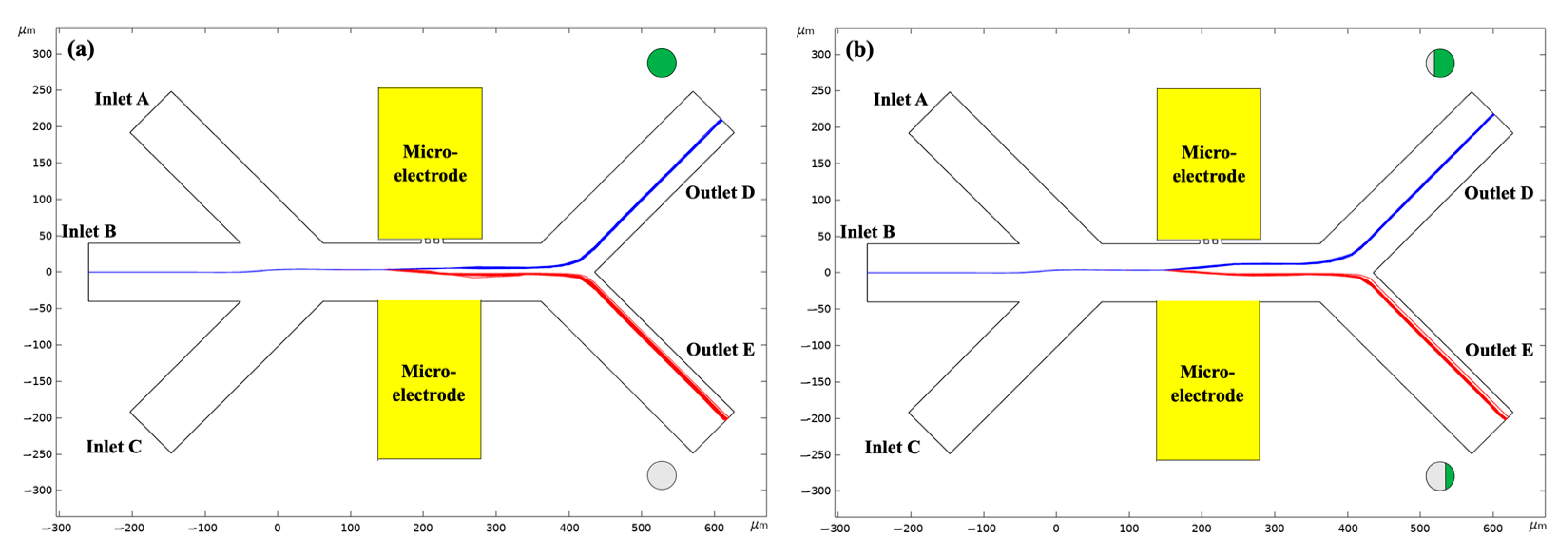
4.2. Effect of the Applied Voltage
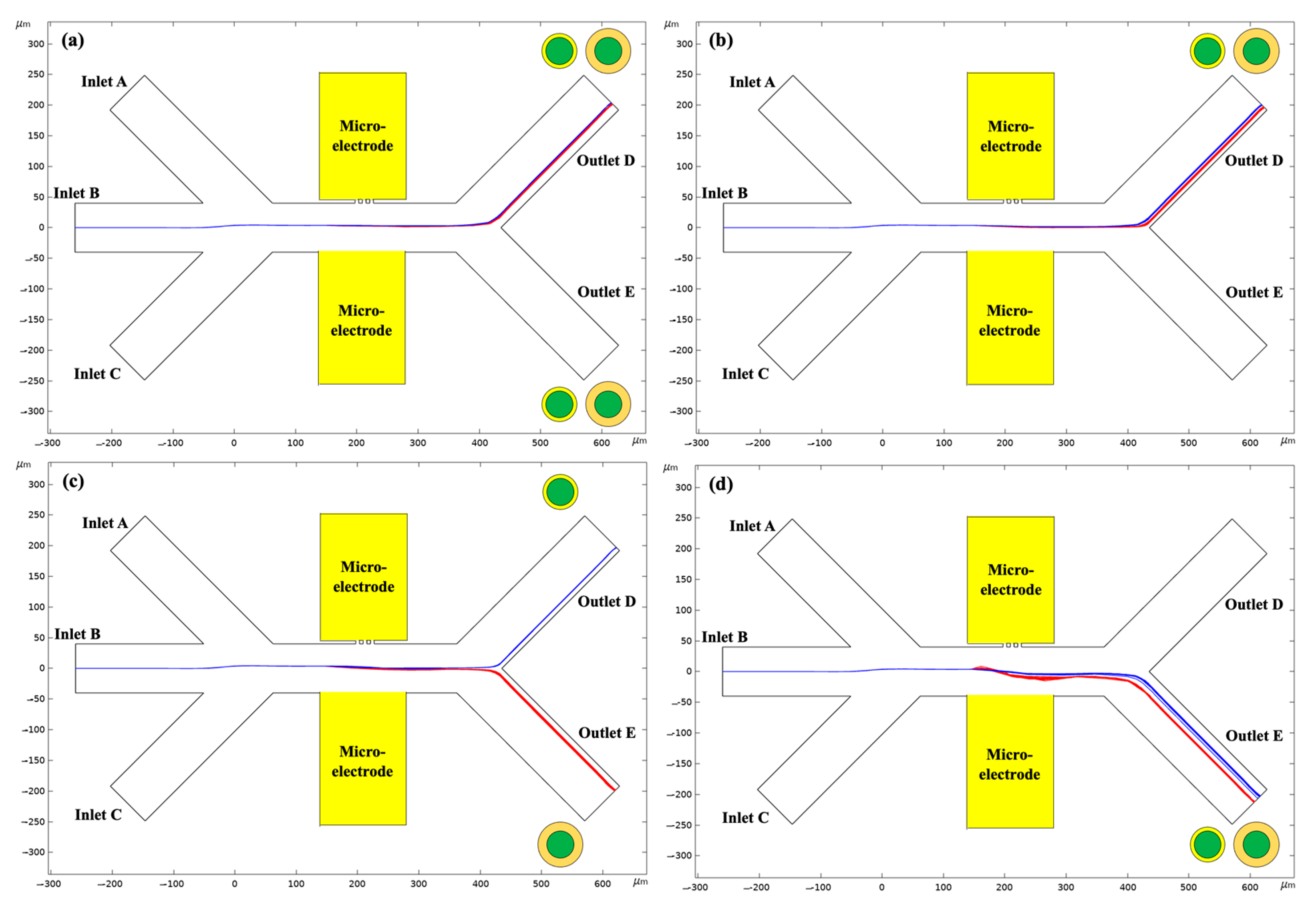
4.3. Effect of the PS Adsorption Coverage
4.4. Effect of the PS Adsorption Thickness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhao, K.; Tong, N.; Wang, J. Separation of microalgae cells in a microfluidic chip based on AC Dielectrophoresis. J. Chem. Technol. Biotechnol. 2022, 98, 140–150. [Google Scholar] [CrossRef]
- Iqbal, H.M.; Bilal, M.; Rasheed, T.; Ahmed, I. High-value compounds from microalgae with industrial exploitability—A review. Front. Biosci. 2017, 9, 319–342. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Li, D.; Chen, S.; Wu, N.; Guan, Y. Improving biological condition assessment accuracy by multimetric index approach with microalgae in streams and lakes. Sci. Total Environ. 2021, 771, 145417. [Google Scholar] [CrossRef] [PubMed]
- Vasistha, S.; Khanra, A.; Clifford, M.; Rai, M. Current advances in microalgae harvesting and lipid extraction processes for improved biodiesel production: A review. Renew. Sustain. Energy Rev. 2021, 137, 110498. [Google Scholar] [CrossRef]
- Daneshvar, E.; Ok, Y.S.; Tavakoli, S.; Sarkar, B.; Shaheen, S.M.; Hong, H.; Luo, Y.; Rinklebe, J.; Song, H.; Bhatnagar, A. Insights into upstream processing of microalgae: A review. Bioresour. Technol. 2021, 329, 124870. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Sun, W.; Yang, T.; Zhu, Z.; Jiang, Y.; Hu, W.; Wei, W.; Zhang, Y.; Yang, H. The toxic effects of polystyrene microplastics on freshwater algae Chlorella pyrenoidosa depends on the different size of polystyrene microplastics. Chemosphere 2022, 308, 136135. [Google Scholar] [CrossRef]
- Zhu, Z.-L.; Wang, S.-C.; Zhao, F.-F.; Wang, S.-G.; Liu, F.-F.; Liu, G.-Z. Joint toxicity of microplastics with triclosan to marine microalgae Skeletonema costatum. Environ. Pollut. 2019, 246, 509–517. [Google Scholar] [CrossRef]
- Zhao, K.; Wei, Y.; Dong, J.; Zhao, P.; Wang, Y.; Pan, X.; Wang, J. Separation and characterization of microplastic and nanoplastic particles in marine environment. Environ. Pollut. 2022, 297, 118773. [Google Scholar] [CrossRef]
- Lagarde, F.; Olivier, O.; Zanella, M.; Daniel, P.; Hiard, S.; Caruso, A. Microplastic interactions with freshwater microalgae: Hetero-aggregation and changes in plastic density appear strongly dependent on polymer type. Environ. Pollut. 2016, 215, 331–339. [Google Scholar] [CrossRef]
- Li, Z.; Yi, X.; Zhou, H.; Chi, T.; Li, W.; Yang, K. Combined effect of polystyrene microplastics and dibutyl phthalate on the microalgae Chlorella pyrenoidosa. Environ. Pollut. 2020, 257, 113604. [Google Scholar] [CrossRef]
- Abinandan, S.; Subashchandrabose, S.R.; Venkateswarlu, K.; Perera, I.A.; Megharaj, M. Acid-tolerant microalgae can withstand higher concentrations of invasive cadmium and produce sustainable biomass and biodiesel at pH 3.5. Bioresour. Technol. 2019, 281, 469–473. [Google Scholar] [CrossRef]
- Balaji, S.; Kalaivani, T.; Sushma, B.; Pillai, C.V.; Shalini, M.; Rajasekaran, C. Characterization of sorption sites and differential stress response of microalgae isolates against tannery effluents from ranipet industrial area—An application towards phycoremediation. Int. J. Phytoremediation 2016, 18, 747–753. [Google Scholar] [CrossRef] [PubMed]
- Sajeesh, P.; Sen, A.K. Particle separation and sorting in microfluidic devices: A review. Microfluid. Nanofluidics 2014, 17, 1–52. [Google Scholar] [CrossRef]
- Zhao, K.; Peng, R.; Li, D. Separation of nanoparticles by a nano-orifice based DC-dielectrophoresis method in a pressure-driven flow. Nanoscale 2016, 8, 18945–18955. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, K.; Li, D. Continuous separation of nanoparticles by type via localized DC-dielectrophoresis using asymmetric nano-orifice in pressure-driven flow. Sens. Actuators B Chem. 2017, 250, 274–284. [Google Scholar] [CrossRef]
- Khoshmanesh, K.; Nahavandi, S.; Baratchi, S.; Mitchell, A.; Kalantar-Zadeh, K. Dielectrophoretic platforms for bio-microfluidic systems. Biosens. Bioelectron. 2011, 26, 1800–1814. [Google Scholar] [CrossRef]
- Zhang, C.; Khoshmanesh, K.; Mitchell, A.; Kalantar-Zadeh, K. Dielectrophoresis for manipulation of micro/nano particles in microfluidic systems. Anal. Bioanal. Chem. 2010, 396, 401–420. [Google Scholar] [CrossRef]
- Zhao, K.; Zhao, P.; Dong, J.; Wei, Y.; Chen, B.; Wang, Y.; Pan, X.; Wang, J. Implementation of an Integrated Dielectrophoretic and Magnetophoretic Microfluidic Chip for CTC Isolation. Biosensors 2022, 12, 757. [Google Scholar] [CrossRef]
- Zhao, K.; Hu, M.; van Baalen, C.; Alvarez, L.; Isa, L. Sorting of heterogeneous colloids by AC-dielectrophoretic forces in a microfluidic chip with asymmetric orifices. J. Colloid Interface Sci. 2023, 634, 921–929. [Google Scholar] [CrossRef]
- Pysher, M.D.; Hayes, M.A. Electrophoretic and Dielectrophoretic Field Gradient Technique for Separating Bioparticles. Anal. Chem. 2007, 79, 4552–4557. [Google Scholar] [CrossRef]
- Kang, Y.; Cetin, B.; Wu, Z.; Li, D. Continuous particle separation with localized AC-dielectrophoresis using embedded electrodes and an insulating hurdle. Electrochim. Acta 2009, 54, 1715–1720. [Google Scholar] [CrossRef]
- Zhao, K.; Li, D. Tunable Droplet Manipulation and Characterization by ac-DEP. ACS Appl. Mater. Interfaces 2018, 10, 36572–36581. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Larasati, L.; Duncker, B.P.; Li, D. Continuous Cell Characterization and Separation by Microfluidic Alternating Current Dielectrophoresis. Anal. Chem. 2019, 91, 6304–6314. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Chen, X.; Ren, Y.; Tang, D.; Jiang, H. Dielectric Characterization and Multistage Separation of Various Cells via Dielectrophoresis in a Bipolar Electrode Arrayed Device. Anal. Chem. 2021, 93, 10220–10228. [Google Scholar] [CrossRef] [PubMed]
- Lapizco-Encinas, B.H. On the Recent Developments of Insulator-Based Dielectrophoresis: A Review. Electrophoresis 2019, 40, 358–375; ISBN 0000000162838. [Google Scholar] [CrossRef] [PubMed]
- Lapizco-Encinas, B.H. Microscale electrokinetic assessments of proteins employing insulating structures. Curr. Opin. Chem. Eng. 2020, 29, 9–16. [Google Scholar] [CrossRef]
- Perez-Gonzalez, V.H.; Gallo-Villanueva, R.C.; Cardenas-Benitez, B.; Martinez-Chapa, S.O.; Lapizco-Encinas, B.H. Simple Approach to Reducing Particle Trapping Voltage in Insulator-Based Dielectrophoretic Systems. Anal. Chem. 2018, 90, 4310–4315. [Google Scholar] [CrossRef]
- Zhao, K.; Li, D. Manipulation and separation of oil droplets by using asymmetric nano-orifice induced DC dielectrophoretic method. J. Colloid Interface Sci. 2018, 512, 389–397. [Google Scholar] [CrossRef] [Green Version]
- Zhao, K.; Li, D. Direct current dielectrophoretic manipulation of the ionic liquid droplets in water. J. Chromatogr. A 2018, 1558, 96–106. [Google Scholar] [CrossRef]
- Ramirez-Murillo, C.J.; de los Santos-Ramirez, J.M.; Perez-Gonzalez, V.H. Toward Low-Voltage Dielectrophoresis-Based Microfluidic Systems: A Review. Electrophoresis 2021, 42, 565–587; ISBN 0000000345. [Google Scholar] [CrossRef]
- Tottori, S.; Misiunas, K.; Keyser, U.F.; Bonthuis, D.J. Nonlinear Electrophoresis of Highly Charged Nonpolarizable Particles. Phys. Rev. Lett. 2019, 123, 014502. [Google Scholar] [CrossRef] [Green Version]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995; ISBN 0521019109/9780521019101/0521431964/9780521431965. [Google Scholar]
- Morgan, H.; Green, N.G. AC Electrokinetics: Colloids and Nanoparticles; Research Studies Press: Baldock, UK, 2003; ISBN 0863802559. [Google Scholar]
- Zhang, L.; Zhu, Y. Dielectrophoresis of Janus particles under high frequency ac-electric fields. Appl. Phys. Lett. 2010, 96, 141902. [Google Scholar] [CrossRef]
- Li, D. Encyclopedia of Microfluidics and Nanofluidics; Springer: New York, NY, USA, 2013; Volume 1, ISBN 978-3-642-27758-0. [Google Scholar]
- Nahavandi, M. Continuous-Flow Separation of Malaria-Infected Human Erythrocytes Using DC Dielectrophoresis: An Electrokinetic Modeling and Simulation. Ind. Eng. Chem. Res. 2016, 55, 5484–5499. [Google Scholar] [CrossRef]
- Das, D.; Biswas, K.; Das, S. A microfluidic device for continuous manipulation of biological cells using dielectrophoresis. Med. Eng. Phys. 2014, 36, 726–731. [Google Scholar] [CrossRef] [PubMed]


| Parameters | Values |
|---|---|
| 80 | |
| (F/m) | 8.85 × 10−12 |
| (kg/m3) | 1000 |
| 1 × 10−3 | |
| (kg/m3) | 1050 |
| ) | 0.1 |
| (S/m) | 0.5 |
| (S/m) | 1 × 10−8 |
| (S/m) | 1 × 10−16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, T.; Zhao, K.; Zhang, J.; Zhang, K. DC-Dielectrophoretic Manipulation and Isolation of Microplastic Particle-Treated Microalgae Cells in Asymmetric-Orifice-Based Microfluidic Chip. Micromachines 2023, 14, 229. https://doi.org/10.3390/mi14010229
Gao T, Zhao K, Zhang J, Zhang K. DC-Dielectrophoretic Manipulation and Isolation of Microplastic Particle-Treated Microalgae Cells in Asymmetric-Orifice-Based Microfluidic Chip. Micromachines. 2023; 14(1):229. https://doi.org/10.3390/mi14010229
Chicago/Turabian StyleGao, Tianbo, Kai Zhao, Jiaqi Zhang, and Kaihuan Zhang. 2023. "DC-Dielectrophoretic Manipulation and Isolation of Microplastic Particle-Treated Microalgae Cells in Asymmetric-Orifice-Based Microfluidic Chip" Micromachines 14, no. 1: 229. https://doi.org/10.3390/mi14010229
APA StyleGao, T., Zhao, K., Zhang, J., & Zhang, K. (2023). DC-Dielectrophoretic Manipulation and Isolation of Microplastic Particle-Treated Microalgae Cells in Asymmetric-Orifice-Based Microfluidic Chip. Micromachines, 14(1), 229. https://doi.org/10.3390/mi14010229







