Approximate Packing of Binary Mixtures of Cylindrical Particles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cylindrical Particle Generation
2.2. Discrete Element Method
2.3. Calculation of Planar Packing Fraction
2.4. Voronoi Tessellation
3. Results and Discussion
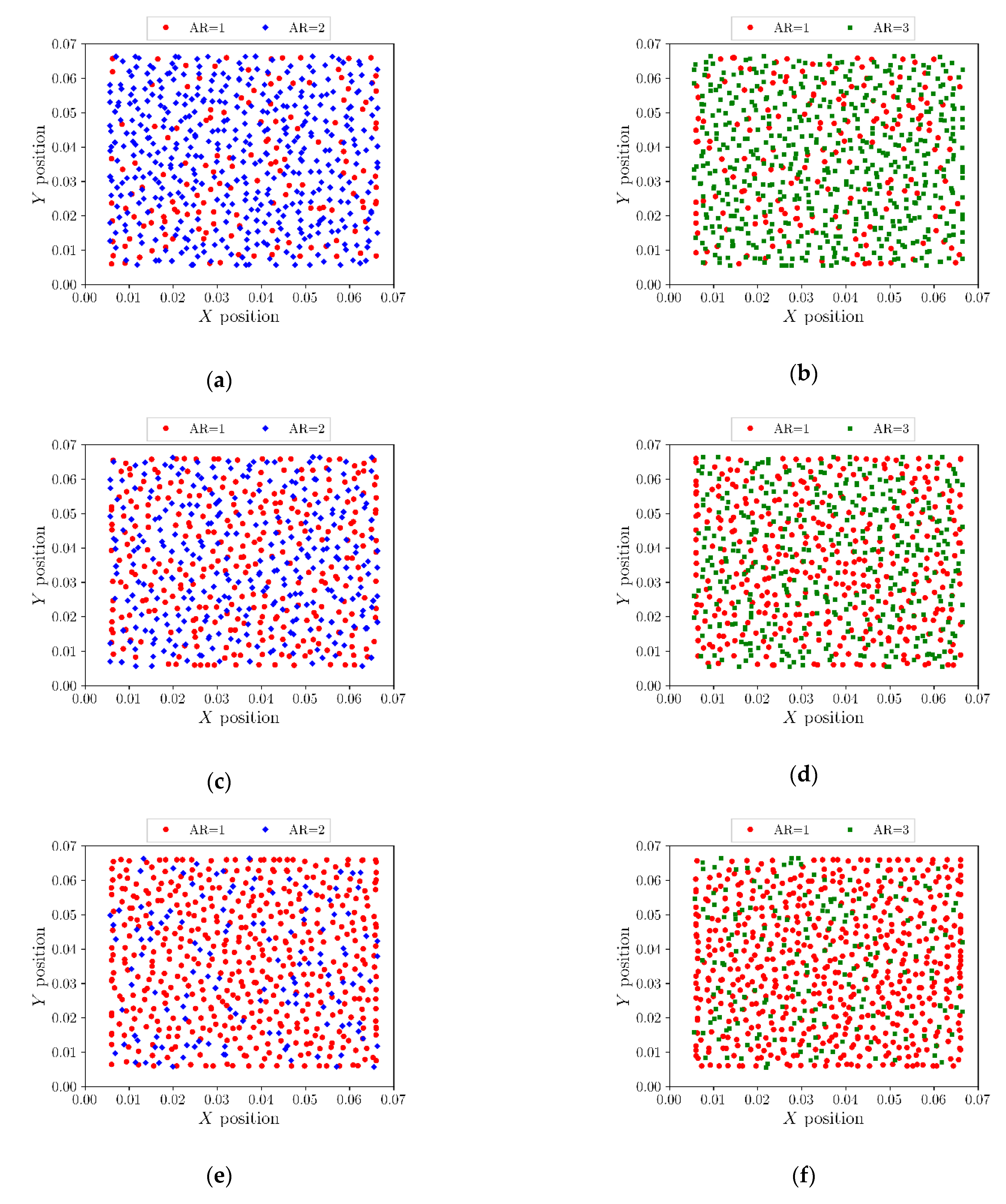
3.1. DEM Simulation Results
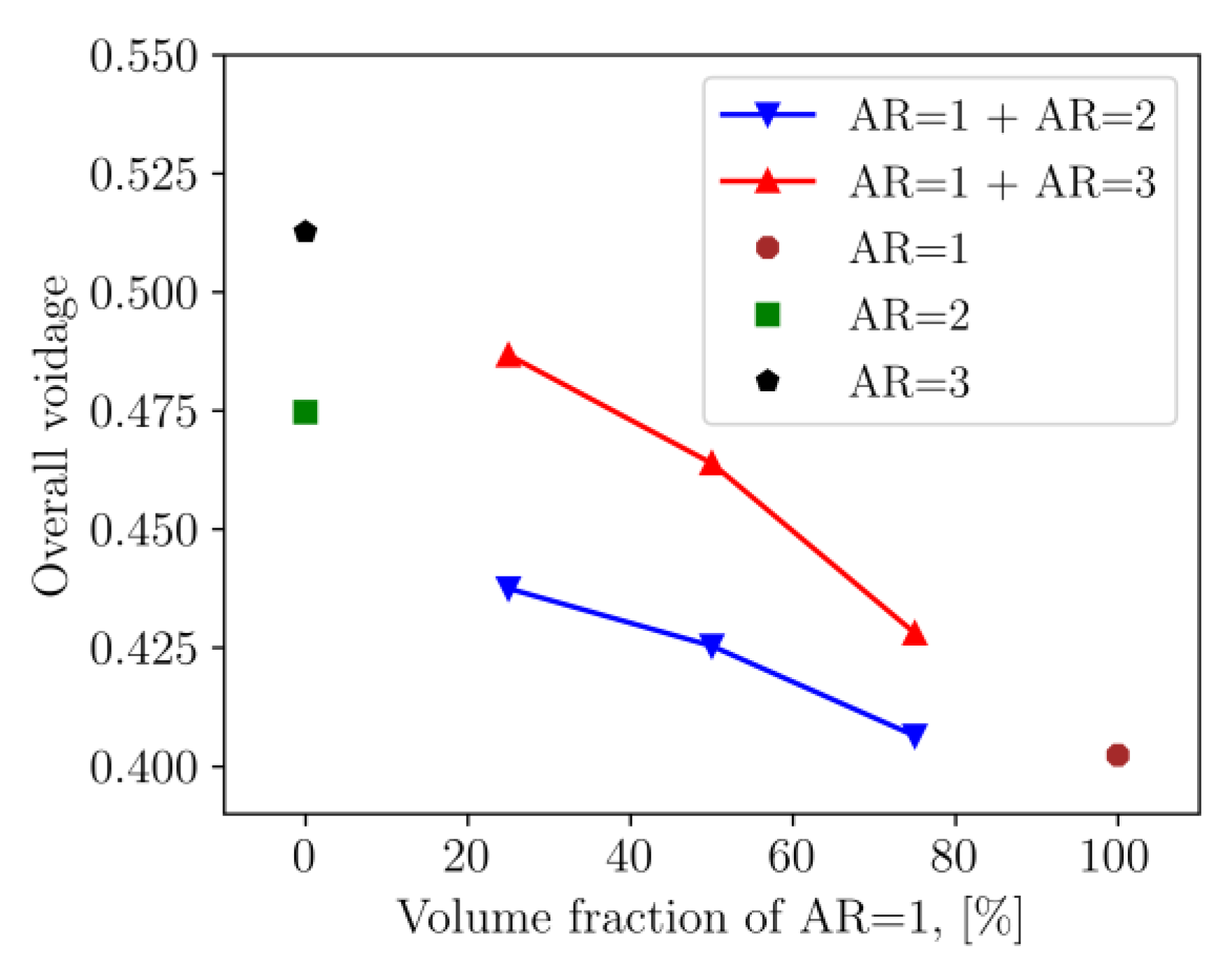
3.2. Planar Packing Fraction
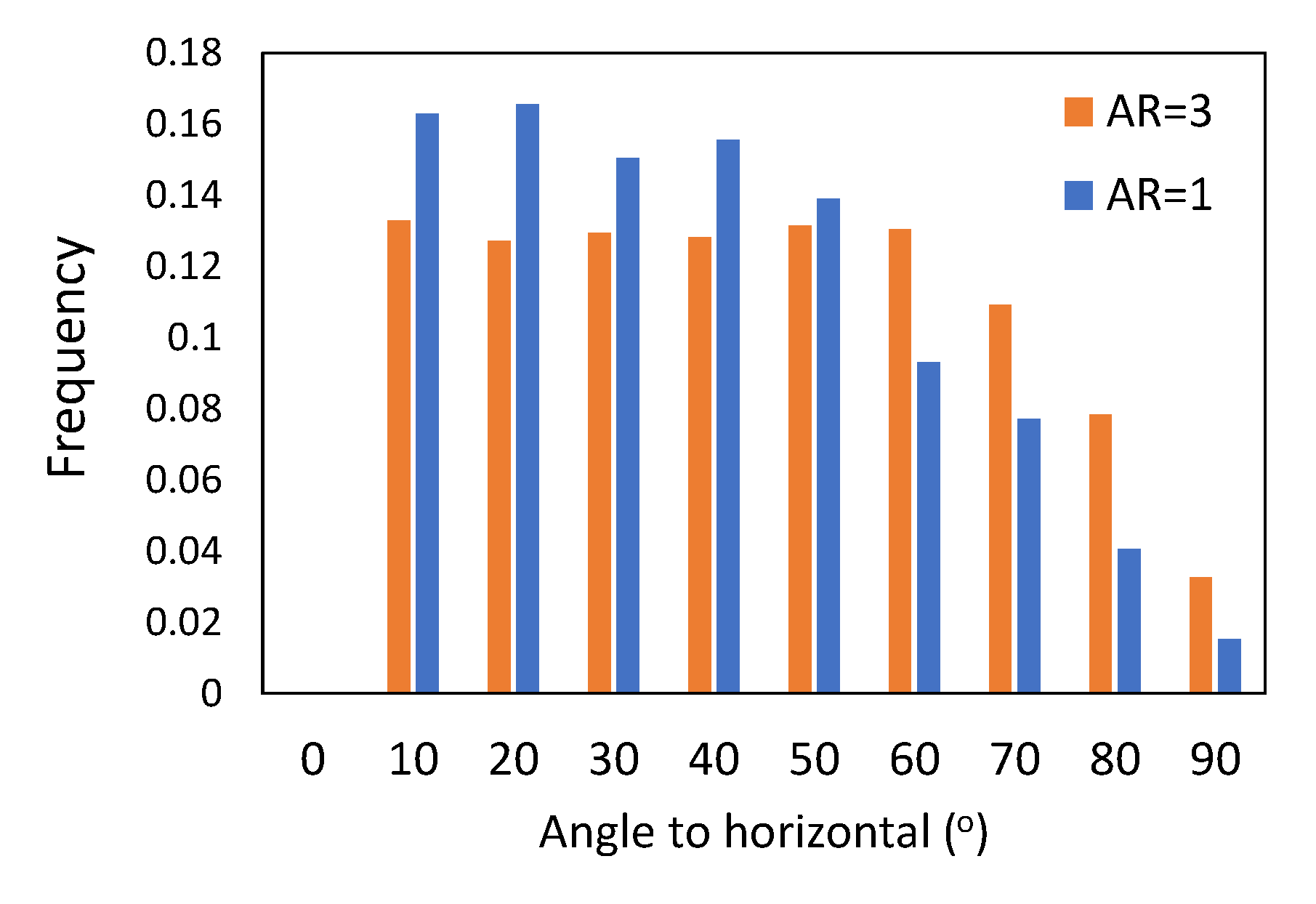
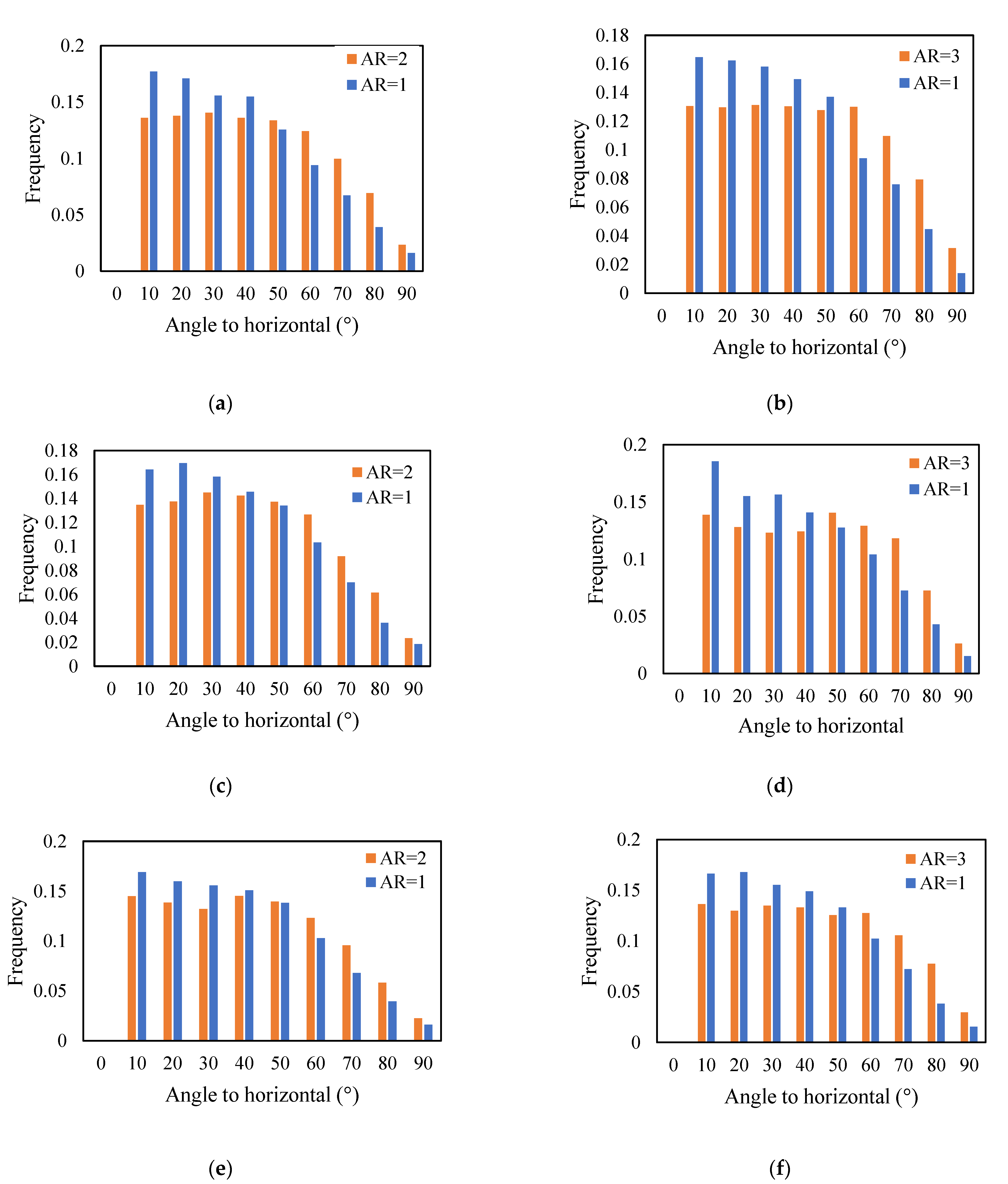
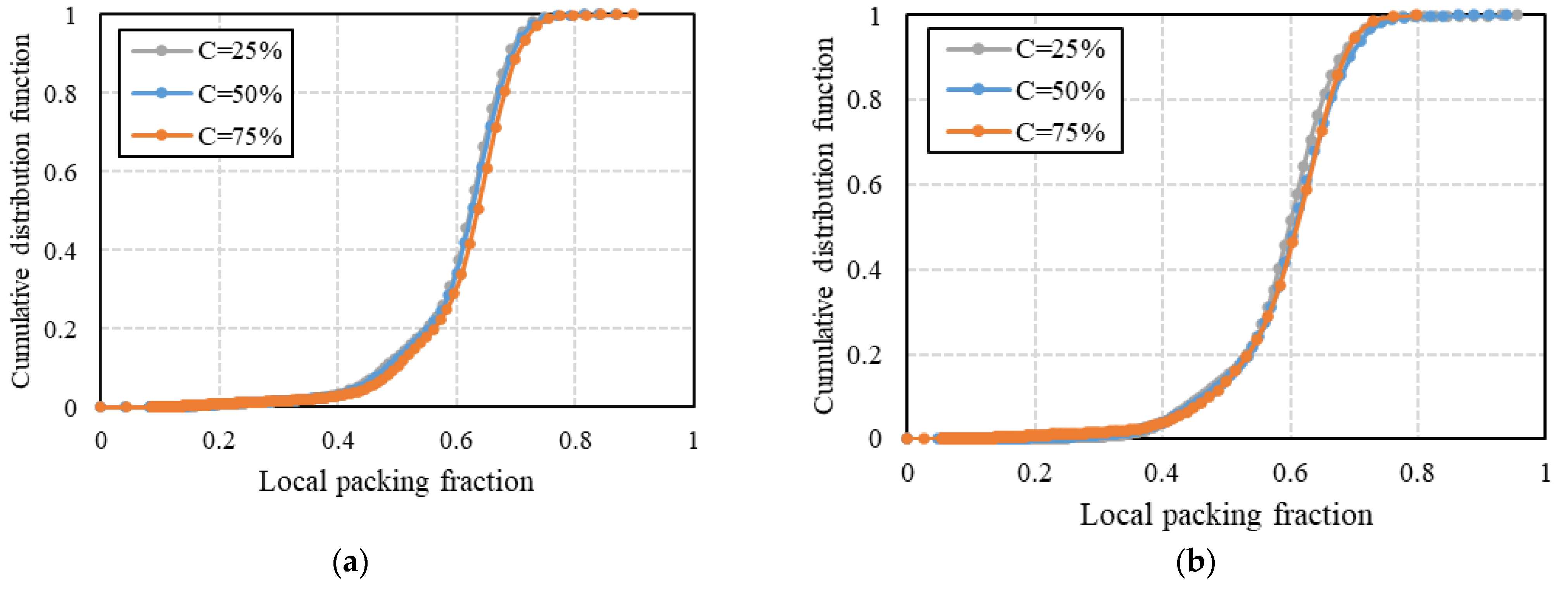
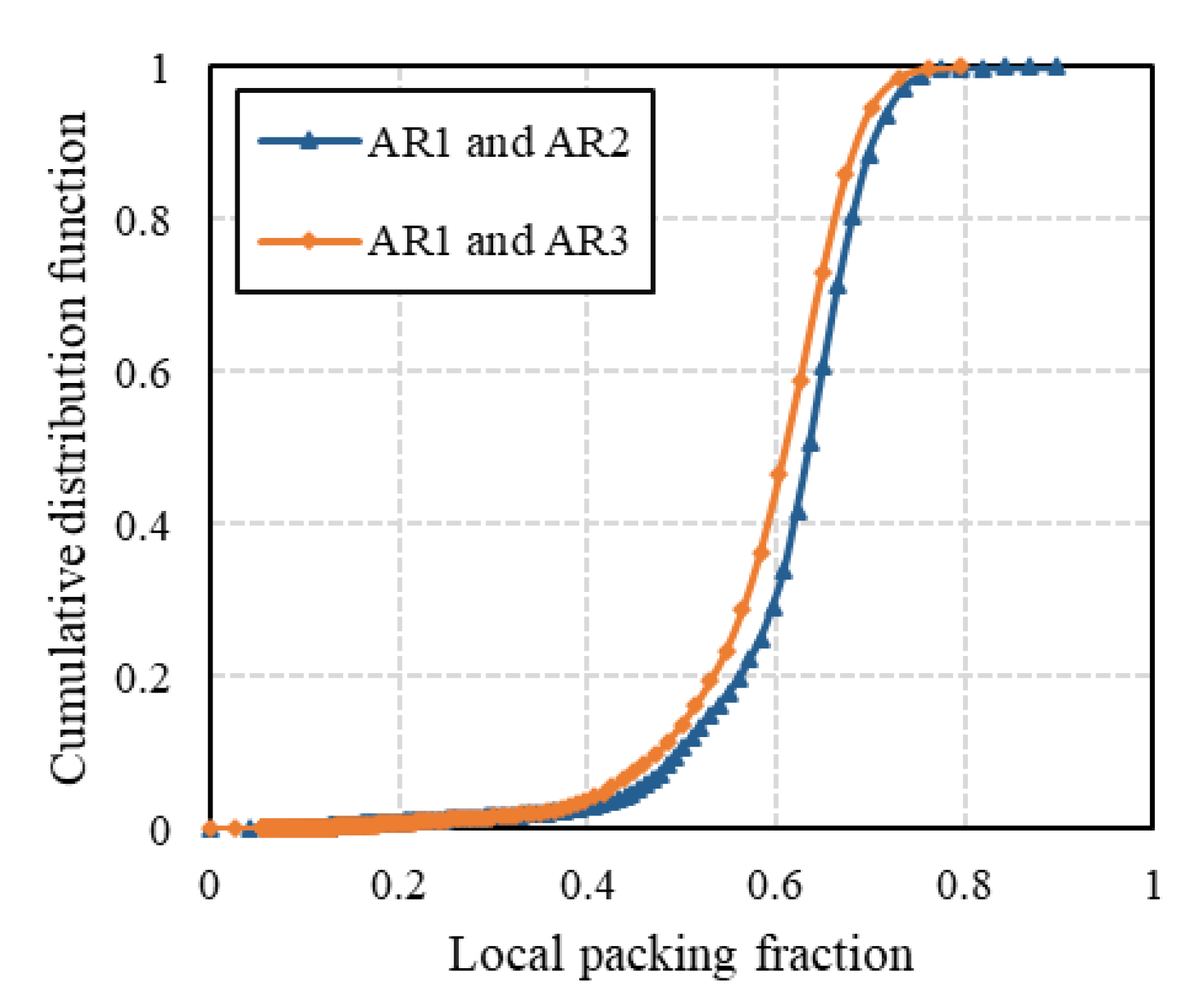
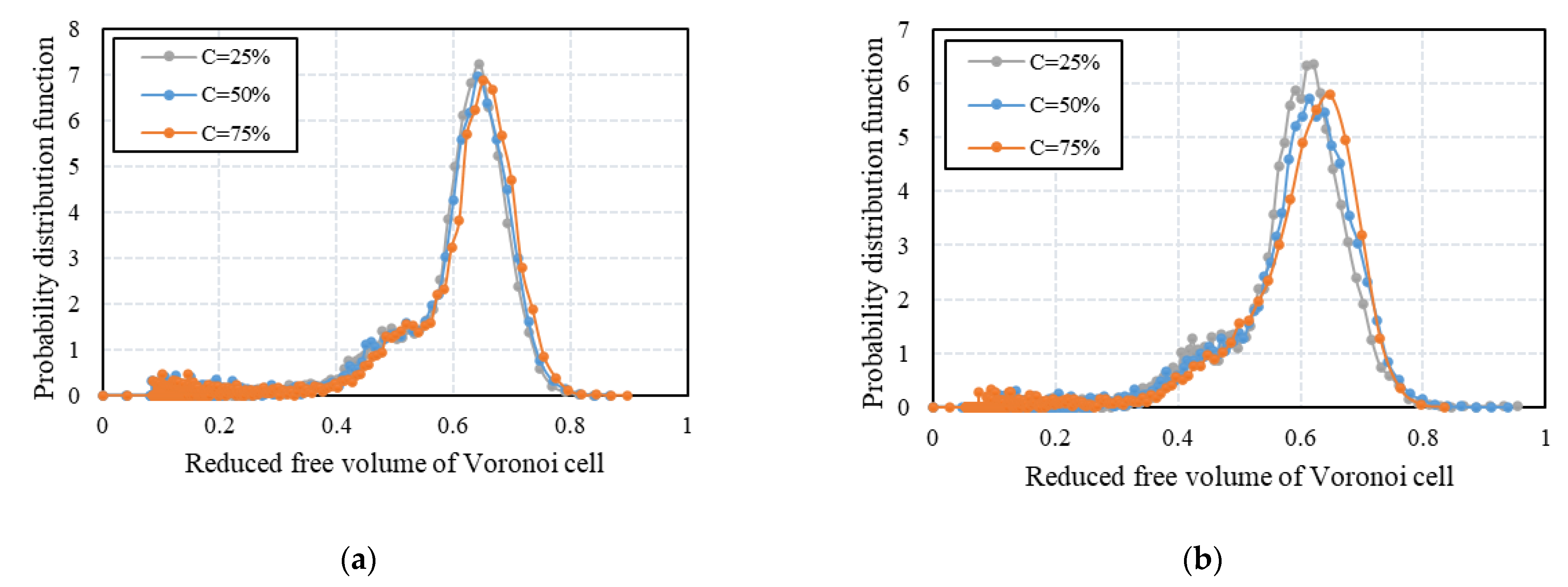
3.3. Local Packing Structure Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dixon, A.G.; Taskin, M.E.; Nijemeisland, M.; Stitt, E.H. Wall-to-particle heat transfer in steam reformer tubes: CFD comparison of catalyst particles. Chem. Eng. Sci. 2008, 63, 2219–2224. [Google Scholar] [CrossRef]
- Motlagh, A.H.A.; Hashemabadi, S.H. 3D CFD simulation and experimental validation of particle-to-fluid heat transfer in a randomly packed bed of cylindrical particles. Int. Commun. Heat Mass Transf. 2008, 35, 1183–1189. [Google Scholar] [CrossRef]
- Meng, L.; Lu, P.; Li, S.; Zhao, J.; Li, T. Shape and size effects on the packing density of binary spherocylinders. Powder Technol. 2012, 228, 284–294. [Google Scholar] [CrossRef]
- Yu, A.B.; Zou, R.P.; Standish, N. Modifying the Linear Packing Model for Predicting the Porosity of Nonspherical Particle Mixtures. Ind. Eng. Chem. Res. 1996, 35, 3730–3741. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Lattanzi, A.M.; Stickel, J.J. Hopper flows of mixtures of spherical and rod-like particles via the multisphere method. AIChE J. 2020, 66, e16882. [Google Scholar] [CrossRef]
- Williams, J.R.; Pentland, A.P. Superquadrics and Modal Dynamics for Discrete Elements in Interactive Design. Eng. Comput. 1992, 9, 115–127. [Google Scholar] [CrossRef]
- Soltanbeigi, B.; Podlozhnyuk, A.; Papanicolopulos, S.-A.; Kloss, C.; Pirker, S.; Ooi, J.Y. DEM study of mechanical characteristics of multi-spherical and superquadric particles at micro and macro scales. Powder Technol. 2018, 329, 288–303. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Xu, L.; Umbanhowar, P.B.; Lueptow, R.M. Discrete element simulation of cylindrical particles using super-ellipsoids. Particuology 2019, 46, 55–66. [Google Scholar] [CrossRef]
- Wang, S.; Marmysh, D.; Ji, S. Construction of irregular particles with superquadric equation in DEM. Theor. Appl. Mech. Lett. 2020, 10, 68–73. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Cylindrical object contact detection for use in discrete element method simulations. Part I: Contact detection algorithms. Chem. Eng. Sci. 2010, 65, 5852–5862. [Google Scholar] [CrossRef]
- Guo, Y.; Wassgren, C.; Ketterhagen, W.; Hancock, B.; Curtis, J. Some computational considerations associated with discrete element modeling of cylindrical particles. Powder Technol. 2012, 228, 193–198. [Google Scholar] [CrossRef]
- Gan, J.; Yu, A. DEM simulation of the packing of cylindrical particles. Granul. Matter 2020, 22, 1–19. [Google Scholar] [CrossRef]
- Pankratov, A.; Romanova, T.; Litvinchev, I. Packing Oblique 3D Objects. Mathematics 2020, 8, 1130. [Google Scholar] [CrossRef]
- Wang, L.; An, X.; Wu, Y.; Qian, Q.; Zou, R.; Dong, K. DEM simulation of vibrated packing densification of mono-sized regular octahedral particles. Powder Technol. 2021, 384, 29–35. [Google Scholar] [CrossRef]
- Zhao, B.; An, X.; Zhao, H.; Gou, D.; Shen, L.; Sun, X. DEM simulation on random packings of binary tetrahedron-sphere mixtures. Powder Technol. 2020, 361, 160–170. [Google Scholar] [CrossRef]
- Jaggannagari, S.R.; Desu, R.K.; Reimann, J.; Gan, Y.; Moscardini, M.; Annabattula, R.K. DEM simulations of vibrated sphere packings in slender prismatic containers. Powder Technol. 2021, 393, 31–59. [Google Scholar] [CrossRef]
- Desu, R.K.; Moorthy, A.; Annabattula, R.K. DEM simulation of packing mono-sized pebbles into prismatic containers through different filling strategies. Fusion Eng. Des. 2018, 127, 259–266. [Google Scholar] [CrossRef]
- Pola, V.R.M.; Desu, R.K.; Annabattula, R.K. Voxelization based packing analysis for discrete element simulations of non-spherical particles. arXiv 2021, arXiv:2110.14151. [Google Scholar] [CrossRef]
- Aste, T. Variations around disordered close packing. J. Phys. Condens. Matter 2005, 17, S2361–S2390. [Google Scholar] [CrossRef]
- Zhao, S.; Evans, T.M.; Zhou, X.; Zhou, S. Discrete element method investigation on thermally-induced shakedown of granular materials. Granul. Matter 2016, 19, 11. [Google Scholar] [CrossRef]
- Akhmetov, Z.; Boribayeva, A.; Berkinova, Z.; Yermukhambetova, A.; Golman, B. Microstructural features of ternary powder compacts. Chem. Eng. Trans. 2019, 74, 385–390. [Google Scholar] [CrossRef]
- Zharbossyn, A.; Berkinova, Z.; Boribayeva, A.; Yermukhambetova, A.; Golman, B. Analysis of Tortuosity in Compacts of Ternary Mixtures of Spherical Particles. Materials 2020, 13, 4487. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Evans, T.M.; Zhou, X. Three-dimensional Voronoi analysis of monodisperse ellipsoids during triaxial shear. Powder Technol. 2018, 323, 323–336. [Google Scholar] [CrossRef]
- Schaller, F.M.; Neudecker, M.; Saadatfar, M.; Delaney, G.W.; Schröder-Turk, G.E.; Schröter, M. Local Origin of Global Contact Numbers in Frictional Ellipsoid Packings. Phys. Rev. Lett. 2015, 114, 158001. [Google Scholar] [CrossRef] [Green Version]
- Schröder-Turk, G.E.; Mickel, W.; Kapfer, S.C.; Klatt, M.A.; Schaller, F.M.; Hoffmann, M.J.F.; Kleppmann, N.; Armstrong, P.; Inayat, A.; Hug, D.; et al. Minkowski Tensor Shape Analysis of Cellular, Granular and Porous Structures. Adv. Mater. 2011, 23, 2535–2553. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, J.; Guo, N. Universality of internal structure characteristics in granular media under shear. Phys. Rev. E 2020, 101, 012906. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, S.; Zhao, J.; Zhou, X. Three-dimensional Voronoi analysis of realistic grain packing: An XCT assisted set Voronoi tessellation framework. Powder Technol. 2021, 379, 251–264. [Google Scholar] [CrossRef]
- Schaller, F.M.; Kapfer, S.C.; Hilton, J.E.; Cleary, P.W.; Mecke, K.; De Michele, C.; Schilling, T.; Saadatfar, M.; Schröter, M.; Delaney, G.W.; et al. Non-universal Voronoi cell shapes in amorphous ellipsoid packs. EPL—Europhys. Lett. 2015, 111, 24002. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Yu, Z.; Jin, W.; Yuan, Y.; Li, S. Uniform and decoupled shape effects on the maximally dense random packings of hard superellipsoids. Powder Technol. 2018, 338, 67–78. [Google Scholar] [CrossRef]
- Dong, K.; Wang, C.; Yu, A. Voronoi analysis of the packings of non-spherical particles. Chem. Eng. Sci. 2016, 153, 330–343. [Google Scholar] [CrossRef]
- Boribayeva, A.; Iniyatova, G.; Uringaliyeva, A.; Golman, B. Porous Structure of Cylindrical Particle Compacts. Micromachines 2021, 12, 1498. [Google Scholar] [CrossRef] [PubMed]
- Barr, A.H. Superquadrics and Angle-Preserving Transformations. IEEE Comput. Graph. Anim. 1981, 1, 11–23. [Google Scholar] [CrossRef] [Green Version]
- Podlozhnyuk, A.; Pirker, S.; Kloss, C. Efficient implementation of superquadric particles in Discrete Element Method within an open-source framework. Comput. Part. Mech. 2017, 4, 101–118. [Google Scholar] [CrossRef] [Green Version]
- Aspherix®, DCS Computing GmbH, Linz, Austria. 2021. Available online: https://www.aspherix-dem.com/ (accessed on 29 November 2022).
- Wang, J.; Lei, M.; Yang, H.; Xu, K.; Xu, S.; Zhao, P.; Song, Y. Effects of coefficient of friction and coefficient of restitution on static packing characteristics of polydisperse spherical pebble bed. Particuology 2021, 57, 1–9. [Google Scholar] [CrossRef]
- Yao, D.; Liu, X.; Wang, J.; Fan, W.; Li, M.; Fu, H.; Zhang, H.; Yang, X.; Zou, Q.; An, X. Numerical insights on the spreading of practical 316 L stainless steel powder in SLM additive manufacturing. Powder Technol. 2021, 390, 197–208. [Google Scholar] [CrossRef]
- Zou, R.-P.; Lin, X.-Y.; Yu, A.; Wong, P. Packing of Cylindrical Particles with a Length Distribution. J. Am. Ceram. Soc. 1997, 80, 646–652. [Google Scholar] [CrossRef]
- Tangri, H.; Guo, Y.; Curtis, J.S. Packing of cylindrical particles: DEM simulations and experimental measurements. Powder Technol. 2017, 317, 72–82. [Google Scholar] [CrossRef]
- Zhang, W.; Thompson, K.E.; Reed, A.H.; Beenken, L. Relationship between packing structure and porosity in fixed beds of equilateral cylindrical particles. Chem. Eng. Sci. 2016, 61, 8060–8074. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, H.; Geng, Z. Computational study of particle packing process and fluid flow inside Polydisperse cylindrical particles fixed beds. Powder Technol. 2019, 354, 19–29. [Google Scholar] [CrossRef]


| Sample | Cylinder 1 | Cylinder 2 | Cylinder 3 |
|---|---|---|---|
 |  |  | |
| d, mm | 3 | 2.381 | 2.080 |
| AR (h/d) | 1 | 2 | 3 |
| h, mm | 3 | 4.752 | 6.240 |
| V, mm3 | 21.206 | 21.206 | 21.206 |
| a, mm | 1.5 | 1.191 | 1.04 |
| b, mm | 1.5 | 1.191 | 1.04 |
| c, mm | 1.5 | 2.381 | 3.12 |
| 10 | 10 | 10 | |
| 2 | 2 | 2 |
| Properties | Value | |
|---|---|---|
| Container size | width × thick × height, m | 0.064 × 0.064 × 0.13 |
| Mechanical properties | Young’s modulus, [Pa] | 2.2 × 108 |
| Poisson ratio | 0.3 | |
| Restitution coefficient | 0.64 | |
| Friction coefficient | 0.6 | |
| DEM parameters | Time-step, Δt [s] | 10−5 |
| Gravity, g [m/s2] | 9.81 | |
| Particles physical properties | Density, [kg/cm3] | 7980 |
| Volume Fraction of AR = 1 | AR = 1 | AR = 2 | AR = 3 | |
|---|---|---|---|---|
| Binary mixture of AR = 1 and AR = 2 | C = 25% | 3000 | 9000 | 0 |
| C = 50% | 6000 | 6000 | 0 | |
| C = 75% | 9000 | 3000 | 0 | |
| Binary mixture of AR = 1 and AR = 3 | C = 25% | 3000 | 0 | 9000 |
| C = 50% | 6000 | 0 | 6000 | |
| C = 75% | 9000 | 0 | 3000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iniyatova, G.; Yermukhambetova, A.; Boribayeva, A.; Golman, B. Approximate Packing of Binary Mixtures of Cylindrical Particles. Micromachines 2023, 14, 36. https://doi.org/10.3390/mi14010036
Iniyatova G, Yermukhambetova A, Boribayeva A, Golman B. Approximate Packing of Binary Mixtures of Cylindrical Particles. Micromachines. 2023; 14(1):36. https://doi.org/10.3390/mi14010036
Chicago/Turabian StyleIniyatova, Gulfairuz, Assiya Yermukhambetova, Aidana Boribayeva, and Boris Golman. 2023. "Approximate Packing of Binary Mixtures of Cylindrical Particles" Micromachines 14, no. 1: 36. https://doi.org/10.3390/mi14010036
APA StyleIniyatova, G., Yermukhambetova, A., Boribayeva, A., & Golman, B. (2023). Approximate Packing of Binary Mixtures of Cylindrical Particles. Micromachines, 14(1), 36. https://doi.org/10.3390/mi14010036








