Capillary Underfill Flow Simulation as a Design Tool for Flow-Optimized Encapsulation in Heterogenous Integration †
Abstract
:1. Introduction
2. Materials and Experimental Methods
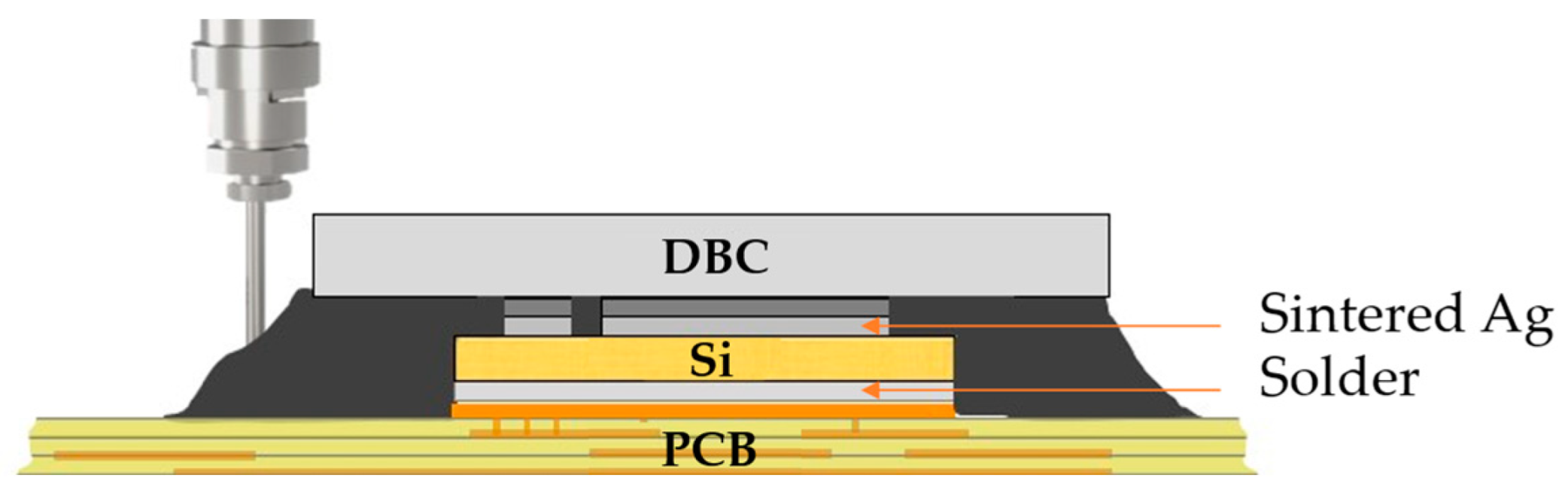
2.1. Vertical Integration Packaging Concept
2.2. Test Setup
- To retain a representative material composition, the flow was monitored using thinned FR4 and Al2O3 substrates. For die imitation, a copper layer was attached via solder/sinter preforms. Substrate materials and dimensions are listed in Table 1;
- Test samples for flow calibration without any overhangs within the gap were illuminated from underneath to guarantee high-contrast images;
- To include flow-optimizing design elements, dam underfill was applied before soldering. Benefits of this material include its limited wetting characteristics and its capacity to accommodate fluctuating gap dimensions;
- After setup, the gap height of each specimen was measured using confocal laser scanning microscopy. Considering substrate warping caused by thermal expansion during the joining process, average gap heights were computed with polynomial fitting;
- Translucency of the thinned substrates enabled real-time monitoring of the black-colored underfill, captured from a top view (xy-plane). Accordingly, this approach is well-suited for identifying voids across the entire gap height.
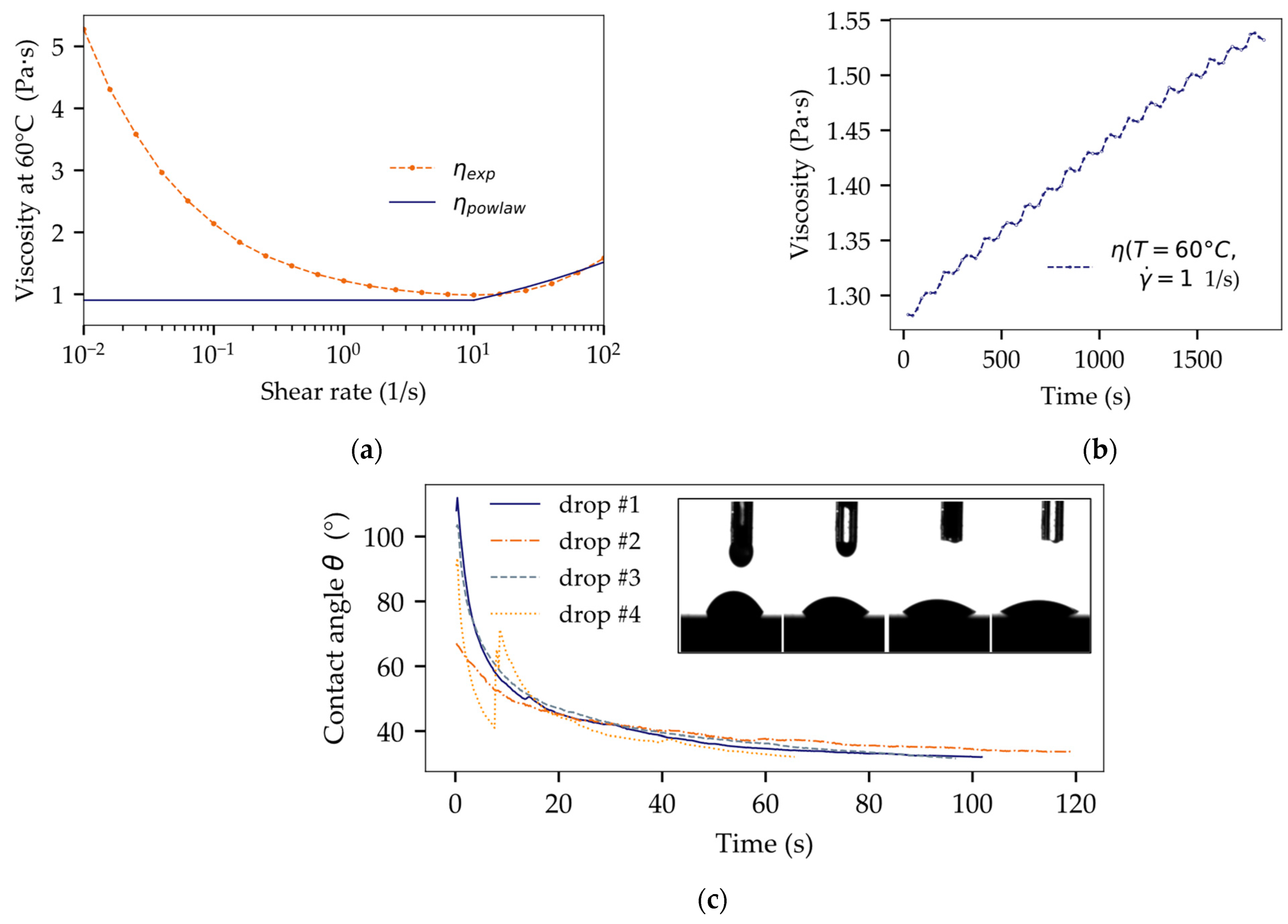
2.3. Material Characterization
2.4. Virtual Mapping: Post-Processing of Flow Recordings
3. Numerical Simulation
3.1. Governing Equations
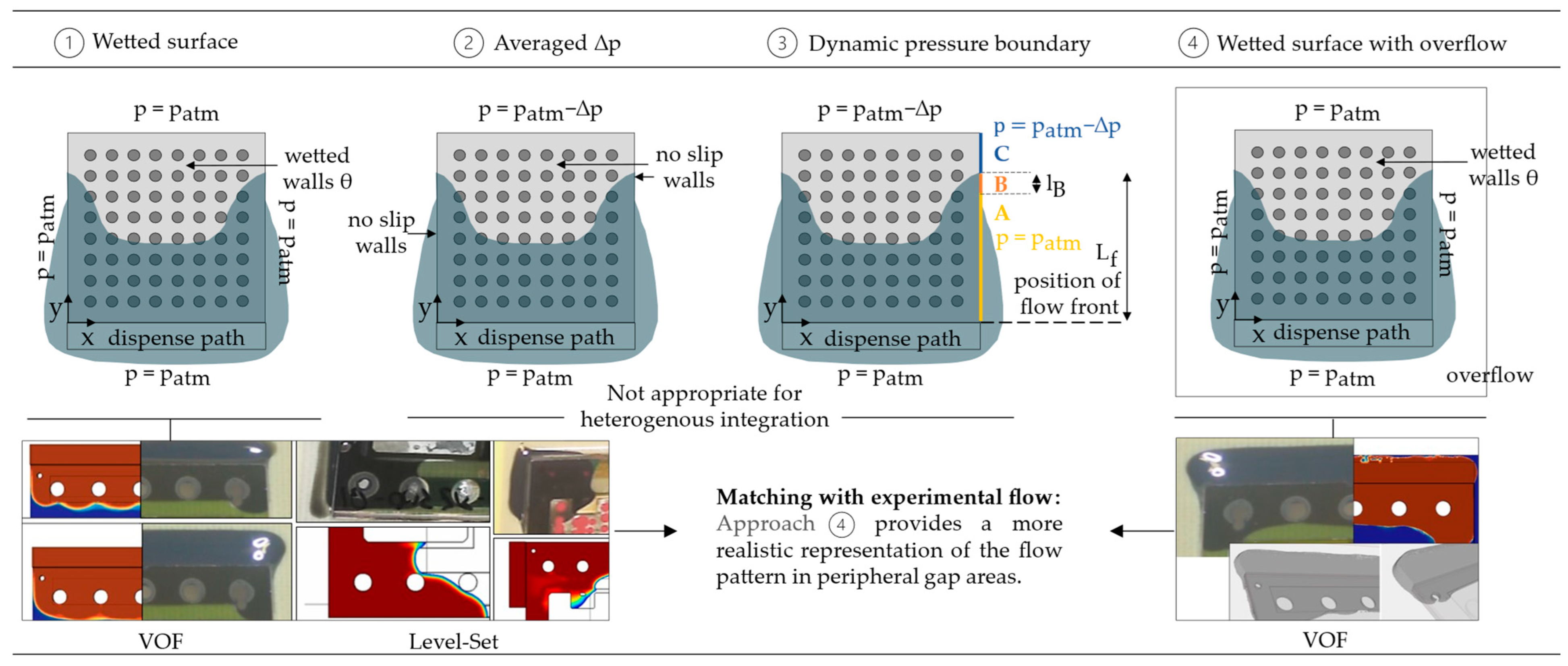
3.2. Computational Domain and Boundary Conditions
3.3. Implementation of Varying Dispensing Patterns
3.4. Coupling Two-Phase Flow with Heat Transfer
3.5. Grid Convergence Study
3.6. Parametric Optimization of VOF Model
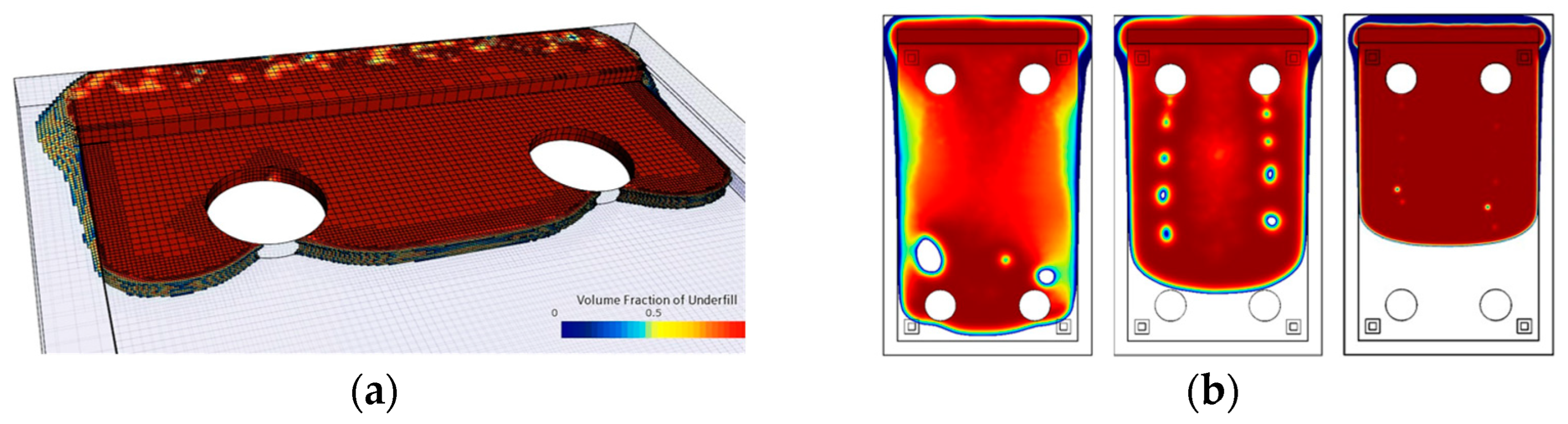
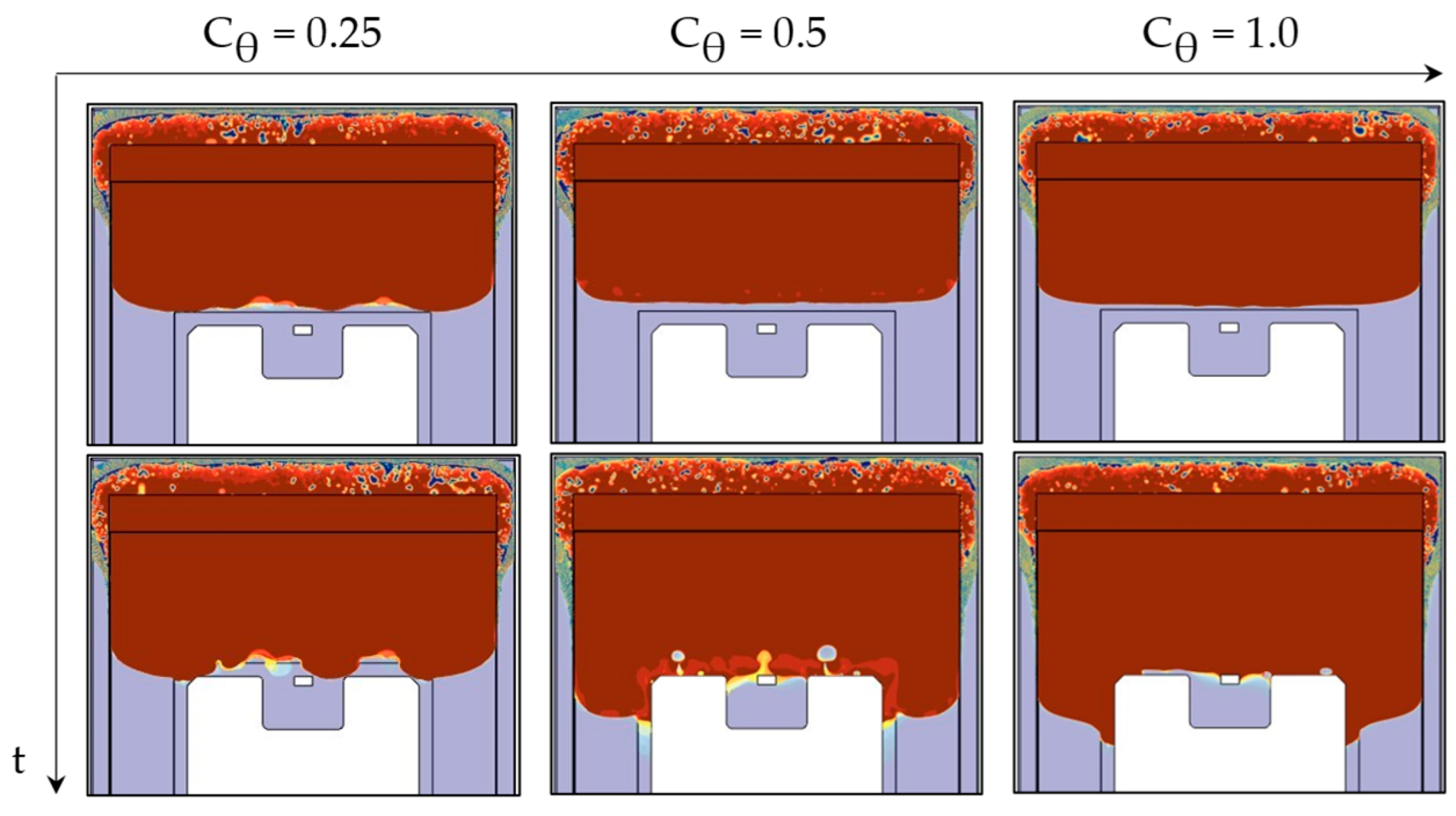
3.6.1. Angle Factor, Blending Criterion, and HRIC Scheme
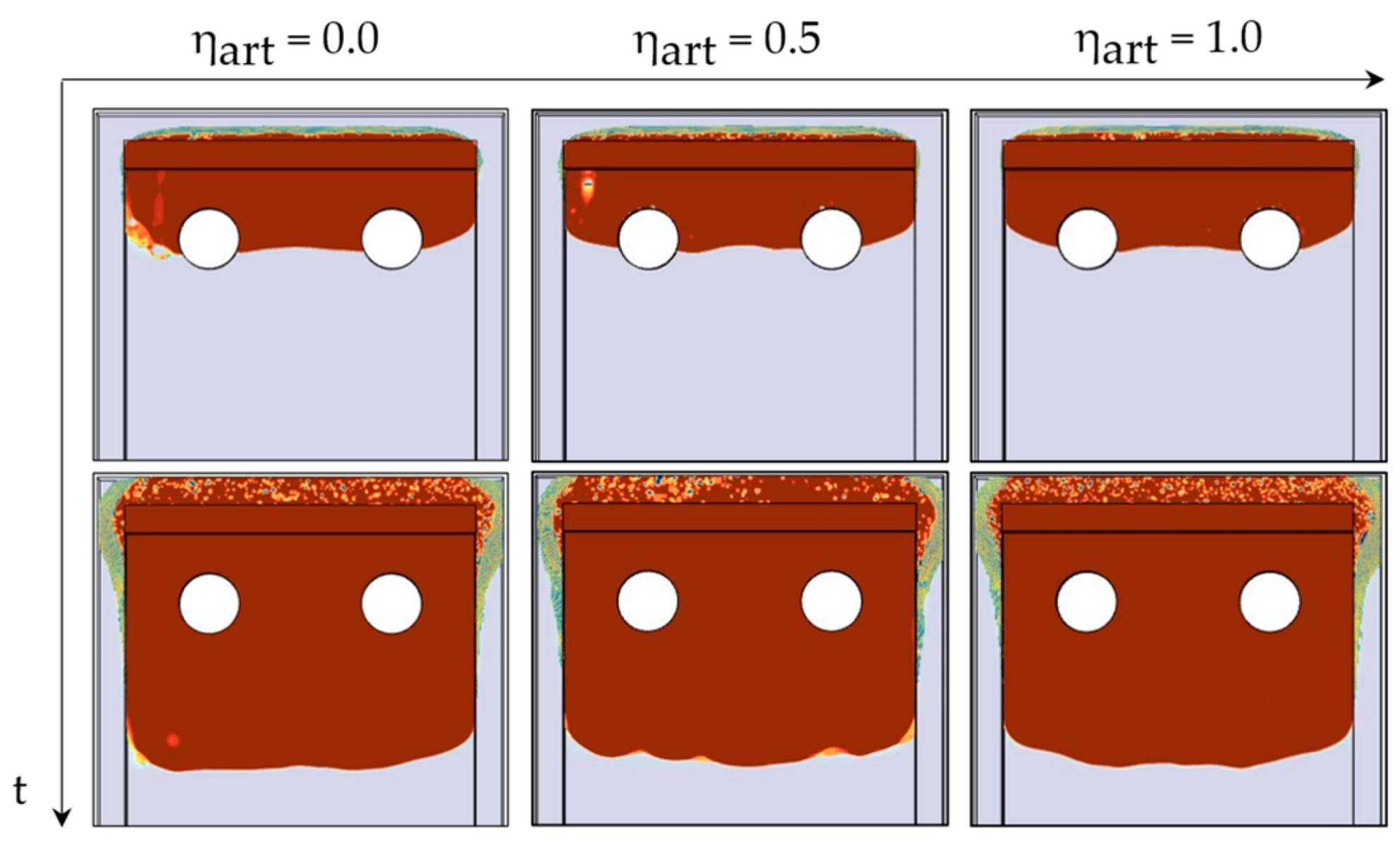
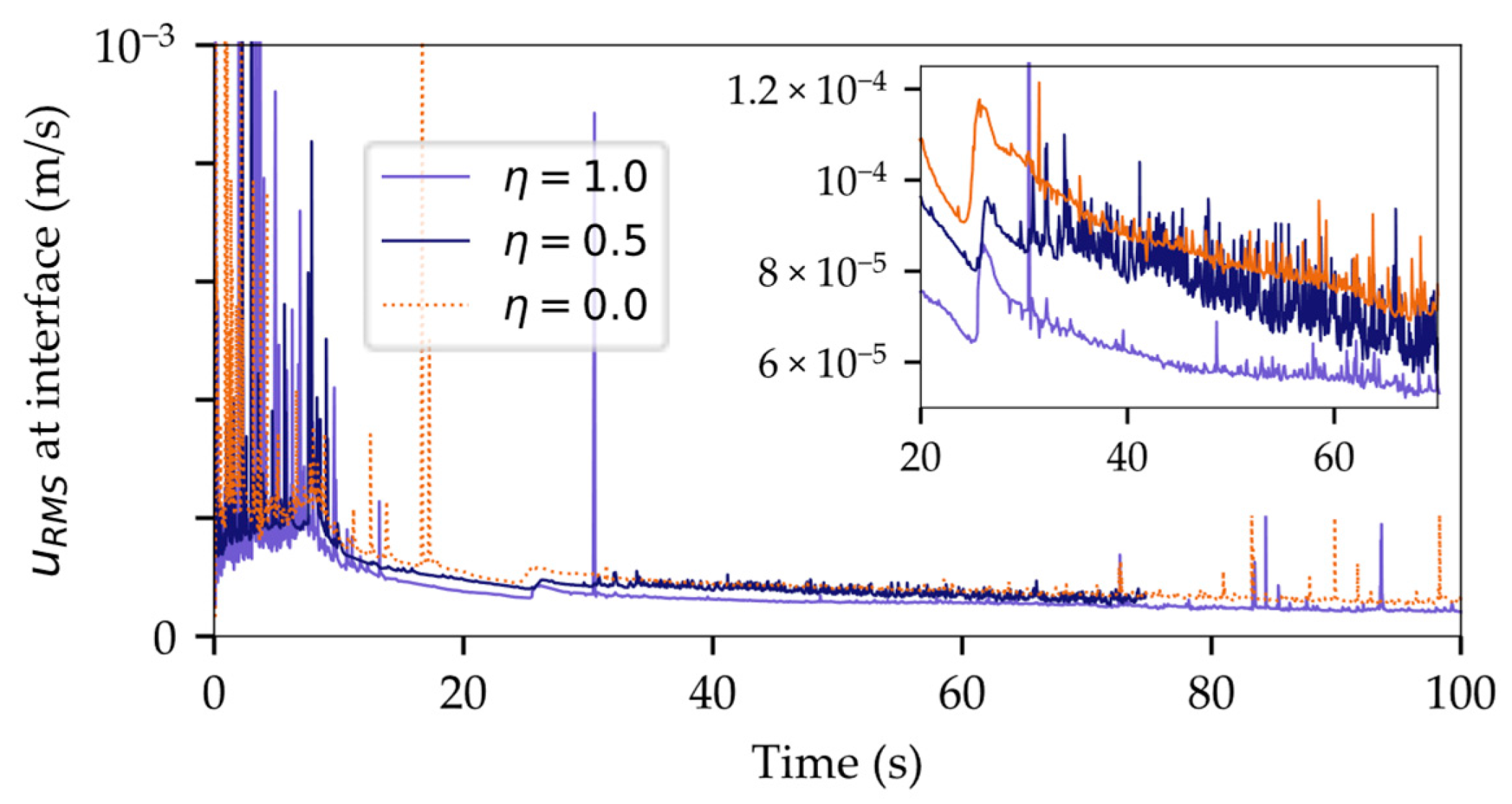
3.6.2. Interfacial Artificial Viscosity
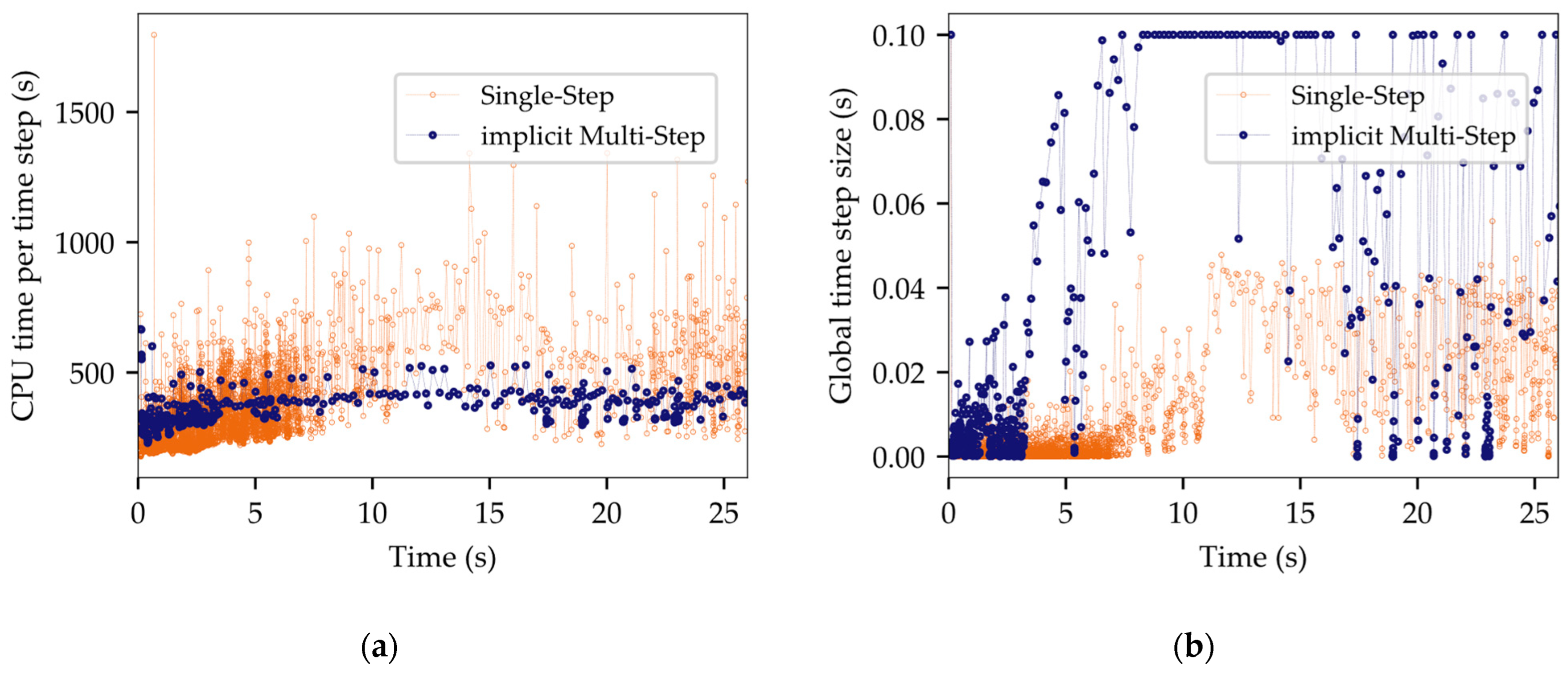
3.6.3. Implicit Multi-Stepping
4. Experimental and Numerical Results
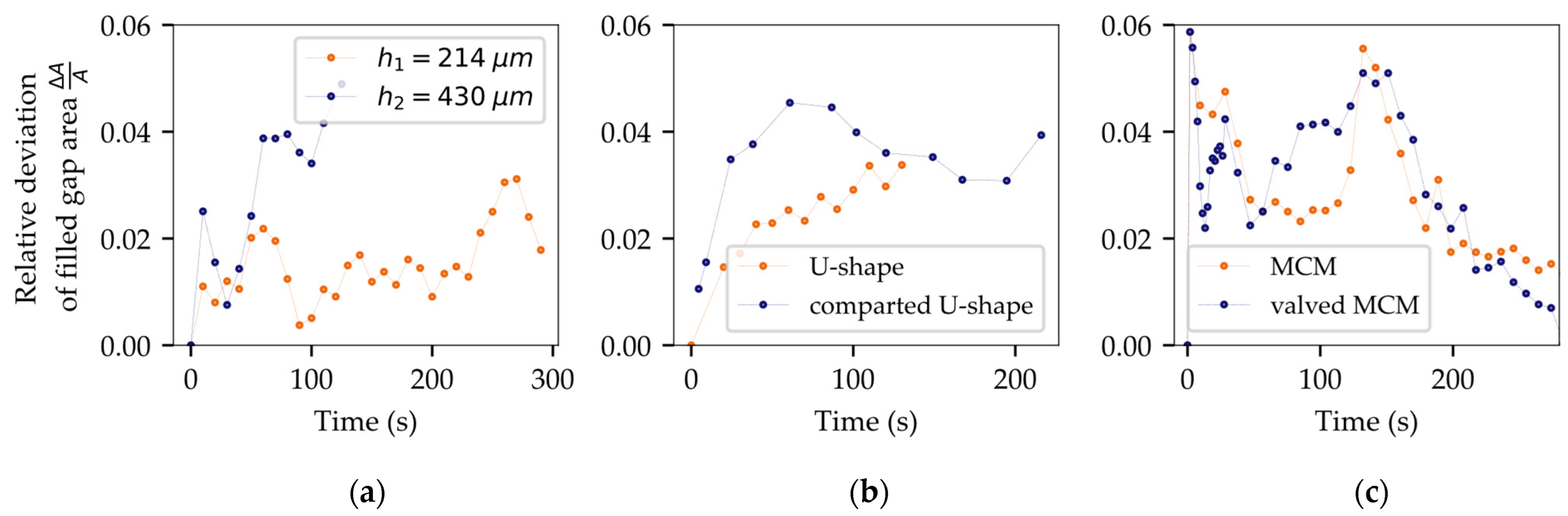
4.1. VOF Sensitivity Study
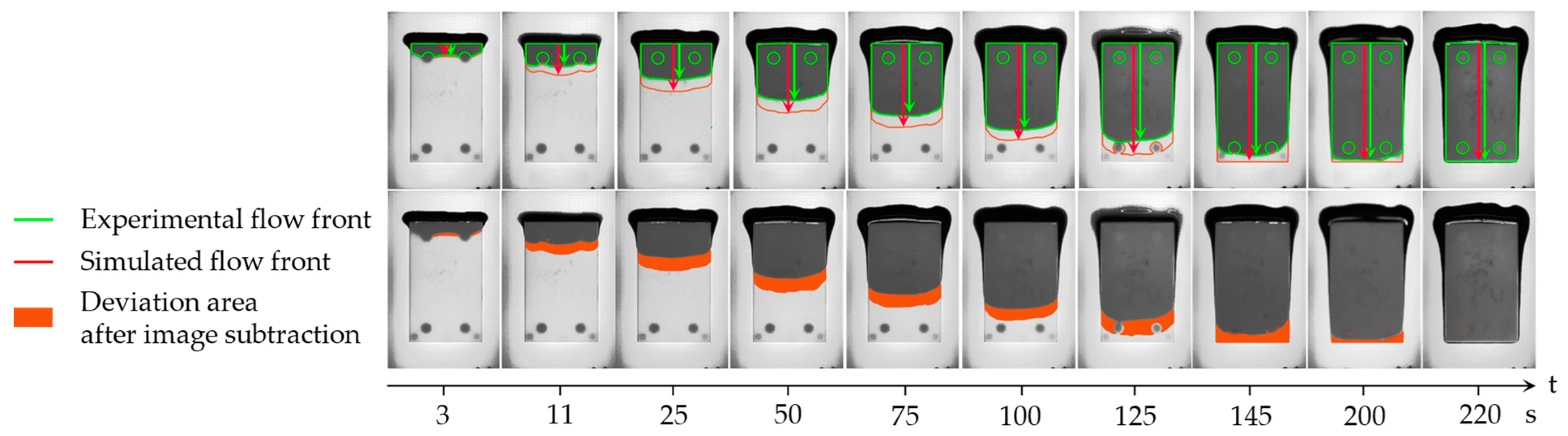
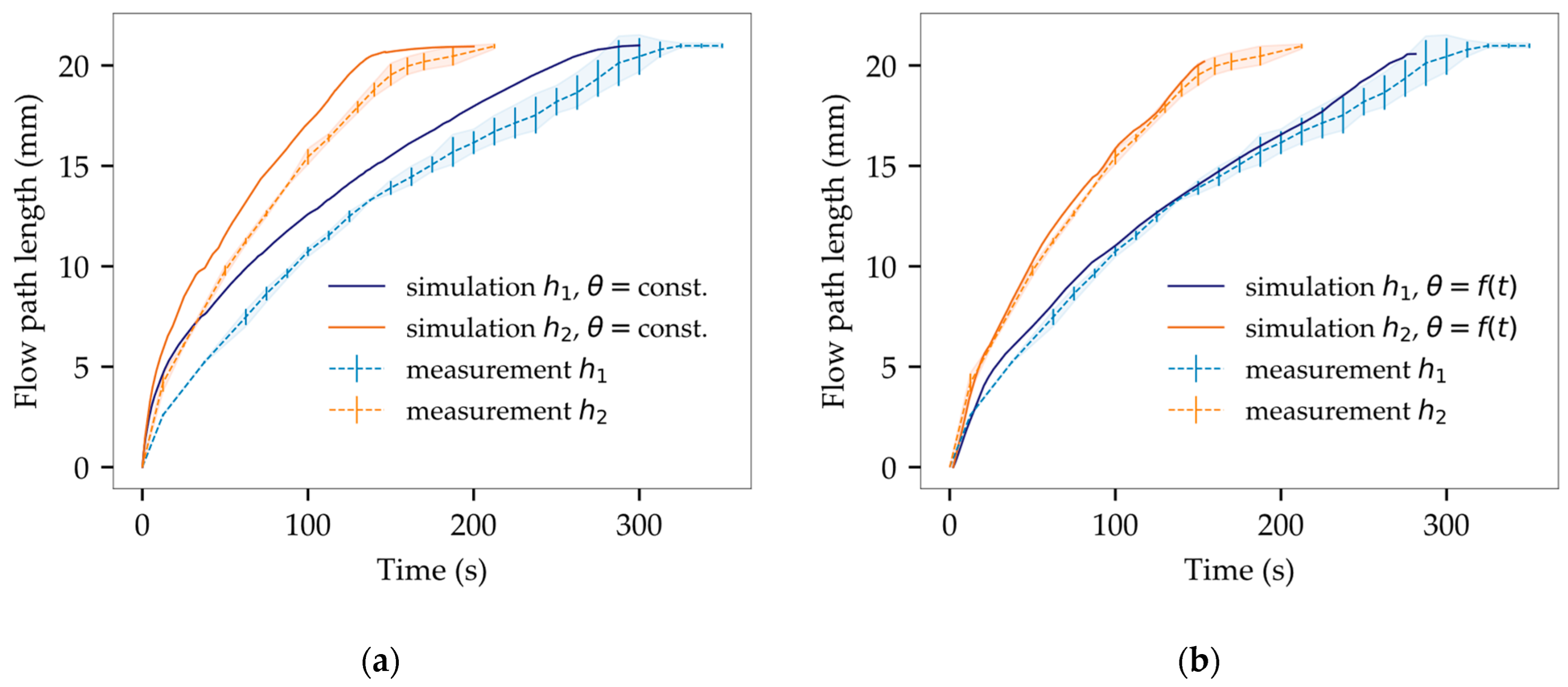
4.2. Experimental Verification
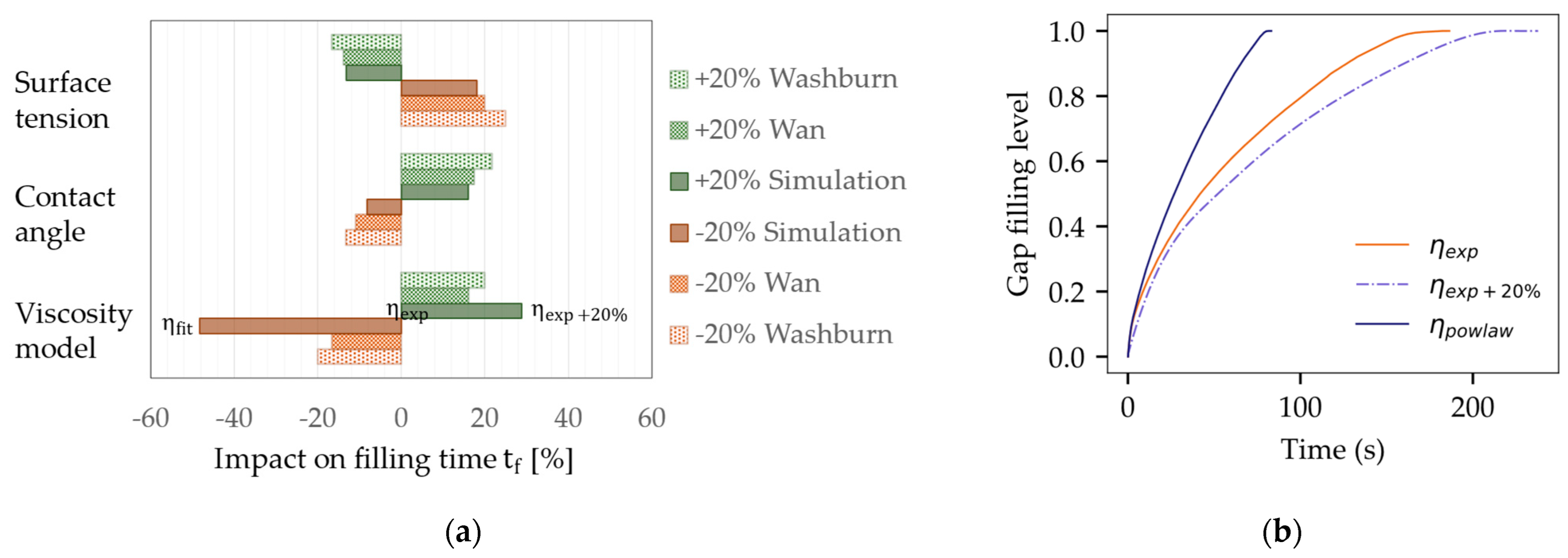
- Simplified inlet condition: simulation assumes complete wetting of the gap, whereas several seconds are necessary for adequate material deposition;
- Heat transfer within underfill is neglected: since the underfill was not preheated before application, it undergoes a temperature transition from room temperature to 60 °C, resulting in a lower initial experimental flow velocity;
- Time-dependency of the contact angle : in alignment with time-dependent sessile drop measurements (Figure 2c), the equilibrium contact angle is reached not before 60 s. This dynamic aspect was not considered in the previous model, contributing to temporal discrepancies.
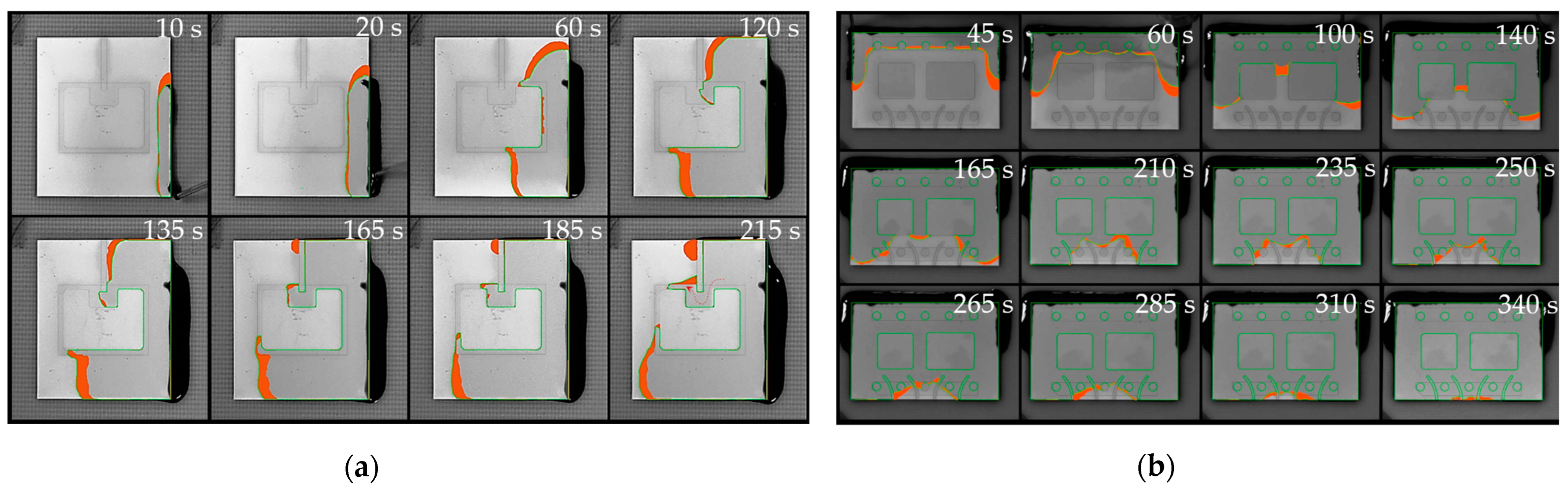
- Figure 16a illustrates a filling scenario of a single IGBT chip with emitter and gate pad being mounted on a ceramic substrate. The model accurately replicated critical flow behavior near the gate interconnection with a low average deviation of only 2.55%. The deep indentation of the sintered joint and the resulting passage around the gate do not allow for void-free filling and inevitably lead to air being trapped between emitter and gate. The simulation has convincingly replicated this behavior.
- In Figure 16b, a common scenario is depicted where the geometric configuration results in irregularly shaped flow fronts, giving rise to uncontrolled merging of multiple free surfaces and, consequently, an increased likelihood of air entrapment. Once again, the simulation showed impressive agreement with the experimental results (2.84% deviation). Minor deviations of the interface primarily resulted from shape deviations and indentations in the joining zones within the experimental setup. Meniscus-shaped solder joints and areas of non-densified, porous sintering material seem to have an impact on the flow along the lateral chip surfaces.
5. Design Studies for Targeted Flow Manipulation
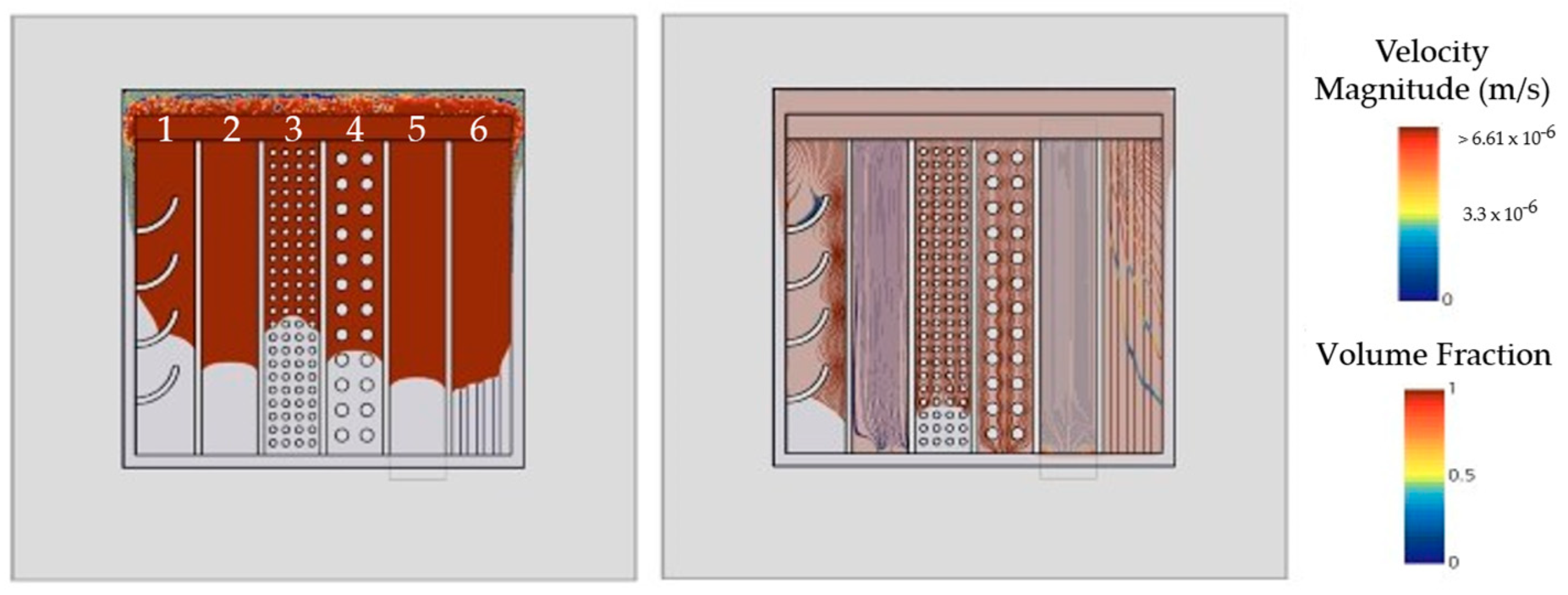
5.1. Flow Speed Adjustment
- Arch-shaped flow barriers decelerate and redirect the flow, tilting the interface orientation towards the outer periphery. This mechanism can also transport unavoidable voids to a less critical peripheral gap area;
- A flat layer (100 µm) was introduced to slow down the flow by reducing the cross-sectional height. Vice versa, to intentionally accelerate the flow, the inclusion of non-functional metallization areas with easily wettable surfaces is an option. Note that any additional layer will reduce gap height, weakening the accelerating effect;
- Higher bump pitch for more manageable flow behavior;
- Stands as a reference flow without any modifications;
- Additional layers for lowering the contact angle are more efficient, if incorporated in a striped shape instead of full coverage. This can be beneficial when substrate depressions are not a viable option to increase the local gap height.
5.2. Gap Compartmentation
5.3. Enforcing Chip-Near Confluence
5.4. Experimental Validation of Design Element Viability
- The results in Figure 20a confirm successful flow control by routing the underfill through the gate channel without air entrapment. Below the semiconductor, the experimental flow propagates slightly faster than the simulation because of non-planarity occurring during assembly. The rise in temperature during soldering triggers the shrinkage of the dam material, leading to substrate tilting, which was not included in the geometry model. Discrepancies between the experiment and the simulation still demonstrate good agreement with only 3.34% deviation.
- Figure 20b highlights the benefit of arcuate valve-like features and confirms, once again, the accuracy of the simulation (2.84% deviation). The numerical as well as the experimental results demonstrated successful void prevention for both fully obstructing and half-height dam elements. Based on this finding, flow control measures do not necessarily need to adopt constricting dam designs. The redirection of flow can also be achieved through partial gap blockage or sharply designed recesses, offering a viable alternative without adverse consequences like substrate tilting or warping.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of symbols: | List of abbreviations: | |||
| Dynamic viscosity | AMR | Adaptive Mesh Refinement | ||
| Interpolated measurement viscosity data | ATS | Adaptive Time Step model | ||
| Fitted power law viscosity | CFD | Computational Fluid Dynamics | ||
| Interfacial artificial viscosity | CFL | Courant–Friedrichs–Lewy condition | ||
| Fixed initial viscosity for low shear rates | CTE | Coefficient of Thermal Expansion | ||
| m | Flow consistency index (power law) | DBC | Direct Bonded Copper | |
| n | 1 | Flow behavior index (power law) | DDS | Differential Downwind Scheme |
| 1/s | Zero shear rate limit of power law definition | DICOM | Digital Imaging and Communications in Medicine | |
| 1/s | Asymptotic shear rate limit of power law | EMC | Epoxy Molding Compound | |
| ° | Contact angle | FCBGA | Flip-Chip Ball-Grid-Array | |
| m/s | Velocity field | FCP | Flip-Chip Package | |
| Pa | Pressure field | FEM | Finite Element Method | |
| 1 | Volume Fraction of underfill | FSI | Fluid–Structure Interaction | |
| 1 | Volume Fraction of air | FVM | Finite Volume Method | |
| ρ | kg/m³ | Mass density | GIC | Grid Convergence Index |
| m/s² | Gravity | HRIC | High-Resolution Interface-Capturing scheme | |
| N/m | Volumetric force | IGBT | Insulated-Gate Bipolar Transistor | |
| N/m | Surface tension | LBM | Lattice–Boltzmann Method | |
| 1 | Interface normal | LS | Level-Set | |
| 1 | Interface curvature of the free surface | MCM | Multi-Chip Module | |
| 1 | Laplace–Beltrami operator of identity mapping | PCB | Printed Circuit Board | |
| 1 | Free surface | ROI | Region of Interest | |
| Pa | Young–Laplace capillary pressure gradient | SFT | Free Surface Tension | |
| m | Gap height | Si/SiC | Silicon/Silicon Carbide | |
| Pa | Atmospheric pressure | MOSFET | Metal-Oxide-Semiconductor Field-Effect Transistor | |
| 1 | Mesh scaling factor | UDS | Upwind Differential Scheme | |
| 1 | Order of accuracy for GCI calculation | URF | Under-Relaxation Factor | |
| 1 | Safety factor (1.25 for three iterations) | VOF | Volume of Fluid | |
| - | Simulated target value for mesh iteration | |||
| - | True numerical target value | |||
| s | Filling time for 90% gap coverage | |||
| h | Required solver time | |||
| ° | Angle between interface and cell face normal | |||
| 1 | Angle factor of HRIC blending criterion | |||
| 1 | Blended normalized cell face value | |||
| m/s | Root mean square of interface velocity magnitude for time t | |||
| m/s | Interfacial velocity component in x, y, z | |||
| 1 | Number of cells at interface | |||
References
- Yole Développement. Status of the Power Module Packaging Industry 2021. Available online: https://s3.i-micronews.com/uploads/2021/11/YINTR21196_Status_of_the_Power_Module_Packaging_Industry_2021_Sample.pdf (accessed on 20 August 2023).
- Weidner, K.; Kaspar, M.; Seliger, N. Planar interconnect technology for power module system integration. In Proceedings of the 7th International Conference on Integrated Power Electronics Systems (CIPS), Nuremberg, Germany, 6–8 March 2012. [Google Scholar]
- Liang, Z. Planar-bond-all: A technology for three-dimensional integration of multiple packaging functions into advanced power modules. In Proceedings of the IEEE International Workshop on Integrated Power Packaging (IWIPP), Chicago, IL, USA, 3–6 May 2015. [Google Scholar]
- Scheuermann, U. Reliability of planar SKiN interconnect technology. In Proceedings of the 7th International Conference on Integrated Power Electronics Systems (CIPS), Nuremberg, Germany, 6–8 March 2012. [Google Scholar]
- Yin, L.; Nagarkar, K.; Gowda, A.; Kapusta, C.; Tuominen, R.; Gillespie, P.; Sherman, D.; Johnson, T.; Hayashibe, S.; Ito, H.; et al. POL-kw modules for high power applications. In Proceedings of the IEEE 67th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 3 August 2017. [Google Scholar]
- Wang, M.; Mei, Y.; Liu, W.; Xie, Y.; Fu, S.; Li, X.; Lu, G. Reliability Improvement of a Double-Sided IGBT Module by Lowering Stress Gradient Using Molybdenum Buffers. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1637–1648. [Google Scholar] [CrossRef]
- Jeon, J.; Seong, J.; Lim, J.; Kim, M.K.; Kim, T.; Yoon, S.W. Finite Element and Experimental Analysis of Spacer Designs for Reducing the Thermomechanical Stress in Double-Sided Cooling Power Modules. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3883–3891. [Google Scholar] [CrossRef]
- Cao, J.; Li, J.; Mei, Y.-H. A Double-Sided Bidirectional Power Module with Low Heat Concentration and Low Thermomechanical Stress. IEEE Trans. Power Electron. 2021, 36, 9763–9766. [Google Scholar] [CrossRef]
- Ding, C.; Liu, H.; Ngo, K.D.; Burgos, R.; Lu, G.Q. A Double-Side Cooled SiC MOSFET Power Module with Sintered-Silver Interposers: I-Design, Simulation, Fabrication, and Performance Characterization. IEEE Trans. Power Electron. 2021, 36, 11672–11680. [Google Scholar] [CrossRef]
- Pavlicek, N.; Liu, C.; Qayyum, U. Thermal and Thermomechanical Investigations of Power Semiconductor Pre-Packages. In Proceedings of the 2022 IEEE 9th Electronics System-Integration Technology Conference (ESTC), Sibiu, Romania, 13–16 September 2022. [Google Scholar]
- Thomas, T.; Nguyen, T.D.; Blechert, M.; Hoffmann, S.; Obst, M.; Becker, K.F.; Braun, T.; Dreissigacker, M.; Schneider-Ramelow, M. Packaging Platform for low to medium Power Packages. In Proceedings of the 2022 IEEE 9th Electronics System-Integration Technology Conference (ESTC), Sibiu, Romania, 13–16 September 2022. [Google Scholar]
- Ng, F.C.; Abas, M.A. Underfill Flow in Flip-Chip Encapsulation Process: A Review. J. Electron. Packag. 2022, 144, 010803. [Google Scholar] [CrossRef]
- Miyazawa, R.; Marushima, C.; Aoki, T.; Horibe, A.; Hisada, T. CFD Simulation Analysis and Experimental Study of Capillary Underfill Flow in Heterogeneous Integration. In Proceedings of the 2021 IEEE 71st Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 1 June–4 July 2021. [Google Scholar]
- Gan, Z.L.; Abas, A.; Ishak, M.H.H.; Abdullah, M.Z.; Ngang, J.L. Comparative Study of Pressurized and Capillary Underfill Flow Using Lattice Boltzmann Method. Arabia. J. Sci. Eng. 2019, 44, 7627–7652. [Google Scholar] [CrossRef]
- Ishak, M.H.H.; Abdullah, M.Z.; Aziz, M.A.; Saad, A.A.; Abdullah, M.K.; Loh, W.K.; Ooi, R.C.; Ooi, C.K. Study on the Fluid–Structure Interaction at Different Layout of Stacked Chip in Molded Packaging. Arab. J. Sci. Eng. 2017, 42, 4743–4757. [Google Scholar] [CrossRef]
- Ramdan, D.; Abdullah, M.Z.; Khor, C.; Leong, W.C.; Loh, W.K.; Ooi, C.K.; Ooi, R.C. Fluid/Structure Interaction Investigation in PBGA Packaging. IEEE Trans. Compon. Packag. Manuf. Technol. 2012, 2, 1786–1795. [Google Scholar] [CrossRef]
- Yang, C.; Young, W.B. The Effective Permeability of the Underfill Flow Domain in Flip-Chip Packaging. Appl. Math. Modell. 2013, 37, 1177–1186. [Google Scholar] [CrossRef]
- Abas, A.; Haslinda, M.S.; Ishak, M.H.H.; Nurfatin, A.S.; Abdullah, M.Z.; Ani, F.C. Effect of ILU Dispening Types for Different Solder Bump Arrangements on CUF Encapsulation Process. Microelectron. Eng. 2016, 163, 83–97. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, H.J.; Kim, J.M.; Shin, Y.E. Dynamic Filling Characteristics of a Capillary Driven Underfill Process in Flip-Chip Packaging. Mater. Trans. 2011, 52, 1998–2003. [Google Scholar] [CrossRef]
- Ng, F.C.; Abas, A.; Abdullah, M.Z. Finite Volume Method Study on Contact Line Jump Phenomena and Dynamic Contact Angle of Underfill Flow in Flip-Chip of Various Bump Pitches. IOP Conf. Ser. Mater. Sci. Eng. 2019, 530, 012012. [Google Scholar] [CrossRef]
- Ng, F.C.; Zawawi, M.H.; Abas, M.A. Spatial Analysis of Underfill Flow in Flip-Chip Encapsulation. Solder. Surf. Mount Technol. 2020, 33, 112–127. [Google Scholar] [CrossRef]
- Chen, D.L.; Chang, H.J.; Chen, T.Y.; Hu, Y.H.; Chen, T.B.; Pan, C.H.; Yang, Y.S.; Hwang, S.J. A Study of Underfill Dispensing Patterns in Flip-Chip Packaging. In Proceedings of the International Conference on Electronics Packaging (ICEP), Kumamoto, Japan, 19–22 April 2023. [Google Scholar]
- Stencel, L.C.; Strogies, J.; Müller, B.; Knofe, R.; Borwieck, C.; Heimann, M. Digital twin as a tool for evaluating and optimizing flow behavior in encapsulating processes. In Proceedings of the 2022 IEEE 9th Electronics System-Integration Technology Conference (ESTC), Sibiu, Romania, 13–16 September 2022. [Google Scholar]
- Stencel, L.C.; Strogies, J.; Knofe, R.; Müller, B.; Borwieck, C.; Heimann, M. Two-Phase Flow Simulation of Capillary Underfilling as a Design Tool for Heterogenous Integration. In Proceedings of the 2023 24th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Graz, Austria, 16–19 April 2023. [Google Scholar]
- De Beeck, J.O.; De Malsche, W.; Tezcan, D.S.; De Moor, P.; Desmet, G. Impact of the limitations of state-of-the-art micro-fabrication processes on the performance of pillar array columns for liquid chromatography. J. Chromatogr. A 2012, 1239, 35–48. [Google Scholar] [CrossRef]
- Nagrath, S.; Sequist, L.V.; Maheswaran, S.; Bell, D.W.; Irimia, D.; Ulkus, L.; Smith, M.R.; Kwak, E.L.; Digumarthy, S.; Muzikansky, A.; et al. Isolation of rare circulating tumour cells in cancer patients by microchip technology. Nature 2007, 450, 1235–1239. [Google Scholar] [CrossRef]
- Vangelooven, J.; De Malsche, W.; De Beeck, J.O.; Eghbali, H.; Gardeniers, H.; Desmet, G. Design and evaluation of flow distributors for microfabricated pillar array columns. Lab. Chip 2010, 10, 349–356. [Google Scholar] [CrossRef]
- Nguyen, L.; Quentin, C.; Fine, P.; Cobb, B.; Bayyuk, S.; Yang, H.; Bidstrup-Allen, S.A. Underfill of flip chip on laminates: Simulation and validation. IEEE Trans. Compon. Packag. Technol. 1999, 22, 168–176. [Google Scholar] [CrossRef]
- Luo, W.; Liang, J.J.; Zhang, Y.; Zhou, H.M. An analytical model for the underfill flow driven by capillary forces in chip packaging. In Proceedings of the 2016 17th International Conference on Electronic Packaging Technology (ICEPT), Wuhan, China, 16–19 August 2016. [Google Scholar]
- Häußermann, T. Simulation des Underfill-Prozesses bei Flip Chip-Anwendungen. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2009. [Google Scholar]
- Fan, L.; Tison, C.K.; Wong, C.P. Study on underfill/solder adhesion in flip-chip encapsulation. IEEE Trans. Adv. Packag. 2002, 25, 473–480. [Google Scholar]
- MathWorks. MATLAB Release 2022a; The MathWorks, Inc.: Natick, MA, USA, 2022. [Google Scholar]
- Yushkevich, P.A.; Piven, J.; Hazlett, H.C.; Smith, R.G.; Ho, S.; Gee, J.C.; Gerig, G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage 2006, 31, 1116–1128. [Google Scholar] [CrossRef]
- COMSOL Multiphysics® v. 5.6. COMSOL AB: Stockholm, Sweden, 2020.
- Siemens Digital Industries Software. Simcenter STAR-CCM+, version 2210; Siemens: Munich, Germany, 2022. [Google Scholar]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Fine, P.; Cobb, B.; Nguyen, L. Flip chip underfill flow characteristics and prediction. IEEE Trans. Compon. Packag. Technol. 2000, 23, 420–427. [Google Scholar] [CrossRef]
- Young, W.B.; Yang, W.L. The effect of solder bump pitch on the underfill flow. IEEE Trans. Adv. Packag. 2002, 25, 537–542. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, K.; Wang, Y. A novel model for simulating the racing effect in capillary-driven underfill process in flip chip. J. Micromech. Microeng. 2018, 28, 045002. [Google Scholar] [CrossRef]
- Phillips, T.S.; Roy, C.J. A New Extrapolation-Based Uncertainty Estimator for Computational Fluid Dynamics. J. Verif. Valid. Uncert. Dec. 2016, 1, 041006. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Muzaferija, S. A two-fluid NavierStokes solver to simulate water entry. In Proceedings of the Twenty-Second Symposium on Naval Hydrodynamics, Washington, DC, USA, 9–14 August 1998. [Google Scholar]
- Berndt, J.C.; Perić, R.; Abdel-Maksoud, M. Improved Simulation of Flows with Free-Surface Waves by Optimizing the Angle Factor in the HRIC Interface-Sharpening Scheme. J. Appl. Fluid Mech. 2020, 14, 909–920. [Google Scholar]
- Inguva, V.; Schulz, A.; Kenig, E. On methods to reduce spurious currents within VOF solver frameworks. Part 1: A review of the static bubble/droplet. Chem. Prod. Process Model. 2020, 17, 121–135. [Google Scholar] [CrossRef]
- Wörner, M.; Sabisch, W.; Grötzbach, G.; Cacuci, D.G. Volume-averaged conservation equations for volume-of-fluid interface tracking. In Proceedings of the 4th International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Elhamady, A.K.M.A. Mitigation of Spurious Currents in Multiphase Flow Simulation at Low Capillary Numbers. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2022. [Google Scholar]
- Yu, M.L.; Giraldo, F.X.; Peng, M.; Wang, Z.J. Localized artificial viscosity stabilization of discontinuous Galerkin methods for nonhydrostatic mesoscale atmospheric modeling. Mon. Weather Rev. 2015, 143, 4823–4845. [Google Scholar] [CrossRef]
- Schwiebert, M.K.; Leong, W. Underfill flow as viscous flow between parallel plates driven by capillary action. In Proceedings of the Seventeenth IEEE/CPMT International Electronics Manufacturing Technology Symposium, Austin, TX, USA, 2–4 October 1995. [Google Scholar]
- Wan, J.W.; Zhang, W.J.; Bergstrom, D.J. An analytical model for predicting the underfill flow characteristics in flip-chip encapsulation. IEEE Trans. Adv. Packag. 2005, 28, 481–487. [Google Scholar] [CrossRef]
- Wan, J. Analysis and Modeling of Underfill Flow Driven by Capillary Action in Flip-Chip. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]
- Darbois Texier, B.; Laurent, P.; Stoukatch, S.; Dorbolo, S. Wicking through a confined micropillar array. Microfluid Nanofluid 2016, 20, 53. [Google Scholar] [CrossRef]
- Young, W.B. Modeling of a Non-Newtonian Flow Between Parallel Plates in a Flip Chip Encapsulation. Microelectron. Reliab. 2010, 50, 995–999. [Google Scholar] [CrossRef]
- Young, W.B. Effect on Filling Time for a Non-Newtonian Flow During the Underfilling of a Flip Chip. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 1048–1053. [Google Scholar] [CrossRef]
- Young, W.B. Non-Newtonian Flow Formulation of the Underfill Process in Flip-Chip Packaging. IEEE Trans. Compon. Packag. Manuf. Technol. 2011, 1, 2033–2037. [Google Scholar] [CrossRef]
- Wan, J.W.; Zhang, W.J.; Bergstrom, D.J. Numerical Modeling for the Underfill Flow in Flip-Chip Packaging. IEEE Trans. Compon. Packag. Technol. 2009, 32, 227–234. [Google Scholar] [CrossRef]
- Luo, W.; Liang, J.J.; Zhang, Y.; Zhou, H.M. The effect of gap height on non-Newtonian underfill flow in chip packaging: Experiments and simulations. In Proceedings of the 17th International Conference on Electronic Packaging Technology (ICEPT), Wuhan, China, 16–19 August 2016. [Google Scholar]
- Han, S.; Wang, K.K. Analysis of the Flow of Encapsulant During Underfill Encapsulation of Flip-Chips. IEEE Trans. Compon. Packag. 1997, 20, 424–433. [Google Scholar]
- Young, W.B. Capillary Impregnation into Cylinder Banks. J. Colloid Interface Sci. 2004, 273, 576–580. [Google Scholar] [CrossRef]
- Young, W.B.; Yang, W.L. Underfill of Flip-Chip: The Effect of Contact Angle and Solder Bump Arrangement. IEEE Trans. Adv. Packag. 2006, 29, 647–653. [Google Scholar] [CrossRef]






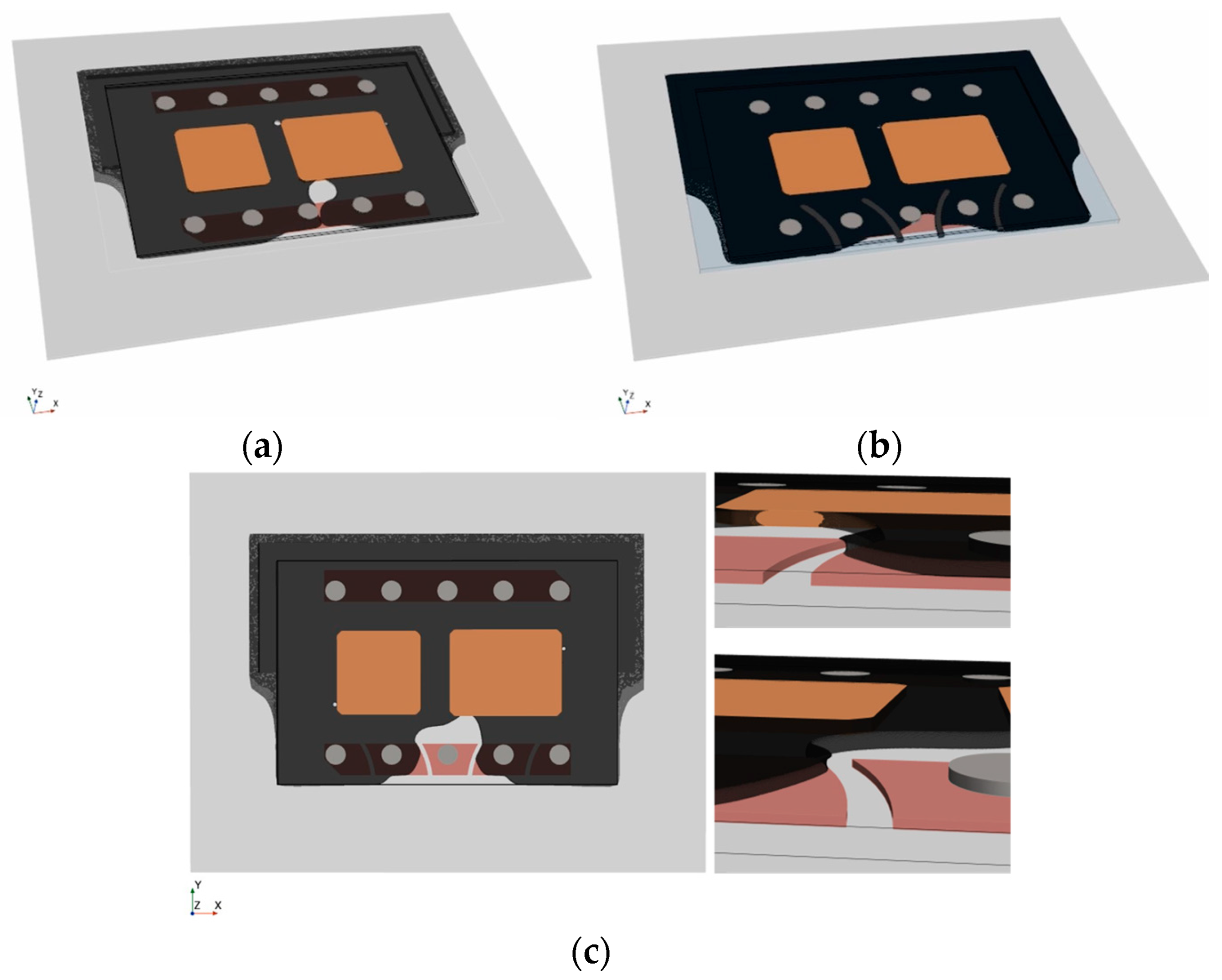
| Flow Calibration | IGBTs | Multi-Chip Module | |||
|---|---|---|---|---|---|
| FR4 | 800 µm | FR4 | 800 µm | FR4 | 800 µm |
| Al2O3 | 360 µm | Al2O3 | 360 µm | Al2O3 | 360 µm |
| - | - | Cu | 120 µm | - | - |
| 214 µm | SnSb5 | 110 µm | SnSb5 | 110 µm | |
| 430 µm | Sintered Ag | 80 µm | |||
| 12.7 mm × 21 mm 1 | 21 mm × 25.4 mm 1 | 25.4 mm × 38.6 mm 1 | |||
| Filler Type | Filler Content (%) | Max Particle (µm) | Density (kg/m³) | |
| Quartz | 67 | 1.5 | 1730 | |
| Viscosity | Power law fit | |||
| ) | n (1) | (1/s) | (1/s) | |
| (see Figure 2a) | 0.54 | 1.22 | 10 | 100 |
| Gelling effect at 60 °C, ): | ||||
| Surface Tension at 60 °C | (mN/m) | |||
| SFT | Dispersive | Polar | ||
| 25 | 24.52 | 0.22 | ||
| Contact angle at 60 °C (°) | ||||
| FR4 | Al2O3 | Cu | SnSb5 | Ag |
| 35 | 25 | 33 | 30 [30] | 25 [31] |
| Level-Set | VOF | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r = 2 | AMR | (s) | p | (s) | (h) | r = 2 | AMR | (s) | (s) | (h) | |
| 2 | 96.55 | 1.33 | 101.39 | 293.41 | 4 | 63.82 | 1.82 | 64.21 | 206.48 | ||
| 1 | 89.20 | 41.38 | 3 | 62.82 | 42.43 | ||||||
| 0 | 70.69 | 8.85 | 2 | 59.31 | 25.22 | ||||||
| 6.27% | 0.77% | ||||||||||
| 17.08% | 2.76% | ||||||||||
| Continua Model | Parameter | Previous Model | Modified Model |
|---|---|---|---|
| AMR | Max. Refinement Level | 3 | 3 |
| Transition Width | 6 | 6 | |
| Delta Time (s) | 0.1 | 0.1 | |
| ATS | Max. CFL Limit | 0.4 | 1.0 |
| Multiphase Interaction | Semi-implicit Surface Tension | enabled | Enabled |
| Interface Artificial Viscosity | 0.1 | 1.0 | |
| HRIC | 0.5 | 0.5 | |
| 1.0 | 1.0 | ||
| Sharpening Factor | 0.0 | 0.1 | |
| Angle Factor | 0.05 | 1.0 | |
| Segregated Flow | Enhanced Stability Treatment | enabled | enabled |
| URF Velocity | 0.8 | 0.8 | |
| URF Pressure | 0.2 | 0.2 | |
| Segregated VOF | Solution Strategy | Single-Step | Multi-Step |
| URF VOF | 0.9 | 0.9 | |
| Number of Steps | 1 | 3 |
| Flow Calibration | IGBTs | Multi-Chip Module | |||
|---|---|---|---|---|---|
| = 214 µm | 1.48% | U-shape | 2.55% | Dual-Chip | 2.84% |
| = 430 µm | 3.04% | Comparted | 3.34% | Valved MCM | 2.79% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stencel, L.C.; Strogies, J.; Müller, B.; Knofe, R.; Borwieck, C.; Heimann, M. Capillary Underfill Flow Simulation as a Design Tool for Flow-Optimized Encapsulation in Heterogenous Integration. Micromachines 2023, 14, 1885. https://doi.org/10.3390/mi14101885
Stencel LC, Strogies J, Müller B, Knofe R, Borwieck C, Heimann M. Capillary Underfill Flow Simulation as a Design Tool for Flow-Optimized Encapsulation in Heterogenous Integration. Micromachines. 2023; 14(10):1885. https://doi.org/10.3390/mi14101885
Chicago/Turabian StyleStencel, Lisa Christin, Jörg Strogies, Bernd Müller, Rüdiger Knofe, Carsten Borwieck, and Matthias Heimann. 2023. "Capillary Underfill Flow Simulation as a Design Tool for Flow-Optimized Encapsulation in Heterogenous Integration" Micromachines 14, no. 10: 1885. https://doi.org/10.3390/mi14101885
APA StyleStencel, L. C., Strogies, J., Müller, B., Knofe, R., Borwieck, C., & Heimann, M. (2023). Capillary Underfill Flow Simulation as a Design Tool for Flow-Optimized Encapsulation in Heterogenous Integration. Micromachines, 14(10), 1885. https://doi.org/10.3390/mi14101885








