Multiphysics Modeling and Analysis of Sc-Doped AlN Thin Film Based Piezoelectric Micromachined Ultrasonic Transducer by Finite Element Method
Abstract
:1. Introduction
2. PMUT Modeling and Simulation
2.1. FEM Modeling of PMUT
2.2. Evaluation of PMUT Properties
3. Results and Discussion
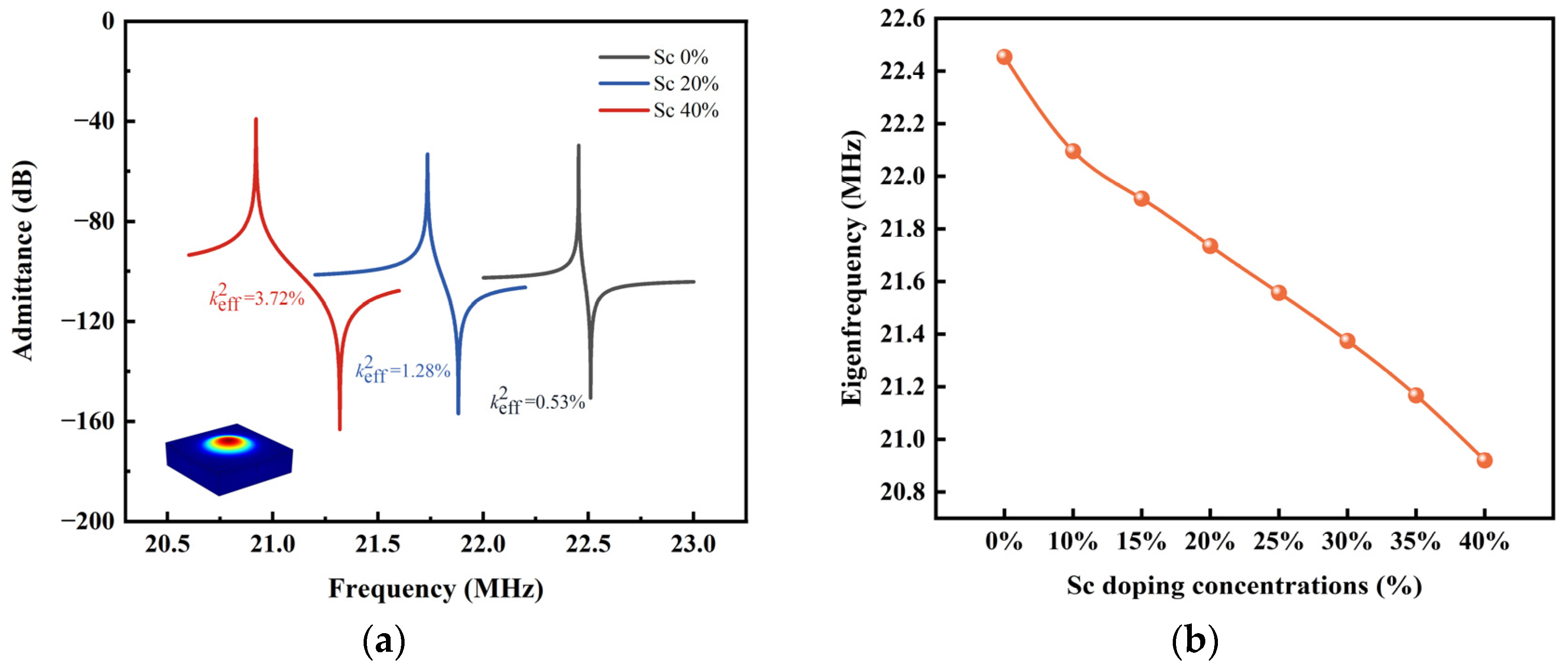
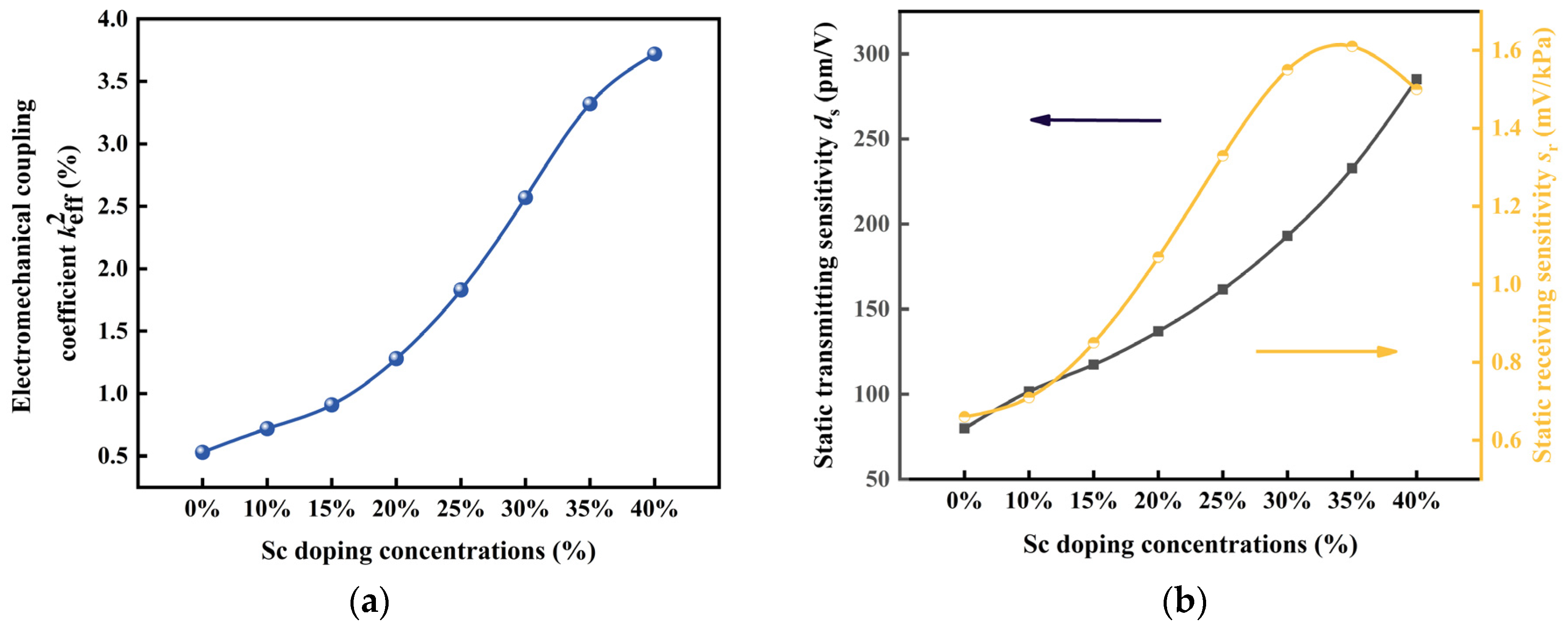
3.1. Effect of Sc Concentration on PMUT Cells
3.2. Design and Optimizing of PMUT Array
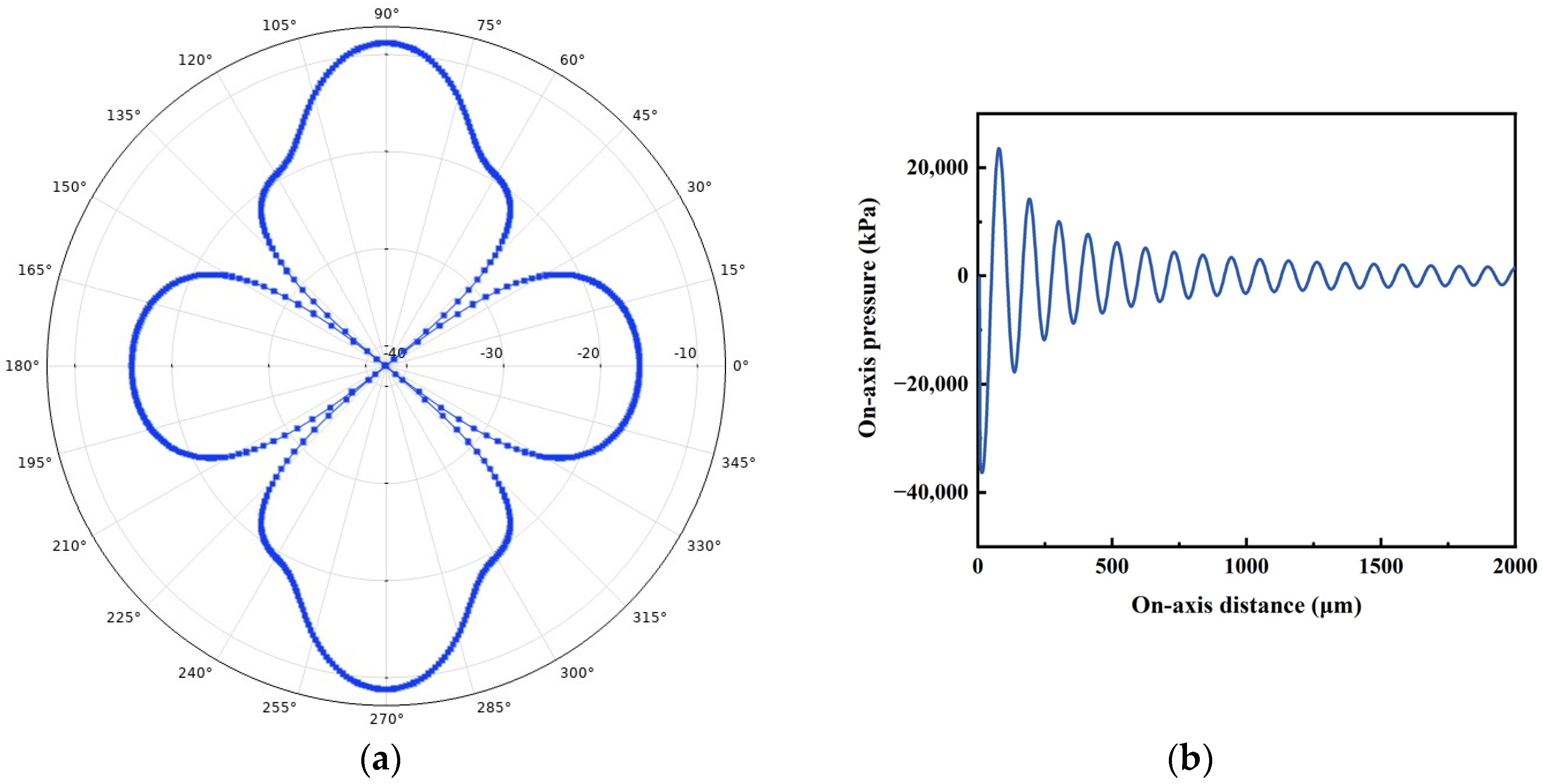
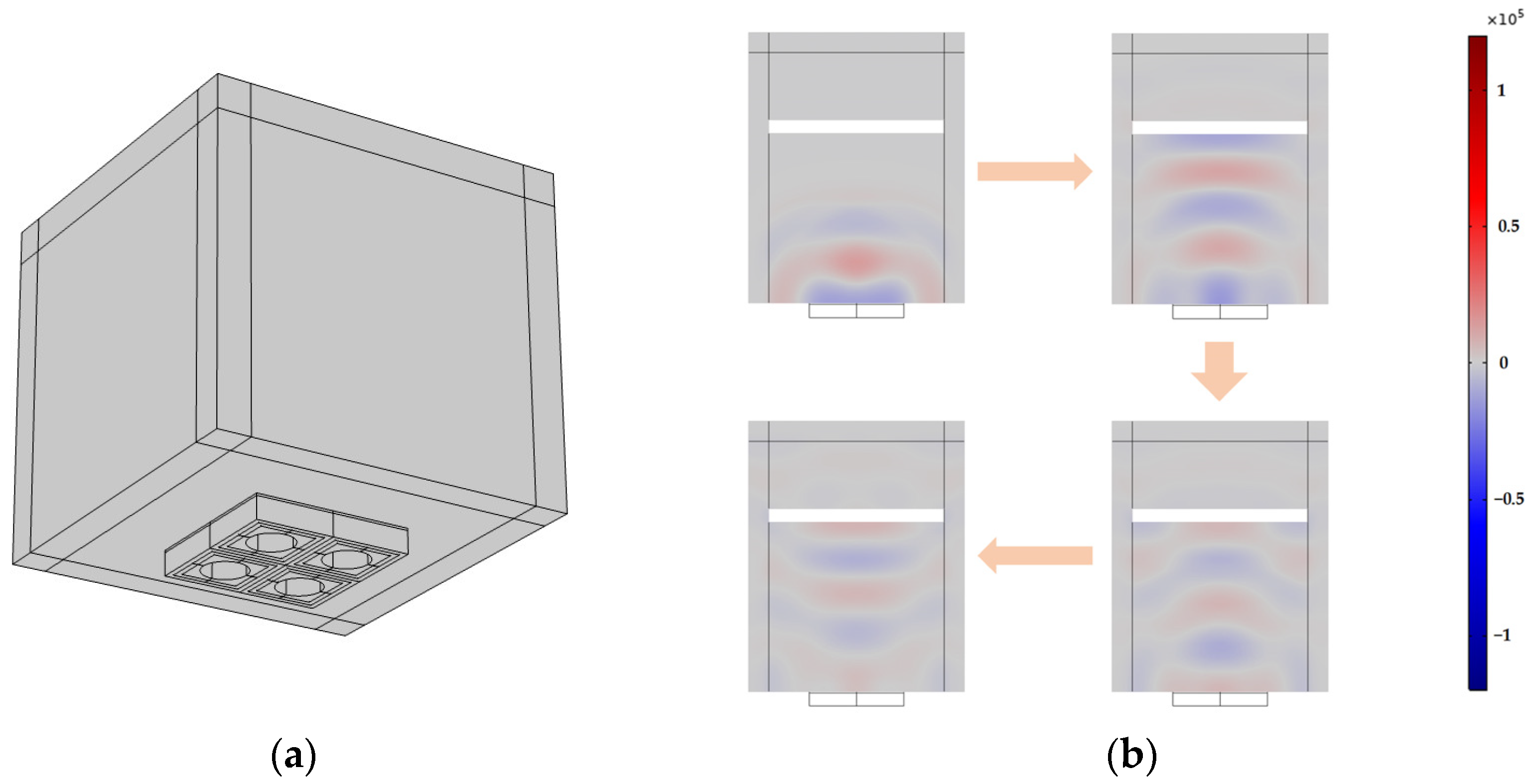
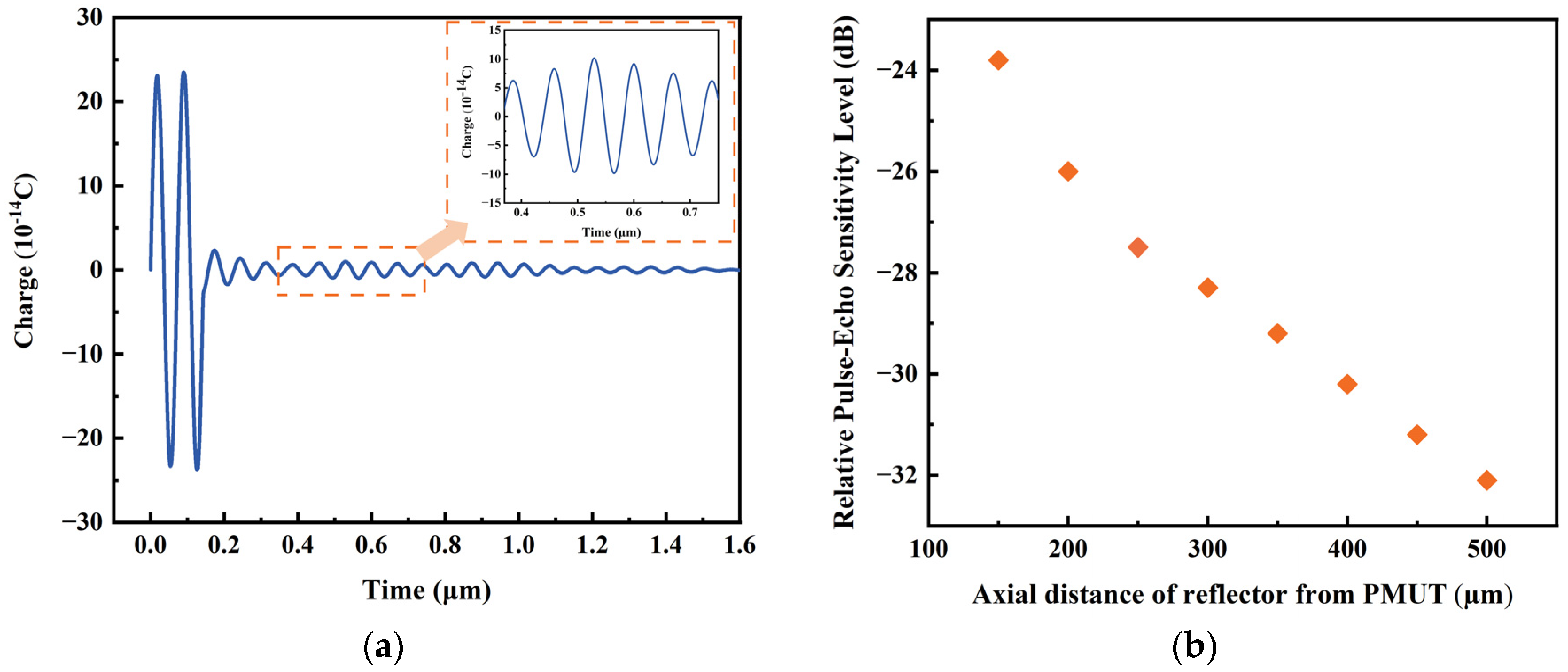
3.2.1. Static Analysis
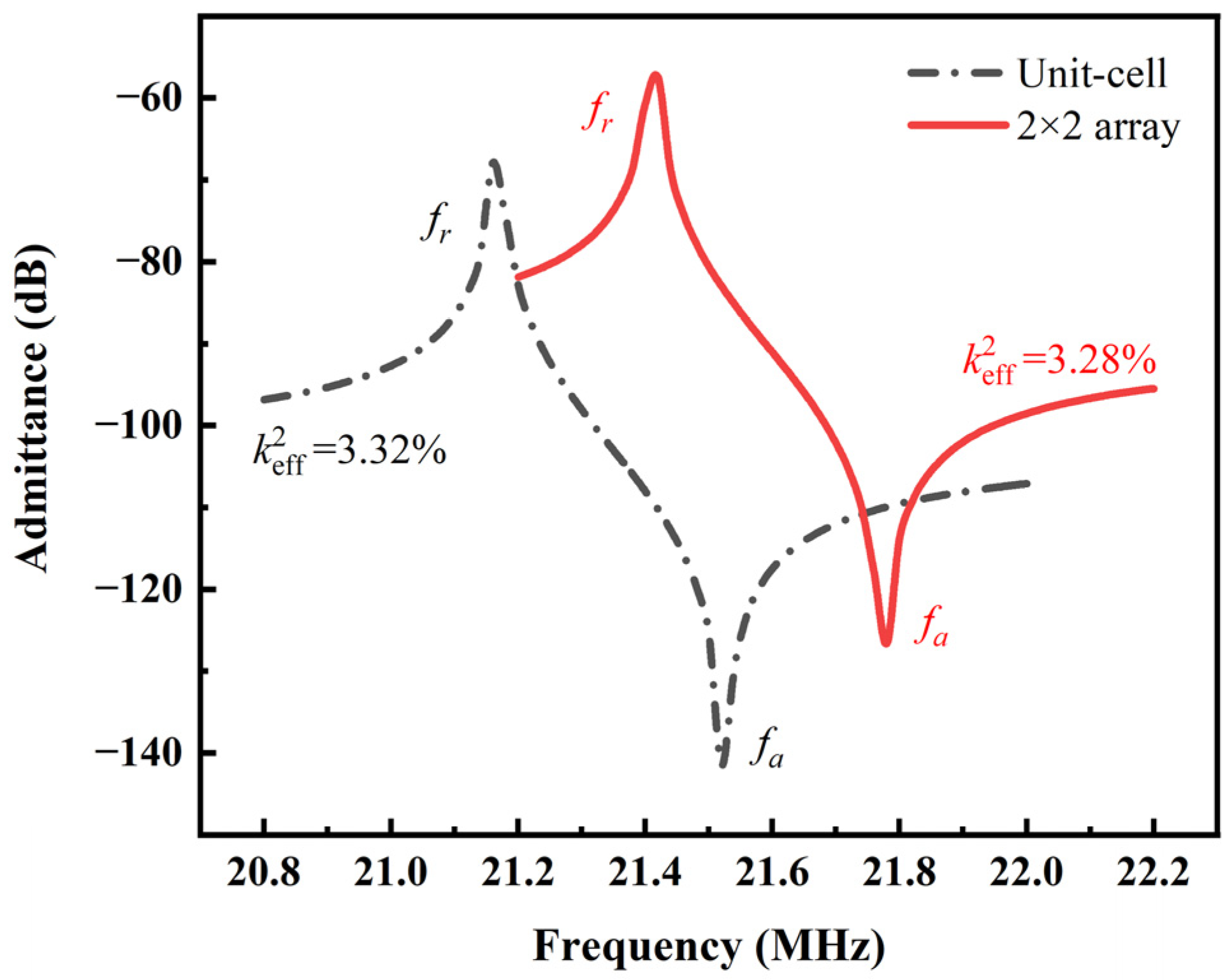
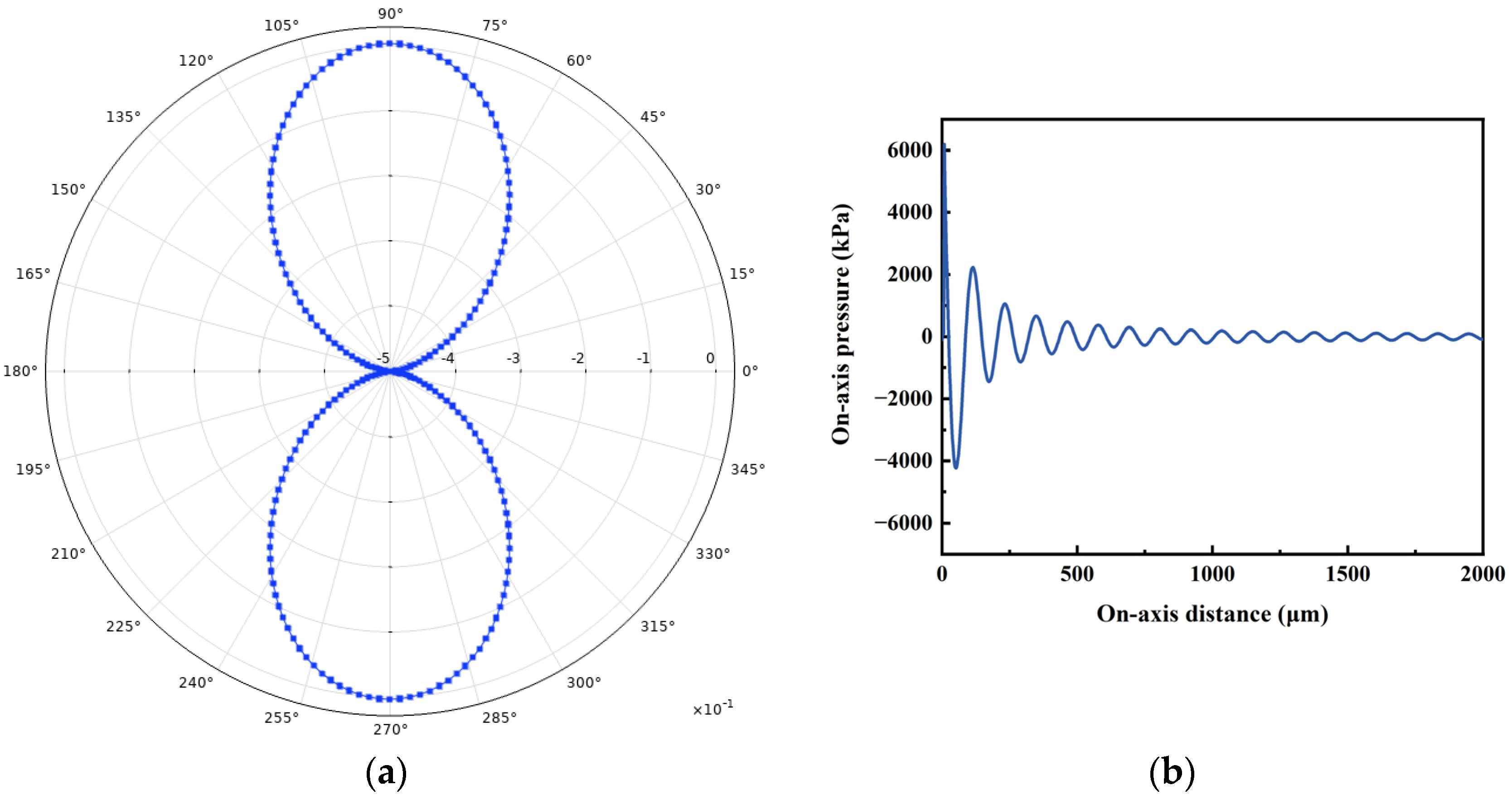
3.2.2. Dynamic Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Przybyla, R.J.; Shelton, S.E.; Guedes, A.; Izyumin, I.I.; Kline, M.H.; Horsley, D.A.; Boser, B.E. In-Air Rangefinding With an AlN Piezoelectric Micromachined Ultrasound Transducer. IEEE Sens. J. 2011, 11, 2690–2697. [Google Scholar] [CrossRef]
- Przybyla, R.J.; Tang, H.Y.; Shelton, S.E.; Horsley, D.A.; Boser, B.E. 12.1 3D ultrasonic gesture recognition. In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014; pp. 210–211. [Google Scholar]
- Arnau, A. Piezoelectric Transducer and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 99–116. [Google Scholar]
- Huang, D.H.; Wang, J.L.; Song, C.H.; Zhao, Y.J. Ultrasound-responsive matters for biomedical applications. Innovation 2023, 4, 100421. [Google Scholar] [CrossRef]
- Dausch, D.E.; Gilchrist, K.H.; Carlson, J.B.; Hall, S.D.; Castellucci, J.B.; von Ramm, O.T. In vivo real-time 3-D intracardiac echo using PMUT arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1754–1764. [Google Scholar] [CrossRef]
- Ferrer-Costa, C.; Gelpi, J.L.; Zamakola, L.; Parraga, I.; de la Cruz, X.; Orozco, M. PMUT: A web-based tool for the annotation of pathological mutations on proteins. Bioinformatics 2005, 21, 3176–3178. [Google Scholar] [CrossRef] [PubMed]
- Sadeghpour, S.; Kraft, M.; Puers, R. Design and fabrication strategy for an efficient lead zirconate titanate based piezoelectric micromachined ultrasound transducer. J. Micromech. Microeng. 2019, 29, 125002. [Google Scholar] [CrossRef]
- Qiu, Y.; Gigliotti, J.V.; Wallace, M.; Griggio, F.; Demore, C.E.; Cochran, S.; Trolier-McKinstry, S. Piezoelectric micromachined ultrasound transducer (PMUT) arrays for integrated sensing, actuation and imaging. Sensors 2015, 15, 8020–8041. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Chu, F.; Liu, X.; Li, Y.; Rong, J.; Jiang, H. AlN-based piezoelectric micromachined ultrasonic transducer for photoacoustic imaging. Appl. Phys. Lett. 2013, 103, 031118. [Google Scholar] [CrossRef]
- Smyth, K.; Bathurst, S.; Sammoura, F.; Kim, S.G. Analytic solution for N-electrode actuated piezoelectric disk with application to piezoelectric micromachined ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1756–1767. [Google Scholar] [CrossRef]
- Dangi, A.; Pratap, R. System level modeling and design maps of PMUTs with residual stresses. Sens. Actuators A Phys. 2017, 262, 18–28. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, H.; Wang, Q.; Fung, S.; Tsai, J.M.; Daneman, M.; Boser, B.E.; Horsley, D.A. Waveguide piezoelectric micromachined ultrasonic transducer array for short-range pulse-echo imaging. Appl. Phys. Lett. 2015, 106, 193506. [Google Scholar] [CrossRef]
- Chen, M.Z.; Zhang, Q.Z.; Zhao, X.Y.; Wang, F.F. Design and analysis of piezoelectric micromachined ultrasonic transducer using high coupling PMN-PT single crystal thin film for ultrasound imaging. Smart Mater. Struct. 2021, 30, 055006. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Z.; Yang, H.; Jiang, H.; Xie, H. A ceramic PZT-based PMUT array for endoscopic photoacoustic imaging. J. Microelectromech. Syst. 2020, 29, 1038–1043. [Google Scholar] [CrossRef] [PubMed]
- Akasheh, F.; Myers, T.; Fraser, J.D.; Bose, S.; Bandyopadhyay, A. Development of piezoelectric micromachined ultrasonic transducers. Sens. Actuators A Phys. 2004, 111, 275–287. [Google Scholar] [CrossRef]
- Akiyama, M.; Kamohara, T.; Kano, K.; Teshigahara, A.; Takeuchi, Y.; Kawahara, N. Enhancement of piezoelectric response in scandium aluminum nitride alloy thin films prepared by dual reactive cosputtering. Adv. Mater. 2009, 21, 593–596. [Google Scholar] [CrossRef] [PubMed]
- Shelton, S.; Chan, M.L.; Park, H. CMOS-compatible AlN piezoelectric micromachined ultrasonic transducers. In Proceedings of the 2009 IEEE International Ultrasonics Symposium, Rome, Italy, 20–23 September 2009; pp. 402–405. [Google Scholar]
- Akiyama, M.; Kano, K.; Teshigahara, A. Influence of growth temperature and scandium concentration on piezoelectric response of scandium aluminum nitride alloy thin films. Appl. Phys. Lett. 2009, 95, 162107. [Google Scholar] [CrossRef]
- Lu, Y.; Reusch, M.; Kurz, N.; Ding, A.; Christoph, T.; Prescher, M.; Kirste, L.; Ambacher, O. Elastic modulus and coefficient of thermal expansion of piezoelectric Al1−xScxN (up to x = 0.41) thin films. APL Mater. 2018, 6, 076105. [Google Scholar] [CrossRef]
- Choi, H.S.; Ding, J.L.; Bandyopadhyay, A.; Anderson, M.J.; Bose, S. Characterization and modeling of a piezoelectric micromachined ultrasonic transducer with a very large length/width aspect ratio. J. Micromech. Microeng. 2008, 18, 025037. [Google Scholar] [CrossRef]
- Lu, Y.; Horsley, D.A. Modeling, fabrication, and characterization of piezoelectric micromachined ultrasonic transducer arrays based on cavity SOI wafers. J. Microelectromech. Syst. 2015, 24, 1142–1149. [Google Scholar] [CrossRef]
- Muralt, P.; Ledermann, N.; Paborowski, J.; Barzegar, A.; Gentil, S.; Belgacem, B.; Petitgrand, S.; Bosseboeuf, A.; Setter, N. T Piezoelectric micromachined ultrasonic transducers based on PZT thin films. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 2276–2288. [Google Scholar] [CrossRef]
- Caro, M.A.; Zhang, S.; Riekkinen, T.; Ylilammi, M.; Moram, M.A.; Lopez-Acevedo, O.; Molarius, J.; Laurila, T. Piezoelectric coefficients and spontaneous polarization of ScAlN. J. Phys. Condens. Matter 2015, 27, 245901. [Google Scholar] [CrossRef]
- Haider, S.T.; Shah, M.A.; Lee, D.; Hur, S. A Review of the Recent Applications of Aluminum Nitride-Based Piezoelectric Devices. IEEE Access J. 2023, 11, 58779–58795. [Google Scholar] [CrossRef]
- Chen, M.Z.; Zhang, Q.Z.; Zhao, X.Y.; Wang, F.F. Modeling and simulation of aluminum nitride-based piezoelectric micromachined ultrasonic transducer for ultrasound imaging. In Proceedings of the 2019 14th Symposium on Piezoelectricity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019; pp. 1–5. [Google Scholar]
- Meeker, T.R. Publication and proposed revision of ANSI/IEEE standard 176–1987. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 717–772. [Google Scholar]
- Guo, J.Q.; Liu, C.C.; Tao, H.; Miao, J.M. Model of scandium doped aluminum nitride based PMUT with high transmitting performance. In Proceedings of the 2017 Symposium on Piezoelectricity, Acoustic Waves and Device Applications (SPAWDA), Chengdu, China, 27–30 October 2017; pp. 211–216. [Google Scholar]
- Lu, Y.; Tang, H.Y.; Fung, S.; Boser, B.E.; Horsley, D.A. Pulse-echo ultrasound imaging using an AlN piezoelectric micromachined ultrasonic transducer array with transmit beam-forming. J. Microelectromech. Syst. 2015, 25, 179–187. [Google Scholar] [CrossRef]
- Peng, J.; Lau, S.T.; Chao, C.; Dai, J.Y.; Chan, H.L.W.; Luo, H.S.; Zhu, B.P.; Zhou, Q.F.; Shung, K.K. PMN-PT single crystal thick films on silicon substrate for high-frequency micromachined ultrasonic transducers. Appl. Phys. A 2010, 98, 233. [Google Scholar] [CrossRef]
- Mikaël, W.; Alexandre, R.; Vincent, L.; Raphaël, A.; William, D. Three-dimensional modelling of micromachined-ultrasonic-transducer arrays operating in water. Ultrasonics 2005, 43, 457–465. [Google Scholar]
- Zhang, Y.; Yan, X.-H.; Liao, W.-B.; Zhao, K. Effects of Nitrogen Content on the Structure and Mechanical Properties of (Al0.5CrFeNiTi0.25)Nx High-Entropy Films by Reactive Sputtering. Entropy 2018, 20, 624. [Google Scholar] [CrossRef]
- Liao, W.B.; Lan, S.; Gao, L.B.; Zhang, H.T.; Xu, S.; Song, J.; Wang, X.L.; Lu, Y. Nanocrystalline high-entropy alloy (CoCrFeNiAl0.3) thin-film coating by magnetron sputtering. Thin Solid Film 2017, 638, 383–388. [Google Scholar] [CrossRef]


| Material Coefficient | PZT | AlN |
|---|---|---|
| 200–400 | ||
| Parameter | Value |
|---|---|
| Thickness of top Pt | 200 nm |
| Thickness of ScAlN | 780 nm |
| Thickness of bottom Mo | 190 nm |
| Thickness of SiO2 | 350 μm |
| Thickness of the top layer Si | 2 μm |
| Thickness of SiO2 | 1 μm |
| Radius of top Pt | 20 μm |
| Side length of ScAlN | 50 μm |
| Radius of etching | 20 μm |
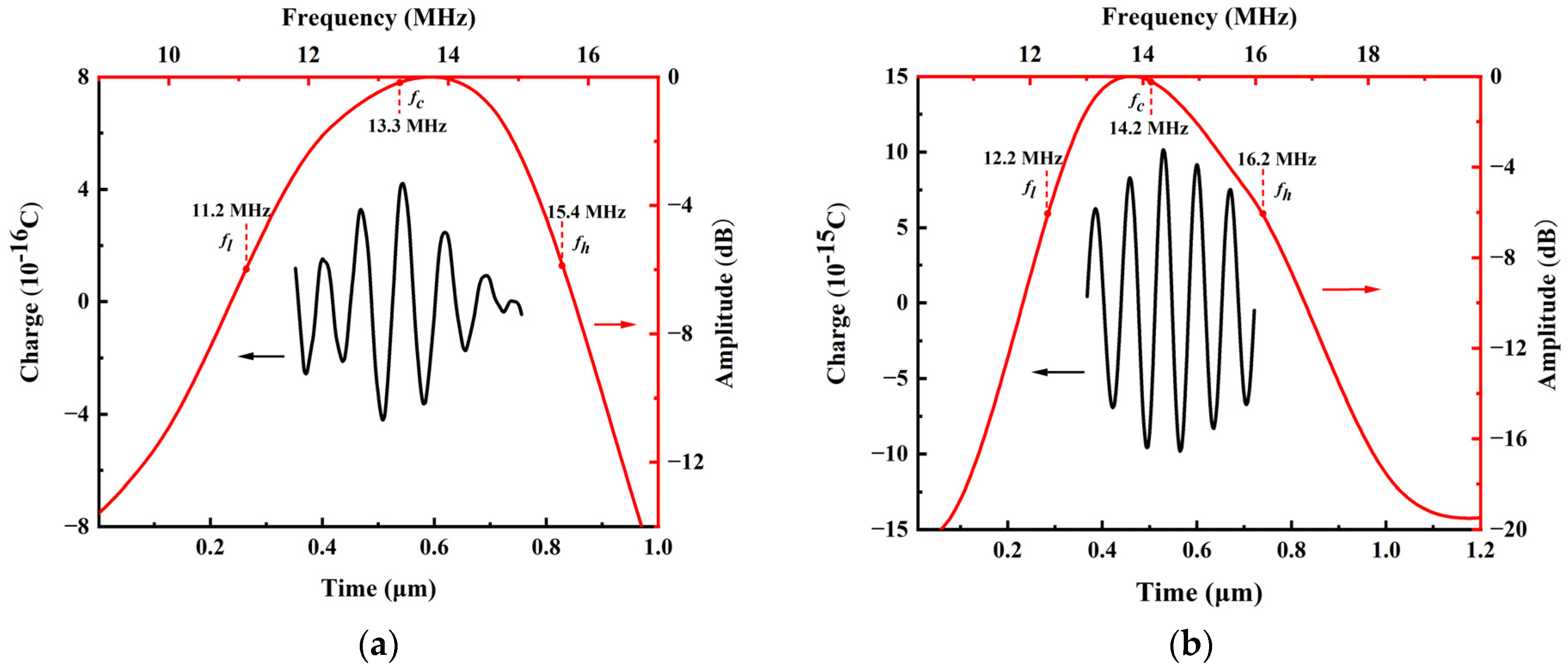
| Parameter | 35% Sc PMUT Cell | 35% Sc 2 × 2 PMUT Array |
|---|---|---|
| Relative pulse-echo sensitivity level (dB) | −43 | −27 |
| Lower/upper −6 dB (MHz) | 11.2/15.4 | 12.2/16.2 |
| Center frequency (MHz) | 13.3 | 14.2 |
| Bandwidth (−6 dB) | 31.6% | 28.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhang, Q.; Chen, M.; Liu, Y.; Zhu, J.; Yang, J.; Wang, F.; Tang, Y.; Zhao, X. Multiphysics Modeling and Analysis of Sc-Doped AlN Thin Film Based Piezoelectric Micromachined Ultrasonic Transducer by Finite Element Method. Micromachines 2023, 14, 1942. https://doi.org/10.3390/mi14101942
Liu X, Zhang Q, Chen M, Liu Y, Zhu J, Yang J, Wang F, Tang Y, Zhao X. Multiphysics Modeling and Analysis of Sc-Doped AlN Thin Film Based Piezoelectric Micromachined Ultrasonic Transducer by Finite Element Method. Micromachines. 2023; 14(10):1942. https://doi.org/10.3390/mi14101942
Chicago/Turabian StyleLiu, Xiaonan, Qiaozhen Zhang, Mingzhu Chen, Yaqi Liu, Jianqiu Zhu, Jiye Yang, Feifei Wang, Yanxue Tang, and Xiangyong Zhao. 2023. "Multiphysics Modeling and Analysis of Sc-Doped AlN Thin Film Based Piezoelectric Micromachined Ultrasonic Transducer by Finite Element Method" Micromachines 14, no. 10: 1942. https://doi.org/10.3390/mi14101942
APA StyleLiu, X., Zhang, Q., Chen, M., Liu, Y., Zhu, J., Yang, J., Wang, F., Tang, Y., & Zhao, X. (2023). Multiphysics Modeling and Analysis of Sc-Doped AlN Thin Film Based Piezoelectric Micromachined Ultrasonic Transducer by Finite Element Method. Micromachines, 14(10), 1942. https://doi.org/10.3390/mi14101942






