Research on an Enhanced Detuned-Loading Effect in Integrated Two-Section DFB Lasers with High Modulation Bandwidths
Abstract
:1. Introduction
2. Principle and Design
2.1. Principle of the REC Technique
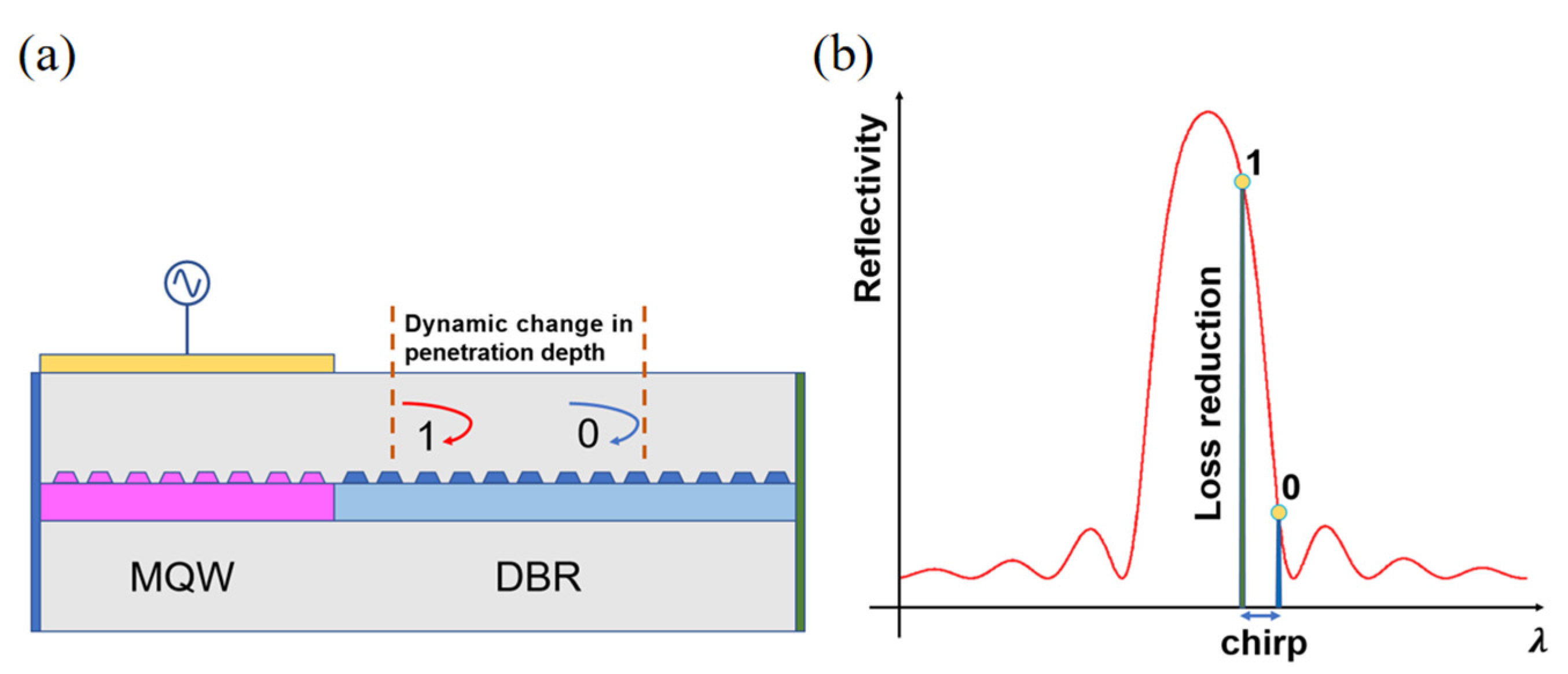
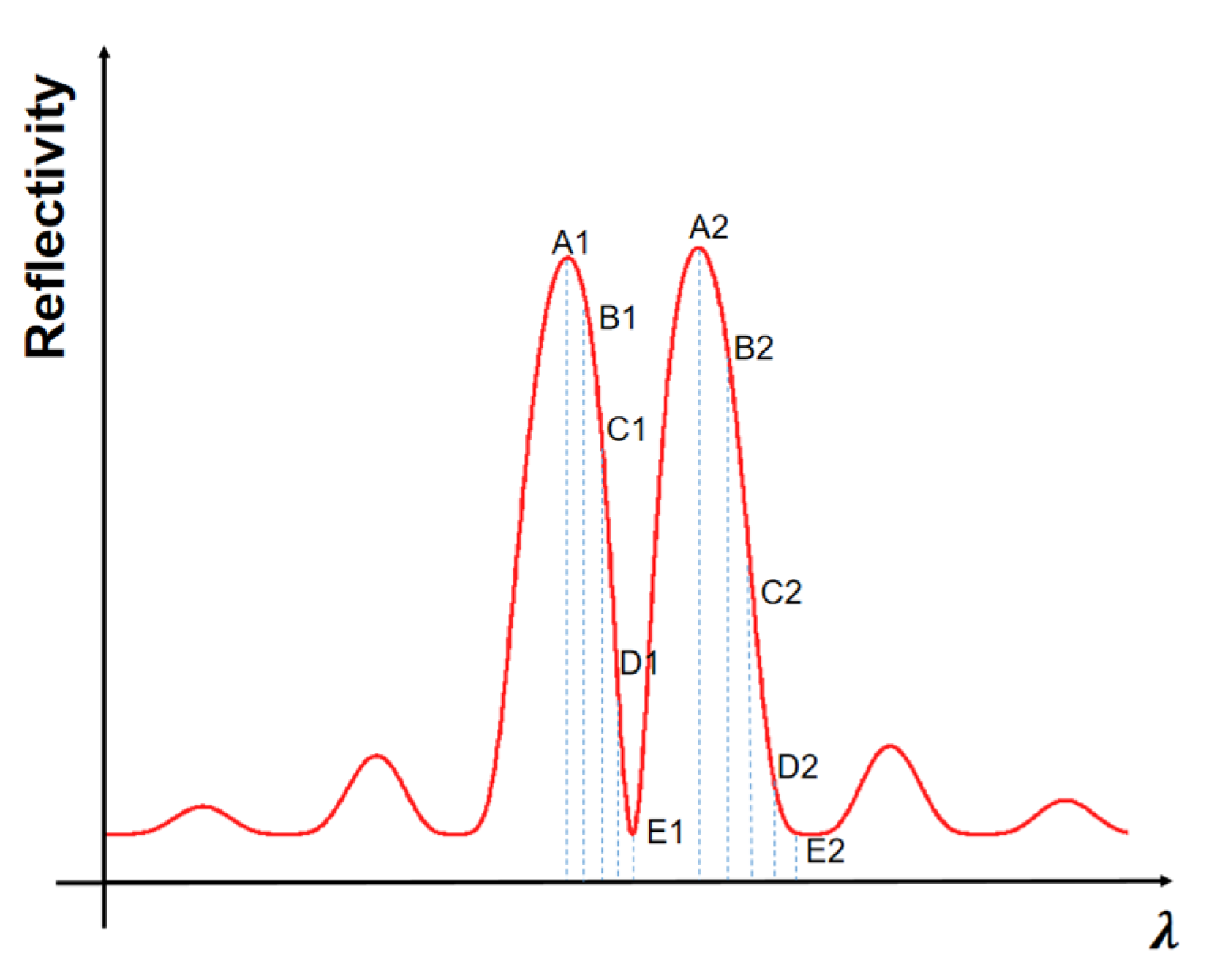
2.2. Principle of the Detuned-Loading Effect
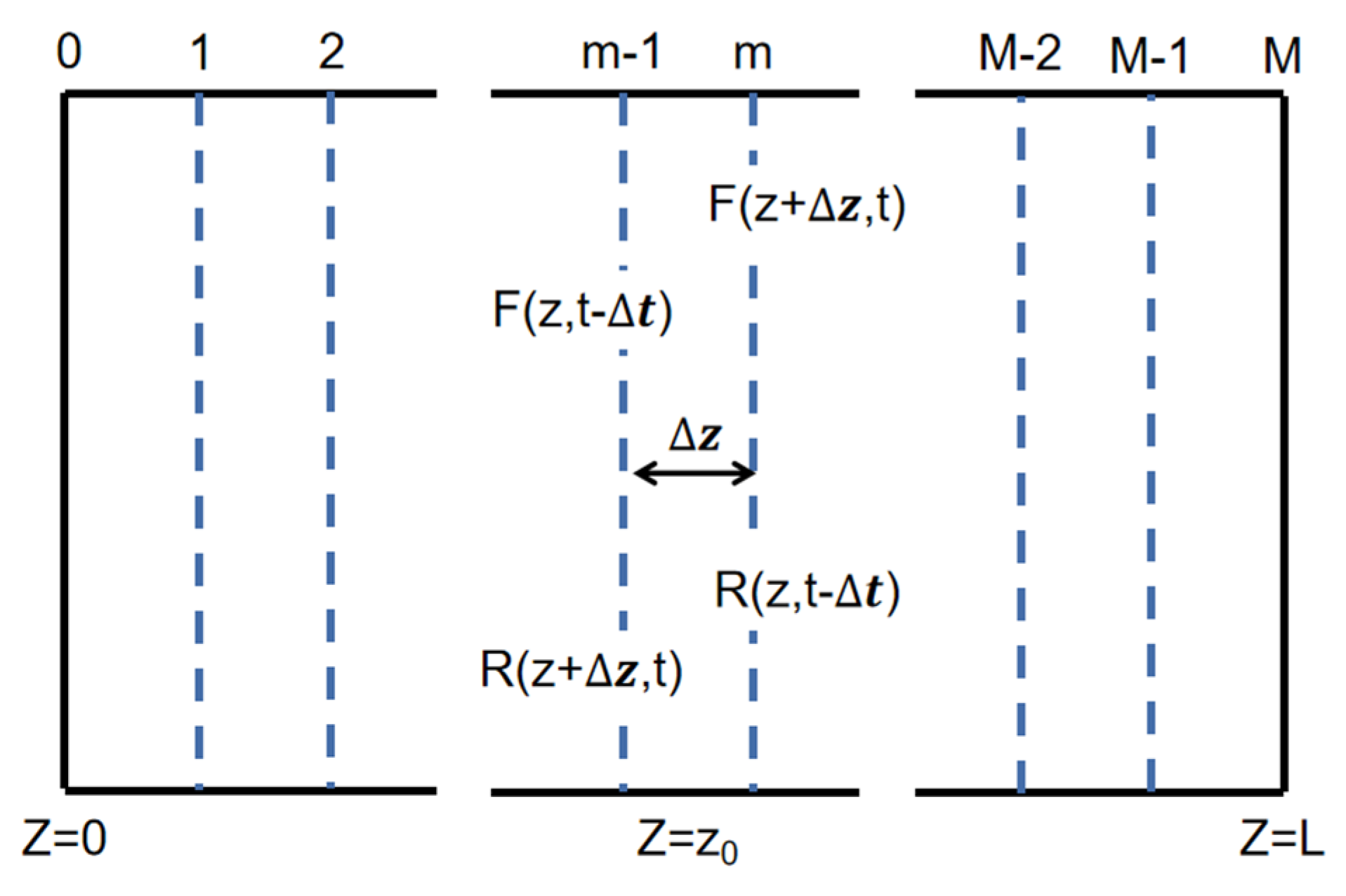
2.3. Principle of the Simulation
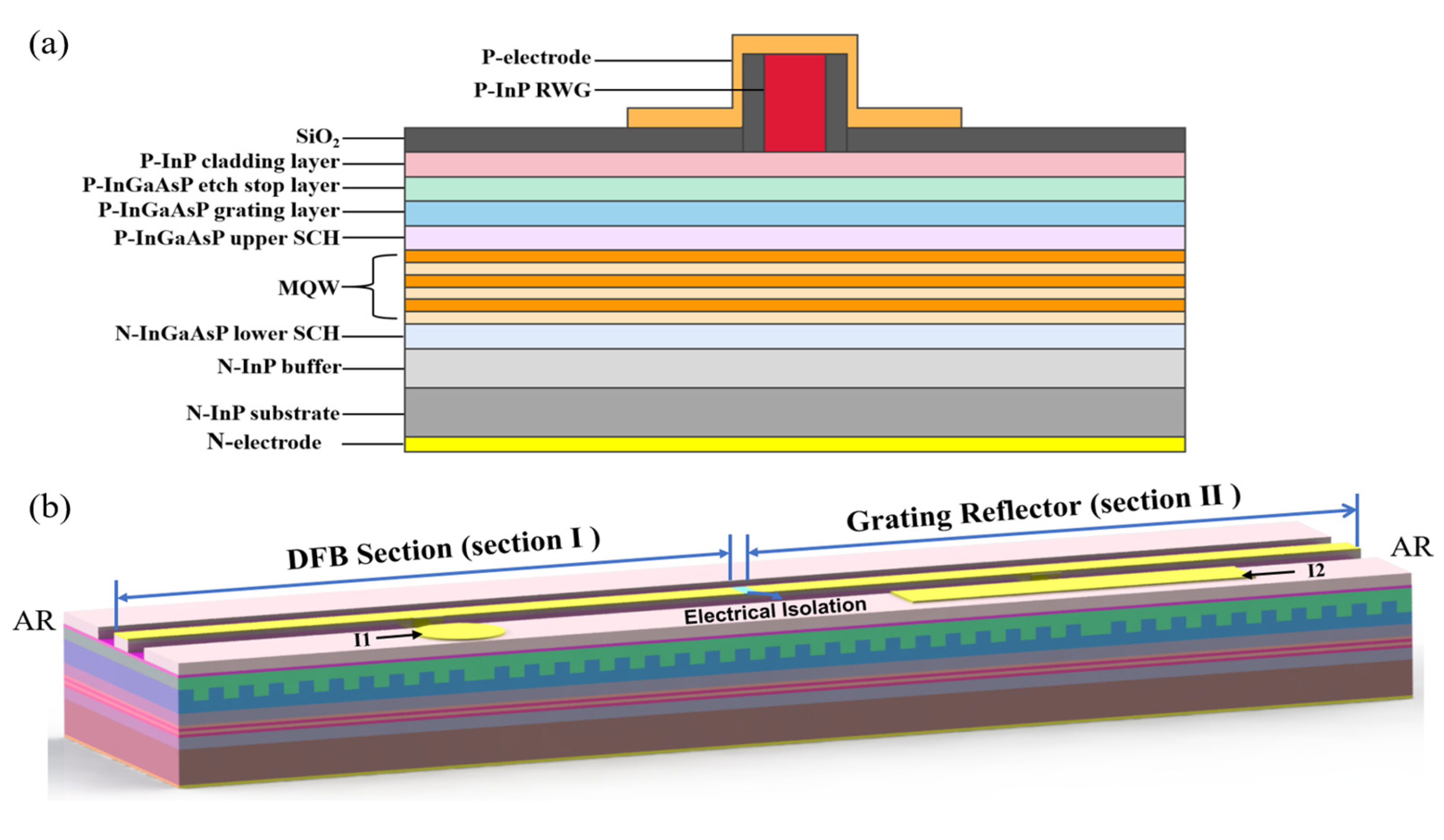
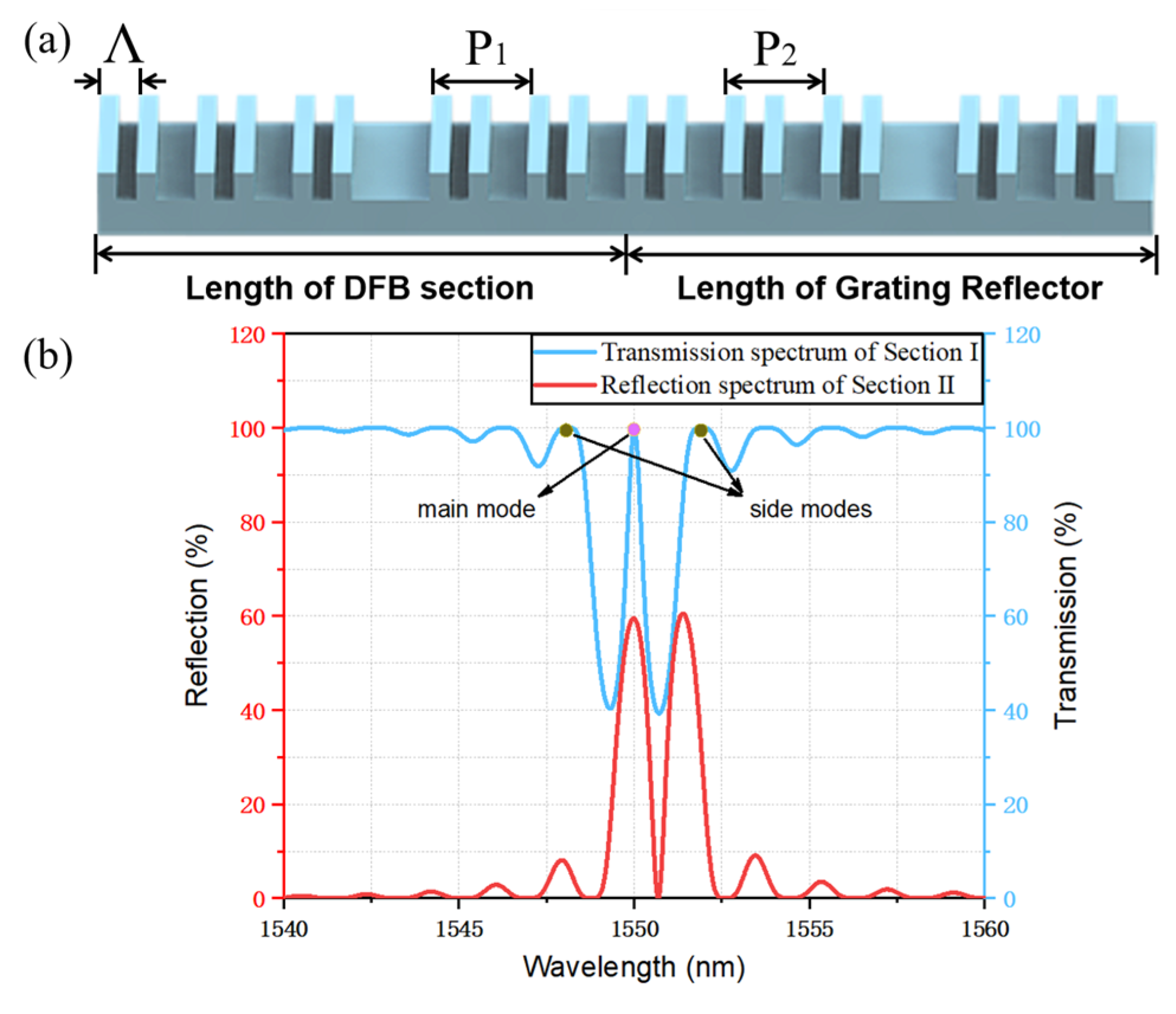
2.4. The Design of the TS-DFB Laser
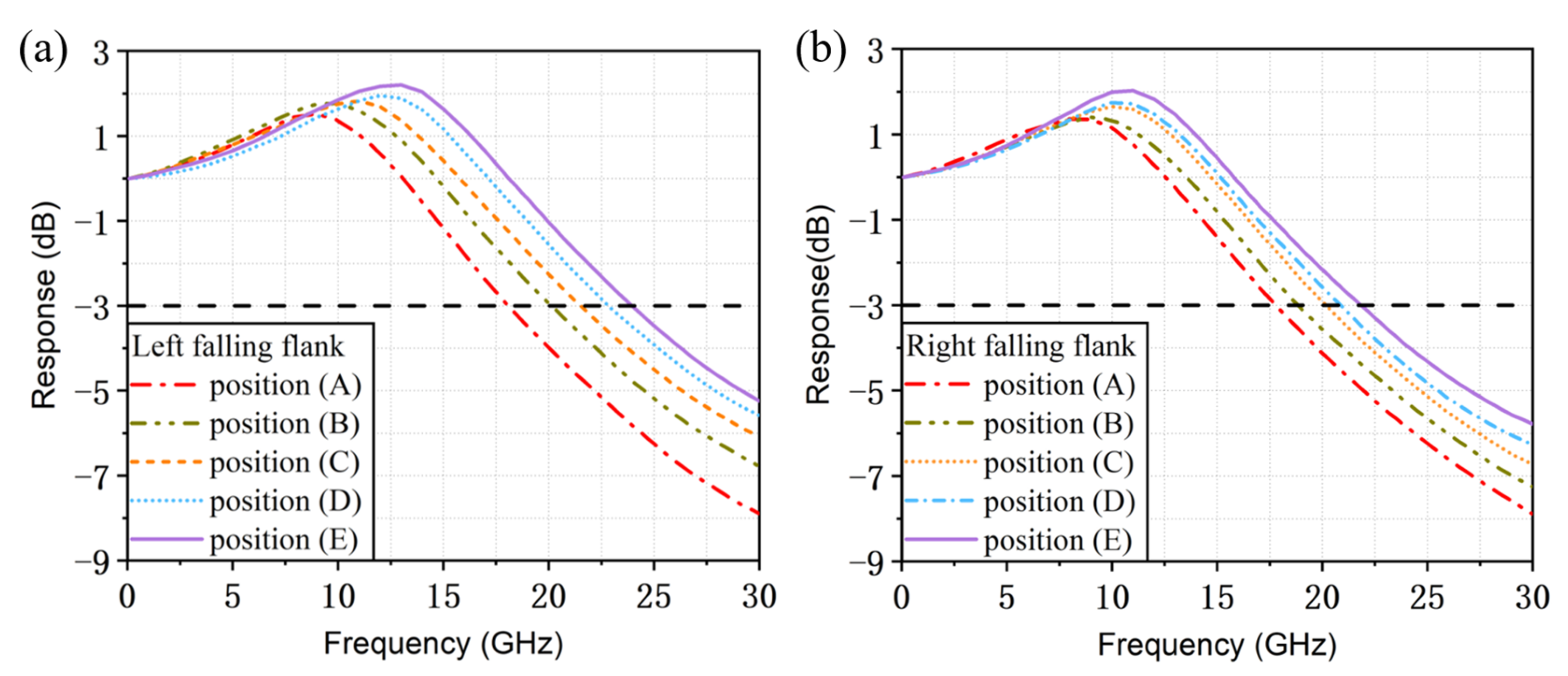
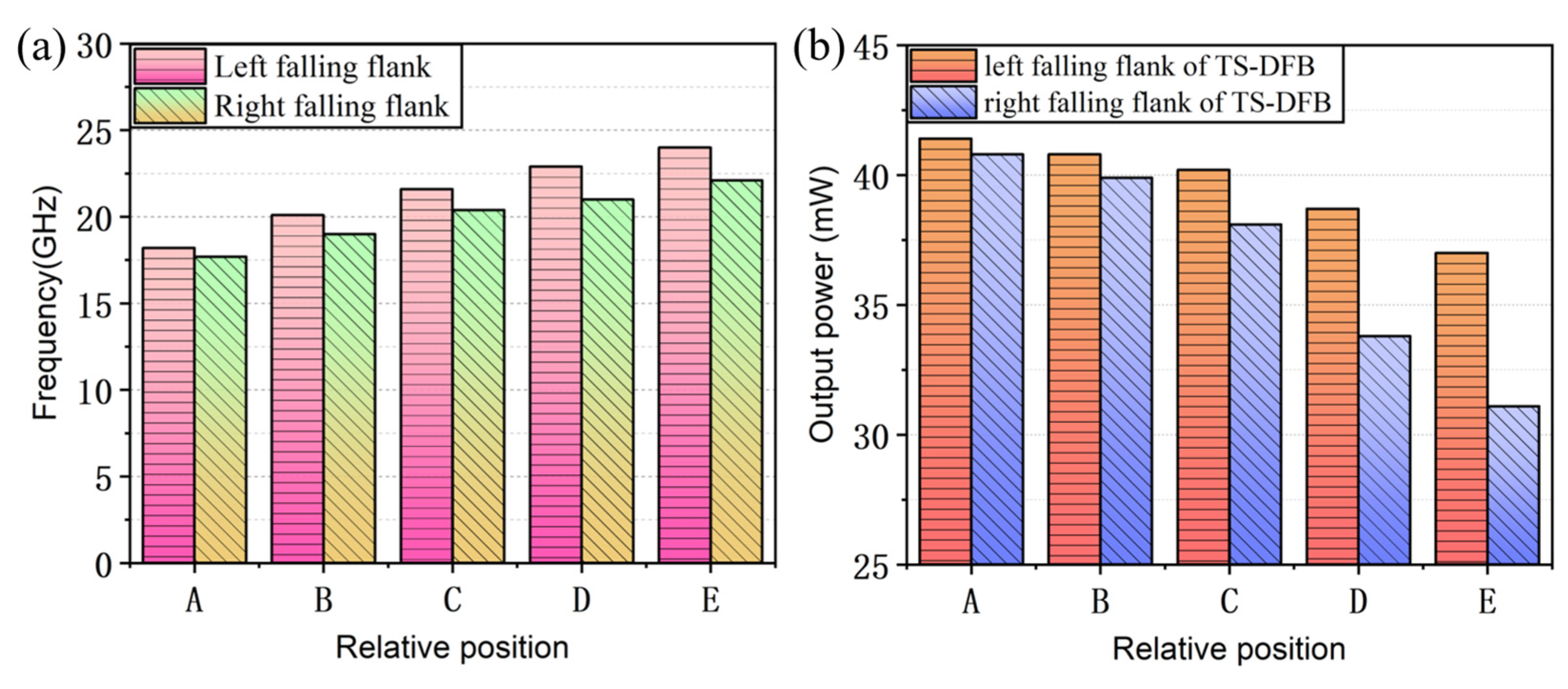
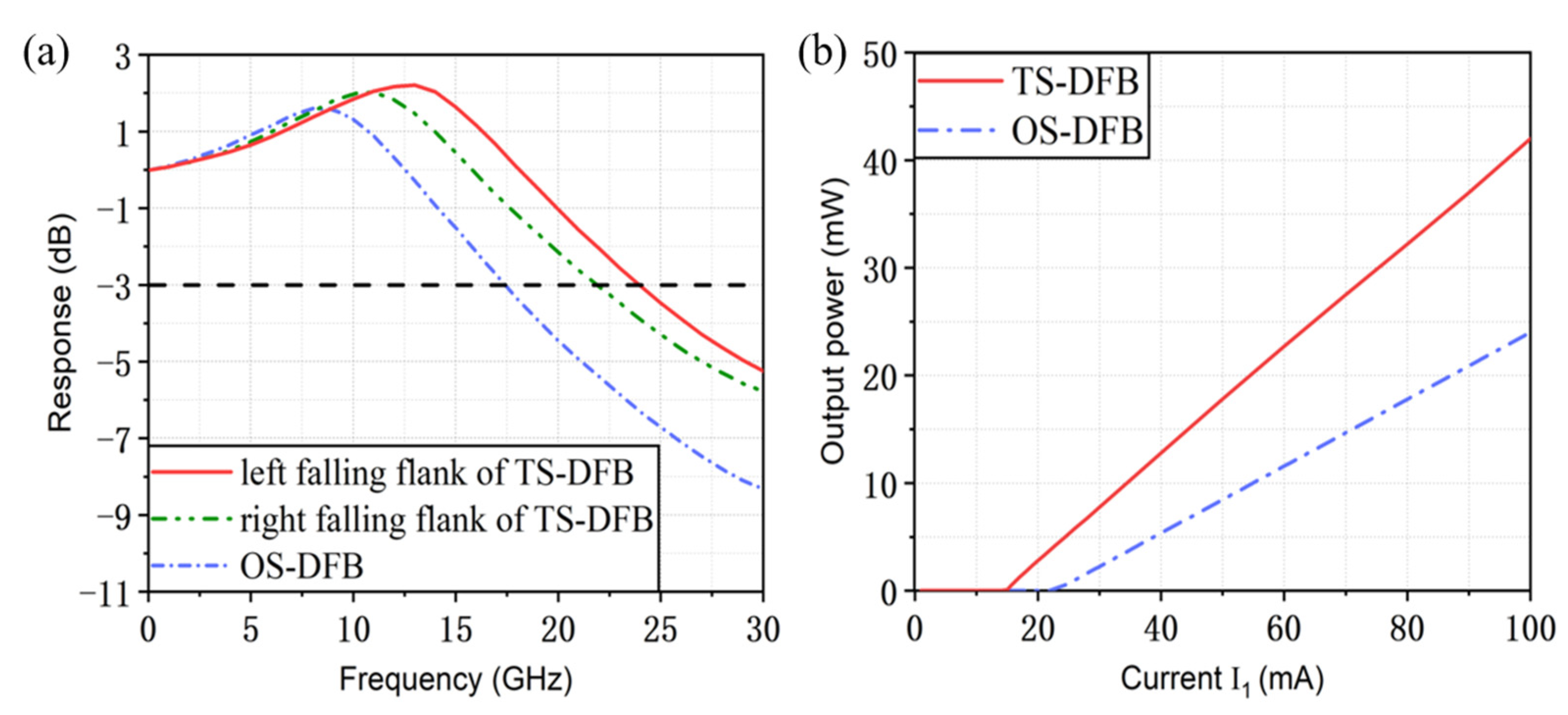
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ReferencesTakiguchi, T.; Hanamaki, Y.; Kadowaki, T.; Tanaka, T.; Takemi, M.; Tomita, N.; Mihashi, Y.; Omura, E. High speed 1.3-μm AlGaInAs DFB-LD with lambda/4-shift grating. In Proceedings of the 2001 International Conference on Indium Phosphide and Related Materials, Nara, Japan, 14–18 May 2001. [Google Scholar]
- Kobayashi, W.; Tadokoro, T.; Ito, T.; Fujisawa, T.; Yamanaka, T.; Shibata, Y.; Kohtoku, M. High-speed operation at 50 Gb/s and 60-km SMF transmission with 1.3-μm InGaAlAs-based DML. In Proceedings of the ISLC 2012 International Semiconductor Laser Conference, San Diego, CA, USA, 7–10 October 2012. [Google Scholar]
- Zhang, C.; Srinivasan, S.; Tang, Y.; Heck, M.J.; Davenport, M.L.; Bowers, J.E. Low threshold and high speed short cavity distributed feedback hybrid silicon lasers. Opt. Express 2014, 22, 10202–10209. [Google Scholar] [CrossRef] [PubMed]
- Uomi, K.; Nakano, H.; Chinone, N. Ultrahigh-speed 1.55-μm lambda/4-shifted DFB PIQ-BH lasers with bandwidth of 17 GHz. Electron. Lett. 1989, 10, 668–669. [Google Scholar] [CrossRef]
- Matsuda, M.; Uetake, A.; Simoyama, T.; Okumura, S.; Takabayashi, K.; Ekawa, M.; Yamamoto, T. 1.3-μm-Wavelength AlGaInAs Multiple-Quantum-Well Semi-Insulating Buried-Heterostructure Distributed-Reflector Laser Arrays on Semi-Insulating InP Substrate. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 241–247. [Google Scholar] [CrossRef]
- Nakahara, K.; Wakayama, Y.; Kitatani, T.; Taniguchi, T.; Fukamachi, T.; Sakuma, Y.; Tanaka, S. Direct Modulation at 56 and 50 Gb/s of 1.3-μm InGaAlAs Ridge-Shaped-BH DFB Lasers. IEEE Photon. Technol. Lett. 2015, 27, 534–536. [Google Scholar] [CrossRef]
- Oberg, M.; Kjebon, O.; Lourdudoss, S.; Nilsson, S.; Backbom, L.; Streubel, K.; Wallin, J. Increased modulation bandwidth up to 20 GHz of a detuned-loaded DBR laser. IEEE Photon. Technol. Lett. 1994, 6, 161–163. [Google Scholar] [CrossRef]
- Kjebon, O.; Schatz, R.; Carlsson, C.; Akram, M.N. Experimental evaluation of detuned loading effects on distortion in edge emitting DBR lasers. In Proceedings of the 2002 International Topical Meeting on Microwave Photonics, Awaji, Japan, 5–8 November 2002. [Google Scholar]
- Chaciński, M.; Schatz, R. Impact of Losses in the Bragg Section on the Dynamics of Detuned Loaded DBR Lasers. IEEE J. Quantum Electron. 2010, 46, 1360–1367. [Google Scholar] [CrossRef]
- Matsui, Y.; Schatz, R.; Carey, G.; Sudo, T.; Roxlo, C. Direct modulation laser technology toward 50-GHz bandwidth. In Proceedings of the 2016 International Semiconductor Laser Conference, Kobe, Japan, 12–15 September 2016. [Google Scholar]
- Xu, Y.; Gu, H.; Fang, T.; Li, L.; Nie, Y.; Zhang, Y. Direct Modulation Bandwidth Improvement in Two-section DFB Lasers Based on the Detuned Loading Effect. In Proceedings of the 2022 Asia Communications and Photonics Conference, Shenzhen, China, 5–8 November 2022. [Google Scholar]
- Sun, C.; Liu, D.; Xiong, B.; Luo, Y.; Wang, J.; Hao, Z.; Han, Y.; Wang, L.; Li, H. Modulation Characteristics Enhancement of Monolithically Integrated Laser Diodes Under Mutual Injection Locking. IEEE J. Sel. Top. Quant. 2015, 21, 628–635. [Google Scholar] [CrossRef]
- Mao, Y.; Ren, Z.; Zhang, R.; Wang, H.; Huang, Y.; Ji, C.; Kan, Q.; Wang, W. Extending the direct modulation bandwidth by mutual injection locking in integrated coupled DFB lasers. In Proceedings of the 2017 IEEE Photonics Conference, Orlando, FL, USA, 1–5 October 2017. [Google Scholar]
- Zhao, W.; Mao, Y.; Lu, D.; Huang, Y.; Zhao, L.; Kan, Q.; Wang, W. Modulation Bandwidth Enhancement of Monolithically Integrated Mutually Coupled Distributed Feedback Laser. Appl. Sci. 2020, 10, 4375. [Google Scholar] [CrossRef]
- Matsui, Y.; Pham, T.; Ling, W.A.; Schatz, R.; Carey, G.; Daghighian, H.; Sudo, T.; Roxlo, C. 55-GHz bandwidth short-cavity distributed reflector laser and its application to 112-Gb/s PAM-4. In Proceedings of the 2016 Optical Fiber Communications Conference and Exhibition, Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Yamaoka, S.; Diamantopoulos, N.P.; Nishi, H.; Nakao, R.; Fujii, T.; Takeda, K.; Hiraki, T.; Kanazawa, S.; Tanobe, H.; Kakitsuka, T.; et al. 239.3-Gbit/s net rate PAM-4 transmission using directly modulated membrane lasers on high-thermal-conductivity SiC. In Proceedings of the 45th European Conference on Optical Communication, Dublin, Ireland, 22–26 September 2019. [Google Scholar]
- Che, D.; Matsui, Y.; Schatz, R.; Rodes, R.; Khan, F.; Kwakernaak, M.; Sudo, T. 200-Gb/s Direct Modulation of a 50-GHz Class Laser with Advanced Digital Modulations. J. Light. Technol. 2021, 39, 845–852. [Google Scholar] [CrossRef]
- Sulikhah, S.; Tsao, H.W. Improvement on Direct Modulation Responses and Stability by Partially Corrugated Gratings Based DFB Lasers With Passive Feedback. IEEE Photonics J. 2021, 13, 4900214. [Google Scholar] [CrossRef]
- Lu, L.; Shi, Y.; Chen, X. Four channel DFB laser array based on the reconstruction-equivalent-chirp technique for 1.3 µm CWDM systems. In Proceedings of the 2013 Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference, Anaheim, CA, USA, 17–21 March 2013. [Google Scholar]
- Li, L.; Lu, L.; Li, S.; Guo, R.; Shi, Y.; Chen, X. Phase-shifted distributed feedback laser with linearly chirped grating fabricated by reconstruction equivalent chirp technique. Opt. Laser Technol. 2014, 61, 57–61. [Google Scholar] [CrossRef]
- Kim, B.S.; Chung, Y.; Lee, J.S. An efficient split-step time-domain dynamic modeling of DFB/DBR laser diodes. IEEE J. Quantum Electron. 2000, 36, 787–794. [Google Scholar]
- Zhang, L.M.; Yu, S.F.; Nowell, M.C.; Marcenac, D.D.; Carroll, J.E.; Plumb, R.G.S. Dynamic analysis of radiation and side-mode suppression in a second-order DFB laser using time-domain large-signal traveling wave model. IEEE J. Quantum Electron. 1994, 30, 1389–1395. [Google Scholar] [CrossRef]
- Fernandes, C.A. Transfer matrix modelling in DFB lasers. Microelectron. Eng. 1998, 43, 553–560. [Google Scholar] [CrossRef]
- Morrison, G.B.; Cassidy, D.T. A probability-amplitude transfer matrix model for distributed-feedback laser structures. IEEE J. Quantum Electron. 2000, 36, 633–640. [Google Scholar] [CrossRef]



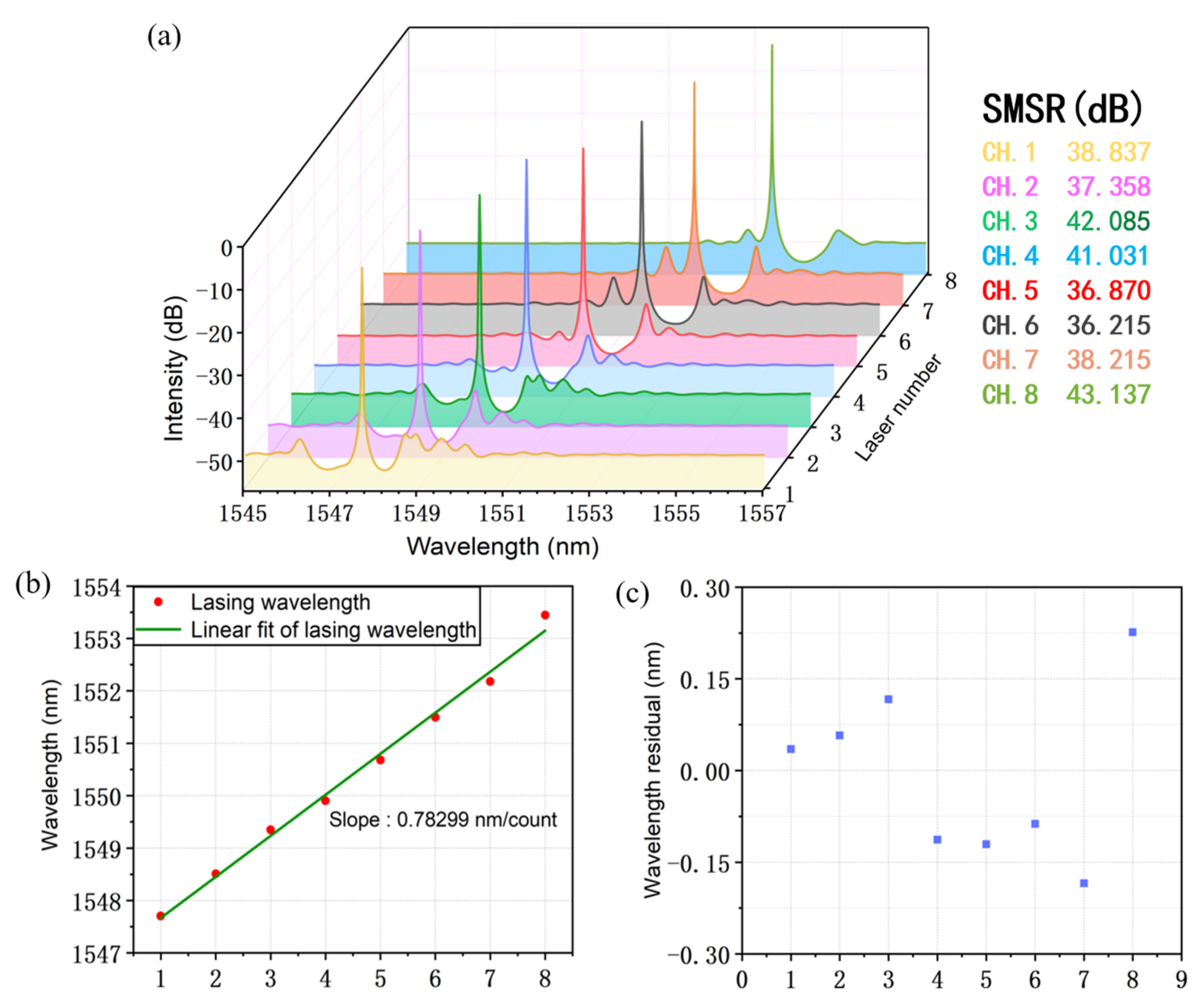
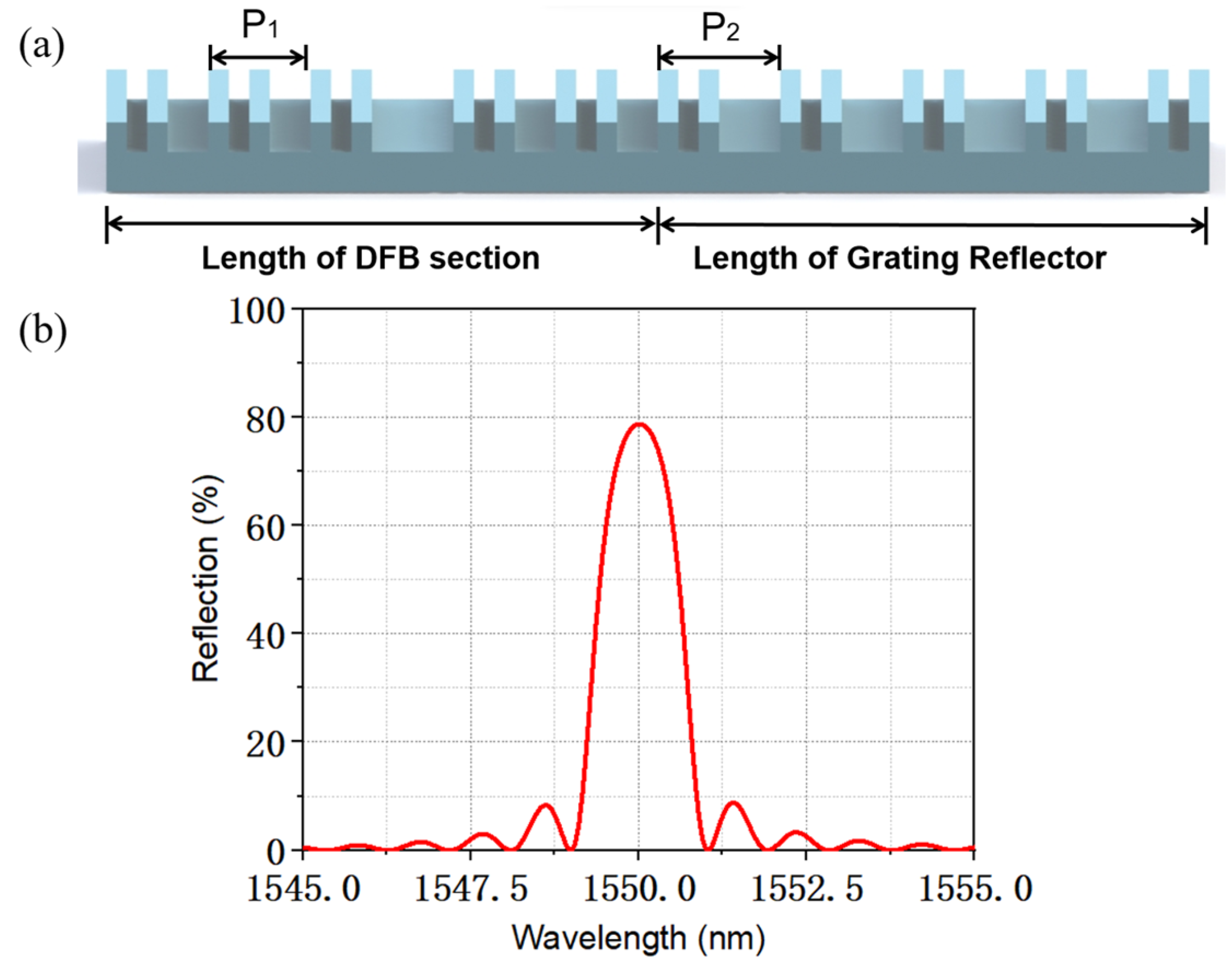
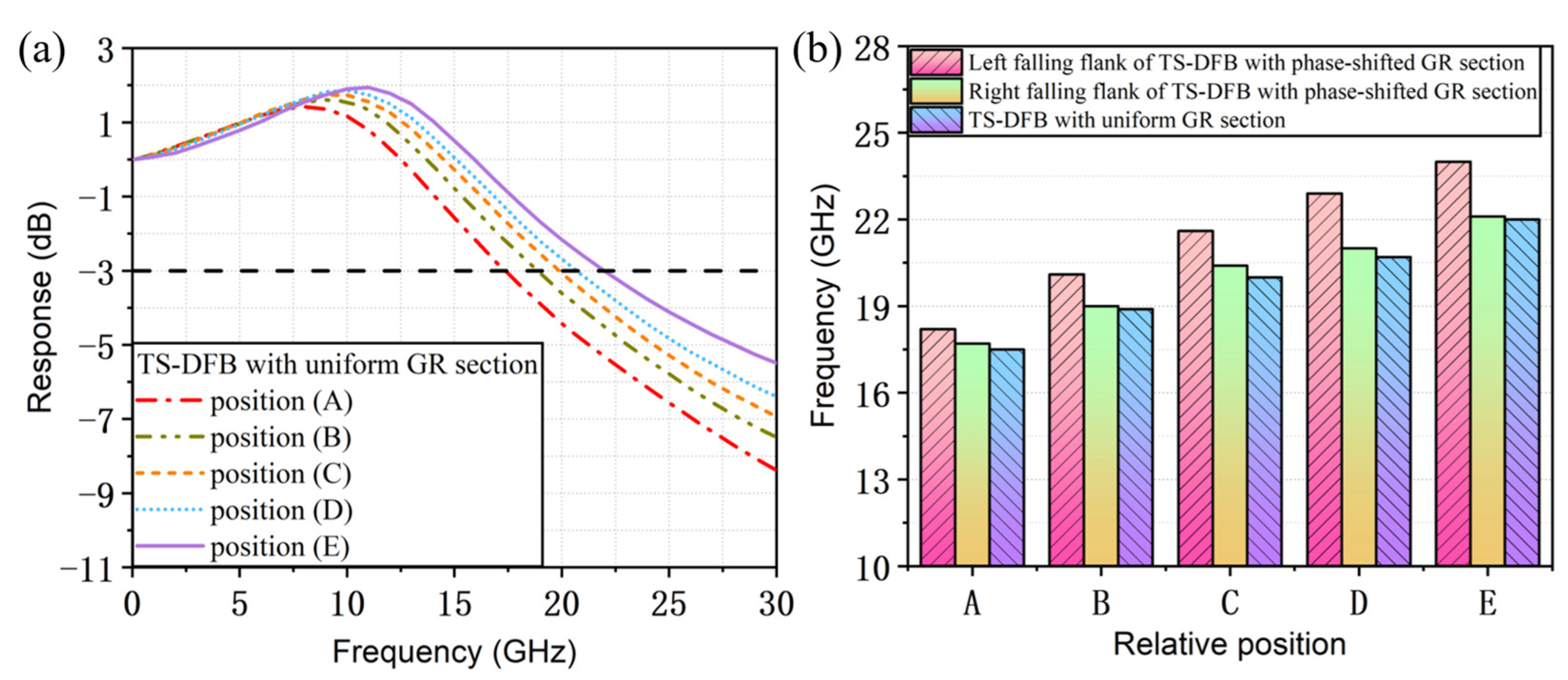
| Parameter | Symbol | Value |
|---|---|---|
| Seed grating period (nm) | Λ0 | 256.71 |
| Sampling period of DFB section (μm) | P1 | 4.189 |
| Length of DFB section (μm) | L1 | 400 |
| Length of grating reflector (μm) | L2 | 400 |
| Active layer width (μm) | Wa | 2 |
| Active layer thickness (μm) | da | 48 |
| Effective refractive index | neff | 3.204 |
| Group refractive index | ng | 3.6 |
| Linewidth enhancement factor | αh | 2 |
| Gain coefficient (cm−1) | g | 1100 |
| Internal loss (cm−1) | α | 10 |
| Optical confinement factor | Γ | 0.1 |
| Monomolecular recombination coefficient (109 s−1) | A | 1 |
| Bimolecular recombination coefficient (10−10 cm3 s−1) | B | 1 |
| Auger recombination coefficient (10−29 cm6 s−1) | C | 7.5 |
| Transparency carrier density (1024 m−3) | Ntr | 1 |
| Nonlinear gain saturation coefficient (10−23 m−3) | ε | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Gu, H.; Ma, G.; Guan, S.; Fang, T.; Chen, X. Research on an Enhanced Detuned-Loading Effect in Integrated Two-Section DFB Lasers with High Modulation Bandwidths. Micromachines 2023, 14, 1994. https://doi.org/10.3390/mi14111994
Zhang Y, Gu H, Ma G, Guan S, Fang T, Chen X. Research on an Enhanced Detuned-Loading Effect in Integrated Two-Section DFB Lasers with High Modulation Bandwidths. Micromachines. 2023; 14(11):1994. https://doi.org/10.3390/mi14111994
Chicago/Turabian StyleZhang, Yunshan, Hongming Gu, Guolong Ma, Shijian Guan, Tao Fang, and Xiangfei Chen. 2023. "Research on an Enhanced Detuned-Loading Effect in Integrated Two-Section DFB Lasers with High Modulation Bandwidths" Micromachines 14, no. 11: 1994. https://doi.org/10.3390/mi14111994
APA StyleZhang, Y., Gu, H., Ma, G., Guan, S., Fang, T., & Chen, X. (2023). Research on an Enhanced Detuned-Loading Effect in Integrated Two-Section DFB Lasers with High Modulation Bandwidths. Micromachines, 14(11), 1994. https://doi.org/10.3390/mi14111994




