High-Bandwidth Repetitive Trajectory Tracking Control of Piezoelectric Actuators via Phase–Hysteresis Hybrid Compensation and Feedforward–Feedback Combined Control
Abstract
:1. Introduction
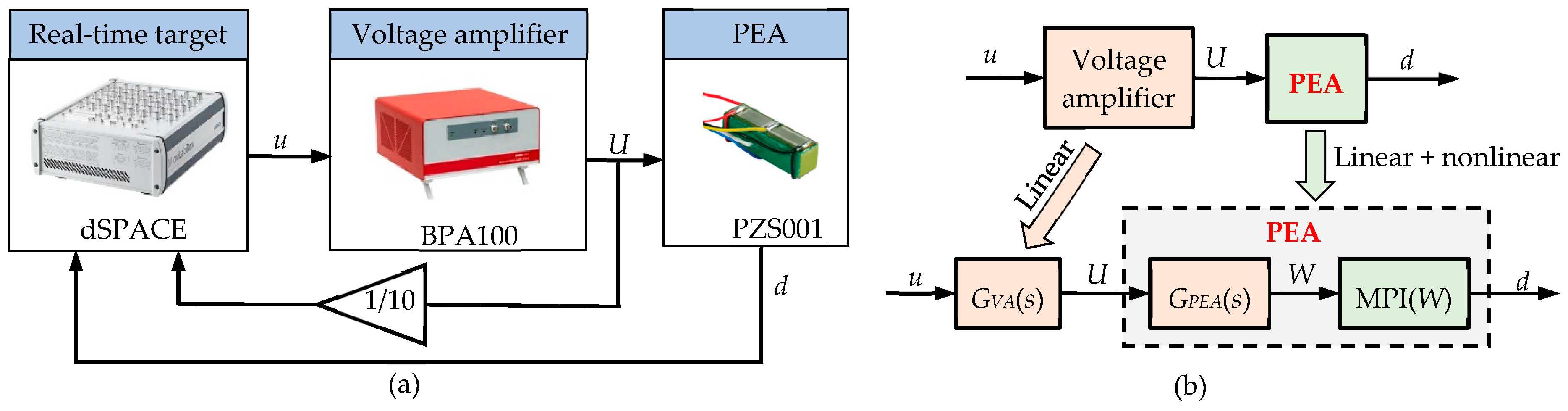
2. High-Bandwidth Hysteresis Dynamics Hybrid Modeling of the VA-PEA Module
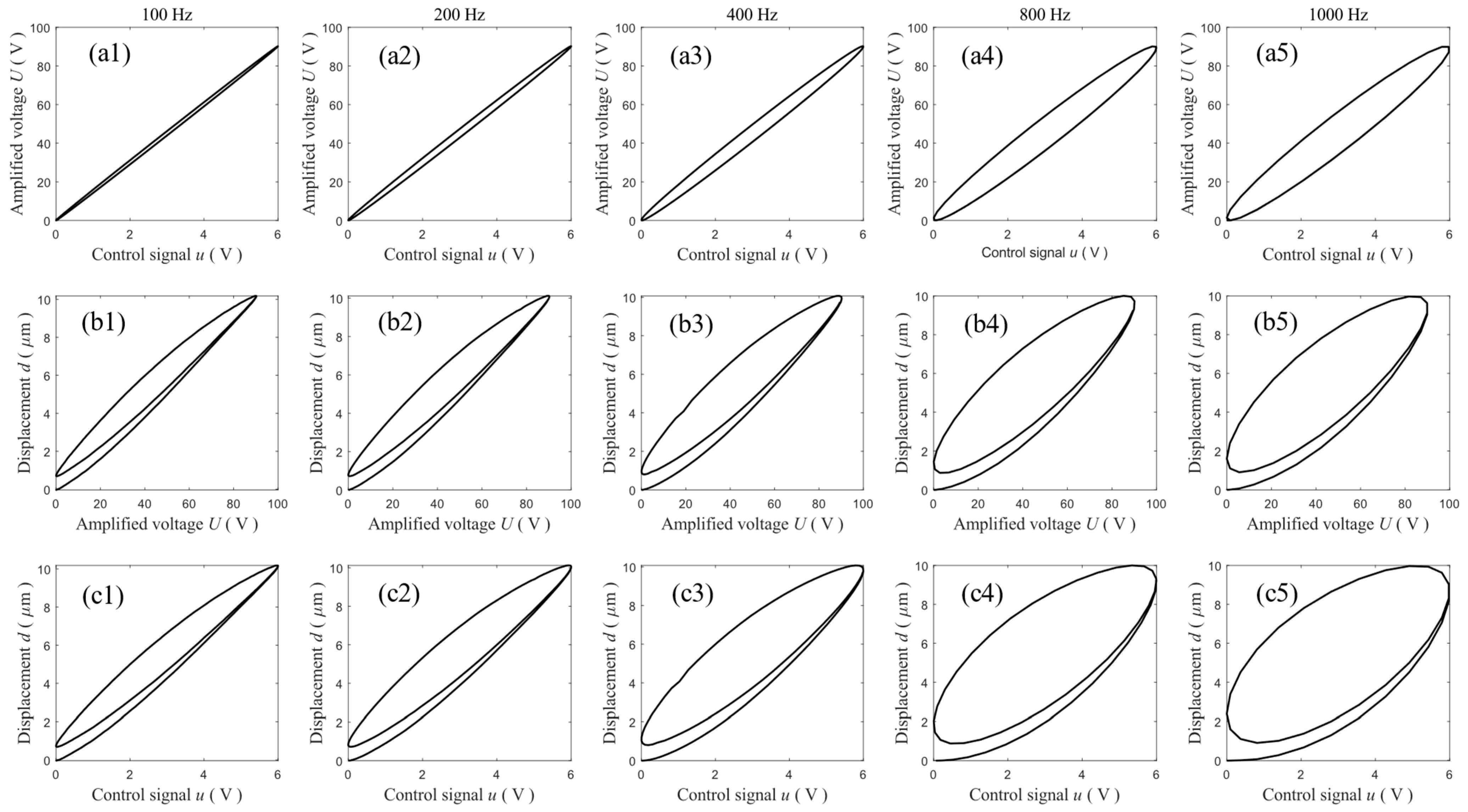
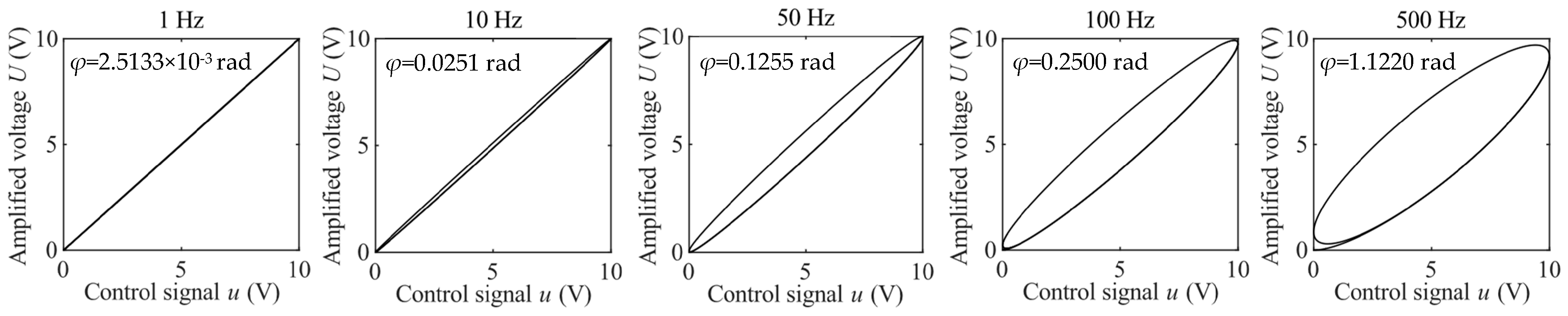
2.1. Characteristics of the Measured Hysteresis of the VA-PEA Module
2.2. The Hysteresis-like Loops of a Linear Dynamic System
2.3. Hysteresis Dynamics Hybrid Modeling of the VA-PEA Module
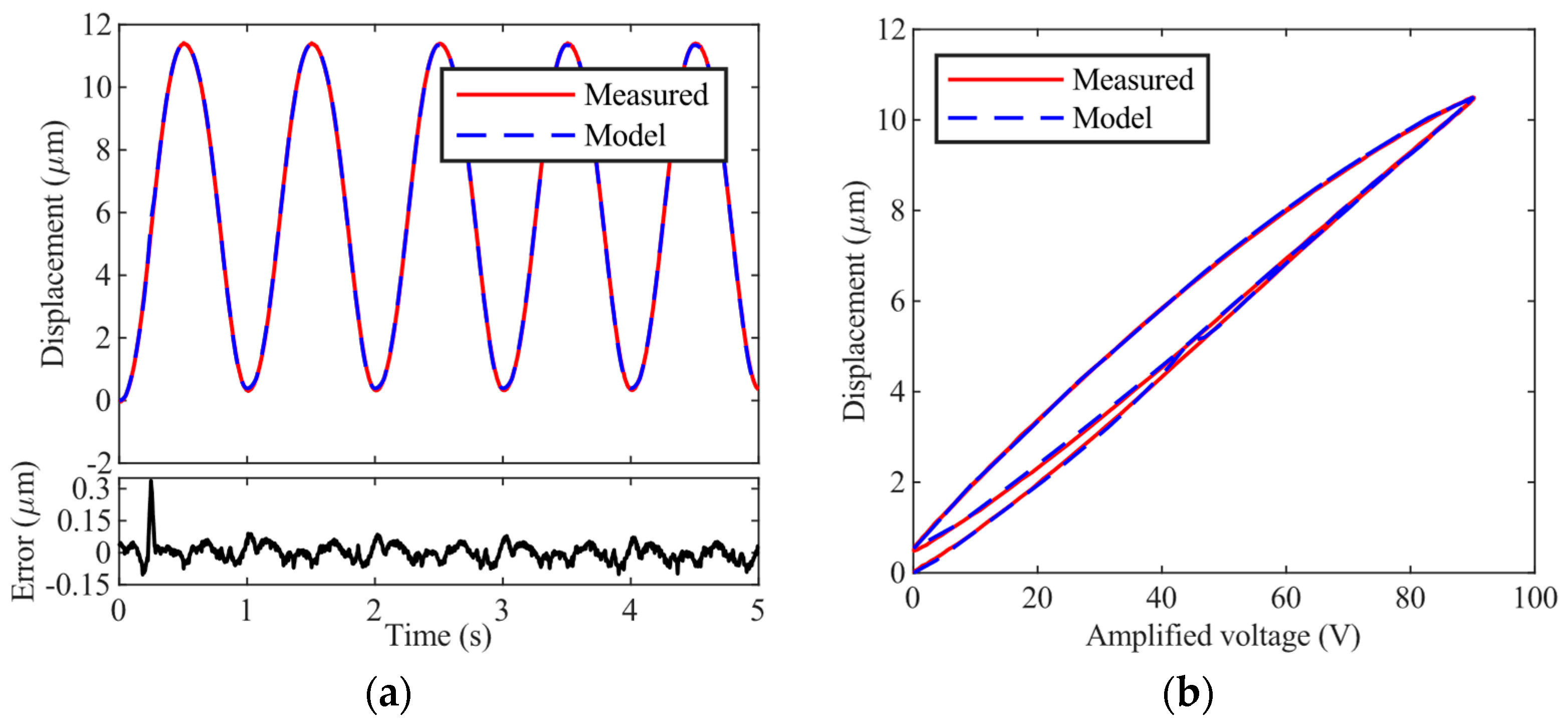
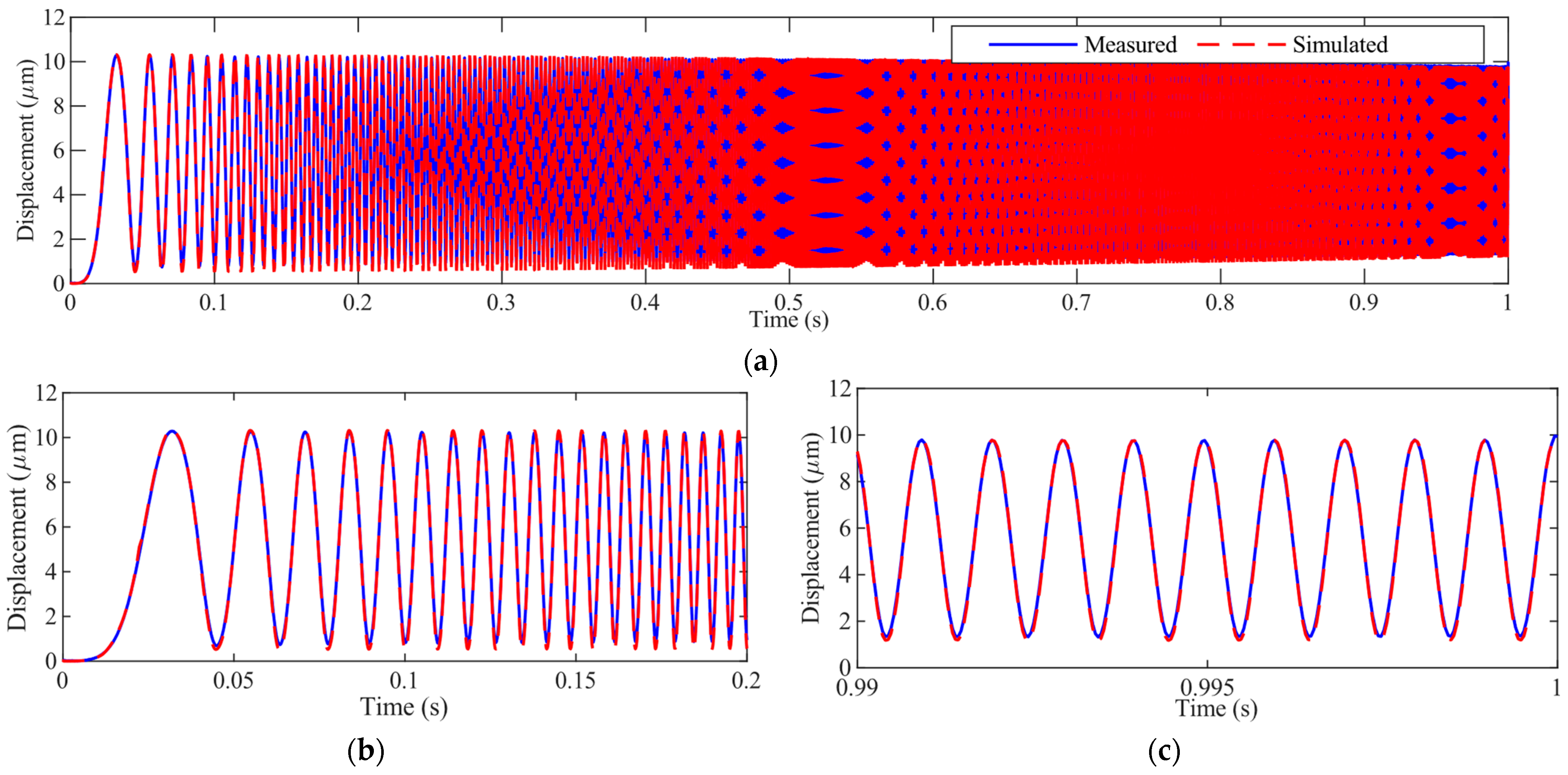
2.4. Parameter Identification
3. Phase–Hysteresis Hybrid Compensation Strategy
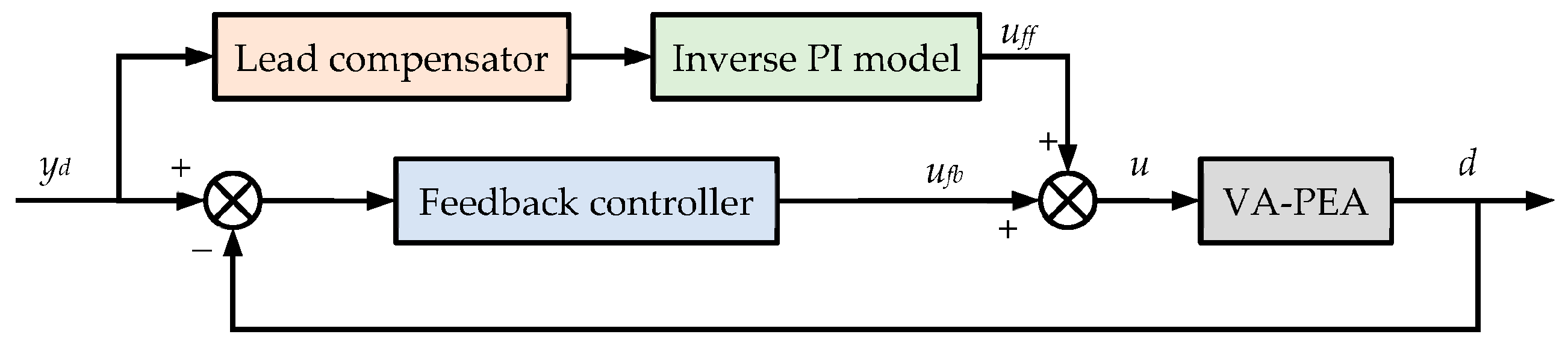
3.1. Lead Compensator and Inverse PI Model
3.2. UKF-Based PID Controller
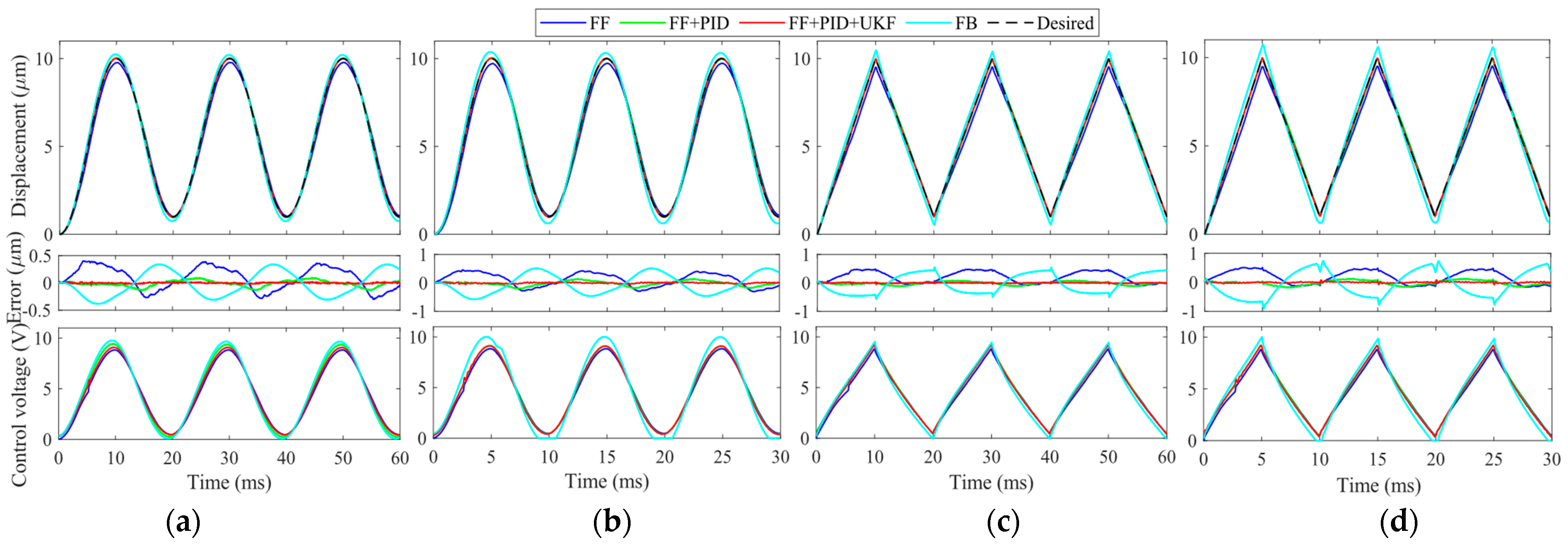
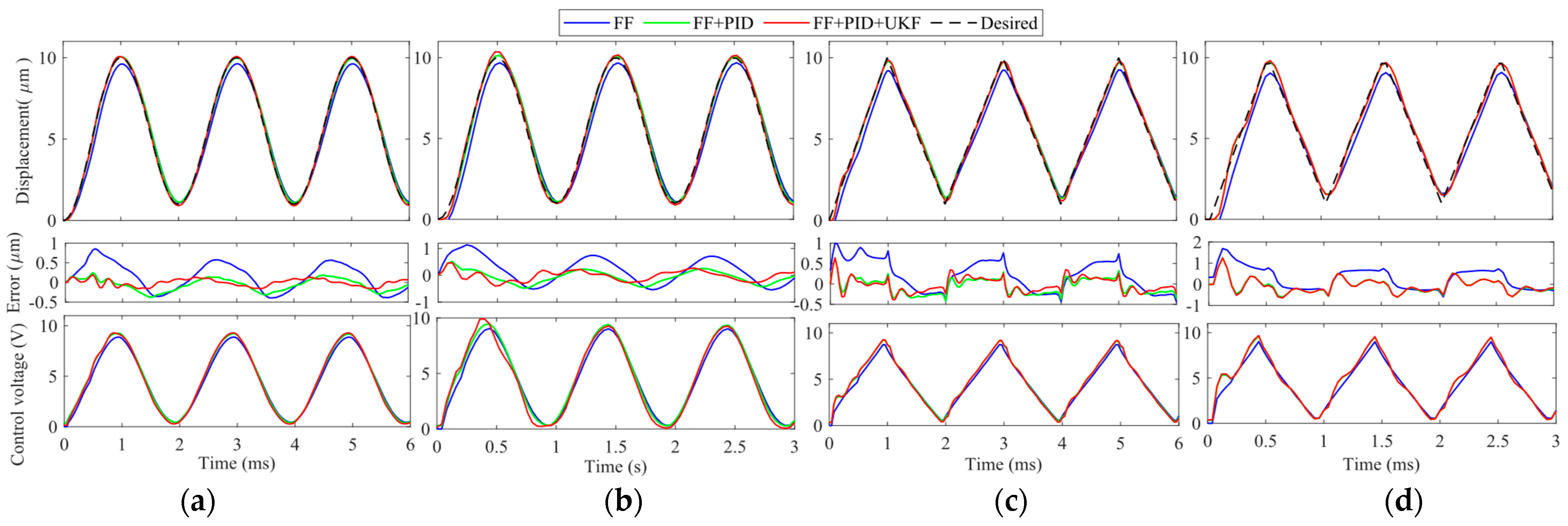
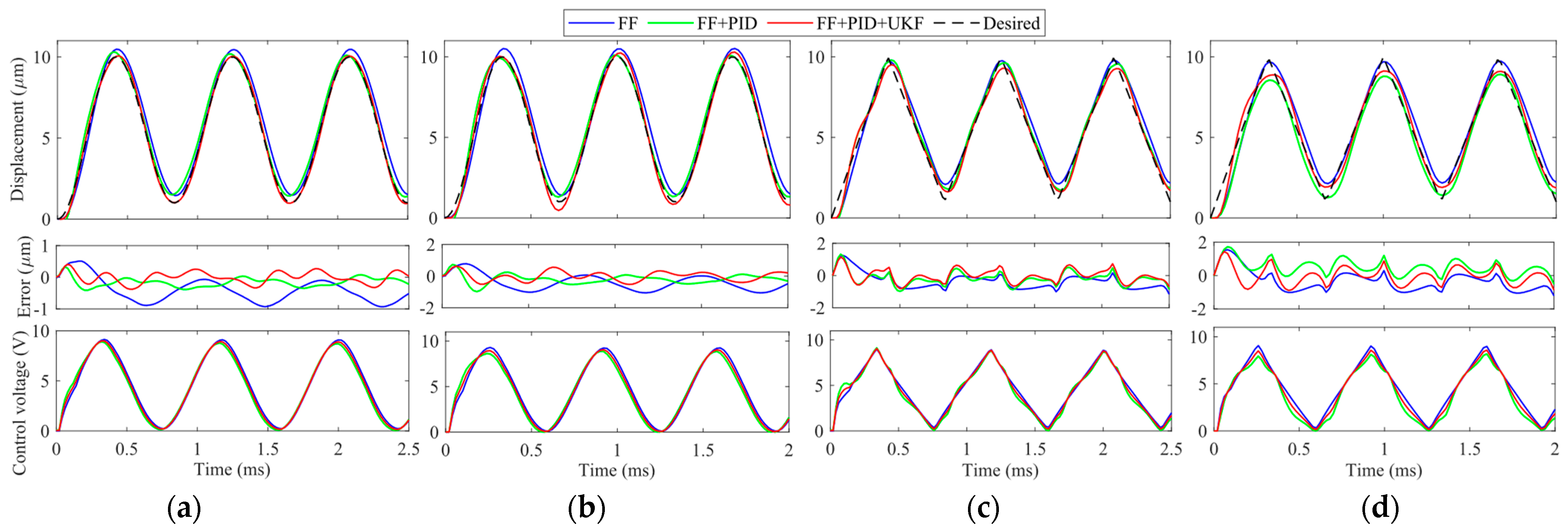
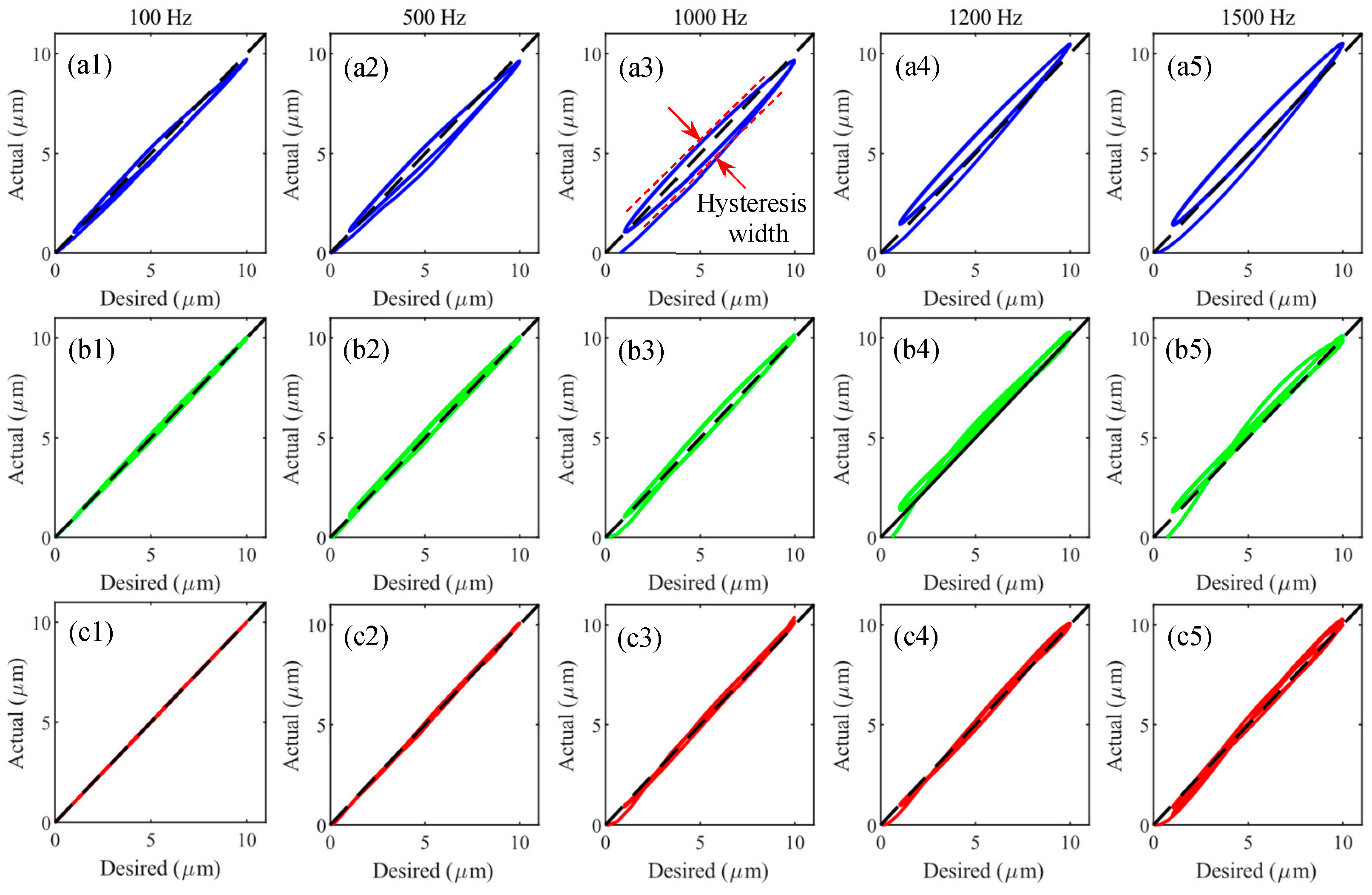
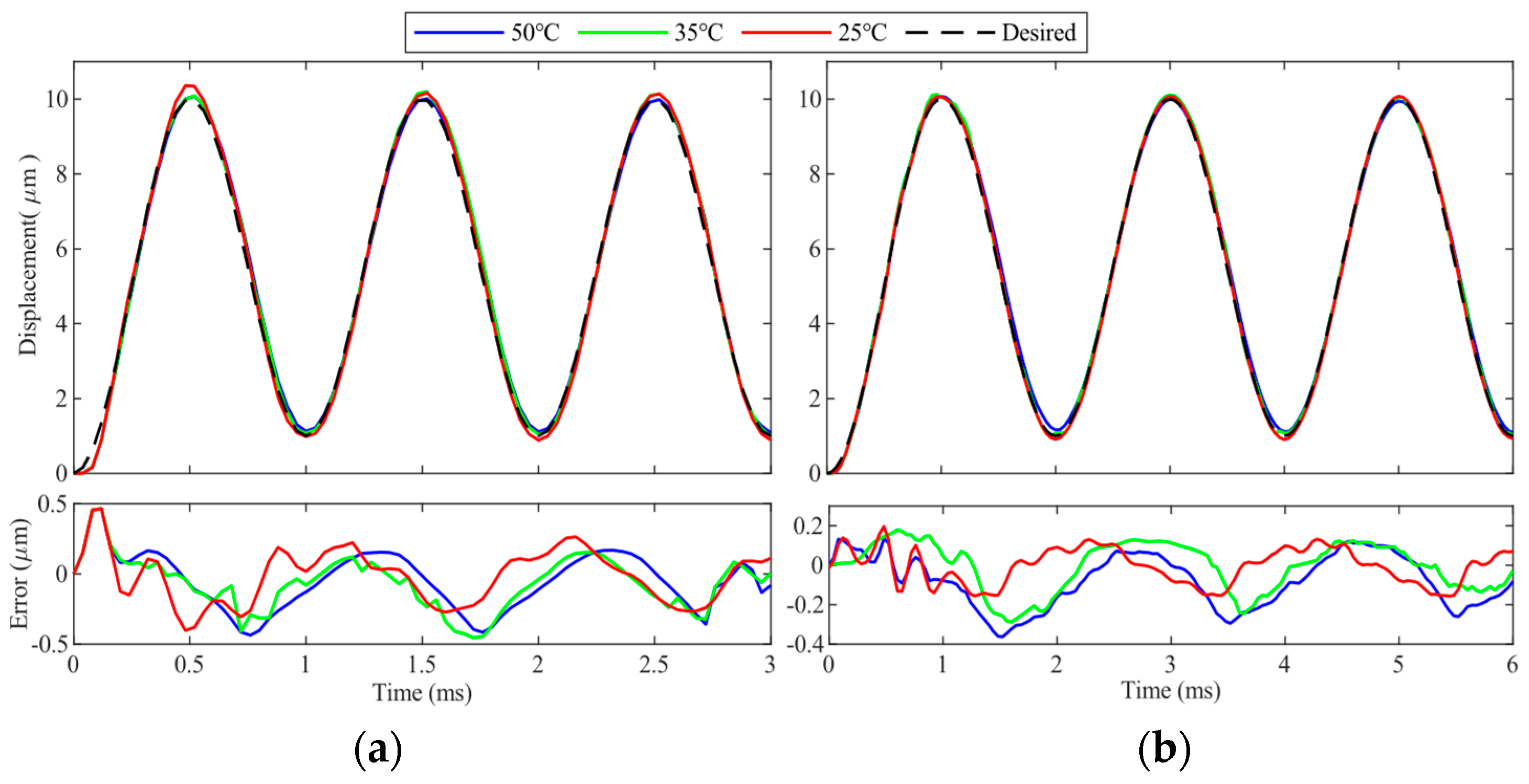
4. Experimental Verifications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Wang, Y.; Chen, X. Online hysteresis identification and compensation for piezoelectric actuators. IEEE Trans. Ind. Electron. 2020, 67, 5595–5603. [Google Scholar] [CrossRef]
- Qin, Y.; Duan, H. Single-neuron adaptive hysteresis compensation of piezoelectric actuator based on hebb learning rules. Micromachines 2020, 11, 84. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Li, C.; Xia, F.; Zhu, Y.; Zhao, J.; Youcef-Toumi, K. Charge controller with decoupled and self-compensating configurations for linear operation of piezoelectric actuators in a wide bandwidth. IEEE Trans. Ind. Electron. 2019, 66, 5392–5402. [Google Scholar] [CrossRef]
- Tao, Y.-D.; Li, H.-X.; Zhu, L.-M. Rate-dependent hysteresis modeling and compensation of piezoelectric actuators using Gaussian process. Sens. Actuators A Phys. 2019, 295, 357–365. [Google Scholar] [CrossRef]
- Ramirez-Laboreo, E.; Roes, M.G.L.; Sagues, C. Hybrid dynamical model for reluctance actuators including saturation, hysteresis, and eddy currents. IEEE/ASME Trans. Mechatron. 2019, 24, 1396–1406. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Li, C.-X.; Zhu, L.-M.; Su, C.-Y. Modeling and identification of piezoelectric-actuated stages cascading hysteresis nonlinearity with linear dynamics. IEEE/ASME Trans. Mechatron. 2016, 21, 1792–1797. [Google Scholar] [CrossRef]
- Qin, Y.; Jia, R. Adaptive hysteresis compensation of piezoelectric actuator using direct inverse modelling approach. Micro Nano Lett. 2018, 13, 180–183. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B.; Chen, X.; Li, Z.; Peng, Y.; Su, C.-Y. Adaptive implicit inverse control for a class of discrete-time hysteretic nonlinear systems and its application. IEEE/ASME Trans. Mechatron. 2020, 25, 2112–2122. [Google Scholar] [CrossRef]
- Zhang, Q.; Dong, Y.; Peng, Y.; Luo, J.; Xie, S.; Pu, H. Asymmetric bouc–wen hysteresis modeling and inverse compensation for piezoelectric actuator via a genetic algorithm–based particle swarm optimization identification algorithm. J. Intell. Mater. Syst. Struct. 2019, 30, 1263–1275. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, X.; Zhou, L. Modeling and identification of the rate-dependent hysteresis of piezoelectric actuator using a modified prandtl-ishlinskii model. Micromachines 2017, 8, 114. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakotondrabe, M.; Aljanaideh, O. Further results on hysteresis compensation of smart micropositioning systems with the inverse prandtl–ishlinskii compensator. IEEE Trans. Control Syst. Technol. 2016, 24, 428–439. [Google Scholar] [CrossRef]
- Liu, W.; Cheng, L.; Hou, Z.-G.; Yu, J.; Tan, M. An inversion-free predictive controller for piezoelectric actuators based on a dynamic linearized neural network model. IEEE/ASME Trans. Mechatron. 2015, 21, 214–226. [Google Scholar] [CrossRef]
- Cailliez, J.; Boudaoud, M.; Liang, S.; Regnier, S. Robust hybrid control of an atomic force microscope for the characterization of interaction force regions at the nanoscale. IEEE Trans. Control Syst. Technol. 2021, 29, 1689–1703. [Google Scholar] [CrossRef]
- Li, L.; Huang, W.-W.; Wang, X.; Chen, Y.-L.; Zhu, L. Periodic-disturbance observer using spectrum-selection filtering scheme for cross-coupling suppression in atomic force microscopy. IEEE Trans. Autom. Sci. Eng. 2023, 20, 2037–2048. [Google Scholar] [CrossRef]
- Merry, R.J.E.; Ronde, M.J.C.; van de Molengraft, R.; Koops, K.R.; Steinbuch, M. Directional repetitive control of a metrological AFM. IEEE Trans. Control Syst. Technol. 2011, 19, 1622–1629. [Google Scholar] [CrossRef]
- Lagrange, D.; Mauran, N.; Schwab, L.; Legrand, B. Low Latency Demodulation for High-Frequency Atomic Force Microscopy Probes. IEEE Trans. Control Syst. Technol. 2021, 29, 2264–2270. [Google Scholar] [CrossRef]
- Ragazzon, M.R.P.; Ruppert, M.G.; Harcombe, D.M.; Fleming, A.J.; Gravdahl, J.T. Lyapunov estimator for high-speed demodulation in dynamic mode atomic force microscopy. IEEE Trans. Control Syst. Technol. 2018, 26, 765–772. [Google Scholar] [CrossRef]
- Ruppert, M.G.; Karvinen, K.S.; Wiggins, S.L.; Reza Moheimani, S.O. A Kalman filter for amplitude estimation in high-speed dynamic mode atomic force microscopy. IEEE Trans. Control Syst. Technol. 2016, 24, 276–284. [Google Scholar] [CrossRef]
- Wang, A.; Cheng, L.; Yang, C.; Hou, Z.-G. An adaptive fuzzy predictive controller with hysteresis compensation for piezoelectric actuators. Cogn. Comput. 2020, 12, 736–747. [Google Scholar] [CrossRef]
- Qin, Y.; Duan, H.; Han, J. Direct inverse hysteresis compensation of piezoelectric actuators using adaptive Kalman filter. IEEE Trans. Ind. Electron. 2022, 69, 9385–9395. [Google Scholar] [CrossRef]
- Huang, D.; Min, D.; Jian, Y.; Li, Y. Current-cycle iterative learning control for high-precision position tracking of piezoelectric actuator system via active disturbance rejection control for hysteresis compensation. IEEE Trans. Ind. Electron. 2020, 67, 8680–8690. [Google Scholar] [CrossRef]
- Zhou, Z.; Tan, Y.; Liu, X. State estimation of dynamic systems with sandwich structure and hysteresis. Mech. Syst. Signal Process. 2019, 126, 82–97. [Google Scholar] [CrossRef]
- Li, R.; Cao, K.; Yu, X.; Zeng, M. Modeling and compensation algorithms of asymmetric nonlinearity for piezoelectric actuators based on madelung’s rules. IEEE Trans. Ind. Electron. 2021, 68, 11359–11368. [Google Scholar] [CrossRef]
- Qin, Y.; Tian, Y.; Zhang, D.; Shirinzadeh, B.; Fatikow, S. A novel direct inverse modeling approach for hysteresis compensation of piezoelectric actuator in feedforward applications. IEEE/ASME Trans. Mechatron. 2013, 18, 981–989. [Google Scholar] [CrossRef]
- Liu, Y.F.; Shan, J.J.; Gabbert, U. Feedback/feedforward control of hysteresis-compensated piezoelectric actuators for high-speed scanning applications. Smart Mater. Struct. 2014, 24, 015012. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, W.; Hou, Z.-G.; Yu, J.; Tan, M. Neural-network-based nonlinear model predictive control for piezoelectric actuators. IEEE Trans. Ind. Electron. 2015, 62, 7717–7727. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef]
- Wan, E.A.; Merwe, R.V.D. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 1–4 October 2000; pp. 153–158. [Google Scholar]


| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| ri | 0 | 3.7101 | 21.1438 | 32.1438 | 40.5758 | 45.1003 | 47.1873 | 69.81 | 81.5687 | 90.6485 |
| whi | 8.437 × 10−3 | 2.851 × 10−3 | 7.517 × 10−4 | 1.856 × 10−9 | 3.019 × 10−3 | −0.0179 | 0.0140 | 1.695 × 10−3 | 2.404 × 10−3 | −0.2041 |
| ci | 8.8816 | / | 2.5262 | / | −2.9198 | / | 0.6430 | / | 0.1342 | / |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1306 | 3.0631 | 3.9282 | 5.5533 | 4.9691 | 5.5667 | 7.6329 | 9.4221 | 10.9181 | |
| 1.4874 | −0.3781 | −0.1677 | −0.1395 | 4.9229 | −0.0918 | −4.6767 | −0.1370 | −0.0595 | −0.0485 | |
| 3.700 × 10−9 | / | −35.166 | / | 7.045 × 10−4 | / | −0.0462 | / | 9.4131 | / |
| Trajectory | Controller | RMSE (μm)/MAE (μm) | |||||
|---|---|---|---|---|---|---|---|
| 50 Hz | 100 Hz | 500 Hz | 1000 Hz | 1200 Hz | 1500 Hz | ||
| Sinusoidal | FB | 0.2311/0.2042 | 0.3466/0.3062 | / | / | / | / |
| FF | 0.2255/0.1972 | 0.2605/0.2308 | 0.3783/0.3268 | 0.5178/0.4405 | 0.5630/0.4912 | 0.6391/0.5339 | |
| FF + PID | 0.0582/0.0663 | 0.0880/0.0694 | 0.1691/0.1414 | 0.2452/0.2064 | 0.2124/0.1785 | 0.3446/0.2699 | |
| FF + PID + UKF | 0.0096/0.0078 | 0.0172/0.0141 | 0.0909/0.0764 | 0.1893/0.1583 | 0.1813/0.1473 | 0.2914/0.2420 | |
| Triangular | FB | 0.3312/0.3059 | 0.4497/0.4030 | / | / | / | / |
| FF | 0.2846/0.2260 | 0.2890/0.2423 | 0.4313/0.3665 | 0.5957/0.4910 | 0.5981/0.5025 | 0.6980/0.5713 | |
| FF + PID | 0.0587/0.0485 | 0.0884/0.0755 | 0.2035/0.1761 | 0.3932/0.3136 | 0.4393/0.3464 | 0.6596/0.5356 | |
| FF + PID + UKF | 0.0113/0.0087 | 0.0196/0.0146 | 0.1842/0.1548 | 03539/0.2816 | 0.3821/0.3189 | 0.5118/0.4011 | |
| 100 Hz | 500 Hz | 1000 Hz | 1200 Hz | 1500 Hz | |
|---|---|---|---|---|---|
| FF | 0.5400 | 0.8852 | 1.1889 | 1.2198 | 1.2992 |
| FF + PID | 0.2488 | 0.4396 | 0.6982 | 0.7096 | 1.2121 |
| FF + PID + UKF | 0.0644 | 0.2492 | 0.6124 | 0.6264 | 0.8146 |
| 25 °C | 35 °C | 50 °C | |
|---|---|---|---|
| 500 Hz | 0.0909 | 0.1172 | 0.1361 |
| 1000 Hz | 0.1893 | 0.1968 | 0.2034 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, J.; Wu, H.; Qin, Y.; Han, J. High-Bandwidth Repetitive Trajectory Tracking Control of Piezoelectric Actuators via Phase–Hysteresis Hybrid Compensation and Feedforward–Feedback Combined Control. Micromachines 2023, 14, 2009. https://doi.org/10.3390/mi14112009
Yuan J, Wu H, Qin Y, Han J. High-Bandwidth Repetitive Trajectory Tracking Control of Piezoelectric Actuators via Phase–Hysteresis Hybrid Compensation and Feedforward–Feedback Combined Control. Micromachines. 2023; 14(11):2009. https://doi.org/10.3390/mi14112009
Chicago/Turabian StyleYuan, Jie, Haitao Wu, Yanding Qin, and Jianda Han. 2023. "High-Bandwidth Repetitive Trajectory Tracking Control of Piezoelectric Actuators via Phase–Hysteresis Hybrid Compensation and Feedforward–Feedback Combined Control" Micromachines 14, no. 11: 2009. https://doi.org/10.3390/mi14112009
APA StyleYuan, J., Wu, H., Qin, Y., & Han, J. (2023). High-Bandwidth Repetitive Trajectory Tracking Control of Piezoelectric Actuators via Phase–Hysteresis Hybrid Compensation and Feedforward–Feedback Combined Control. Micromachines, 14(11), 2009. https://doi.org/10.3390/mi14112009








