A Novel Electrokinetic-Based Technique for the Isolation of Circulating Tumor Cells
Abstract
:1. Introduction
2. Governing Equations
3. Numerical Method
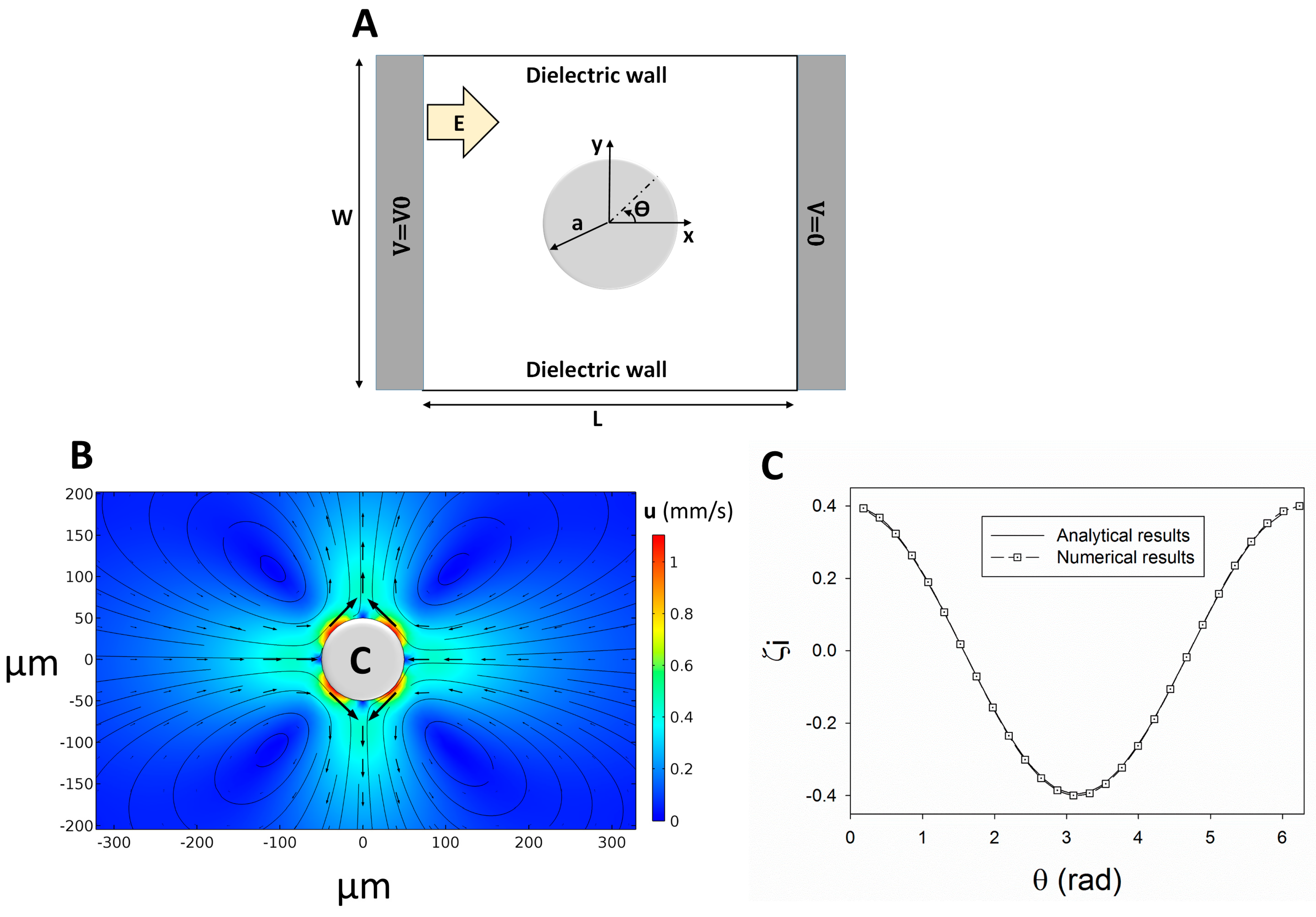
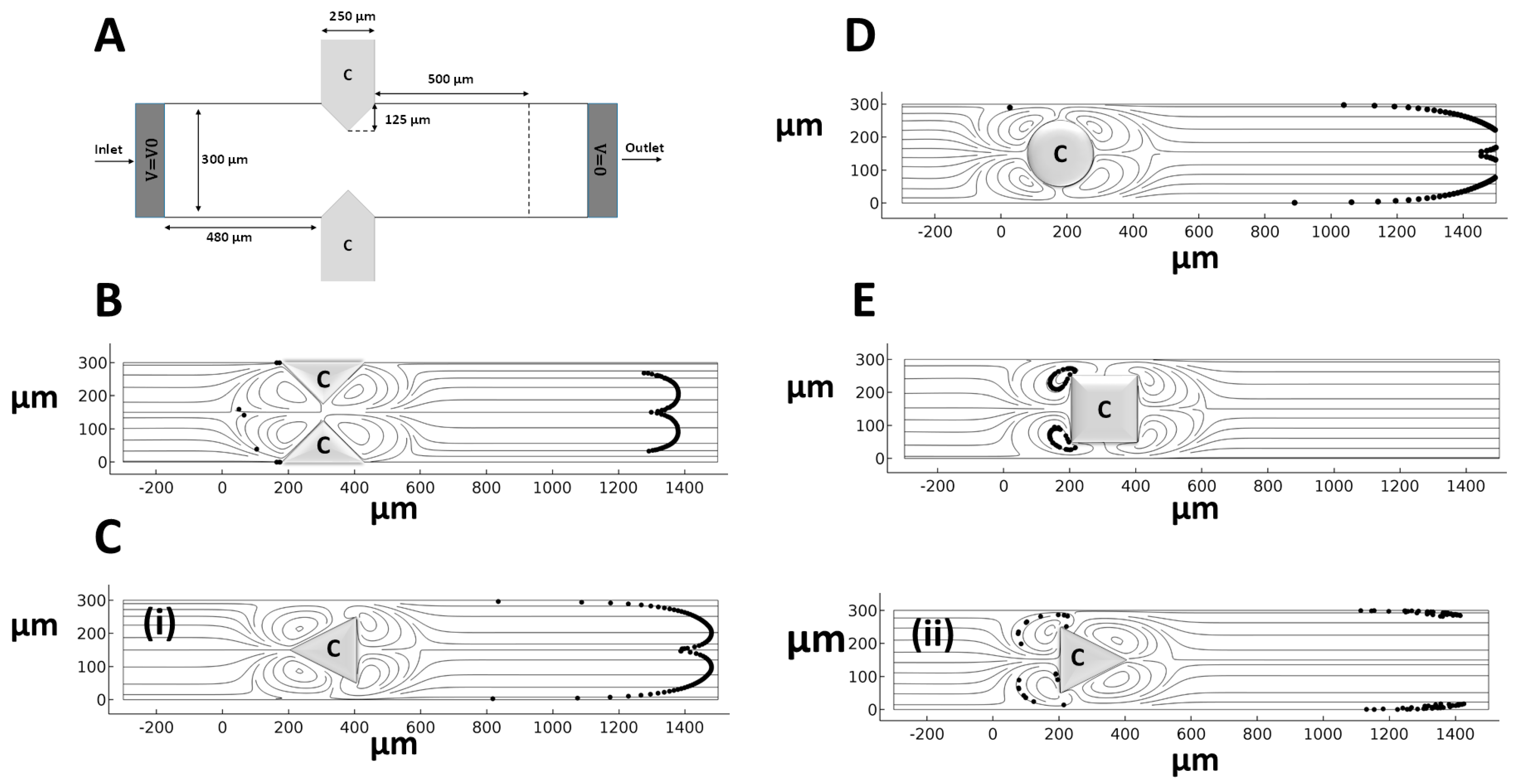
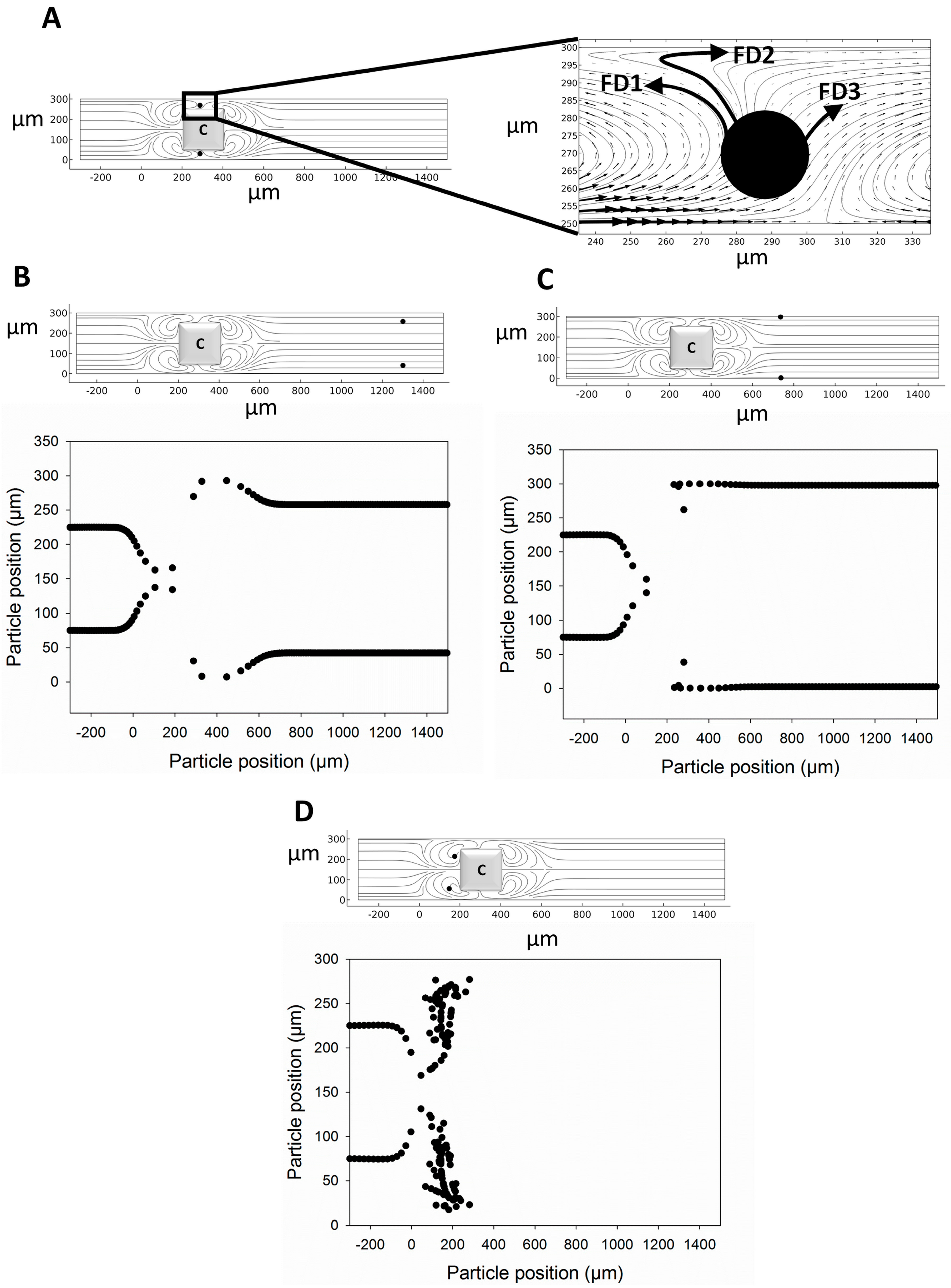
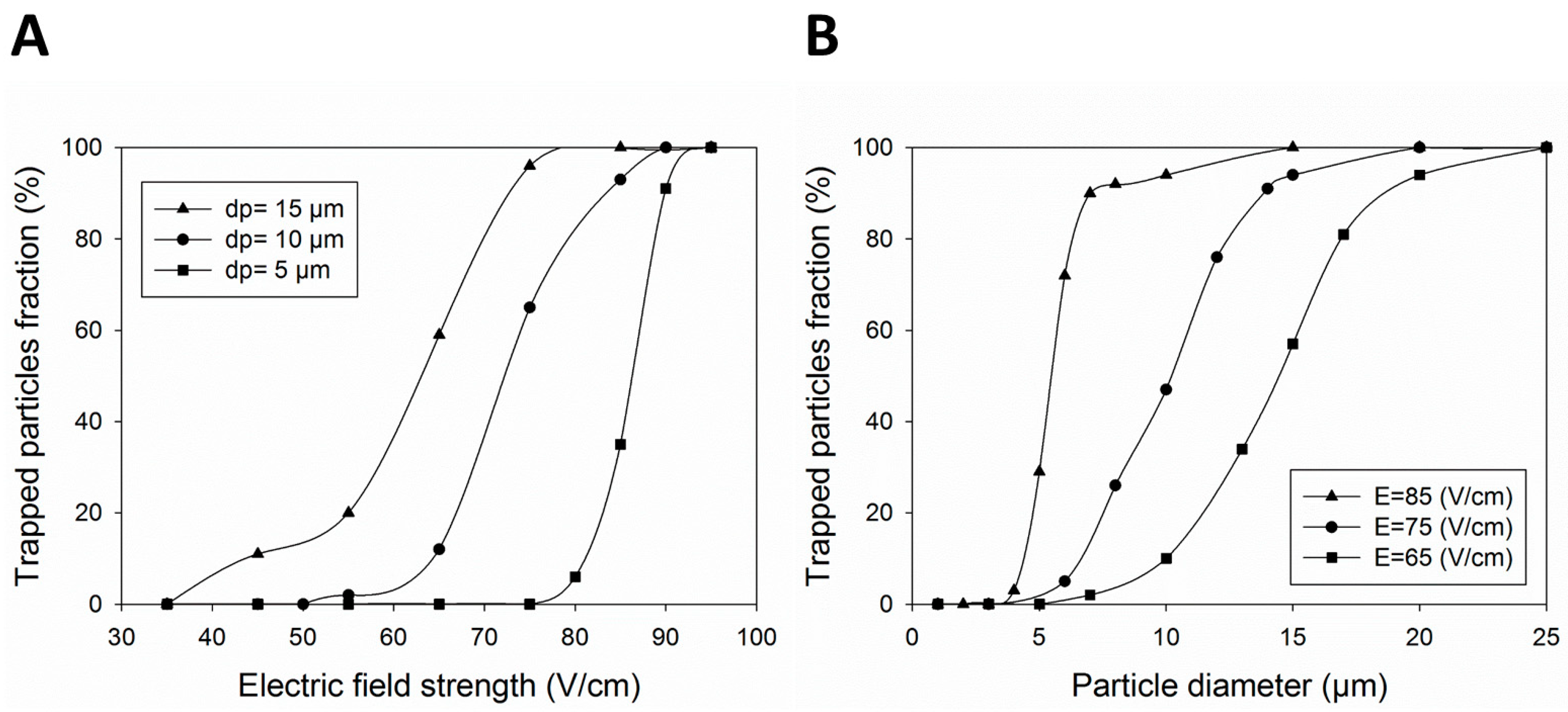
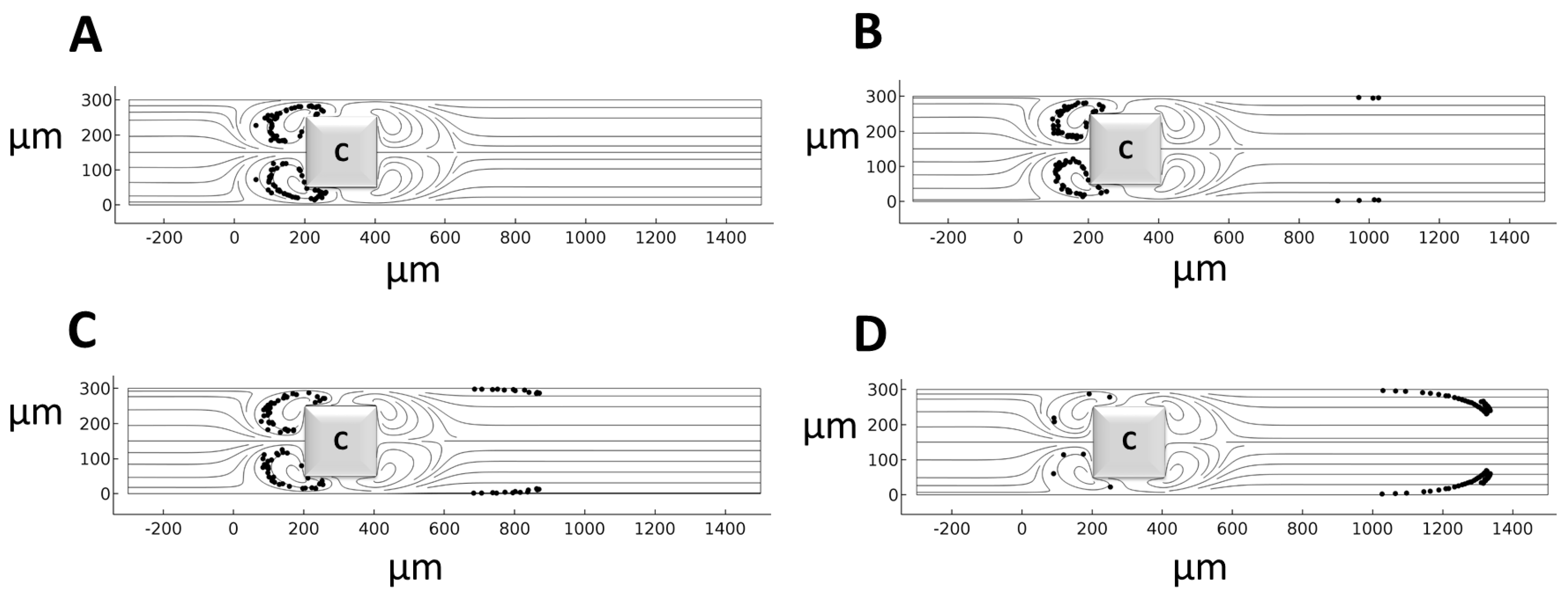
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhagat, A.A.S.; Bow, H.; Hou, H.W.; Tan, S.J.; Han, J.; Lim, C.T. Microfluidics for cell separation. Med. Biol. Eng. Comput. 2010, 48, 999–1014. [Google Scholar] [CrossRef]
- Safavieh, M.; Kaul, V.; Khetani, S.; Singh, A.; Dhingra, K.; Kanakasabapathy, M.K.; Draz, M.S.; Memic, A.; Kuritzkes, D.R.; Shafiee, H. Paper microchip with a graphene-modified silver nano-composite electrode for electrical sensing of microbial pathogens. Nanoscale 2017, 9, 1852–1861. [Google Scholar] [CrossRef] [PubMed]
- Valente, K.P.; Khetani, S.; Kolahchi, A.R.; Sanati-Nezhad, A.; Suleman, A.; Akbari, M. Microfluidic technologies for anticancer drug studies. Drug Discov. Today 2017, 22, 1654–1670. [Google Scholar] [CrossRef] [PubMed]
- Conteduca, D.; Brunetti, G.; Barth, I.; Quinn, S.D.; Ciminelli, C.; Krauss, T.F. Multiplexed Near-Field Optical Trapping Exploiting Anapole States. ACS Nano 2023, 17, 16695–16702. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D. Inertial microfluidics. Lab Chip 2009, 9, 3038–3046. [Google Scholar] [CrossRef] [PubMed]
- Khetani, S.; Mohammadi, M.; Nezhad, A.S. Filter-based isolation, enrichment, and characterization of circulating tumor cells. Biotechnol. Bioeng. 2018, 115, 2504–2529. [Google Scholar] [CrossRef] [PubMed]
- Pamme, N.; Manz, A. On-chip free-flow magnetophoresis: Continuous flow separation of magnetic particles and agglomerates. Anal. Chem. 2004, 76, 7250–7256. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.; Madadi, H.; Casals-Terré, J.; Sellarès, J. Hydrodynamic and direct-current insulator-based dielectrophoresis (H-DC-iDEP) microfluidic blood plasma separation. Anal. Bioanal. Chem. 2015, 407, 4733–4744. [Google Scholar] [CrossRef]
- Mohammadi, M.; Zare, M.J.; Madadi, H.; Sellarès, J.; Casals-Terré, J. A new approach to design an efficient micropost array for enhanced direct-current insulator-based dielectrophoretic trapping. Anal. Bioanal. Chem. 2016, 408, 5285–5294. [Google Scholar] [CrossRef]
- Safavieh, M.; Khetani, S.; Juillard, F.; Kaul, V.; Kanakasabapathy, M.K.; Kaye, K.M.; Shafiee, H. Electrical response of a B lymphoma cell line latently infected with Kaposi’s sarcoma herpesvirus. Biosens. Bioelectron. 2016, 80, 230–236. [Google Scholar] [CrossRef]
- El Deeb, S.; Al-Harrasi, A.; Khan, A.; Al-Broumi, M.; Al-Thani, G.; Alomairi, M.; Elumalai, P.; Sayed, R.A.; Ibrahim, A.E. Microscale thermophoresis as a powerful growing analytical technique for the investigation of biomolecular interaction and the determination of binding parameters. Methods Appl. Fluoresc. 2022, 10, 042001. [Google Scholar] [CrossRef]
- Collins, D.J.; Khoo, B.L.; Ma, Z.; Winkler, A.; Weser, R.; Schmidt, H.; Han, J.; Ai, Y. Selective particle and cell capture in a continuous flow using micro-vortex acoustic streaming. Lab Chip 2017, 17, 1769–1777. [Google Scholar] [CrossRef] [PubMed]
- Naderi, M.M.; Barilla, L.; Zhou, J.; Papautsky, I.; Peng, Z. Elasto-Inertial Focusing Mechanisms of Particles in Shear-Thinning Viscoelastic Fluid in Rectangular Microchannels. Micromachines 2022, 13, 2131. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Zhou, J.; Naderi, M.M.; Peng, Z.; Papautsky, I. Evolution of focused streams for viscoelastic flow in spiral microchannels. Microsyst. Nanoeng. 2023, 9, 73. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Ren, Y.; Tao, Y.; Hou, L.; Jiang, H. Large-scale single particle and cell trapping based on rotating electric field induced-charge electroosmosis. Anal. Chem. 2016, 88, 11791–11798. [Google Scholar] [CrossRef]
- Tao, Y.; Ren, Y.; Liu, W.; Wu, Y.; Jia, Y.; Lang, Q.; Jiang, H. Enhanced particle trapping performance of induced charge electroosmosis. Electrophoresis 2016, 37, 1326–1336. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Continuous-Flow Trapping and Localized Enrichment of Micro-and Nano-Particles with Induced-Charge Electrokinetics. Soft Matter 2017, 14, 1056–1066. [Google Scholar] [CrossRef]
- Salimian Rizi, F.; Talebi, S.; Manshadi, M.K.; Mohammadi, M. Separation of bacteria smaller than 4 µm from other blood components using insulator-based dielectrophoresis: Numerical simulation approach. Biomech. Model. Mechanobiol. 2023, 22, 825–836. [Google Scholar] [CrossRef]
- Rizi, F.S.; Talebi, S.; Manshadi, M.K.; Mohammadi, M. Combination of the insulator-based dielectrophoresis and hydrodynamic methods for separating bacteria smaller than 3 μm in bloodstream infection: Numerical simulation approach. Sep. Sci. Plus 2023, 6, 2200055. [Google Scholar] [CrossRef]
- Daghighi, Y.; Sinn, I.; Kopelman, R.; Li, D. Experimental validation of induced-charge electrokinetic motion of electrically conducting particles. Electrochim. Acta 2013, 87, 270–276. [Google Scholar] [CrossRef]
- Squires, T.M. Induced-charge electrokinetics: Fundamental challenges and opportunities. Lab Chip 2009, 9, 2477–2483. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Li, D. Mixing and flow regulating by induced-charge electrokinetic flow in a microchannel with a pair of conducting triangle hurdles. Microfluid. Nanofluid. 2008, 5, 65–76. [Google Scholar] [CrossRef]
- Harnett, C.K.; Templeton, J.; Dunphy-Guzman, K.A.; Senousy, Y.M.; Kanouff, M.P. Model based design of a microfluidic mixer driven by induced charge electroosmosis. Lab Chip 2008, 8, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Li, D. Micromixing using induced-charge electrokinetic flow. Electrochim. Acta 2008, 53, 5827–5835. [Google Scholar] [CrossRef]
- Daghighi, Y.; Li, D. Numerical study of a novel induced-charge electrokinetic micro-mixer. Anal. Chim. Acta 2013, 763, 28–37. [Google Scholar] [CrossRef]
- Gangwal, S.; Cayre, O.J.; Bazant, M.Z.; Velev, O.D. Induced-charge electrophoresis of metallodielectric particles. Phys. Rev. Lett. 2008, 100, 058302. [Google Scholar] [CrossRef] [PubMed]
- Kilic, M.S.; Bazant, M.Z. Induced-charge electrophoresis near a wall. Electrophoresis 2011, 32, 614–628. [Google Scholar] [CrossRef]
- Wu, Z.; Li, D. Induced-charge electrophoretic motion of ideally polarizable particles. Electrochim. Acta 2009, 54, 3960–3967. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, W.; Jia, Y.; Tao, Y.; Shao, J.; Ding, Y.; Jiang, H. Induced-charge electroosmotic trapping of particles. Lab Chip 2015, 15, 2181–2191. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, J.; Liu, W.; Lang, Q.; Tao, Y.; Hu, Q.; Hou, L.; Jiang, H. Scaled particle focusing in a microfluidic device with asymmetric electrodes utilizing induced-charge electroosmosis. Lab Chip 2016, 16, 2803–2812. [Google Scholar] [CrossRef]
- Liu, W.; Shao, J.; Ren, Y.; Liu, J.; Tao, Y.; Jiang, H.; Ding, Y. On utilizing alternating current-flow field effect transistor for flexibly manipulating particles in microfluidics and nanofluidics. Biomicrofluidics 2016, 10, 034105. [Google Scholar] [CrossRef]
- Chen, X.; Ren, Y.; Liu, W.; Feng, X.; Jia, Y.; Tao, Y.; Jiang, H. A Simplified Microfluidic Device for Particle Separation with Two Consecutive Steps: Induced Charge Electro-osmotic Prefocusing and Dielectrophoretic Separation. Anal. Chem. 2017, 89, 9583–9592. [Google Scholar] [CrossRef]
- Zhang, F.; Li, D. A novel particle separation method based on induced-charge electro-osmotic flow and polarizability of dielectric particles. Electrophoresis 2014, 35, 2922–2929. [Google Scholar] [CrossRef]
- Song, Y.; Wang, C.; Li, M.; Pan, X.; Li, D. Focusing particles by induced charge electrokinetic flow in a microchannel. Electrophoresis 2016, 37, 666–675. [Google Scholar] [CrossRef]
- Plaks, V.; Koopman, C.D.; Werb, Z. Circulating tumor cells. Science 2013, 341, 1186–1188. [Google Scholar] [CrossRef]
- Follain, G.; Herrmann, D.; Harlepp, S.; Hyenne, V.; Osmani, N.; Warren, S.C.; Timpson, P.; Goetz, J.G. Fluids and their mechanics in tumour transit: Shaping metastasis. Nat. Rev. Cancer 2020, 20, 107–124. [Google Scholar] [CrossRef]
- Cengel, Y.; Cimbala, J. Ebook: Fluid Mechanics Fundamentals and Applications (Si Units); McGraw Hill: New York, NY, USA, 2013. [Google Scholar]
- Wall, S. The history of electrokinetic phenomena. Curr. Opin. Colloid Interface Sci. 2010, 15, 119–124. [Google Scholar] [CrossRef]
- Dehghan Manshadi, M.K.; Khojasteh, D.; Mohammadi, M.; Kamali, R. Electroosmotic micropump for lab-on-a-chip biomedical applications. Int. J. Numer. Model. Electron. Netw. Devices Fields 2016, 29, 845–858. [Google Scholar] [CrossRef]
- Ye, C.; Li, D. 3-D transient electrophoretic motion of a spherical particle in a T-shaped rectangular microchannel. J. Colloid Interface Sci. 2004, 272, 480–488. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, Y.; Li, D. Electrophoretic motion of ideally polarizable particles in a microchannel. Electrophoresis 2009, 30, 773–781. [Google Scholar] [CrossRef]
- Daghighi, Y.; Gao, Y.; Li, D. 3D numerical study of induced-charge electrokinetic motion of heterogeneous particle in a microchannel. Electrochim. Acta 2011, 56, 4254–4262. [Google Scholar] [CrossRef]
- Zhao, K.; Li, D. Numerical studies of manipulation and separation of Janus particles in nano-orifice based DC-dielectrophoretic microfluidic chips. J. Micromech. Microeng. 2017, 27, 095007. [Google Scholar] [CrossRef]
- Tang, G.; Yan, D.; Yang, C.; Gong, H.; Chai, C.; Lam, Y. Joule heating and its effects on electrokinetic transport of solutes in rectangular microchannels. Sens. Actuators A Phys. 2007, 139, 221–232. [Google Scholar] [CrossRef]
- Gao, J.; Yin, X.-F.; Fang, Z.-L. Integration of single cell injection, cell lysis, separation and detection of intracellular constituents on a microfluidic chip. Lab Chip 2004, 4, 47–52. [Google Scholar] [CrossRef]
- Squires, T.M.; Bazant, M.Z. Induced-charge electro-osmosis. J. Fluid Mech. 2004, 509, 217–252. [Google Scholar] [CrossRef]
- Sajeesh, P.; Sen, A.K. Particle separation and sorting in microfluidic devices: A review. Microfluid. Nanofluid. 2014, 17, 1–52. [Google Scholar] [CrossRef]
- Gu, Y.; Li, D. The ζ-potential of glass surface in contact with aqueous solutions. J. Colloid Interface Sci. 2000, 226, 328–339. [Google Scholar] [CrossRef]

| Material Properties | |
|---|---|
| Electrolyte density (ρ) | 998 kg/m3 |
| Viscosity (µ) | 0.001 Pa·s |
| Particle diameter | 1–25 µm |
| Cell density | 1050 kg/m3 |
| BCs | |
| Non-conducting walls | Slip velocity (Equation (4)) with ζ (V) |
| Conducting walls | Slip velocity (Equation (4)) with ζi (V) |
| Inlet | No viscous stress Electric potential (V0) Release of 100 particles |
| Outlet | No viscous stress Zero voltage (ground) Particle escape |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manshadi, M.K.D.; Saadat, M.; Mohammadi, M.; Sanati Nezhad, A. A Novel Electrokinetic-Based Technique for the Isolation of Circulating Tumor Cells. Micromachines 2023, 14, 2062. https://doi.org/10.3390/mi14112062
Manshadi MKD, Saadat M, Mohammadi M, Sanati Nezhad A. A Novel Electrokinetic-Based Technique for the Isolation of Circulating Tumor Cells. Micromachines. 2023; 14(11):2062. https://doi.org/10.3390/mi14112062
Chicago/Turabian StyleManshadi, Mohammad K. D., Mahsa Saadat, Mehdi Mohammadi, and Amir Sanati Nezhad. 2023. "A Novel Electrokinetic-Based Technique for the Isolation of Circulating Tumor Cells" Micromachines 14, no. 11: 2062. https://doi.org/10.3390/mi14112062
APA StyleManshadi, M. K. D., Saadat, M., Mohammadi, M., & Sanati Nezhad, A. (2023). A Novel Electrokinetic-Based Technique for the Isolation of Circulating Tumor Cells. Micromachines, 14(11), 2062. https://doi.org/10.3390/mi14112062







