Design of Optoelectronic Tracking Platform Driven by Ultrasonic Motor with a Novel Limiter
Abstract
:1. Introduction
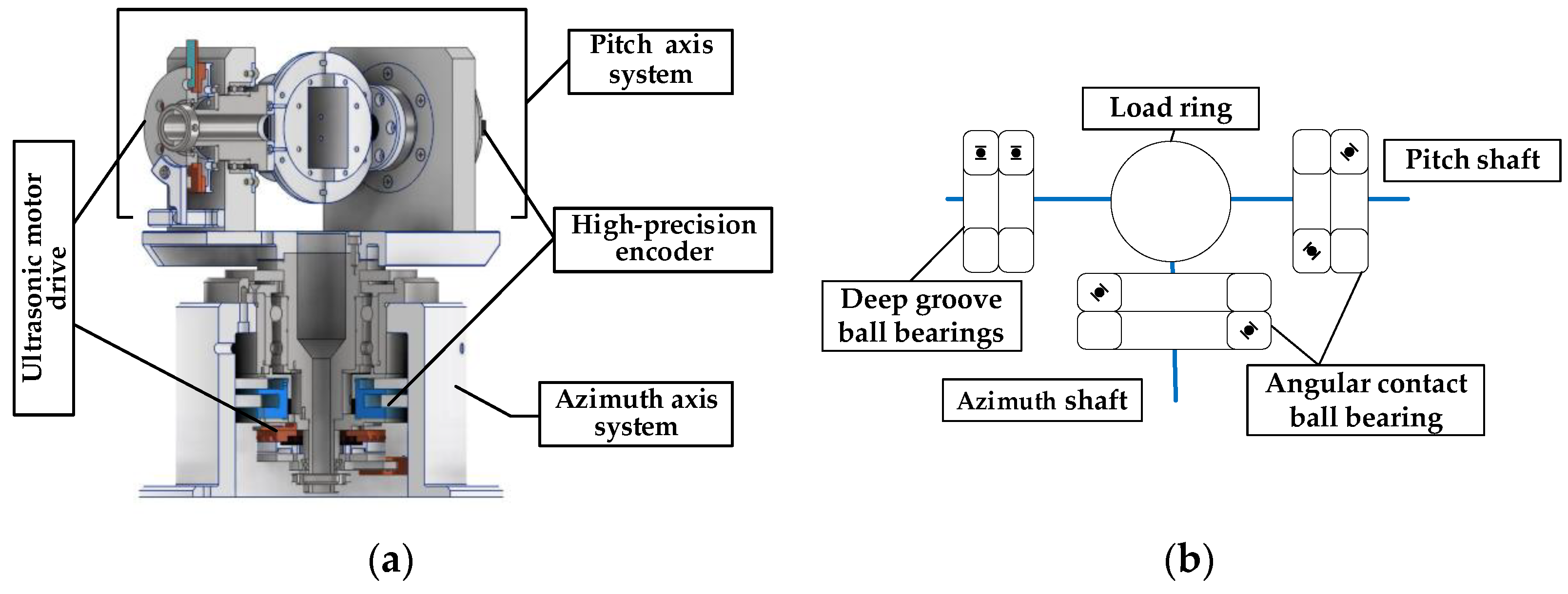
2. Structure of Tracking Platform
2.1. Main Structure
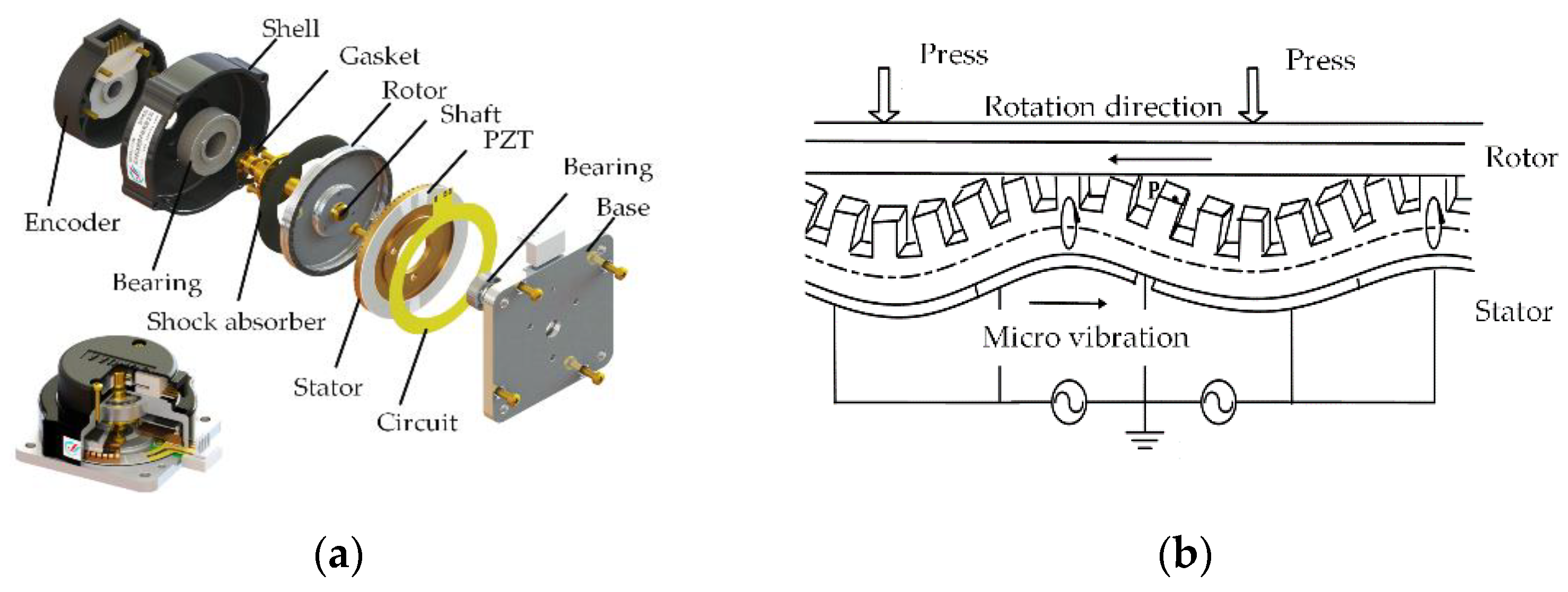
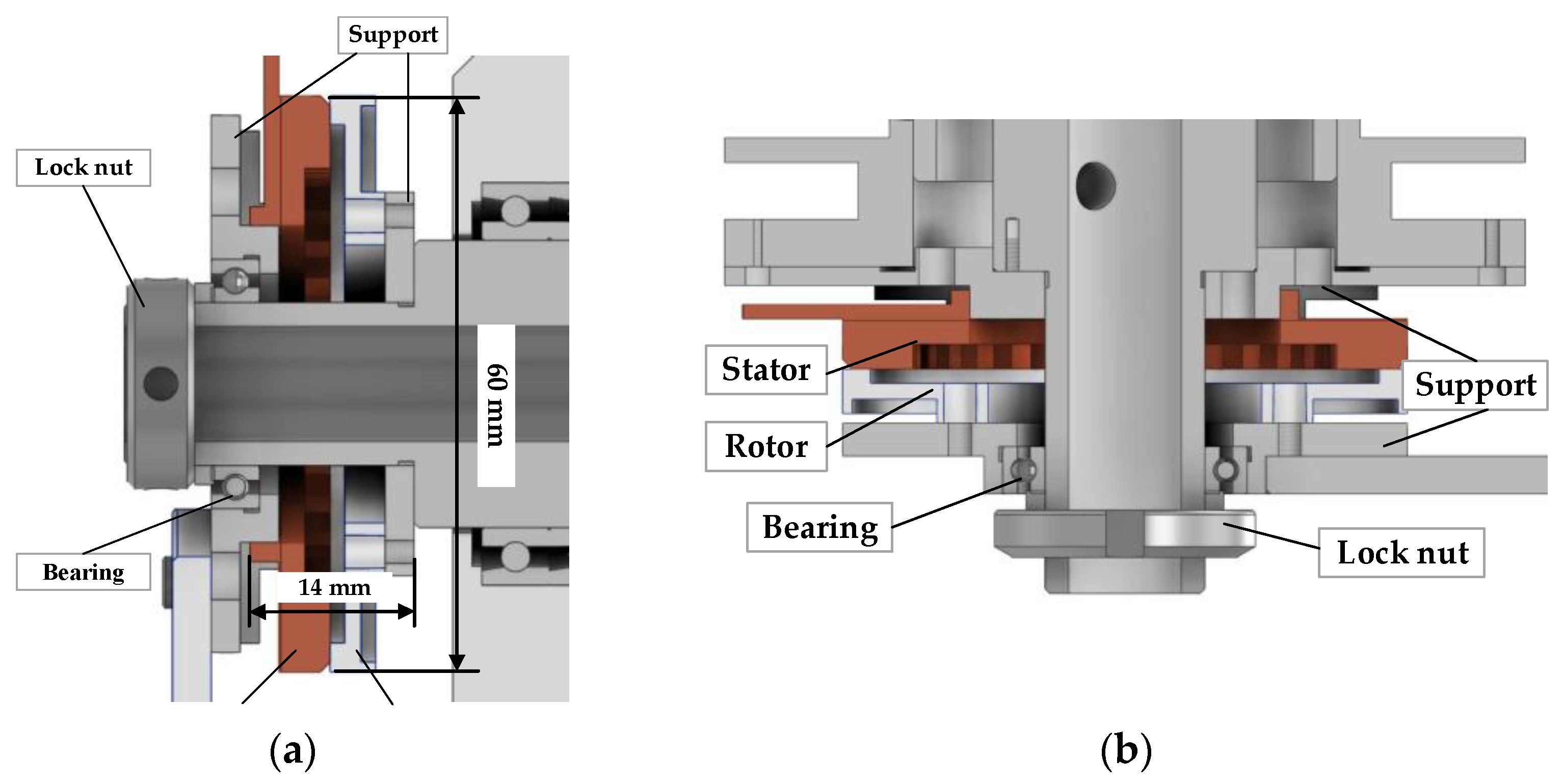
2.2. Ultrasonic Motor Drive Unit
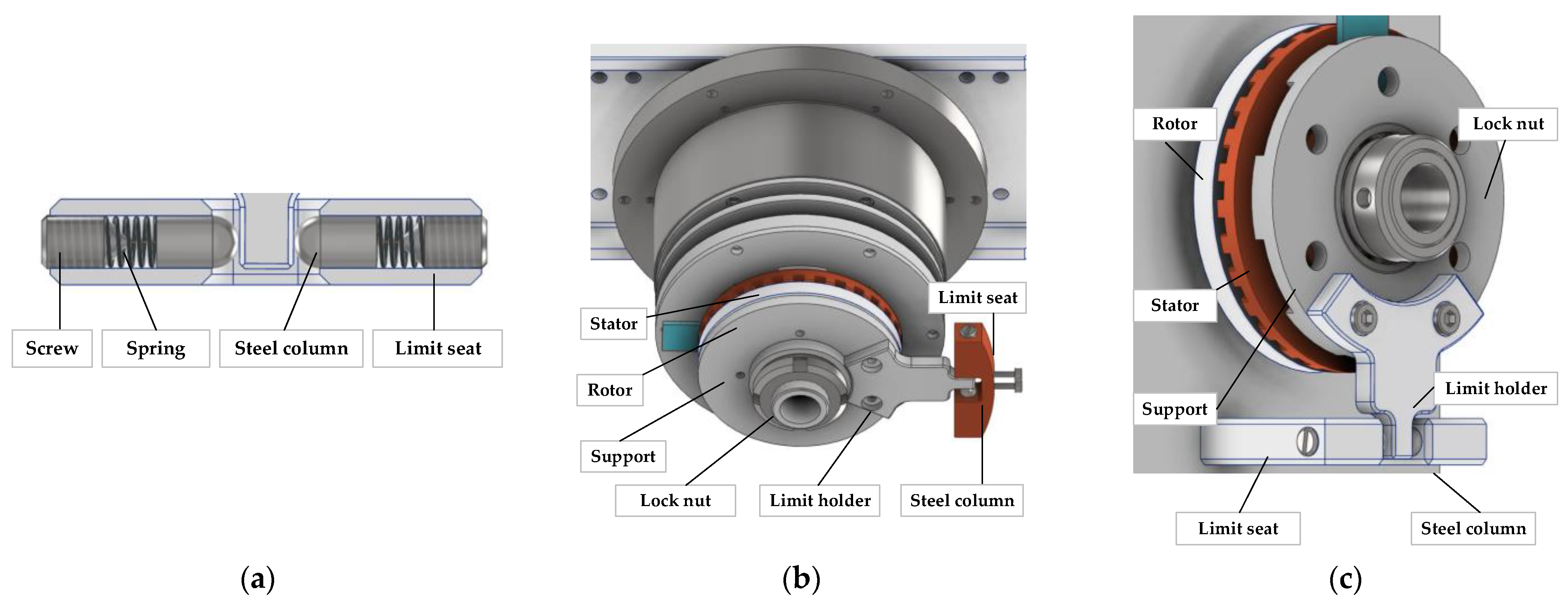
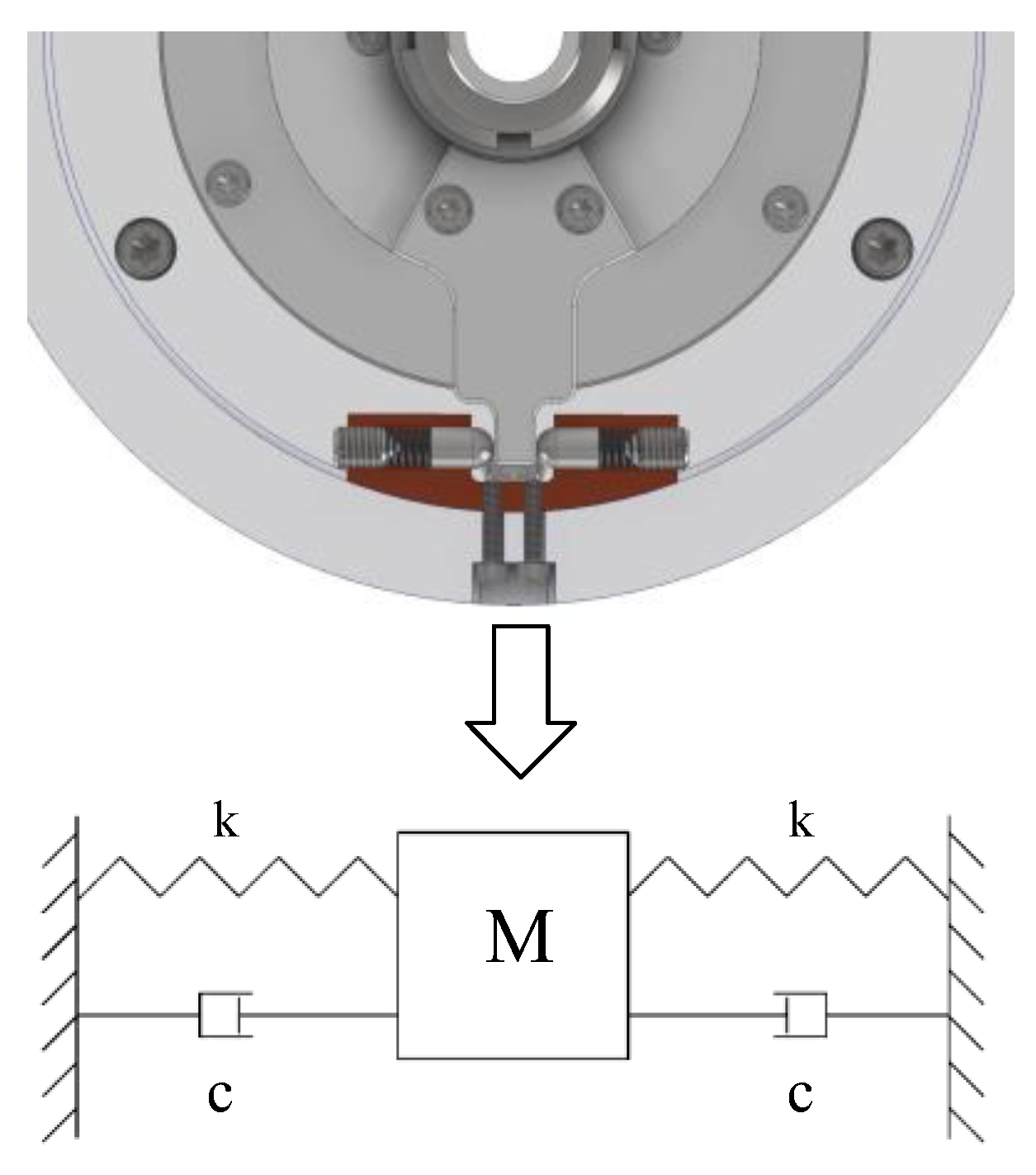
2.3. Mechanical Angle Limiter
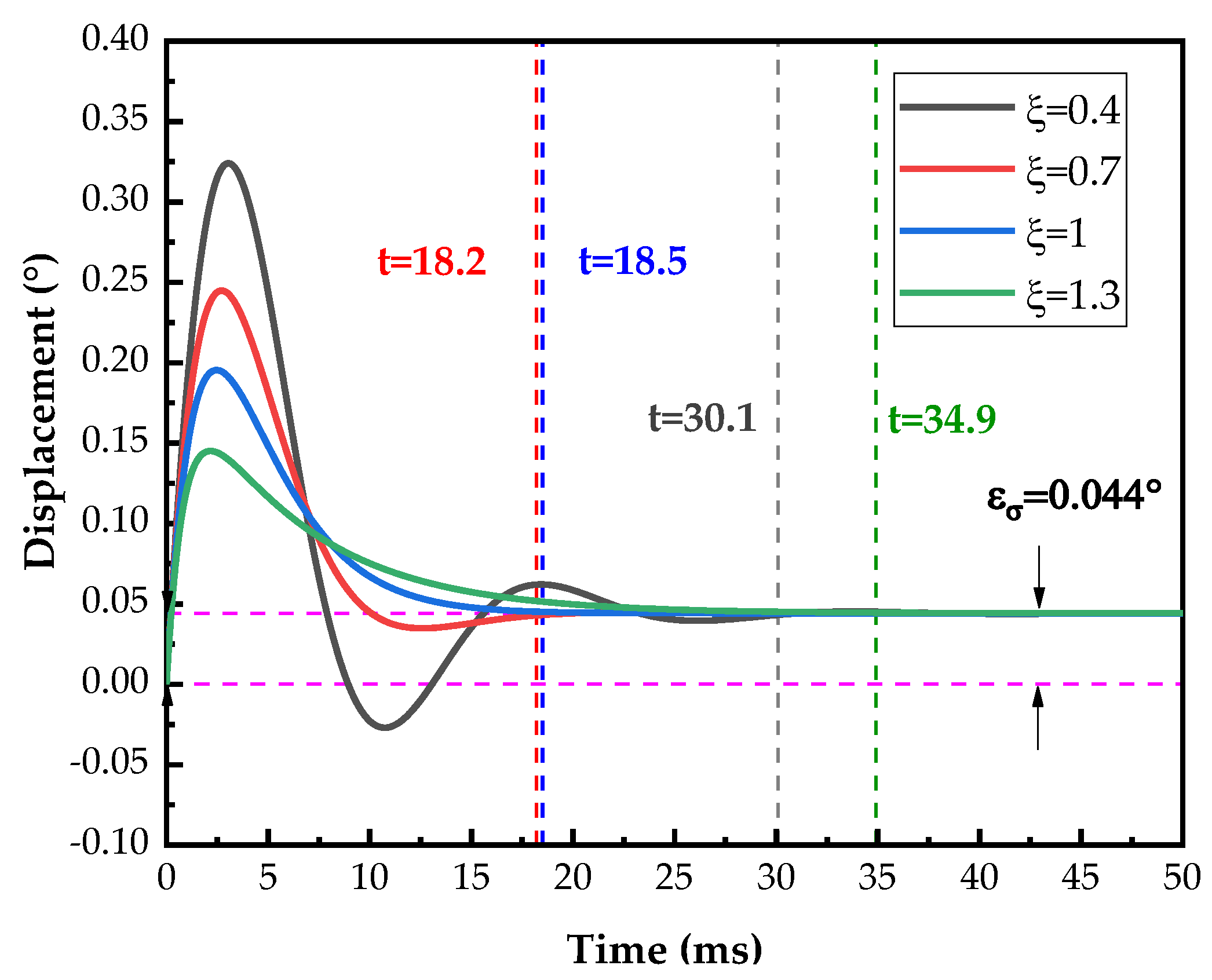
3. Shaft Motion Characteristics
Dynamic Characteristics
4. Experimental Analysis
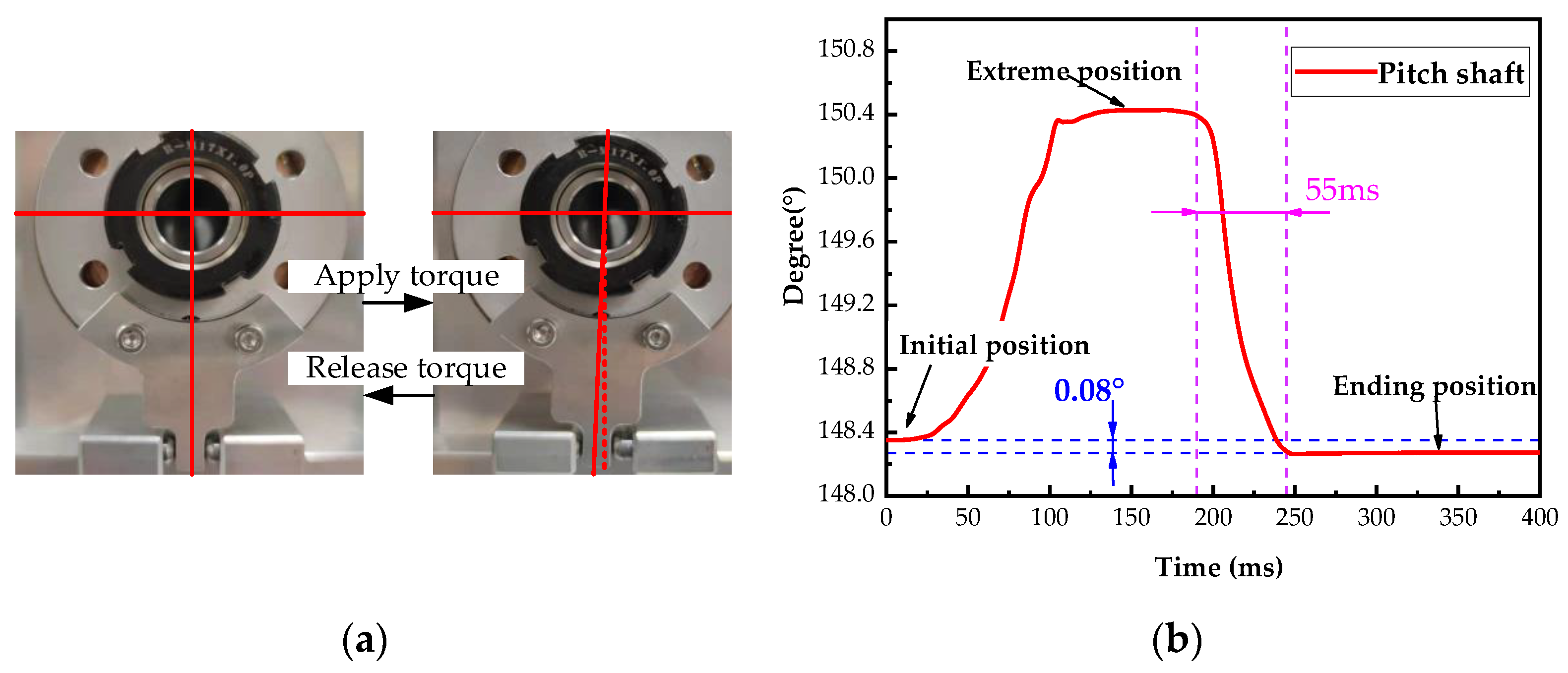
4.1. Response Characteristics at Limit Position
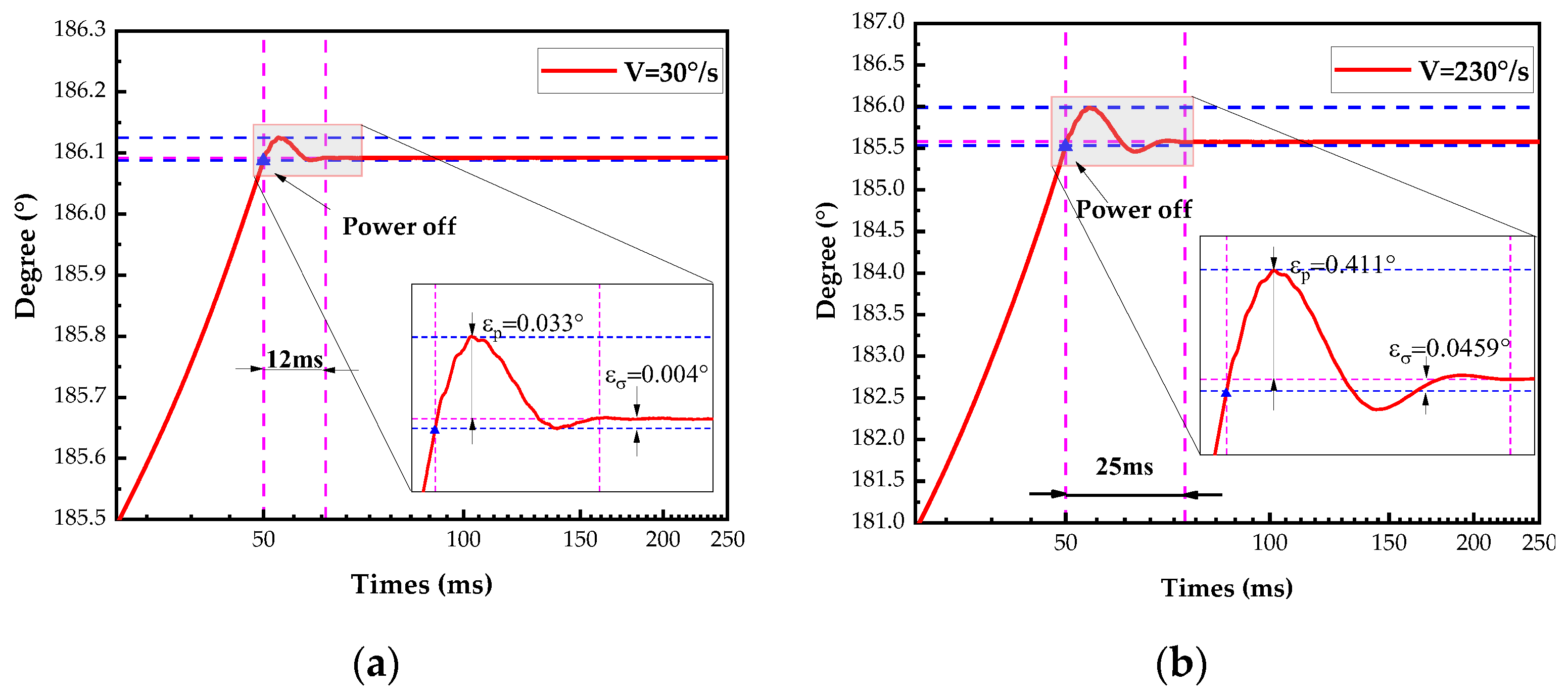
4.2. Response Characteristics at Different Velocities
4.2.1. The Complete Response of the Shaft
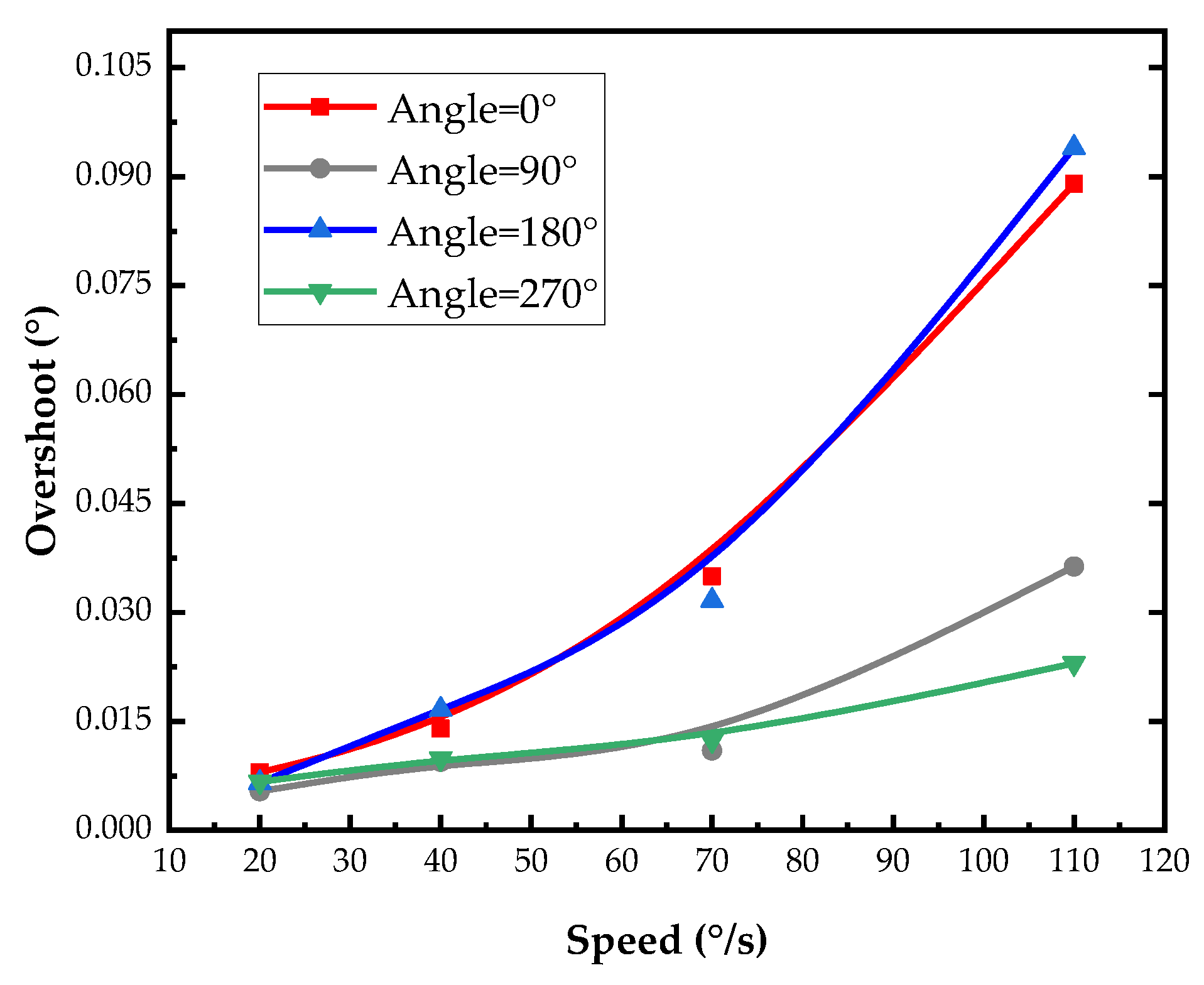
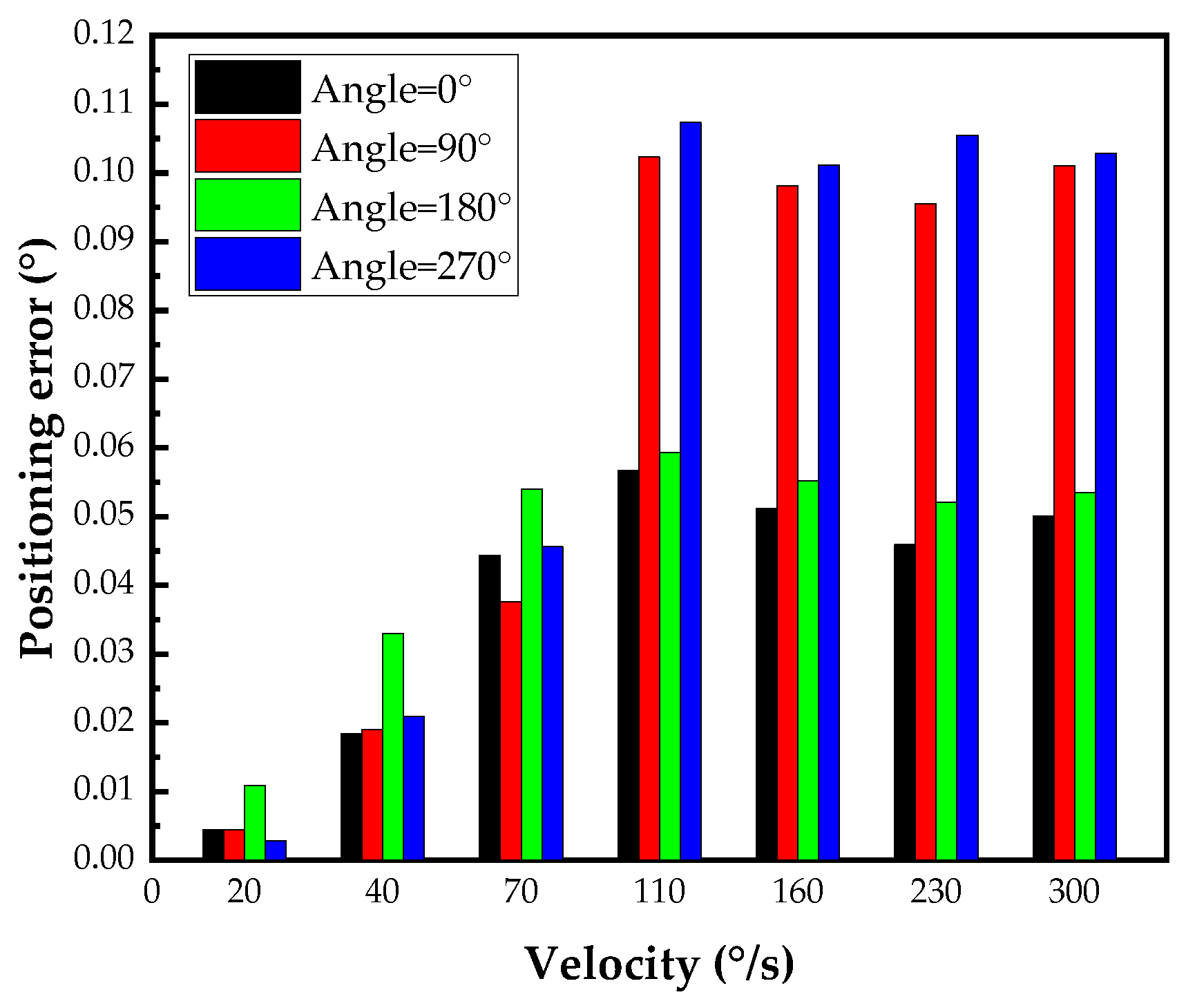
4.2.2. Shaft Overshoot and Positioning Error
5. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Masten, M.K.; Yang, W.; Ma, J.; Stockum, L.A. New tracking and measuring control system for optical and electronic theodolite. In Acquisition, Tracking, and Pointing XVI; SPIE: Bellingham, WA, USA, 2002; pp. 118–123. [Google Scholar]
- Hilkert, J.M. Inertially stabilized platform technology Concepts and principles. IEEE Control Syst. 2008, 28, 26–46. [Google Scholar] [CrossRef]
- Favell, N.B. Range-Finding with a Theodolite in Topographical Surveying. Emp. Surv. Rev. 2013, 5, 364–368. [Google Scholar] [CrossRef]
- Nguyen, T.T. High precision laser tracker system for contactless position measurement. In Proceedings of the 2011 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 25–27 November 2011. [Google Scholar]
- Li, G.; Gu, B.; Yang, D.; Wang, G.; Wang, Y. Structure Design and Analysis of the Special Mounting and Tracking System of the LAMOST. Proc. SPIE Int. Soc. Opt. Eng. 2003, 4837, 284–294. [Google Scholar]
- Thompson, W.E.; Walter, R.E.; Danny, H.; Donaldson, J.; Merritt, P.H. Stabilized Inertial Measurement System (SIMS). In Laser Weapons Technology III; SPIE: Bellingham, WA, USA, 2002; pp. 57–68. [Google Scholar]
- Gendreau, K.C.; Leitner, J.; Markley, L.; Cash, W.C.; Shipley, A.F. Requirements and Options for a Stable Inertial Reference Frame for a 100 µarcsecond Imaging Telescope. Proc. SPIE Int. Soc. Opt. Eng. 2003, 4852, 117–133. [Google Scholar]
- Masten, M.K.; Jono, T.; Toyoshima, M.; Takahashi, N.; Yamawaki, T.; Nakagawa, K.; Yamamoto, A.; Stockum, L.A. Laser tracking test under satellite microvibrational disturbances by OICETS ATP system. In Acquisition, Tracking, and Pointing XVI; SPIE: Bellingham, WA, USA, 2002; pp. 97–104. [Google Scholar]
- Campbell, M.F.; Reese, E.O. SOAR 4.2 Meter Telescope: Evolution of drive and pointing performance from early predictions to final testing. In Large Ground-Based Telescopes; SPIE: Bellingham, WA, USA, 2003; pp. 308–316. [Google Scholar]
- Hong, H.; Zhao, Z.; Xu, J.; Yuan, X. Tribo-dynamics Analysis of Satellite-bone Multi-axis Linkage System. J. Appl. Nonlinear Dyn. 2015, 4, 239–250. [Google Scholar]
- Wang, J.; Chen, T.; Qi, C.; Fang, Z. Method to improve the capability of electro-optical theodolite to track fast moving target. Proc. Spie Int. Soc. Opt. Eng. 2001, 4564, 238–244. [Google Scholar]
- Masten, M.K.; Ruffatto, D.; Brown, H.D.; Pohle, R.H.; Reiley, M.F.; Haddock, D.D.; Stockum, L.A. Stabilized high-accuracy optical tracking system (SHOTS). In Acquisition, Tracking, and Pointing XV; SPIE: Bellingham, WA, USA, 2001; pp. 10–18. [Google Scholar]
- Šabanović, A. Challenges in Motion Control Systems. IEEJ J. Ind. Appl. 2017, 6, 107–116. [Google Scholar] [CrossRef]
- Ruderman, M.; Iwasaki, M.; Chen, W.-H. Motion-control techniques of today and tomorrow: A review and discussion of the challenges of controlled motion. IEEE Ind. Electron. Mag. 2020, 14, 41–55. [Google Scholar] [CrossRef]
- Zhao, C. Ultrasonic Motors: Technologies and Applications; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- ADR-F Series. Available online: https://akribis-sys.com/products/frameless-rotary-motors/adr-f-series (accessed on 27 October 2023).
- Wu, Z.; Chen, Z.; Xu, B.; Pang, S.; Lin, F. Realization of Control Algorithm for Vehicle Optoelectronic Tracking Platform Based on Sliding Mode Control and Active Disturbance Rejection Control Optimized by Differential Evolution Algorithm. IEEE Access 2023, 11, 60386–60397. [Google Scholar] [CrossRef]
- Hu, X.; Han, S.; Liu, Y.; Wang, H. Two-Axis Optoelectronic Stabilized Platform Based on Active Disturbance Rejection Controller with LuGre Friction Model. Electronics 2023, 12, 1261. [Google Scholar] [CrossRef]
- Jiang, W.; Rao, C.; Cho, M.K.; Wei, K.; Zhang, X.; Wu, F.; Zhang, A.; Zhang, Y.; Xian, H.; Zhou, L.; et al. First observations on the 127-element adaptive optical system for 1.8m telescope. In Proceedings of the 5th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Large Mirrors and Telescopes, Dalian, China, 26–29 April 2010. [Google Scholar]
- Du, F.; Lewis, H.; Wang, D.; Bridger, A. The ultra-low speed research on friction drive of large telescope. In Advanced Software and Control for Astronomy; SPIE: Bellingham, WA, USA, 2006. [Google Scholar]
- Mohd Romlay, F.R.; Wan Yusoff, W.A.; Mat Piah, K.A. Increasing the efficiency of traveling wave ultrasonic motor by modifying the stator geometry. Ultrasonics 2016, 64, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Shogo Kumamoto, K.H.K.T. Improvement of driving efficiency of ultrasonic motor by improvement of vibration configuration. In Proceedings of the IEEE International Ultrasonics Symposium Proceedings, Chicago, IL, USA, 3–6 September 2014; pp. 2129–2132. [Google Scholar]
- Shi, J.; Lv, F.; Liu, B. Self-tuning speed control of ultrasonic motor combined with efficiency optimization. Int. J. Control. Autom. Syst. 2014, 12, 93–101. [Google Scholar] [CrossRef]
- Odomari, S.; Hieu, N.T.; Uchida, K.; Senjyu, T.; Yona, A. Robust Position Control for Ultrasonic Motor Using Variable Structure System Observer in Non-linear Observer. Electr. Power Compon. Syst. 2011, 39, 1769–1782. [Google Scholar] [CrossRef]
- Chen, N.; Zheng, J.; Jiang, X.; Fan, S.; Fan, D. Analysis and control of micro-stepping characteristics of ultrasonic motor. Front. Mech. Eng. 2020, 15, 585–599. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, W.; Liu, J.; Yang, X. A High-Power Linear Ultrasonic Motor Using Bending Vibration Transducer. IEEE Trans. Ind. Electron. 2013, 60, 5160–5166. [Google Scholar] [CrossRef]
- Chau, K.T.; Bin, S.; Min-Qiang, H.; Jin, L.; Ying, F. Microstepping control of ultrasonic stepping motors. IEEE Trans. Ind. Appl. 2006, 42, 436–442. [Google Scholar] [CrossRef]
- Chu, X.; Xing, Z.; Li, L.; Gui, Z. High resolution miniaturized stepper ultrasonic motor using differential composite motion. Ultrasonics 2004, 41, 737–741. [Google Scholar] [CrossRef]
- Ko, H.-P.; Jeong, H.; Koc, B. Piezoelectric actuator for mobile auto focus camera applications. J. Electroceram. 2008, 23, 530–535. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, G.; Nakamura, K.; Ueha, S. A robot finger joint driven by hybrid multi-DOF piezoelectric ultrasonic motor. Sens. Actuators A Phys. 2011, 169, 206–210. [Google Scholar] [CrossRef]
- Yong, Y.K.; Mohemani, S.O.R. Design of an Inertially Counterbalanced Z -Nanopositioner for High-Speed Atomic Force Microscopy. IEEE Trans. Nanotechnol. 2013, 12, 137–145. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, S.; Chu, X.; Gao, S.; Zhong, Z.; Zhu, C. Ultrasonic micro-motor with multilayer piezoelectric ceramic and chamfered driving tips. Rev. Sci. Instrum. 2016, 87, 095108. [Google Scholar] [CrossRef] [PubMed]
- Ogahara, Y.; Maeno, T. Torque characteristics analysis of a traveling wave type ultrasonic motor impressed high load torque in low speed rangeange. In Proceedings of the IEEE Ultrasonics Symposium, Montreal, QC, Canada, 23–27 August 2004; pp. 2271–2274. [Google Scholar]
- Zhang, B.; Wang, Z.; Wang, T. Development of two-axis non-magnetic turntable based on ultrasonic motor. Adv. Mech. Eng. 2019, 11, 1687814019828582. [Google Scholar] [CrossRef]
- Riddoch, D.J.; Cicirello, A.; Hills, D.A. Response of a mass-spring system subject to Coulomb damping and harmonic base excitation. Int. J. Solids Struct. 2020, 193–194, 527–534. [Google Scholar] [CrossRef]
- Kong, X.; Li, H.; Wu, C. Dynamics of 1-dof and 2-dof energy sink with geometrically nonlinear damping: Application to vibration suppression. Nonlinear Dyn. 2017, 91, 733–754. [Google Scholar] [CrossRef]
- Marino, L.; Cicirello, A. Coulomb friction effect on the forced vibration of damped mass–spring systems. J. Sound Vib. 2022, 535, 117085. [Google Scholar] [CrossRef]

| Motor Classification | Manufacturers | Stall Torque/ (N/m) | Speed without Load/(r/min) | Weight/ g | Maximum Efficiency/% | Self-Locking |
|---|---|---|---|---|---|---|
| EM, DC, Brush | Maxon | 0.0127 | 5200 | 38 | 70 | No |
| EM, DC, Brush | Aeroflcx | 0.00988 | 4000 | 256 | 20 | No |
| EM, Alternating voltage/current, Three phases | Astro | 0.0755 | 11,500 | 340 | 20 | No |
| EM, DC, Brushless | Akribis | 1.95 | 1500 | 350 | 80 | No |
| USM, Traveling wave type, 60 | PDLab | 1.2 | 180 | 250 | 30 | Yes |
| USM, Traveling wave type, 60 | Proposed USM | 1.5 | 180 | 285 | 30 | Yes |
| Parameter | Value |
|---|---|
| Size | 174 mm × 208 mm × 170 mm |
| Azimuth angle | 360° × N |
| Pitch angle | −80°/s~80°/s |
| Positioning accuracy | <0.02° |
| Positioning time | <2 s |
| Angular velocity | 0.005°/s~180°/s |
| Angular acceleration | >120°/s2 |
| Self-locking torque | >2.5 Nm |
| Parameter | Description | Value |
|---|---|---|
| J (kg·m2) | Rotational inertia | 8 × 10−5 |
| l (mm) | Length of limit holder | 45 |
| k (N·mm) | Elasticity of spring | 3.9 |
| lz (mm) | Eccentric gravity center | 0.75 |
| G (g) | Weight of load | 93 |
| Author | Motor | Positioning Accuracy | Positioning Time | Self-Locking Torque |
|---|---|---|---|---|
| Proposed platform | USM | <0.02° (open-loop, velocities < 30°/s) | <12 ms | >2.5 Nm |
| Bo Zhang [34] | USM | <0.00017° (closed-loop) | 0.5 s~2 s | >4.4 Nm |
| Zhaolong Wu [17] | PMSM | <0.057°(closed-loop) | <15 ms (tracking unit step) | - |
| Xueyan Hu [18] | PMSM | 0.0542° (closed-loop) | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Pan, S.; Chen, L. Design of Optoelectronic Tracking Platform Driven by Ultrasonic Motor with a Novel Limiter. Micromachines 2023, 14, 2067. https://doi.org/10.3390/mi14112067
Liang Y, Pan S, Chen L. Design of Optoelectronic Tracking Platform Driven by Ultrasonic Motor with a Novel Limiter. Micromachines. 2023; 14(11):2067. https://doi.org/10.3390/mi14112067
Chicago/Turabian StyleLiang, Yongjin, Song Pan, and Lei Chen. 2023. "Design of Optoelectronic Tracking Platform Driven by Ultrasonic Motor with a Novel Limiter" Micromachines 14, no. 11: 2067. https://doi.org/10.3390/mi14112067
APA StyleLiang, Y., Pan, S., & Chen, L. (2023). Design of Optoelectronic Tracking Platform Driven by Ultrasonic Motor with a Novel Limiter. Micromachines, 14(11), 2067. https://doi.org/10.3390/mi14112067






