Design of a Femtosecond Laser Percussion Drilling Process for Ni-Based Superalloys Based on Machine Learning and the Genetic Algorithm
Abstract
:1. Introduction
2. Materials and Methods
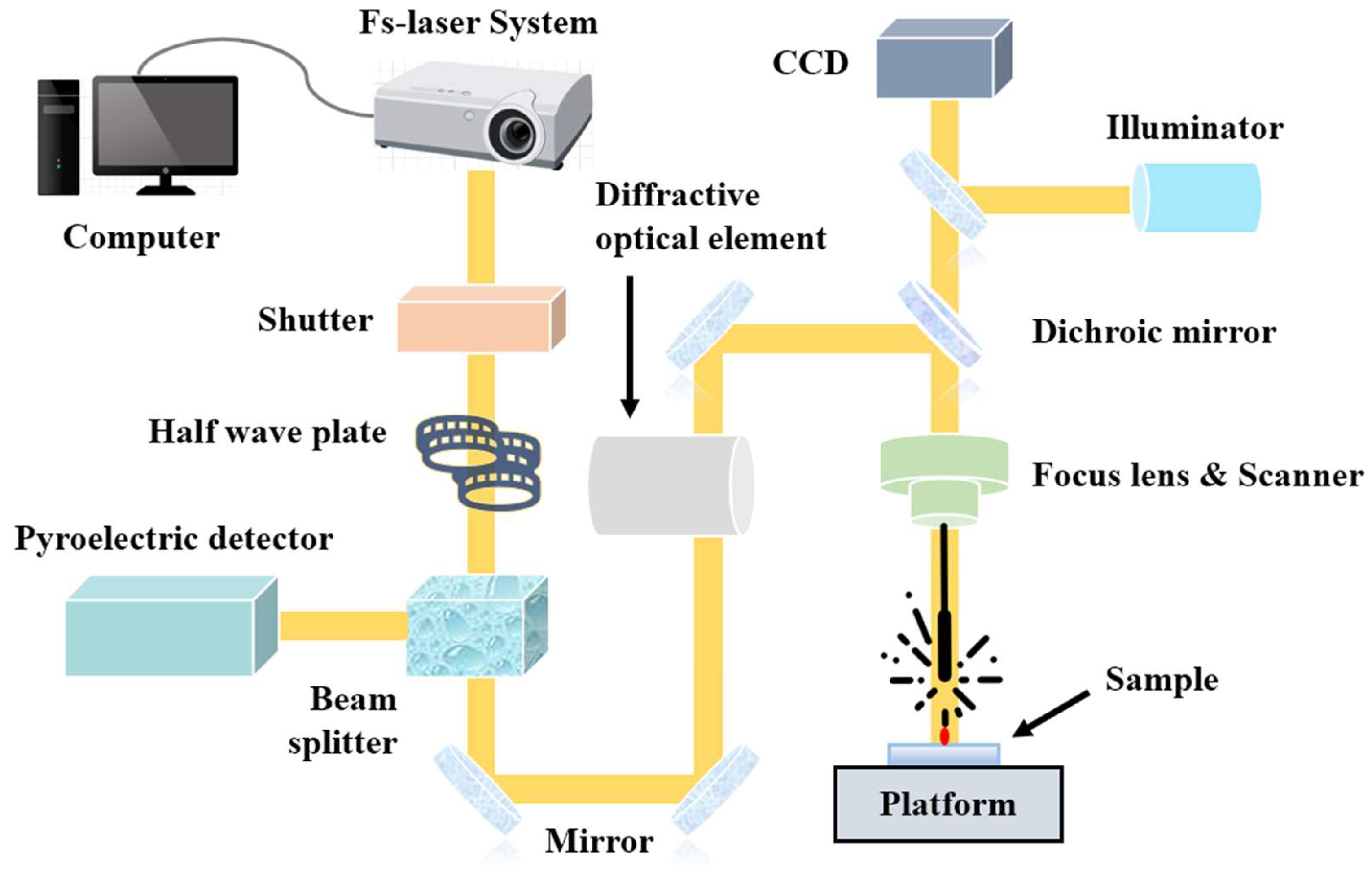
2.1. Materials and Experimental Facilities
2.2. Simulation of Machine Learning
3. Results and Discussion
3.1. Dataset Collection
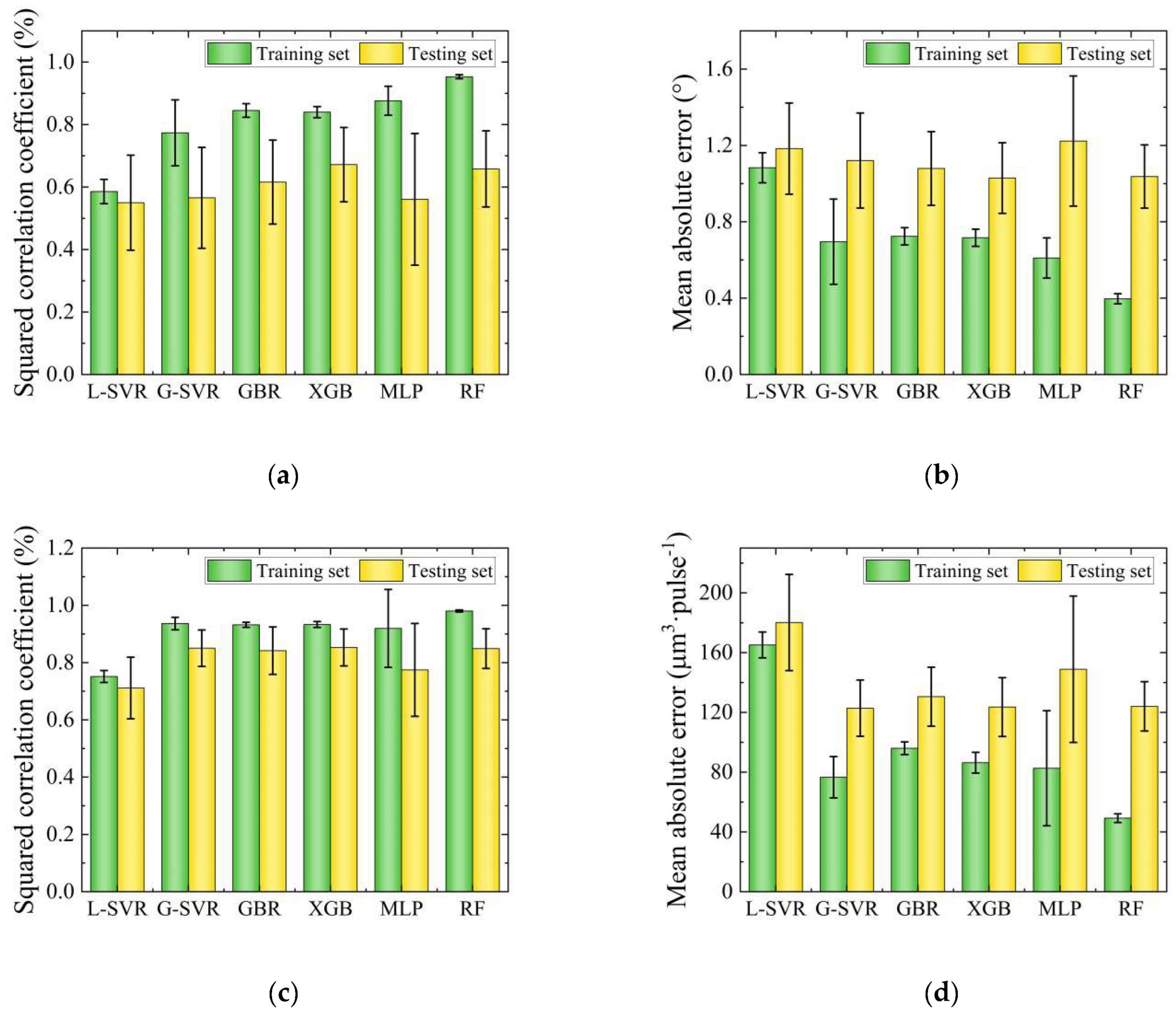
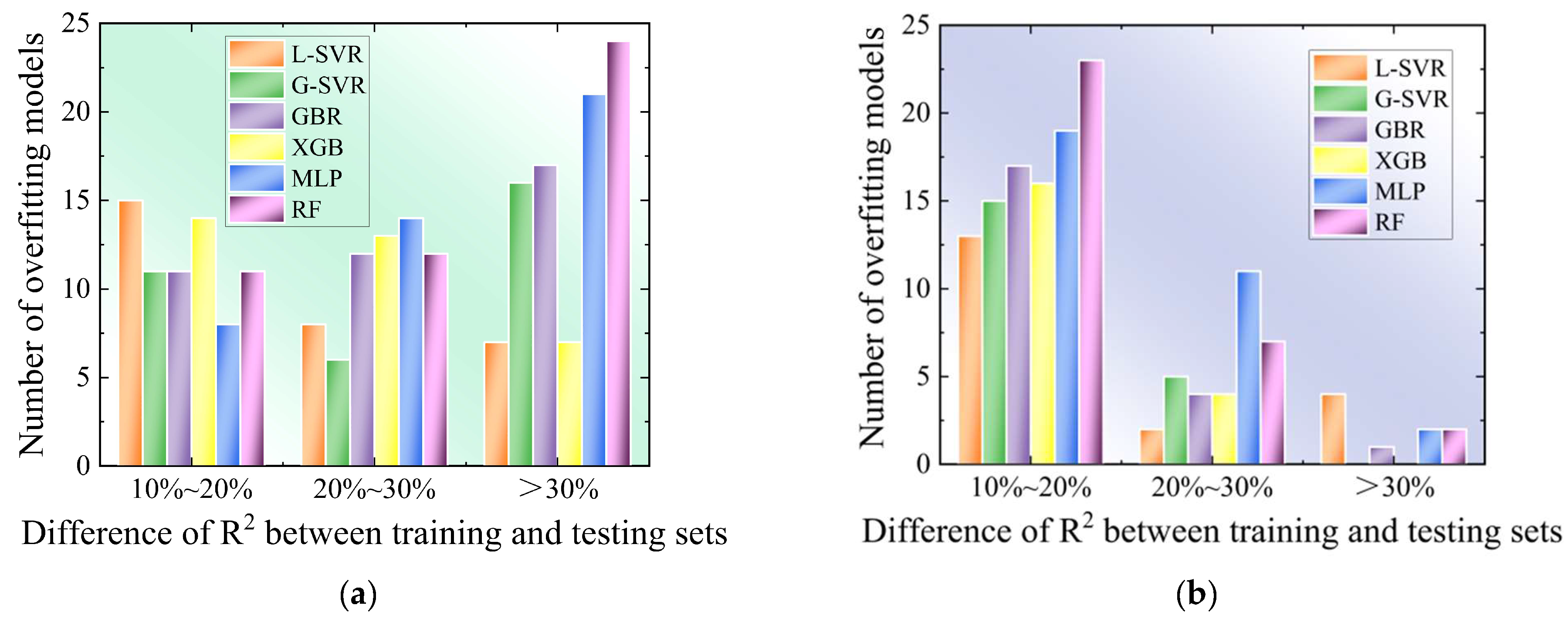
3.2. Selection of Machine Learning Algorithms
3.3. Feature Analysis and Building Prediction Models
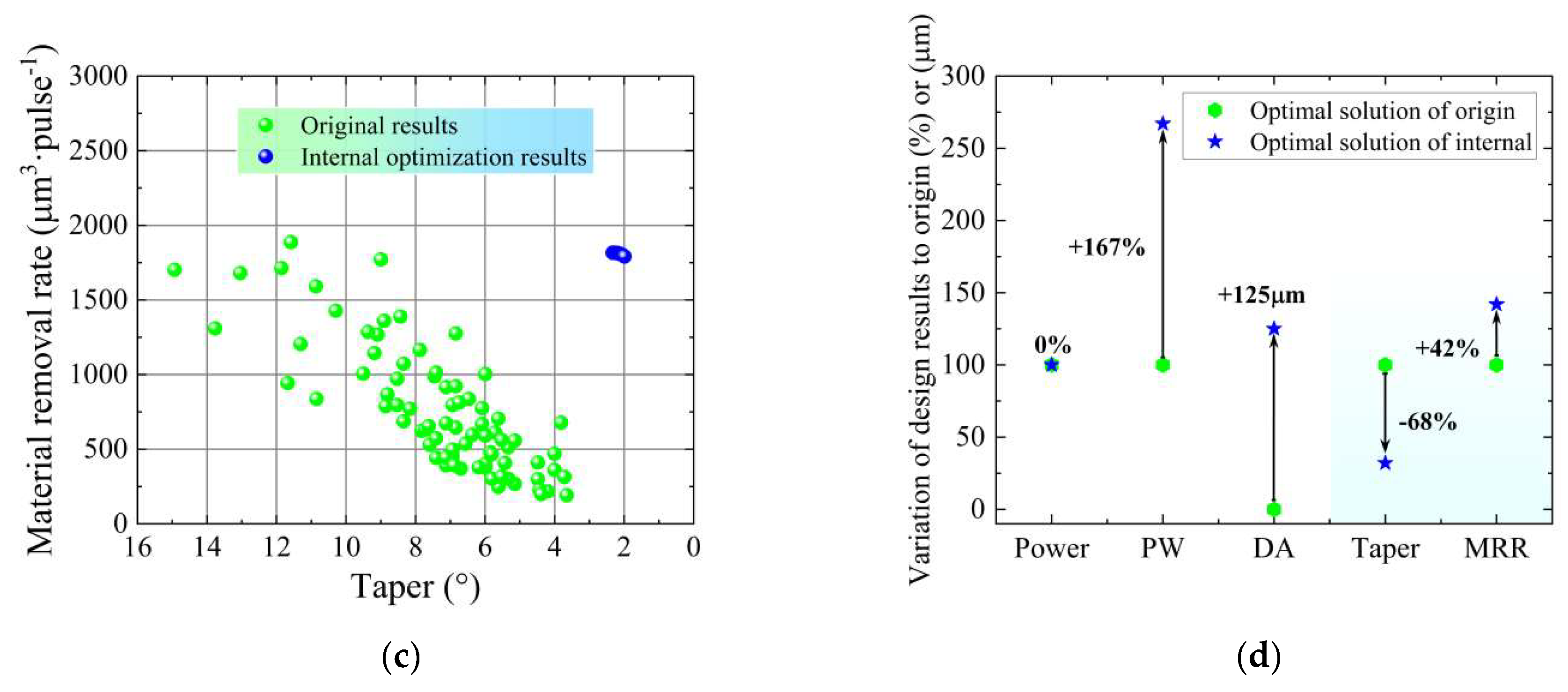
3.4. Process Design within the Range of the Original Dataset
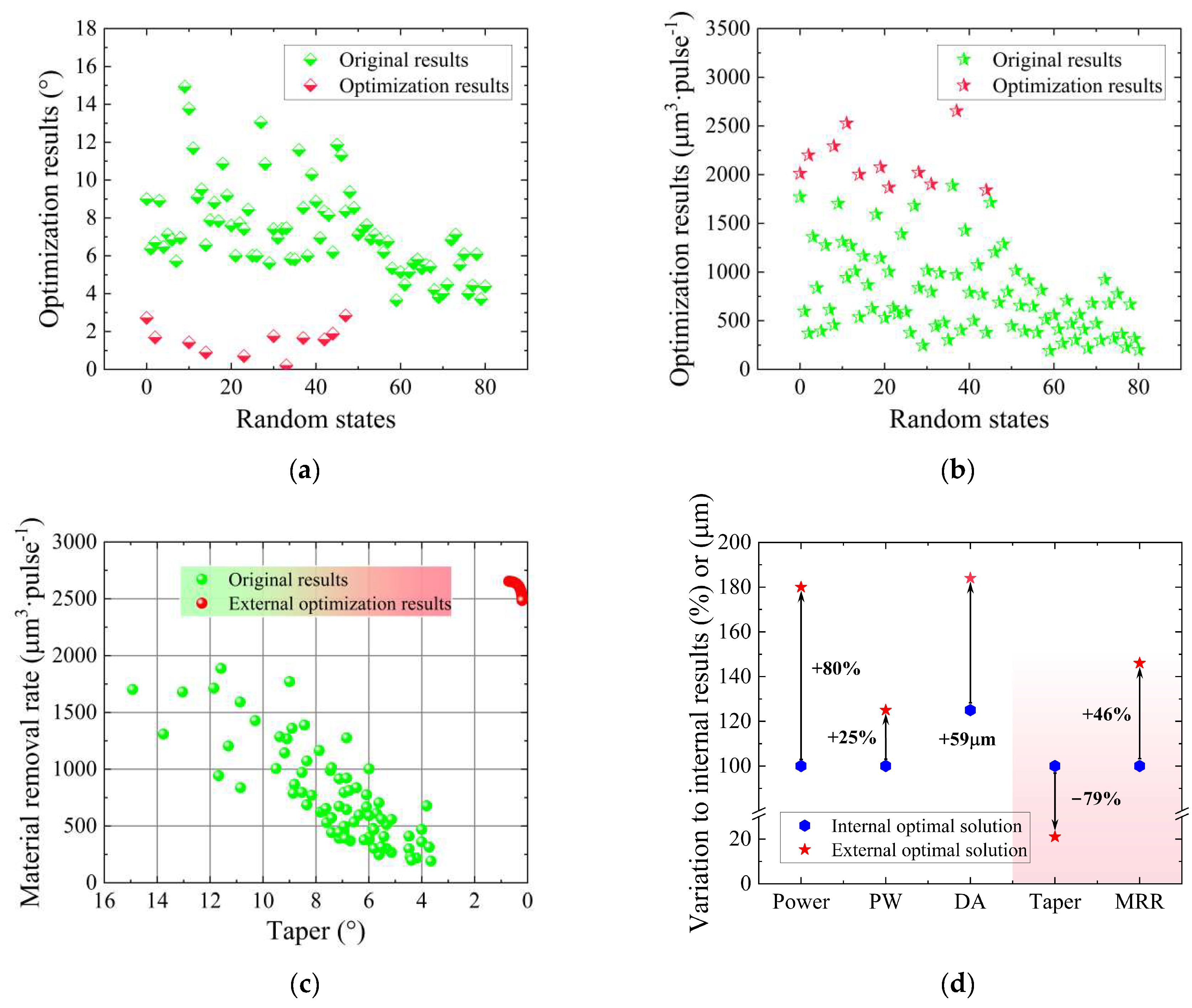
3.5. Process Design Outside of the Range of the Original Dataset
4. Conclusions
- Through a comparison of generalization ability and overfitting analysis, six machine learning methods were gradually refined. G-SVR, GBR and XGB were selected for the further establishment of the prediction model owing to their good levels of accuracy and stability. In addition, it was observed that the frequency feature had the lowest Pearson correlation coefficient and MDA value for both taper and the MRR.
- To enhance the model accuracy and reduce overfitting, G-SVR, GBR and XGB prediction models were established using three input features, excluding the frequency feature based on the feature analysis. Among these, the G-SVR prediction model demonstrated higher accuracy for taper and the MRR; the R2 values using the training set and testing set were 69.5% and 62.9% for taper, and 90% and 85.8% for the MRR, respectively, while the MAE values in the training set and testing set were 0.865° and 1.03° for taper, and 97.1 and 115 μm3·pulse−1 for MRR, respectively.
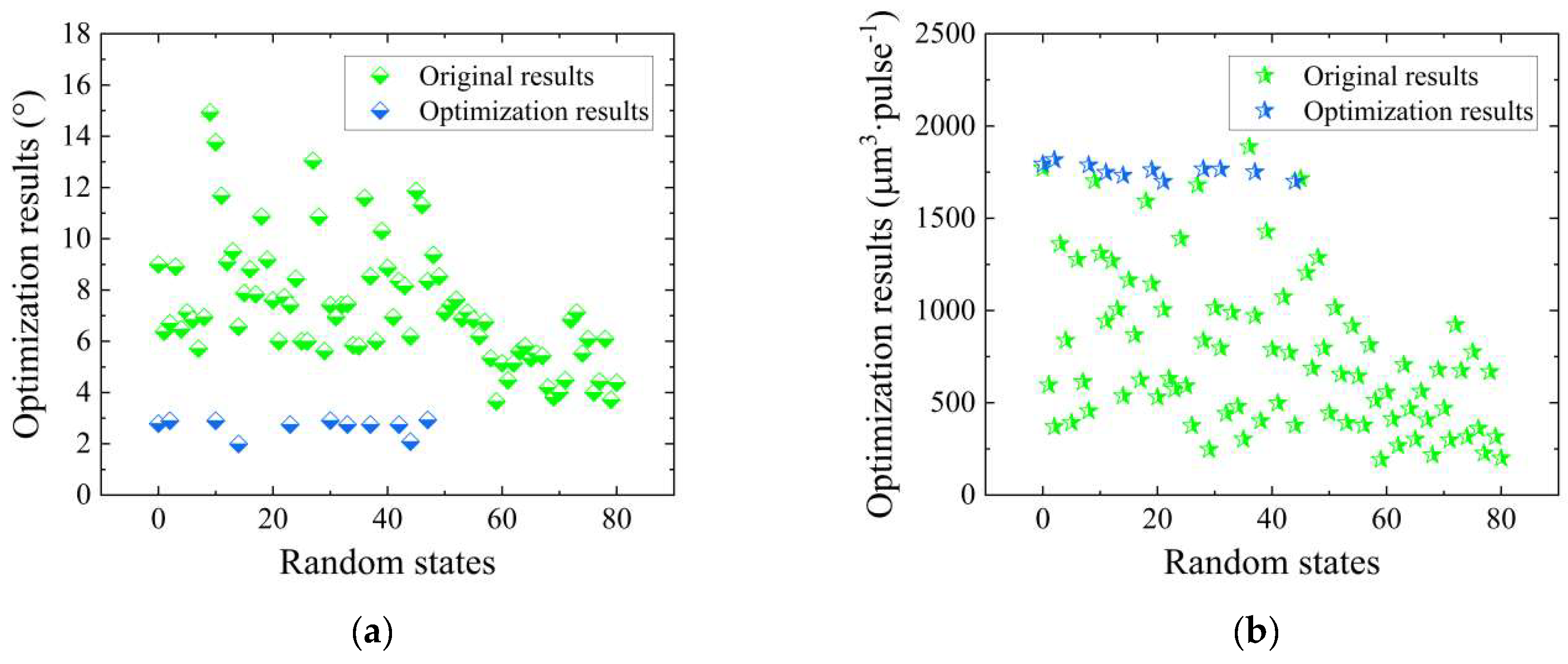
- Combined with the GA, the double-objective performance was optimized within the range of original data. The optimal result for taper was reduced by 68%, while the MRR was increased by 42% compared to the original optimal data.
- To achieve more generalized design outcomes, the GA was employed to optimize the double-objective performance outside the original data range. As a result, taper and the MRR were reduced and increased by 79% and 46% respectively, compared to the optimal results within the original data range. Furthermore, taper and the MRR were reduced and increased by 93% and 107%, respectively, compared to the original optimum data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Zhang, Z.; Yang, Z.; Wang, C. Femtosecond Laser-Induced Evolution of Surface Micro-Structure in Depth Direction of Nickel-Based Alloy. Appl. Sci. 2022, 12, 8464. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, Y. Electrochemical machining of complex components of aero-engines: Developments, trends, and technological advances. Chin. J. Aeronaut. 2021, 34, 28–53. [Google Scholar] [CrossRef]
- Sato, A.; Chiu, Y.L.; Reed, R.C. Oxidation of nickel-based single-crystal superalloys for industrial gas turbine applications. Acta Mater. 2011, 59, 225–240. [Google Scholar] [CrossRef]
- Yang, Z.; Ji, P.; Zhang, Z.; Ju, Y.; Wang, Z.; Zhang, Q.; Wang, C.; Xu, W. Fundamental 3D simulation of the femtosecond laser ablation for cooling hole drilling on Ni and Fe based aero-engine components. Opt. Commun. 2020, 475, 126237. [Google Scholar] [CrossRef]
- Bunker, R.S. A review of shaped hole turbine film-cooling technology. J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Dutta, S.; Kaur, I.; Singh, P. Review of Film Cooling in Gas Turbines with an Emphasis on Additive Manufacturing-Based Design Evolutions. Energies 2022, 15, 6968. [Google Scholar] [CrossRef]
- Wong, Y.S.; Rahman, M.; Lim, H.S.; Han, H.; Ravi, N. Investigation of micro-EDM material removal characteristics using single RC-pulse discharges. J. Mater. Process. Technol. 2003, 140, 303–307. [Google Scholar] [CrossRef]
- Duan, W.; Mei, X.; Fan, Z.; Li, J.; Wang, K.; Zhang, Y. Electrochemical corrosion assisted laser drilling of micro-hole without recast layer. Optik 2020, 202, 163577. [Google Scholar] [CrossRef]
- Qi, Y.; Qi, H.; Chen, A.; Hu, Z. Improvement of aluminum drilling efficiency and precision by shaped femtosecond laser. Appl. Surf. Sci. 2014, 317, 252–256. [Google Scholar] [CrossRef]
- Butkute, A.; Jonusauskas, L. 3D Manufacturing of Glass Microstructures Using Femtosecond Laser. Micromachines 2021, 12, 499. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Zhang, Y.; Wang, C.; Zhang, S.; Yang, Z.; Xu, W. Optimization of low-power femtosecond laser trepan drilling by machine learning and a high-throughput multi-objective genetic algorithm. Opt. Laser Technol. 2022, 148, 107688. [Google Scholar] [CrossRef]
- Wen, Z.; Pei, H.; Yang, H.; Wu, Y.; Yue, Z. A combined CP theory and TCD for predicting fatigue lifetime in single-crystal superalloy plates with film cooling holes. Int. J. Fatigue 2018, 111, 243–255. [Google Scholar] [CrossRef]
- Wang, R.; Wang, K.; Fan, Z.; Sun, X.; Dong, X.; Mei, X.; Zhang, W. A comparative study on high pulse energy femtosecond laser drilling of high-aspect-ratio holes under different pressure conditions. J. Manuf. Process. 2023, 85, 492–502. [Google Scholar] [CrossRef]
- Corcoran, A.; Sexton, L.; Seaman, B.; Ryan, P.; Byrne, G. The laser drilling of multi-layer aerospace material systems. J. Mater. Process. Technol. 2002, 123, 100–106. [Google Scholar] [CrossRef]
- Gurav, M.M.; Gupta, U.; Dabade, U.A. Quality evaluation of precision micro holes drilled using pulsed Nd:YAG laser on aerospace nickel-based superalloy. Mater. Today Proc. 2019, 19, 575–582. [Google Scholar] [CrossRef]
- Feng, Q.; Picard, Y.; McDonald, J.; Van Rompay, P.; Yalisove, S.; Pollock, T. Femtosecond laser machining of single-crystal superalloys through thermal barrier coatings. Mater. Sci. Eng. A 2006, 430, 203–207. [Google Scholar] [CrossRef]
- Chaki, S.; Bathe, R.N.; Ghosal, S.; Padmanabham, G. Multi-objective optimization of pulsed Nd:YAG laser cutting process using integrated ANN–NSGAII model. J. Intell. Manuf. 2015, 29, 175–190. [Google Scholar] [CrossRef]
- D’Addona, D.M.; Genna, S.; Leone, C.; Matarazzo, D. Prediction of Poly-methyl-methacrylate Laser Milling Process Characteristics Based on Neural Networks and Fuzzy Data. Procedia CIRP 2016, 41, 981–986. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Jiang, R.; Zhang, X.; Xiong, Y.; Mao, Z. Investigation on geometric precision and surface quality of microholes machined by ultrafast laser. Opt. Laser Technol. 2020, 121, 105834. [Google Scholar] [CrossRef]
- Wang, R.; Dong, X.; Wang, K.; Sun, X.; Fan, Z.; Duan, W. Two-step approach to improving the quality of laser micro-hole drilling on thermal barrier coated nickel base alloys. Opt. Lasers Eng. 2019, 121, 406–415. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Z.; Jing, X.; Yang, Z.; Xu, W. Optimization of multistage femtosecond laser drilling process using machine learning coupled with molecular dynamics. Opt. Laser Technol. 2022, 156, 108442. [Google Scholar] [CrossRef]
- Wang, M.; Yang, L.; Zhang, S.; Wang, Y. Experimental investigation on the spiral trepanning of K24 superalloy with femtosecond laser. Opt. Laser Technol. 2018, 101, 284–290. [Google Scholar] [CrossRef]
- Kurani, A.; Doshi, P.; Vakharia, A.; Shah, M. A Comprehensive Comparative Study of Artificial Neural Network (ANN) and Support Vector Machines (SVM) on Stock Forecasting. Ann. Data Sci. 2021, 10, 183–208. [Google Scholar] [CrossRef]
- Liu, X.; Xu, P.; Zhao, J.; Lu, W.; Li, M.; Wang, G. Material machine learning for alloys: Applications, challenges and perspectives. J. Alloys Compd. 2022, 921, 165984. [Google Scholar] [CrossRef]
- Ilyas, N.; Shahzad, A.; Kim, K. Convolutional-neural network-based image crowd counting: Review, categorization, analysis, and performance evaluation. Sensors 2020, 20, 43. [Google Scholar] [CrossRef] [PubMed]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- van der Aalst, W.M.P.; Rubin, V.; Verbeek, H.M.W.; van Dongen, B.F.; Kindler, E.; Günther, C.W. Process mining: A two-step approach to balance between underfitting and overfitting. Softw. Syst. Model. 2008, 9, 87–111. [Google Scholar] [CrossRef]
- Reddy, G.T.; Reddy, M.P.K.; Lakshmanna, K.; Kaluri, R.; Rajput, D.S.; Srivastava, G.; Baker, T. Analysis of Dimensionality Reduction Techniques on Big Data. IEEE Access 2020, 8, 54776–54788. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, T.-H.; Ergün, T. The instability of the Pearson correlation coefficient in the presence of coincidental outliers. Financ. Res. Lett. 2015, 13, 243–257. [Google Scholar] [CrossRef]
- Wei, J.; Chu, X.; Sun, X.Y.; Xu, K.; Deng, H.X.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Han, H.; Yu, R.; Li, B.; Zhang, Y. Multi-objective optimization of corrugated tube inserted with multi-channel twisted tape using RSM and NSGA-II. Appl. Therm. Eng. 2019, 159, 113731. [Google Scholar] [CrossRef]





| Variables | Maximum | Minimum | Average | Standard Deviation | |
|---|---|---|---|---|---|
| Inputs | Power (W) | 20 | 5 | 11.67 | 6.28 |
| Pulse width (fs) | 800 | 300 | 533.33 | 206.76 | |
| Frequency (kHz) | 200 | 100 | 150 | 41.08 | |
| Defocusing amount (μm) | 150 | −150 | 0 | 123.24 | |
| Outputs | Taper (°) | 14.93 | 3.65 | 7.28 | 2.34 |
| Material removal rate (μm3·pulse−1) | 1887.67 | 192.21 | 757.68 | 421.37 |
| Type | Population | Generation | Crossover | Mutation |
|---|---|---|---|---|
| Single-objective optimization | 50 | 200 | 0.9 | 0.09 |
| Double-objective optimization | 100 | 500 | 0.9 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Yu, Y.; Sun, R.; Zhao, W.; Guo, H.; Zhang, Z.; Wang, C. Design of a Femtosecond Laser Percussion Drilling Process for Ni-Based Superalloys Based on Machine Learning and the Genetic Algorithm. Micromachines 2023, 14, 2110. https://doi.org/10.3390/mi14112110
Zhao Z, Yu Y, Sun R, Zhao W, Guo H, Zhang Z, Wang C. Design of a Femtosecond Laser Percussion Drilling Process for Ni-Based Superalloys Based on Machine Learning and the Genetic Algorithm. Micromachines. 2023; 14(11):2110. https://doi.org/10.3390/mi14112110
Chicago/Turabian StyleZhao, Zhixi, Yunhe Yu, Ruijia Sun, Wanrong Zhao, Hao Guo, Zhen Zhang, and Chenchong Wang. 2023. "Design of a Femtosecond Laser Percussion Drilling Process for Ni-Based Superalloys Based on Machine Learning and the Genetic Algorithm" Micromachines 14, no. 11: 2110. https://doi.org/10.3390/mi14112110
APA StyleZhao, Z., Yu, Y., Sun, R., Zhao, W., Guo, H., Zhang, Z., & Wang, C. (2023). Design of a Femtosecond Laser Percussion Drilling Process for Ni-Based Superalloys Based on Machine Learning and the Genetic Algorithm. Micromachines, 14(11), 2110. https://doi.org/10.3390/mi14112110








