Research on Geometric Constraint Strategies for Controlling the Diameter of Micro-Shafts Manufactured via Wire Electric Discharge Grinding
Abstract
:1. Introduction
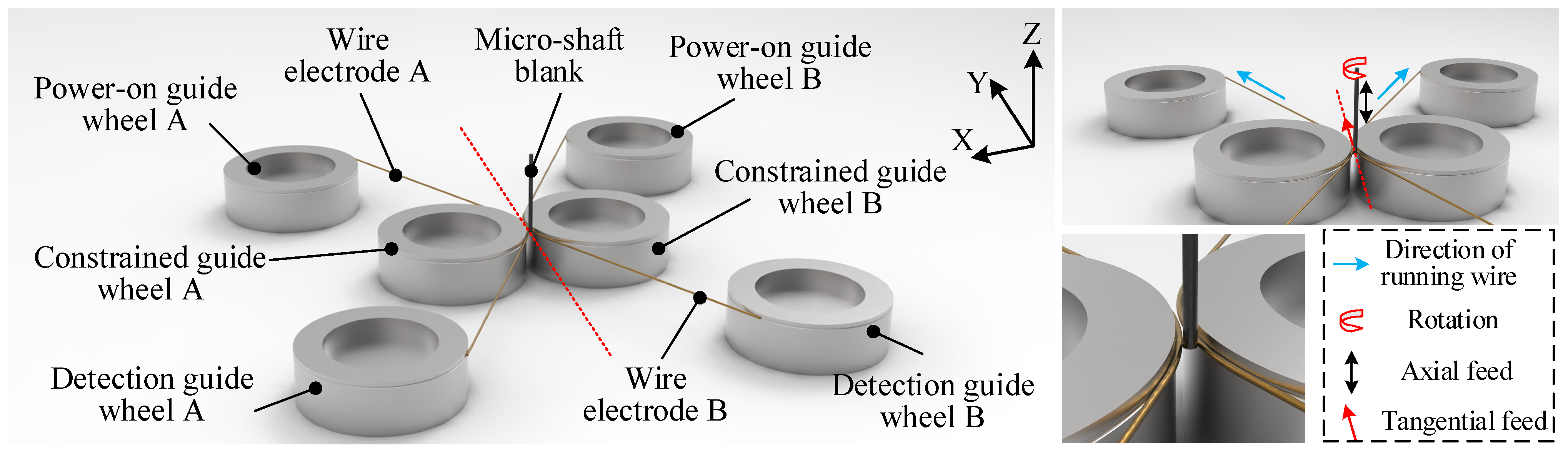
2. The TMTF–WEDG Method and Analysis
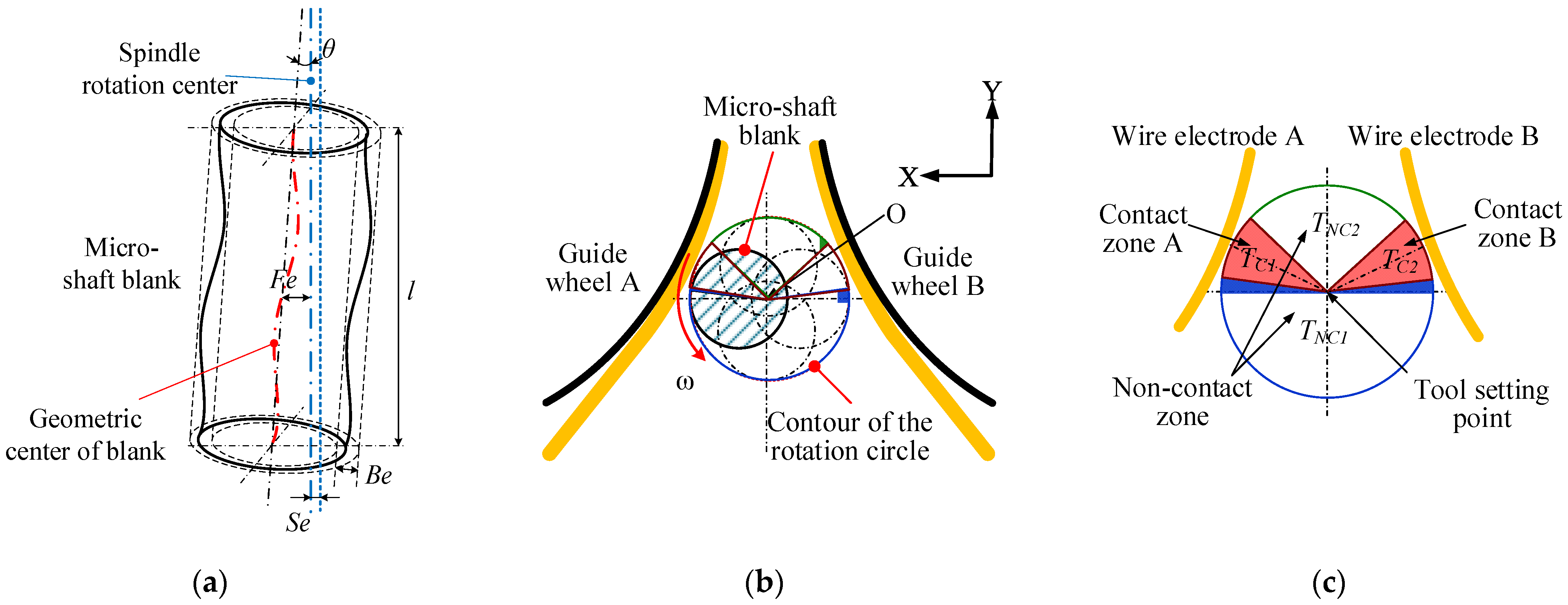
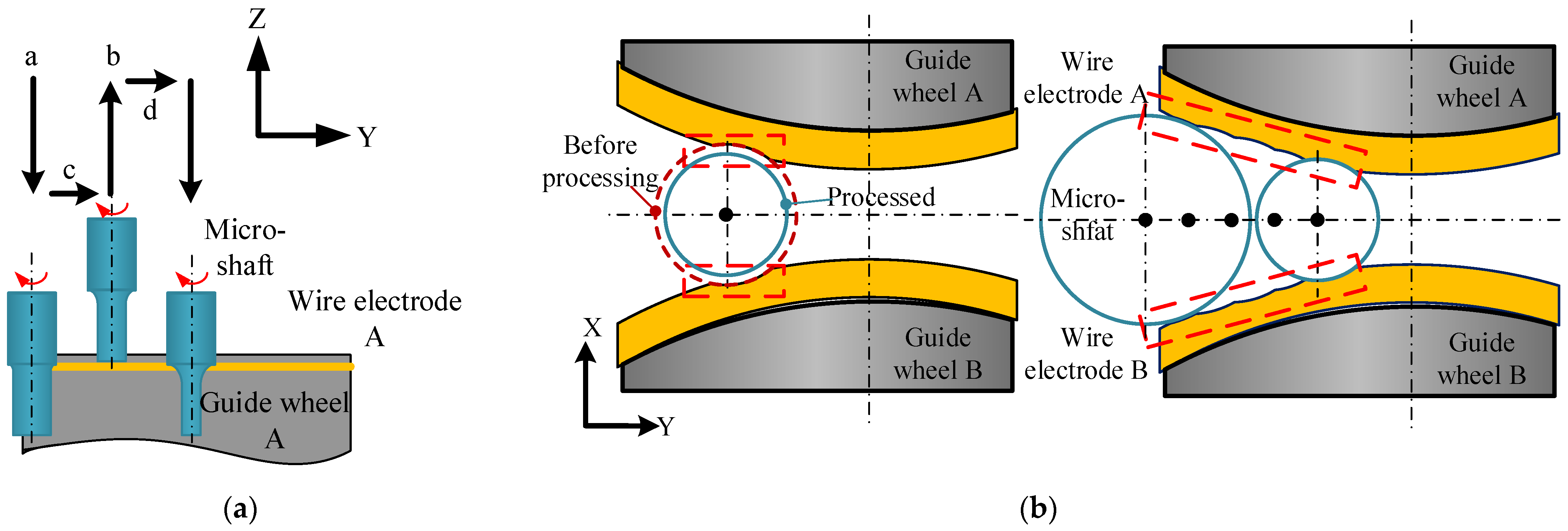
2.1. The TMTF–WEDG Method and Device
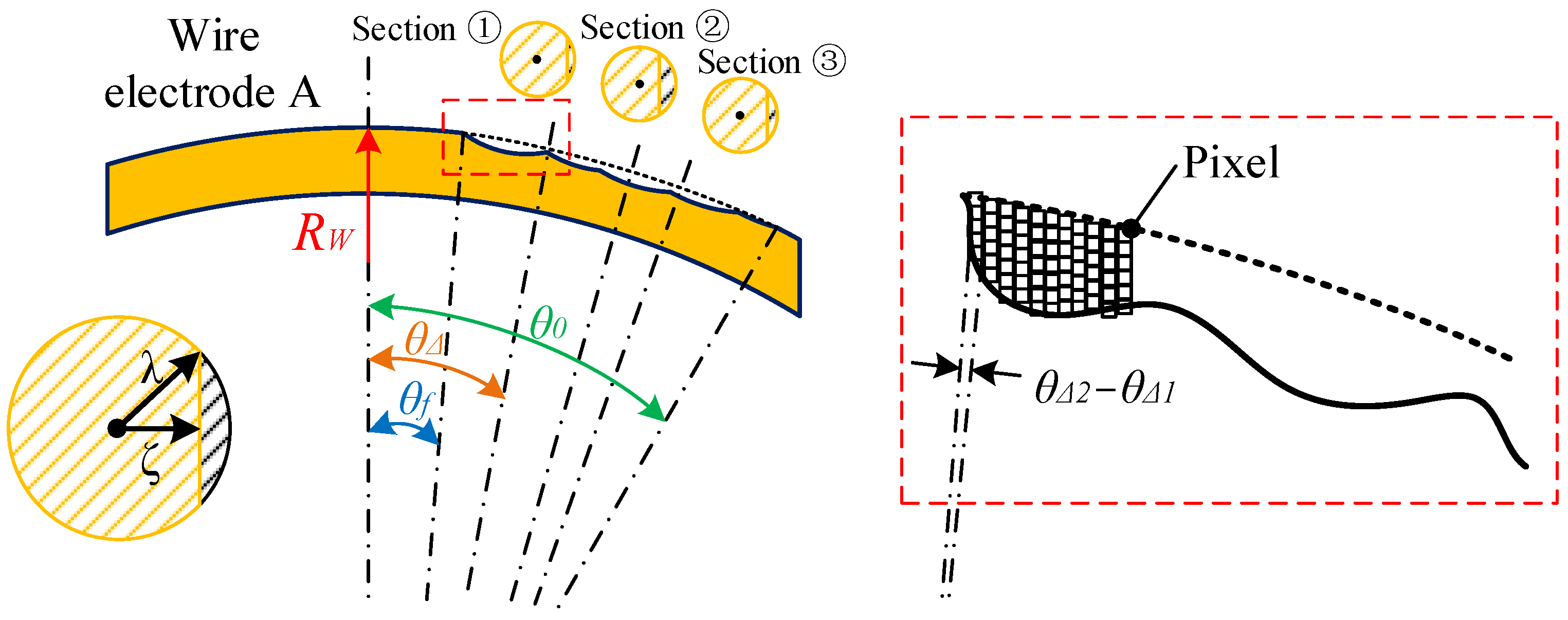
2.2. Keypoints Analysis of Geometric Constraints on the Diameter of Micro-Shafts
- The tangential feed path of the micro-shafts should be the symmetrical centerline of the narrow slit formed via the twin–mirroring–wire electrodes;
- The diameter of the micro-shafts is controlled by the distance of the tangential feed;
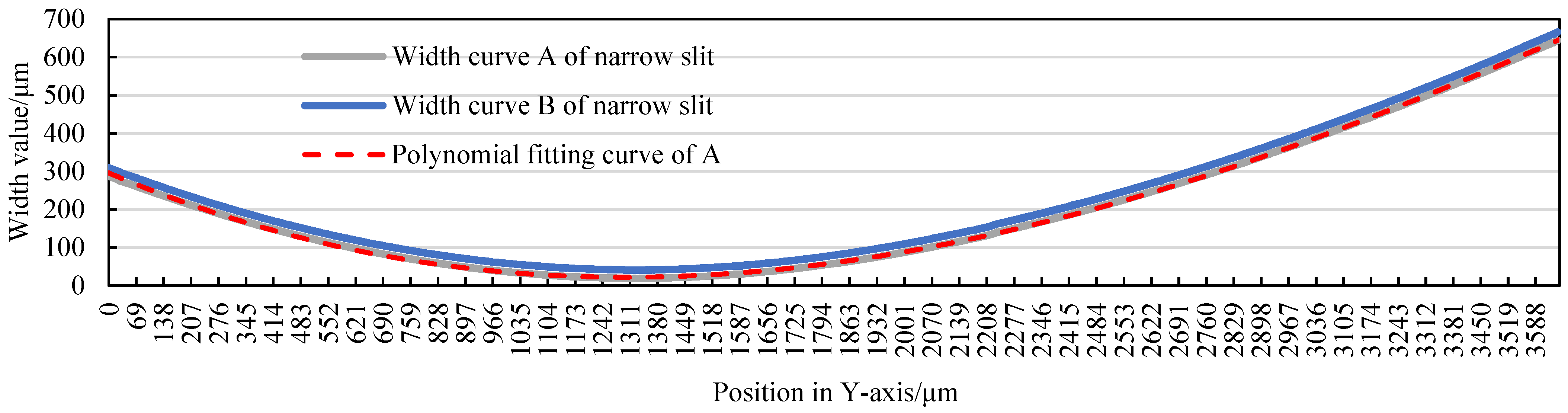
- The width of the narrow slit can be precisely controlled and adjusted to achieve different minimum limit values of micro-shaft diameters;
- The boundary on both sides of the narrow slit, namely the boundaries of the twin–mirroring–wire electrodes, should be stable and free from fluctuations.
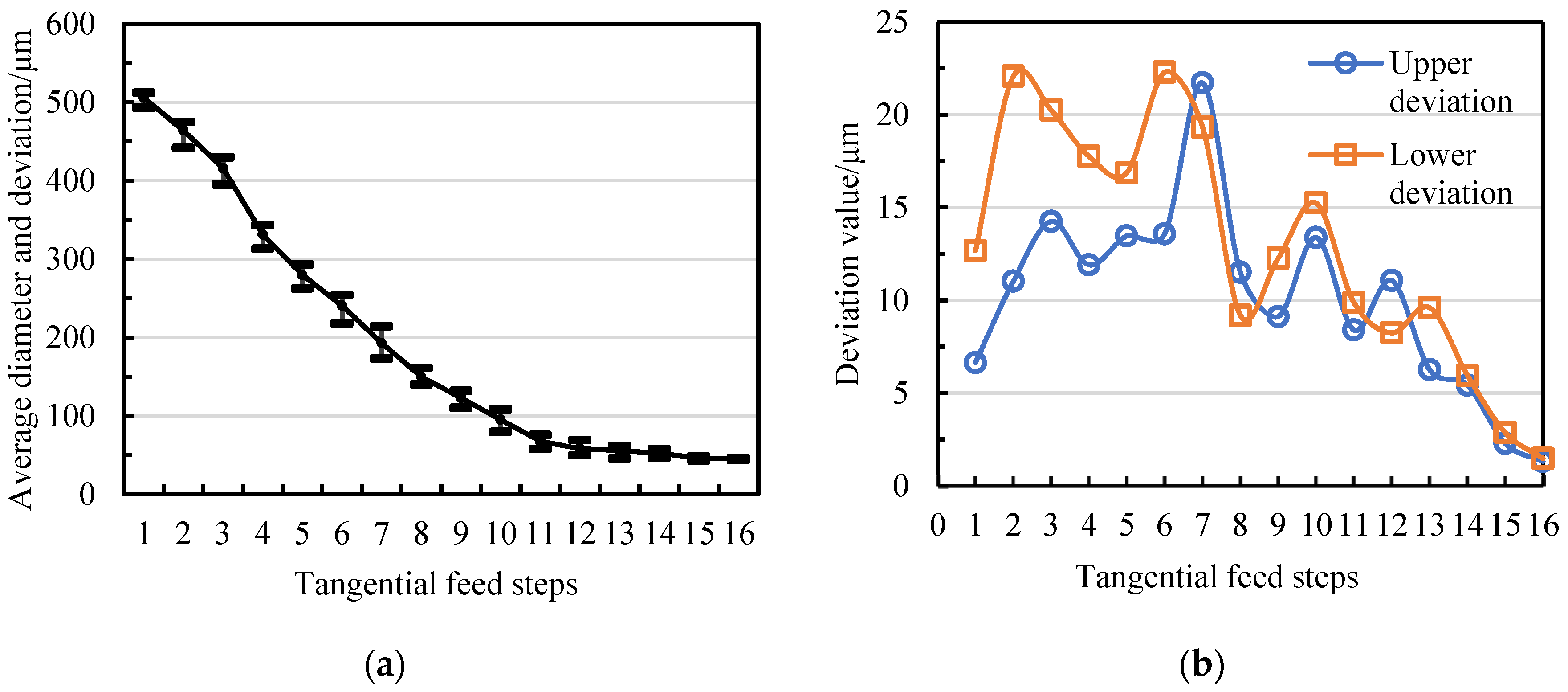
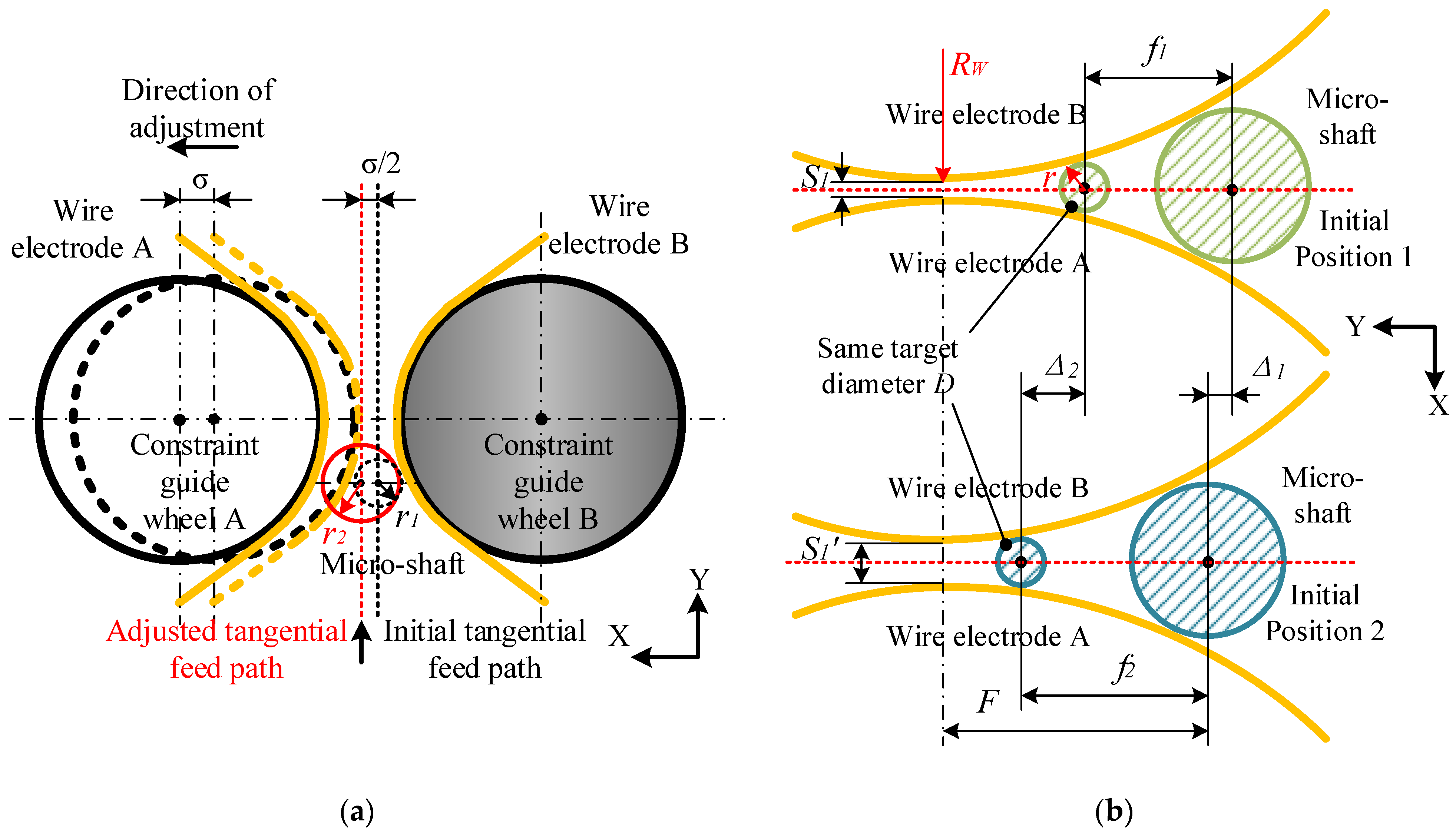
3. Geometric Constraint Strategy for Micro-Shaft Diameter Control
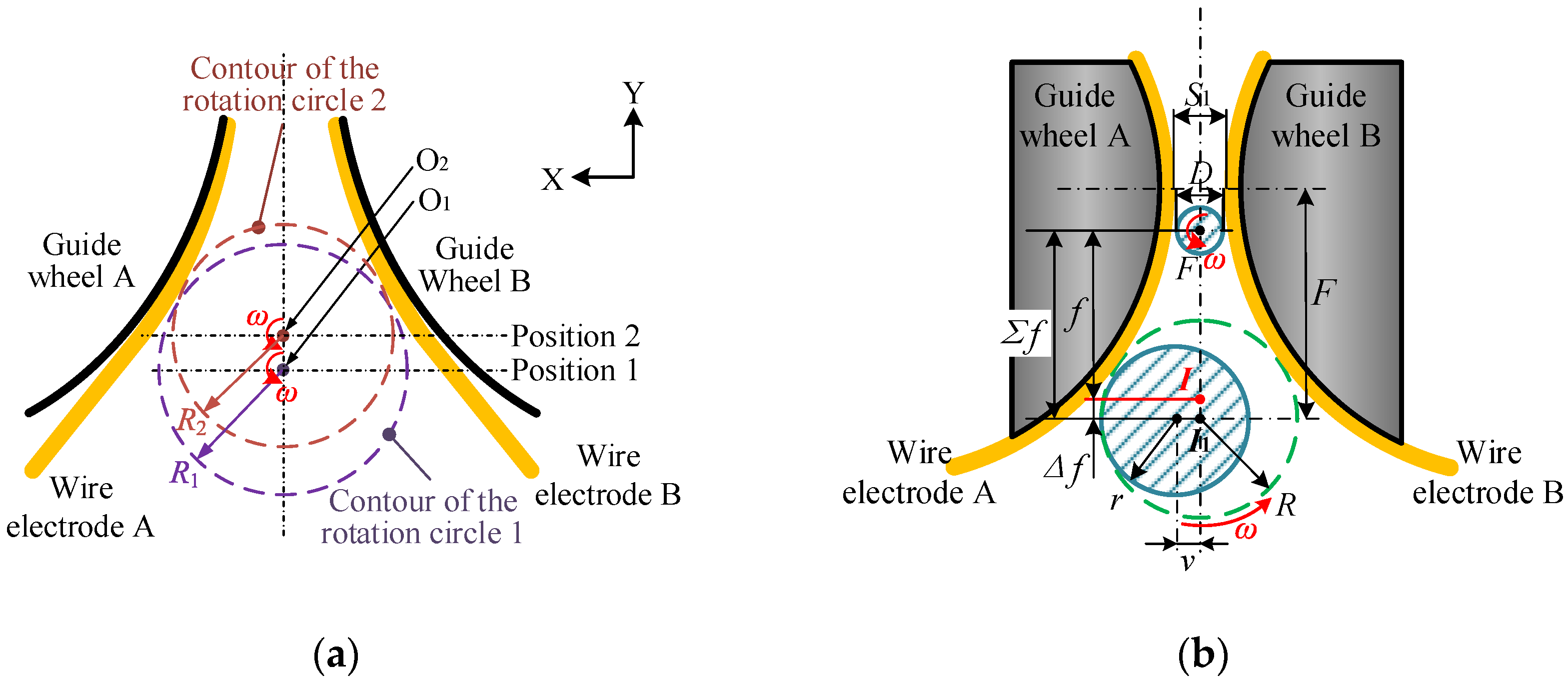
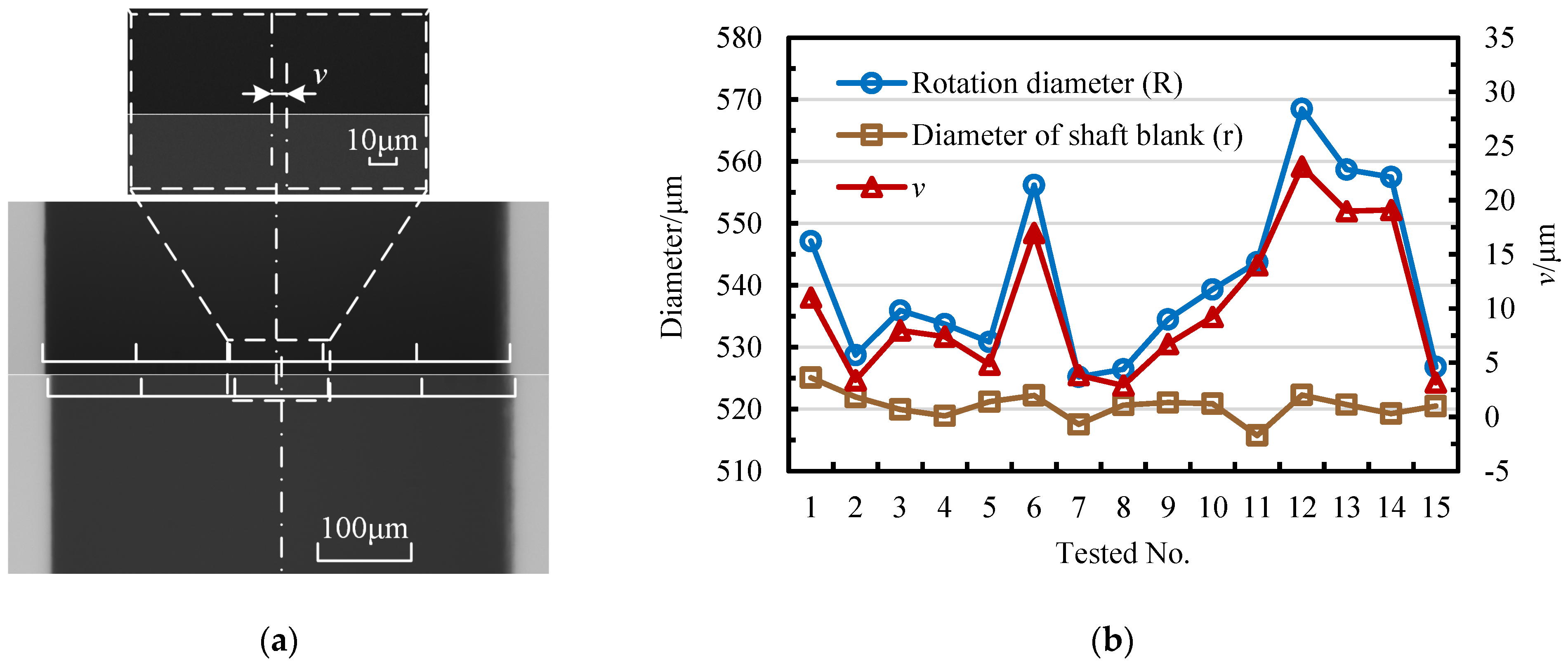
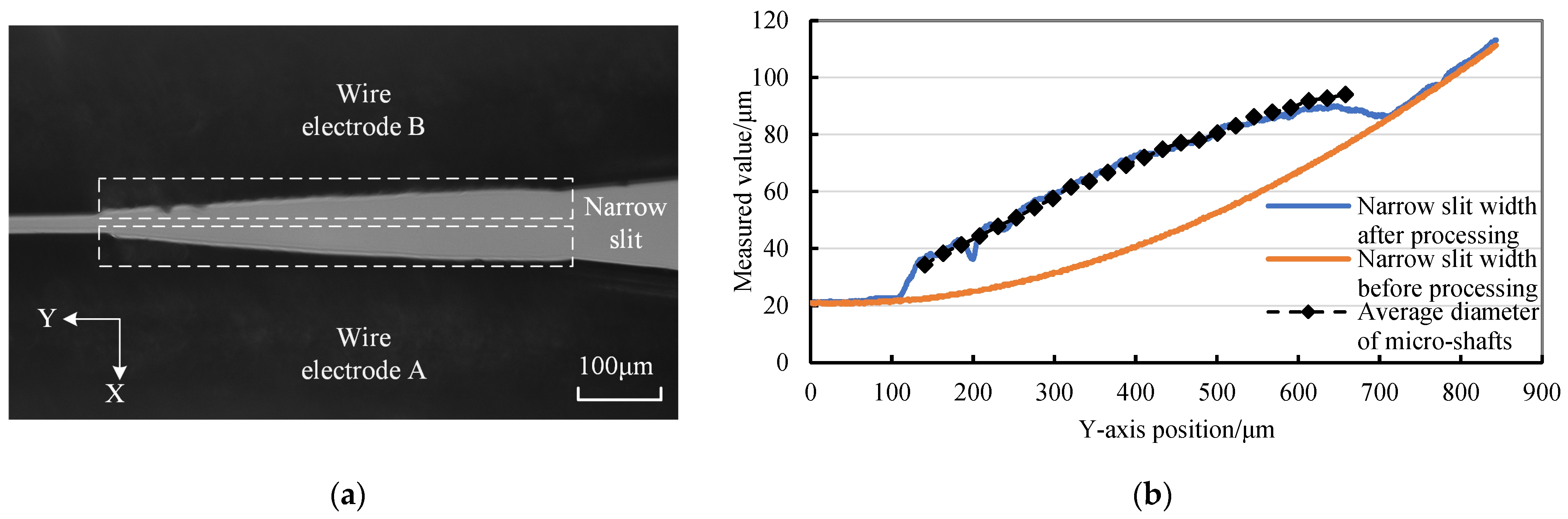
3.1. Tool-Setting and Tangential Feed Distance
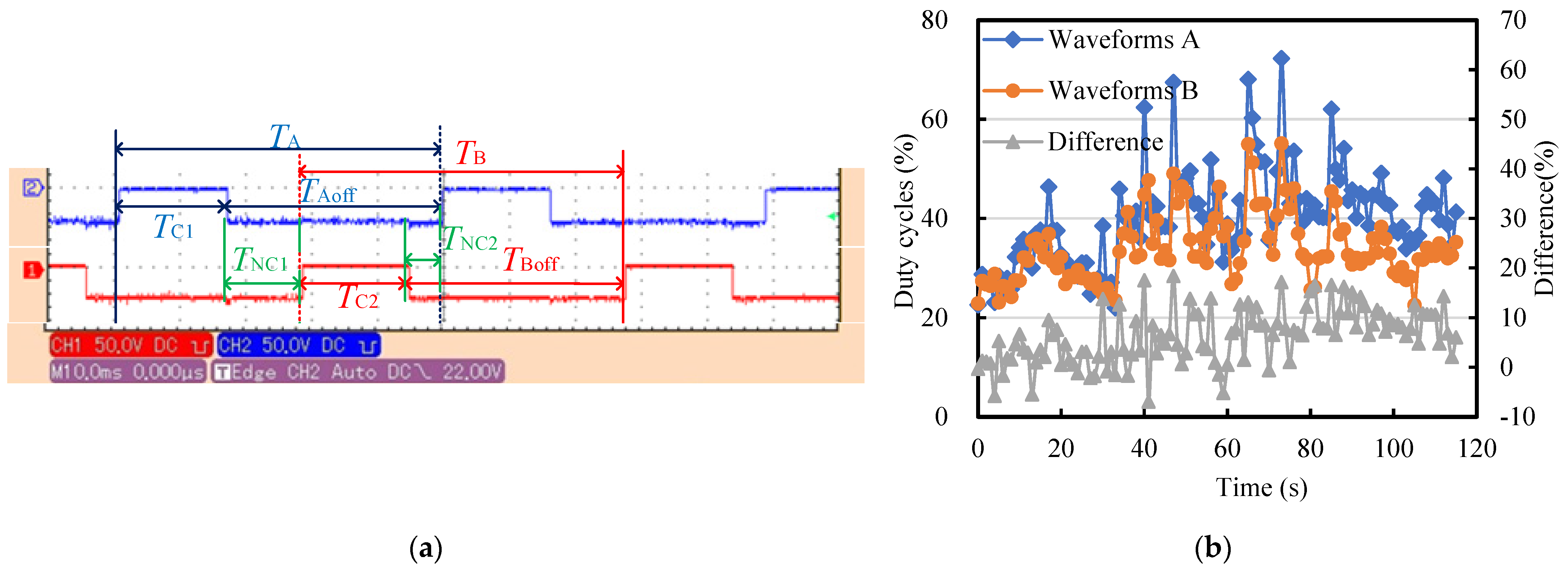
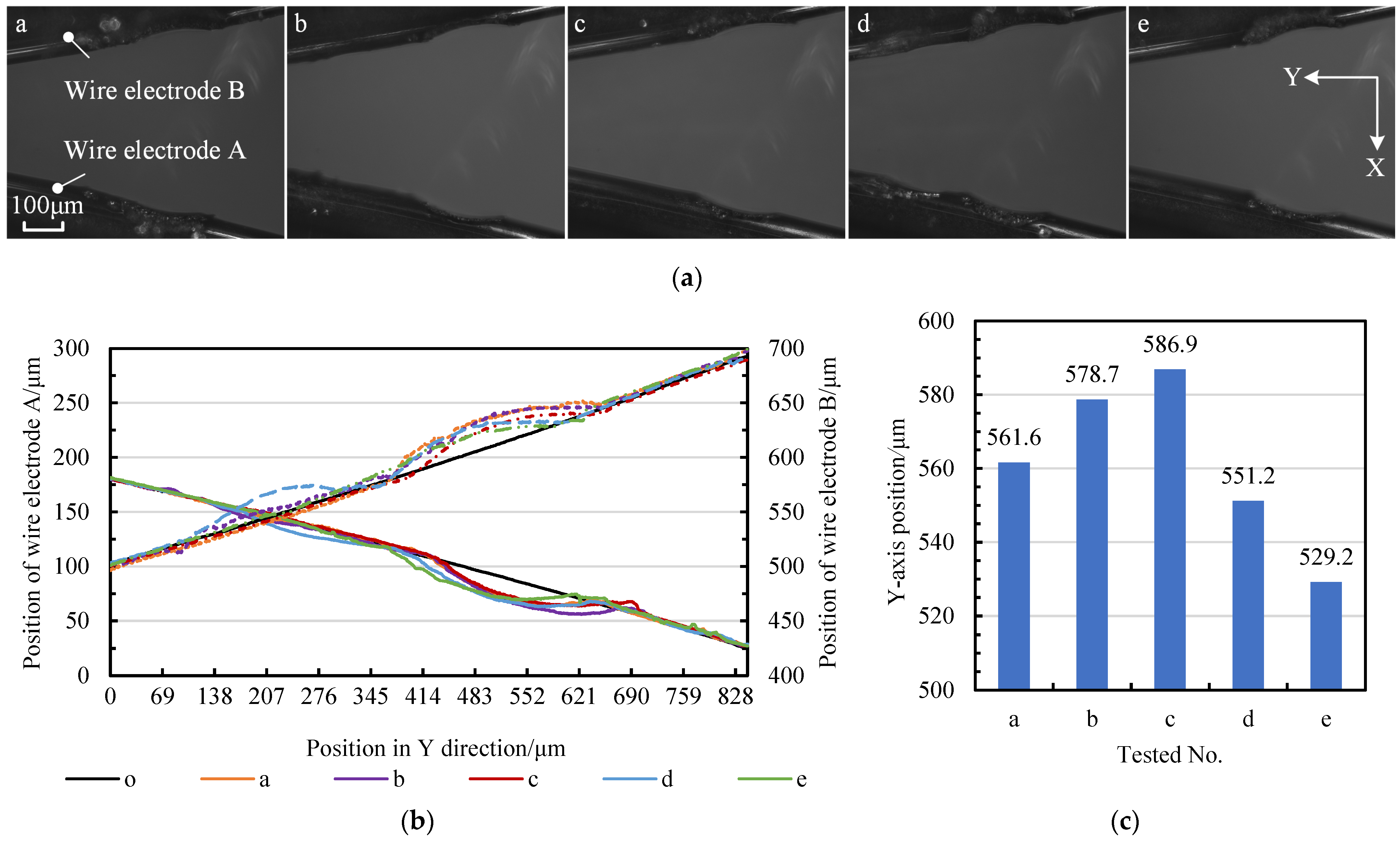
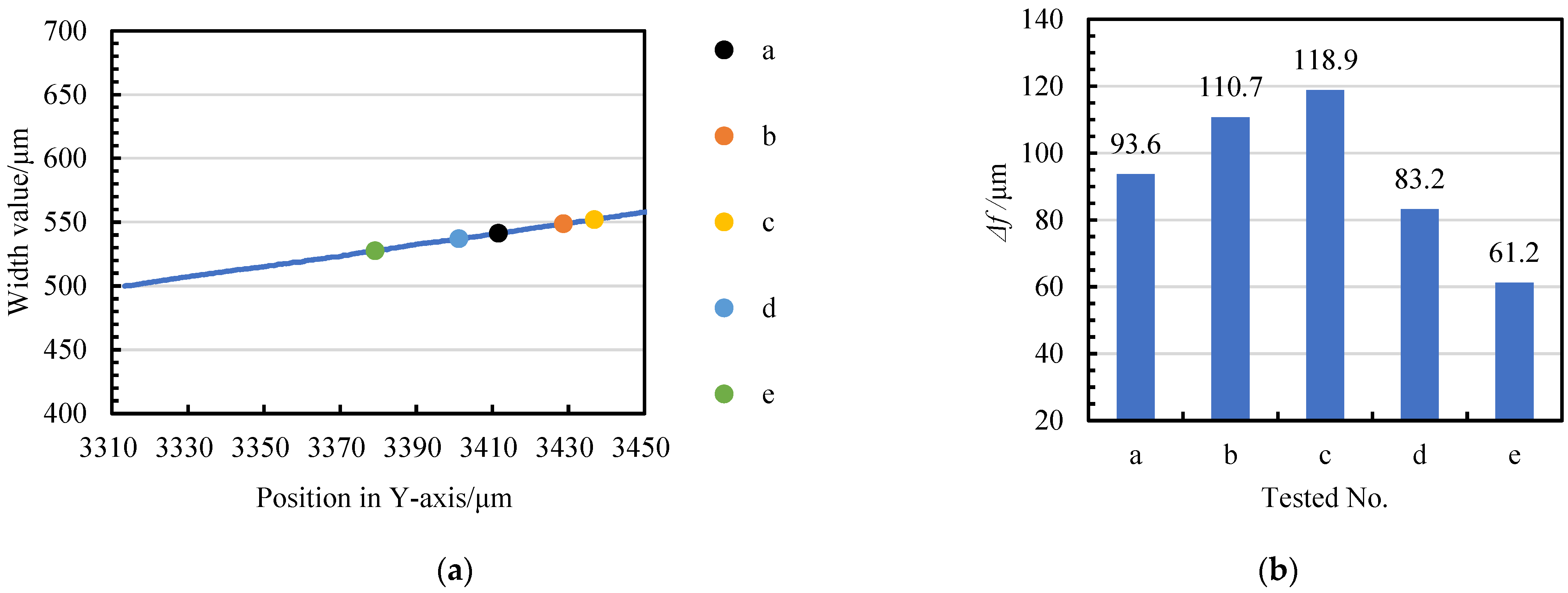
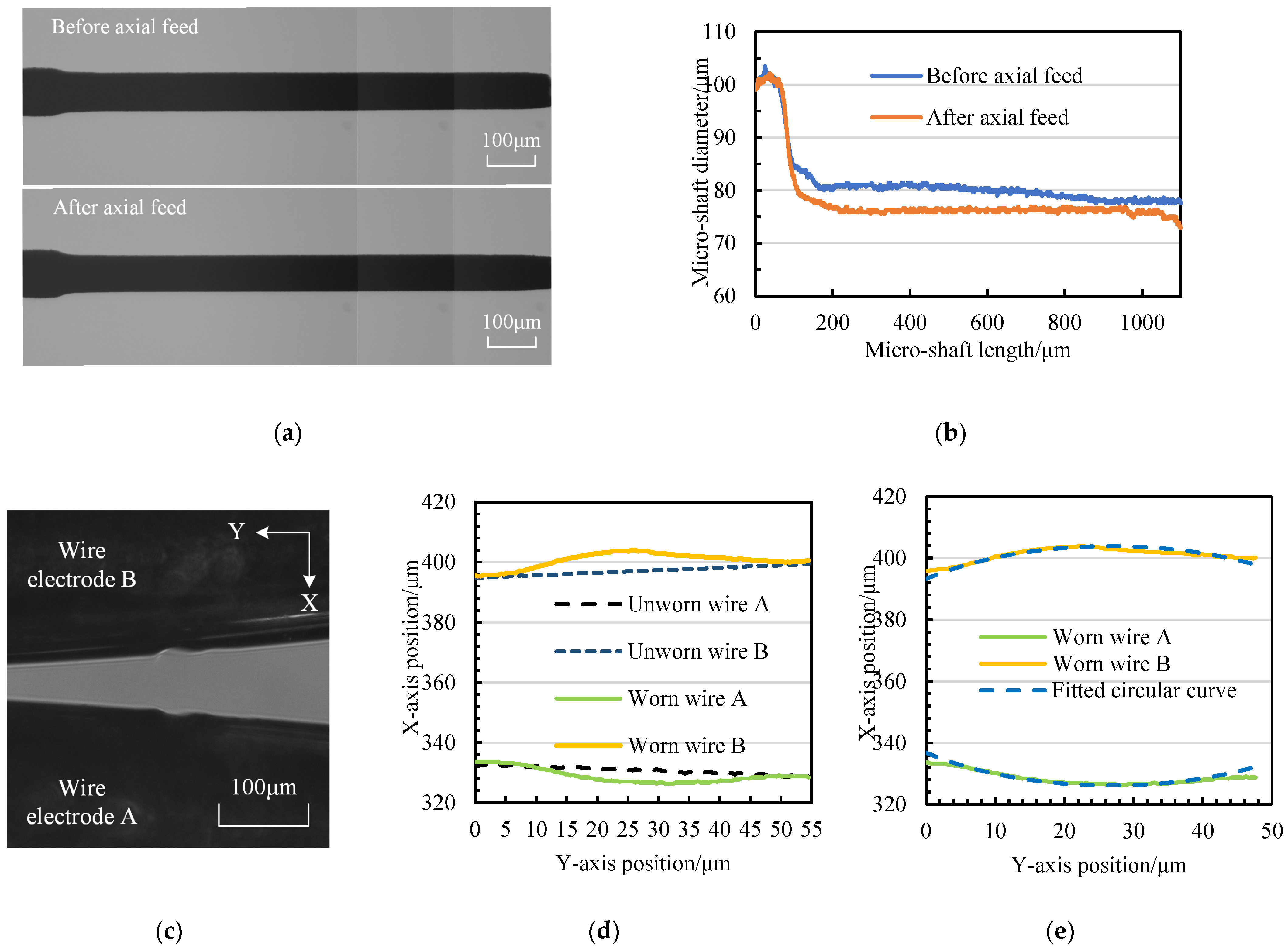
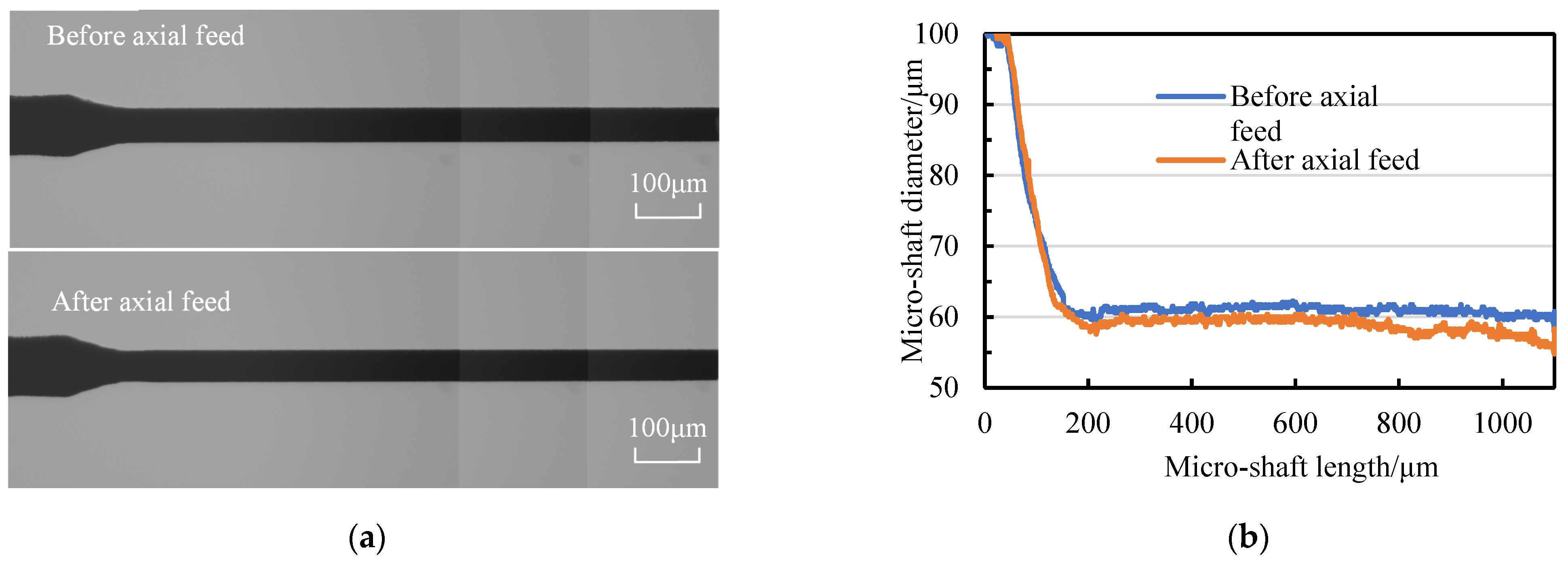
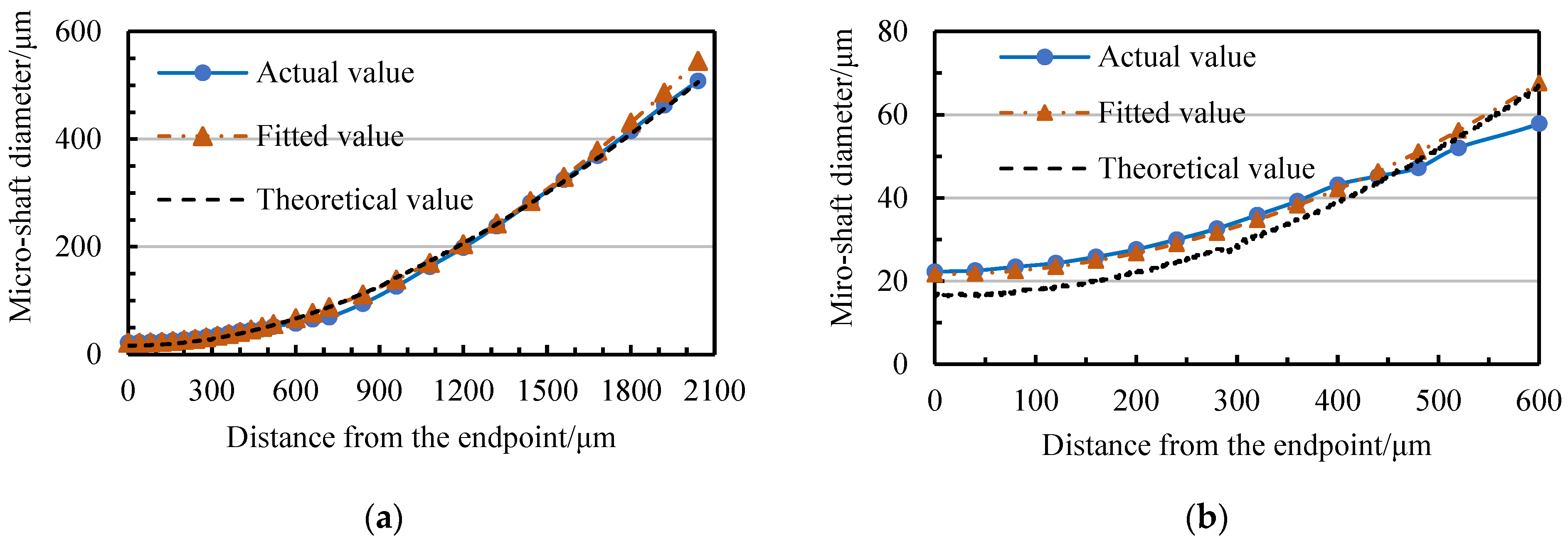
3.2. The Relationship between the Material Removal Amount of Micro-Shafts and Wire-Electrode Wear
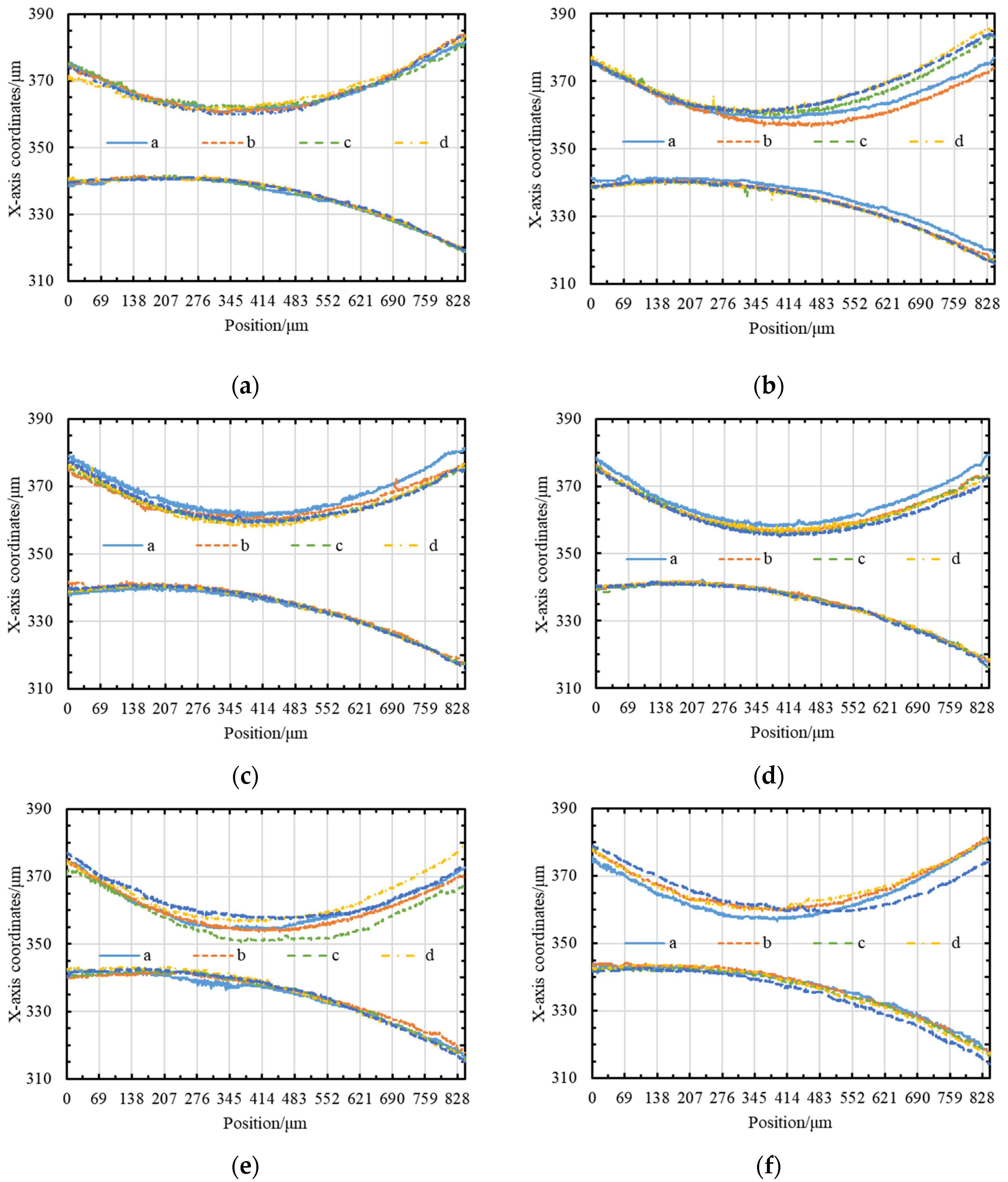
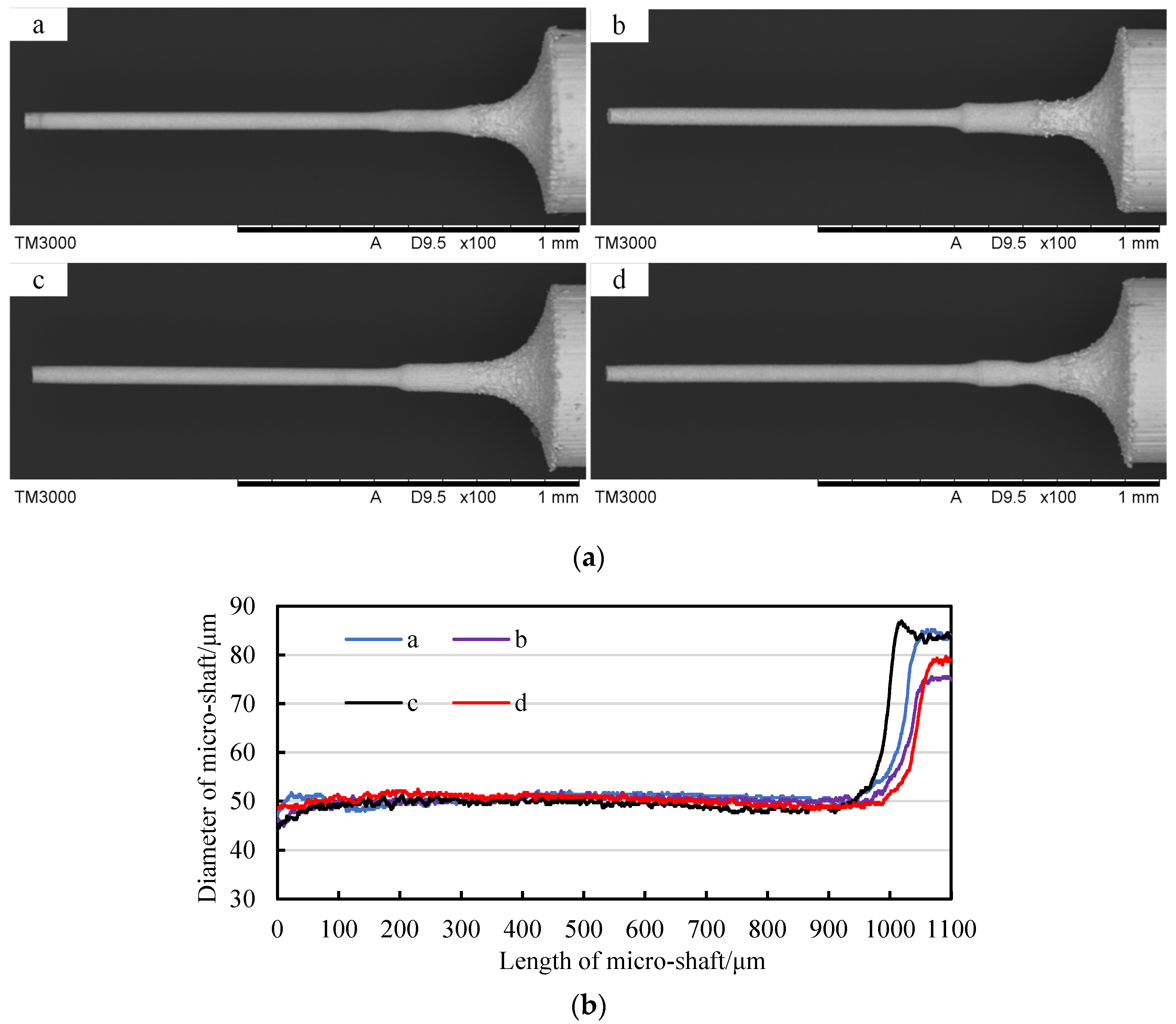
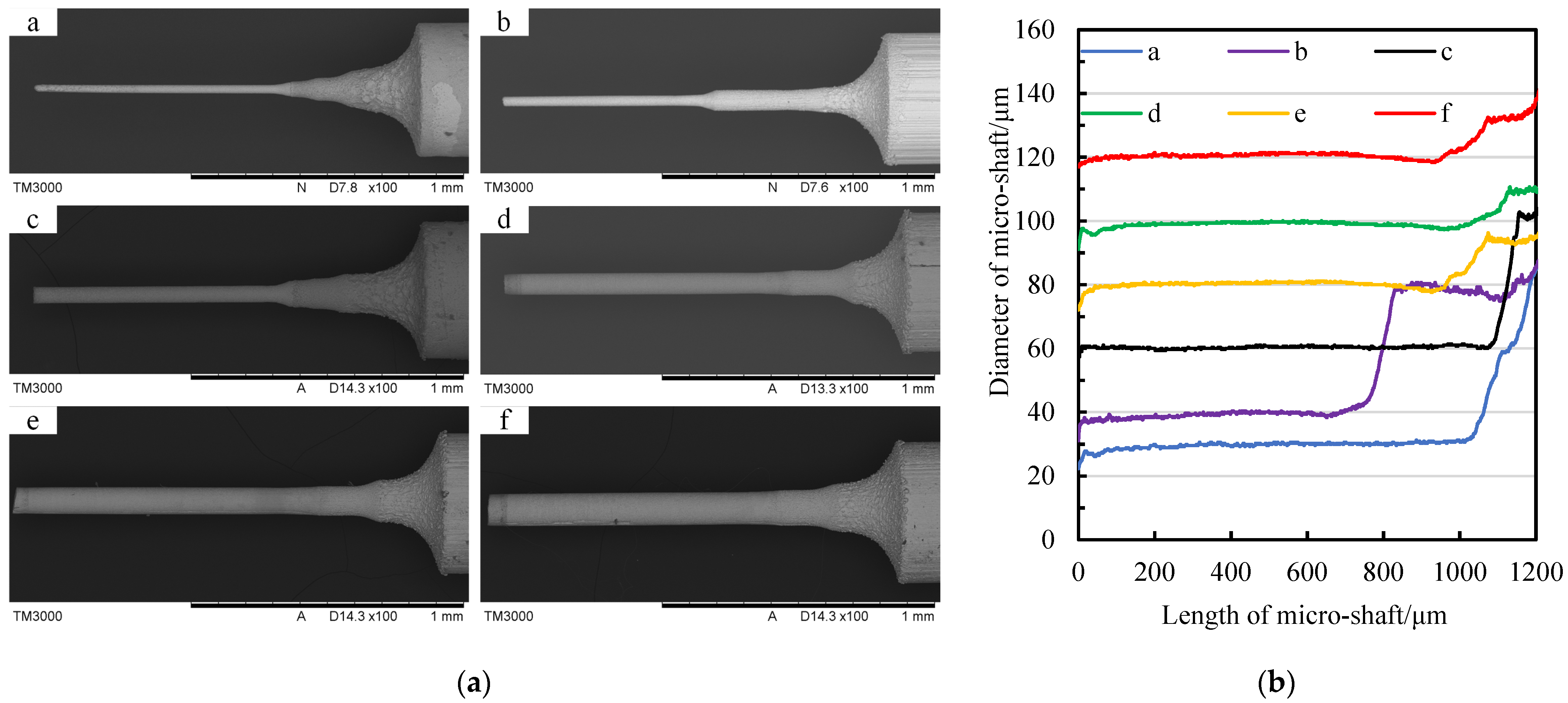
4. Repetitive Machining of Micro-Shafts with Different Diameters
5. Conclusions
- In the TMTF-WEDG process, the narrow slit formed via twin-mirroring-wire electrodes can geometrically constrain the micro-shaft diameter arbitrarily by controlling tangential feed distance. The geometric constraint strategy includes the tool-setting method, the tangential feed distance compensation, and the equation for the relationship between tangential distance and diameter variation;
- The geometric constraint strategy solves the matter of the tangential feed distance change caused by the fluctuation in the tool-setting position and the wire wear caused by the wire electrodes being stationary under a tension force to maintain the high accuracy of micro-shafts;
- Supported via a geometric constraint strategy, both high-precision repetitive machining of micro-shafts with a certain diameter and any target diameter are flexibly achieved without any interruption in the process. For instance, the result shows four micro-shafts with diameters of 50 µm and a consistency of ±1.5 µm and a series of micro-shafts with diameters ranging from 30 µm to 120 µm and a diameter accuracy of ±2 µm.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, T.C.; Wang, Y.X. Micro/nano-fabrication technologies for cell biology. Med. Biol. Eng. Comput. 2010, 48, 1023–1032. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.T.; Chu, C.Y. Fabrication and testing of a novel biopotential electrode array. J. Mater. Process. Technol. 2017, 250, 345–356. [Google Scholar] [CrossRef]
- Marauska, S.; Jahns, R.; Kirchhof, C.; Claus, M.; Quandt, E.; Knöchel, R.; Wagner, B. Highly sensitive wafer-level packaged MEMS magnetic field sensor based on magnetoelectric composites. Sens. Actuators A Phys. 2013, 189, 321–327. [Google Scholar] [CrossRef]
- Huang, T.W.; Sheu, D.Y. Micro ball-ended tips stylus fabrication with pipe-electrode by micro-EDM process. Procedia CIRP 2020, 95, 590–593. [Google Scholar] [CrossRef]
- Asad, A.B.M.A.; Masaki, T.; Rahman, M.; Lim, H.S.; Wong, Y.S. Tool-based micro-machining. J. Mater. Process. Technol. 2008, 192–193, 204–211. [Google Scholar] [CrossRef]
- Oliaei, S.N.B.; Karpat, Y.; Davim, J.P. Micro tool design and fabrication: A review. J. Manuf. Process. 2018, 36, 496–519. [Google Scholar] [CrossRef]
- Rahman, M.; Asad, A.B.M.A.; Masaki, T. A multiprocess machine tool for compound micromachining. Int. J. Mach. Tools Manuf. 2010, 50, 344–356. [Google Scholar] [CrossRef]
- Singh, S.K.; Mali, H.S. Microfeatures and microfabrication: Current role of micro-electric discharge machining. J. Micromech. Microeng. 2019, 29, 043002. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rahman, M.; Mia, M.; Asad, A.B.M.A.; Fardin, A. Manufacturing of Al Alloy Microrods by Micro Cutting in a Micromachining Center. Micromachines 2019, 10, 831. [Google Scholar] [CrossRef]
- Sun, Y.; Jin, L.Y.; Liu, M.J.; Gong, Y.D.; Wen, X.L.; Yin, G.Q.; Wen, Q. A comprehensive review on fabrication of ultra small micro tools via electrical discharge machining-based methods. Int. J. Adv. Manuf. Technol. 2022, 118, 703–735. [Google Scholar] [CrossRef]
- Hourmand, M.; Sarhan, A.A.D.; Sayuti, M. Micro-electrode fabrication processes for micro-EDM drilling and milling: A state-of-the-art review. Int. J. Adv. Manuf. Technol. 2017, 91, 1023–1056. [Google Scholar] [CrossRef]
- Masuzawa, T.; Fujino, M.; Kobayashi, K.; Suzuki, T.; Kinoshita, N. Wire electro-discharge grinding for micro-machining. CIRP Ann. Manuf. Technol. 1985, 34, 431–434. [Google Scholar] [CrossRef]
- Lim, H.S.; Wong, Y.S.; Rahman, M.; Lee, M.K.E. A study on the machining of high-aspect ratio micro-structures using micro-EDM. J. Mater. Process. Technol. 2003, 140, 318–325. [Google Scholar] [CrossRef]
- Li, Y.; Guo, M.; Zhou, Z.Y.; Hu, M. Micro electro discharge machine with an inchworm type of micro feed mechanism. Precis. Eng. 2002, 26, 7–14. [Google Scholar] [CrossRef]
- Huang, S.H.; Huang, F.Y.; Yan, B.H. Fracture strength analysis of micro WC-shaft manufactured by micro-electro-discharge machining. Int. J. Adv. Manuf. Technol. 2005, 26, 68–77. [Google Scholar] [CrossRef]
- Wu, Y.Y.; Huang, T.W.; Sheu, D.Y. Desktop Micro-EDM System for High-Aspect Ratio Micro-Hole Drilling in Tungsten Cemented Carbide by Cut-Side Micro-Tool. Micromachines 2020, 11, 675. [Google Scholar] [CrossRef]
- Chern, G.L.; Wu, Y.J.E.; Cheng, J.C.; Yao, J.C. Study on burr formation in micro-machining using micro-tools fabricated by micro-EDM. Precis. Eng. 2007, 31, 122–129. [Google Scholar] [CrossRef]
- Kuo, C.L.; Huang, J.D. Fabrication of series-pattern microdisk electrode and its application in machining micro-slit of less than 10μm. Int. J. Mach. Tools Manuf. 2004, 44, 545–553. [Google Scholar] [CrossRef]
- Rees, A.; Brousseau, E.; Dimov, S.S.; Bigot, S.; Griffiths, C.A. Development of surface roughness optimization and prediction for the process of wire electro-discharge grinding. Int. J. Adv. Manuf. Technol. 2013, 64, 1395–1410. [Google Scholar] [CrossRef]
- Sun, Y.; Gong, Y.D. Experimental study on the microelectrodes fabrication using low speed wire electrical discharge turning (LS-WEDT) combined with multiple cutting strategy. J. Mater. Process. Technol. 2017, 250, 121–131. [Google Scholar] [CrossRef]
- Li, Z.K.; Bai, J.C.; Cao, Y.; Wang, Y.Q.; Zhu, G.Z. Fabrication of microelectrode with large aspect ratio and precision machining of micro-hole array by micro-EDM. J. Mater. Process. Technol. 2019, 268, 70–79. [Google Scholar] [CrossRef]
- Rees, A.; Dimov, S.S.; Ivanov, A.; Herrero, A.; Uriarte, L.G. Micro-electrode discharge machining: Factors affecting the quality of electrodes produced on the machine through the process of wire electro-discharge machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2007, 221, 409–418. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Bai, J.C. Diameter control of microshafts in wire electrical discharge grinding. Int. J. Adv. Manuf. Technol. 2014, 72, 1747–1757. [Google Scholar] [CrossRef]
- Zou, Z.; Guo, Z.; Huang, Q.; Yue, T.; Liu, J.; Chen, X. Precision EDM of Micron-Scale Diameter Hole Array Using in-Process Wire Electro-Discharge Grinding High-Aspect-Ratio Microelectrodes. Micromachines 2021, 12, 17. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tong, H.; Li, Y. Precision machining of micro tool electrodes in micro EDM for drilling array micro holes. Precis. Eng. 2015, 39, 100–106. [Google Scholar] [CrossRef]
- Sheu, D.Y. Microelectrode tools manufacturing by hybrid circuits Twin-Wire electrodischarge grinding. Mater. Manuf. Process. 2010, 25, 1142–1147. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Bellotti, M.; Jia, J.Y.; Li, Z.; Yang, S.Q.; Qian, J.; Reynaerts, D. Fabrication of micro rods by twin-mirroring-wire tangential feed micro electrical discharge grinding. Precis. Eng. 2020, 66, 482–495. [Google Scholar] [CrossRef]
- Jia, J.Y.; Wang, Y.Q.; Li, Z.; Yang, S.Q.; Qian, J.; Reynaerts, D. Accuracy improvement of micro-shafts fabricated by the twin-mirroring-wire tangential feed electrical discharge grinding. J. Mater. Process. Technol. 2020, 286, 116808. [Google Scholar] [CrossRef]







| Parameters | Values | |||
|---|---|---|---|---|
| Roughing | Semi–Finishing | Finishing | ||
| RC pulse power supply | Voltage | 120 V | 100 V | 40 V |
| Capacitance | 68 nF | 470 pF | 47 pF | |
| Resistance | 1000 Ω | |||
| Feed rate in Z direction | 50 μm/s | 30 μm/s | 20 μm/s | |
| Feed length per step in the Y direction | 30 μm | 20 μm | 10 μm | |
| Spindle speed | 1200 rpm | |||
| Wire speed | Nearly 0.11 mm/s | 0 | ||
| Wire tension | 14~15 N | |||
| Dielectric fluid | Deionized water | |||
| Micro-shafts blank | Tungsten (Ø 0.5 mm) | |||
| Wire electrodes | Brass (Ø 0.250−0.002 mm) (5 kg/roll) 1 | |||
| Index Values | Narrow-Slit Width A | Narrow-Slit Width B |
|---|---|---|
| Narrow-slit width | S1 = 18 μm | S1′ = 40 μm |
| Tangential feed distance | f1 ≈ 1600 μm | f2 ≈ 1800 μm |
| Initial position difference | Δ1 ≈ 50 μm | |
| Finish position difference | Δ2 ≈ 250 μm | |
| Motor Control Variable Settings | The Linear Velocity of the Wire Electrodes | Average of Fluctuations | |
|---|---|---|---|
| Wire Electrode A | Wire Electrode B | ||
| 10 | 107 μm/s | 0.93 μm | 2.34 μm |
| 20 | 213.5 μm/s | 2.07 μm | 5.65 μm |
| 40 | 427 μm/s | 1.12 μm | 3.91 μm |
| 60 | 640.5 μm/s | 0.87 μm | 3.47 μm |
| 80 | 854 μm/s | 2.07 μm | 6.49 μm |
| 100 | 1067.5 μm/s | 2.45 μm | 5.99 μm |
| Micro-Shaft | a | b | c | d |
|---|---|---|---|---|
| f | 1517.5 μm | |||
| Δf | 125 μm | 98 μm | 60 μm | 116 μm |
| Σf | 1642.5 μm | 1615.5 μm | 1577.5 μm | 1633.5 μm |
| Micro-Shaft | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| Target value | Ø 30 μm | Ø 40 μm | Ø 60 μm | Ø 80 μm | Ø 100 μm | Ø 120 μm |
| Average value | Ø 29.66 μm | Ø 39.44 μm | Ø 60.35 μm | Ø 79.98 μm | Ø 99.81 μm | Ø 120.29 μm |
| f | 1732.9 μm | 1611.2 μm | 1440.6 μm | 1312.4 μm | 1204.8 μm | 1110.2 μm |
| Δf | 8 μm | 162 μm | 141 μm | 33 μm | 65 μm | 71 μm |
| Σf | 1740.9 μm | 1773.2 μm | 1581.6 μm | 1345.4 μm | 1269.8 μm | 1181.2 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Li, Z.; Hu, B.; Wang, Y.; Wang, J.; Li, C.; Xiang, W. Research on Geometric Constraint Strategies for Controlling the Diameter of Micro-Shafts Manufactured via Wire Electric Discharge Grinding. Micromachines 2023, 14, 2178. https://doi.org/10.3390/mi14122178
Jia J, Li Z, Hu B, Wang Y, Wang J, Li C, Xiang W. Research on Geometric Constraint Strategies for Controlling the Diameter of Micro-Shafts Manufactured via Wire Electric Discharge Grinding. Micromachines. 2023; 14(12):2178. https://doi.org/10.3390/mi14122178
Chicago/Turabian StyleJia, Jianyu, Zan Li, Bo Hu, Yanqing Wang, Jing Wang, Congbo Li, and Wenfeng Xiang. 2023. "Research on Geometric Constraint Strategies for Controlling the Diameter of Micro-Shafts Manufactured via Wire Electric Discharge Grinding" Micromachines 14, no. 12: 2178. https://doi.org/10.3390/mi14122178
APA StyleJia, J., Li, Z., Hu, B., Wang, Y., Wang, J., Li, C., & Xiang, W. (2023). Research on Geometric Constraint Strategies for Controlling the Diameter of Micro-Shafts Manufactured via Wire Electric Discharge Grinding. Micromachines, 14(12), 2178. https://doi.org/10.3390/mi14122178






