1. Introduction
With the emergence of small-caliber intelligent ammunition and unmanned and small-load combat platforms, fuses have more application requirements with respect to the miniaturization of detonation sequences [
1]. A reduction in volume of a detonation sequence provides more space for the ammunition warhead and circuit design. A flyer-type detonation sequence uses the detonation products of the primary microexplosive to drive the microflyer to detonate the booster explosive. The flyer-type detonation sequence is smaller than the volume and charge amount of the detonator. Moreover, the flyer can maintain a higher velocity within several millimeters, which is significantly lower than the energy-attenuation rate of the shock wave; at the same time, the safe and arm (S&A) devices no longer need a special-shaped booster, so the structure of the detonation sequence is simpler.
Gerald proposed three design schemes of the detonation sequence of flyers driven by in situ explosives to initiate booster explosives: a linear size of the detonation sequence of less than 1 mm and a charge of less than 10 mg, deposition of a plastic flyer (p-xylene, polyimide, etc.) on the initiating explosive layer, and etching through holes on the back of the base as acceleration chamber. Cyclotrimethylene trinitramine (RDX), HNS, pentaerythritol tetranitrate (PETN), cyclotetramethylene tetranitramine (HMX)/Viton A–95/5 (PBXN-5), triaminotrinitrobenzene (TATB)/RDX/Viton-60/35/5 (PBXN-7), or PETN/silicone resin-80/20 (PBXN-301) were detonated after the flyer was accelerated using in situ explosives [
2]. The U.S. Army designed a micro detonation sequence of a titanium flyer driven by a hexanitrohexaazaisowurtzitane (CL-20)-based ink explosive (EDF-11) to detonate the booster explosives [
3,
4,
5]. The micro detonation sequence designed by the U.S. Navy used pressed or in situ silver azide (Ag(N
3)
2, φ 2 mm × 0.5 mm, and 6 mg) or in situ copper azide (Cu(N
3)
2) as primary explosives; the stainless steel flyer (0.3 mm~1 mm thick) was accelerated to detonate EDF-11 explosives, and the EDF-11 was laterally exported to generate a shock wave or drive the flyer to detonate CL-20/proprietary binders-97.75/2.25 (RSI-007)/PBXN-5 [
6,
7,
8]. A micro detonation sequence for a 25 mm~40 mm grenade was proposed by the American Kaman Company; the rotor carries Pb(N
3)
2 (a slurry charge) to the release position, which is aligned with the lead styphnate (LTNR) of the igniter; the Pb(N
3)
2 shears the nickel-cobalt alloy to form a flyer; and the flyer accelerates in the base of booster and detonates the booster HNS-IV [
9]. Wang’s research showed that lead azide with a size of φ 1.6 mm × 2 mm (with a weight of approximately 14 mg) could drive a stainless steel flyer that was 30 μm thick to successfully initiate HNS-IV [
10]. Xie proposed a micro detonation sequence of a titanium flyer driven by Cu(N
3)
2; the CL-20 based booster explosive could be reliably detonated when the Cu(N
3)
2 weighed about 7.5 mg [
11,
12]. Tan used a simulation to analyze the speeds of flyers composed of different materials and thicknesses using different densities and sizes of tetraammine-cis-bis (5-nitro-2
H-tetrazolato-
N2) cobalt (III) perchlorate (BNCP) [
13]. Zeng proposed a micro detonation sequence of HNS-IV initiated by a titanium flyer that was driven by microsized copper azide and found that the diameter and thickness of the charge and the length of the accelerating chamber significantly affected the velocity of the flyer and that the material of flyer was related to the shape of the flyer [
14,
15,
16].
The azide-type primary explosive has a short detonation distance and certain power, and it is often used as the primary charge in a detonator. The output performance of microsized lead azide was proved [
17,
18], and the pressing characteristics of microsized lead azide was studied [
19]. Copper azide and silver azide are relatively sensitive, while the sensitivity of lead azide is relatively low, making it the most widely used primary explosive at present. There is little research on the mechanism of microflyers driven by microsized lead azide.
The velocity of a flyer is an important parameter when measuring the detonation ability, but whether the booster explosive can be detonated is also related to the type of booster explosive; the material, shape, and size of the flyer; and other factors. The impact initiation criterion, which is related to the properties of the flyer and explosive, the velocity of the flyer, and the structural parameters, is a reliable tool that can be used to judge whether the flyer successfully detonated the booster explosive. The pressure peak, duration, and particle velocity of the incident shock wave are used to analyze the initiation of the booster explosive.
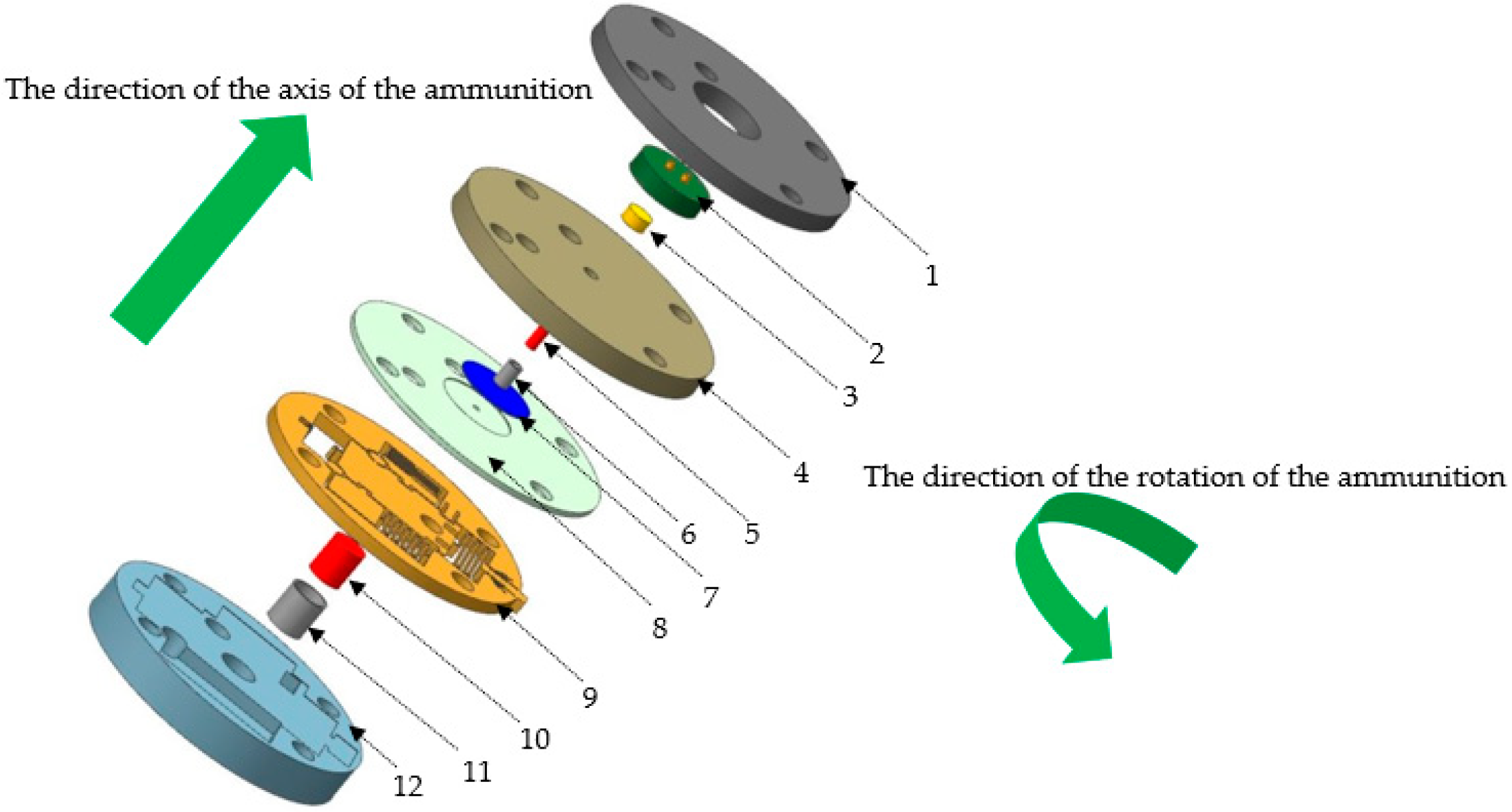
Figure 1 shows a structural diagram of a MEMS detonation system. Such systems are usually composed of a microdetonation sequence and a micro S&A device. The ignition layer is composed of a semiconductor bridge and a lead styphnate, which can ignite lead azide, and the charge of the LTNR weighs a milligram. The primary explosive is lead azide, which is pressed with several milligrams of charge and is a millimeter in size. When the S&A device is armed, the detonation product of the primary explosive shears the titanium flyer, which accelerates in the shear hole of the upper cover plate of the micro S&A device and the detonation hole of the micro S&A device, and then detonates the HNS-IV booster explosive. In this study, we examined the relationship between the important influencing factors of a microflyer driven by microsized lead azide and the initiation ability based on the initiation criterion.
2. Materials and Methods
2.1. Materials
In this study, a microscale semiconductor bridge (SCB) was used for ignition. The material of the SCB was monocrystalline silicon with a size of 20 × 50 × 4 μm at 60°. The doping element was phosphorus, the doping concentration was 4 × 1019·cm−3, and the resistance value was about 4 Ω~5 Ω. It was fabricated using a deep reactive ion etching (DRIE) process in the micro/nano laboratory of Peking University.
The proportion of ignition agent was: 1 g weight of LTNR; 6% concentration of polyvinyl acetate, and 0.5 mL~1 mL. The average particle size after drying was about 70 μm, and the particles had a hexagonal prism shape. The production process of LTNR was as follows: sodium styphnate was prepared via the reaction of styphnic acid and sodium bicarbonate, and LTNR was formed via the reaction of sodium styphnate and lead(II) nitrate. The styphnic acid (chemically pure) was acquired from Xi’an Qinghua Co., Ltd. (Xi’an, China); lead(II) nitrate, an analytical reagent (AR), was acquired from Xilong Chemical Co., Ltd. (Shantou, China); the sodium bicarbonate (AR) was acquired from Tianjin Dengfeng Chemical Reagent Factory (Tianjin, China); and the polyvinyl acetate (AR) was acquired from Hubei Guangao Biotechnology Co., Ltd. (Tianmen, China). The ignition agent was applied to the SCB, aired for 20 min, and then applied again; after 60 min of airing, it was dried at 50 °C~60 °C for 4 h.
The primary explosive was carboxymethyl cellulose-lead azide (CMC-Pb(N3)2) with an average particle size of 5 μm and a columnar shape. Lead(II) acetate solution with a concentration of 14% and sodium azide solution with a concentration of 5.5% were added to a solution composed of 0.1% sodium carboxymethyl cellulose solution and 0.1% sodium tartrate solution. After the reaction, the solution was filtered, washed, and dried. The lead(II) acetate (AR) was acquired from Sinopharm Chemical Reagent Co., Ltd. (Shanghai, China); the sodium azide (AR) was acquired from Shanghai Qiyuan Biotechnology Co., Ltd. (Shanghai, China); the sodium carboxymethyl cellulose (AR) was acquired from Jiangsu Taize Biotechnology Co., Ltd. (Suzhou, China); and the sodium tartrate (AR) was acquired from Tianjin Jinhui Taiya Chemical Reagent Co., Ltd. (Tianjin, China). The lead azide was weighed multiple times using an electronic balance (with an accuracy of 0.1 mg), and multiple pressings were performed by using a small pressing mold (for submillimeter pressing) and a precision servo press machine (the pressure, speed, and time could be set in the program with an accuracy of ± 1 N). Finally, the lead azide was pressed into a micro tube shell.
The average particle size of the booster HNS-IV was 0.8 μm in a long rod shape. The HNS was used as the raw material and dimethylformamide was used as the solvent (1 g of HNS was added to 6 mL of dimethylformamide solvent). The HNS was dissolved by heating and then purified via recrystallization at a low temperature; and then the HNS-IV was obtained via mechanical grinding. The HNS (technically pure) was acquired from Xi’an Qinghua Co., Ltd. (Xi’an, China); and the dimethylformamide (AR) was acquired from Shaanxi Xintong Chemical Co., Ltd. (Xi’an, China). The HNS-IV was pressed into the tube shell at one time using a hand press machine.
2.2. Criteria of Flyer Impact Initiation
At present, the common initiation criteria are the p-τ criterion, the James criterion, and the Π-τ criterion. The theories and fitting methods of these three initiation criteria are introduced below.
2.2.1. Theory of the p-τ Initiation Criterion
On the basis of energy conservation, Walker and Wasely proposed the concept of the critical initiation energy of explosives. After the flyer strikes the explosive, the explosive is detonated when the energy
E loaded on the unit area of the explosive is greater than the critical initiation threshold energy density
Ec [
20] (
Ec is a constant related to the properties of the explosive):
where
E represents the energy density in MJ·m
−2,
p represents the pressure in Gpa,
u represents the particle velocity in km·s
−1, and
τ represents the action time of the incident shock wave in μs.
Table A1 in
Appendix A lists the main symbols in this study and the corresponding explanations and units. The relation between
p,
D,
ρ, and
u is:
where
D represents the shock wave velocity in km·s
−1, and
ρ represents the density in g·cm
−3. Equation (2) can be substituted into Equation (1) to obtain:
The critical condition for initiation of explosives is:
When the shock wave pressure produced by the impact of the flyer on the explosive changes slightly, the shock wave velocity
D inside the explosive is constant, and the shock wave impedance
ρD of the explosive can be considered as a constant [
21]. The initiation criterion is:
The initiation criterion
Cini is a constant related to the properties of explosives. For high-energy heterogeneous explosives,
D is used in the power function of
p, and the initiation criterion is [
21]:
In Formula (6),
n is a constant related to the properties of explosives. When
pnτ >
Cini, it means that the explosive is detonated; on the contrary, it means that the explosive cannot be detonated. The shock initiation of explosive is related to the pressure
p and the shock wave action time
τ [
22].
2.2.2. Theory of the James Initiation Criterion
On the basis of the p-τ initiation criterion, James proposed an initiation criterion that is applicable to larger impact pressures, wider types of explosives, and more shapes of the flyer. The concept of the particle specific kinetic energy Σ is proposed as Σ = u2/2, MJ·kg−1.
The James initiation criterion can be expressed as [
23]:
In Formula (7), Σc is a constant related to the properties of explosives. The energy density Ec and particle specific kinetic energy Σc jointly determine whether the explosive detonates. When Σc/Σ + Ec/E > 1, it means that the explosive is detonated; otherwise, it means that the explosive cannot be detonated.
2.2.3. Theory of the Π-τ Initiation Criterion
On the basis of James’s research, Welle and Kim proposed the concept of power flux Π where Π = pu in GW·cm−2. The power flux Π is used instead of the particle specific kinetic energy Σ. The power flux Π is the derivative of the energy density E for the action time τ, which is not only related to the impact strength but also represents the energy rate transmitted to the explosive per unit area.
The
Π-
τ criterion, which is defined by the energy density
E, power flux
Π, and action time
τ, can be expressed as [
24,
25]:
In Formula (8), Πc is a constant related to the properties of explosives. When Π > Πc + (Ec/τΠc), the explosive is detonated; otherwise, the explosive cannot be detonated.
2.2.4. Parameter-Fitting Process of the Three Initiation Criteria for HNS-IV
The calculation method of the shock wave parameters and the fitting process of the initiation criteria of the HNS-IV are introduced below. The formula to calculate the pressure p and particle velocity u of the incident shock wave is [
21]:
where subscripts e and f represent explosives and flyers, respectively;
A represents the intercept of the Hugoniot line in km·s
−1;
S represents the slope of the Hugoniot line (dimensionless); and
vf is the flyer velocity in km·s
−1.
The calculation formulas of the action time of the explosives for flyers with different shapes are different [
23]. The action time of the shock wave of the flat-nosed rod-shaped flyer is:
The action time of the shock wave of the sphere/round-nosed rod-shaped flyer is:
The action time of the shock wave of the plate-shaped flyer is:
where
df represents the diameter of the flyer in μm,
Ce represents the sound velocity inside the explosive in km·s
−1,
δf represents flyer thickness in μm, and
Df is the shock wave velocity in the flyer in km·s
−1.
The first three columns and the last three columns of
Table 1 provide the respective experimental data of the critical velocities for initiating HNS-IV using polyimide and aluminum flyers with different sizes. According to the velocity and size of the flyer, the Hugoniot parameters of the flyer and HNS-IV in
Table 2, the pressure
p, particle velocity
u, and action time
τ of the incident shock wave in the HNS-IV are calculated by using the Formula (9)~(12), and then the energy density
E, specific kinetic energy
Σ, and power flux
Π are obtained.
The parameter-fitting process of the initiation criterion is shown in
Figure 2.
The Hugoniot parameters of the booster explosive and flyers are shown in
Table 2.
2.3. Simulation of The Microflyer Driven by Microsized Lead Azide
2.3.1. Design of Simulation
In order to provide data support for the parameter design of the microdetonation sequence and to study the laws of a flyer driven by a microcharge, a simulation model of a microflyer driven by microsized lead azide was established, and the velocity of the flyer corresponding to the microdetonation sequence with different structural parameters was obtained. Based on
Section 2.2, parameters such as the pressure
p, particle velocity
u, and action time
τ could be calculated. Furthermore, the relationship between the structural parameters of the microdetonation sequence and the initiation ability of the flyer was analyzed in combination with the shock initiation criterion.
Studying the relationship between the key influencing factors and the velocity of the flyer can better reveal the mechanism of detonation transmission. The influencing factors of lead azide are the diameter, height, density, and constraint conditions of the charge. In the MEMS detonation system, the diameter of the primary explosive is at the level of 1 mm [
2,
3,
4,
5,
6,
7,
8,
9], so the simulation range of the diameter should be about 1 mm; in [
17,
18], the output performance of lead azide with a charge height of 0.6 mm~3 mm was verified, so the charge height in the simulation was also set in this range. The common density of lead azide is more than 3 g·cm
−3, and the crystal density is slightly larger than 4 g·cm
−3, so the density range in the simulation was set to 2 g·cm
−3~4 g·cm
−3. At present, the commonly used metal and non-metal materials of the tube shell are aluminum, stainless steel, and organic glass; the materials (nickel, silicon, and copper) of S&A devices may also be used as the constraint materials of the primary explosive. The influence factors of the flyer were the thickness and material: the thickness of a polyimide flyer in an explosive foil initiator (EFI) is generally less than 100 μm, and the thickness of a flyer matched with a microcharge is generally larger than that of the EFI. So, the larger the charge, the greater the thickness of the matching flyer. In the simulation, the thickness of the flyer was designed to be 30 μm~200 μm. Polyimide is a commonly used material for EFIs; aluminum, copper, and stainless steel are also used as flyer materials for conventional charges, and titanium flyers are also used in some small detonators. Therefore, the performance of these types of flyers driven by a microcharge was evaluated. The main influencing factors of the acceleration chamber were the material and aperture: in an EFI, there is no S&A device, and the acceleration chamber is a separate device; its main materials are sapphire and stainless steel with high strength. In the MEMS detonation system, the flyer is sheared by the cover plate of the S&A device and accelerates in the detonating hole of the S&A device. At this time, the material used for the acceleration chamber is the same as that of the S&A (nickel, silicon, and copper); therefore, the performance of these materials as acceleration chambers was studied. The aperture of the acceleration chamber limited the diameter of the flyer, and there was an optimal matching relationship between the aperture of the acceleration chamber and the diameter of the lead azide. Considering that the common diameter of the lead azide was 0.9 mm, the aperture of the acceleration chamber was set to 0.3 mm~1.5 mm. Structural design parameters were optimized in combination with the shock initiation criterion.
2.3.2. Simulation Model
The simulation model of the microflyer driven by a microsized charge was established as shown in
Figure 3. The Eulerian algorithm was applied to the explosive and air; the Lagrange algorithm was applied to the constraint of the lead azide, acceleration chamber, and flyer; the outflow boundary was applied to the air domain; the mesh size was 0.025 mm × 0.025 mm; and the Gauss points were distributed from the center of the flyer to the radial edge. The initiation point was located at the center of one side of the explosive.
The state equation and constitutive model were mainly used to describe the mechanical behavior of materials in the mechanical simulation of the explosion. The state equation described the thermodynamic behavior of the material, and the constitutive model considered the strength effect of the material. The Jones–Wilkins–Lee (JWL) state equation was used to describe the work behavior of the detonation products of the lead azide, and the acquisition of its parameters was based on the experimental data of the relationship between the density and detonation velocity of the lead azide [
31]. The shock state equation and the Johnson–Cook constitutive model were used for the constraint, acceleration chamber, and titanium flyer, and the ideal gas state equation was used for air.
2.4. PDV Test
In order to carry out simulation research, the accuracy of the simulation model should be evaluated by comparing the consistency of the flyer velocity–time curve in the simulation and test. The velocity of flyer is the most important parameter used to evaluate the initiation ability of the detonation sequence. Difficulties with the velocity test include the high transient process and the miniaturization of the target to be tested [
32]. The PDV system uses the Doppler effect to calculate the velocity of moving objects according to the difference in frequency between the reflected laser frequency and the reference laser frequency. Compared with other speed-measurement methods, it has the advantages of a high precision, a wide range, and simple composition. The principle of the PDV system is shown in
Figure 4.
The principle of the PDV system was as follows: the laser emitted by the laser source was divided into two channels by the fiber coupler, one of which was used as the reference laser that was shined into the next fiber coupler; the other entered the circulator and then irradiated the flyer, and the frequency changed after being reflected by the flyer, which was called the signal laser. The signal laser was transmitted to the next fiber coupler after passing through the circulator, and a frequency difference occurred with the reference laser that was detected by the detector. Finally, the frequency-difference signal was recorded by the oscilloscope.
The frequency of the reference laser and signal laser met the following relationship:
where
f0 is the frequency of the reference laser in Hz,
fd is the frequency of the signal laser in Hz,
C is the speed of light in km·s
−1, and
vf(
t) is the velocity of the flyer changing with time in km·s
−1. The frequency difference can be expressed as:
The light speed, frequency, and wavelength of the reference laser satisfied the following relationship:
where
λ0 is the wavelength of the reference laser in nm.
When substituting Formulas (15) and (16) into Formula (14), the relationship between the flyer velocity
vf(
t) and frequency difference Δ
f could be obtained:
Therefore, the flyer velocity could be calculated by detecting the frequency difference of the laser caused by the flyer’s motion. Using a Fourier transform, the velocity–time curve of the flyer could be obtained by processing the frequency-difference signal Δf with the MATLAB program.
The test system was mainly composed of the test device of the flyer driven by a microcharge, an organic glass sheet, an optical fiber probe, the PDV, a laser amplifier, and a laser source (
Figure 5).
In
Section 2.3.1, it was introduced that the diameter of the lead azide was at the 1 mm level, so the diameter of the lead azide in this experiment was submillimeter (0.9 mm); when the pressing pressure was 188 MPa, the corresponding theoretical density of 3.83 g·cm
−3 was used as the charge density of the lead azide [
19], which was also close to that used in the literature [
17,
18]. According to the preliminary simulation results, the flyer had a relatively high speed when the charge height was 1.2 mm, the thickness of the titanium flyer was 0.1 mm, and the aperture of the stainless steel acceleration chamber was 0.6 mm. Therefore, the flyer velocity–time curve under the above design parameters was obtained by the PDV test.
The test process was as follows:
Fix the optical fiber probe with a steel protective sleeve with the optical fiber probe clamp.
Fix the organic glass sheet on the path between the flyer and the probe to prevent the flyer from damaging the probe, and collect the flyer.
Assemble the flyer-type microdetonation sequence in the fixture, and fix the fixture position so that the optical fiber probe is aligned with the central axis of the acceleration chamber.
Check the continuity of the test circuit and oscilloscope settings, and fire after the inspection.
Read the original frequency difference signal from the oscilloscope, and obtain the flyer velocity–time curve through fast Fourier transform.
2.5. Steel Dent Test
According to the relationship between the design parameters and the velocity and detonation ability of the flyer, a prototype of the microdetonation sequence was designed. The main difference from the device used in the PDV test was that the SCB was placed on a printed circuit board (replacing the electrode plug), which reduced the volume, and then HNS-IV was added as a booster explosive.
After the test, the steel dent depth produced by the reaction of HNS-IV was used to verify whether the flyer had a reliable detonation function under the design parameters. When the prototype was placed on the steel block and the preset initiation energy was input, the following phenomena could occur in HNS-IV: a. the booster explosive was only knocked out of the pit by the flyer, and no steel dent is generated; b. deflagration of the booster explosive occurred, and some of the booster explosive was black, some of the booster explosive was burned out, and no steel dent is generated; c. most of the booster explosive was consumed, thereby resulting in a shallow steel dent; e. the booster explosive was completely consumed, thereby resulting in a deep steel dent, and the depth of the steel dent was consistent with the corresponding charge amount. Obviously, only the last case could show that the flyer had a reliable detonation capability and could verify the rationality of the previous parameter design.
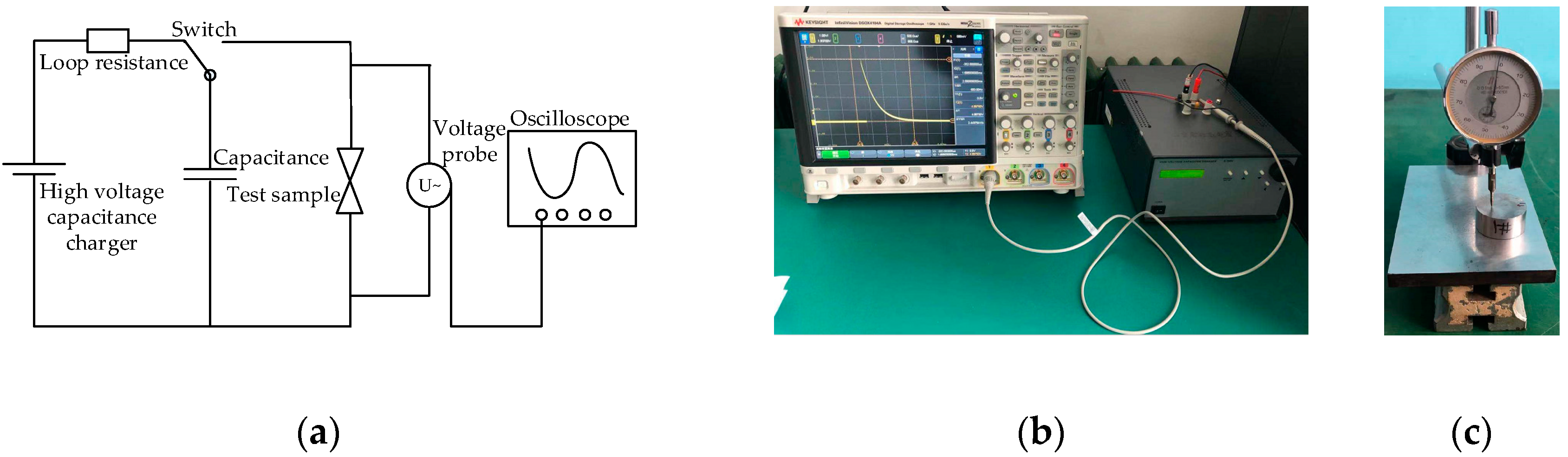
The main equipment used in the steel dent test were: the microdetonation sequence, a high-voltage capacitance charger, a KEYSIGHT DSOX4104A oscilloscope, a VICTOR VC9807+ multimeter, a steel dent tester, and a steel block (φ 35 mm × 16 mm). The test principle and equipment are shown in
Figure 6.
The main process of the steel dent test was as follows:
Set the firing voltage and oscilloscope parameters, then short-circuit the firing circuit.
Assemble the microdetonation sequence prototype.
Connect the prototype pin wire and firing circuit, remove the short-circuit cap of the pin wire, and close the explosion-proof box and test room.
Outside the test room, measure whether the resistance of the semiconductor bridge is within the normal range through the firing circuit.
Determine the test parameter settings again and ignite.
Save the ignition voltage data, record the status of samples, and measure the depth of the steel dent.
4. Discussion
The concept of the critical initiation criterion is similar to the concept of the energy absorbed by energetic materials [
37], both of which involve the energy characteristics inside the explosives. It is worth noting that due to factors of the booster explosive and the test itself [
37], it was better to leave a certain margin when using the critical initiation criterion for the design. Bowden and Guo obtained the
p-
τ and James criteria of HNS-IV by fitting [
38,
39], and Guo verified the accuracy of the criteria via simulation; the fitting accuracy of the James criterion was not high, and the
p-
τ criterion was proved to be more suitable for one-dimensional shock initiation. Tong obtained the
p-
τ criterion of HNS-IV by fitting the experimental [
26] and theoretical data [
40], and the applicable time obtained from the experimental data is within 0.0013 μs, which was less than 0.137 μs found in this study. Wang found the minimum all-firing voltage of HNS-IV initiated via EFI [
41], obtained a flyer velocity that corresponded to the minimum all-firing voltage via PDV, and then obtained the all-firing
p-
τ initiation criterion of HNS-IV: the applicable maximum pressure was 13 GPa, which was less than the 27 GPa found in this study. The fitting range in this study was larger, and the fitting effects of the three common initiation criteria were compared. Compared with the
p-
τ criterion, the
Π-
τ criterion and the James criterion were more suitable for a wider range of explosive types, flyer shapes, pressures, and action times [
23,
24]. The fitting accuracy of the
Π-
τ criterion was higher than that of the James criterion, so it could be used to assist in the design of the microdetonation sequence.
In this paper, the relationship between the design parameters and initiation ability was revealed from the perspective of mechanics by combining the design parameters with an initiation criterion. In some of the literature, the influencing factors of flyers driven by different sizes and types of explosives were reported, but these influencing factors were not comprehensive enough and only the flyer velocity was obtained, so the detonation ability of the flyer could not be judged. Regarding the relationship between the velocity of the flyer driven by PBXN-5 and the density of the flyer (titanium, stainless steel, or copper), the diameter of the charge (1.5 mm~5 mm) and the thickness of the flyer (0.1 mm~0.5 mm) were studied via simulation [
42], and the conclusions were consistent with those of this paper, which not only revealed the negative correlation between the flyer’s density and velocity, but also the morphology of the flyer after shearing. The sensitivity of PBNX-5 was relatively low, and the critical size was larger than that of the primary explosive, which was not suitable for driving the flyer as a primary charge. The test results showed that the BNCP with a size of φ 3 mm × 8 mm could drive a titanium flyer with a thickness of 0.1 mm to reach a speed of about 3600 m/s [
13,
43], but the charge size was quite different from that used in this study, and it was impossible to compare the difference between Pb(N
3)
2 and BNCP in driving the flyer. The simulation results showed that the velocity of the flyer with a diameter of 1 mm driven by Cu(N
3)
2 did not increase significantly after the charge height was 0.6 mm; in this study, the diameter of the Pb(N
3)
2 was 0.9 mm, and when the charge height was 1.8 mm, the velocity of the flyer tended to be stable, which was similar to the growth law of the output pressure of Pb(N
3)
2 [
17]. Due to the high sensitivity of Cu(N
3)
2, it was difficult to test its output pressure. The experimental results confirmed that the titanium flyer could remain intact under the action of Cu(N
3)
2; while copper, aluminum, and polyimide showed different degrees of damage [
14,
15,
16]. This study verified that under the action of Pb(N
3)
2, the titanium flyer could still remain intact while the polyimide flyer was incomplete; therefore, the matching of the titanium flyer and the microcharge was the best. Liu studied the relationship between the design parameters and the kinetic energy of a titanium flyer driven by PBXN-5 (diameter: 5 mm) [
44], and Mu studied the relationship between the design parameters and the kinetic energy per unit area of a titanium flyer driven by lead azide (size: φ 1.2 mm × 2 mm) [
45]. Compared with other studies, it was an improvement to use the kinetic energy of the flyer or the kinetic energy per unit area as a characterization parameter, but it was still rough and directly affected the relevant conclusions because the energy absorbed by the explosives only accounted for a portion of the kinetic energy of the flyer [
37]. In the current study, it was more reasonable to use the incident shock wave parameters formed in the explosive as the initiation criterion when the flyer struck the explosive. In summary, the previous studies only focused on the velocity, kinetic energy, or kinetic energy per unit area of the flyer, and these three parameters could not accurately reflect the initiation ability of the flyer. In the current paper, the initiation mechanism could be revealed more clearly by combining the design parameters with an initiation criterion. Moreover, the design parameters used in the current paper were more comprehensive.
In this study, a prototype of HNS-IV detonated by a titanium flyer driven by microsized Pb(N
3)
2 was designed. The steel dent test confirmed that the prototype had a reliable detonation transmission function. The purpose of the design of the prototype was to make the size or charge amount of the primary explosive as small as possible under the premise of meeting the detonation transmission function. The U.S. military used Ag(N
3)
2 (φ 2 mm × 0.5 mm; 6 mg), Cu(N
3)
2, or energetic ink explosives to drive flyers to detonate EDF-11 explosives [
3,
4,
5,
6,
7,
8]. The Kaman Company used a slurry of Pb(N
3)
2 to drive a flyer to detonate HNS-IV explosives [
9]. The volume and charge of Ag(N
3)
2 used by the U.S. military were larger than that of the Pb(N
3)
2 used in the current study (φ 0.9 mm × 1.8 mm and 4.6 mg, respectively), but the charge height was smaller. This may have been because the sensitivity of EDF-11 is higher than that of HNS-IV, and the in situ process maturity of the U.S. military is high. Kaman’s design idea was consistent with that of this paper, but the literature we found did not introduce specific design parameters. In the literature [
12], when the size and weight of Cu(N
3)
2 were φ 2 mm × 1.5 mm and 7.5 mg, respectively, a titanium flyer with a thickness of 30 μm~50 μm could be driven to detonate a CL-20-based booster explosive. The size and charge amount of Cu(N
3)
2 used in the literature were larger than that of the Pb(N
3)
2 used in the current paper, which may have been related to the in situ synthesis process. Wang used lead azide (φ 1.6 mm × 2 mm; 14.4 mg) to drive a stainless steel flyer (with a thickness of 30 μm) to detonate HNS-IV [
10]; in the latest research results published by their group, the size and charge of the lead azide (φ 1.2 mm × 2 mm; 8.1 mg) were further reduced [
46], which was close to the level used in the current study. The size or charge amount of the Pb(N
3)
2 used in this paper can be further reduced based on the following aspects: (a) increase the charge diameter appropriately to reduce the charge height; (b) reduce the thickness of the flyer properly to improve the power flux of the flyer; (c) design the diameter of the acceleration chamber to be designed closer to the diameter of the charge; and (d) encapsulate the outside of the prototype to reduce the leakage of the detonation products.
5. Conclusions
According to the shock-initiation theory, the Π-τ initiation criterion of HNS-IV was fitted. The simulation model of the microflyer driven by microsized lead azide was established. The ratio of the RMSE to the simulation value was 7.82%.
Based on the Π-τ initiation criterion, the relationships between various design parameters and the velocity of the flyer, the power flux, and the action time were studied; the results were as follows. Titanium was the best flyer material; based on the premise of satisfying the forming effect, the thinner flyer should be selected; the aperture of accelerating chamber should be consistent with the diameter of the primary explosive; sapphire and metal were the most suitable materials for the acceleration chamber; the material with a high shock wave impedance should be selected for the restraint of the primary explosive; and the velocity and power flux of the flyer increased linearly or exponentially with the increase in the density, diameter, and height of the primary explosive.
A microdetonation sequence for HNS-IV detonated by a titanium microflyer driven by microsized lead azide was designed. When the weight of the lead azide was 4.6 mg, the microflyer successfully detonated the HNS-IV, and the average depth of the steel dent was 0.39 mm.