Numerical Modeling Using Immersed Boundary-Lattice Boltzmann Method and Experiments for Particle Manipulation under Standing Surface Acoustic Waves
Abstract
1. Introduction
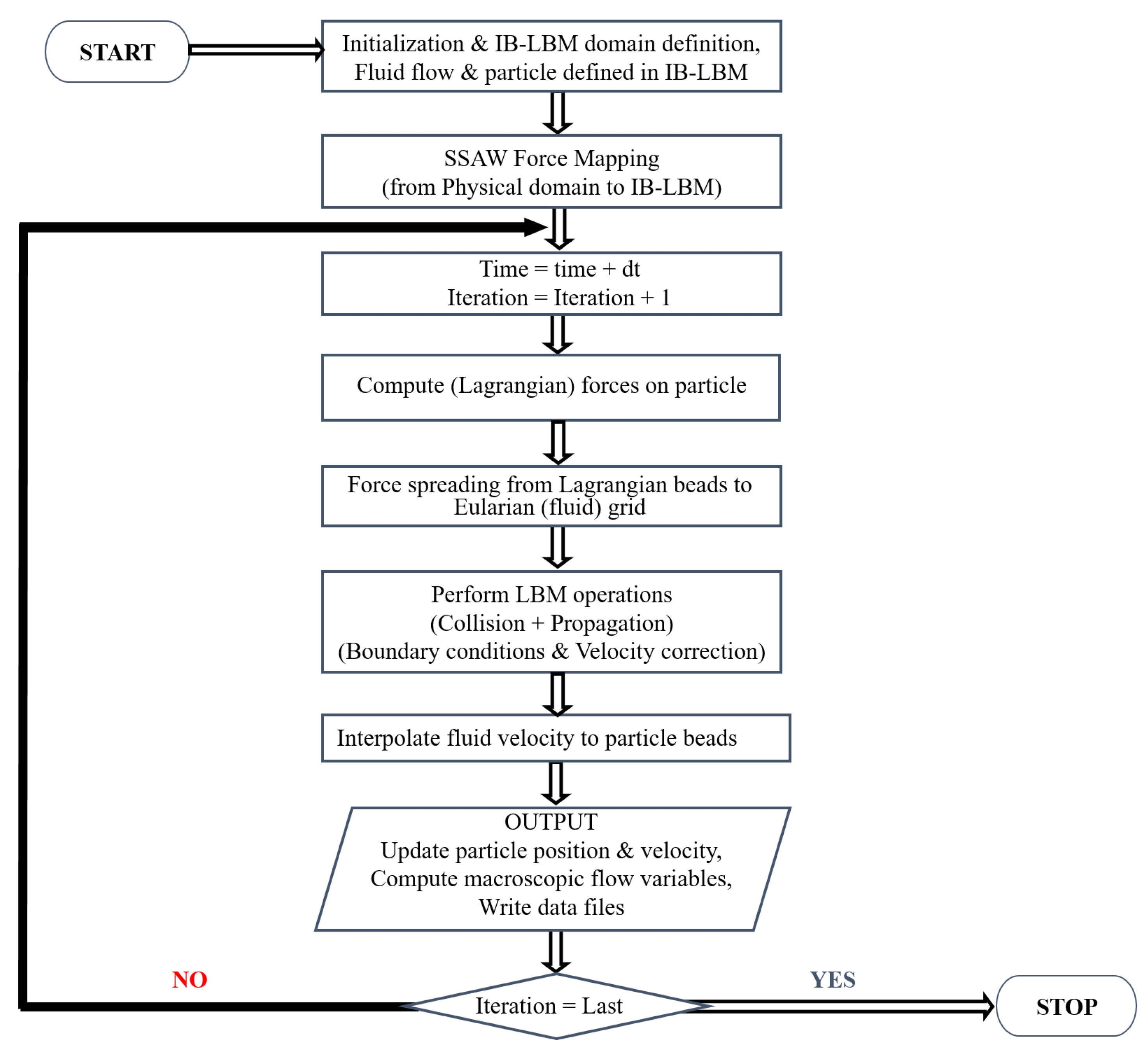
2. Mathematical Modeling
2.1. Model for Fluid, Particle, and Their Interaction
2.2. Parameter Mapping from Physical to LBM Domain
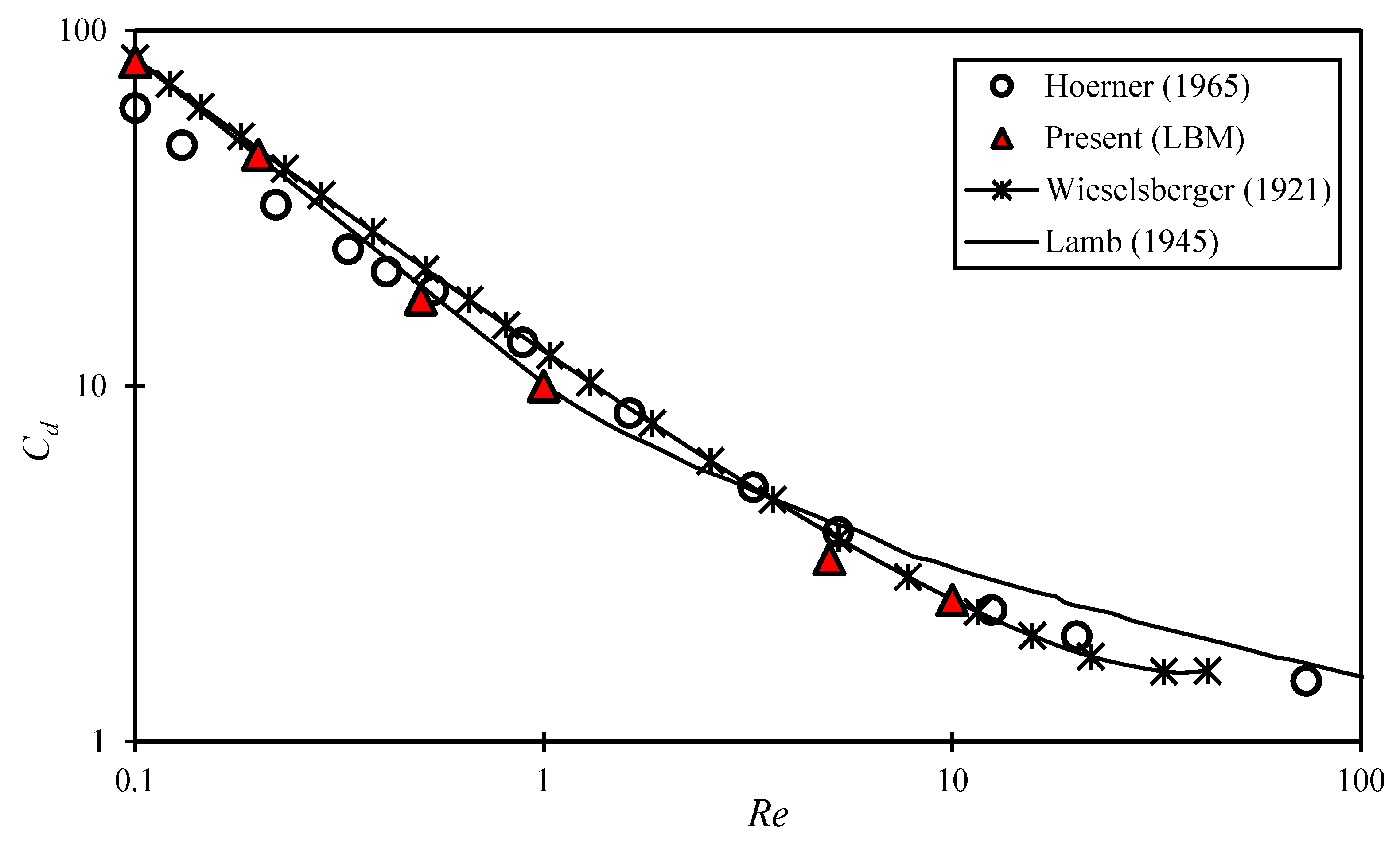
3. Verification and Validation
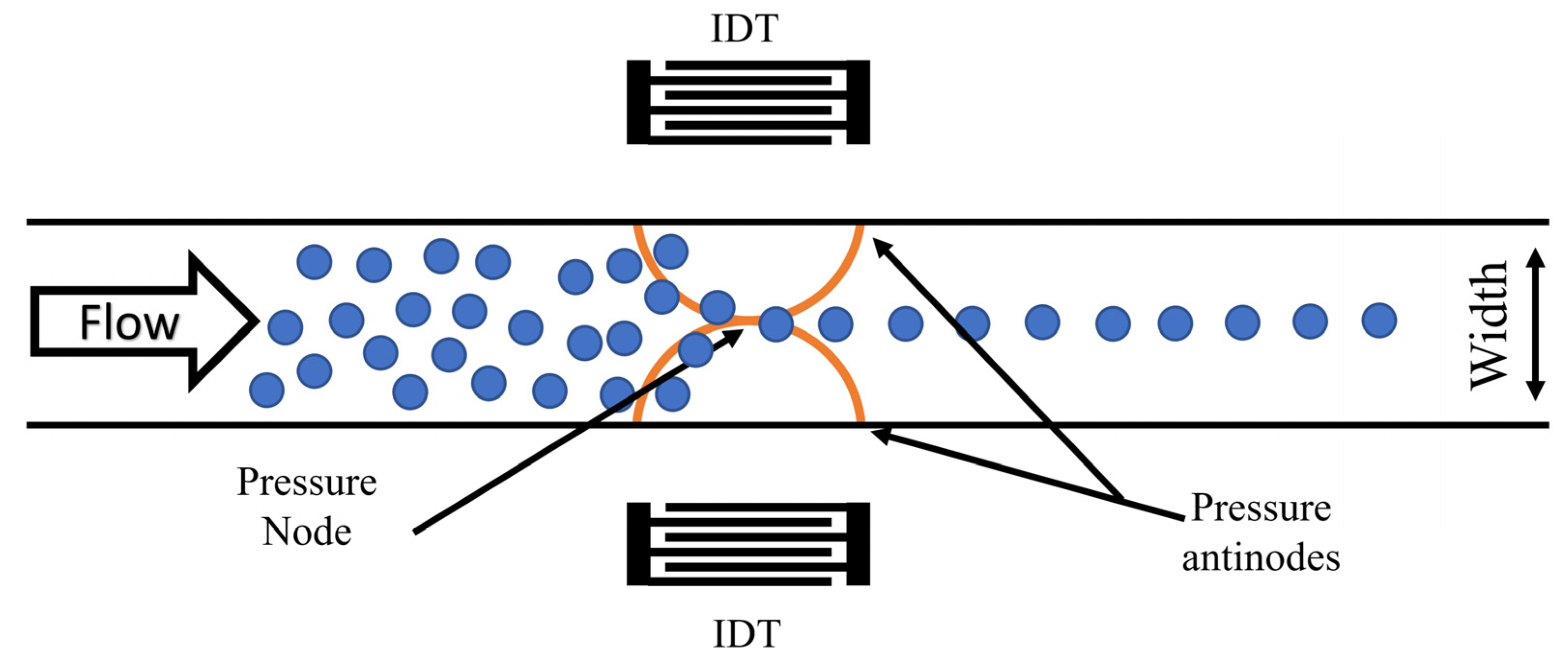
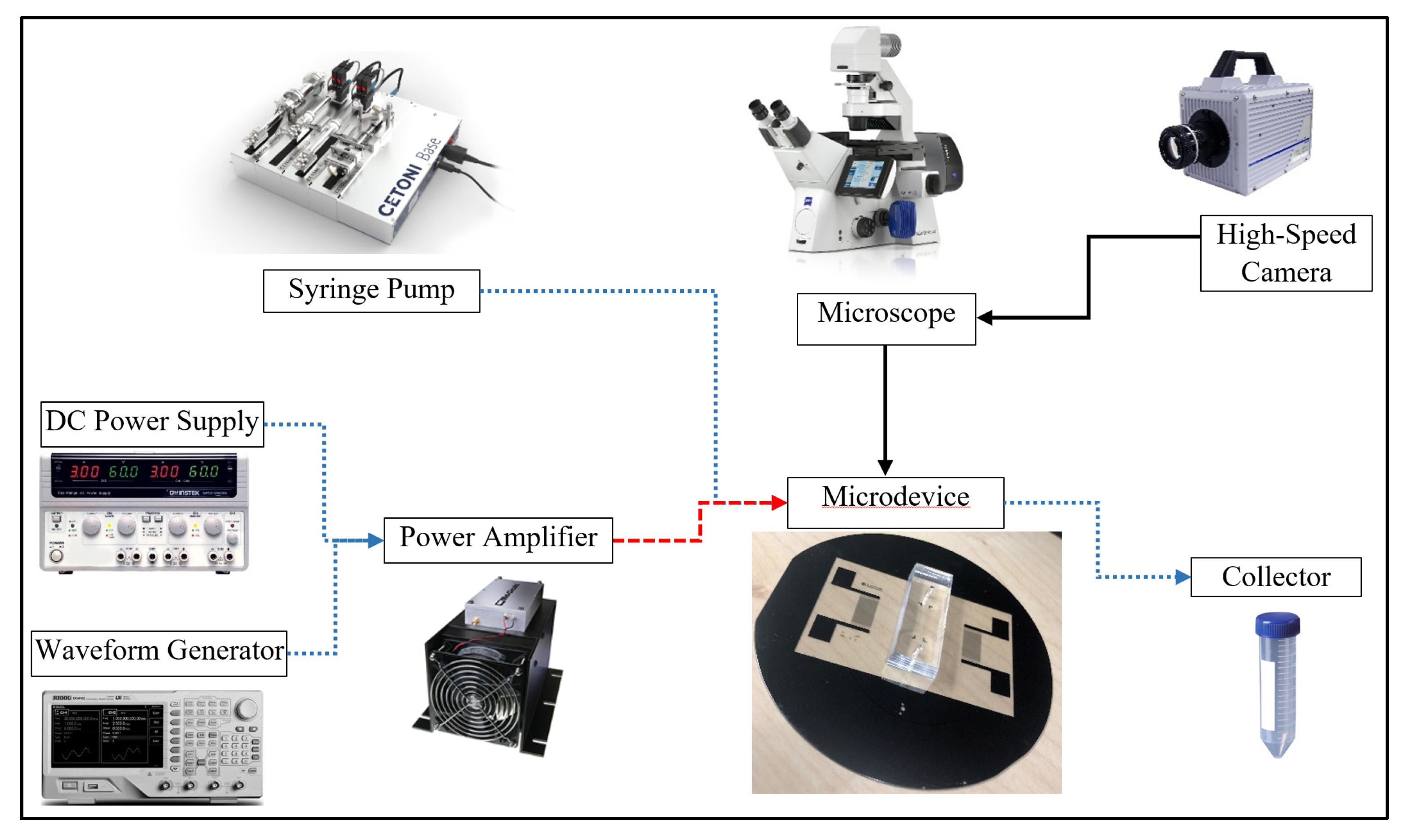
4. Device Design and Experimental Setup
5. Results and Discussion
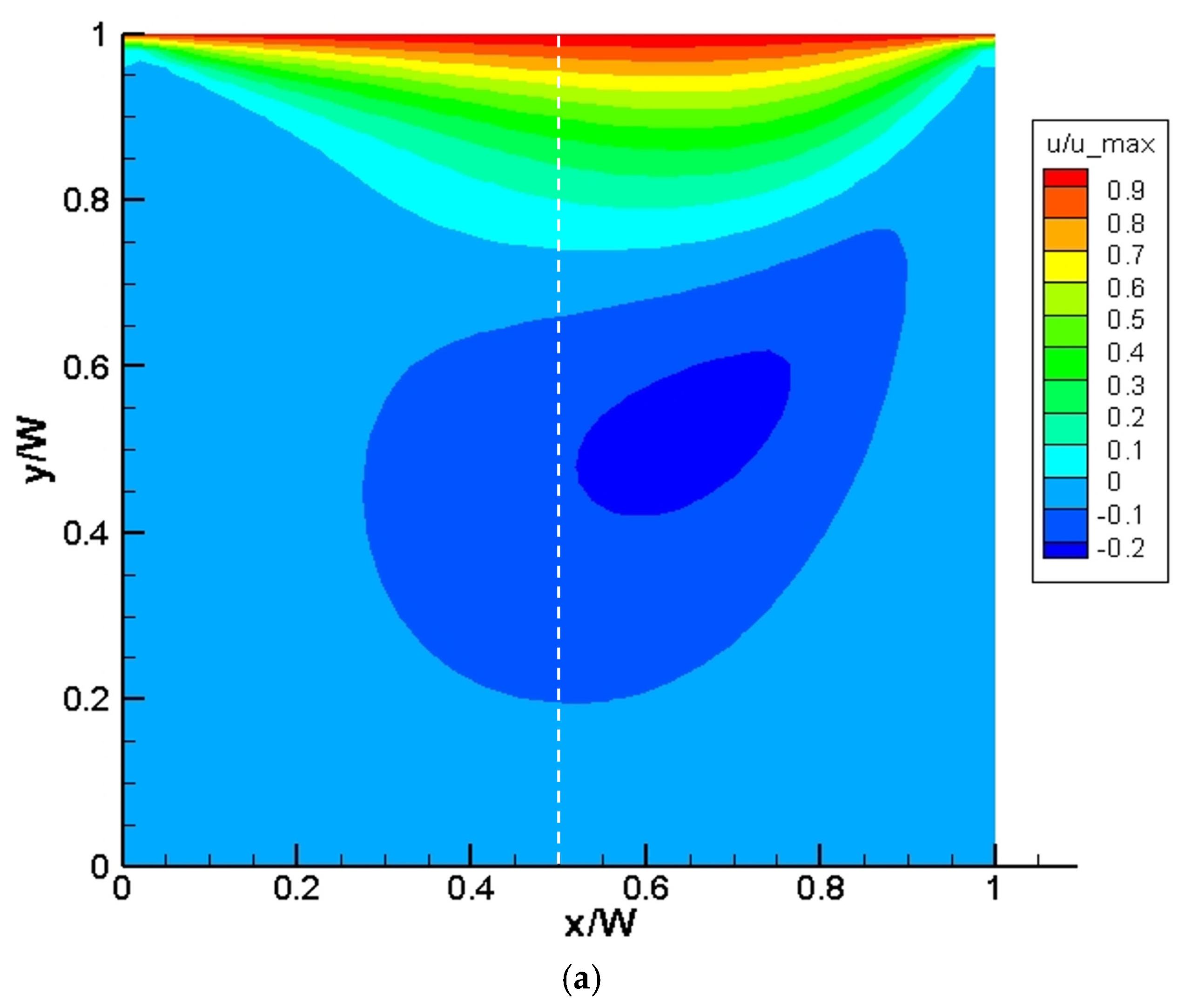
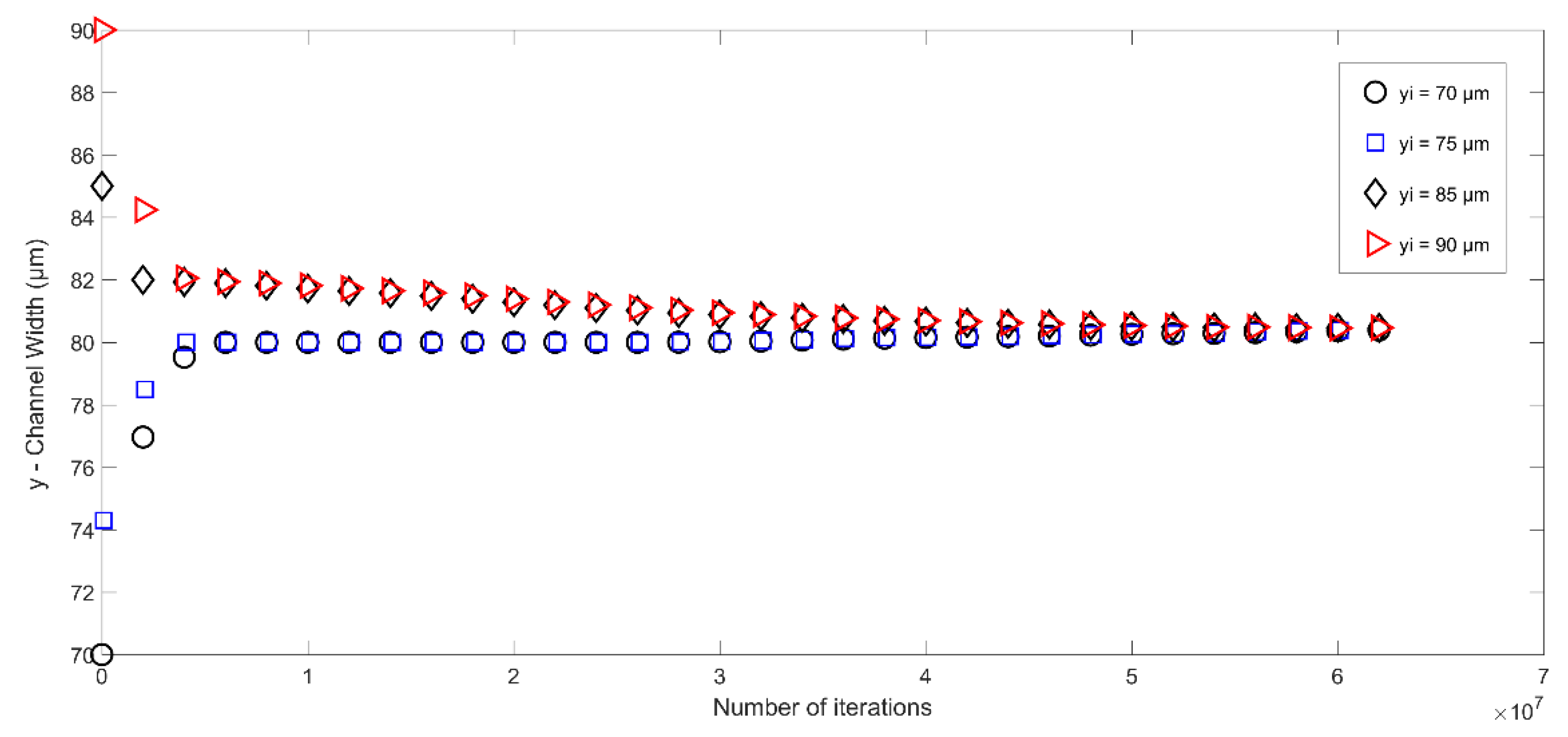
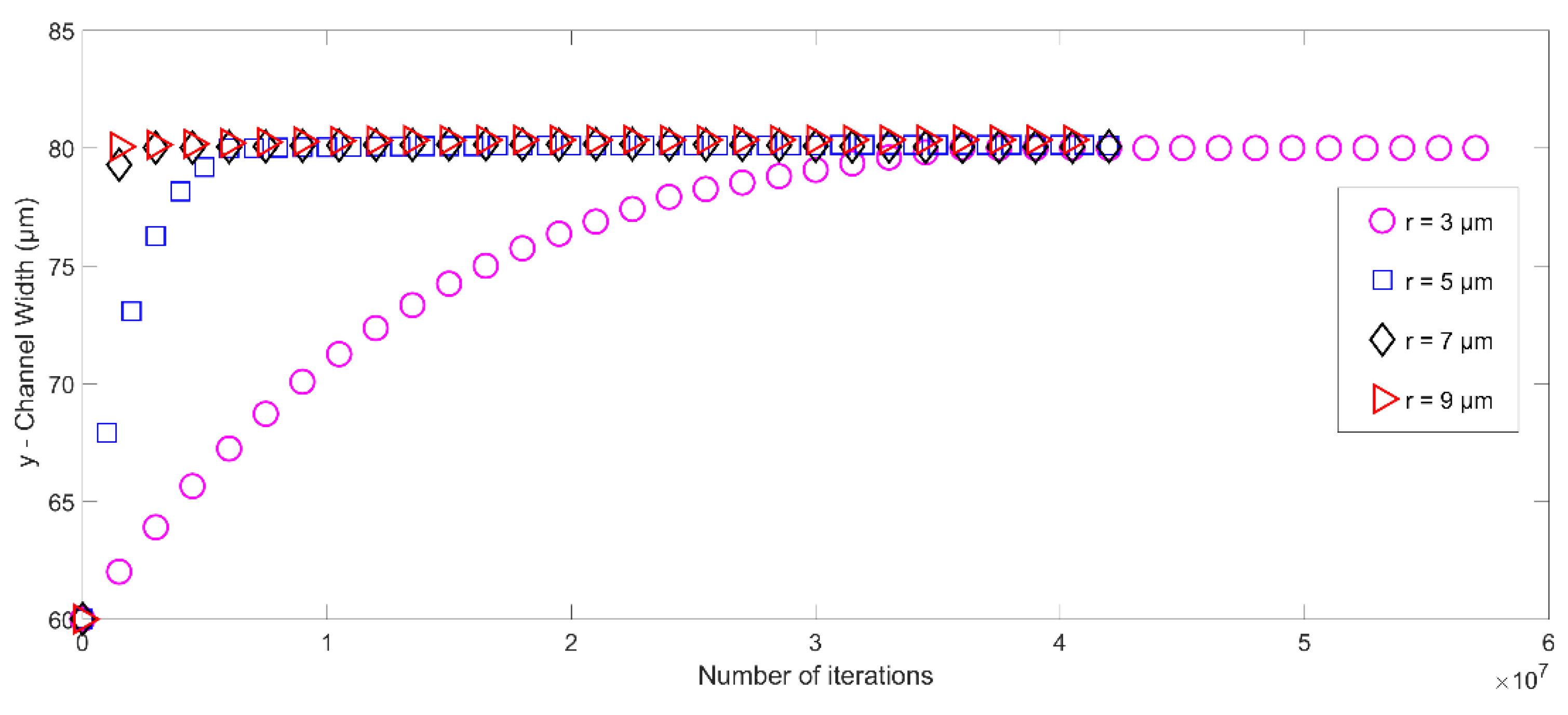
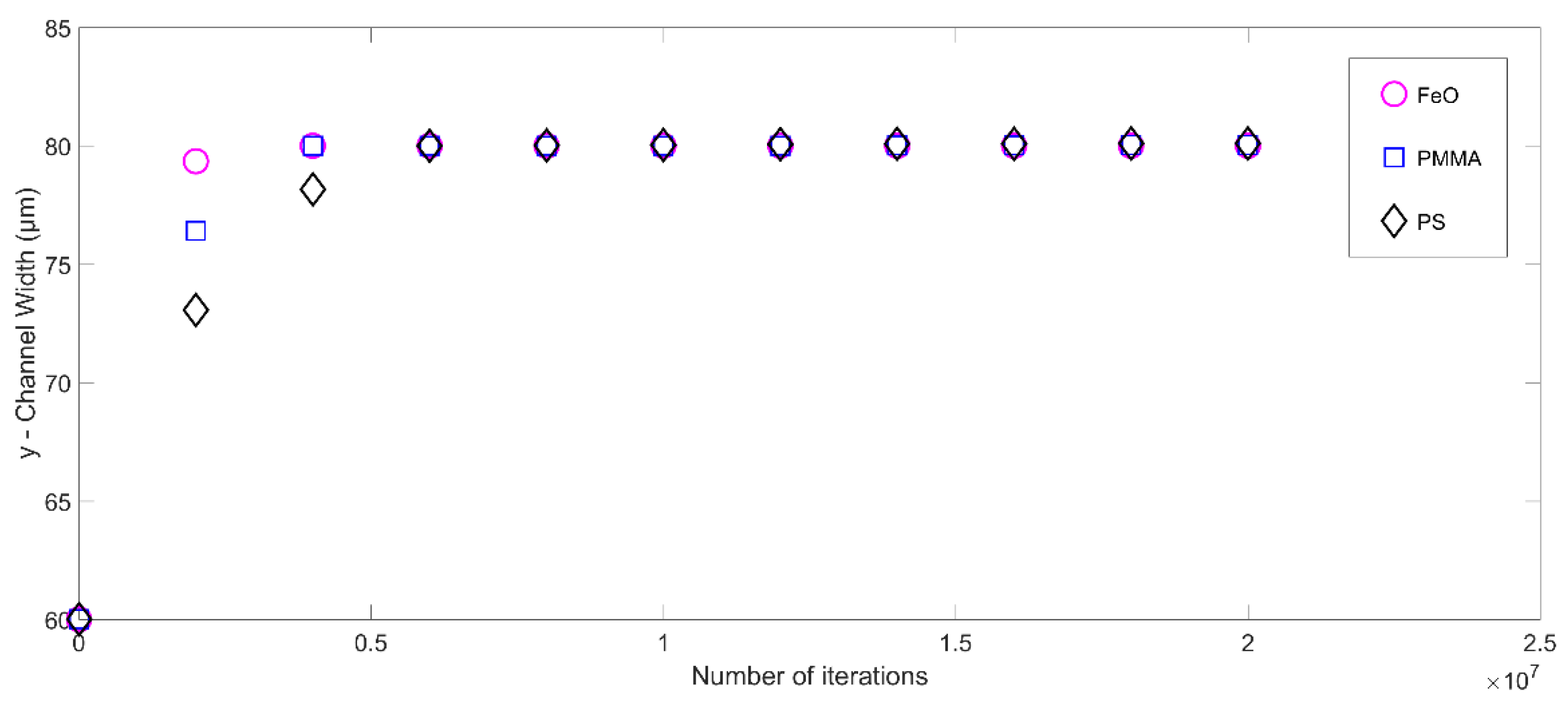
5.1. Microparticle Focusing at the Centerline of the Microchannel
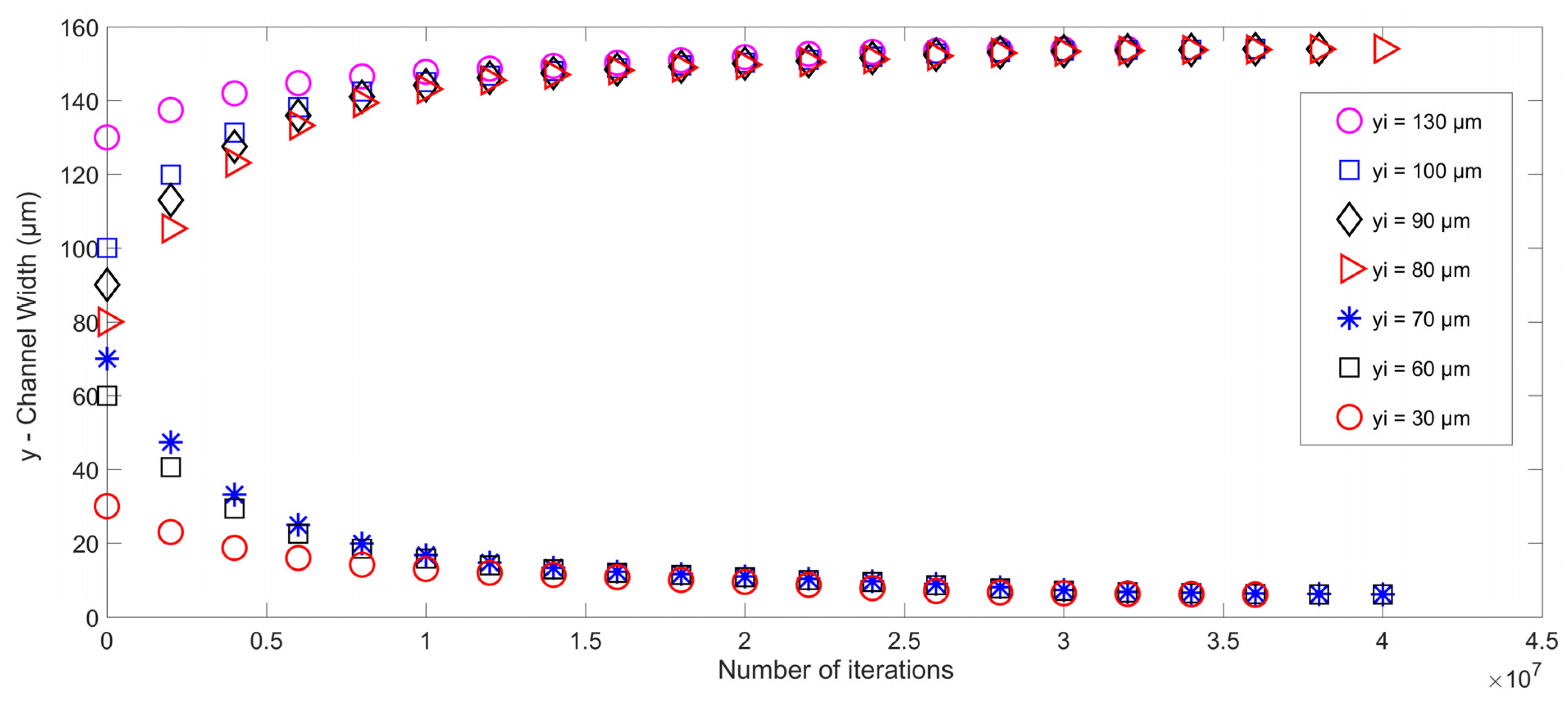
5.2. Microparticle Focusing at the Sides of the Microchannel
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, S.; Joseph, N.; Feng, S.; Jellicoe, M.; Raston, C.L. Application of microfluidic technology in food processing. Food Funct. 2020, 11, 5726–5737. [Google Scholar] [CrossRef] [PubMed]
- Livak-Dahl, E.; Sinn, I.; Burns, M. Microfluidic Chemical Analysis Systems. Annu. Rev. Chem. Biomol. Eng. 2011, 2, 325–353. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Yu, C.; Xie, X. Microfluidics for Environmental Applications. In Microfluidics in Biotechnology; Springer: Cham, Switzerland, 2020; pp. 267–290. [Google Scholar]
- Al-Ali, A.; Waheed, W.; Abu-Nada, E.; Alazzam, A. A review of active and passive hybrid systems based on Dielectrophoresis for the manipulation of microparticles. J. Chromatogr. A 2022, 1676, 463268. [Google Scholar] [CrossRef] [PubMed]
- Alhammadi, F.; Waheed, W.; El-Khasawneh, B.; Alazzam, A. Continuous-flow cell dipping and medium exchange in a microdevice using dielectrophoresis. Micromachines 2018, 9, 223. [Google Scholar] [CrossRef]
- Sajeesh, P.; Sen, A.K. Particle separation and sorting in microfluidic devices: A review. Microfluid. Nanofluid. 2014, 17, 1–52. [Google Scholar] [CrossRef]
- Zborowski, M.; Chalmers, J.J. Magnetophoresis: Fundamentals and applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1999; pp. 1–23. [Google Scholar]
- Destgeer, G.; Lee, K.H.; Jung, J.H.; Alazzam, A.; Sung, H.J. Continuous separation of particles in a PDMS microfluidic channel via travelling surface acoustic waves (TSAW). Lab A Chip 2013, 13, 4210–4216. [Google Scholar] [CrossRef]
- Zhang, H.; Tu, E.; Hagen, N.D.; Schnabel, C.A.; Paliotti, M.J.; Hoo, W.S.; Nguyen, P.M.; Kohrumel, J.R.; Butler, W.F.; Chachisvillis, M. Time-of-flight optophoresis analysis of live whole cells in microfluidic channels. Biomed. Microdevices 2004, 6, 11–21. [Google Scholar] [CrossRef]
- Waheed, W.; Alazzam, A.; Mathew, B.; Christoforou, N.; Abu-Nada, E. Lateral fluid flow fractionation using dielectrophoresis (LFFF-DEP) for size-independent, label-free isolation of circulating tumor cells. J. Chromatogr. B 2018, 1087, 133–137. [Google Scholar] [CrossRef]
- Lau, A.Y.; Hung, P.J.; Wu, A.R.; Lee, L.P. Open-access microfluidic patch-clamp array with raised lateral cell trapping sites. Lab A Chip 2006, 6, 1510–1515. [Google Scholar] [CrossRef]
- Gao, Y.; Magaud, P.; Baldas, L.; Wang, Y. Inertial migration of neutrally buoyant spherical particles in square channels at moderate and high Reynolds numbers. Micromachines 2021, 12, 198. [Google Scholar] [CrossRef]
- Soliman, A.M.; Eldosoky, M.A.; Taha, T.E. Analysis improvement of standing surface acoustic wave microfluidic devices for bio-particles separation. Int. J. Comput. Appl. Technol. 2017, 55, 244–256. [Google Scholar] [CrossRef]
- Lenshof, A.; Laurell, T. Acoustophoresis. In Encyclopedia of Nanotechnology; Springer: Dordrecht, The Netherlands, 2012; pp. 45–50. [Google Scholar]
- Mathew, B.; Alazzam, A.; El-Khasawneh, B.; Maalouf, M.; Destgeer, G.; Sung, H.J. Model for tracing the path of microparticles in continuous flow microfluidic devices for 2D focusing via standing acoustic waves. Sep. Purif. Technol. 2015, 153, 99–107. [Google Scholar] [CrossRef]
- Nam, J.; Lee, Y.; Shin, S. Size-dependent microparticles separation through standing surface acoustic waves. Microfluid. Nanofluid. 2011, 11, 317–326. [Google Scholar] [CrossRef]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Waheed, W.; Alazzam, A.; Al-Khateeb, A.N.; Abu-Nada, E. Dissipative particle dynamics for modeling micro-objects in microfluidics: Application to dielectrophoresis. Biomech. Model. Mechanobiol. 2020, 19, 389–400. [Google Scholar] [CrossRef]
- Waheed, W.; Alazzam, A.; Al-Khateeb, A.N.; Sung, H.J.; Abu-Nada, E. Investigation of DPD transport properties in modeling bioparticle motion under the effect of external forces: Low Reynolds number and high Schmidt scenarios. J. Chem. Phys. 2019, 150, 054901. [Google Scholar] [CrossRef]
- Teschner, T.-R.; Könözsy, L.; Jenkins, K.W. Progress in particle-based multiscale and hybrid methods for flow applications. Microfluid. Nanofluid. 2016, 20, 68. [Google Scholar] [CrossRef]
- Mohamad, A. Lattice Boltzmann Method; Springer: Cham, Switzerland, 2011; Volume 70. [Google Scholar]
- Hardy, J.; Pomeau, Y.; De Pazzis, O. Time evolution of a two-dimensional classical lattice system. Phys. Rev. Lett. 1973, 31, 276. [Google Scholar] [CrossRef]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier-Stokes equation. In Lattice Gas Methods for Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2019; pp. 11–18. [Google Scholar]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 1988, 61, 2332. [Google Scholar] [CrossRef]
- Hsu, J.-C.; Hsu, C.-H.; Huang, Y.-W. Acoustophoretic control of microparticle transport using dual-wavelength surface acoustic wave devices. Micromachines 2019, 10, 52. [Google Scholar] [CrossRef]
- Gantner, A.; Hoppe, R.H.; Köster, D.; Siebert, K.; Wixforth, A. Numerical simulation of piezoelectrically agitated surface acoustic waves on microfluidic biochips. Comput. Vis. Sci. 2007, 10, 145–161. [Google Scholar] [CrossRef]
- Barnkob, R.; Augustsson, P.; Laurell, T.; Bruus, H. Measuring the local pressure amplitude in microchannel acoustophoresis. Lab A Chip 2010, 10, 563–570. [Google Scholar] [CrossRef]
- Muller, P.B.; Barnkob, R.; Jensen, M.J.H.; Bruus, H. A numerical study of microparticle acoustophoresis driven by acoustic radiation forces and streaming-induced drag forces. Lab A Chip 2012, 12, 4617–4627. [Google Scholar] [CrossRef]
- Nama, N.; Barnkob, R.; Mao, Z.; Kähler, C.J.; Costanzo, F.; Huang, T.J. Numerical study of acoustophoretic motion of particles in a PDMS microchannel driven by surface acoustic waves. Lab A Chip 2015, 15, 2700–2709. [Google Scholar] [CrossRef]
- Mao, Z.; Xie, Y.; Guo, F.; Ren, L.; Huang, P.-H.; Chen, Y.; Rufo, J.; Costanzo, F.; Huang, T.J. Experimental and numerical studies on standing surface acoustic wave microfluidics. Lab A Chip 2016, 16, 515–524. [Google Scholar] [CrossRef]
- Guo, F.; Mao, Z.; Chen, Y.; Xie, Z.; Lata, J.P.; Li, P.; Ren, L.; Liu, J.; Yang, J.; Dao, M. Three-dimensional manipulation of single cells using surface acoustic waves. Proc. Natl. Acad. Sci. USA 2016, 113, 1522–1527. [Google Scholar] [CrossRef]
- Skov, N.R.; Bruus, H. Modeling of microdevices for SAW-based acoustophoresis—A study of boundary conditions. Micromachines 2016, 7, 182. [Google Scholar] [CrossRef]
- Bach, J.S.; Bruus, H. Theory of pressure acoustics with viscous boundary layers and streaming in curved elastic cavities. J. Acoust. Soc. Am. 2018, 144, 766–784. [Google Scholar] [CrossRef]
- O’Rorke, R.; Collins, D.; Ai, Y. A rapid and meshless analytical model of acoustofluidic pressure fields for waveguide design. Biomicrofluid. 2018, 12, 024104. [Google Scholar] [CrossRef]
- Ni, Z.; Yin, C.; Xu, G.; Xie, L.; Huang, J.; Liu, S.; Tu, J.; Guo, X.; Zhang, D. Modelling of SAW-PDMS acoustofluidics: Physical fields and particle motions influenced by different descriptions of the PDMS domain. Lab A Chip 2019, 19, 2728–2740. [Google Scholar] [CrossRef]
- Skov, N.R.; Sehgal, P.; Kirby, B.J.; Bruus, H. Three-dimensional numerical modeling of surface-acoustic-wave devices: Acoustophoresis of micro-and nanoparticles including streaming. Phys. Rev. Appl. 2019, 12, 044028. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann method. Springer Int. Publ. 2017, 10, 4–15. [Google Scholar]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Eggleton, C.D.; Popel, A.S. Large deformation of red blood cell ghosts in a simple shear flow. Phys. Fluids 1998, 10, 1834–1845. [Google Scholar] [CrossRef]
- Feng, Z.-G.; Michaelides, E.E. The immersed boundary-Lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, H.; Huang, D.; Zhou, L. The Immersed Boundary-Lattice boltzmann method parallel model for fluid-structure interaction on heterogeneous platforms. Math. Probl. Eng. 2020, 2020, 3913968. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815. [Google Scholar] [CrossRef]
- Karimnejad, S.; Delouei, A.A.; Basagaoglu, H.; Nazari, M.; Shahmardan, M.M.; Falcucci, G.; Lauricella, M.; Succi, S. A Review on Contact and Collision Methods for Multi-body Hydrodynamic problems in Complex Flows. arXiv 2022, arXiv:2211.11728. [Google Scholar] [CrossRef]
- Delouei, A.A.; Nazari, M.; Kayhani, M.; Ahmadi, G. A non-Newtonian direct numerical study for stationary and moving objects with various shapes: An immersed boundary–Lattice Boltzmann approach. J. Aerosol Sci. 2016, 93, 45–62. [Google Scholar] [CrossRef]
- Munson, B.; Okiishi, T.; Huebsch, W.; Rothmayer, A. Fundamentals of Fluid Mechanics, 7th ed.; Munson: Traverse City, MI, USA, 2013. [Google Scholar]
- Sukop, M.; Thorne, D.T., Jr. Lattice Boltzmann Modeling; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ghia, U.; Ghia, K.N.; Shin, C. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics; Tata McGraw-Hill Education: New York, NY, USA, 1979. [Google Scholar]
- Hoerner, S.F. Fluid-Dynamic Drag; Hoerner Fluid Dynamics: Vancouver, WA, USA, 1965. [Google Scholar]
- Wieselsberger, C.v. Neuere feststellungen uber die gesetze des flussigkeits und luftwiderstands. Phys. Z. 1921, 22, 321. [Google Scholar]
- Zhang, Y.; Chen, X. Particle separation in microfluidics using different modal ultrasonic standing waves. Ultrason. Sonochem. 2021, 75, 105603. [Google Scholar] [CrossRef]
- Mazalan, M.B.; Noor, A.M.; Wahab, Y.; Yahud, S.; Zaman, W.S.W.K. Current Development in Interdigital Transducer (IDT) Surface Acoustic Wave Devices for Live Cell In Vitro Studies: A Review. Micromachines 2021, 13, 30. [Google Scholar] [CrossRef]
- Al-Ali, A.; Waheed, W.; Abu-Nada, E.; Alazzam, A. Fabrication of acoustic microfluidic platforms for particle manipulation. In Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 4 February–April 2020; pp. 1–4. [Google Scholar]
- Al-Ali, A.; Waheed, W.; Abu-Nada, E.; Mathew, B.; Sung, H.J.; Alazzam, A. A microfluidic platform with castellated electrodes to separate cancer cells from blood cells. In Proceedings of the 2020 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Toronto, ON, Canada, 13–17 July 2020; pp. 1–6. [Google Scholar]
- Simon, G.; Pailhas, Y.; Andrade, M.A.; Reboud, J.; Marques-Hueso, J.; Desmulliez, M.P.; Cooper, J.M.; Riehle, M.O.; Bernassau, A.L. Particle separation in surface acoustic wave microfluidic devices using reprogrammable, pseudo-standing waves. Appl. Phys. Lett. 2018, 113, 044101. [Google Scholar] [CrossRef]




| Property | Conversion Factor (C.F.) | ||
|---|---|---|---|
| Channel width, | 160 μm | 80 | 2 μm |
| Water density, | 1027 kg/m3 | 1 | 1027 kg/m3 |
| Particle density, | 1050 kg/m3 | 1.05 | 1000 kg/m3 |
| Fluid Viscosity, | 1 × 10−6 m2/s | 0.0167 | 6 × 10−5 m2/s |
| Particle | Particle Density | Particle Compressibility |
|---|---|---|
| Polystyrene (PS) | 1050 kg/m3 | 2.49 × 10−10 pa−1 |
| Iron Oxide (FeO) | 1500 kg/m3 | 1.5× 10−11pa−1 |
| Poly(Methyl Methacrylate) (PMMA) | 1200 kg/m3 | 1.7 × 10−10 pa−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehhi, F.; Waheed, W.; Al-Ali, A.; Abu-Nada, E.; Alazzam, A. Numerical Modeling Using Immersed Boundary-Lattice Boltzmann Method and Experiments for Particle Manipulation under Standing Surface Acoustic Waves. Micromachines 2023, 14, 366. https://doi.org/10.3390/mi14020366
Alshehhi F, Waheed W, Al-Ali A, Abu-Nada E, Alazzam A. Numerical Modeling Using Immersed Boundary-Lattice Boltzmann Method and Experiments for Particle Manipulation under Standing Surface Acoustic Waves. Micromachines. 2023; 14(2):366. https://doi.org/10.3390/mi14020366
Chicago/Turabian StyleAlshehhi, Fatima, Waqas Waheed, Abdulla Al-Ali, Eiyad Abu-Nada, and Anas Alazzam. 2023. "Numerical Modeling Using Immersed Boundary-Lattice Boltzmann Method and Experiments for Particle Manipulation under Standing Surface Acoustic Waves" Micromachines 14, no. 2: 366. https://doi.org/10.3390/mi14020366
APA StyleAlshehhi, F., Waheed, W., Al-Ali, A., Abu-Nada, E., & Alazzam, A. (2023). Numerical Modeling Using Immersed Boundary-Lattice Boltzmann Method and Experiments for Particle Manipulation under Standing Surface Acoustic Waves. Micromachines, 14(2), 366. https://doi.org/10.3390/mi14020366








