Comparative Study about Dimensional Accuracy and Surface Finish of Constant-Breadth Cams Manufactured by FFF and CNC Milling
Abstract
:1. Introduction
2. Materials and Methods
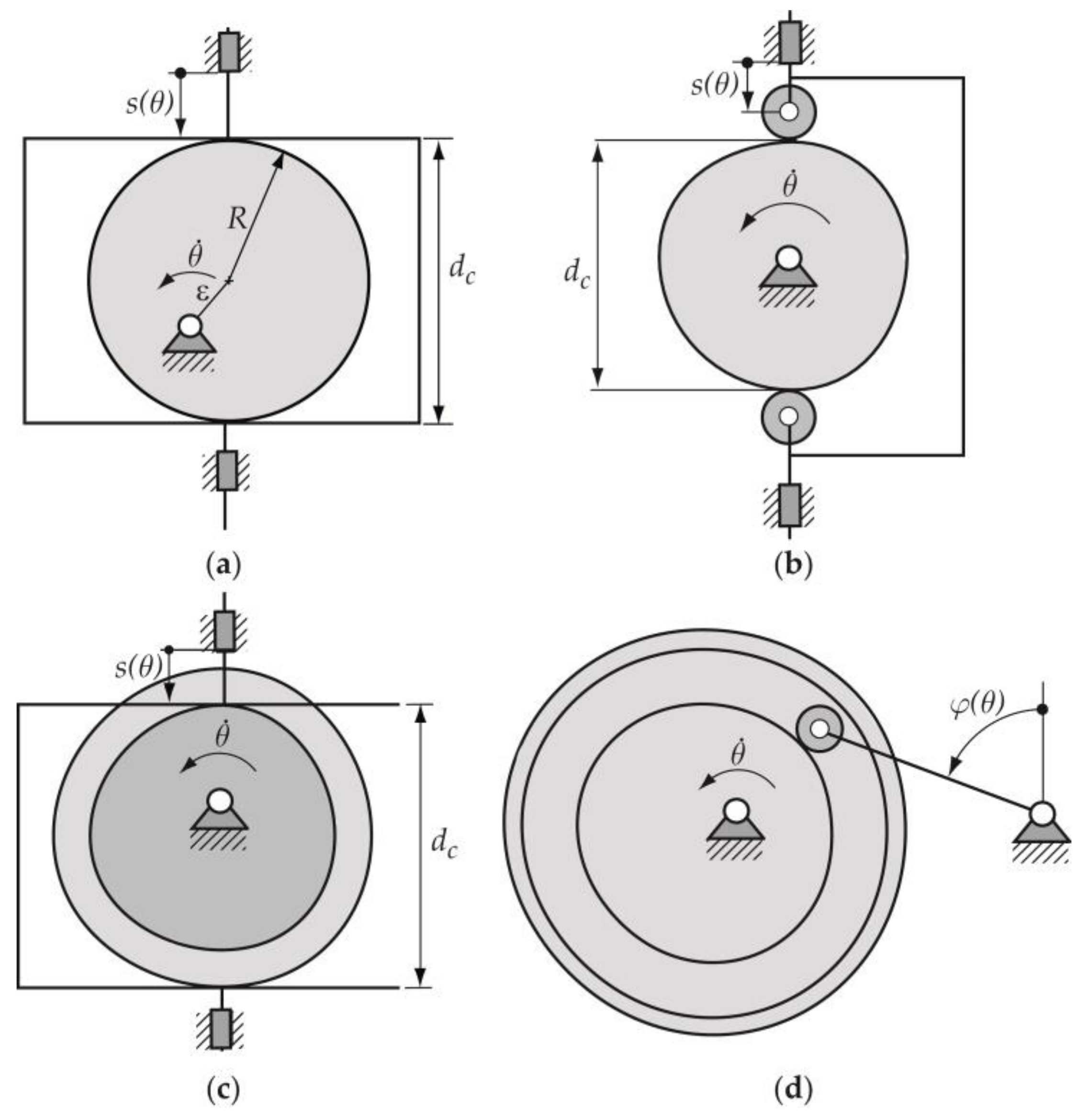
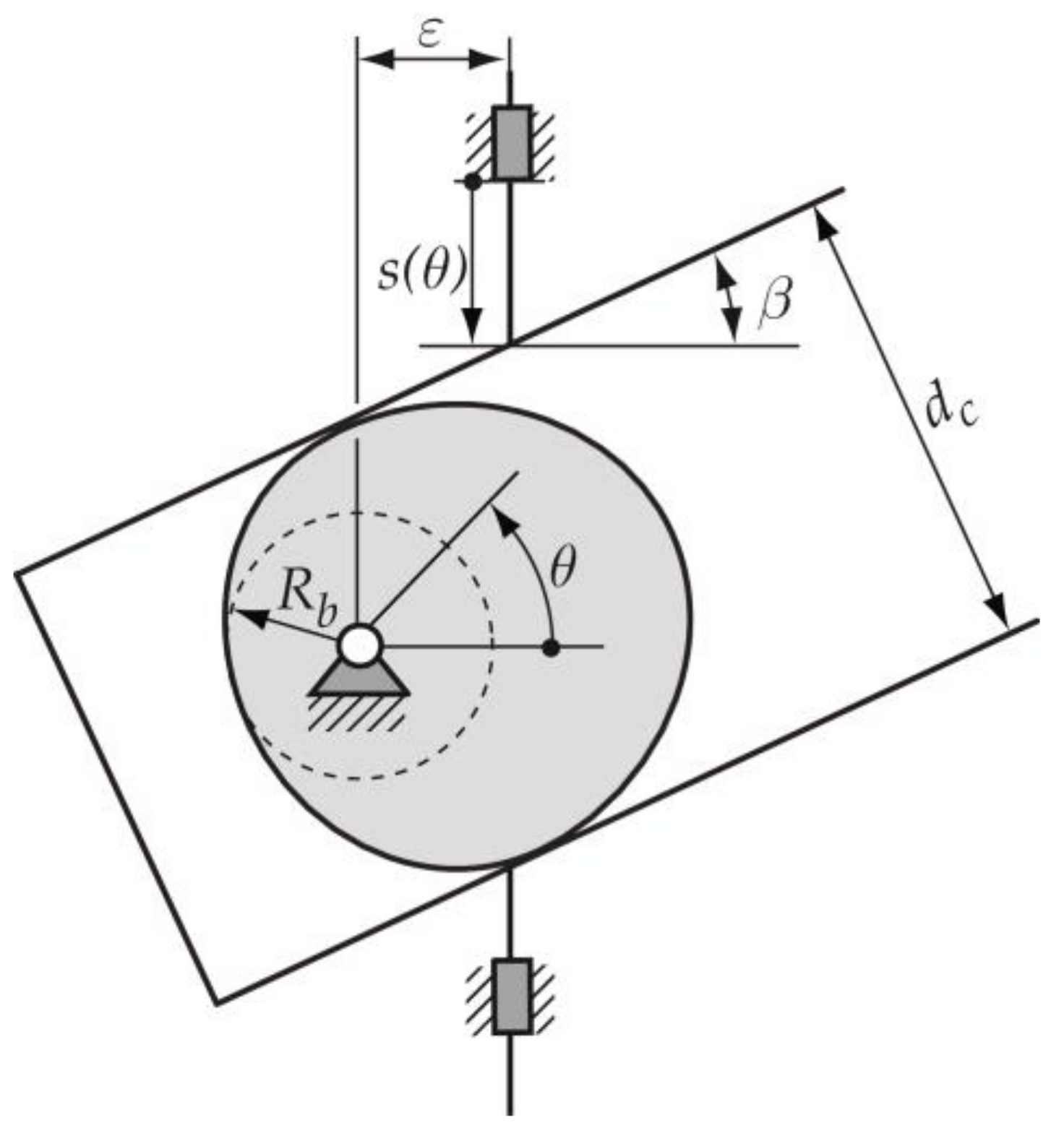
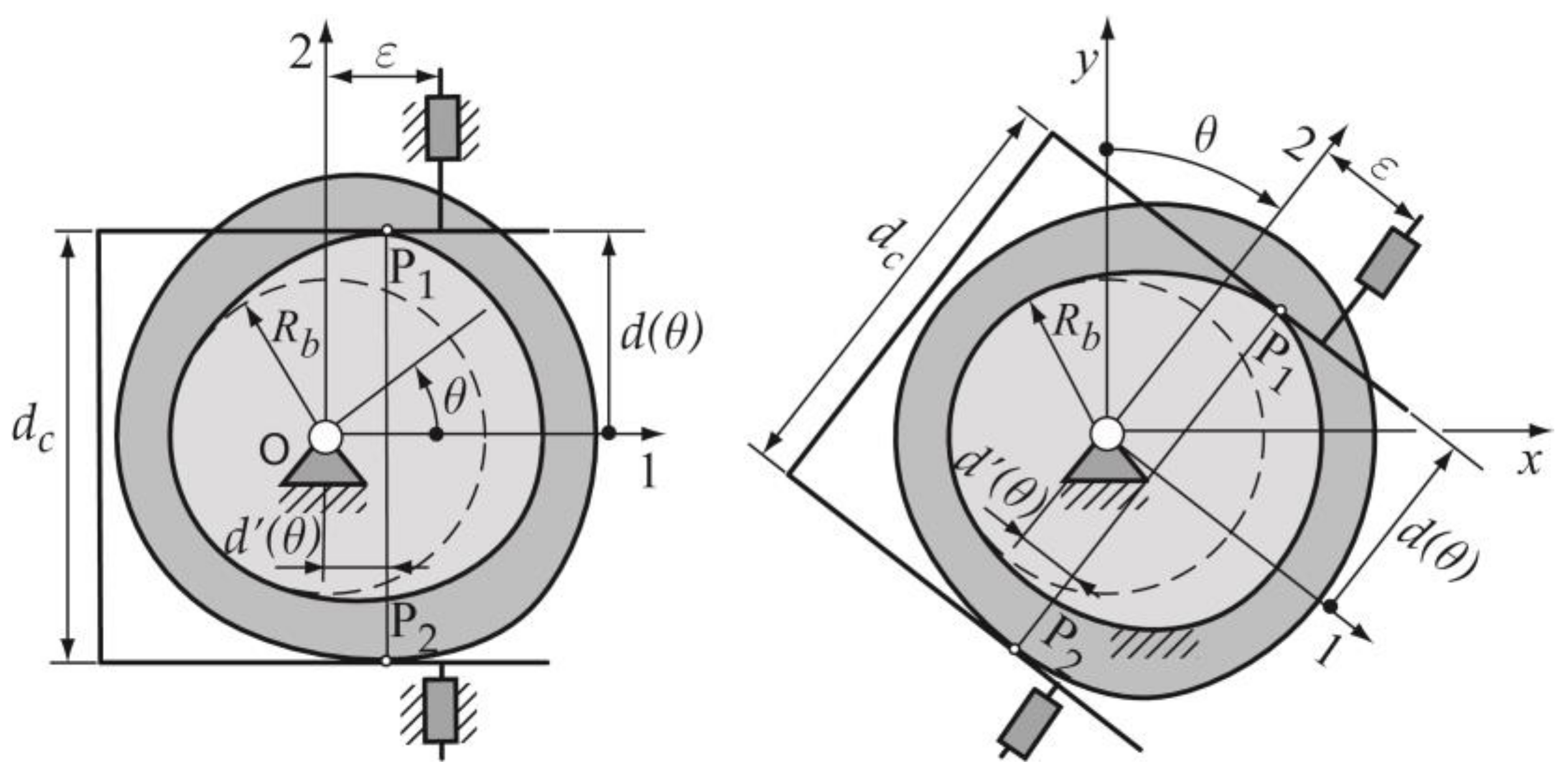
2.1. Design Process of the Cam–Follower Mechanism
- Designing the displacement law. The designer defines the displacement law of the follower according to the movement required by the technological process or function that must be met by the mechanism. As mentioned in Section 1, the displacement law for this particular type of constant-breadth cam mechanism with a double-translating follower must meet a design restriction (expression 1) [2,3,4]. Thus, consists of two segments: the designed segment and the calculated segment.
- 2.
- Obtaining the cam profile that drives a certain type of follower according to the designed displacement law.
- 3.
- Verifying that the cam profile obtained does not present geometric characteristics that prevent the right contact between the cam and follower. In the case here exposed, the curvature radii of the cam profile must always be positive, in order to guarantee correct contact between the cam and the follower. The expression to calculate is as follows [1]:
2.2. Manufacturing Processes of the Cams
2.2.1. Manufacturing Processes of the 3D-Printed Cams
2.2.2. CNC Milling of the Cams
2.3. Measuring Process of the Cams
3. Results
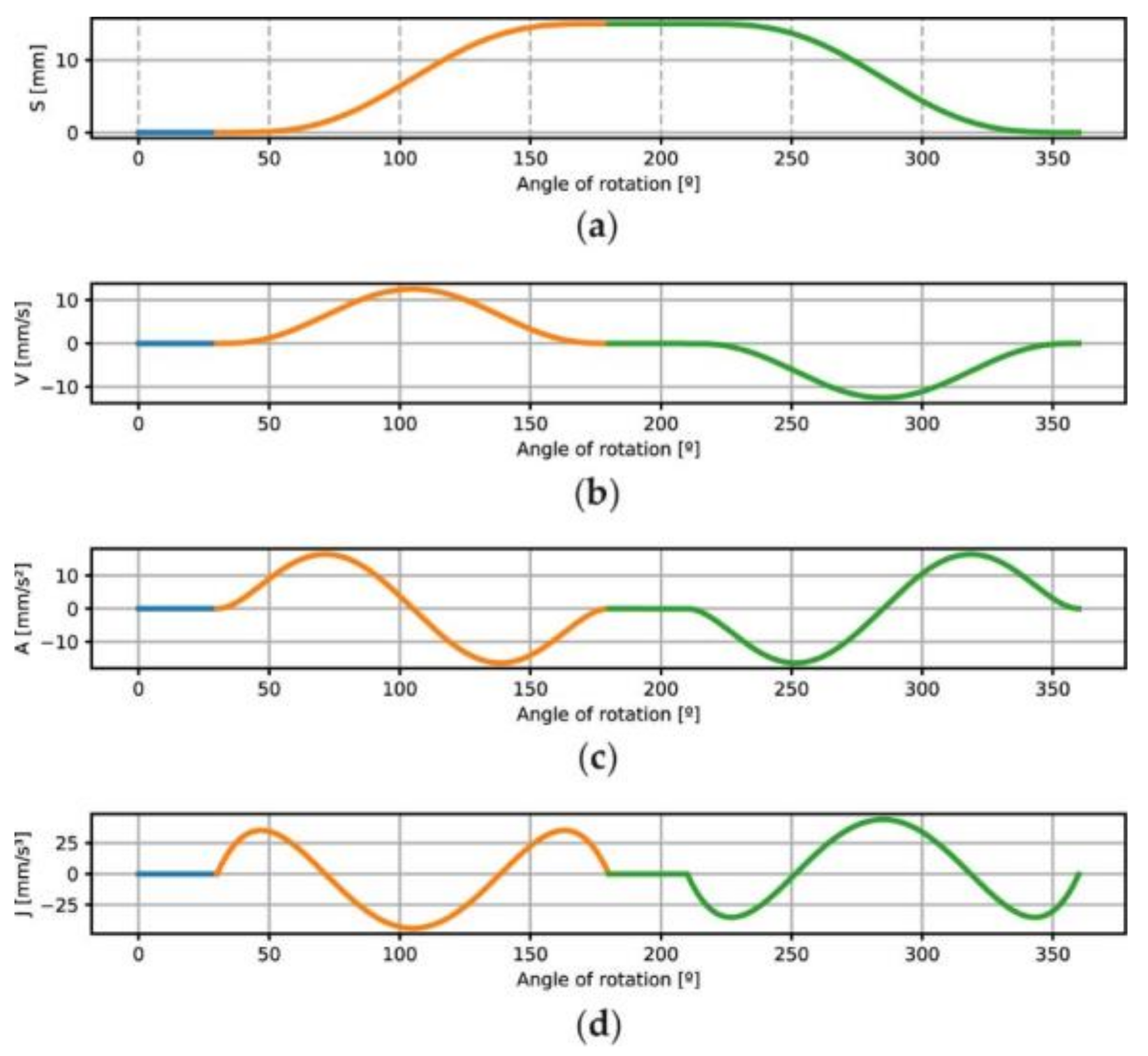
3.1. Dimensions
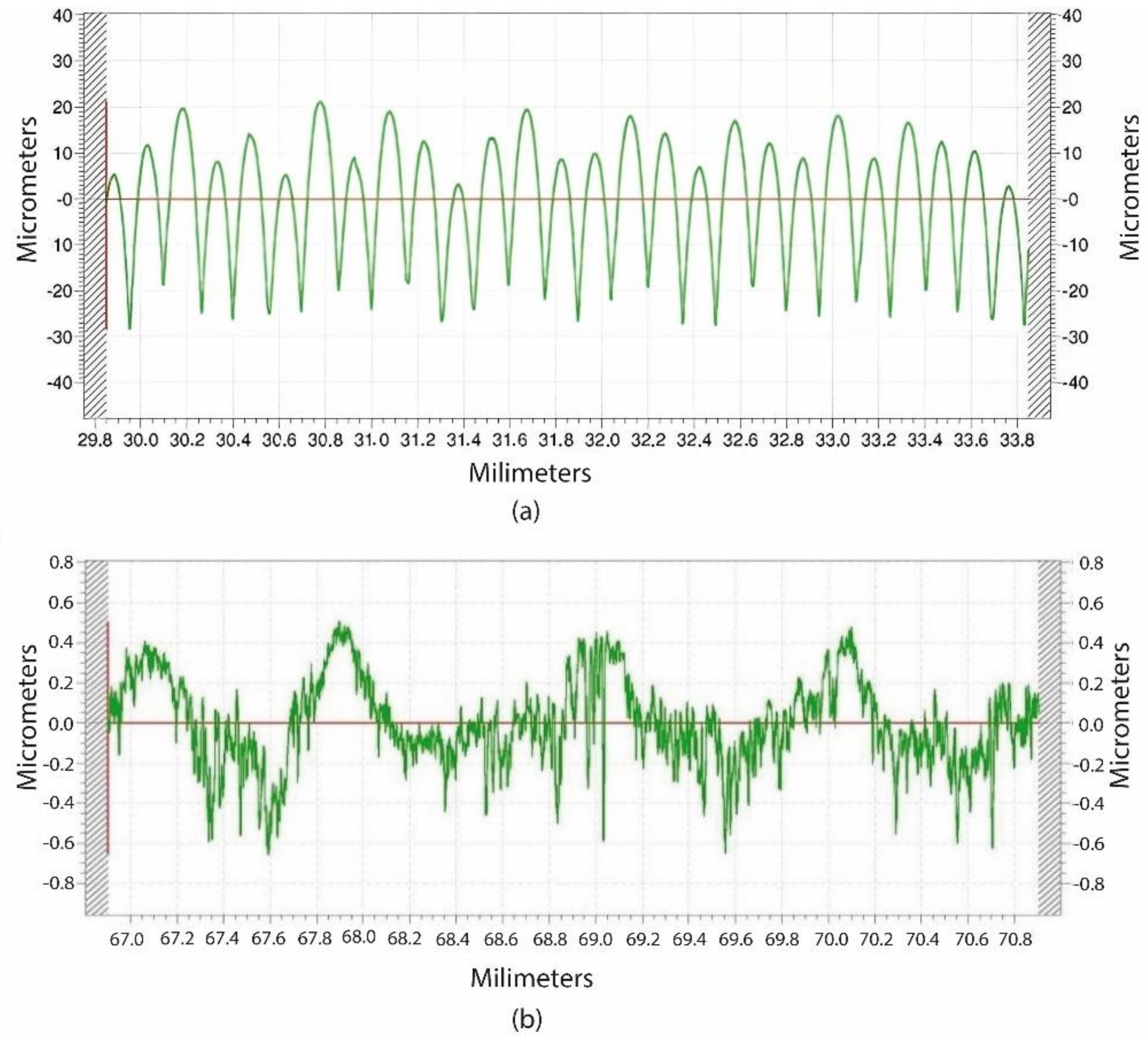
3.2. Surface Roughness
4. Discussion
5. Conclusions
- Two principal design desmodromic constraints must be considered in the design process of a constant-breadth cam that drives a double flat-translating follower. The first constraint is that the motion law s(θ) consists of two segments: the designed segment, which can only be designed in the interval from 0 to 180° of cam rotation), and the calculated segment, which is obtained using the expression 1. The second constraint is that the value of the constant-breadth cam dc is equal to the diameter of the base circle plus the maximum displacement of the cam follower.
- Similar dimensional relative errors were obtained for the 3D-printed cams and the machined parts when the x, y plane was considered (maximum relative error of 0.75%). However, when the z direction was considered, which is orthogonal to the depositing plane of the printed layers, higher dimensional relative errors were reported for the 3D-printed cams (up to 1.64%) than for the machined ones (up to 0.54 %);
- As for the surface finish on the lateral surface (working face) of the cams, the average roughness Ra was around 20 times higher for the 3D-printed cams (10.41 µm) than for the machined ones (0.50 µm).
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cardona, S.; Zayas, E.E.; Jordi, L. Radius of curvature and sliding velocity in constant-breadth cam mechanisms. Mech. Mach. Theory 2014, 81, 181–192. [Google Scholar] [CrossRef]
- Zayas, E.E.; Cardona, S.; Jordi, L. Analysis and synthesis of the displacement function of the follower in constant-breadth cam mechanisms. Mech. Mach. Theory 2009, 44, 1938–1949. [Google Scholar] [CrossRef]
- Ye, Z.; Smith, M.R. Synthesis of constant-breadth cam mechanisms. Mech. Mach. Theory 2002, 37, 941–953. [Google Scholar] [CrossRef]
- Cardona, S.; Zayas, E.E.; Jordi, L.; Català, P. Synthesis of displacement functions by Bézier curves in constant-breadth cams with parallel flat-faced double translating and oscillating followers. Mech. Mach. Theory 2013, 62, 51–62. [Google Scholar] [CrossRef]
- Lugosi, R.; Brauer, M.; Cook, J. Assembled camshaft for I.C. engines with forged powder metal cams. SAE Trans. 1987, 96, 455–465. [Google Scholar]
- Luis Pérez, C.J.; Luri Irigoyen, R.; Fuertes Bonel, J.P.; León Iriarte, J.; Salcedo Pérez, D.; Puertas Arbizu, I. Experimental and fem analysis of wear behaviour in AA5083 ultrafine-grained cams. Metals 2020, 10, 479. [Google Scholar] [CrossRef]
- Röhrle, M.D. The camshaft in the course of time. MTZ Worldw. 2002, 63, 7–9. [Google Scholar] [CrossRef]
- Liu, T.; Deng, Z.; Luo, C.; Li, Z.; Lv, L.; Zhuo, R. Chatter detection in camshaft high-speed grinding process based on VMD parametric optimization. Meas. J. Int. Meas. Confed. 2022, 187, 110133. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Zayas-Figueras, E.; Montaña-Faiget, À. Comparative study of flank cams manufactured by wedm and milling processes. Metals 2020, 10, 1159. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, Y.; Song, P.; Liu, L. Spatial-temporal motion control via composite cam-follower mechanisms. ACM Trans. Graph. 2021, 40, 1–15. [Google Scholar] [CrossRef]
- Cheng, Y.; Song, P.; Lu, Y.; Chew, W.J.J.; Liu, L. Exact 3D Path Generation via 3D Cam-Linkage Mechanisms. ACM Trans. Graph. 2022, 41, 1–13. [Google Scholar] [CrossRef]
- Xiang, J.; Cai, Z.; Zhang, Y.; Wang, W. A micro-cam actuated linear peristaltic pump for microfluidic applications. Sens. Actuators A Phys. 2016, 251, 20–25. [Google Scholar] [CrossRef]
- Almeida, A.; Andrews, G.; Jaiswal, D.; Hoshino, K. The Actuation Mechanism of 3D Printed Flexure-Based Robotic Microtweezers. Micromachines 2019, 10, 470. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhou, H.; Zhao, D.; Guan, X.; Li, G.; Feng, F. Online approach to measuring relative location of spatial geometric features of long rotating parts. Meas. J. Int. Meas. Confed. 2022, 187, 110317. [Google Scholar] [CrossRef]
- Hou, Y.; Tan, Q.; Li, Q.; Song, Y.; Li, G. Measurement of the cam spacing on camshaft by binocular vision. Int. J. Multimed. Ubiquitous Eng. 2016, 11, 139–146. [Google Scholar] [CrossRef]
- Kiraci, E.; Palit, A.; Donnelly, M.; Attridge, A.; Williams, M.A. Comparison of in-line and off-line measurement systems using a calibrated industry representative artefact for utomotive dimensional inspection. Meas. J. Int. Meas. Confed. 2020, 163, 108027. [Google Scholar]
- Jeong, Y.; Lee, W.; Lee, K. Accuracy evaluation of dental models manufactured by CAD/CAM milling method and 3D printing method. J. Adv. Prosthodont. 2018, 10, 245–251. [Google Scholar] [CrossRef]
- Wang, S.; Wu, Z.; Peng, D.; Li, W.; Chen, S.; Liu, S. An angle displacement sensor using a simple gear. Sens. Actuators A Phys. 2018, 270, 245–251. [Google Scholar] [CrossRef]
- Li, S.; Zeng, L.; Feng, P.; Yu, D. An accurate probe pre-travel error compensation model for five-axis on-machine inspection system. Precis. Eng. 2020, 62, 256–264. [Google Scholar] [CrossRef]
- Stoup, J.; Doiron, T. A novel high accuracy micrometer for the measurement of diameter. Metrologia 2021, 58, 025002. [Google Scholar] [CrossRef]
- Notabug.org: “Free Code Hosting”. Program That Helps in the Design Process of a Follower-Cam Mechanism. Available online: https://notabug.org/anengineer/qtcam (accessed on 4 May 2022).
- Zayas Figueras, E.E. Aportación al Estudio de Levas Desmodrómicas. Ph.D. Thesis, Universitat Politècnica de Catalunya Barcelona Tech UPC, Barcelona, Spain, 2001. [Google Scholar]
- Cimatech. Available online: https://www.cimatech.com/productos/cimatron/cimatech-productos-cimatron.html (accessed on 29 September 2022).
- Buj, I.; Vivancos, J.; González, H. Influence of feed, eccentricity and helix angle on topography obtained in side milling processes. Int. J. Mach. Tools Manuf. 2011, 51, 889–897. [Google Scholar]
- Buj-Corral, I.; Domínguez-Fernández, A.; Durán-Llucià, R. Influence of print orientation on surface roughness in fused deposition modeling (FDM) processes. Materials 2019, 12, 3834. [Google Scholar] [CrossRef] [PubMed]
- Buj-Corral, I.; Zayas-Figueras, E.E. Comparative study about dimensional accuracy and orm errors of FFF printed spur gears using PLA and Nylon. Polym. Test. 2023, 117, 107862. [Google Scholar] [CrossRef]
- Beniak, J.; Križan, P.; Šooš, Ľ; Matuš, M. Research on Shape and Dimensional Accuracy of FDM Produced Parts. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Phuket, Thailand, 11–14 December 2018. [Google Scholar]
- Pennington, R.C.; Hoekstra, N.L.; Newcomer, J.L. Significant factors in the dimensional accuracy of fused deposition modelling. J. Process Mech. Eng. 2005, 219, 89–92. [Google Scholar] [CrossRef]
- Zharylkassyn, B.; Perveen, A.; Talamona, D. Effect of process parameters and materials on the dimensional accuracy of FDM parts. Mater. Today Proc. 2021, 44, 1307–1311. [Google Scholar] [CrossRef]
- Popescu, D.; Amza, C.G.; Marinescu, R.; Iacob, M.C.; Căruţaşu, N.L. Investigations on Factors Affecting 3D-Printed Holes Dimensional Accuracy and Repeatability. Appl. Sci. 2023, 13, 41. [Google Scholar] [CrossRef]
- Robthbart, H. Chapter 10: Cam Manufacturing. In Cam Design Handbook: Cam Size and Profile Determination, Numerical Controls for Manufacturing, Computer Aided Design Thecniques; Rohtbart, H., Ed.; McGraw-Hill Companies: New York, NY, USA, 2004; pp. 285–296. [Google Scholar]
- Buj-Corral, I.; Bagheri, A.; Sivatte-Adroer, M. Effect of Printing Parameters on Dimensional Error, Surface Roughness and Porosity of FFF Printed Parts with Grid Structure. Polymers 2021, 13, 1213. [Google Scholar] [CrossRef]
- Galantucci, L.M.; Lavecchia, F.; Percoco, G. Experimental study aiming to enhance the surface finish of fused deposition modeled parts. CIRP Ann. 2009, 58, 189–192. [Google Scholar] [CrossRef]
- Hartcher-O’Brien, J.; Evers, J.; Tempelman, E. Surface roughness of 3D printed materials: Comparing physical measurements and human perception. Mater. Today Commun. 2019, 19, 300–305. [Google Scholar] [CrossRef]
- Agulló, J.; Cardona, S. Assessment of Surface Roughness (Valoración de la Rugosidad Superficial); Asociación Nacional de la Máquina—Herramienta: San Sebastián, Spain, 1974. [Google Scholar]
- Norton, R. Cam Materials and Manufacturing. In Cam Design and Manufacturing Handbook; Norton, R., Ed.; Industrial Press Inc.: New York, NY, USA, 2009; Chapter 14; pp. 467–470. [Google Scholar]
- Veera Ajay, C.; Pradeep, B.A.; Boopathi, C.; Sanjeev, R.K.; Meganathan, V. Comparison of geometrical accuracy and surface finish of cam profile generated by wire-EDM and CNC milling machine. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Sathyamangalam, India, 10–11 September 2019. [Google Scholar]

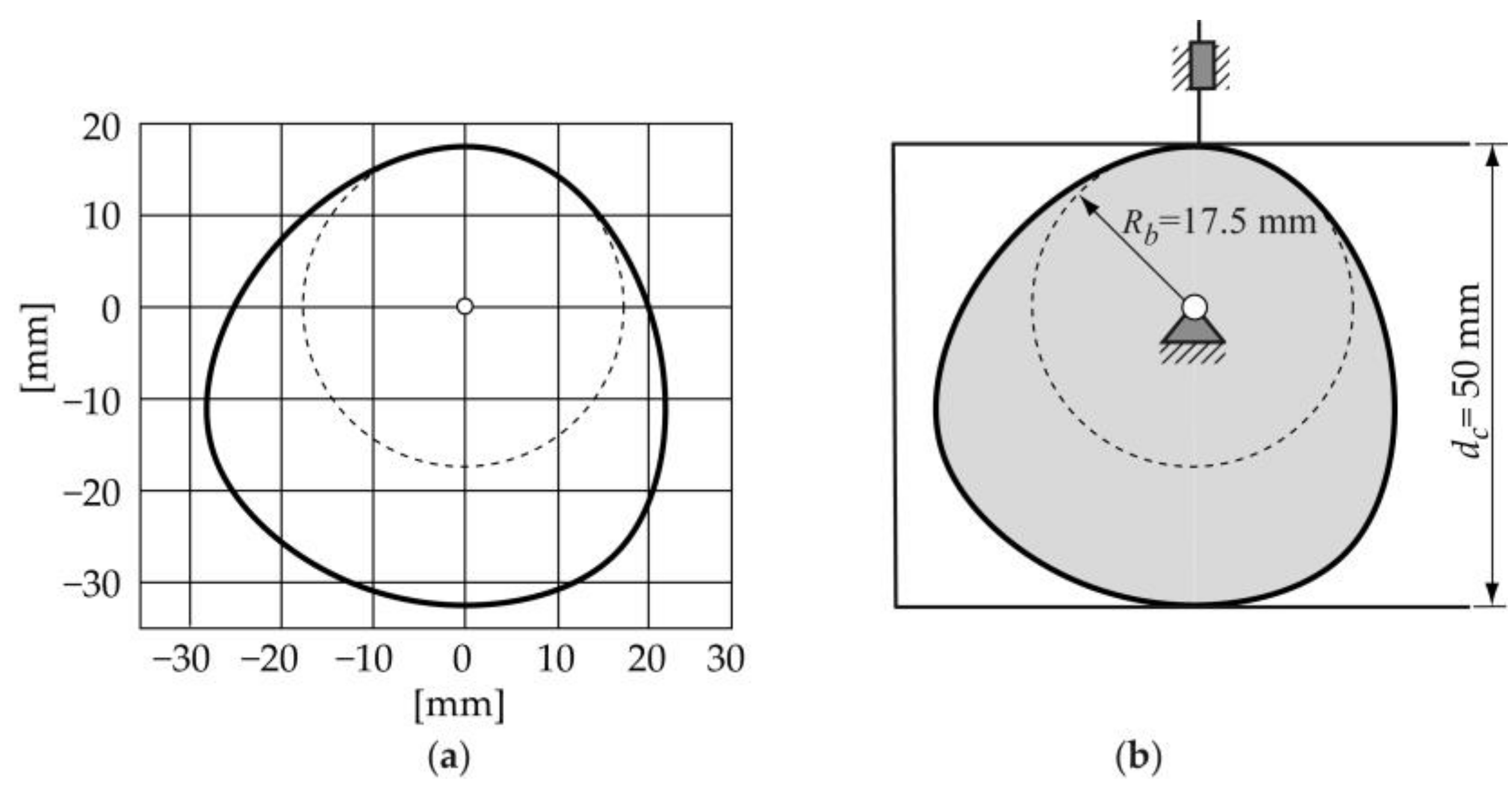
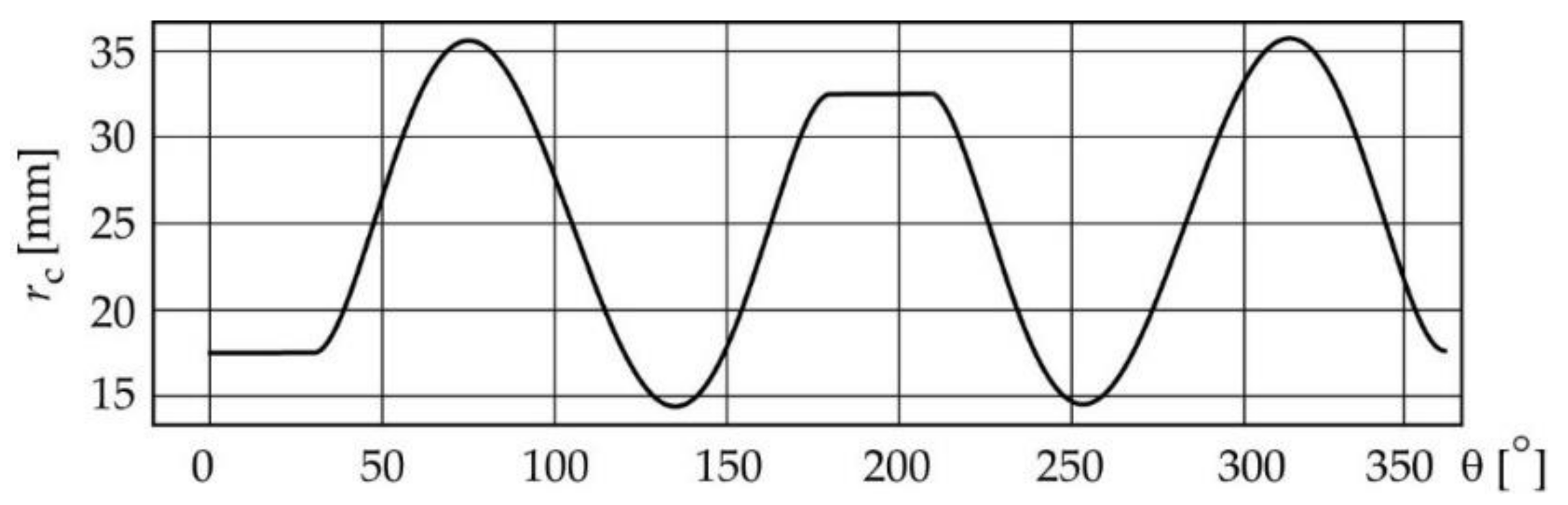
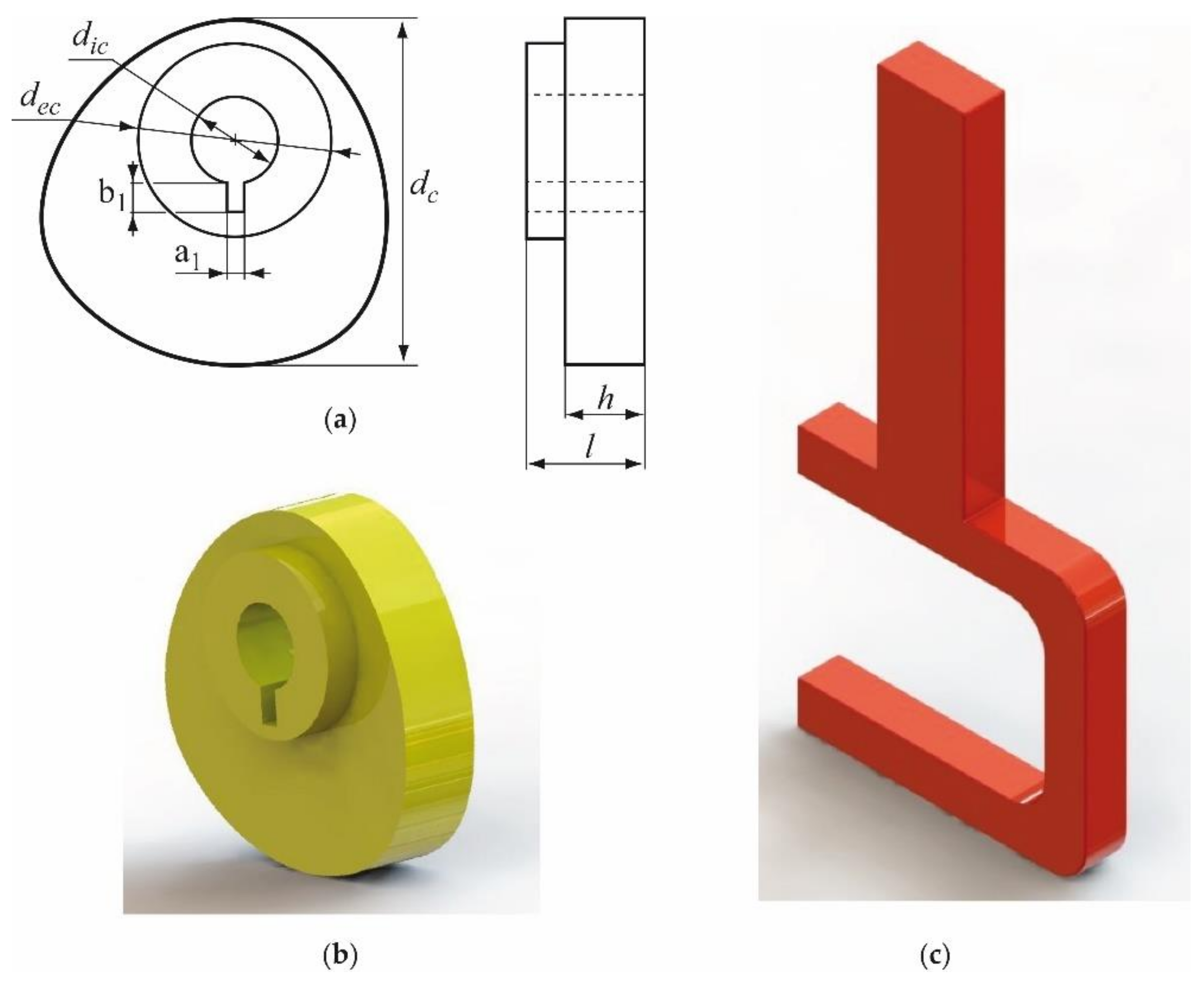






| Geometric Parameter [Units] | Numerical Value |
|---|---|
| Radius of the base circle of the cam [mm] | 17.5 |
| Breadth of the cam [mm] | 50 |
| Offset of the translating follower ε [mm] | 0 |
| Inclination angle of the translating follower β [°] | 0 |
| Parameter [Units] | Numerical Value |
|---|---|
| Nozzle diameter [mm] | 0.4 |
| Infill ratio [%] | 18 |
| Print speed [mm/s] | 60 |
| Infill pattern | Linear |
| Shell thickness [mm] | 0.4 |
| Layer height [mm] | 0.15 |
| Printing head temperature [°C] | 200 |
| Build plate temperature [°C] | 60 |
| Raster angle [°] | 45 |
| Number of wall lines | 3 |
| Operation Number | Operation (Machine Tool) | Tool | Fixture System | Cutting Conditions |
|---|---|---|---|---|
| 1 | Cutting off of the starting cylinder (band saw machine) | Band saw | Bench vice | Cutting speed: 30 m/min |
| 2 | Face milling (CNC machine centre) | Face milling tool of diameter 40 mm and z = 8 | Bench vice | Cutting speed: 150 m/min; feed speed: 955 mm/min; depth of cut: 2 mm |
| 3 | Rough contour milling of the cam hub (CNC machine centre) | Face milling tool of diameter 25 mm and z = 4 | Bench vice | Cutting speed: 120 m/min; feed speed: 611 mm/min; depth of cut: 5.40 mm |
| 4 | Rough contour milling of the cam profile (CNC machine centre) | Face milling tool of diameter 25 mm and z = 4 | Bench vice | Cutting speed: 120 m/min; feed speed: 611 mm/min; depth of cut: 20 mm |
| 5 | Marking of the cam hole (CNC machine centre) | Drilling tool of angle 90° and diameter 12 mm and z = 2 | Bench vice | Cutting speed: 95 m/min; feed speed: 302 mm/min; depth of cut: 5 mm |
| 6 | Drilling of the cam hole (CNC machine centre) | Drilling tool of angle 120° and diameter 12 mm and z = 2 | Bench vice | Cutting speed: 95 m/min; feed speed: 302 mm/min; cutting length: 22 mm |
| 7 | Contour milling of the keyway of 6 × 4.36 mm (CNC machine centre) | Face milling tool of diameter 4 mm and z = 2 | Bench vice | Cutting speed: 120 m/min; feed speed: 1910 mm/min; depth of cut: 22 mm |
| 8 | Contour milling of the cam profile (CNC machine centre) | Face milling tool of diameter 10 mm and z = 4 | Bench vice | Cutting speed: 120 m/min; feed speed: 1528 mm/min; depth of cut: 15 mm |
| 9 | Contour milling of the cam’s hub (CNC machine centre) | Face milling tool of diameter 10 mm and z = 4 | Bench vice | Cutting speed: 120 m/min; feed speed: 1528 mm/min; depth of cut: 5.40 mm |
| 10 | Cutting off the machined cylinder (band saw machine) | Band saw | Bench vice | Cutting speed: 30 m/min |
| 11 | Face milling to final length of the cam of 17.40 mm, obtaining a width of the working face of 12 mm (CNC machine centre) | Face milling tool of diameter 40 mm and z = 8 | Bench vice | Cutting speed: 150 m/min; feed speed: 955 mm/min; depth of cut: 2 mm |
| Cam Manufacturing Process | Parameter | Theoretical Value (mm) | Mean Value (mm) | Standard Deviation (mm) | Relative Error (%) |
|---|---|---|---|---|---|
| 3D-printed | dc | 50 | 49.98 | 0.06 | 0.12 |
| dic | 12 | 11.91 | 0.05 | 0.75 | |
| l | 15 | 15.17 | 0.01 | 1.16 | |
| h | 12 | 12.20 | 0.01 | 1.64 | |
| Machined | dc | 50 | 49.99 | 0.06 | 0.07 |
| dic | 12 | 11.97 | 0.01 | 0.30 | |
| l | 17.40 | 17.31 | 0.08 | 0.54 | |
| h | 12 | 11.99 | 0.09 | 0.08 |
| Cam Manufacturing Process | Mean Value [µm] | Standard Deviation [µm] |
|---|---|---|
| 3D-printed cams | 10.41 | 0.12 |
| Machined cams | 0.50 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zayas-Figueras, E.E.; Buj-Corral, I. Comparative Study about Dimensional Accuracy and Surface Finish of Constant-Breadth Cams Manufactured by FFF and CNC Milling. Micromachines 2023, 14, 377. https://doi.org/10.3390/mi14020377
Zayas-Figueras EE, Buj-Corral I. Comparative Study about Dimensional Accuracy and Surface Finish of Constant-Breadth Cams Manufactured by FFF and CNC Milling. Micromachines. 2023; 14(2):377. https://doi.org/10.3390/mi14020377
Chicago/Turabian StyleZayas-Figueras, Enrique E., and Irene Buj-Corral. 2023. "Comparative Study about Dimensional Accuracy and Surface Finish of Constant-Breadth Cams Manufactured by FFF and CNC Milling" Micromachines 14, no. 2: 377. https://doi.org/10.3390/mi14020377
APA StyleZayas-Figueras, E. E., & Buj-Corral, I. (2023). Comparative Study about Dimensional Accuracy and Surface Finish of Constant-Breadth Cams Manufactured by FFF and CNC Milling. Micromachines, 14(2), 377. https://doi.org/10.3390/mi14020377








