Design and Testing of a Novel Nested, Compliant, Constant-Force Mechanism with Millimeter-Scale Strokes
Abstract
1. Introduction
1.1. Background
1.2. Motivation
1.3. Contribution
2. Design and Modeling Analysis of a Compliant CFM
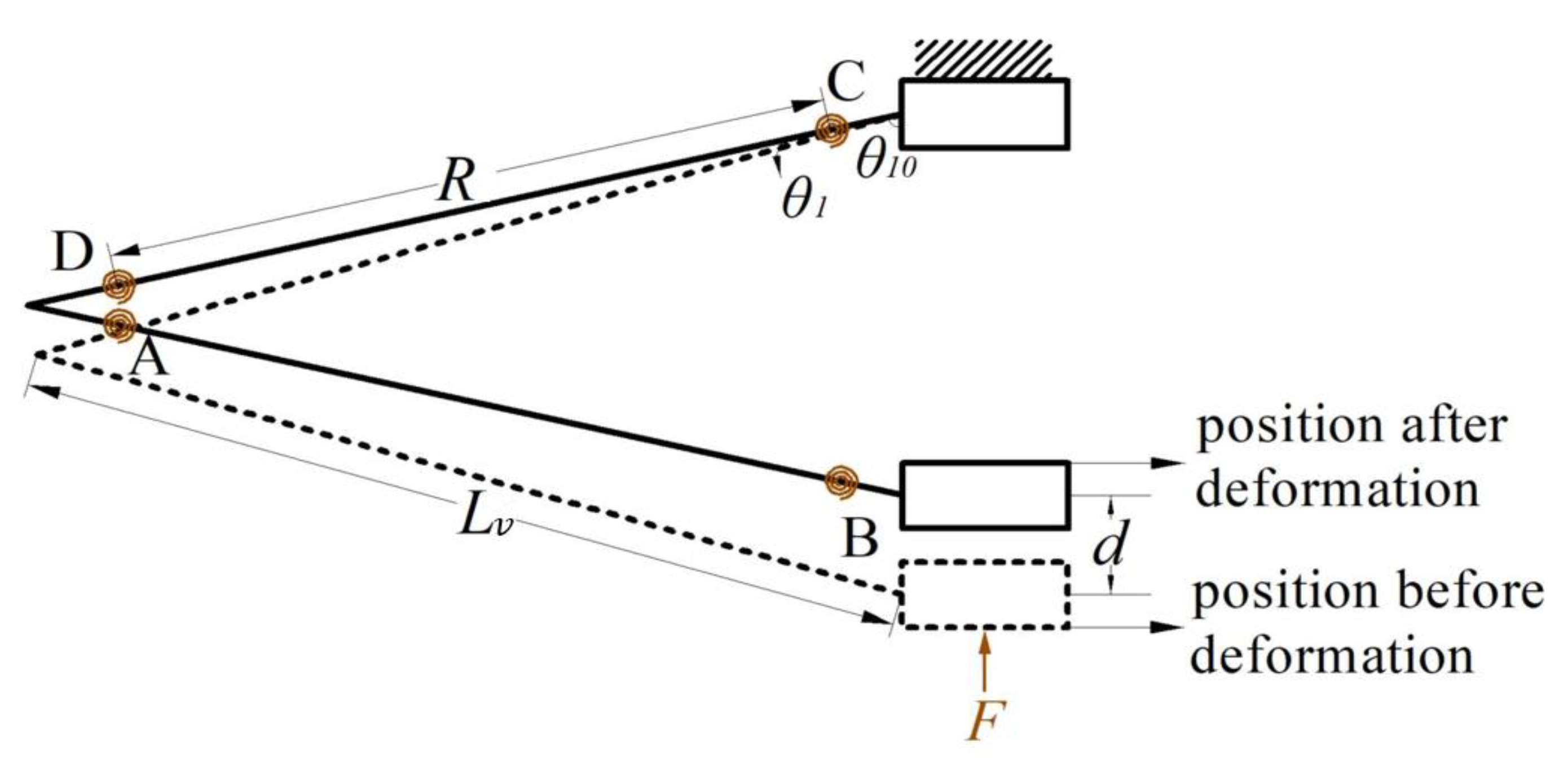
2.1. Mechanism Design
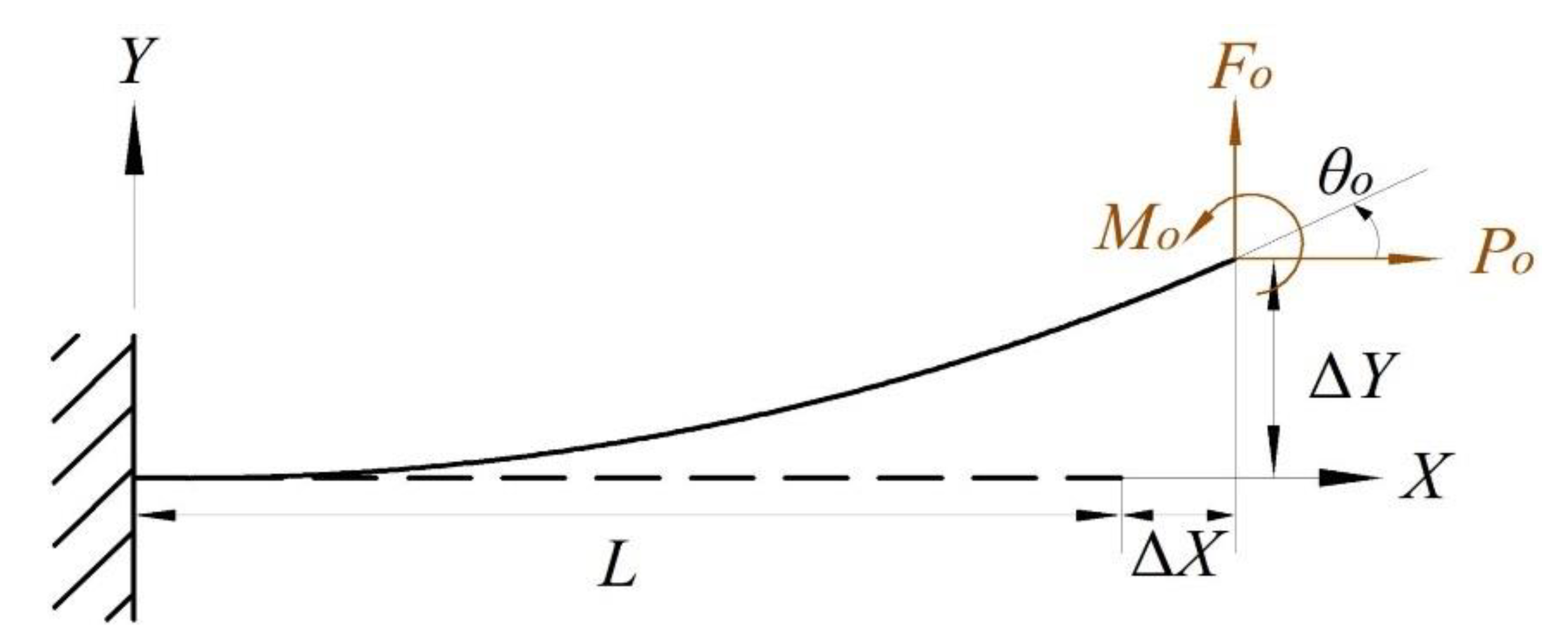
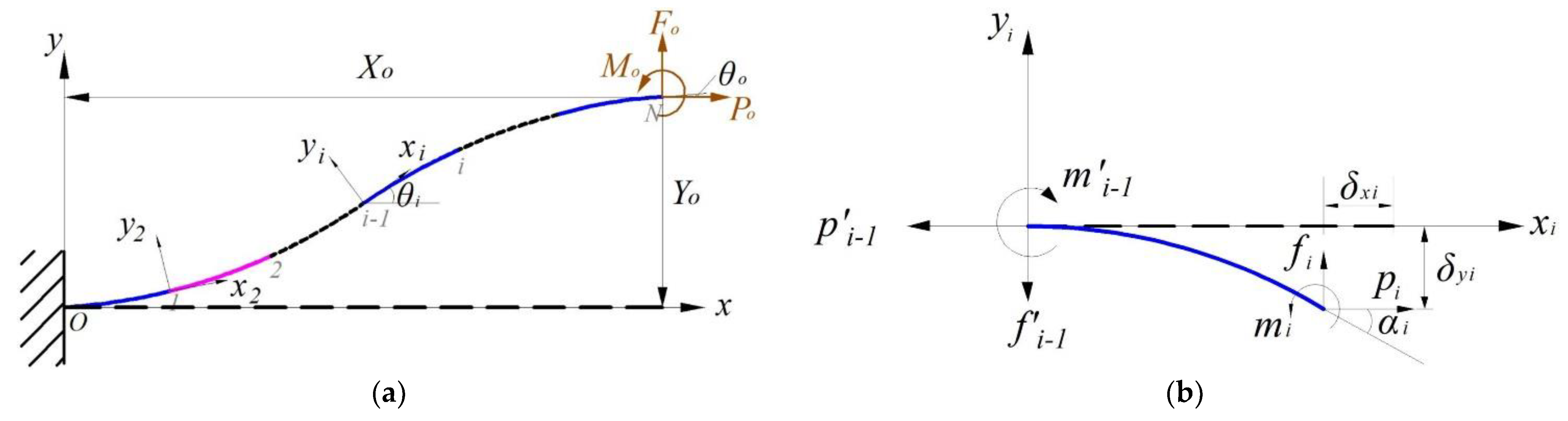
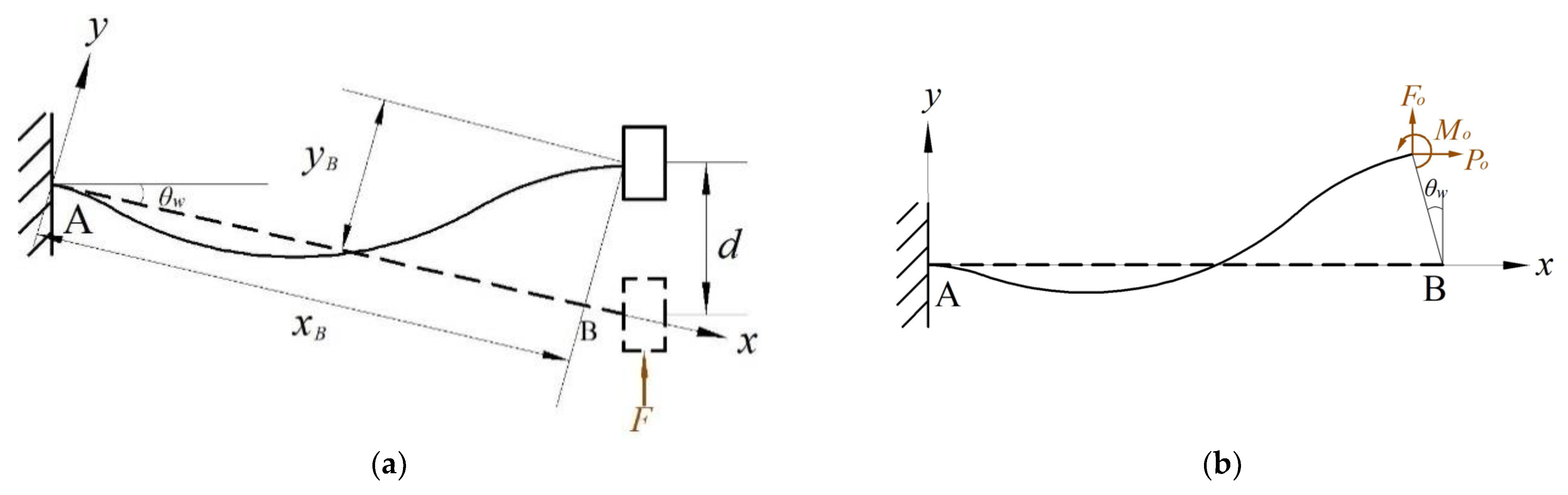
2.2. Analytical Modeling of the CFM
2.2.1. V-Shaped Beam
2.2.2. Bi-Stable Beam
3. FEA and Parameter Analysis
3.1. Finite Element Analysis
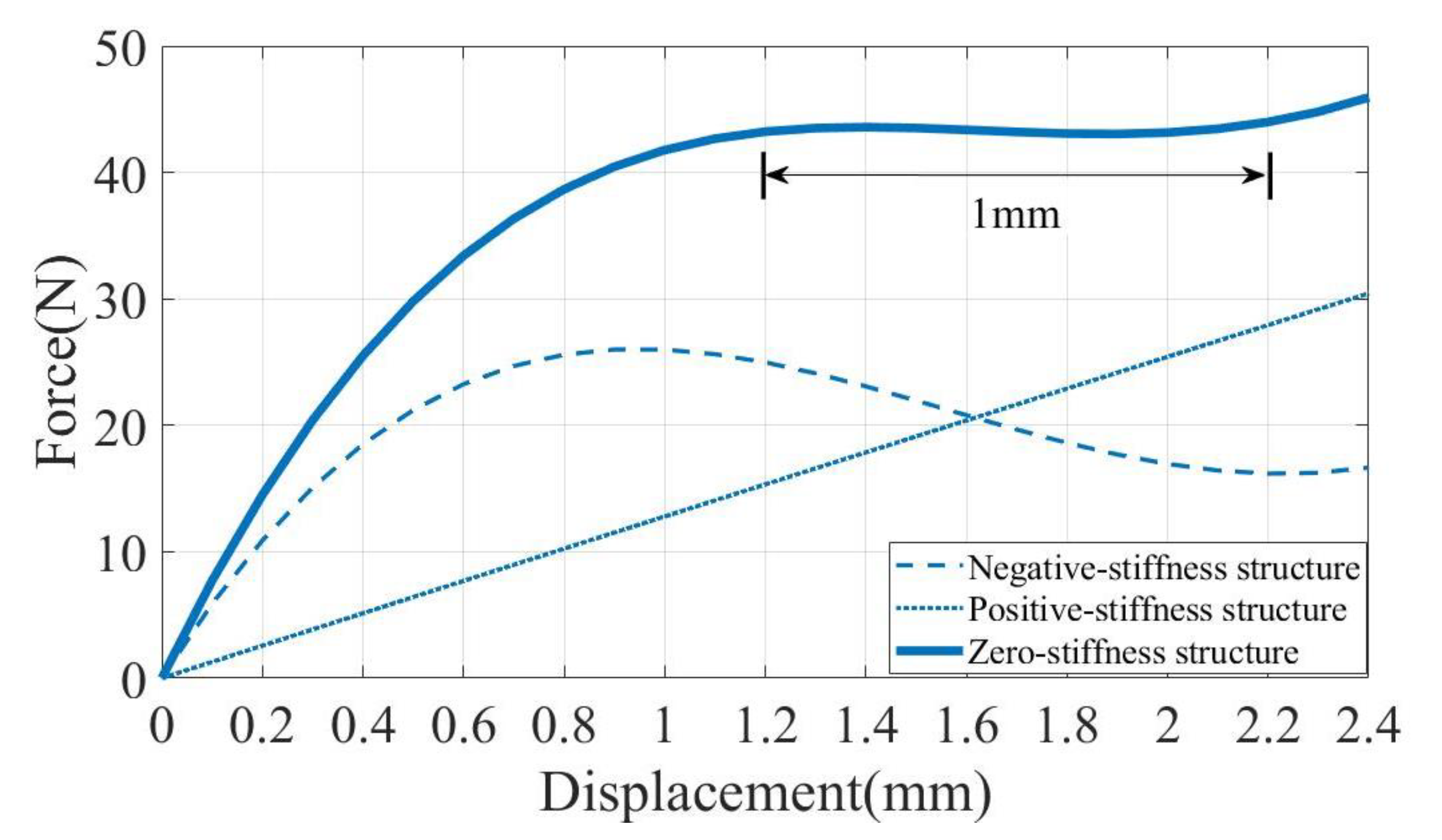
3.2. Parameter Analysis
4. Experimental Study
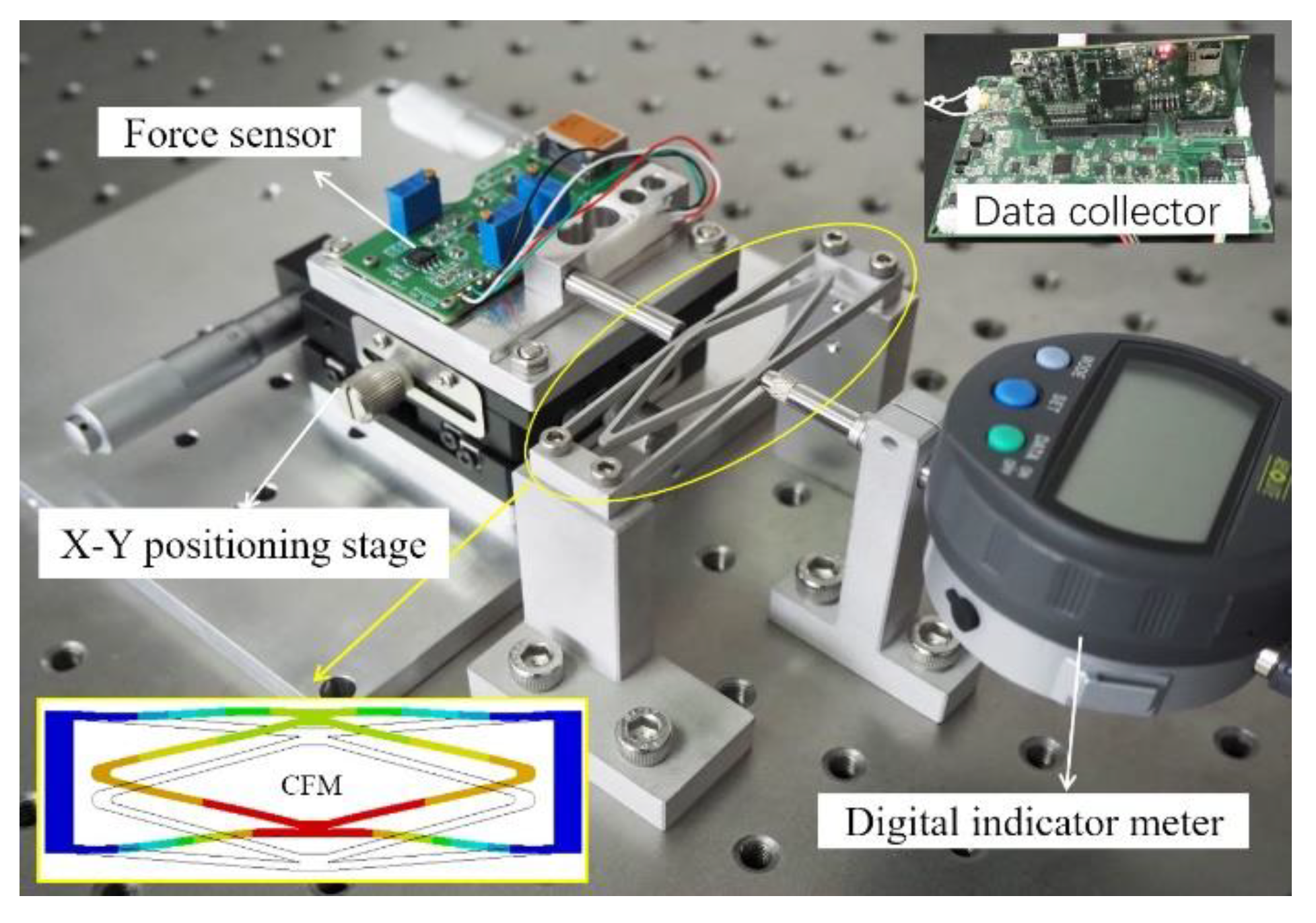
4.1. Prototype Fabrication
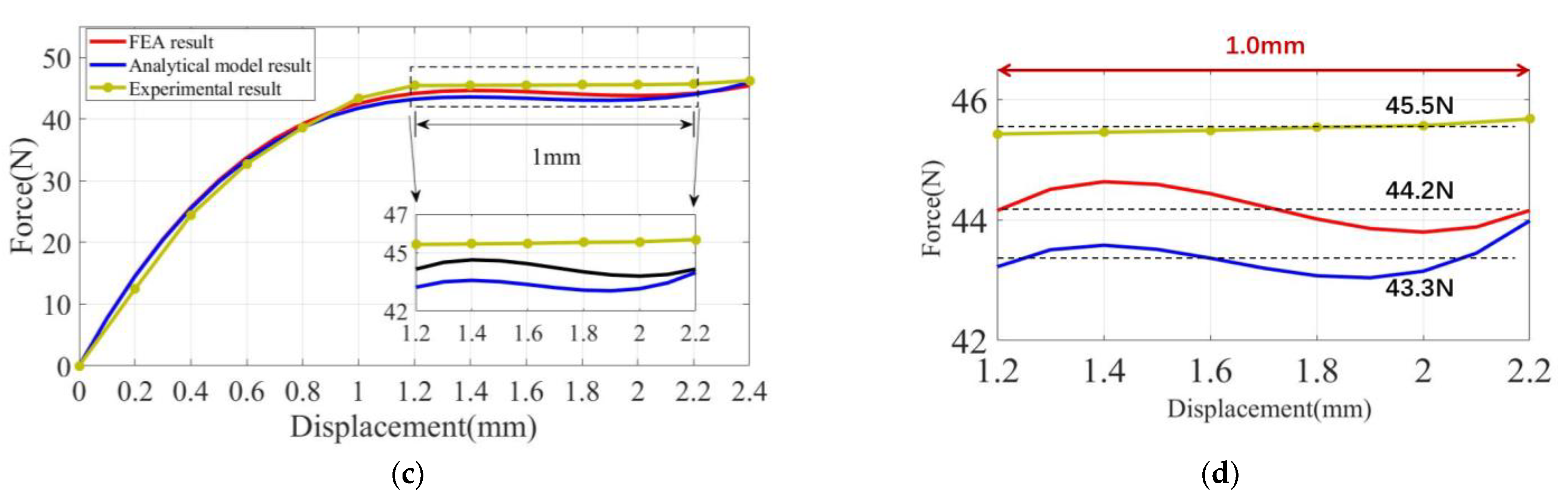
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Fan, L.; Li, Y.; Wei, T.; Wang, C.; Li, F.; Sun, D. Development of cell-carrying magnetic microrobots with bioactive nanostructured titanate surface for enhanced cell adhesion. Micromachines 2021, 12, 1572. [Google Scholar] [CrossRef]
- Kaaliveetil, S.; Yang, J.; Alssaidy, S.; Li, Z.; Cheng, Y.H.; Menon, N.H.; Basuray, S. Microfluidic Gas Sensors: Detection Principle and Applications. Micromachines 2022, 13, 1716. [Google Scholar] [CrossRef]
- Lu, S.; Yan, P.; Zhang, B. Long stroke displacement measurement with reduced coupling error supporting high precision control of a beam flexure-based micro-stage. Rev. Sci. Instrum. 2020, 91, 073701. [Google Scholar] [CrossRef]
- Chen, X.; Deng, Z.; Hu, S.; Gao, X.; Gao, J. Research on three-stage amplified compliant mechanism-based piezo-driven microgripper. Adv. Mech. Res. 2020, 12, 1–12. [Google Scholar] [CrossRef]
- Xu, Q. Adaptive discrete-time sliding mode impedance control of a piezoelectric microgripper. IEEE Trans. Robot. 2013, 29, 663–673. [Google Scholar] [CrossRef]
- Zhang, R.; Chu, J.; Wang, H.; Chen, Z. A multipurpose electrothermal micro-gripper for biological micro-manipulation. Microsyst. Technol. 2013, 19, 89–97. [Google Scholar] [CrossRef]
- Yang, S.; Xu, Q. Design of a micro-electromechanical systems microgripper with integrated electrothermal actuator and force sensor. Int. J. Adv. Robot. Syst. 2016, 13, 1–10. [Google Scholar] [CrossRef]
- Zhang, T.; Xiao, M.; Zou, Y.B.; Xiao, J.D.; Chen, S.Y. Robotic curved surface tracking with a neural network for angle identification and constant force control based on reinforcement learning. Int. J. Precis. Eng. Manuf. 2020, 21, 869–882. [Google Scholar] [CrossRef]
- Zhang, T.; Yu, Y.; Yang, L.X.; Xiao, M.; Chen, S.Y. Robot grinding system trajectory compensation based on co-kriging method and constant-force control based on adaptive iterative algorithm. Int. J. Precis. Eng. Manuf. 2020, 21, 1637–1651. [Google Scholar] [CrossRef]
- Miao, Y.; Zheng, J. Optimization design of compliant constant-force mechanism for apple picking actuator. Comput. Electron. Agric. 2020, 170, 105232. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, Q. Design of a new passive end-effector based on constant-force mechanism for robotic polishing. Robot. Comput. Int. Manuf. 2022, 74, 102278. [Google Scholar] [CrossRef]
- Liu, C.H.; Hsu, M.C.; Chen, T.L.; Chen, Y. Optimal design of a compliant constant-force mechanism to deliver a nearly constant output force over a range of input displacements. Soft Robot. 2020, 7, 758–769. [Google Scholar] [CrossRef]
- Wang, P.; Yang, S.; Xu, Q. Design and optimization of a new compliant rotary positioning stage with constant output torque. Int. J. Precis. Eng. Manuf. 2018, 19, 1843–1850. [Google Scholar] [CrossRef]
- Wang, D.A.; Chen, J.H.; Pham, H.T. A constant-force bistable micromechanism. Sensor. Actua. A Phys. 2013, 189, 481–487. [Google Scholar] [CrossRef]
- Chen, Y.H.; Lan, C.C. An adjustable constant-force mechanism for adaptive end-effector operations. J. Mech. Design. 2012, 134, 031005. [Google Scholar] [CrossRef]
- Xu, Q. Design of a large-stroke bistable mechanism for the application in constant-force micropositioning stage. J. Mech. Robot. 2017, 9, 011006. [Google Scholar] [CrossRef]
- Ding, B.; Li, X.; Li, Y. FEA-based optimization and experimental verification of a typical flexure-based constant force module. Sensor. Actua. A Phys. 2021, 332, 113083. [Google Scholar] [CrossRef]
- Ding, B.; Zhao, J.; Li, Y. Design of a spatial constant-force end-effector for polishing/deburring operations. Int. J. Adv. Manuf. Technol. 2021, 116, 3507–3515. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, C.; Wang, F.; Lu, K.; Yuan, Y.; Yang, M.; Zhang, D. Design of a flexure-based mechanism possessing low stiffness and constant force. Rev. Sci. Instrum. 2019, 90, 105005. [Google Scholar] [CrossRef]
- Tolman, K.A.; Merriam, E.G.; Howell, L.L. Compliant constant-force linear-motion mechanism. Mech. Mach. Theory. 2016, 106, 68–79. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, P.; Wang, H. A curved-beam based quasi-constant force mechanism supporting large range and force sensitive robotic manipulation. Mech. Mach. Theory. 2022, 172, 104799. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Xu, Q. Design and control of a novel compliant constant-force gripper based on buckled fixed-guided beams. IEEE/ASME Trans. Mech. 2016, 22, 476–486. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Q. Design of a compliant constant force gripper mechanism based on buckled fixed-guided beam. In Proceedings of the 2016 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Paris, France, 8 September 2016; pp. 1–6. [Google Scholar]
- Liu, Y.; Xu, Q. Design and analysis of a micro-gripper with constant force mechanism. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12ߝ15 June 2016; pp. 2142–2147. [Google Scholar]
- Zhang, X.; Xu, Q. Design and testing of a novel 2-DOF compound constant-force parallel gripper. Precis. Eng. 2019, 56, 53–61. [Google Scholar] [CrossRef]
- Ye, T.; Ling, J.; Kang, X.; Feng, Z.; Xiao, X. A novel two-stage constant force compliant microgripper. J. Mech. Des. 2021, 143, 053302. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Q. Design of a flexure-based constant-force XY precision positioning stage. Mech. Mach. Theory. 2017, 108, 1–13. [Google Scholar] [CrossRef]
- Chen, Y.H.; Lan, C.C. Design of a constant-force snap-fit mechanism for minimal mating uncertainty. Mech. Mach. Theory 2012, 55, 34–50. [Google Scholar] [CrossRef]
- Weight, B.L.; Mattson, C.A.; Magleby, S.P.; Howell, L.L. Configuration selection, modeling, and preliminary testing in support of constant force electrical connectors. J. Electron. Packag. 2007, 129, 236–246. [Google Scholar] [CrossRef]
- Meaders, J.C.; Mattson, C.A. Optimization of near-constant force springs subject to mating uncertainty. Struct. Multidiscip. Optimization 2010, 41, 1–15. [Google Scholar] [CrossRef]
- Howell, L.L.; Midha, A.; Norton, T.W. Evaluation of Equivalent Spring Stiffness for Use in a Pseudo-Rigid-Body Model of Large-Deflection Compliant Mechanisms. J. Mech. Des. 1996, 118, 126–131. [Google Scholar] [CrossRef]
- Ma, F.; Chen, G. Modeling large planar deflections of flexible beams in compliant mechanisms using chained beam-constraint-model. J. Mech. Robot. 2016, 8, 021018. [Google Scholar] [CrossRef]
- Awtar, S.; Slocum, A.H.; Sevincer, E. Characteristics of beam-based flexure modules. J. Mech. Design. 2007, 129, 625–639. [Google Scholar] [CrossRef]
- Wang, P.; Xu, Q. Design and testing of a flexure-based constant-force stage for biological cell micromanipulation. IEEE Trans. Autom. Sci. Eng. 2017, 15, 1114–1126. [Google Scholar] [CrossRef]
- Ding, B.; Li, X.; Li, Y. Configuration design and experimental verification of a variable constant-force compliant mechanism. Robotica 2022, 40, 3463–3475. [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, P. A Large Range Constant Force Microgripper With a Three-Stage Compliant Amplification Mechanism. IEEE Access 2022, 10, 58225–58232. [Google Scholar] [CrossRef]






| Parameters | Numerical Value |
|---|---|
| Young’s modulus | 71 Gpa |
| Density | 2810 kg/m3 |
| Poisson’s ratio | 0.33 |
| Parameters | Numerical Value | |
|---|---|---|
| Bi-stable beam | Length | 32.5 mm |
| Tilt angle | 3.7° | |
| Thickness | 1.0 mm | |
| Width | 3.1 mm | |
| V-shaped beam | Length | 27.22 mm |
| Angle | 25.4 | |
| Thickness | 1.1 mm | |
| Width | 3.1 mm | |
| Performance | Experiment | FEA | Model | Error |
|---|---|---|---|---|
| Constant force (N) | 45.5 | 44.2 | - | 5% |
| - | 43.3 | 3% | ||
| Constant stroke (mm) | 1.0 | 1.0 | 1.0 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Lu, S.; Liu, P.; Yan, P. Design and Testing of a Novel Nested, Compliant, Constant-Force Mechanism with Millimeter-Scale Strokes. Micromachines 2023, 14, 480. https://doi.org/10.3390/mi14020480
Qin X, Lu S, Liu P, Yan P. Design and Testing of a Novel Nested, Compliant, Constant-Force Mechanism with Millimeter-Scale Strokes. Micromachines. 2023; 14(2):480. https://doi.org/10.3390/mi14020480
Chicago/Turabian StyleQin, Xuejiao, Shuaishuai Lu, Pengbo Liu, and Peng Yan. 2023. "Design and Testing of a Novel Nested, Compliant, Constant-Force Mechanism with Millimeter-Scale Strokes" Micromachines 14, no. 2: 480. https://doi.org/10.3390/mi14020480
APA StyleQin, X., Lu, S., Liu, P., & Yan, P. (2023). Design and Testing of a Novel Nested, Compliant, Constant-Force Mechanism with Millimeter-Scale Strokes. Micromachines, 14(2), 480. https://doi.org/10.3390/mi14020480






