Numerical Simulation Study of Multi-Field Coupling for Laser Cladding of Shaft Parts
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Selection of Experimental Materials
2.2. Build Finite Element Model
- (1)
- The laser energy has a constant Gaussian distribution.
- (2)
- The material properties are assumed to be isotropic.
- (3)
- The concentration of the powder stream ejected from the powder nozzle is Gaussian distributed, and the powder entering the melt pool melts instantaneously.
2.3. Building a Theoretical Model
2.4. Experimental Protocol Setting
3. Analysis of Results
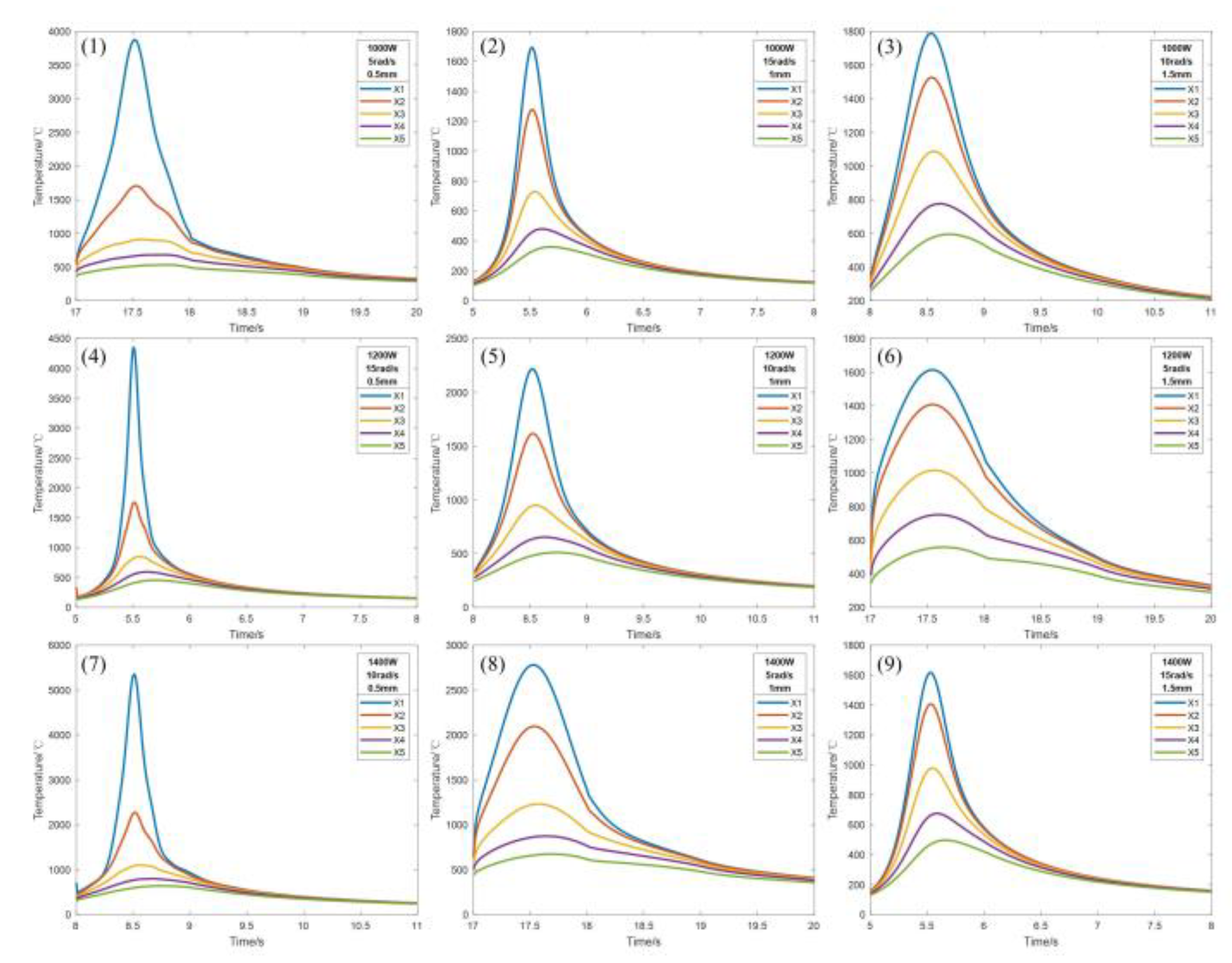
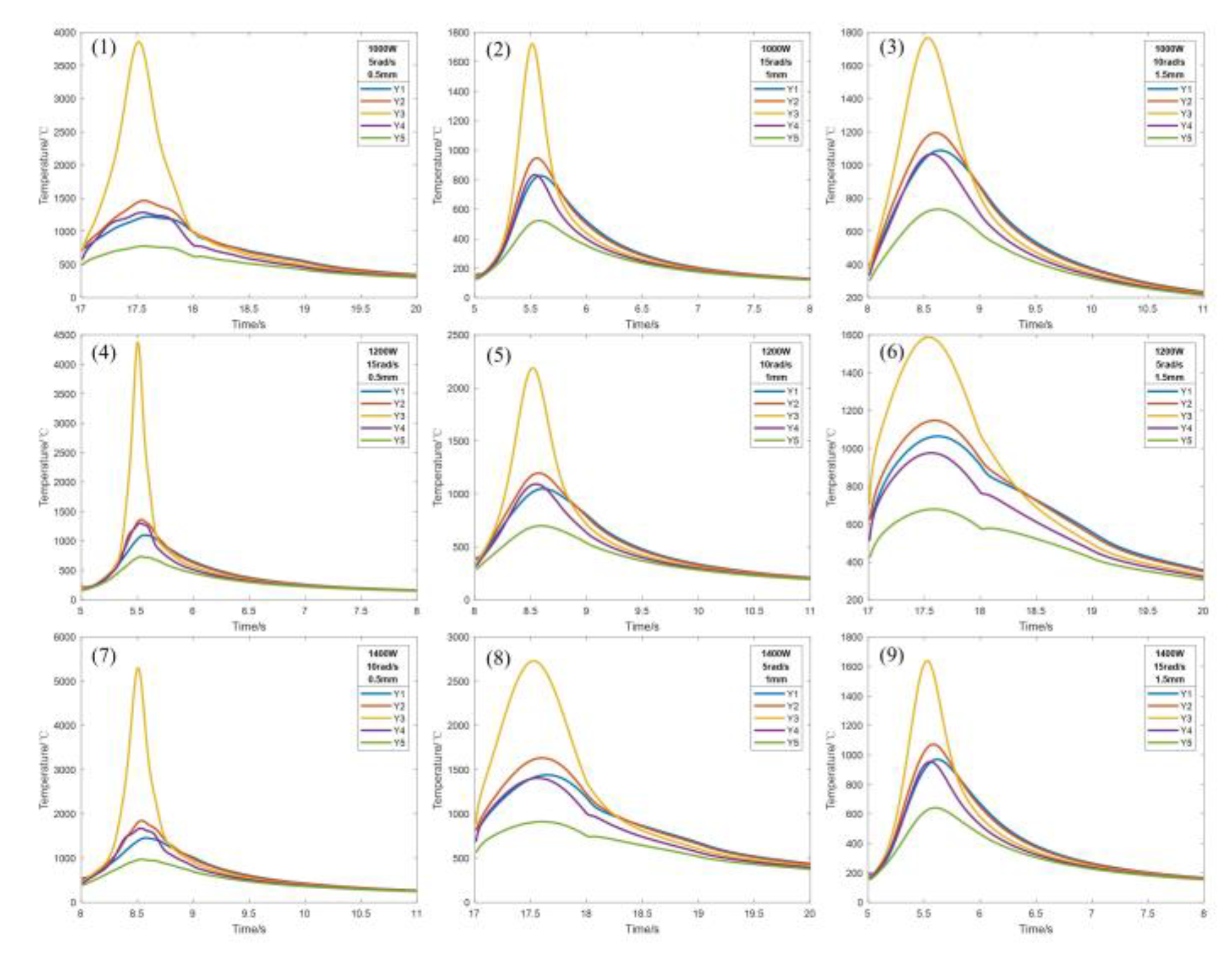
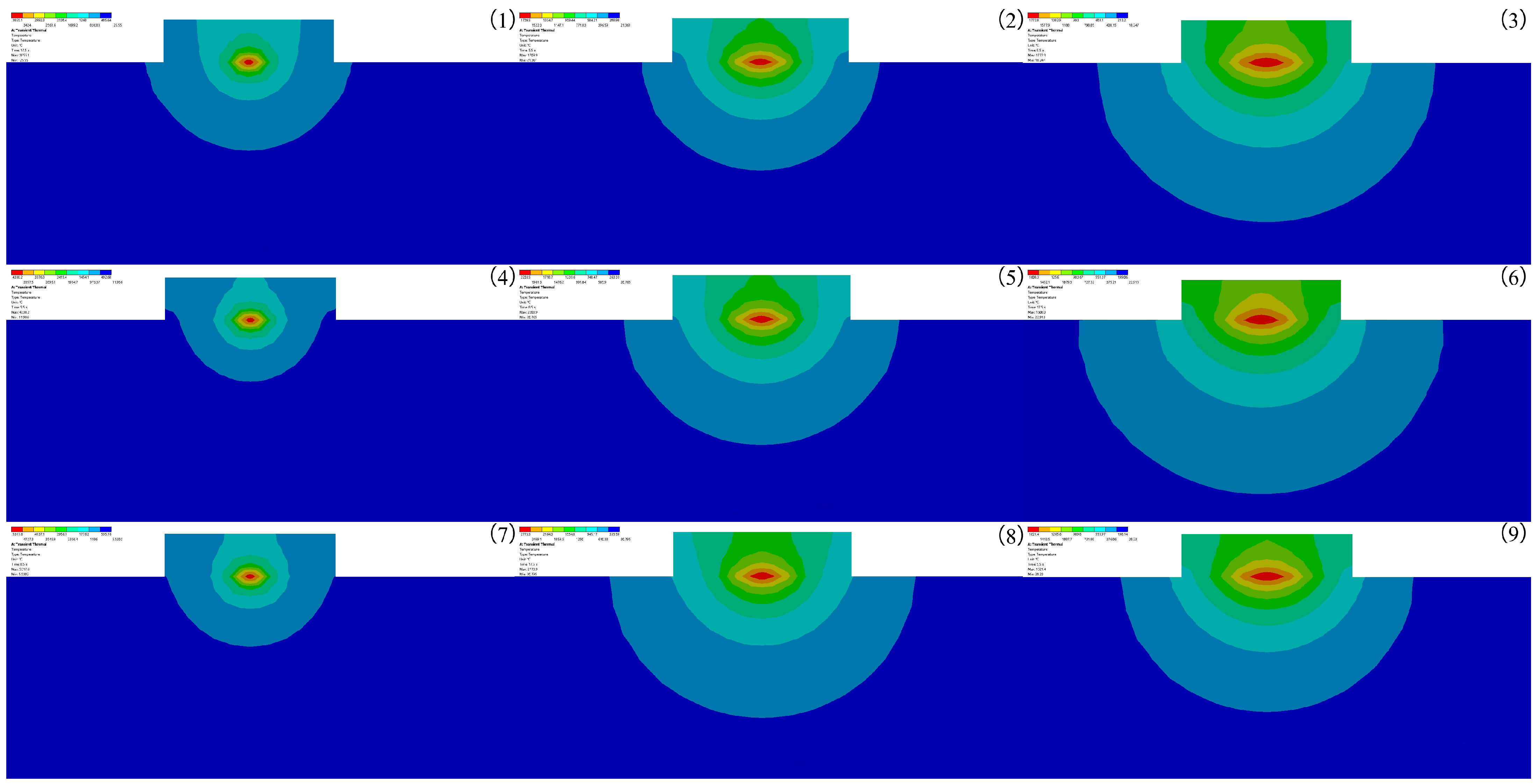
3.1. Simulation Results of Temperature Field under Different Process Parameters
3.2. Analysis of Temperature Field Results
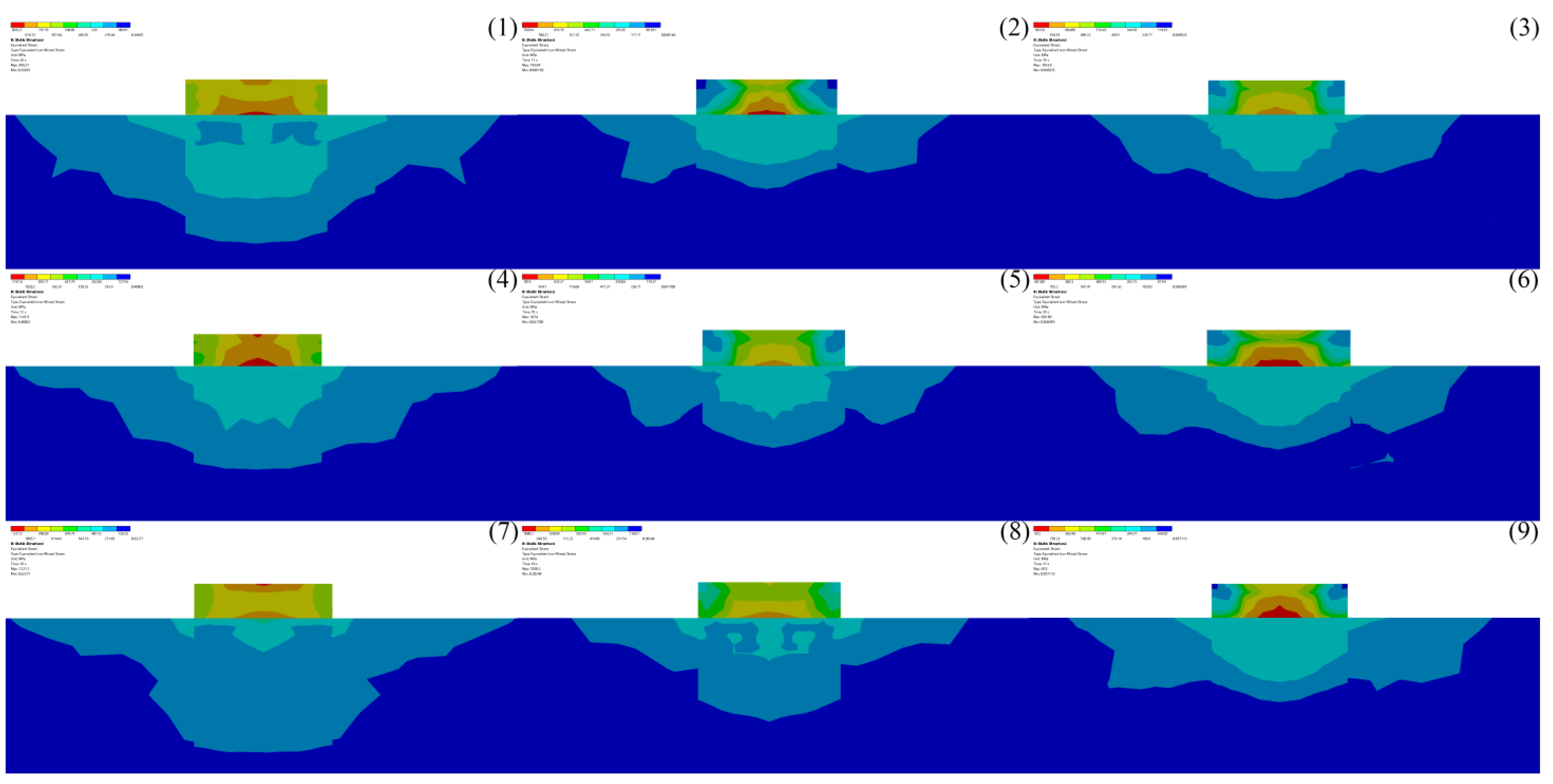
3.3. Analysis of Stress Field Results
3.4. Analysis of Fluid Field Results
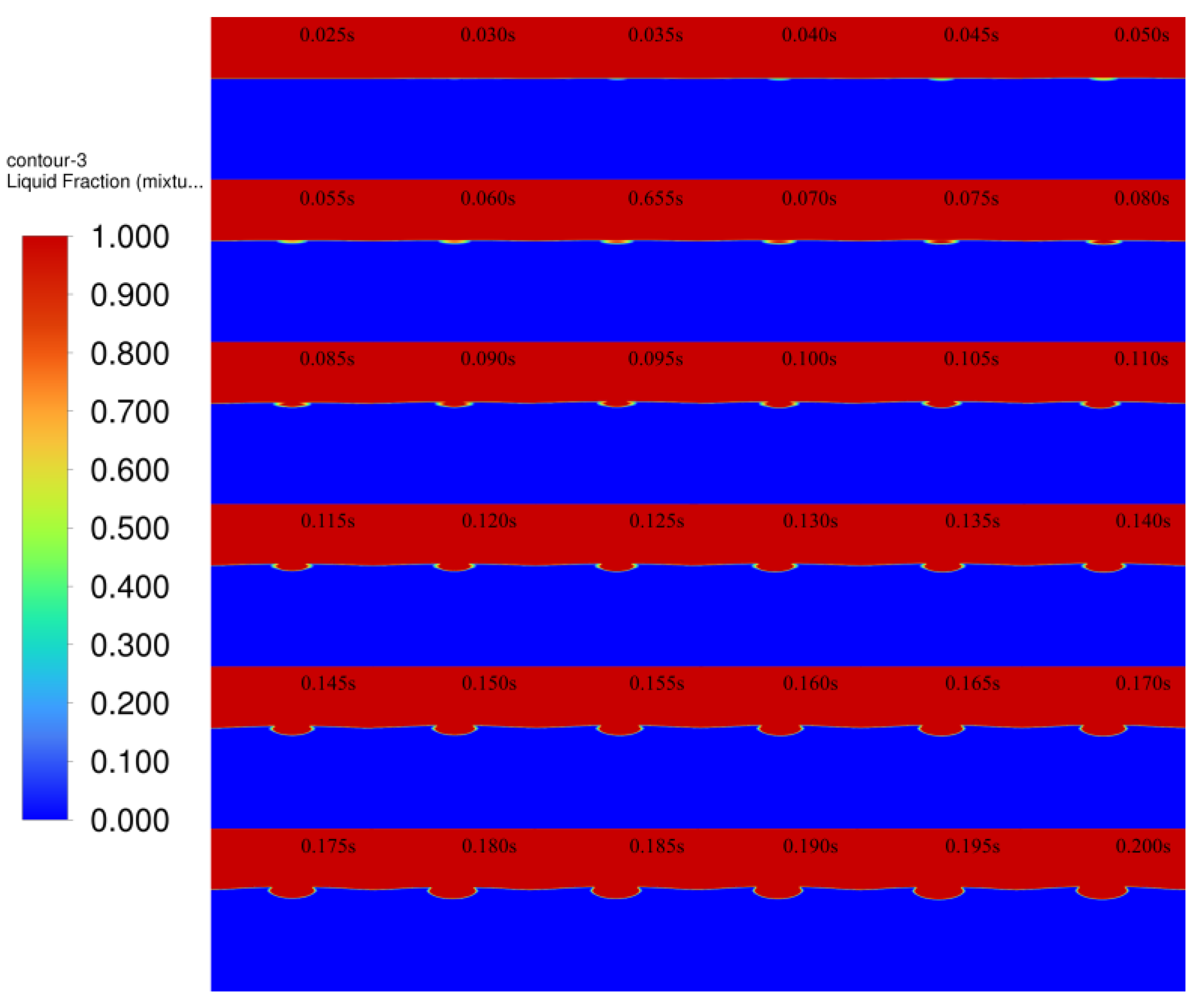
3.4.1. Melting Pool Melting
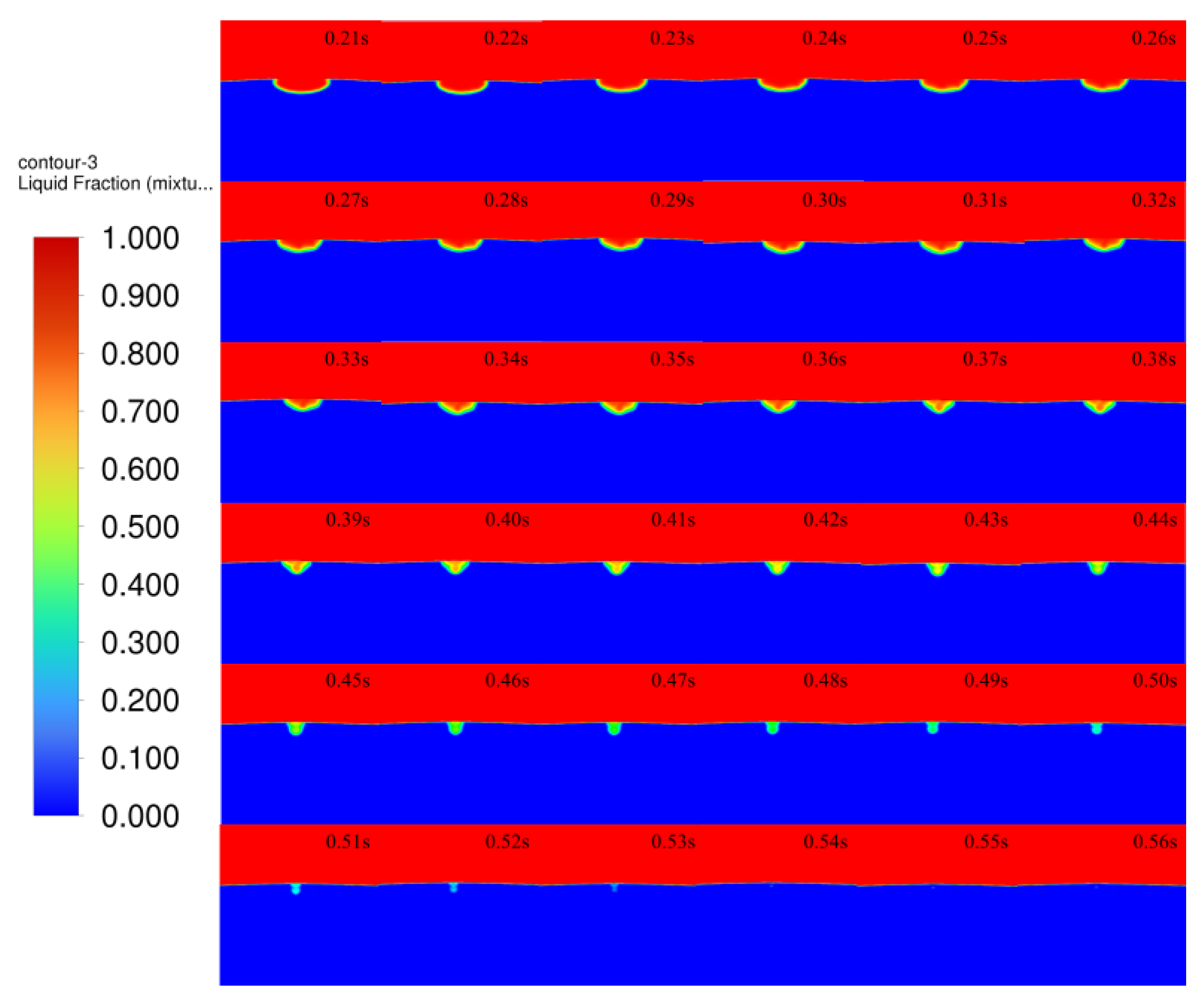
3.4.2. Melt Pool Solidification
3.4.3. Melt Pool Flow
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, H.; Liu, Z.C.; Cong, W.L.; Zhang, H.C. Tensile Fracture Behavior and Failure Mechanism of Additively-Manufactured AISI 4140 Low Alloy Steel by Laser Engineered Net Shaping. Materials 2017, 10, 1283. [Google Scholar] [CrossRef] [Green Version]
- Ozturk, M.; Husem, F.; Karademir, I.; Maleki, E.; Amanov, A.; Unal, O. Fatigue crack growth rate of AISI 4140 low alloy steel treated via shot peening and plasma nitriding. Vacuum 2023, 207, 111552. [Google Scholar] [CrossRef]
- Huang, C.P.; Lin, X.; Liu, F.C.; Cao, J.; Liu, F.G.; Huang, W.D. Effects of cooling condition on microstructure and mechanical properties in laser rapid forming of 34CrNiMo6 thin-wall component. Int. J. Adv. Manuf. Technol. 2016, 825, 1269–1279. [Google Scholar]
- Lashin, M.M.A.; Ibrahim, M.Z.; Khan, M.I.; Guedri, K.; Saxena, K.K.; Eldin, S.M. Fuzzy Control Modeling to Optimize the Hardness and Geometry of Laser Cladded Fe-Based MG Single Track on Stainless Steel Substrate Prepared at Different Surface Roughness. Micromachines 2022, 13, 2191. [Google Scholar] [CrossRef]
- Meng, K.K.; Tan, X.; Shang, F.; Jiang, Z.H. A universal method to fabricate Cu films with superhydrophobic and anti-corrosion properties. Mater. Sci. Technol. 2019, 35, 695–701. [Google Scholar] [CrossRef]
- Koivuluoto, H. A Review of Thermally Sprayed Polymer Coatings. J. Therm. Spray Technol. 2022, 316, 1750–1764. [Google Scholar] [CrossRef]
- Liu, W.; Jiang, S.Q.; Jiao, F. Progress in research of resource-oriented treatment technologies for electroplating sludge. Electroplat. Finish. 2022, 41, 585–592. [Google Scholar]
- Schopphoven, T.; Gasser, A.; Wissenbach, K. Investigations on ultra-high-speed laser material deposition as alternative for hard chrome plating and thermal spraying. J. Laser Appl. 2016, 28, 022501. [Google Scholar] [CrossRef]
- Gateman, S.M.; Halimi, I.; Costa, N.A.R.; Lacasse, R.; Schulz, R.; Moreau, C.; Chromik, R.; Mauzeroll, J. Using macro and micro electrochemical methods to understand the corrosion behavior of stainless-steel thermal spray coatings. npj Mater. Degrad. 2019, 3, 25. [Google Scholar] [CrossRef] [Green Version]
- Tudu, N.; Baruah, M.; Prasad, S.B. Comparison of properties at the interface of deposited IN625 and mixture of IN625 SS304L by laser directed energy deposition and SS304L substrate. Rapid Prototyp. J. 2022; ahead-of-print. [Google Scholar]
- Zhou, Y.; Qu, W.; Zhou, F.; Li, X.; Song, L.; Zhu, Q. Thermo-fluid flow behavior of the IN718 molten pool in the laser directed energy deposition process under magnetic field. Rapid Prototyp. J. 2022; ahead-of-print. [Google Scholar]
- Wang, X.L.; Lei, L.; Yu, H. A Review on Microstructural Features and Mechanical Properties of Wheels/Rails Cladded by Laser Cladding. Micromachines 2021, 122, 152. [Google Scholar] [CrossRef]
- He, Z.Y.; He, W.X.; Yang, H.F.; Zhou, L.; Zhao, H.Y.; Song, X.G. Research Progess in Laser Cladding on Aluminum Alloy Surface. China Surf. Eng. 2021, 346, 33–44. [Google Scholar]
- Raj, D.; Maity, S.R.; Das, B. State-of-the-art review on laser cladding process as an in-situ repair technique. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 2363, 1194–1215. [Google Scholar] [CrossRef]
- Chen, B.; Wang, T.; Xi, X.; Tan, C.; Song, X. Additive manufacturing of Ti-Al functionally graded material by laser based directed energy deposition. Rapid Prototyp. J. 2022; ahead-of-print. [Google Scholar]
- Farzaneh, A.; Khorasani, M.; Farabi, E.; Gibson, I.; Leary, M.; Ghasemi, A.; Rolfe, B. Sandwich structure printing of Ti-Ni-Ti by directed energy deposition. Virtual Phys. Prototyp. 2022, 17, 1006–1030. [Google Scholar] [CrossRef]
- Li, C.; Zhang, D.; Gao, X.; Han, X. Numerical simulation method of the multi-field coupling mechanism for laser cladding 316L powder. Weld. World 2022, 66, 423–440. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, P.; Zha, G.; Zhi, O.Y.; He, D.T. Numerical simulations of temperature and stress field of Fe-Mn-Si-Cr-Ni shape memory alloy coating synthesized by laser cladding. Optik 2021, 242, 167079. [Google Scholar] [CrossRef]
- Yao, F.; Fang, L. Thermal stress cycle simulation in laser cladding process of Ni-based coating on H13 steel. Coatings 2021, 11, 203. [Google Scholar] [CrossRef]
- Farahmand, P.; Kovacevic, R. An experimental-numerical investigation of heat distribution and stress field in single- and multi-track laser cladding by a high-power direct diode laser. Opt. Laser Technol. 2014, 63, 154–168. [Google Scholar] [CrossRef]
- Zhao, S.J.; Qi, W.J.; Huang, Y.H.; Lei, J.F. Numerical Simulation Study on Thermal Cycle Characteristics of Temperature Field of TC4 Surface Laser Cladding Ni60 Based Coating. Surf. Technol. 2020, 49, 301–308. [Google Scholar]
- Li, J.H.; An, X.J.; Yao, F.P. Simulation on Thermal Stress Cycle in Laser Cladding of H13 Steel Ni-Based Coating. Chin. J. Lasers 2021, 48, 33–40. [Google Scholar]
- Xu, M.S.; Zhou, C.H.; Zhang, Z.; Zeng, S.J. Temperature Distribution of Powder-gas-optical Coupling temperature field in Laser Cladding Processes. China Mech. Eng. 2022, 33, 70–77. [Google Scholar]
- Han, X.; Zhang, C.D.; Li, C.; Yu, Z.B.; Zhang, B.G. Study on a multifield coupling mechanism and a numerical simulation method of a pulsed laser deposition process from a disk laser. Appl. Phys. Mater. Sci. Process. 2021, 127, 17. [Google Scholar] [CrossRef]
- Liu, W.W.; Saleheen, K.M.; Al-Hammadi, G.; Daaim, M.; Abdelrahman, A.; Xue, L.; Hua, S.G.; Wang, F.T. Effect of different laser scanning sequences on temperature field and deformation of laser cladding. Opt. Eng. 2022, 614, 046107. [Google Scholar] [CrossRef]
- Liu, H.; Qin, X.; Wu, M.; Ni, M.; Huang, S. Numerical simulation of thermal and stress field of singletrack cladding in wide-beam laser cladding. Int. J. Adv. Manuf. Technol. 2019, 104, 3959–3976. [Google Scholar] [CrossRef]
- Ren, Z.; Wu, M.; Cui, C.; Xia, S. Effects of Temperature Field and CeO2/TiO2 on Material Phase Transition in Laser Cladding. Chin. J. Lasers 2019, 46, 118–125. [Google Scholar]
- Al Hamahmy, M.I.; Deiab, I. Review and analysis of heat source models for additive manufacturing. Int. J. Adv. Manuf. Technol. 2020, 106, 1223–1238. [Google Scholar] [CrossRef]
- Li, C.R.; Hui, S.Y.; Sun, G.Y. Research on the paramenters of Ti Ni Ta memory alloy coating based on temperature field simulation. Laser Infrared 2021, 51, 999–1005. [Google Scholar]
- Luo, X.X.; Gao, C. The research and application of laser cladding repair technology for mine motor rotor shaft. Shaanxi Coal 2018, 37, 25–28. [Google Scholar]
- Wang, S.; Li, C.; Wu, H.T. The Formation of Molten Pool in Laser Cladding of Ni-Cr-Fe-B Alloy Coating. Appl. Laser 2015, 35, 282–287. [Google Scholar]
- Xie, L.Y.; Shi, W.Q.; Wu, T. Numerical Simulation of Temperature Field and Stress Field of Laser Cladding on Curved Substrate Workpiece. Surf. Technol. 2022, 51, 296–303+25. [Google Scholar]
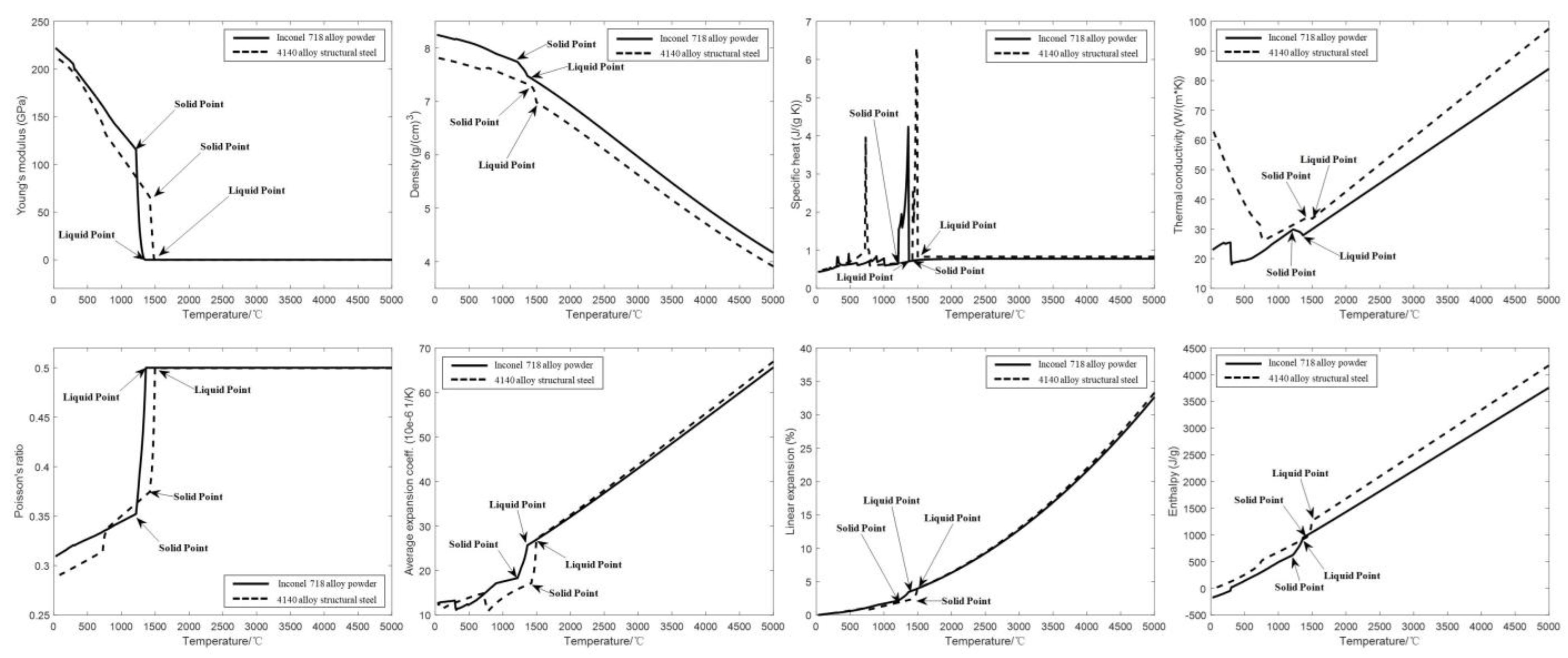
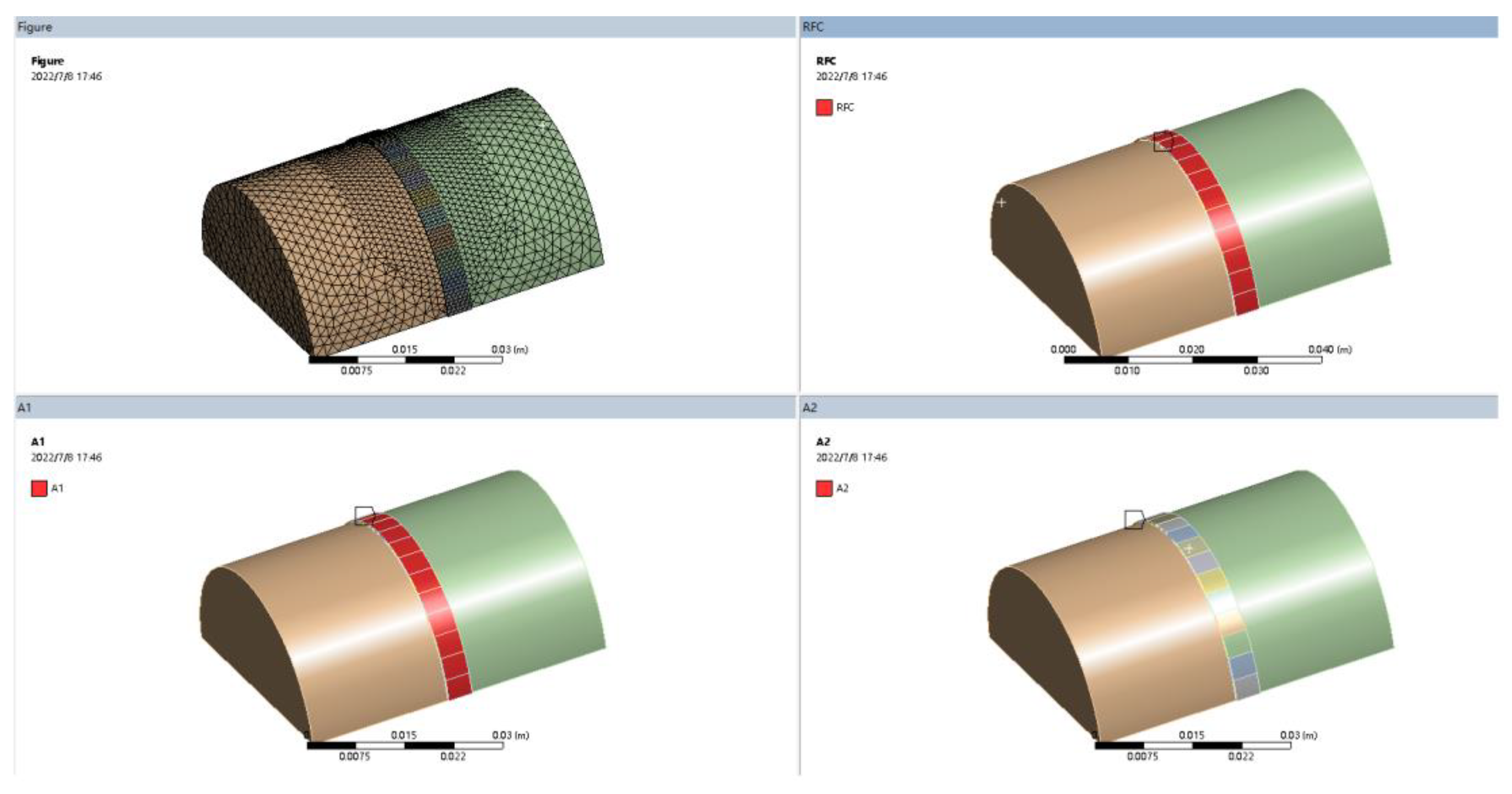
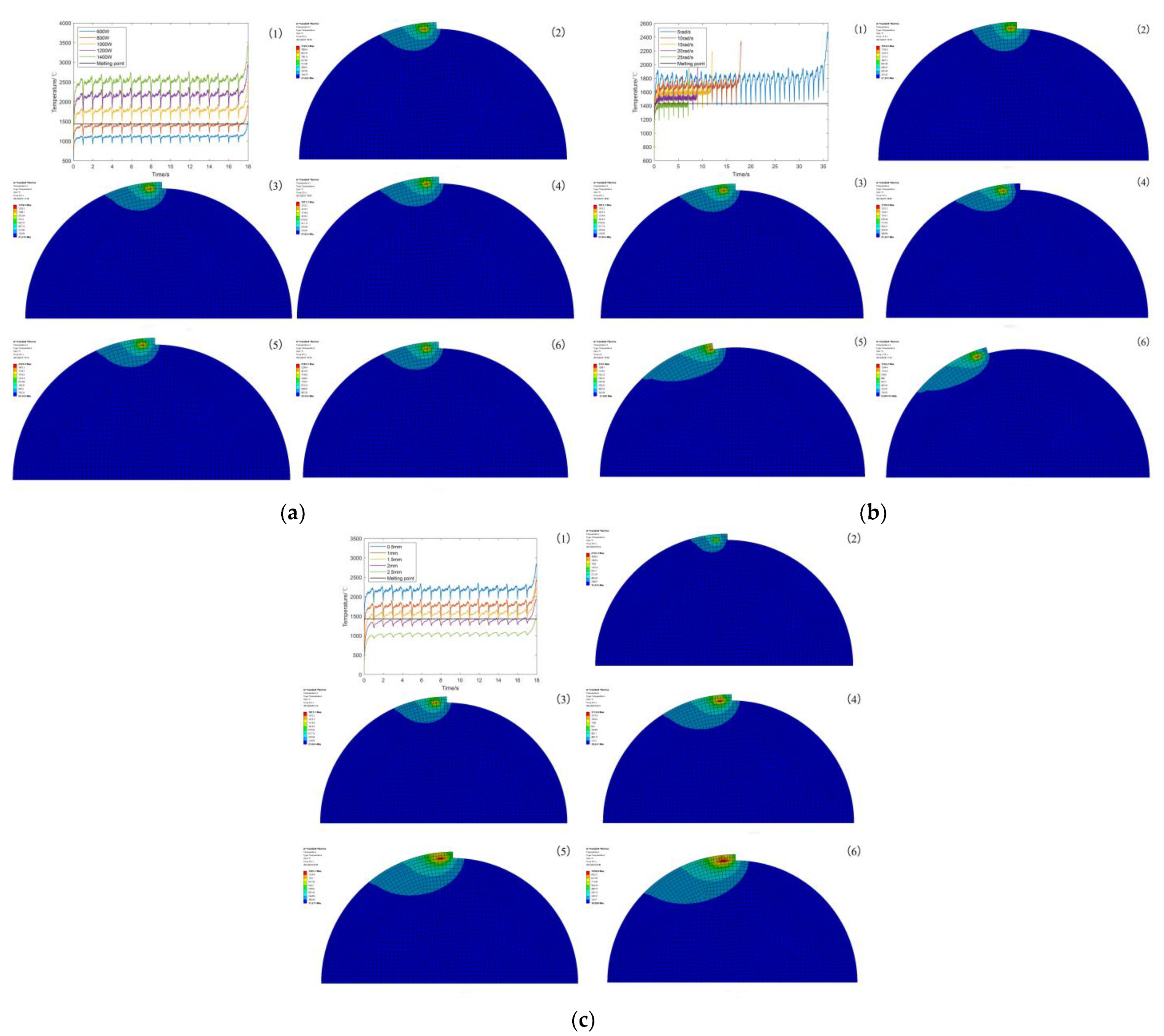
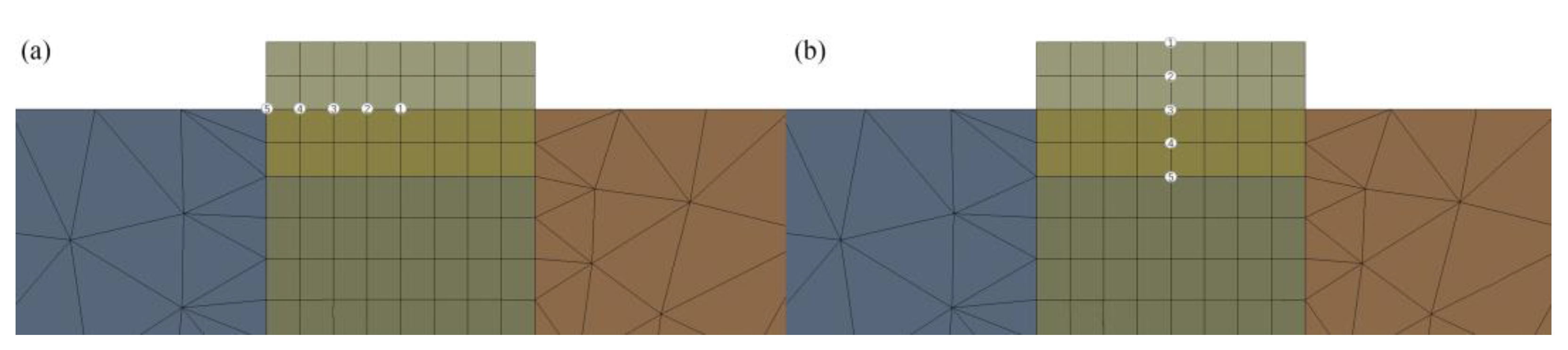







| Element | Cr | Mn | Mo | Ni | Si | C | P | S |
|---|---|---|---|---|---|---|---|---|
| Mass fraction/% | 0.98 | 0.77 | 0.21 | 0.04 | 0.15 | 0.37 | 0.03 | 0.04 |
| Element | Al | Cr | Fe | Mo | Nb |
|---|---|---|---|---|---|
| Mass fraction/% | 0.5 | 19.0 | 18.5 | 3.0 | 5.1 |
| Fixed Factors | Variable Factors |
|---|---|
| Scanning speed 10 rad/s Spot radius 1 mm Remain unchanged | Laser power (W) |
| 600 | |
| 800 | |
| 1000 | |
| 1200 | |
| 1400 | |
| Laser power 1000 W Spot radius 1 mm Remain unchanged | Scanning speed (rad/s) |
| 5 | |
| 10 | |
| 15 | |
| 20 | |
| 25 | |
| Laser power 1000 W Scanning speed 10 rad/s Remain unchanged | Spot radius (mm) |
| 0.5 | |
| 1 | |
| 1.5 | |
| 2 | |
| 2.5 |
| Fixed Factors | Variable Factors | Temperature |
|---|---|---|
| Scanning speed, spot radius certain Change laser power | 600 W | 1129.3 °C |
| 800 W | 1418.6 °C | |
| 1000 W | 1811.1 °C | |
| 1200 W | 2203.9 °C | |
| 1400 W | 2583.1 °C | |
| Laser power, spot radius certain Change scanning speed | 5 rad/s | 1953.6 °C |
| 10 rad/s | 1811.1 °C | |
| 15 rad/s | 1709.9 °C | |
| 20 rad/s | 1454.0 °C | |
| 25 rad/s | 1456.2 °C | |
| Laser power, scanning speed is certain Change spot radius | 0.5 mm | 2134.3 °C |
| 1 mm | 1811.1 °C | |
| 1.5 mm | 1772.8 °C | |
| 2 mm | 1487.7 °C | |
| 2.5 mm | 1058.8 °C |
| No. | Laser Power (W) | Spot Radius (mm) | Scanning Speed (rad/s) |
|---|---|---|---|
| 1 | 1000 | 0.5 | 5 |
| 2 | 1000 | 1 | 15 |
| 3 | 1000 | 1.5 | 10 |
| 4 | 1200 | 0.5 | 15 |
| 5 | 1200 | 1 | 10 |
| 6 | 1200 | 1.5 | 5 |
| 7 | 1400 | 0.5 | 10 |
| 8 | 1400 | 1 | 5 |
| 9 | 1400 | 1.5 | 15 |
| No. | Laser Power (W) | Spot Radius (mm) | Scanning Speed (rad/s) | Thermal Stress Maximum (Mpa) |
|---|---|---|---|---|
| 1 | 1000 | 0.5 | 5 | 986 |
| 2 | 1000 | 1 | 15 | 796 |
| 3 | 1000 | 1.5 | 10 | 1033 |
| 4 | 1200 | 0.5 | 15 | 1147 |
| 5 | 1200 | 1 | 10 | 1074 |
| 6 | 1200 | 1.5 | 5 | 881 |
| 7 | 1400 | 0.5 | 10 | 1221 |
| 8 | 1400 | 1 | 5 | 1068 |
| 9 | 1400 | 1.5 | 15 | 853 |
| Source of Difference | Sum of Squares | df | Root Mean Square | F | P |
|---|---|---|---|---|---|
| Intercept | 1,630,250 | 1 | 1,630,249.797 | 124.897 | 0.008 ** |
| Laser power (W) | 1,193,225 | 2 | 596,612.392 | 45.708 | 0.021 ** |
| Spot radius (mm) | 362,394.3 | 2 | 181,197.157 | 13.882 | 0.067 |
| Scanning speed (rad/s) | 50,754.89 | 2 | 25,377.444 | 1.944 | 0.34 |
| Residual | 26,105.56 | 2 | 13,052.778 | ||
| R2: 0.836 | * p < 0.05 | ** p < 0.01 |
| Item | Level | Thermal Stress Maximum | |
|---|---|---|---|
| K-value | Spot radius | 0.5 | 3354 |
| 1 | 2938 | ||
| 1.5 | 2767 | ||
| Scanning speed | 5 | 2935 | |
| 10 | 3328 | ||
| 15 | 2796 | ||
| Laser power | 1000 | 2815 | |
| 1200 | 3102 | ||
| 1400 | 3142 | ||
| K avg value | Spot radius | 0.5 | 1118 |
| 1 | 979.33 | ||
| 1.5 | 922.33 | ||
| Scanning speed | 5 | 978.33 | |
| 10 | 1109.33 | ||
| 15 | 932 | ||
| Laser power | 1000 | 938.33 | |
| 1200 | 1034 | ||
| 1400 | 1047.33 | ||
| Optimal level | 1000 | 1.5 | 15 |
| R | −109 | −195.67 | −177.33 |
| Number of levels | 3 | 3 | 3 |
| Number of repetitions per level r | 3 | 3 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Ma, C.; Yang, J.; Li, M.; Zhao, Q.; Ma, H.; Jia, X. Numerical Simulation Study of Multi-Field Coupling for Laser Cladding of Shaft Parts. Micromachines 2023, 14, 493. https://doi.org/10.3390/mi14020493
Zhao C, Ma C, Yang J, Li M, Zhao Q, Ma H, Jia X. Numerical Simulation Study of Multi-Field Coupling for Laser Cladding of Shaft Parts. Micromachines. 2023; 14(2):493. https://doi.org/10.3390/mi14020493
Chicago/Turabian StyleZhao, Changlong, Chen Ma, Junbao Yang, Ming Li, Qinxiang Zhao, Hongnan Ma, and Xiaoyu Jia. 2023. "Numerical Simulation Study of Multi-Field Coupling for Laser Cladding of Shaft Parts" Micromachines 14, no. 2: 493. https://doi.org/10.3390/mi14020493
APA StyleZhao, C., Ma, C., Yang, J., Li, M., Zhao, Q., Ma, H., & Jia, X. (2023). Numerical Simulation Study of Multi-Field Coupling for Laser Cladding of Shaft Parts. Micromachines, 14(2), 493. https://doi.org/10.3390/mi14020493





