A New Analytical Large-Signal Model for Quasi-Ballistic Transport in InGaAs HEMTs Accommodating Dislocation Scattering
Abstract
:1. Introduction
2. Model Development
2.1. InGaAs HEMT Devices
2.2. A New 2DEG Charge Density Model
2.3. Calculation of Surface Potential
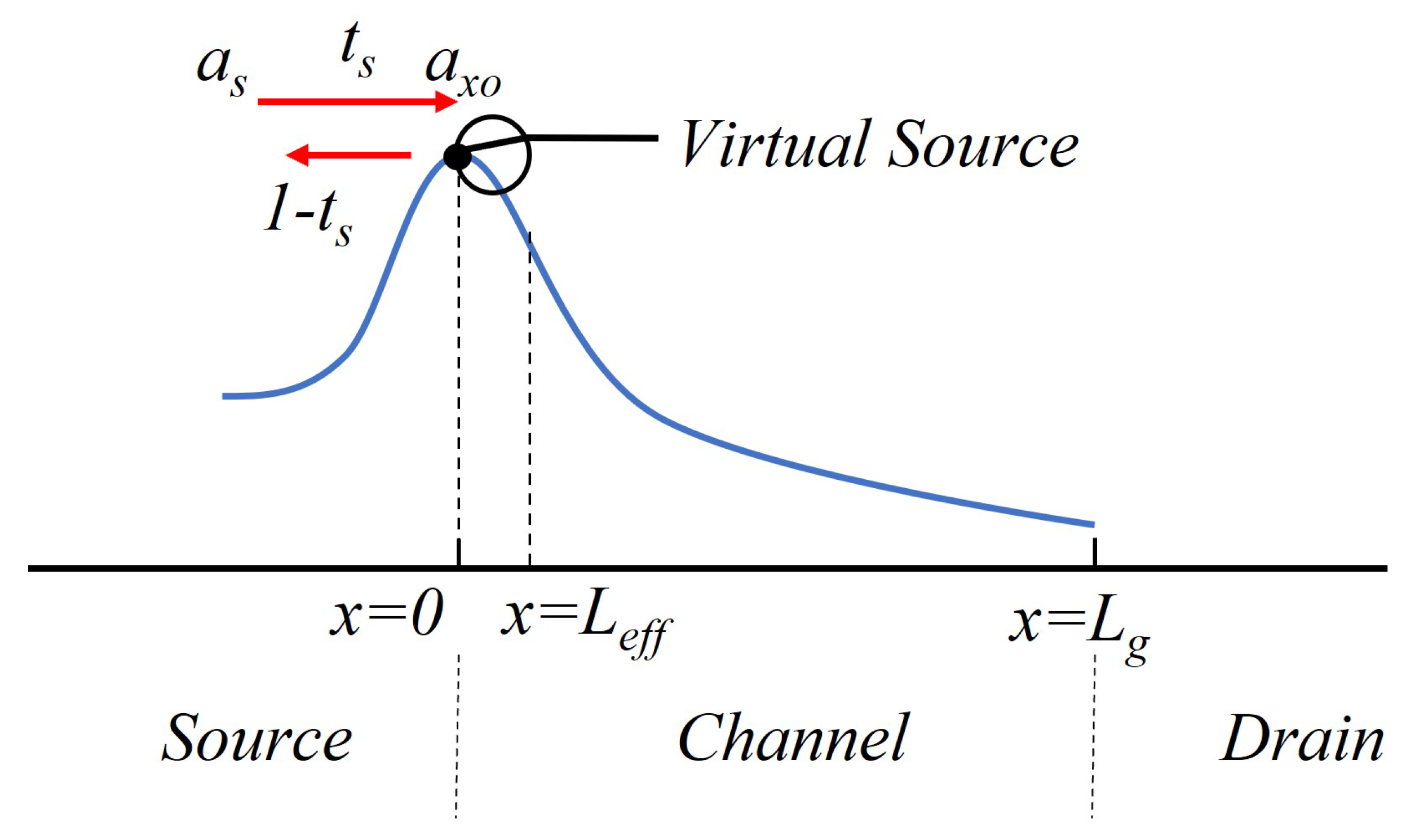
2.4. Drain Current Model
2.5. Capacitance Model
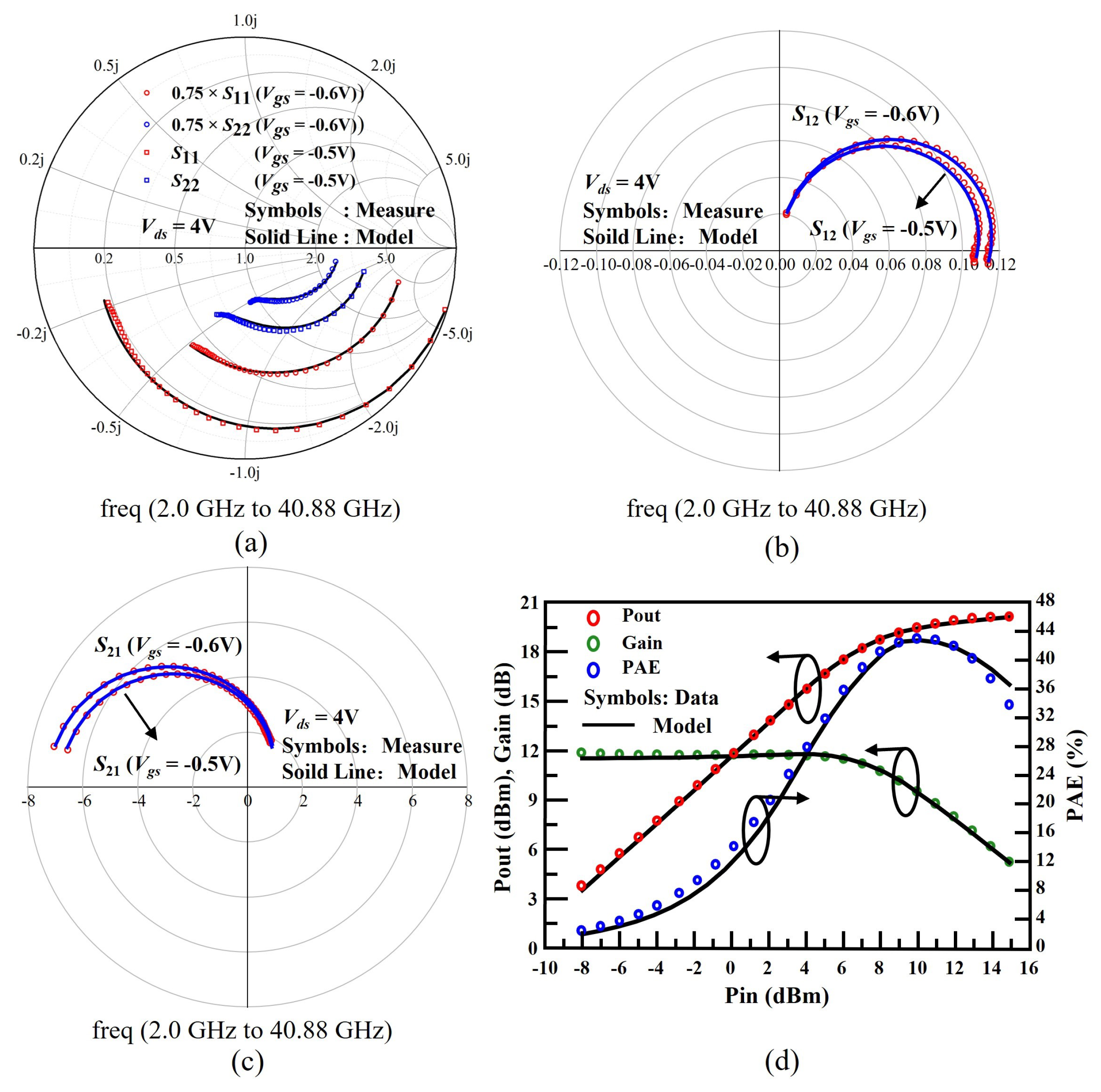
3. Model Verification and Discussion
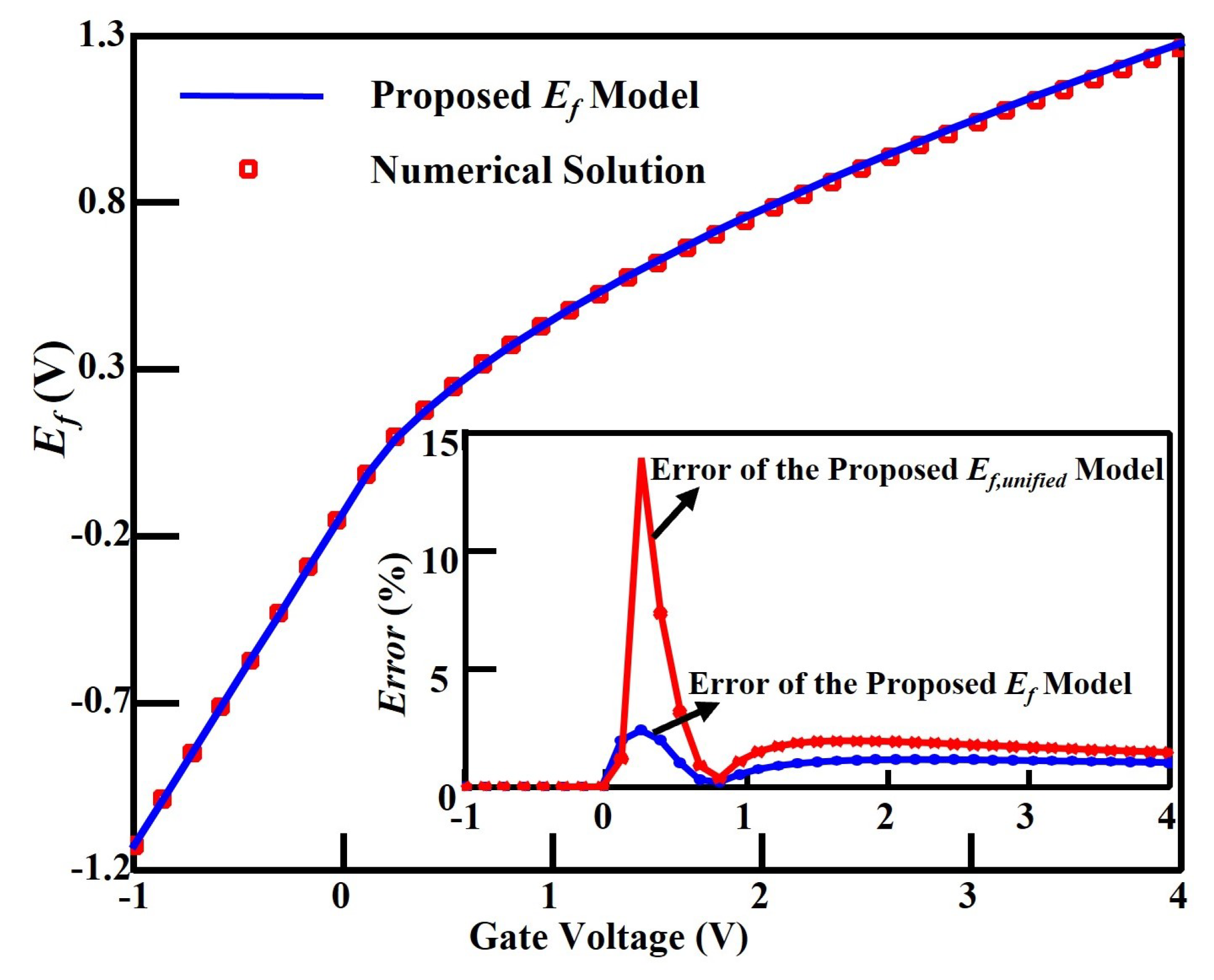
3.1. Comparison to Numerical Simulations
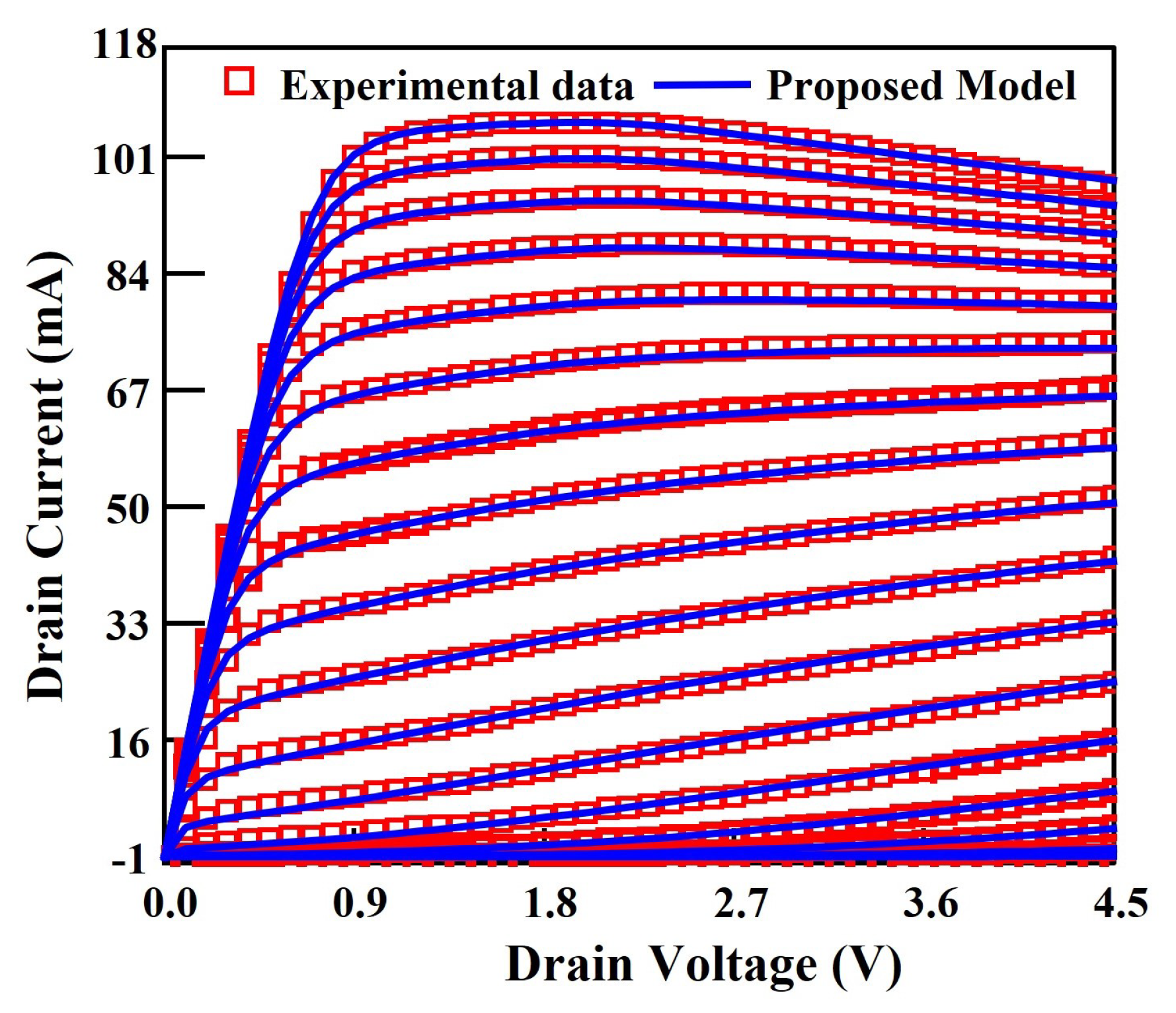
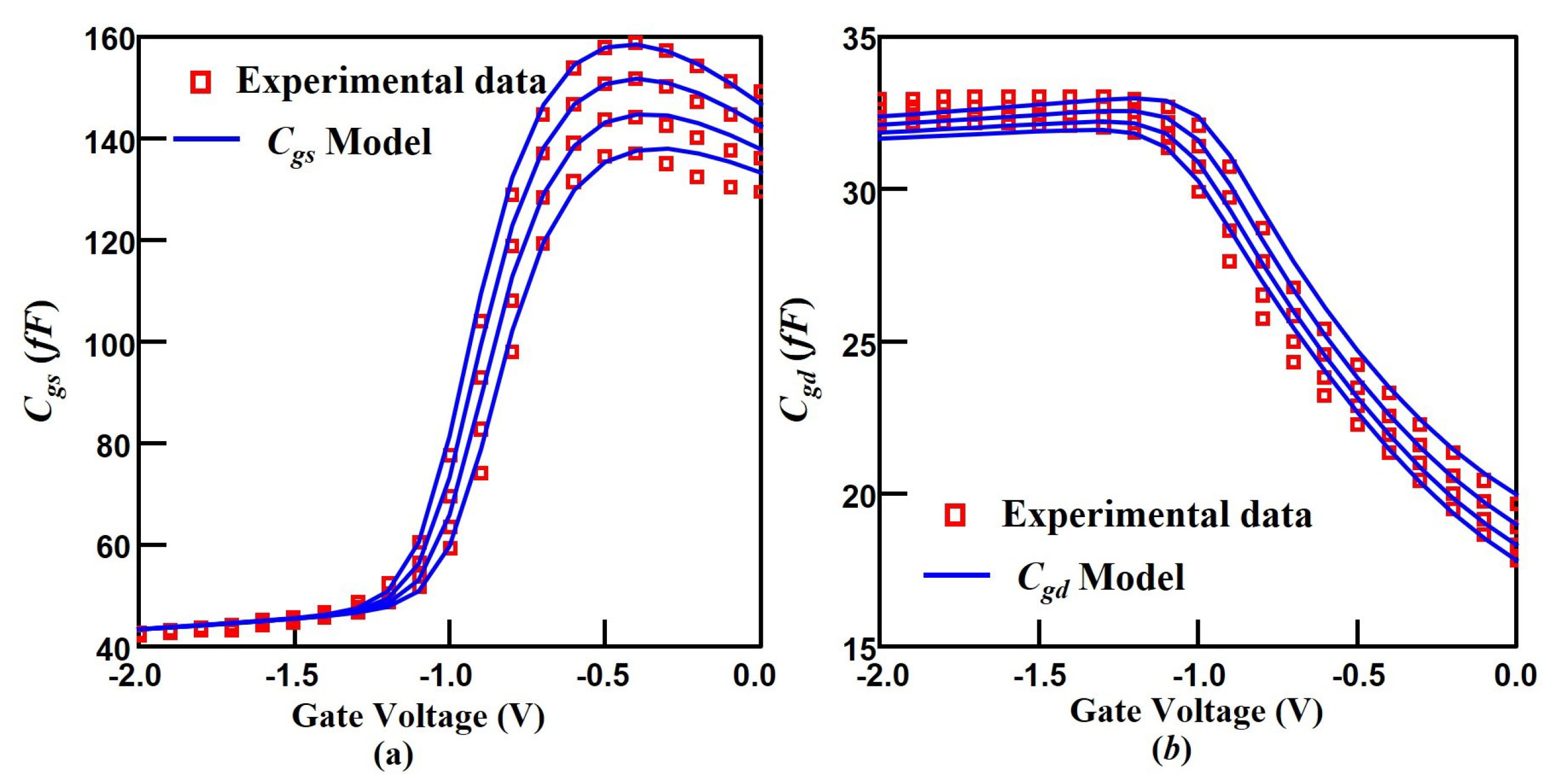
3.2. Comparison to Experimental Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martinie, S.; Munteanu, D.; Le Carval, G.; Autran, J.L. New Unified Analytical Model of Backscattering Coefficient From Low- to High-Field Conditions in Quasi-Ballistic Transport. IEEE Electron Device Lett. 2008, 29, 1392–1394. [Google Scholar] [CrossRef]
- Dasgupta, A.; Ghosh, S.; Chauhan, Y.S.; Khandelwal, S. ASM-HEMT: Compact model for GaN HEMTs. In Proceedings of the 2015 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Singapore, 1–4 June 2015; pp. 495–498. [Google Scholar] [CrossRef]
- Khandelwal, S.; Yigletu, F.; Iniguez, B.; Fjeldly, T.A. Analytical modeling of surface-potential and drain current in AlGaAs/GaAs HEMT devices. In Proceedings of the 2012 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Singapore, 21–23 November 2012; pp. 183–185. [Google Scholar]
- Martinie, S.; Munteanu, D.; Carval, G.L.; Autran, J.L. Physics-Based Analytical Modeling of Quasi-Ballistic Transport in Double-Gate MOSFETs: From Device to Circuit Operation. IEEE Trans. Electron Devices 2009, 56, 2692–2702. [Google Scholar] [CrossRef]
- Wang, H.; Gildenblat, G. Scattering matrix based compact MOSFET model. In Proceedings of the Digest. International Electron Devices Meeting, San Francisco, CA, USA, 8–11 December 2002; pp. 125–128. [Google Scholar]
- Khakifirooz, A.; Nayfeh, O.M.; Antoniadis, D. A simple semiempirical short-channel MOSFET current–voltage model continuous across all regions of operation and employing only physical parameters. IEEE Trans. Electron Devices 2009, 56, 1674–1680. [Google Scholar] [CrossRef]
- Wei, L.; Mysore, O.; Antoniadis, D. Virtual-source-based self-consistent current and charge FET models: From ballistic to drift-diffusion velocity-saturation operation. IEEE Trans. Electron Devices 2012, 59, 1263–1271. [Google Scholar] [CrossRef]
- Rahman, A.; Lundstrom, M.S. A compact scattering model for the nanoscale double-gate MOSFET. IEEE Trans. Electron Devices 2002, 49, 481–489. [Google Scholar] [CrossRef]
- Rakheja, S.; Lundstrom, M.S.; Antoniadis, D.A. An improved virtual-source-based transport model for quasi-ballistic transistors—Part I: Capturing effects of carrier degeneracy, drain-bias dependence of gate capacitance, and nonlinear channel-access resistance. IEEE Trans. Electron Devices 2015, 62, 2786–2793. [Google Scholar] [CrossRef]
- Li, K.; Rakheja, S. A unified current-voltage and charge-voltage model of quasi-ballistic III-nitride HEMTs for RF applications. In Proceedings of the 2018 76th Device Research Conference (DRC), Santa Barbara, CA, USA, 24–27 June 2018; pp. 1–2. [Google Scholar]
- Karthik, R.; Sathyakam, P.U.; Mallick, P. Effect of dislocation scattering on electron mobility in GaN. Nat. Sci. 2011, 3, 812–815. [Google Scholar]
- Martin, P.; Lucci, L. A compact model of AlGaN/GaN HEMTs power transistors based on a surface-potential approach. In Proceedings of the 20th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES 2013, Gdynia, Poland, 20–22 June 2013; pp. 92–95. [Google Scholar]
- Delagebeaudeuf, D.; Linh, N.T. Metal-(n) AlGaAs-GaAs two-dimensional electron gas FET. IEEE Trans. Electron Devices 1982, 29, 955–960. [Google Scholar] [CrossRef]
- Householder, A.S. The Numerical Treatment of a Single Nonlinear Equation; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- BSIMSOI 4.6; 1 MOSFET Model of User’s Manual. University of California: Berkeley, CA, USA, 2022.
- Rakheja, S.; Lundstrom, M.S.; Antoniadis, D.A. An improved virtual-source-based transport model for quasi-ballistic transistors—Part II: Experimental verification. IEEE Trans. Electron Devices 2015, 62, 2794–2801. [Google Scholar] [CrossRef]
- Kim, D.H.; Del Alamo, J.A. Lateral and Vertical Scaling of HEMTs for Post-Si-CMOS Logic Applications. IEEE Trans. Electron Devices 2008, 55, 2546–2553. [Google Scholar]
- Rakheja, S.; Lundstrom, M.; Antoniadis, D. A physics-based compact model for FETs from diffusive to ballistic carrier transport regimes. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; pp. 35.1.1–35.1.4. [Google Scholar]
- Zhao, D.; Kuhn, K. Dislocation scattering in n-type modulation doped Al0. 3Ga0. 7As/InxGa1-xAs/Al0. 3Ga0. 7As quantum wells. IEEE Trans. Electron Devices 1991, 38, 2582–2589. [Google Scholar] [CrossRef]



| Quantity | Expression |
|---|---|
| x | |
| z | |
| r |
| Parameter | Values | Parameter | Values |
|---|---|---|---|
| [nm] | 30 | d [nm] | 24 |
| [mV] | 126.3 [18] | ||
| [cm−2] | [19] | [nm] | 4.5 [19] |
| f | 0.5 | 0.035 | |
| 12.65 | [13] |
| Parameter | Values | Parameter | Values |
|---|---|---|---|
| [V] | [m/s] | ||
| [m2/(V·s)] | [cm/s] | ||
| [V−1] | [cm−2] | ||
| [V−2] | [nm] | 4.875 | |
| [V−1] | f | 0.1642 | |
| 1.755 | |||
| [V−2] | 13.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, J.; Wang, J.; Zhao, Z. A New Analytical Large-Signal Model for Quasi-Ballistic Transport in InGaAs HEMTs Accommodating Dislocation Scattering. Micromachines 2023, 14, 1023. https://doi.org/10.3390/mi14051023
Wang J, Liu J, Wang J, Zhao Z. A New Analytical Large-Signal Model for Quasi-Ballistic Transport in InGaAs HEMTs Accommodating Dislocation Scattering. Micromachines. 2023; 14(5):1023. https://doi.org/10.3390/mi14051023
Chicago/Turabian StyleWang, Jinye, Jun Liu, Jie Wang, and Zhenxin Zhao. 2023. "A New Analytical Large-Signal Model for Quasi-Ballistic Transport in InGaAs HEMTs Accommodating Dislocation Scattering" Micromachines 14, no. 5: 1023. https://doi.org/10.3390/mi14051023
APA StyleWang, J., Liu, J., Wang, J., & Zhao, Z. (2023). A New Analytical Large-Signal Model for Quasi-Ballistic Transport in InGaAs HEMTs Accommodating Dislocation Scattering. Micromachines, 14(5), 1023. https://doi.org/10.3390/mi14051023







