An Efficient and Robust Partial Differential Equation Solver by Flash-Based Computing in Memory
Abstract
:1. Introduction
2. Materials and Methods
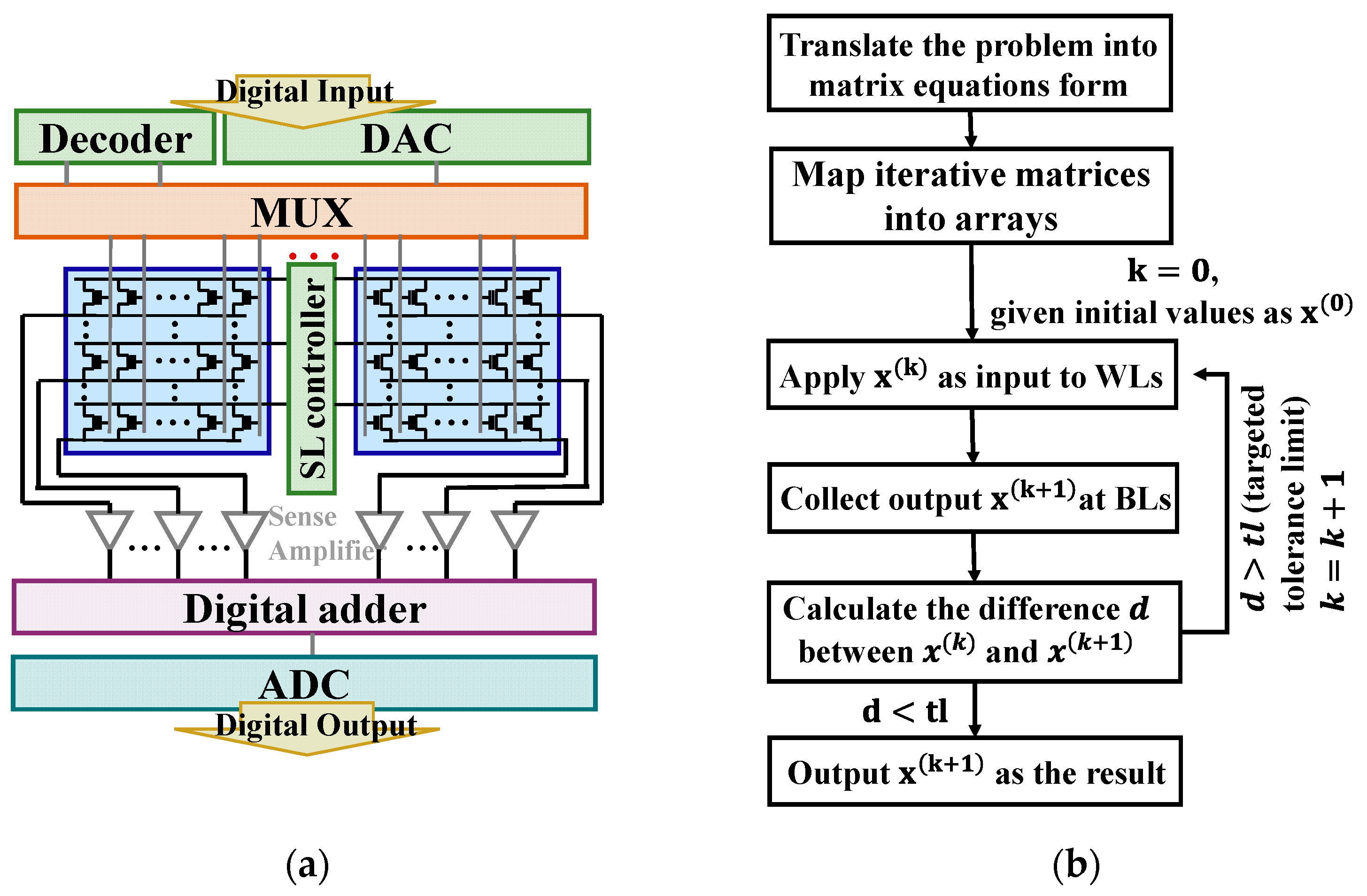
2.1. Architecture
2.2. SRJ Iterative Method
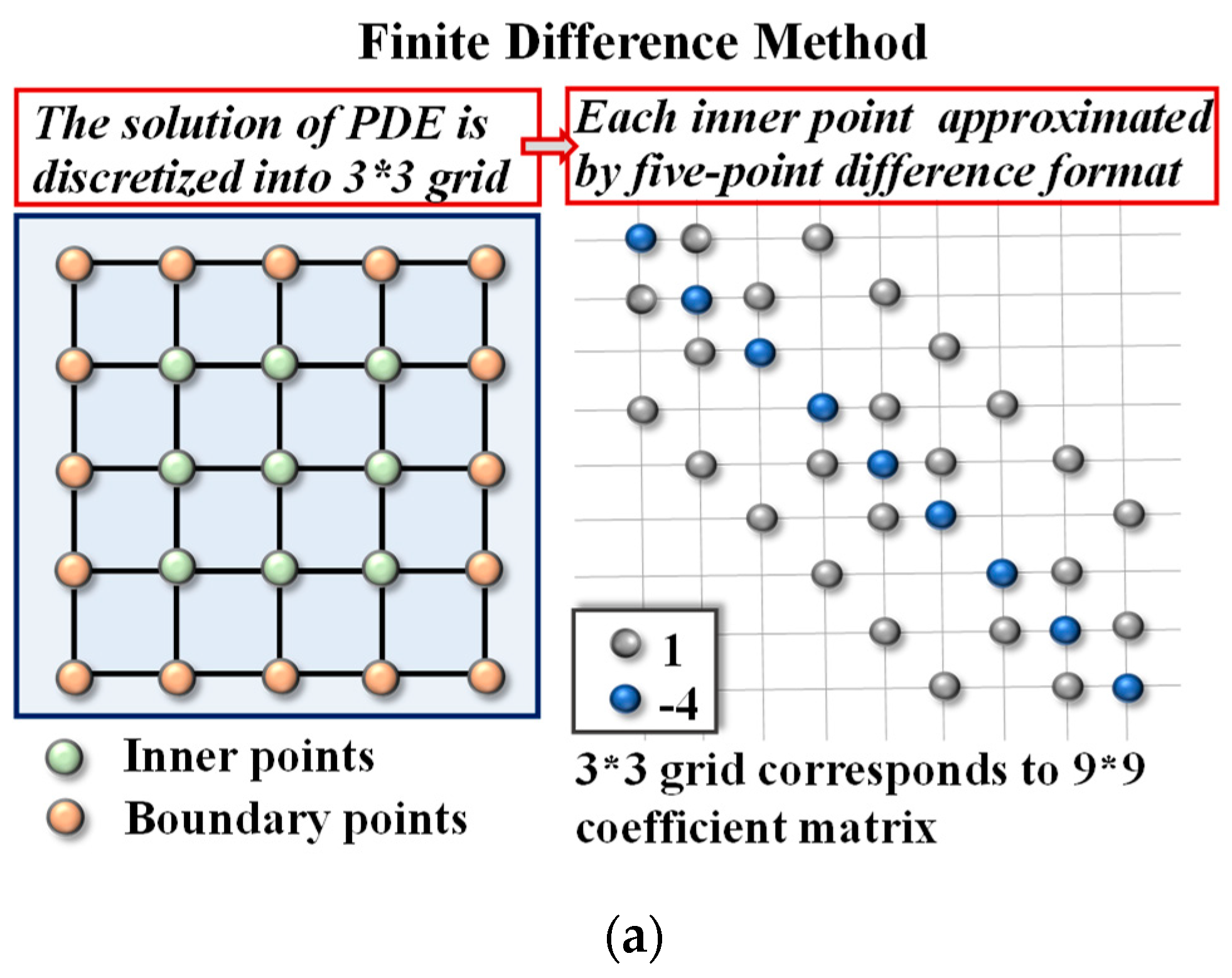
2.3. Pre-Processing
2.4. Mapping Method
3. Results
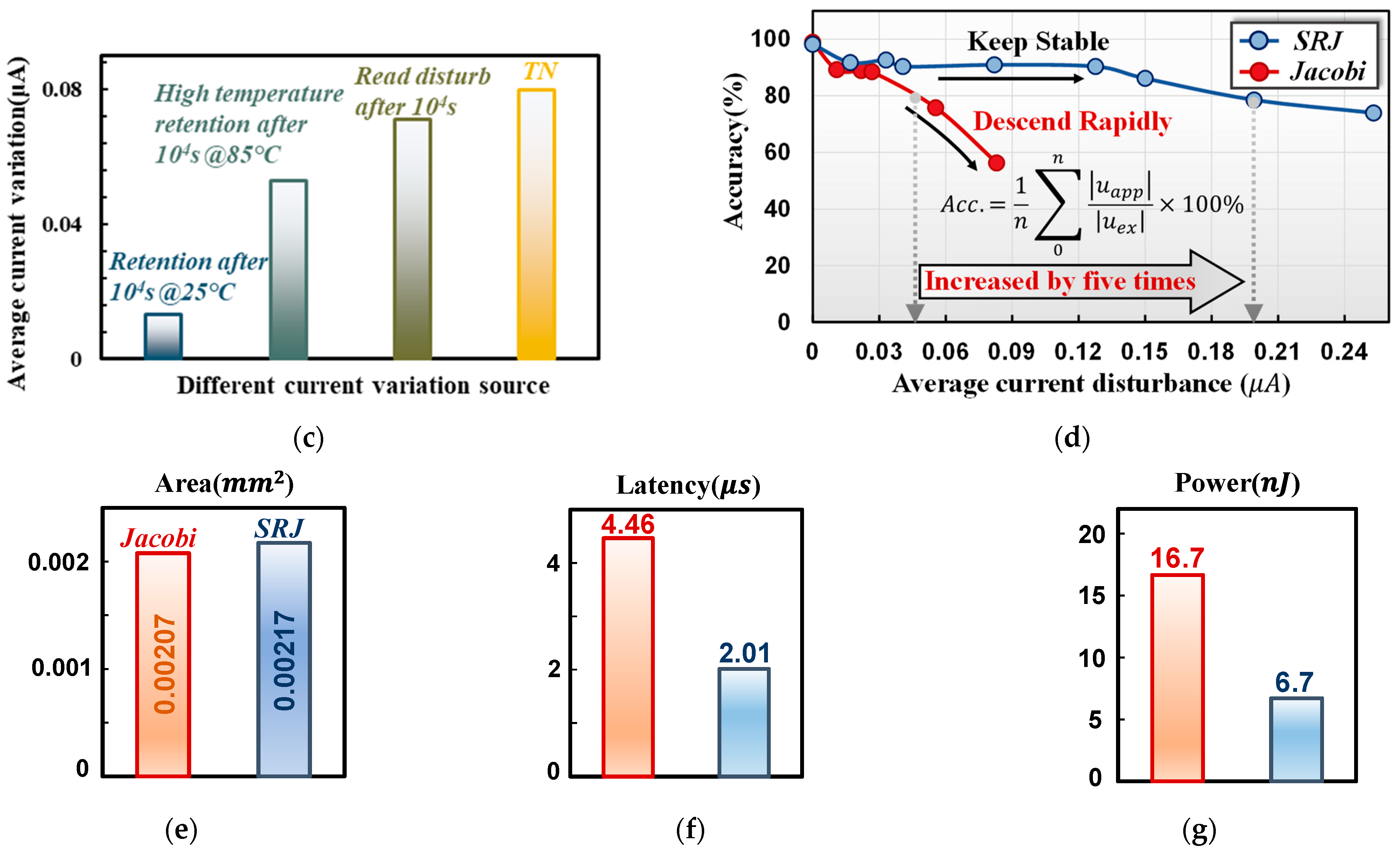
3.1. Accuracy Analysis
3.2. Robustness Performance to Noise
3.3. Power Dissipation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nair, R. Evolution of Memory Architecture. Proc. IEEE 2015, 103, 1331–1345. [Google Scholar] [CrossRef]
- Yu, S.; Sun, X.; Peng, X.; Huang, S. Compute-in-memory with emerging nonvolatile-memories: Challenges and prospects. In Proceedings of the Custom Integrated Circuits Conference (CICC), Boston, MA, USA, 22 March 2020. [Google Scholar]
- Lin, P.; Li, C.; Wang, Z.; Li, Y.; Jiang, H.; Song, W.; Rao, M.; Zhuo, Y.; Upadhyay, N.K.; Barnell, M.; et al. Three-dimensional memristor circuits as complex neural networks. Nat. Electron. 2020, 3, 225–232. [Google Scholar] [CrossRef]
- Xiang, Y.C.; Huang, P.; Zhou, Z.; Han, R.Z.; Jiang, Y.N.; Shu, Q.M.; Su, Z.Q.; Liu, Y.B.; Liu, X.Y.; Kang, J.F. Analog Deep Neural Network Based on NOR Flash Computing Array for High Speed/Energy Efficiency Computation. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019. [Google Scholar]
- Wang, T.; Huang, H.; Wang, X.; Guo, X. An artificial olfactory inference system based on memristive devices. InfoMat 2021, 3, 804–813. [Google Scholar] [CrossRef]
- Wang, H.; Yamamoto, N. Using A Partial Differential Equation with Google Mobility Data to Predict COVID-19 in Arizona. Math. Biosci. Eng. 2020, 17, 4891–4904. [Google Scholar] [CrossRef] [PubMed]
- Dumitrescu, F.; McCaskey, J.; Hagen, G.; Jansen, R.; Morris, D.; Papenbrock, T.; Pooser, C.; Dean, J.; Lougovski, P. Cloud quantum computing of an atomic nucleus. Phys. Rev. Lett. 2018, 120, 210501. [Google Scholar] [CrossRef] [PubMed]
- Al Asaad, B.; Erascu, M. A Tool for Fake News Detection. In Proceedings of the International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 20 September 2018. [Google Scholar]
- Zidan, M.A.; Jeong, Y.; Lee, J.; Chen, B.; Huang, S.; Kushner, M.J.; Lu, W.D. A general memristor-based partial differential equation solver. Nat. Electron. 2018, 1, 411–420. [Google Scholar] [CrossRef]
- Gallo, M.L.; Sebastian, A.; Mathis, R.; Manica, M.; Giefers, H.; Tuma, T.; Bekas, C.; Curioni, A.; Eleftheriou, E. Mixed-Precision In-Memory Computing. Nat. Electron. 2018, 1, 246–253. [Google Scholar] [CrossRef]
- Yang, H.; Huang, P.; Zhou, Z.; Zhang, Y.; Han, R.; Liu, X.; Kang, J. Mixed-Precision Partial Differential Equation Solver Design Based on Nonvolatile Memory. IEEE Trans. Electron Devices 2022, 69, 3708–3715. [Google Scholar] [CrossRef]
- Feng, Y.; Zhan, X.; Chen, J. Flash Memory based Computing-In-Memory to Solve Time-dependent Partial Differential Equations. In Proceedings of the IEEE Silicon Nanoelectronics Workshop (SNW), Honolulu, HI, USA, 13–14 June 2020. [Google Scholar]
- Feng, Y.; Chen, B.; Liu, J.; Sun, Z.; Hu, H.; Zhang, J.; Zhan, X.; Chen, J. Design-Technology Co-Optimizations (DTCO) for General-Purpose Computing In-Memory Based on 55nm NOR Flash Technology. In Proceedings of the IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 11–16 December 2021. [Google Scholar]
- Ames, W.F. Numerical Methods for Partial Differential Equations, 3rd ed.; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Fantini, P.; Ghetti, A.; Marinoni, A.; Ghidini, G.; Visconti, A.; Marmiroli, A. Giant Random Telegraph Signals in Nanoscale Floating-Gate Devices. IEEE Trans. Electron Devices 2007, 28, 1114–1116. [Google Scholar] [CrossRef]
- Wang, R.; Guo, S.; Ren, P.; Luo, M.; Zou, J.; Huang, R. Too noisy at the nanoscale?—The rise of random telegraph noise (RTN) in devices and circuits. In Proceedings of the IEEE International Nanoelectronics Conference (INEC), Chengdu, China, 9–11 May 2016. [Google Scholar]
- Spinelli, A.S.; Malavena, G.; Lacaita, A.L.; Monzio, C. Compagnoni. Random Telegraph Noise in 3D NAND Flash Memories. Micromachines 2021, 12, 703. [Google Scholar] [CrossRef] [PubMed]
- Eneyew, T.K.; Awgichew, G.; Haile, E.; Abie, G.D. Second Refinement of Jacobi Iterative Method for Solving Linear System of Equations. IJCSAM 2019, 5, 41–47. [Google Scholar] [CrossRef]
- Gilbarg, D.; Trudinger, N. Elliptic Partial Differential Equations of Second Order; Springer: Berlin/Heidelberg, Germany, 1977; Volume 224. [Google Scholar]
- Chen, P.Y.; Peng, X.; Yu, S. NeuroSim: A circuit-level macro model for benchmarking neuro-inspired architectures in online learning. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 3067–3080. [Google Scholar] [CrossRef]
- Chen, P.Y.; Peng, X.; Yu, S. NeuroSim+: An integrated device-to-algorithm framework for benchmarking synaptic devices and array architectures. In Proceedings of the International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017. [Google Scholar]
- Choi, Y.; Oh, S.; Qian, C. Vertical organic synapse expandable to 3D crossbar array. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kazemi, A.; Rajaei, R.; Ni, K.; Datta, S.; Niemier, M.; Hu, X.S. A Hybrid FeMFET-CMOS Analog Synapse Circuit for Neural Network Training and Inference. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020. [Google Scholar]
- Sun, Z.; Pedretti, G.; Ambrosi, E. Solving matrix equations in one step with cross-point resistive arrays. Proc. Natl. Acad. Sci. USA 2019, 116, 4123–4128. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Botimer, J.; Chou, T.; Zhang, Z. A 1.87-mm 2 56.9-GOPS Accelerator for Solving Partial Differential Equations. IEEE J. Solid-State Circuits 2020, 55, 1709–1718. [Google Scholar] [CrossRef]
- Ensan, S.S.; Ghosh, S. ReLOPE: Resistive RAM-Based Linear First-Order Partial Differential Equation Solver. IEEE Trans. VLSI Syst. 2021, 29, 237–241. [Google Scholar] [CrossRef]



| CIM Device | Power Dissipation | Accuracy | Residual Norm Error | Latency | |
|---|---|---|---|---|---|
| This Work | NOR Flash (55 nm) | ||||
| Gallo [10] | PCM (90 nm) | per device | --- | ||
| Zidan [9] | RRAM | --- | --- | ||
| Chen [25] | SRAM (180 nm) | --- | --- | --- | |
| Feng [13] | NOR Flash (65 nm) | --- | --- | --- | |
| Ensan [26] | RRAM (65 nm) | --- | --- | ||
| Yang [11] | RRAM (22-nm) &CPU/GPU | --- | --- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Feng, Y.; Wu, J.; Sun, Z.; Bai, M.; Wang, C.; Wang, H.; Zhan, X.; Zhang, J.; Liu, J.; et al. An Efficient and Robust Partial Differential Equation Solver by Flash-Based Computing in Memory. Micromachines 2023, 14, 901. https://doi.org/10.3390/mi14050901
Qi Y, Feng Y, Wu J, Sun Z, Bai M, Wang C, Wang H, Zhan X, Zhang J, Liu J, et al. An Efficient and Robust Partial Differential Equation Solver by Flash-Based Computing in Memory. Micromachines. 2023; 14(5):901. https://doi.org/10.3390/mi14050901
Chicago/Turabian StyleQi, Yueran, Yang Feng, Jixuan Wu, Zhaohui Sun, Maoying Bai, Chengcheng Wang, Hai Wang, Xuepeng Zhan, Junyu Zhang, Jing Liu, and et al. 2023. "An Efficient and Robust Partial Differential Equation Solver by Flash-Based Computing in Memory" Micromachines 14, no. 5: 901. https://doi.org/10.3390/mi14050901
APA StyleQi, Y., Feng, Y., Wu, J., Sun, Z., Bai, M., Wang, C., Wang, H., Zhan, X., Zhang, J., Liu, J., & Chen, J. (2023). An Efficient and Robust Partial Differential Equation Solver by Flash-Based Computing in Memory. Micromachines, 14(5), 901. https://doi.org/10.3390/mi14050901






