Stability Compensation Design and Analysis of a Piezoelectric Ceramic Driver with an Emitter Follower Stage
Abstract
:1. Introduction
2. Materials and Methods
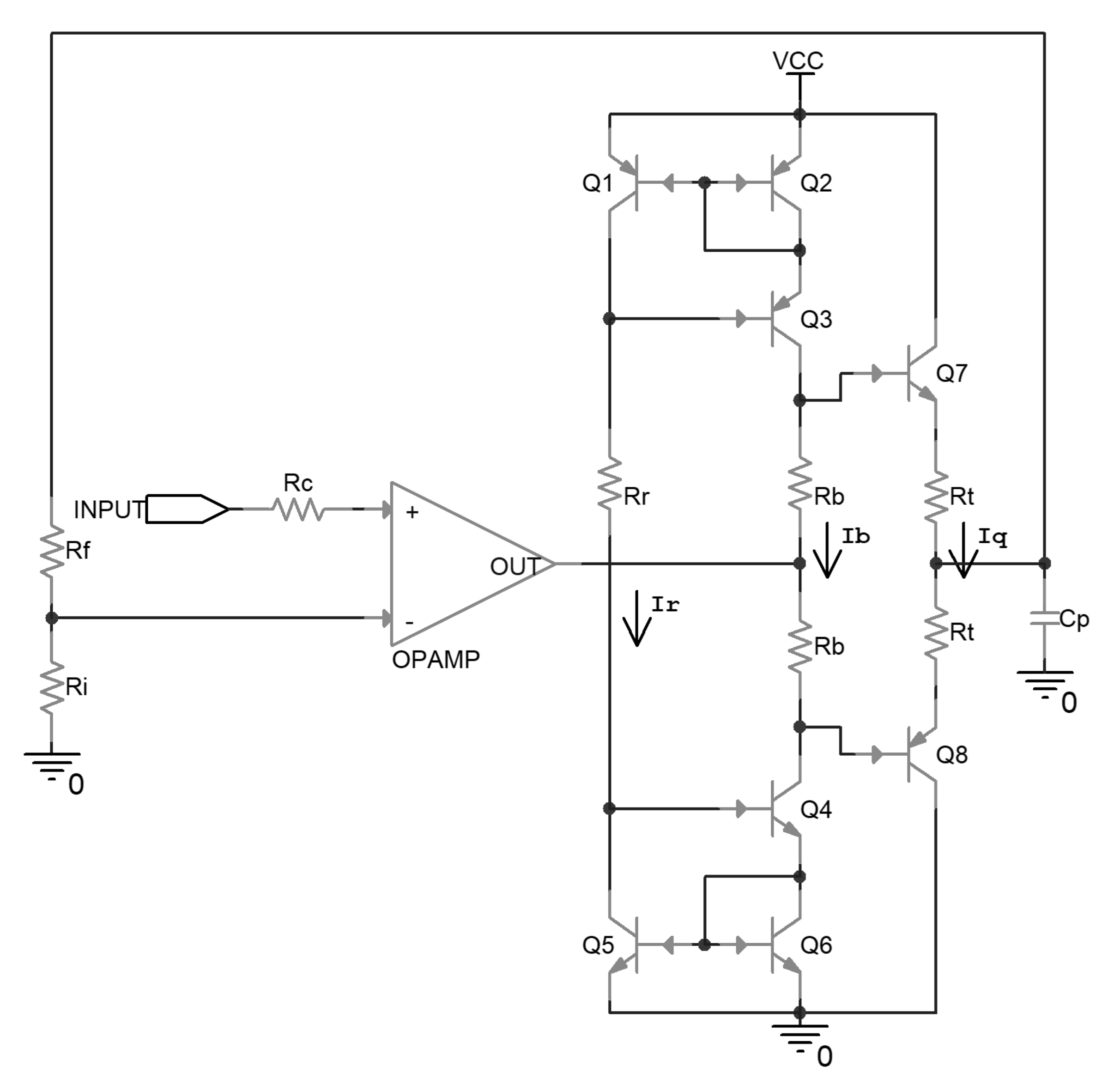
2.1. Piezoelectric Ceramic and Driver Circuit
2.2. Preparation for the Analysis
2.2.1. Determination of the Parameters for the Transistor Model
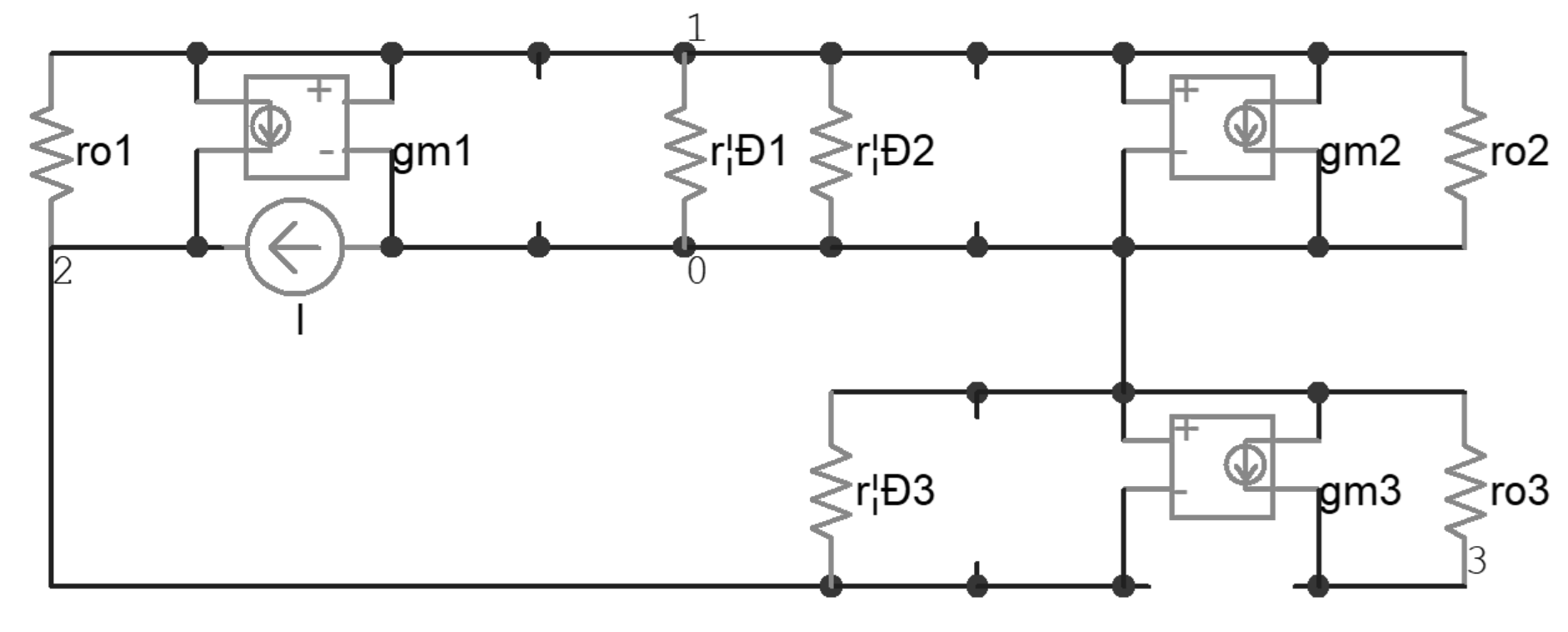
2.2.2. The Effective Impedance of the Current Mirror
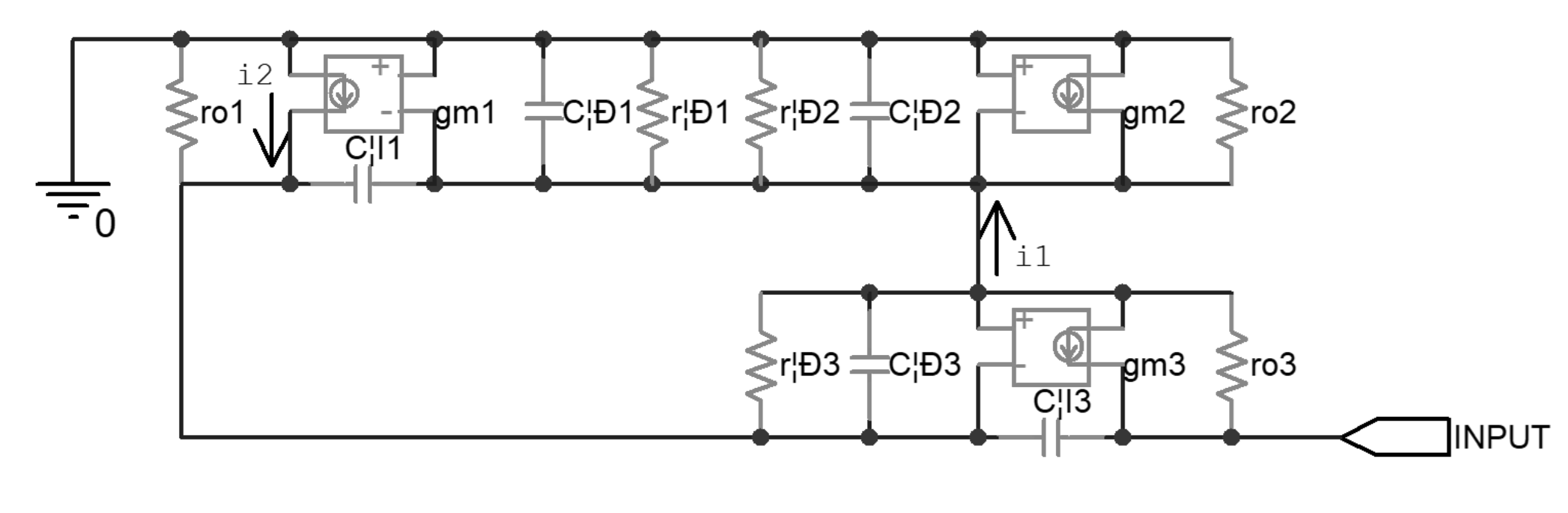
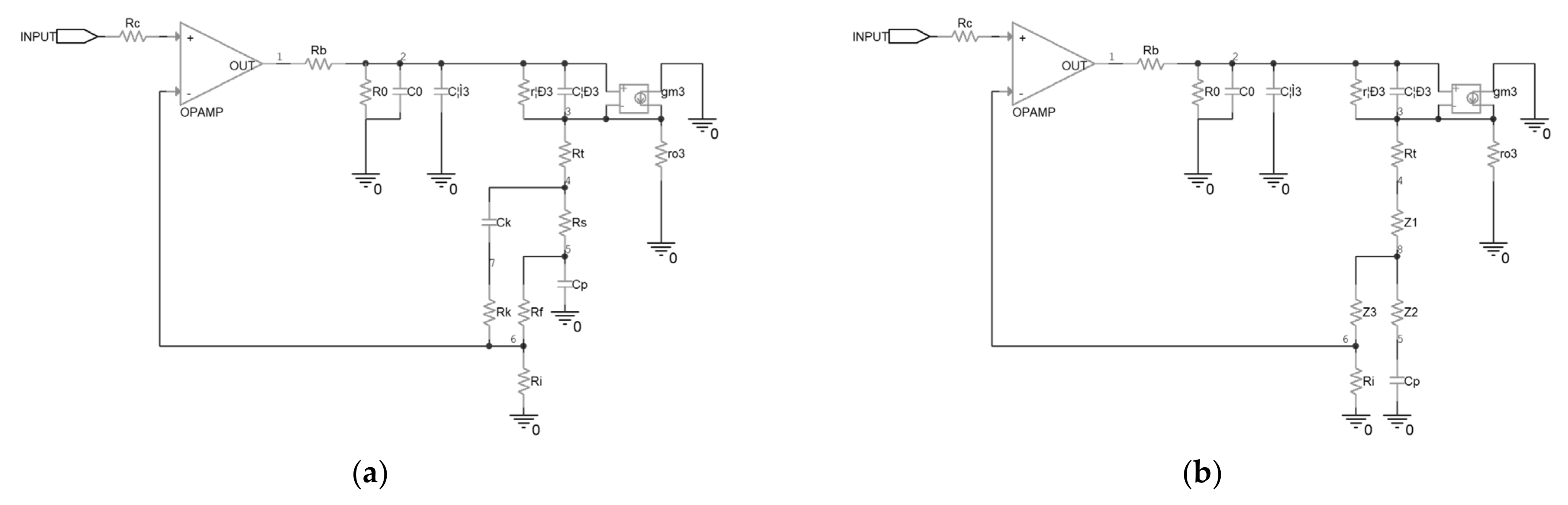
2.3. Analysis of the Uncompensated Driver
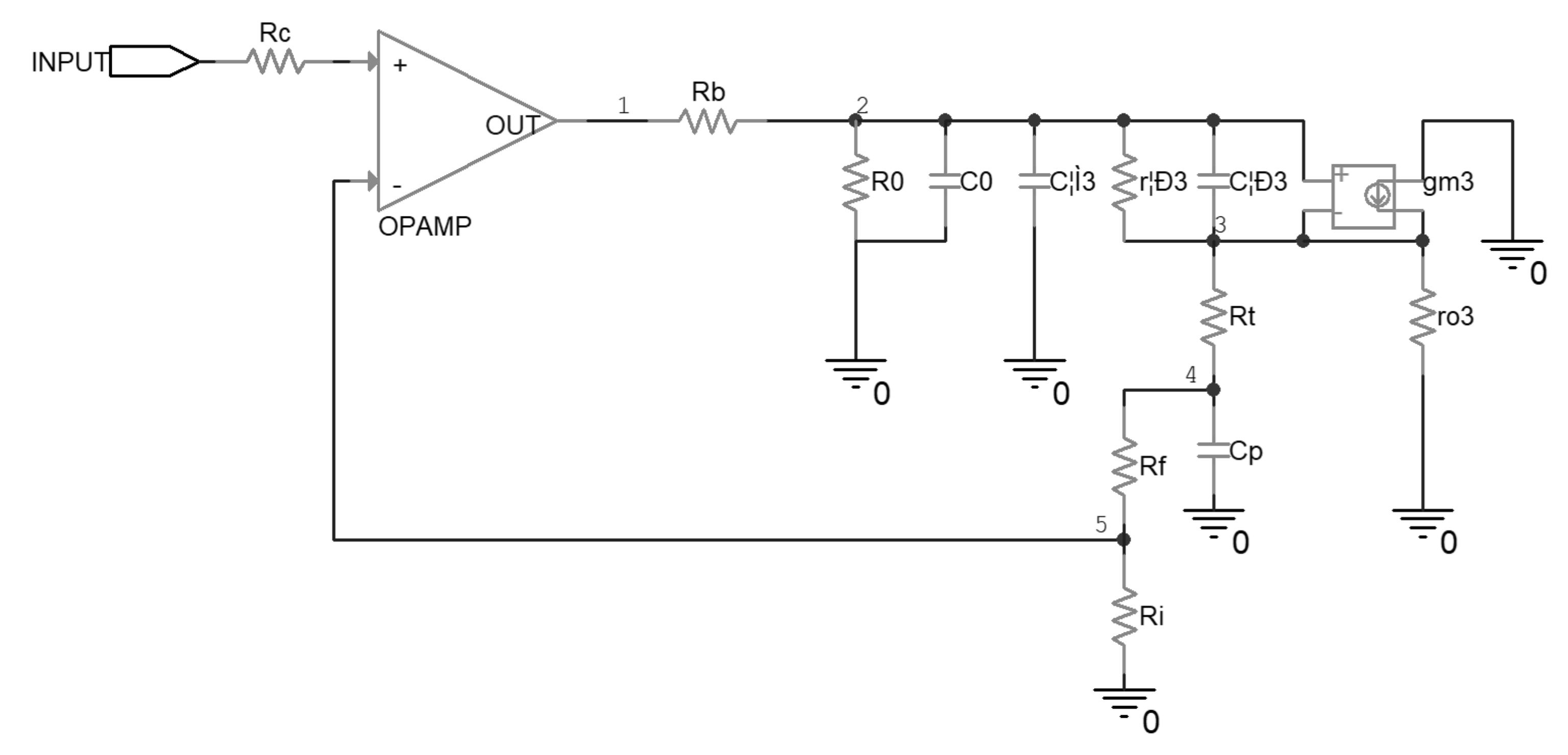
2.4. Design of the Compensated Driver
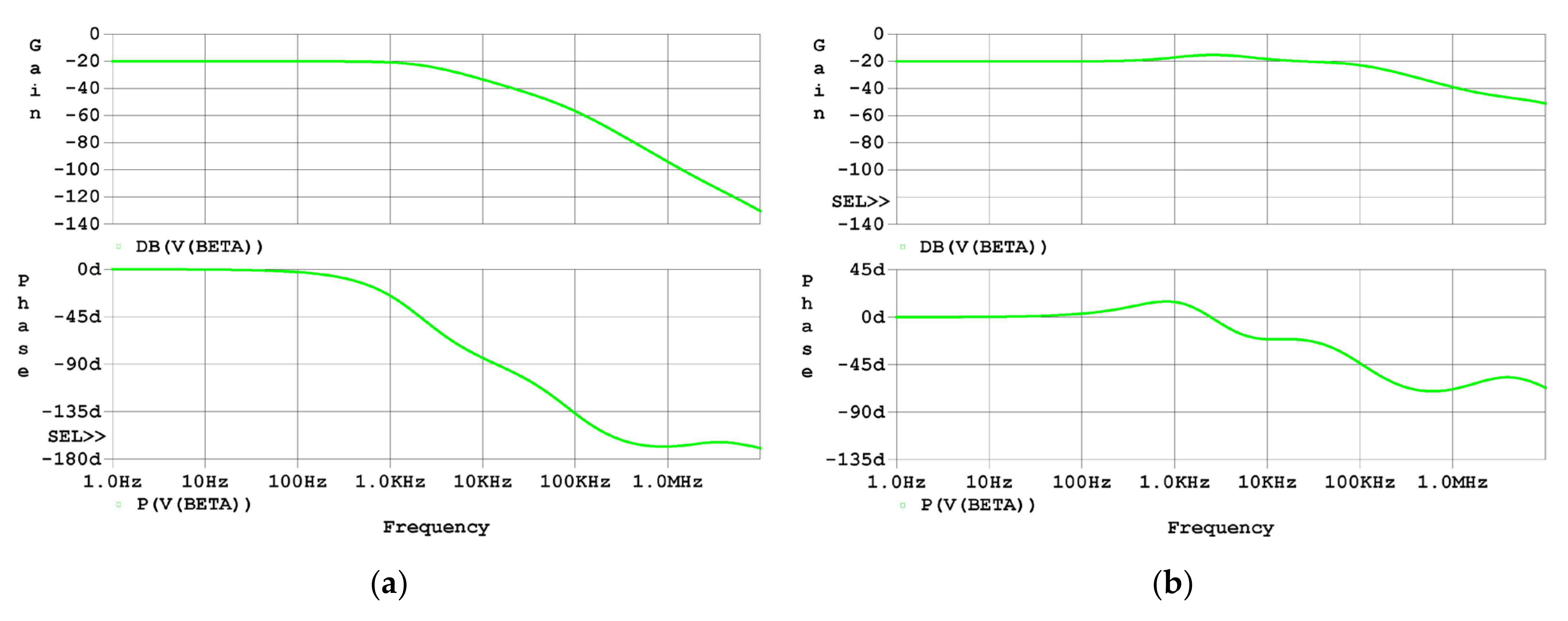
- The one original zero stemming from Cπ stays unchanged and the two original poles stemming from Cp and Cπ change slightly;
- The compensated circuit introduces two zeros stemming from Cp and Ck and one pole stemming from Ck;
- The zeros and poles stemming from Cp and Ck makes the phase shift of β to be 0 degrees at high frequency under proper design;
- The first pole lagging the phase of β in the compensated driver stems from Cπ, and it is at a relatively high frequency. In contrast, the first pole lagging the phase of β in the uncompensated driver stems from Cp, and it is at a relatively low frequency. Thus, the phase margin of the loop gain is increased.
3. Results
3.1. Simulation Results
3.1.1. Frequency Domain Simulation Results
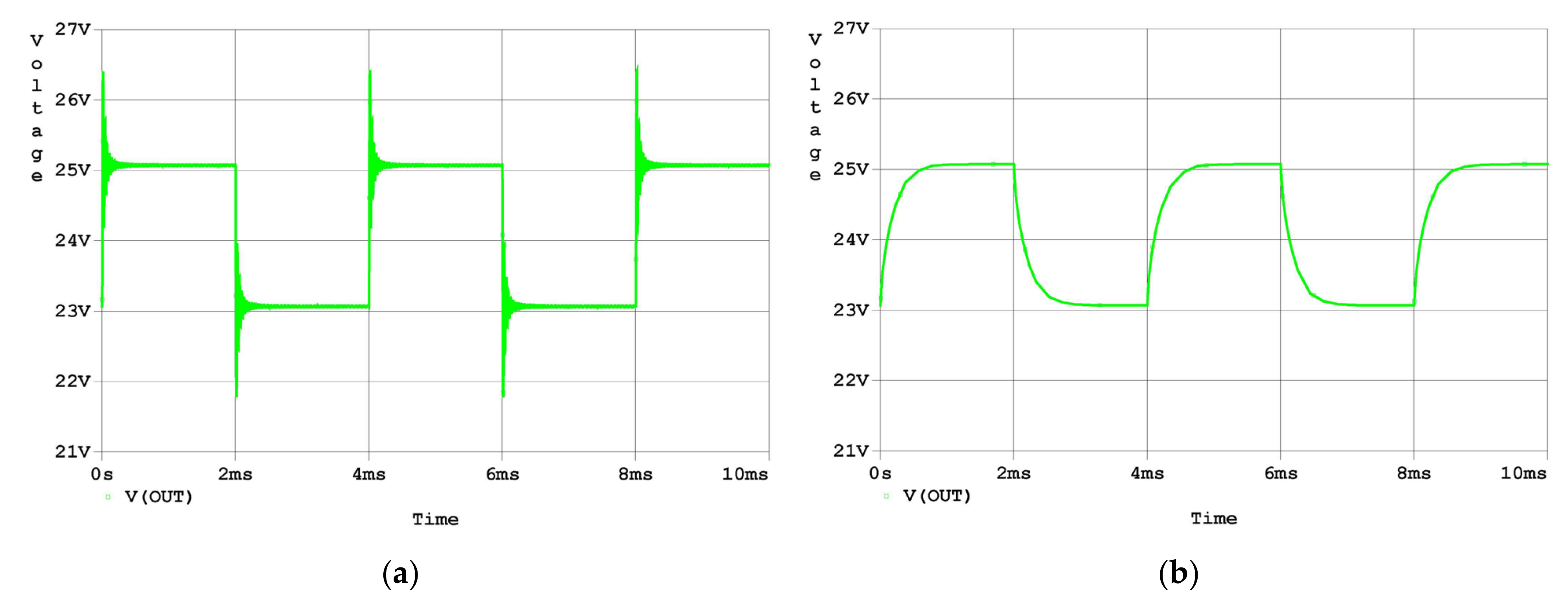
3.1.2. Time-Domain Simulation Results
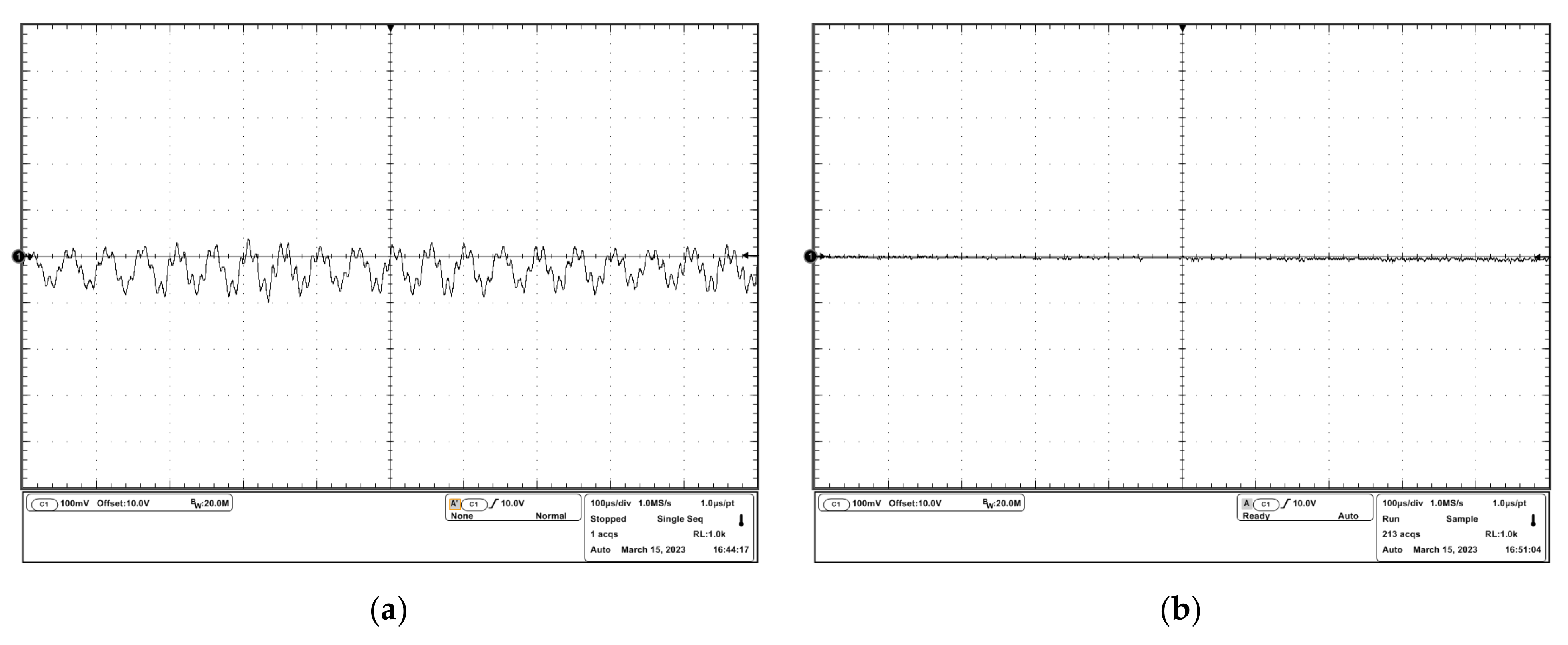
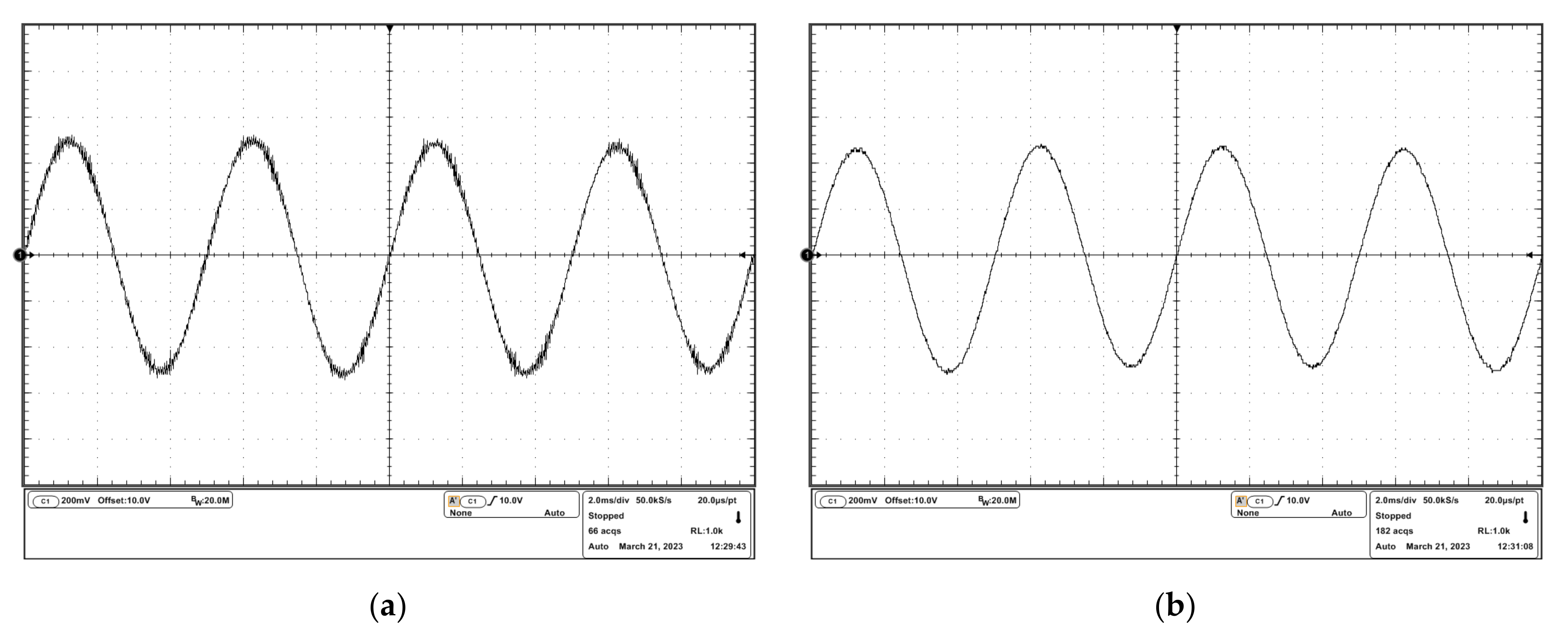
3.2. Experiment Results
3.2.1. Setup of the Experiment
3.2.2. Results of the Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohith, S.; Muralidhara, R.; Navin, K.P.; Kulkarni, S.M.; Adithya, R.U. Development and assessment of large stroke piezo-hydraulic actuator for micro positioning applications. Precis. Eng. 2021, 67, 324–338. [Google Scholar] [CrossRef]
- Zhou, S.; Yan, P. Design and Analysis of a Hybrid Displacement Amplifier Supporting a High-Performance Piezo Jet Dispenser. Micromachines 2023, 14, 322. [Google Scholar] [CrossRef]
- Yasinov, R.; Peled, G.; Feinstein, A.; Karasikov, N. Novel Piezo Motor for a High Precision Motion Axis; SPIE: San Francisco, CA, USA, 2020. [Google Scholar] [CrossRef]
- Jin, H.; Gao, X.; Ren, K.; Liu, J.; Qiao, L.; Liu, M.; Chen, W.; He, Y.; Dong, S.; Xu, Z.; et al. Review on Piezoelectric Actuators Based on High-Performance Piezoelectric Materials. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 3057–3069. [Google Scholar] [CrossRef]
- Jansen, B.; Butler, H.; Filippo, R.D. Active Damping of Dynamical Structures Using Piezo Self Sensing. IFAC-Pap. 2019, 52, 543–548. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Q. Adaptive Sliding Mode Control With Parameter Estimation and Kalman Filter for Precision Motion Control of a Piezo-Driven Microgripper. IEEE Trans. Control Syst. Technol. 2017, 25, 728–735. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, J.; Meng, W.; Zhang, J.; Feng, Q.; Wang, Z.; Hou, Y.; Lu, Q.; Lu, Y. A planar piezoelectric motor of two dimensional XY motions driven by one cross-shaped piezoelectric unit: A new principle. Rev. Sci. Instrum. 2022, 93, 043710. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Zhou, M. Sliding mode control with sigmoid function for the motion tracking control of the piezo-actuated stages. Electron. Lett. 2017, 53, 75–77. [Google Scholar] [CrossRef]
- Zhong, J.; Nishida, R.; Shinshi, T. A digital charge control strategy for reducing the hysteresis in piezoelectric actuators: Analysis, design, and implementation. Precis. Eng. 2021, 67, 370–382. [Google Scholar] [CrossRef]
- Li, P.; Wang, X.; Zhao, L.; Zhang, D.; Guo, K. Dynamic linear modeling, identification and precise control of a walking piezo-actuated stage. Mech. Syst. Signal Process. 2019, 128, 141–152. [Google Scholar] [CrossRef]
- Jalili, H.; Goudarzi, H.; Salarieh, H.; Vossoughi, G. Modeling a multilayer piezo-electric transducer by equivalent electro-mechanical admittance matrix. Sens. Actuators A Phys. 2018, 277, 92–101. [Google Scholar] [CrossRef]
- Ghenna, S.; Bernard, Y.; Daniel, L. Design and experimental analysis of a high force piezoelectric linear motor. Mechatronics 2023, 89, 102928. [Google Scholar] [CrossRef]
- Wei, F.; Wang, X.; Dong, J.; Guo, K.; Sui, Y. Development of a three-degree-of-freedom piezoelectric actuator. Rev. Sci. Instrum. 2023, 94, 025001. [Google Scholar] [CrossRef]
- Massavie, V.; Despesse, G.; Carcouet, S.; Maynard, X. Comparison between Piezoelectric Filter and Passive LC filter in a Class L−Piezo Inverter. Electronics 2022, 11, 3983. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Feng, Y.; Deng, J.; Liu, Y. Development of a novel high bandwidth piezo-hydraulic actuator for a miniature variable swept wing. Int. J. Mech. Sci. 2023, 240, 107926. [Google Scholar] [CrossRef]
- Degefa, T.G.; Wróbel, A.; Płaczek, M. Modelling and Study of the Effect of Geometrical Parameters of Piezoelectric Plate and Stack. Appl. Sci. 2021, 11, 11872. [Google Scholar] [CrossRef]
- Zhou, C.; Yuan, M.; Feng, C.; Ang, W.T. A Modified Prandtl–Ishlinskii Hysteresis Model for Modeling and Compensating Asymmetric Hysteresis of Piezo-Actuated Flexure-Based Systems. Sensors 2022, 22, 8763. [Google Scholar] [CrossRef]
- Yu, Z.; Wu, Y.; Fang, Z.; Sun, H. Modeling and compensation of hysteresis in piezoelectric actuators. Heliyon 2020, 6, e03999. [Google Scholar] [CrossRef]
- Yeh, Y.-L.; Pan, H.-W.; Shen, Y.-H. Model-Free Output-Feedback Sliding-Mode Control Design for Piezo-Actuated Stage. Machines 2023, 11, 152. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, M.; Song, Y.; Zhang, C.; Zhou, M. Hybrid Adaptive Controller Design with Hysteresis Compensator for a Piezo-Actuated Stage. Appl. Sci. 2023, 13, 402. [Google Scholar] [CrossRef]
- Roshandel, E.; Mahmoudi, A.; Kahourzade, S.; Davazdah-Emami, H. DC-DC High-Step-Up Quasi-Resonant Converter to Drive Acoustic Transmitters. Energies 2022, 15, 5745. [Google Scholar] [CrossRef]
- Pai, F.-S.; Hu, H.-L. Driving Circuit Design for Piezo Ceramics Considering Transformer Leakage Inductance. Processes 2023, 11, 247. [Google Scholar] [CrossRef]
- Kobayashi, D.; Kawakatsu, H. High slew rate circuit for high rigidity friction-drive. Jpn. J. Appl. Phys. 2020, 59, SN1008. [Google Scholar] [CrossRef]
- Xu, L.; Li, H.; Li, P.; Ge, C. A High-Voltage and Low-Noise Power Amplifier for Driving Piezoelectric Stack Actuators. Sensors 2020, 20, 6528. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Li, C.; Xia, F.; Zhu, Y.; Zhao, J.; Youcef-Toumi, K. Charge Controller With Decoupled and Self-Compensating Configurations for Linear Operation of Piezoelectric Actuators in a Wide Bandwidth. IEEE Trans. Ind. Electron. 2019, 66, 5392–5402. [Google Scholar] [CrossRef]
- Bazghaleh, M.; Grainger, S.; Cazzolato, B.; Lu, T.; Oskouei, R. Implementation and analysis of an innovative digital charge amplifier for hysteresis reduction in piezoelectric stack actuators. Rev. Sci. Instrum. 2014, 85, 45005. [Google Scholar] [CrossRef] [PubMed]
- Jin, T.; Peng, Y.; Xing, Z.; LEI, L. A Charge Controller for Synchronous Linear Operation of Multiple Piezoelectric Actuators. IEEE Access 2019, 7, 90741–90749. [Google Scholar] [CrossRef]
- Gray, P.R.; Hurst, P.J.; Lewis, S.H.; Meyer, R.G. Analysis and Design of Analog Integrated Circuits, 4th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 517–522. [Google Scholar]
- DeCarlo, R.A.; Lin, P.M. Linear Circuit Analysis: Time Domain, Phasor, and Laplace Transform Approached, 2nd ed.; Oxford University Press: New York, NY, USA, 2001; pp. 111–116. [Google Scholar]
- Franco, S. Design with Operational Amplifiers and Analog Integrated Circuits, 3rd ed.; McGraw-Hill Higher Education: New York, NY, USA, 2002; pp. 348–355. [Google Scholar]
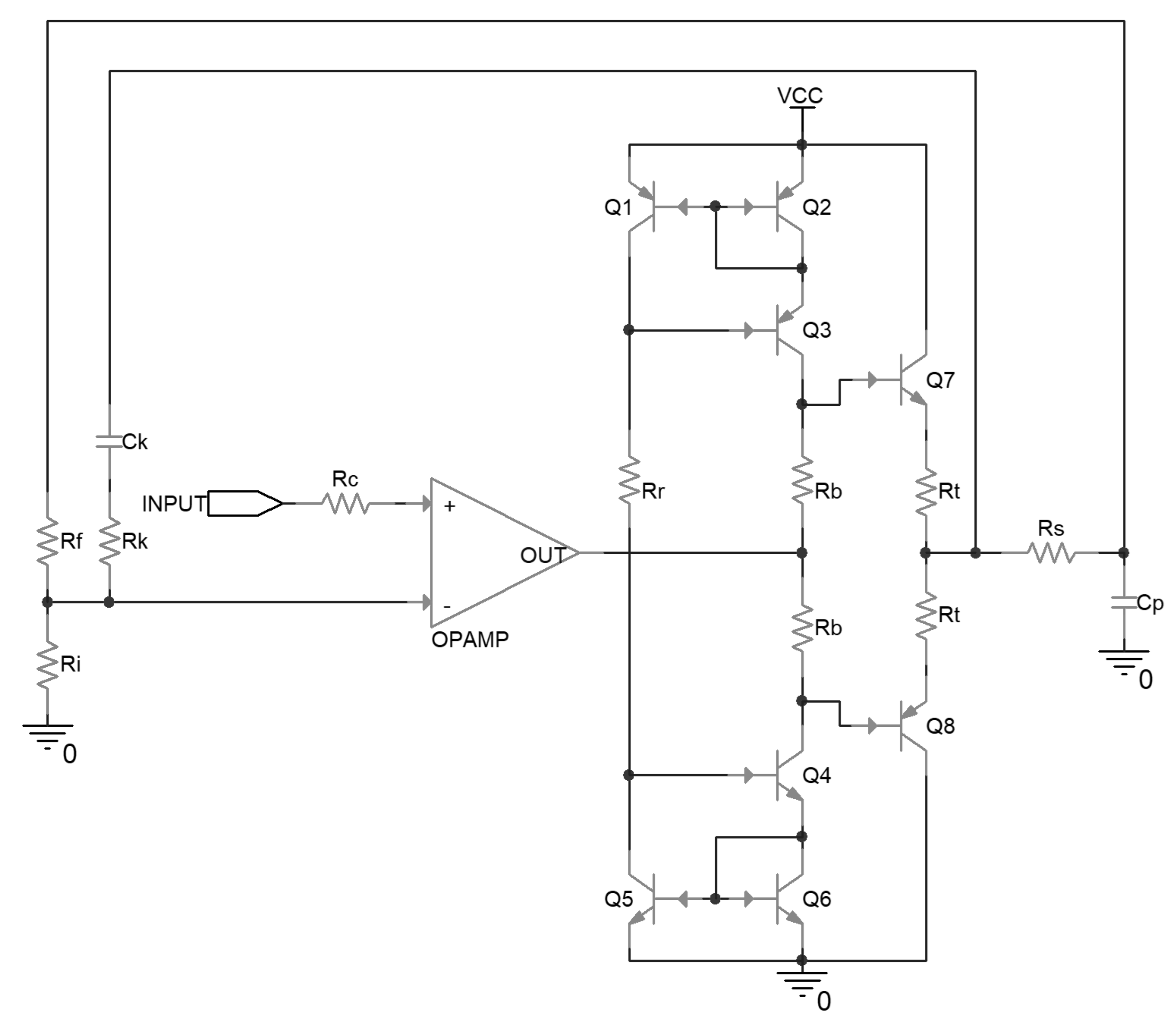



| Dimensions | Nominal Displacement | Blocking Force | Capacitance | Resonant Frequency |
|---|---|---|---|---|
| 7 mm × 7 mm × 18 mm | 15 μm | 1750 N | 3.1 μF | 70 kHz |
| Component | Value |
|---|---|
| OPAMP | OPA547 |
| Rf | 102 kΩ |
| Ri | 11.3 kΩ |
| Rc | 10 kΩ |
| Q1 Q2 Q3 | BC856 |
| Q4 Q5 Q6 | BC846 |
| Rr | 90.9 kΩ |
| Rb | 1 kΩ |
| Q7 | 2SCR586J |
| Q8 | 2SAR586J |
| Rt | 1 Ω |
| Cp | P-887.51 |
| Component | rπ | Cπ | gm | Cμ | ro |
|---|---|---|---|---|---|
| BC856 | 13.0 kΩ | 24 pF | 19.2 mA/V | 14 pF | 27.4 kΩ |
| BC846 | 13.0 kΩ | 8 pF | 19.2 mA/V | 4 pF | 20.0 kΩ |
| 2SCR586J | 13.2 kΩ | 1.3 nF | 18.9 mA/V | 188 pF | 321 kΩ |
| 2SAR586J | 13.2 kΩ | 1.3 nF | 18.9 mA/V | 337 pF | 63 kΩ |
| τμ1 | τπ1 | τπ2 | τπ3 | τμ3 |
|---|---|---|---|---|
| 147 ns | 744 ps | 744 ps | 252 ns | 79 μs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zheng, N.; Wei, F.; Zhou, Y.; Yang, H. Stability Compensation Design and Analysis of a Piezoelectric Ceramic Driver with an Emitter Follower Stage. Micromachines 2023, 14, 914. https://doi.org/10.3390/mi14050914
Wang X, Zheng N, Wei F, Zhou Y, Yang H. Stability Compensation Design and Analysis of a Piezoelectric Ceramic Driver with an Emitter Follower Stage. Micromachines. 2023; 14(5):914. https://doi.org/10.3390/mi14050914
Chicago/Turabian StyleWang, Xueliang, Nan Zheng, Fenglong Wei, Yue Zhou, and Huaijiang Yang. 2023. "Stability Compensation Design and Analysis of a Piezoelectric Ceramic Driver with an Emitter Follower Stage" Micromachines 14, no. 5: 914. https://doi.org/10.3390/mi14050914
APA StyleWang, X., Zheng, N., Wei, F., Zhou, Y., & Yang, H. (2023). Stability Compensation Design and Analysis of a Piezoelectric Ceramic Driver with an Emitter Follower Stage. Micromachines, 14(5), 914. https://doi.org/10.3390/mi14050914





