Role and Effect of Meso-Structuring Surfactants on Properties and Formation Mechanism of Microfluidic-Enabled Mesoporous Silica Microspheres
Abstract
1. Introduction
2. Material and Methods
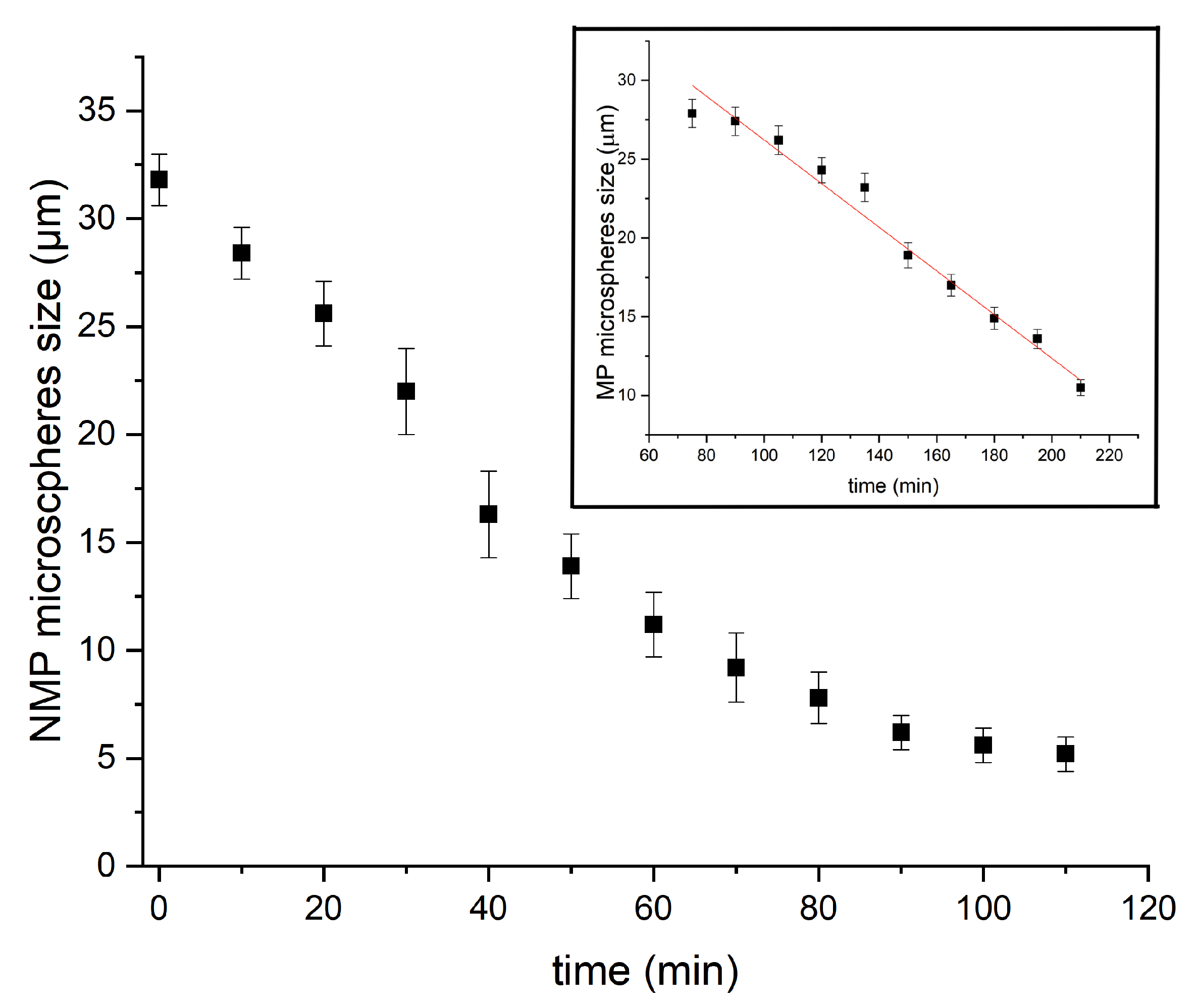
Collection and Condensation of Silica Precursor Droplets
3. Results and Discussion
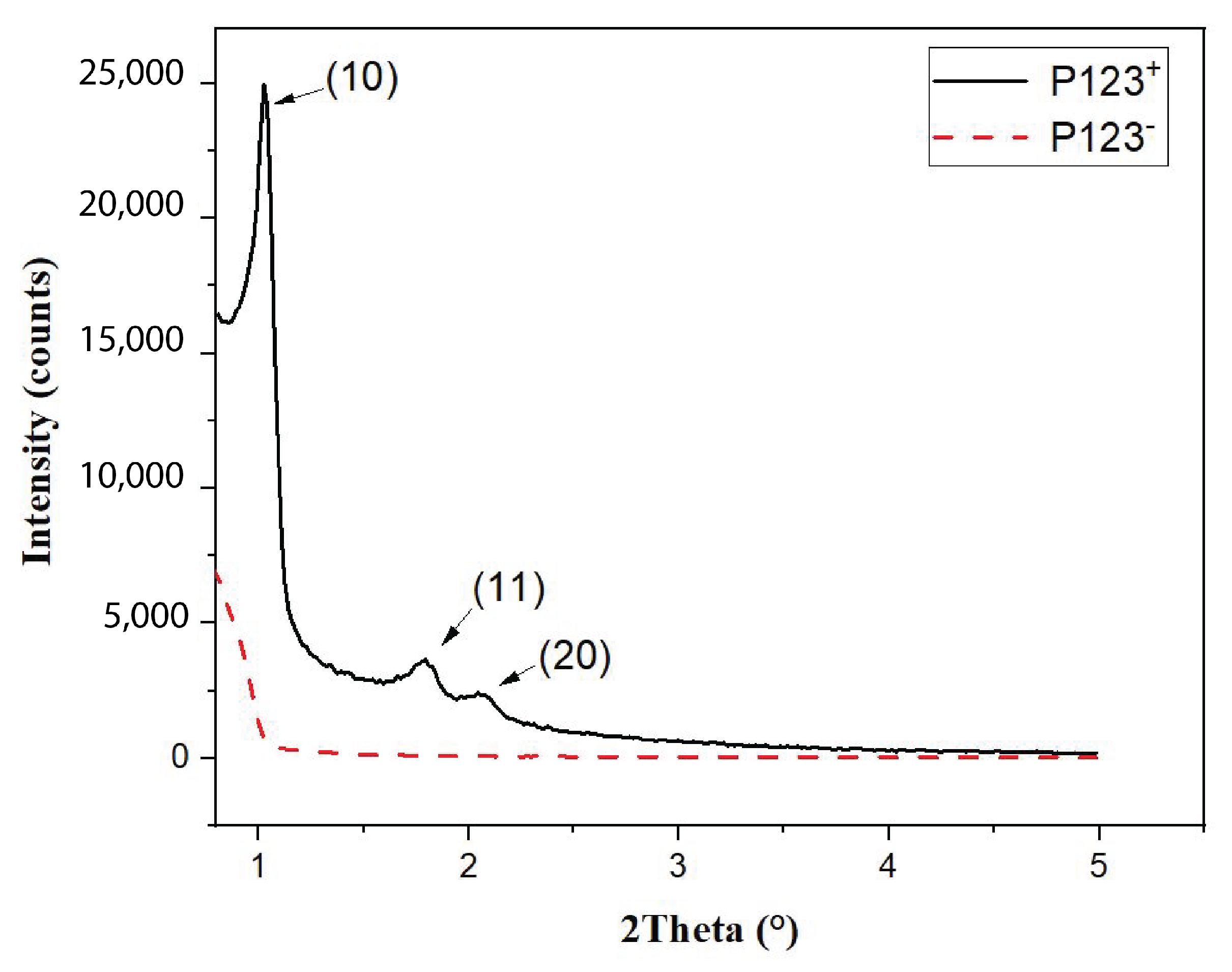
3.1. Structural Characterization of Mesoporous and Non-Mesoporous Silica Microparticles
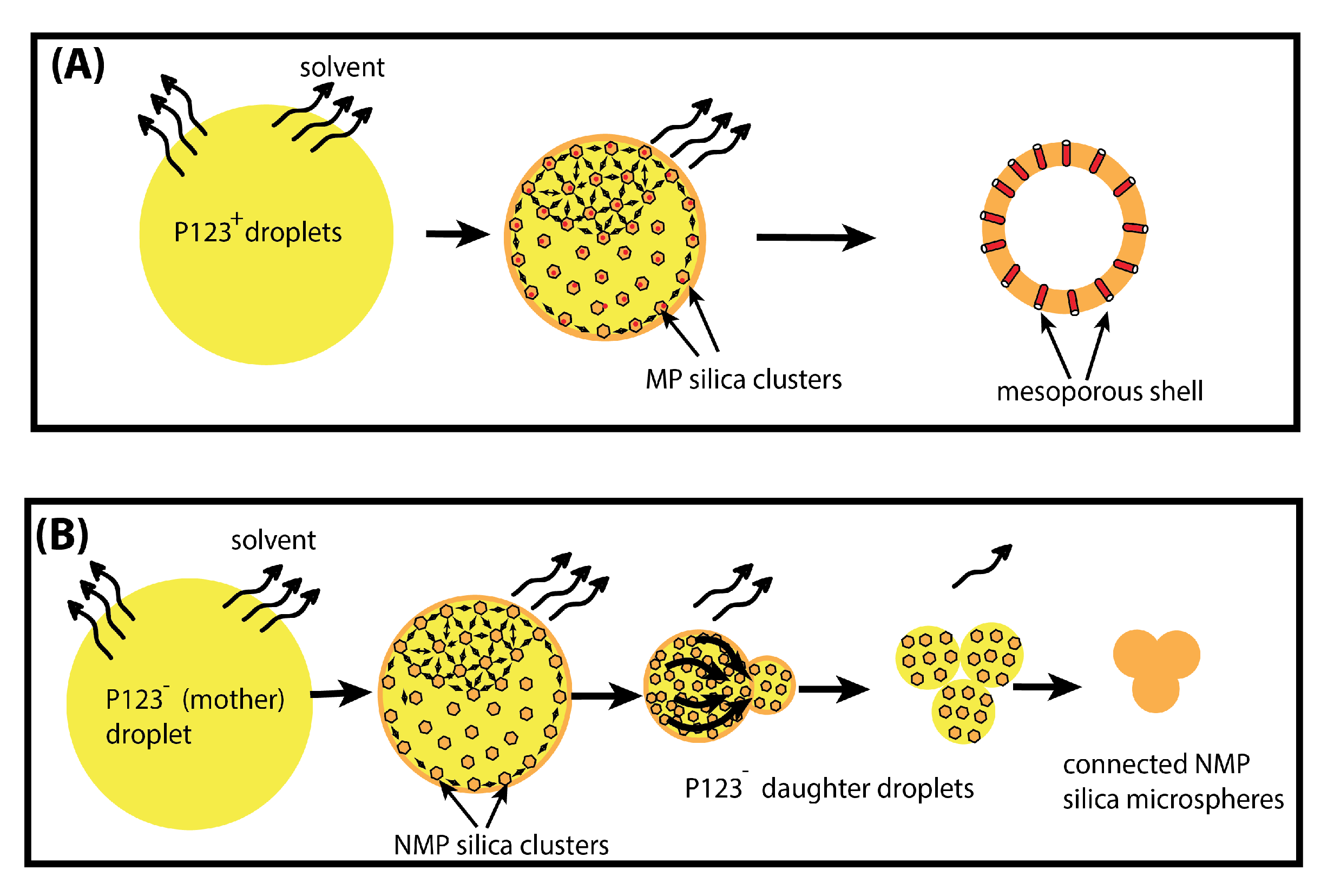
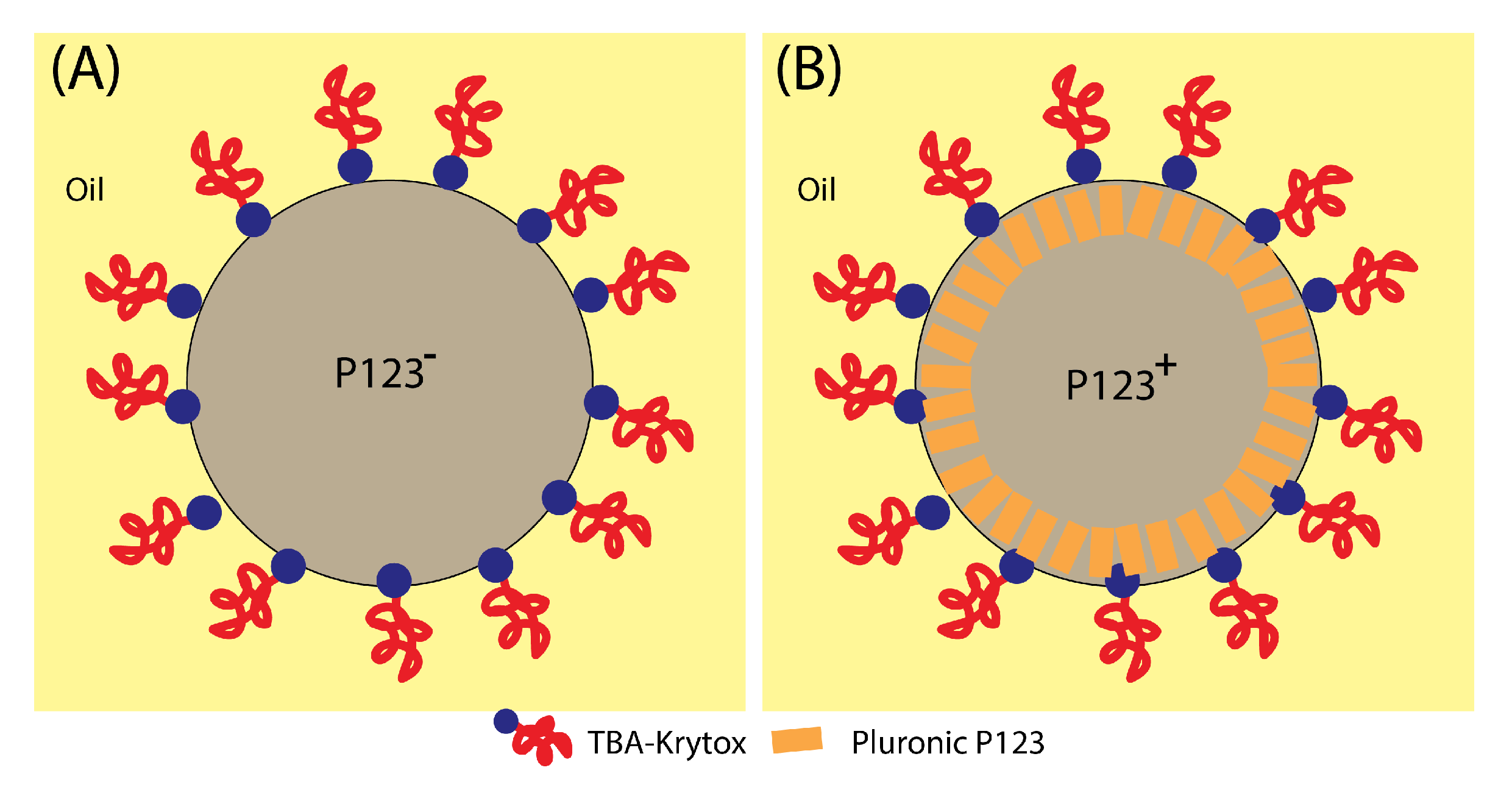
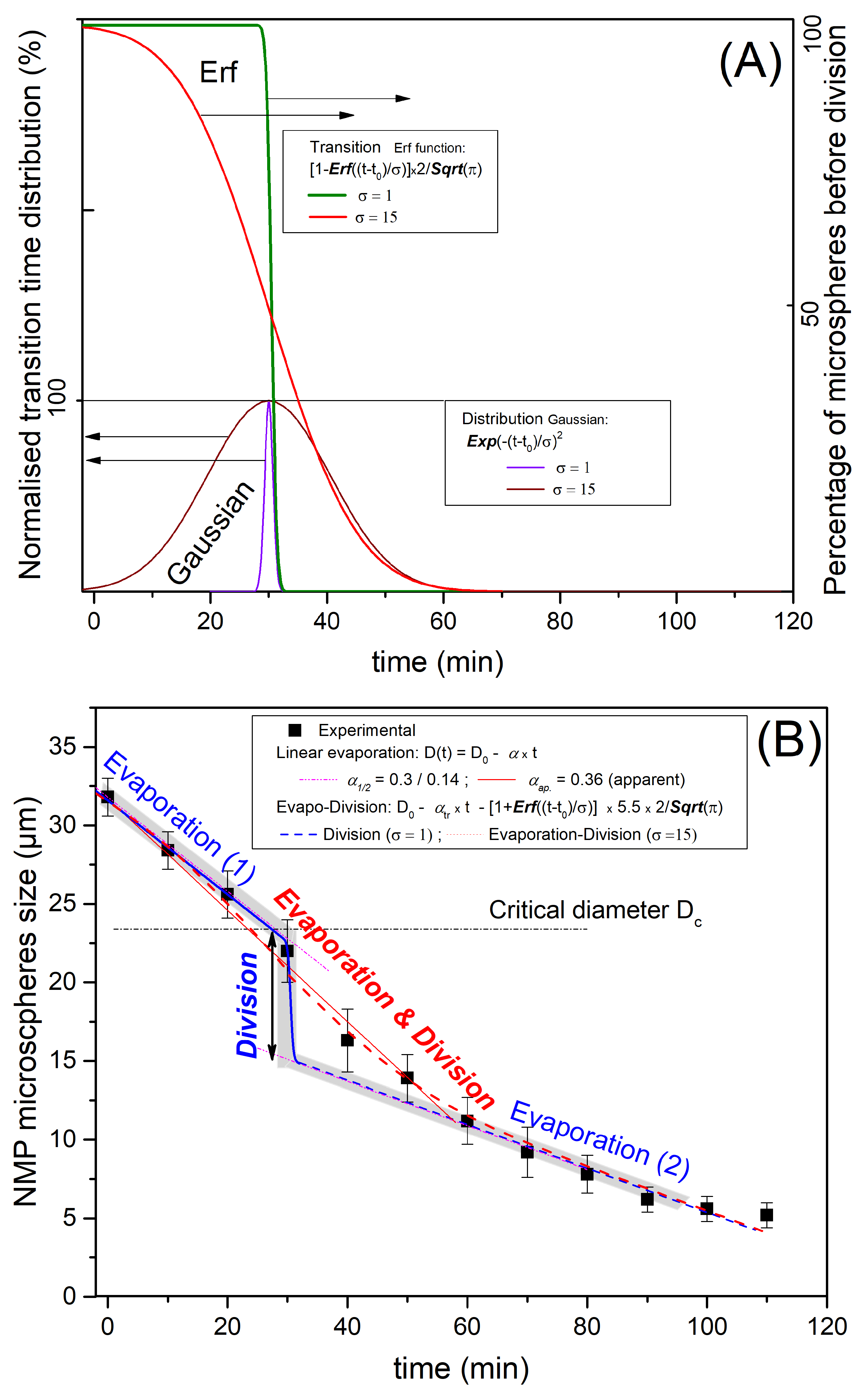
3.2. Suggested Mechanisms for the Formation of Mesoporous and Non-Mesoporous Silica Microspheres
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Slowing, I.I.; Vivero-Escoto, J.L.; Wu, C.W.; Lin, V.S.Y. Mesoporous silica nanoparticles as controlled release drug delivery and gene transfection carriers. Adv. Drug Deliv. Rev. 2008, 60, 1278–1288. [Google Scholar] [CrossRef] [PubMed]
- Radin, S.; Chen, T.; Ducheyne, P. The controlled release of drugs from emulsified, sol gel processed silica microspheres. Biomaterials 2009, 30, 850–858. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Shi, J.; Shen, W.; Dong, X.; Feng, J.; Ruan, M.; Li, Y. Stimuli-Responsive Controlled Drug Release from a Hollow Mesoporous Silica Sphere/Polyelectrolyte Multilayer Core–Shell Structure. Angew. Chem. Int. Ed. 2005, 44, 5083–5087. [Google Scholar] [CrossRef] [PubMed]
- De Vos, D.E.; Dams, M.; Sels, B.F.; Jacobs, P.A. Ordered mesoporous and microporous molecular sieves functionalized with transition metal complexes as catalysts for selective organic transformations. Chem. Rev. 2002, 102, 3615–3640. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Nakamura, T.; Ishi, M.; Yano, M. Reversible control of light reflection of a colloidal crystal film fabricated from monodisperse mesoporous silica spheres. Langmuir 2006, 22, 2444–2446. [Google Scholar] [CrossRef]
- Hossain, K.M.Z.; Patel, U.; Ahmed, I. Development of microspheres for biomedical applications: A review. Prog. Biomater. 2015, 4, 1–19. [Google Scholar] [CrossRef]
- Du, X.; He, J. Spherical silica micro/nanomaterials with hierarchical structures: Synthesis and applications. Nanoscale 2011, 3, 3984–4002. [Google Scholar] [CrossRef]
- Andersson, N.; Kronberg, B.; Corkery, R.; Alberius, P. Combined Emulsion and Solvent Evaporation (ESE) Synthesis Route to Well-Ordered Mesoporous Materials. Langmuir 2007, 23, 1459–1464. [Google Scholar] [CrossRef]
- Olivieri, F.; Castaldo, R.; Cocca, M.; Gentile, G.; Lavorgna, M. Mesoporous silica nanoparticles as carriers of active agents for smart anticorrosive organic coatings: A critical review. Nanoscale 2021, 13, 9091–9111. [Google Scholar] [CrossRef]
- Popat, A.; Hartono, S.B.; Stahr, F.; Liu, J.; Qiao, S.Z.; Qing (Max) Lu, G. Mesoporous silica nanoparticles for bioadsorption, enzyme immobilisation, and delivery carriers. Nanoscale 2011, 3, 2801–2818. [Google Scholar] [CrossRef]
- Stöber, W.; Fink, A.; Bohn, E. Dynamic Pattern Formation in a Vesicle-Generating Microfluidic Device. J. Colloid Interface Sci. 1968, 26, 62–69. [Google Scholar] [CrossRef]
- Lu, Y.; Fan, H.; Stump, A.; Ward, T.L.; Rieker, T.; Brinker, C.J. Aerosol-assisted self-assembly of mesostructured spherical nanoparticles. Nature 1999, 398, 223–226. [Google Scholar] [CrossRef]
- Bchellaoui, N.; Hayat, Z.; Mami, M.; Dorbez-Sridi, R.; El Abed, A.I. Microfluidic-assisted formation of highly monodisperse and mesoporous silica soft microcapsules. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Carroll, N.J.; Rathod, S.B.; Derbins, E.; Mendez, S.; Weitz, D.A.; Petsev, D.N. Droplet-Based Microfluidics for Emulsion and Solvent Evaporation Synthesis of Monodisperse Mesoporous Silica Microspheres. Langmuir 2008, 24, 658–661. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.; Yoo, Y.; Cheng, Z.; Jeong, H.K. Generation of Monodisperse Mesoporous Silica Microspheres with Controllable Size and Surface Morphology in a Microfluidic Device. Adv. Funct. Mater. 2008, 18, 4014–4021. [Google Scholar] [CrossRef]
- Chokkalingam, V.; Weidenhof, B.; Krämer, M.; Herminghaus, S.; Seemann, R.; Maier, W.F. Template-free Preparation of Mesoporous Silica Spheres through Optimized Microfluidics. Chem. Phys. Chem. 2010, 11, 2091–2095. [Google Scholar] [CrossRef]
- Lee, T.Y.; Choi, T.M.; Shim, T.S.; Frijns, R.A.; Kim, S.H. Microfluidic production of multiple emulsions and functional microcapsules. Lab A Chip 2016, 16, 3415–3440. [Google Scholar] [CrossRef]
- Kim, J.W.; Han, S.H.; Choi, Y.H.; Hamonangan, W.M.; Oh, Y.; Kim, S.H. Recent advances in the microfluidic production of functional microcapsules by multiple-emulsion templating. Lab Chip 2022, 22, 2259–2291. [Google Scholar] [CrossRef]
- Hao, N.; Nie, Y.; Zhang, J.X. Microfluidics for silica biomaterials synthesis: Opportunities and challenges. Biomater. Sci. 2019, 7, 2218–2240. [Google Scholar] [CrossRef]
- Kruk, M.; Jaroniec, M.; Sayari, A. Adsorption study of surface and structural properties of MCM-41 materials of different pore sizes. J. Phys. Chem. B 1997, 101, 583–589. [Google Scholar] [CrossRef]
- Duffy, D.C.; Schueller, O.J.; Brittain, S.T.; Whitesides, G.M. Rapid prototyping of microfluidic switches in poly (dimethyl siloxane) and their actuation by electro-osmotic flow. J. Micromech. Microeng. 1999, 9, 211. [Google Scholar] [CrossRef]
- Eggleton, C.D.; Tsai, T.M.; Stebe, K.J. Tip Streaming from a Drop in the Presence of Surfactants. Phys. Rev. Lett. 2001, 87, 048302. [Google Scholar] [CrossRef]
- Baret, J.C. Surfactants in droplet-based microfluidics. Lab A Chip 2012, 12, 422–433. [Google Scholar] [CrossRef] [PubMed]
- Sinha, P.; Datar, A.; Jeong, C.; Deng, X.; Chung, Y.G.; Lin, L.C. Surface area determination of porous materials using the Brunauer–Emmett–Teller (BET) method: Limitations and improvements. J. Phys. Chem. C 2019, 123, 20195–20209. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Y.; Khan, N.; Zhu, C.; Gao, Y. Effects of the Surfactant, Polymer, and Crude Oil Properties on the Formation and Stabilization of Oil-Based Foam Liquid Films: Insights from the Microscale. J. Mol. Liq. 2023, 373, 121194. [Google Scholar] [CrossRef]





| (m2/g) | (cm3/g) | (nm) | |
|---|---|---|---|
| MP | 514 | 0.76 | 5.9 |
| NMP | 80 | 0.27 | 13.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bchellaoui, N.; Xu, Q.; Zhang, X.; Bendeif, E.-E.; Bennacer, R.; El Abed, A.I. Role and Effect of Meso-Structuring Surfactants on Properties and Formation Mechanism of Microfluidic-Enabled Mesoporous Silica Microspheres. Micromachines 2023, 14, 936. https://doi.org/10.3390/mi14050936
Bchellaoui N, Xu Q, Zhang X, Bendeif E-E, Bennacer R, El Abed AI. Role and Effect of Meso-Structuring Surfactants on Properties and Formation Mechanism of Microfluidic-Enabled Mesoporous Silica Microspheres. Micromachines. 2023; 14(5):936. https://doi.org/10.3390/mi14050936
Chicago/Turabian StyleBchellaoui, Nizar, Qisheng Xu, Xuming Zhang, El-Eulmi Bendeif, Rachid Bennacer, and Abdel I. El Abed. 2023. "Role and Effect of Meso-Structuring Surfactants on Properties and Formation Mechanism of Microfluidic-Enabled Mesoporous Silica Microspheres" Micromachines 14, no. 5: 936. https://doi.org/10.3390/mi14050936
APA StyleBchellaoui, N., Xu, Q., Zhang, X., Bendeif, E.-E., Bennacer, R., & El Abed, A. I. (2023). Role and Effect of Meso-Structuring Surfactants on Properties and Formation Mechanism of Microfluidic-Enabled Mesoporous Silica Microspheres. Micromachines, 14(5), 936. https://doi.org/10.3390/mi14050936








