Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives
Abstract
:1. Introduction
2. Methods
2.1. Theoretical Background
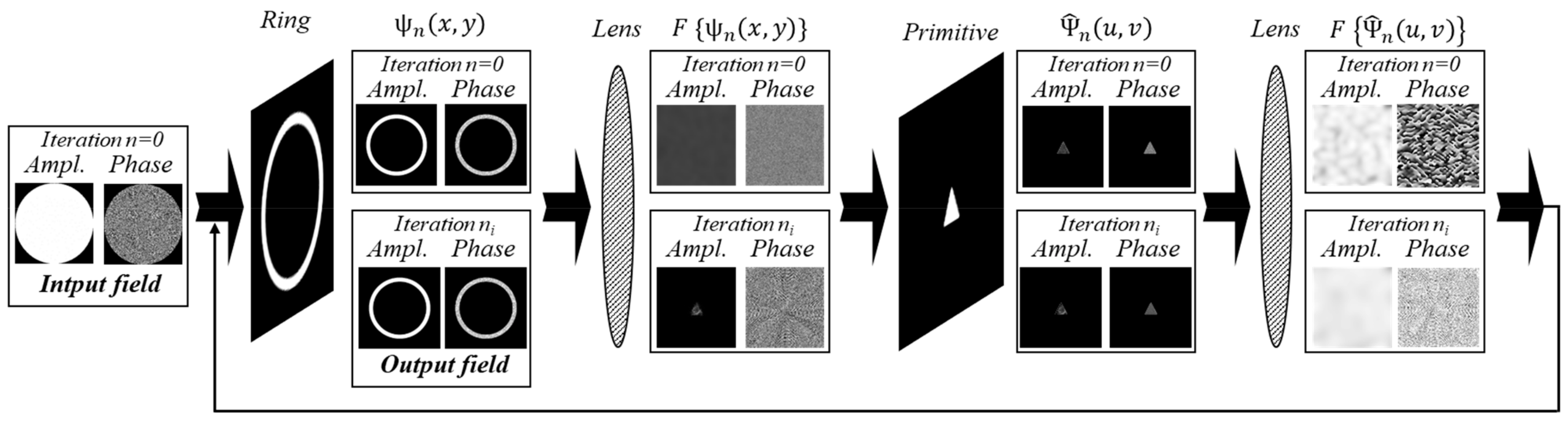
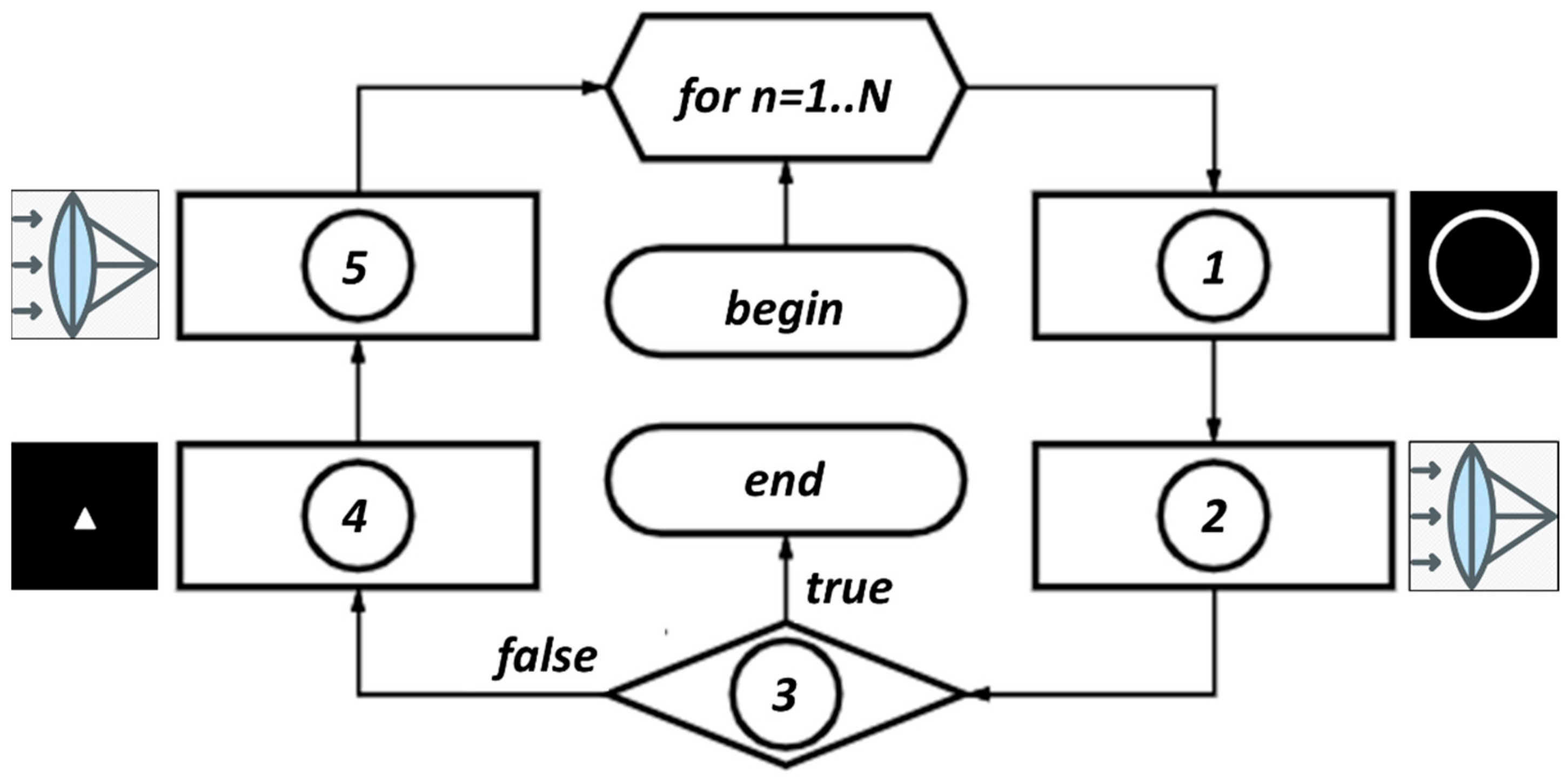
2.2. Iterative Algorithm
3. Calculation Results
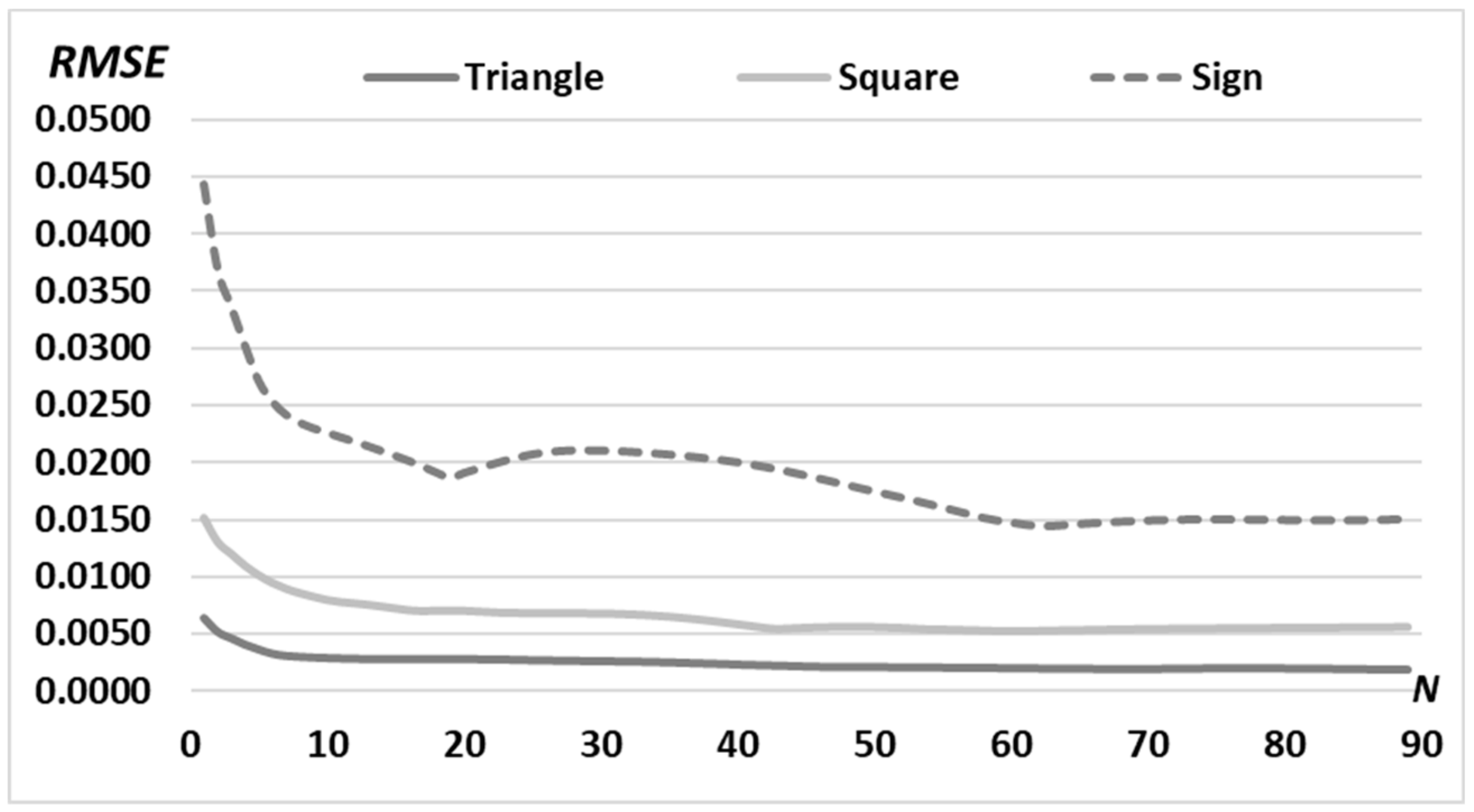
3.1. Simple Primitives
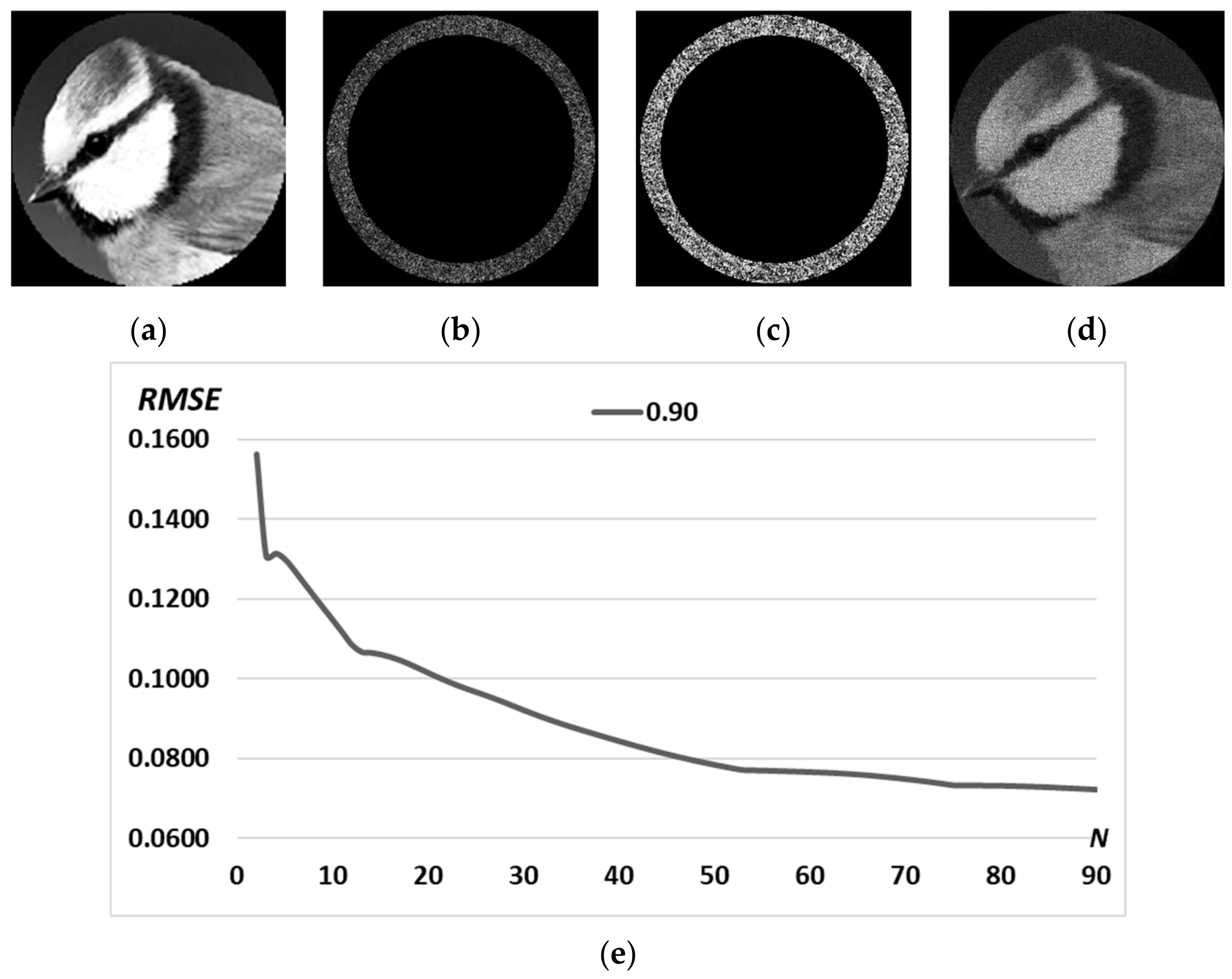
3.2. Complex Patterns
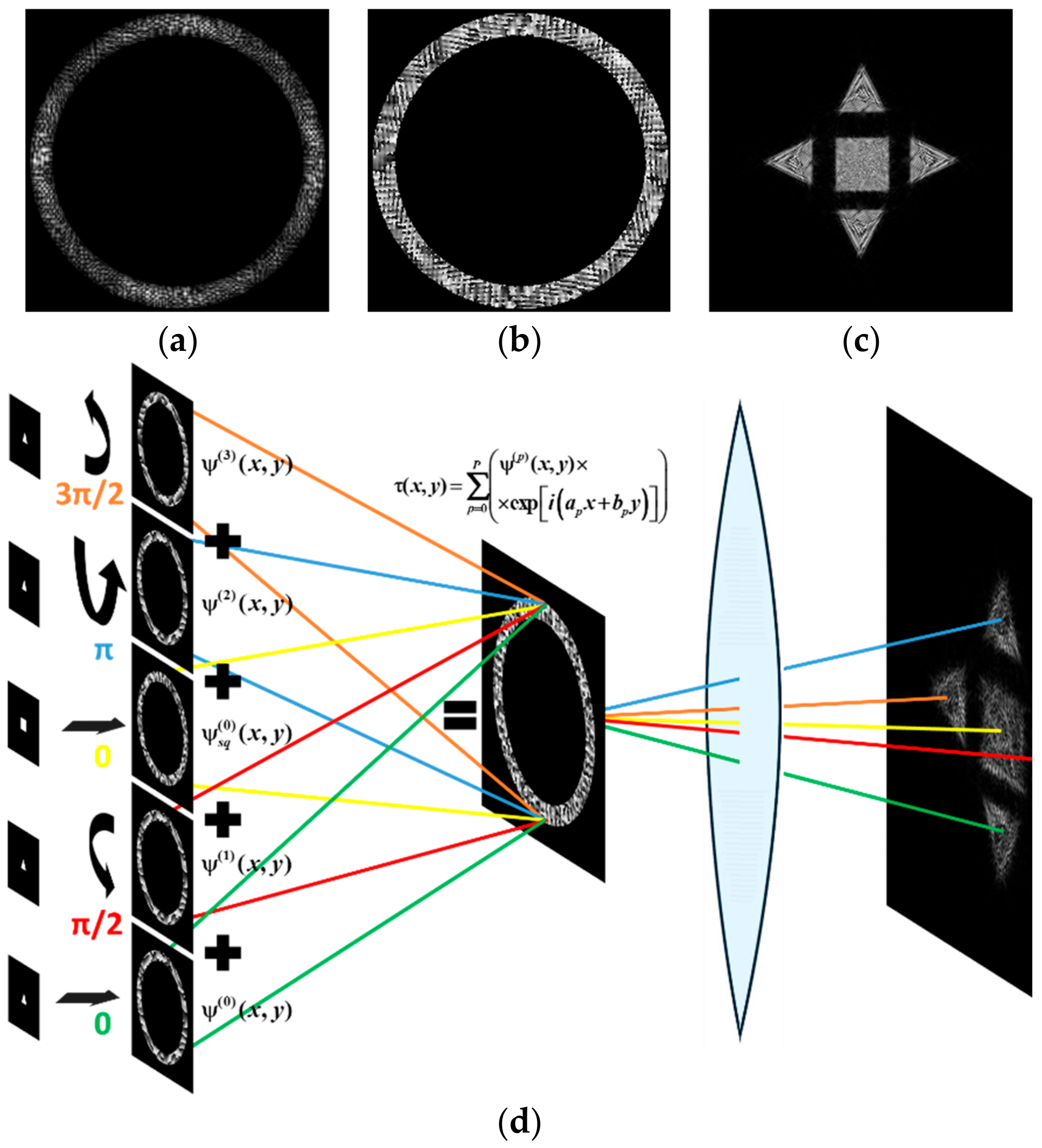
3.3. Superposition of Simple Primitives
4. Simulation and Experimental Results
4.1. Diffraction-Free Properties
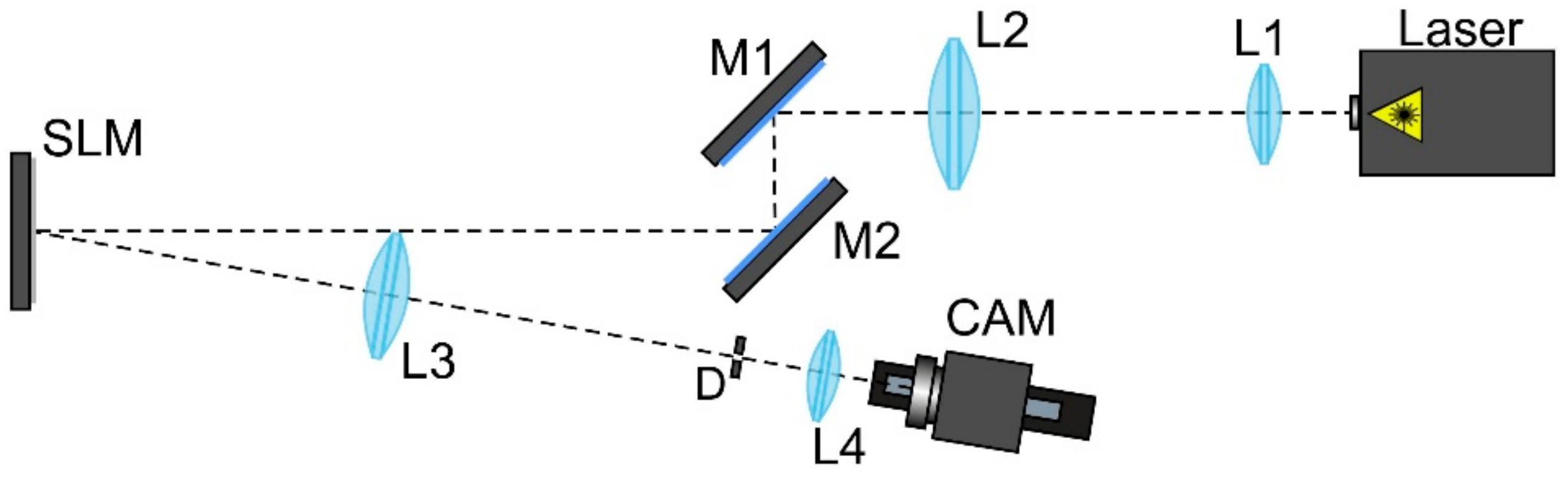
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berezny, A.E.; Prokhorov, A.M.; Sisakian, I.N.; Soifer, V.A. Bessel Optics. Dokl. Akad. Nauk. SSSR 1984, 29, 115–117. [Google Scholar]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-Free Beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Karpeev, S.V.; Butt, M.A. Bessel Beam: Significance and Applications—A Progressive Review. Photonics 2020, 11, 997. [Google Scholar] [CrossRef]
- Gutierrez-Vega, J.C.; Iturbe-Castillo, M.D.; Chavez-Cerda, S. Alternative Formulation for Invariant Optical Fields: Mathieu Beams. Opt. Lett. 2000, 25, 1493–1495. [Google Scholar] [CrossRef]
- Gutiérrez-Vega, J.C.; Iturbe-Castillo, M.D.; Ramırez, G.A.; Tepichın, E.; Rodrıguez-Dagnino, R.M.; Chávez-Cerda, S.; New, G.H.C. Experimental Demonstration of Optical Mathieu Beams. Opt. Commun. 2001, 195, 35–40. [Google Scholar] [CrossRef]
- Bandres, M.A.; Gutierrez-Vega, J.C.; Chavez-Cerda, S. Parabolic Nondiffracting Optical Wave Fields. Opt. Lett. 2004, 29, 44–46. [Google Scholar] [CrossRef] [PubMed]
- López-Mariscal, C.; Bandres, M.A.; Gutiérrez-Vega, J.C.; Chávez-Cerda, S. Observation of Parabolic Nondiffracting Optical Fields. Opt. Express 2005, 13, 2364–2369. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez-Vega, J.C.; Rodrıguez-Masegosa, R.; Chavez-Cerda, S. Focusing Evolution of Generalized Propagation Invariant Optical Fields. J. Opt. A 2003, 5, 276–282. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, Y.; Li, T.; Cannan, D.; Yin, X.; Morandotti, R.; Chen, Z.; Zhang, X. Nonparaxial Mathieu and Weber Accelerating Beams. Phys. Rev. Lett. 2012, 109, 193901. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Ustinov, A.V.; Chávez-Cerda, S. Generalized Parabolic Nondiffracting Beams of Two Orders. J. Opt. Soc. Am. A 2018, 35, 1511–1517. [Google Scholar] [CrossRef]
- Ziolkowski, R.W.; Besieris, I.M.; Shaarawi, A.M. Aperture Realizations of Exact Solutions to Homogeneous-Wave Equations. J. Opt. Soc. Am. A 1993, 10, 75–87. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Mitry, M.J.; Bandres, M.A.; Ruiz, I.; McAuley, K.P.; Cottrell, D.M. Generation of Accelerating Airy and Accelerating Parabolic Beams Using Phase-Only Patterns. Appl. Opt. 2009, 48, 3170–3176. [Google Scholar] [CrossRef] [PubMed]
- Belafhal, A.; Ez-Zariy, L.; Hennani, S.; Nebdi, H. Theoretical Introduction and Generation Method of a Novel Nondiffracting Waves: Olver Beams. Opt. Photon. J. 2015, 5, 234–246. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V. Fractional Airy Beams. J. Opt. Soc. Am. A 2017, 34, 1991–1999. [Google Scholar] [CrossRef]
- McLeod, J.H. The axicon: A New Type of Optical Element. J. Opt. Soc. Am. 1954, 44, 592–597. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K. Generation of High-Order Bessel Beams by Use of an Axicon. Opt. Commun. 2000, 177, 297–301. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Khorin, P.A.; Butt, M.A. Modern Types of Axicons: New Functions and Applications. Sensors 2021, 21, 6690. [Google Scholar] [CrossRef]
- Turunen, J.; Vasara, A.; Friberg, A.T. Holographic Generation of Diffraction-Free Beams. Appl. Opt. 1988, 27, 3959–3962. [Google Scholar]
- Vasara, A.; Turunen, J.; Friberg, A.T. Realization of General Nondiffracting Beams with Computer Generated Holograms. J. Opt. Soc. Am. A. 1989, 6, 1748–1754. [Google Scholar] [CrossRef] [PubMed]
- Paterson, C.; Smith, R. Higher-Order Bessel Waves Produced by Axicon-Type Computer-Generated Holograms. Opt. Commun. 1996, 124, 121–130. [Google Scholar] [CrossRef]
- Chattrapiban, N.; Rogers, E.A.; Cofield, D.; Hill, W.T., III; Roy, R. Generation of Nondiffracting Bessel Beams by Use of a Spatial Light Modulator. Opt. Lett. 2003, 28, 2183–2185. [Google Scholar] [CrossRef]
- Zhai, Z.; Cheng, Z.; Lv, Q.; Wang, X. Tunable Axicons Generated by Spatial Light Modulator with High-Level Phase Computer Generated Holograms. Appl. Sci. 2020, 10, 5127. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Fractional Two-Parameter Parabolic Diffraction-Free Beams. Opt. Commun. 2019, 450, 103–111. [Google Scholar] [CrossRef]
- Thomson, L.C.; Courtial, J. Holographic Shaping of Generalized Self-Reconstructing Light Beams. Opt. Commun. 2008, 281, 1217–1221. [Google Scholar] [CrossRef]
- Goorden, S.A.; Bertolotti, J.; Mosk, A.P. Superpixel-Based Spatial Amplitude and Phase Modulation Using a Digital Micromirror Device. Opt. Express 2014, 22, 17999–18009. [Google Scholar] [CrossRef]
- Anguiano-Morales, M.; Martinez, A.; Iturbe-Castillo, M.D.; Chavez-Cerda, S. Different Field Distributions Obtained with an Axicon and an Amplitude Mask. Opt. Commun. 2008, 281, 401–407. [Google Scholar] [CrossRef]
- Khonina, S.N. Simple Way for Effective Formation Various Nondiffractive Laser Beams. Comput. Opt. 2009, 33, 70–78. [Google Scholar]
- Fedotowsky, A.; Lehovec, K. Far Field Diffraction Patterns of Circular Gratings. Appl. Opt. 1974, 13, 2638–2642. [Google Scholar] [CrossRef]
- Vaity, P.; Rusch, L. Perfect Vortex Beam: Fourier Transformation of a Bessel Beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Quemener, M.; Guenette, J.; Borne, J.; Thibault, S. Toric Lens Analysis as a Focal Ring and Bessel Beam Generator. J. Opt. Soc. Am. A 2020, 37, 1657–1661. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kharitonov, S.I.; Volotovskiy, S.G.; Soifer, V.A. Caustics of Non-Paraxial Perfect Optical Vortices Generated by Toroidal Vortex Lenses. Photonics 2021, 8, 259. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a Twist. Nat. Photon. 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Skidanov, R.V. Dark-Hollow Optical Beams with a Controllable Shape for Optical Trapping in Air. Opt. Express 2015, 23, 8373–8382. [Google Scholar] [CrossRef]
- Rodrigo, J.A.; Alieva, T. Freestyle 3D Laser Traps: Tools for Studying Light-Driven Particle Dynamics and Beyond. Optica 2015, 2, 812–815. [Google Scholar] [CrossRef]
- Suarez, R.A.; Neves, A.A.; Gesualdi, M.R. Optical Trapping with Non-Diffracting Airy Beams Array Using a Holographic Optical Tweezers. Opt. Laser Technol. 2021, 135, 106678. [Google Scholar] [CrossRef]
- Courvoisier, F.; Stoian, R.; Couairon, A. Ultrafast Laser Micro- and Nano-Processing With Nondiffracting and Curved Beams: Invited Paper for the Section: Hot Topics in Ultrafast Lasers. Opt. Laser Technol. 2016, 80, 125–137. [Google Scholar] [CrossRef]
- Syubaev, S.; Zhizhchenko, A.; Vitrik, O.; Porfirev, A.; Fomchenkov, S.; Khonina, S.N.; Kudryashov, S.; Kuchmizhak, A. Chirality of Laser-Printed Plasmonic Nanoneedles Tunable by Tailoring Spiral Shape Pulses. Appl. Surf. Sci. 2019, 470, 526–534. [Google Scholar] [CrossRef]
- Flamm, D.; Chen, K.; Jenne, M.; Schäfer, M.; Grossmann, D.G.; Hellstern, J.; Tillkorn, C.; Kumkar, M. Generalized Non-Diffracting Beams for Ultrafast Materials Processing. Proc. SPIE 2020, 11270, 112700Y. [Google Scholar]
- Vetter, C.; Steinkopf, R.; Bergner, K.; Ornigotti, M.; Nolte, S.; Gross, H.; Szameit, A. Realization of Free-Space Long-Distance Self-Healing Bessel Beams. Laser Photon. Rev. 2019, 13, 1900103. [Google Scholar] [CrossRef]
- Saadati-Sharafeh, F.; Borhanifar, A.; Porfirev, A.; Amiri, P.; Akhlaghi, E.; Khonina, S.N.; Azizian Kalandaragh, Y. The Superposition of the Bessel and Mirrored Bessel Beams and Investigation of Their Self-Healing Characteristics. Optik 2020, 208, 164057. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, Y.; Yan, B.; Zhang, R.; Liu, H.; Lu, Z.; Liu, B. Propagation and Self-Healing Properties of Lommel-Gaussian Beam Through Atmospheric Turbulence. Optoelectron. Lett. 2021, 17, 572–576. [Google Scholar] [CrossRef]
- Sun, P.C.; Mazurenko, Y.; Fainman, Y. Long-Distance Frequency-Division Interferometer for Communication and Quantum Cryptography. Opt. Lett. 1995, 20, 1062–1064. [Google Scholar] [CrossRef]
- Khonina, S.N.; Golub, I. Creating Order with the Help of Randomness: Generating Transversely Random, Longitudinally Invariant Vector Optical Fields. Opt. Lett. 2015, 40, 4070–4073. [Google Scholar] [CrossRef]
- Wang, T.-L.; Gariano, J.A.; Djordjevic, I.B. Employing Bessel-Gaussian Beams to Improve Physical-Layer Security in Free-Space Optical Communications. IEEE Photon. J. 2018, 10, 7907113. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, Z.; Xiang, L.; Xing, D. Extended Depth-of-Field All-Optical Photoacoustic Microscopy with a Dual Non-Diffracting Bessel Beam. Opt. Lett. 2019, 44, 1634–1637. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Dynamic Focal Shift and Extending Depth of Focus Based on the Masking of the Illuminating Beam and Using an Adjustable Axicon. J. Opt. Soc. Am. A 2019, 36, 1039–1047. [Google Scholar] [CrossRef]
- Ren, Y.X.; He, H.; Tang, H.; Wong, K.K. Non-Diffracting Light Wave: Fundamentals and Biomedical Applications. Front. Phys. 2021, 9, 698343. [Google Scholar] [CrossRef]
- Grier, D.G. A Revolution in Optical Manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic Holographic Optical Tweezers. Opt. Commun. 2002, 207, 169175. [Google Scholar] [CrossRef]
- Rodrigo, P.J.; Daria, V.R.; Gluckstad, J. Real-Time Three-Dimensional Optical Micromanipulation of Multiple Particles and Living Cells. Opt. Lett. 2004, 29, 2270–2272. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, J.A.; Alieva, T.; Abramochkin, E.; Castro, I. Shaping of Light Beams Along Curves in Three Dimensions. Opt. Express 2013, 21, 20544–20555. [Google Scholar] [CrossRef] [PubMed]
- Rodrigo, J.A.; Alieva, T. Polymorphic Beams and Nature Inspired Circuits for Optical Current. Sci. Rep. 2016, 6, 35341. [Google Scholar] [CrossRef]
- Khonina, S.N.; Porfirev, A.P. Generation of Multi-Contour Plane Curves Using Vortex Beams. Optik 2021, 229, 166299. [Google Scholar] [CrossRef]
- Zhang, Y.; Belić, M.R.; Sun, J.; Zheng, H.; Chen, H.; Li, C.; Wang, Z.; Zhang, Y. Three-Dimensional Nonparaxial Accelerating Beams from the Transverse Whittaker Integral. Europhys. Let. 2014, 107, 34001. [Google Scholar] [CrossRef]
- Suarez, R.A.; Neves, A.A.; Gesualdi, M.R. Generation and Characterization of an Array of Airy-Vortex Beams. Opt. Commun. 2019, 458, 124846. [Google Scholar] [CrossRef]
- Frolov, A.O.; Khonina, S.N. Modeling the Propagation of Sets of Autofocusing Laser Beams. Proc. SPIE 2021, 11793, 117930I. [Google Scholar]
- Khonina, S.N. Mirror and Circular Symmetry of Autofocusing Beams. Symmetry 2021, 13, 1794. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Khonina, S.N.; Soifer, V.A. Calculation of Phase Formers of Non-Diffracting Images and a Set of Concentric Rings. Optik 1996, 102, 45–50. [Google Scholar]
- Whyte, G.; Courtial, J. Experimental Demonstration of Holographic Three-Dimensional Light Shaping Using a Gerchberg–Saxton Algorithm. New J. Phys. 2005, 7, 117. [Google Scholar] [CrossRef]
- Lopez-Aguayo, S.; Kartashov, Y.V.; Vysloukh, V.A.; Torner, L. Method to Generate Complex Quasi Nondiffracting Optical Lattices. Phys. Rev. Lett. 2010, 105, 013902. [Google Scholar] [CrossRef]
- Kachalov, D.G.; Pavelyev, V.S.; Khonina, S.N.; Skidanov, R.V.; Moiseev, O.Y. Application of the Direct Search in Solving a Problem of Forming Longitudinal Distribution of Intensity. J. Mod. Opt. 2011, 58, 69–76. [Google Scholar] [CrossRef]
- Hsu, W.-F.; Lin, S.-C. Iterative Pixelwise Approach Applied to Computer-Generated Holograms and Diffractive Optical Elements. Appl. Opt. 2018, 57, A189–A196. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Seka, W.; Eberly, J.H.; Huang, H.; Brown, D.L. Experimental Investigation of Bessel Beam Characteristics. Appl. Opt. 1992, 31, 2708. [Google Scholar] [CrossRef] [PubMed]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Durnin, J. Exact Solutions for Nondiffracting Beams. I. The Scalar Theory. J. Opt. Soc. Am. A 1987, 4, 651–654. [Google Scholar] [CrossRef]
- McGloin, D.; Dholakia, K. Bessel Beams: Diffraction in a New Light. Contemp. Phys. 2005, 46, 15–28. [Google Scholar] [CrossRef]
- Courtial, J.; Whyte, G.; Bouchal, Z.; Wagner, J. Iterative Algorithms for Holographic Shaping of Non-Diffracting and Self-Imaging Light Beams. Opt. Express 2006, 140, 2108–2116. [Google Scholar] [CrossRef] [PubMed]
- Mukhametgaleev, I.V.; Khonina, S.N. An Iterative Algorithm for Calculating Images with Diffraction-Free Properties Based on the Selection of a Narrow Spectral Ring. Bull. Samara State Aerosp. Univ. 2010, 4, 238–246. [Google Scholar]
- Khorin, P.A.; Ustinov, A.V. The Formation of Diffraction-Free Beams with a Given Distribution Based on the Whittaker Integral. In Proceedings of the 2020 International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Chafiq, A.; Belafhal, A. Optical Fourier Transform of Pseudo-Nondiffracting Beams. J. Quant. Spectrosc. Radiat. Transf. 2021, 258, 107357. [Google Scholar] [CrossRef]
- Khorin, P.A. Calculation of Diffractive Optical Elements for the Formation of Thin Light Sheet. Jour. Phys. Conf. Series. 2019, 1368, 022014. [Google Scholar] [CrossRef]
- Vettenburg, T.; Dalgarno, H.I.C.; Nylk, J.; Coll-Llado, C.; Ferrier, D.E.K.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-Sheet Microscopy Using an Airy Beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Piksarv, P.; Marti, D.; Le, T.; Unterhuber, A.; Forbes, L.H.; Andrews, M.R.; Stingl, A.; Drexler, W.; Andersen, P.E.; Dholakia, K. Integrated Single- and Two-Photon Light Sheet Microscopy Using Accelerating Beams. Sci. Rep. 2017, 7, 1435. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N.; Balalayev, S.A.; Skidanov, R.V.; Kotlyar, V.V.; Päivänranta, B.; Turunen, J. Encoded Binary Diffractive Element to Form Hyper-Geometric Laser Beams. J. Opt. A Pure Appl. Opt. 2009, 11, 065702. [Google Scholar] [CrossRef]
- Khonina, S.N.; Karpeev, S.V.; Paranin, V.D. A Technique for Simultaneous Detection of Individual Vortex States of Laguerre—Gaussian Beams Transmitted Through an Aqueous Suspension of Microparticles. Opt. Laser. Eng. 2018, 105, 68. [Google Scholar] [CrossRef]



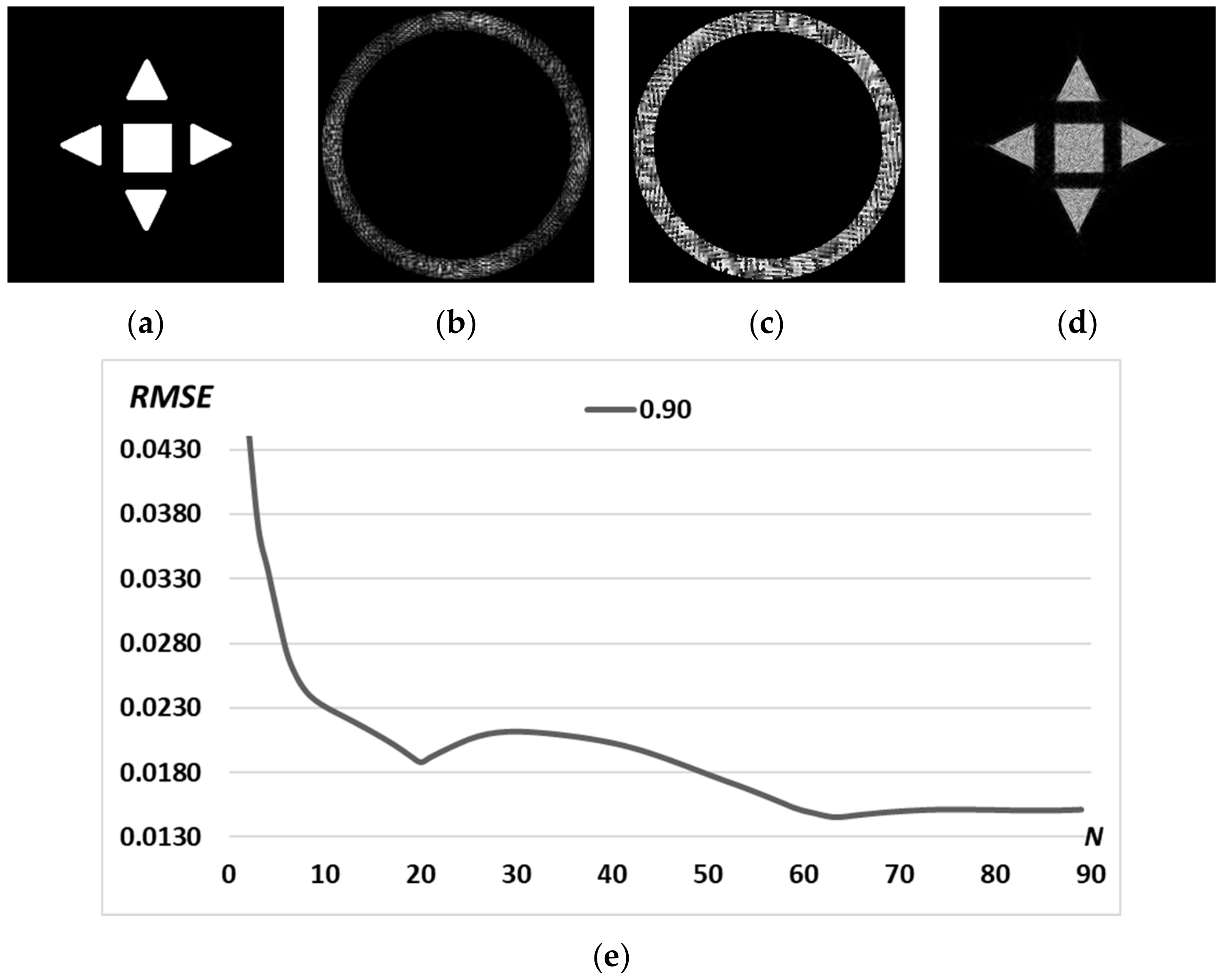




| Iteration, n | 2 | 4 | 10 | 50 | 90 |
|---|---|---|---|---|---|
| Intensity |  |  |  |  |  |
| RMSE | 0.0064 | 0.0046 | 0.0029 | 0.0021 | 0.0019 |
| The Variable Width Δd | 0.20 R0 | 0.25 R0 | 0.30 R0 | 0.35 R0 | 0.40 R0 |
|---|---|---|---|---|---|
| DOE phase |  |  |  |  |  |
| Focal intensity |  |  |  |  |  |
| RMSE | 0.0019 | 0.0015 | 0.0012 | 0.0009 | 0.0005 |
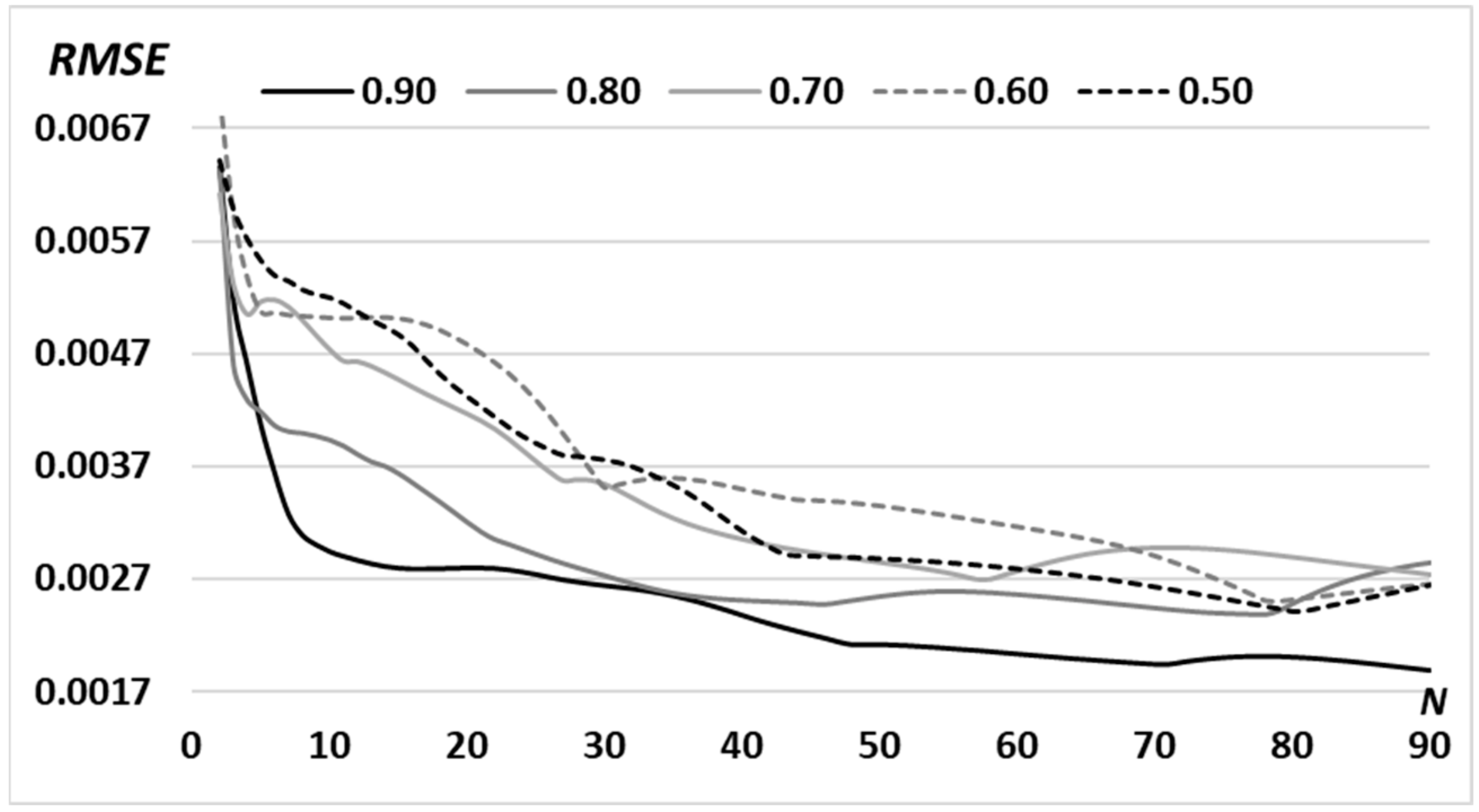
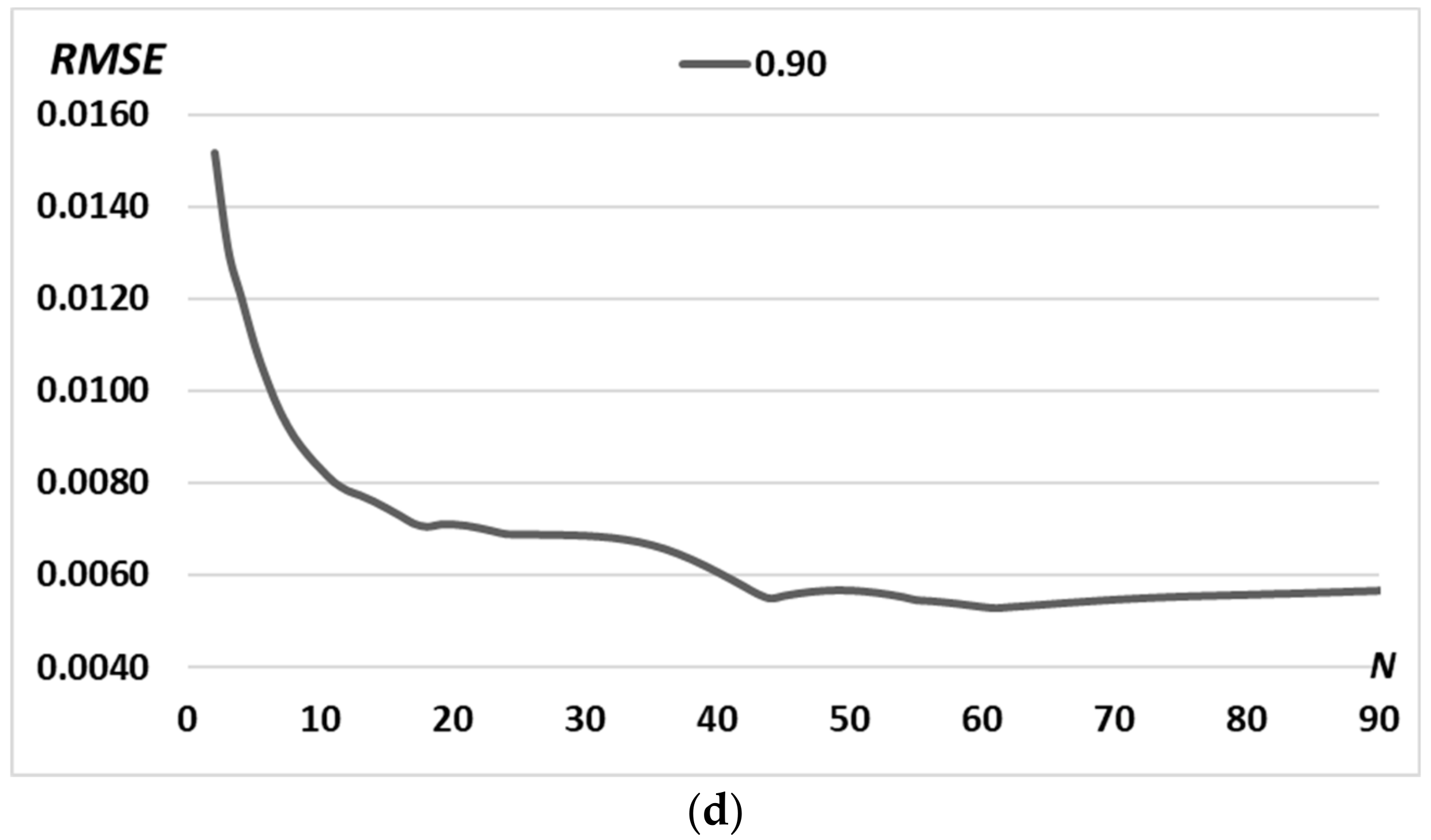
| The Middle Radius of the Ring d | 0.5 R0 | 0.6 R0 | 0.7 R0 | 0.8 R0 | 0.9 R0 |
|---|---|---|---|---|---|
| DOE phase |  |  |  |  |  |
| Focal intensity |  |  |  |  |  |
| RMSE | 0.0028 | 0.0027 | 0.0027 | 0.0026 | 0.0019 |
| Type of Beam | Distance to the Focal Plane Δz, mm | ||||
|---|---|---|---|---|---|
| −75 | −50 | −25 | −15 | 0 | |
| Primitive Triangle with Δd = 0.2 R0 | 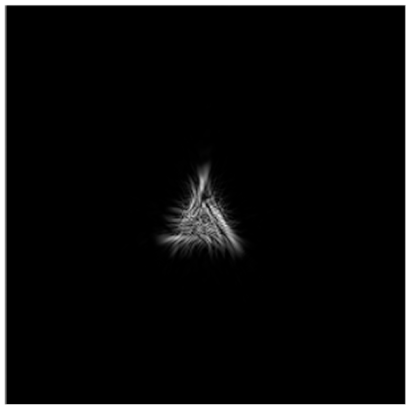 |  |  |  |  |
| Primitive Triangle with Δd = 0.4 R0 | 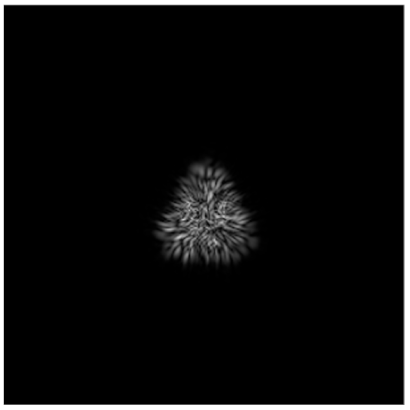 |  |  |  |  |
| Superposition of simple primitives with Δd = 0.2 R0 |  |  |  |  |  |
| Type of Beam | Distance to the Focal Plane Δz, mm | ||||
|---|---|---|---|---|---|
| −75 | −50 | −25 | −15 | 0 | |
| Complex pattern D(u,v) of the “bird” image with Δd = 0.2 R0 |  | 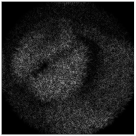 | 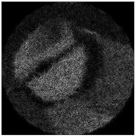 |  | 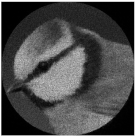 |
| Complex pattern D(u,v) of the “bird” image with Δd = 0.4 R0 |  | 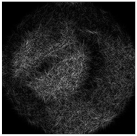 |  | 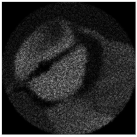 | 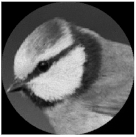 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khorin, P.A.; Porfirev, A.P.; Khonina, S.N. Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives. Micromachines 2023, 14, 989. https://doi.org/10.3390/mi14050989
Khorin PA, Porfirev AP, Khonina SN. Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives. Micromachines. 2023; 14(5):989. https://doi.org/10.3390/mi14050989
Chicago/Turabian StyleKhorin, Pavel A., Alexey P. Porfirev, and Svetlana N. Khonina. 2023. "Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives" Micromachines 14, no. 5: 989. https://doi.org/10.3390/mi14050989
APA StyleKhorin, P. A., Porfirev, A. P., & Khonina, S. N. (2023). Composite Diffraction-Free Beam Formation Based on Iteratively Calculated Primitives. Micromachines, 14(5), 989. https://doi.org/10.3390/mi14050989









