Next-Generation Reconfigurable Nanoantennas and Polarization of Light
Abstract
1. Introduction
2. Polarimetric Formalism
3. Instrumentation Design
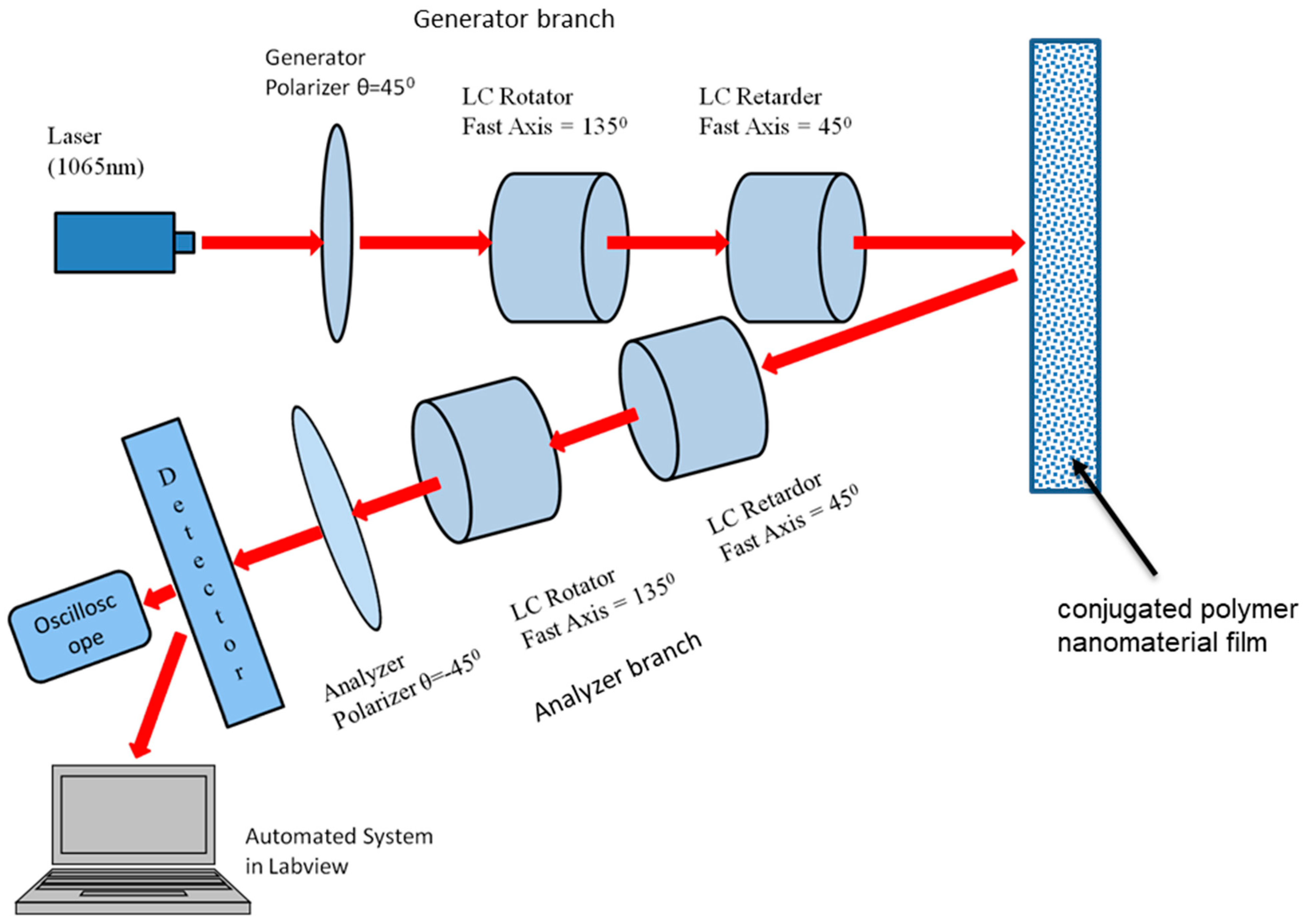
3.1. Polarimetric System Descriprion
3.2. Voltage Calibration of Liquid Crystal Retarders and Rotators
3.3. Calibration Using Known Targets with Known Mueller Matrix (Accuracy Test)
4. Nanofabrication of Polymer Nanomaterials
- (1)
- Thin films of polystyrene (PS) and polybutadiene (PB) domains functionalized with gold nanoparticles
- (2)
- Poly (styrene-b-methyl methacrylate) PS-PMMA used as cast/annealed.
- (3)
- PS-PMMA and PS-PMMA/AuNP
- (1)
- PS-b-PMMA 180 nm
- (2)
- PS-b-PMMA/Au NP 180 nm
- (3)
- PS-b-PMMA/Au NP 120 nm
- (4)
- PS-P2VP (Polystyrene-b-poly)2-vinylpyridine//AuNP
- (1)
- PS-P2VP/Au NPs 105 nm
- (2)
- PS-P2VP/Au NPs 40 nm
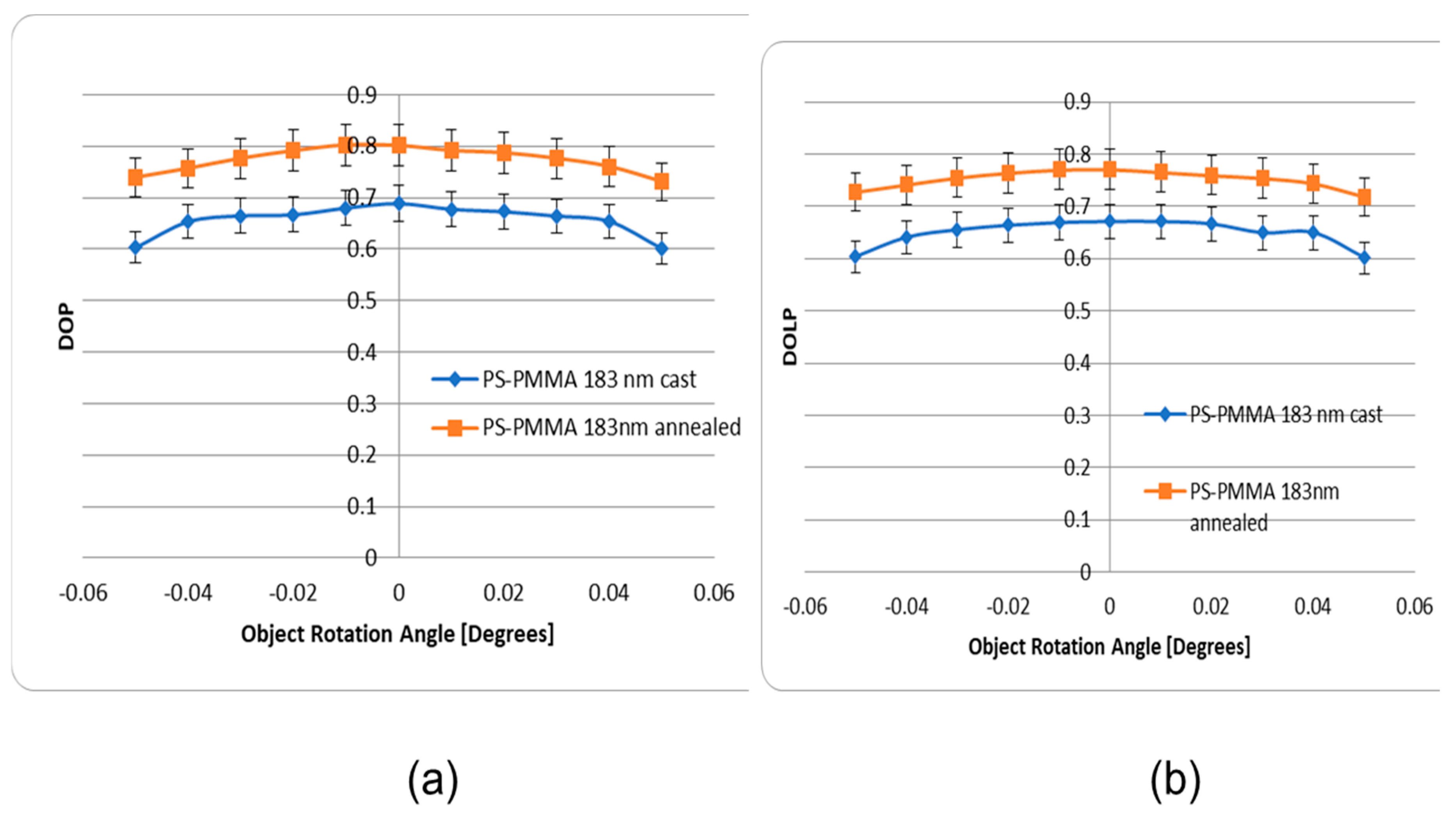
5. Experimental Results and Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LC | Liquid Crystal |
| LHP | Linear Horizontal Polarizer |
| LVP | Linear Vertical Polarizer |
| MM | Mueller Matrix |
| RF | Radiofrequency |
| DOP | Degree of Polarization |
| DOLP | Degree of Linear Polarization |
| LDR | Linear depolarization ratio |
| DOCP | Degree of Circular Polarization |
| HH | Horizontal–Horizontal Measurement State |
| HV | Horizontal–Vertical Measurement State |
| PP | +45°+45° Linear Measurement State |
| RR | Right Circular–Right Circular Measurement State |
| NP | Nanoparticle |
| AuNP | Gold Nanoparticle |
| DNA | Deoxyribonucleic acid |
| PS | Polystyrene |
| PB | Polybutadiene |
| BCP | Block copolymer |
| PMMA | Polymethyl methacrylate |
| PS-b-PMMA | Poly styrene-block-methyl methacrylate |
| PS-b-P2VP | Polystyrene-b-poly(2-vinylpyridine) |
| NIR | Near-Infrared |
References
- Krasnok, A.E.; Maksymov, I.S.; Denisyuk, A.I.; Belov, P.A.; Miroshnichenko, A.E.; Simovski, C.R.; Kivshar, Y.S. Optical nanoantennas. Phys.-Uspekhi 2013, 56, 539. [Google Scholar] [CrossRef]
- Ren, M.; Chen, M.; Wu, W.; Zhang, L.; Liu, J.; Pi, B.; Zhang, X.; Li, Q.; Fan, S.; Xu, J. Linearly polarized light emission from quantum dots with plasmonic nanoantenna arrays. Nano Lett. 2015, 15, 2951–2957. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Salut, R.; Lu, H.; Suarez, M.A.; Martin, N.; Grosjean, T. Subwavelength polarization optics via individual and coupled helical traveling-wave nanoantennas. Light Sci. Appl. 2019, 8, 76. [Google Scholar] [CrossRef] [PubMed]
- Dorrah, A.H.; Rubin, N.A.; Zaidi, A.; Tamagnone, M.; Capasso, F. Metasurface optics for on-demand polarization transformations along the optical path. Nat. Photonics 2021, 15, 287–296. [Google Scholar] [CrossRef]
- Kavankova, I.; Kovar, S.; Valouch, J.; Adamek, M. Review of Nanoantennas Application. Prz. Elektrotechniczny 2023, 1, 13–17. [Google Scholar] [CrossRef]
- Hasan, M.R.; Hellesø, O.G. Dielectric optical nanoantennas. Nanotechnology 2021, 32, 202001. [Google Scholar] [CrossRef]
- Rodríguez-Fortuño, F.J.; Espinosa-Soria, A.; Martínez, A. Exploiting metamaterials, plasmonics and nanoantennas concepts in silicon photonics. J. Opt. 2016, 18, 123001. [Google Scholar] [CrossRef]
- Karki, A.; Yamashita, Y.; Chen, S.; Kurosawa, T.; Takeya, J.; Stanishev, V.; Darakchieva, V.; Watanabe, S.; Jonsson, M.P. Doped semiconducting polymer nanoantennas for tunable organic plasmonics. Commun. Mater. 2022, 3, 48. [Google Scholar] [CrossRef]
- Chen, S.; Kang, E.S.; Shiran Chaharsoughi, M.; Stanishev, V.; Kühne, P.; Sun, H.; Wang, C.; Fahlman, M.; Fabiano, S.; Darakchieva, V.; et al. Conductive polymer nanoantennas for dynamic organic plasmonics. Nat. Nanotechnol. 2020, 15, 35–40. [Google Scholar] [CrossRef]
- Kumar, S.; Tanwar, S.; Sharma, S.K. Nanoantenna—A review on present and future perspective. Int. J. Sci. Eng. Technol. 2016, 4, 240–247. [Google Scholar]
- Yu, N.; Aieta, F.; Genevet, P.; Kats, M.A.; Gaburro, Z.; Capasso, F. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 2012, 2, 6328–6333. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Capasso, F. Tunable structured light with flat optics. Science 2022, 376, eabi6860. [Google Scholar] [CrossRef] [PubMed]
- Krasnok, A.E.; Miroshnichenko, A.E.; Belov, P.A.; Kivshar, Y.S. All-dielectric optical nanoantennas. Opt. Express 2012, 20, 20599–20604. [Google Scholar] [CrossRef] [PubMed]
- Rocco, D.; Locatelli, A.; De Ceglia, D.; Tognazzi, A.; Attilio, Z.; Celebrano, M.; Marco, F.; Antonio, F.; Caputo, R.; De Angelis, C. Manipulating Light with Tunable Nanoantennas and Metasurfaces. In Metamaterials-History, Current State, Applications, and Perspectives; IntechOpen: London, UK, 2022. [Google Scholar]
- Intaravanne, Y.; Chen, X. Recent advances in optical metasurfaces for polarization detection and engineered polarization profiles. Nanophotonics 2020, 9, 1003–1014. [Google Scholar] [CrossRef]
- Dey, S.; Chatterjee, D.; Garboczi, E.J.; Hassan, A.M. Plasmonic nanoantenna optimization using characteristic mode analysis. IEEE Trans. Antennas Propag. 2019, 68, 43–53. [Google Scholar] [CrossRef]
- Farmahini-Farahani, M.; Cheng, J.; Mosallaei, H. Metasurfaces nanoantennas for light processing. J. Opt. Soc. Am. B 2013, 30, 2365–2370. [Google Scholar] [CrossRef]
- Karst, J.; Floess, M.; Ubl, M.; Dingler, C.; Malacrida, C.; Steinle, T.; Ludwigs, S.; Hentschel, M.; Giessen, H. Electrically switchable metallic polymer nanoantennas. Science 2021, 374, 612–616. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Bruck, R.; Traviss, D.; Khokhar, A.Z.; Reynolds, S.; Thomson, D.J.; Mashanovich, G.Z.; Reed, G.T.; Muskens, O.L. Hybrid photon–plasmon coupling and ultrafast control of nanoantennas on a silicon photonic chip. Nano Lett. 2018, 18, 610–617. [Google Scholar] [CrossRef] [PubMed]
- Keyes, D.L.; Lamonte, R.R.; McNally, D.; Bitritto, M. Polymers for Photonics; Photonics Spectra; Wiley Online Library: Hoboken, NJ, USA, 2001; pp. 131–134. [Google Scholar]
- Kensuke, N.; Naka, C.; Chujo, Y. Nanohybridized Synthesis of Metal Nanoparticles and Their Organization; Spinger: Berlin/Heidelberg, Germany, 2009; Volume XVI, p. 191. [Google Scholar]
- Ofir, Y.; Samanta, B.; Rotello, V.M. Polymer and biopolymer mediated self-assembly of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1745–2140. [Google Scholar] [CrossRef]
- Daniel, M.C.; Astruc, D. Gold nanoparticles: Assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis, and nanotechnology. Chem. Rev. 2004, 4, 293–346. [Google Scholar] [CrossRef]
- Neoh, K.G.; Young, T.T.; Looi, N.T.; Kang, E.T.; Tan, K.L. Oxidation−Reduction Interactions between Electroactive Polymer Thin Films and Au(III) Ions in Acid Solution. Chem. Mater. 1997, 9, 2906–2912. [Google Scholar] [CrossRef]
- Braun, E.; Eichen, Y.; Sivan, U.; Ben-Yoseph, G. DNA-templated assembly and electrode attachment of a conducting silver wire. Nature 1998, 391, 775–778. [Google Scholar] [CrossRef] [PubMed]
- Richter, J.; Seidel, R.; Krisch, R.; Mertig, M.; Pompe, W.; Plaschke, J.; Schackert, H.K. Nanoscale Palladium Metallization of DNA. Adv. Mater. 2000, 12, 507–510. [Google Scholar] [CrossRef]
- Mertig, M.; Colombi Ciacchi, L.; Seidel, R.; Pompe, W.; De Vita, A. DNA as a Selective Metallization Template. Nano Lett. 2002, 2, 841–844. [Google Scholar] [CrossRef]
- Harnack, O.; Ford, W.E.; Yasuda, A.; Wessels, J.M. Tris(hydroxymethyl)phosphine-Capped Gold Particles Templated by DNA as Nanowire Precursors. Nano Lett. 2002, 2, 919–923. [Google Scholar] [CrossRef]
- Kumar, A.; Pattarkine, M.; Bhadbhade, M.; Mandale, A.B.; Ganesh, K.N.; Datar, S.S.; Dharmadhikari, C.V.; Sastry, M. Linear Superclusters of Colloidal Gold Particles by Electrostatic Assembly on DNA Templates. Adv. Mater. 2001, 13, 341–344. [Google Scholar] [CrossRef]
- Warner, M.G.; Hutchison, J.E. Linear assemblies of nanoparticles electrostatically organized on DNA scaffolds. Nat. Mater. 2000, 2, 272–277. [Google Scholar] [CrossRef] [PubMed]
- Niemeyer, C.M.; Bürger, W.; Peplies, J. Covalent DNA–Streptavidin Conjugates as Building Blocks for Novel Biometallic Nanostructures. Angew. Chem. Int. Ed. 1998, 37, 2265–2268. [Google Scholar] [CrossRef]
- Djalali, R.; Chen, Y.-F.; Matsui, H. Au Nanowire Fabrication from Sequenced Histidine-Rich Peptide. J. Am. Chem. Soc. 2002, 124, 13660–13661. [Google Scholar] [CrossRef]
- Berven, C.A.; Clarke, L.; Mooster, J.L.; Wybourne, M.N.; Hutchison, J.E. Defect-Tolerant Single-Electron Charging at Room Temperature in Metal Nanoparticle Decorated Biopolymers. Adv. Mater. 2001, 13, 109–113. [Google Scholar] [CrossRef]
- Dujardin, E.; Peet, C.; Stubbs, G.; Culver, J.N.; Mann, S. Organization of Metallic Nanoparticles Using Tobacco Mosaic Virus Templates. Nano Lett. 2003, 2, 413–417. [Google Scholar] [CrossRef]
- Burkett, S.L.; Mann, S. Spatial organization and patterning of gold nanoparticles on self-assembled biolipid tubular templates. Chem. Commun. 1996, 3, 321–326. [Google Scholar] [CrossRef]
- Fullam, S.; Cottel, D.; Rensmo, H.; Fitzmaurice, D. Carbon Nanotube Templated Self-Assembly and Thermal Processing of Gold Nanowires. Adv. Mater. 2000, 12, 1430–1432. [Google Scholar] [CrossRef]
- Jiang, K.; Eitan, A.; Schadler, L.S.; Ajayan, P.M.; Siegel, R.W.; Grobert, N.; Mayne, M.; Reyes, R.M.; Terrones, H.; Terrones, M. Selective Attachment of Gold Nanoparticles to Nitrogen-Doped Carbon Nanotubes. Nano Lett. 2003, 3, 275–277. [Google Scholar] [CrossRef]
- Kirity, A.; Minko, S.; Gorodyska, G.; Stamm, M.; Jaeger, W. Palladium Wire-Shaped Nanoparticles from Single Synthetic Polycation Molecules. Nano Lett. 2002, 2, 881–885. [Google Scholar] [CrossRef]
- Macleod, H.A. Thin-Film Optical Filters; Institute of Physics Publishing Bristol and Philadelphia: Bristol, UK, 2001. [Google Scholar]
- Farrahi, T. Characterization of Functionalized Polymer Nanostructure Thin Films Using Angular Polarimetric Measurements. Master’s Thesis, University of Akron, Akron, OH, USA, 2014. [Google Scholar]
- Zhang, R.; Singh, G.; Dang, A.; Dai, L.; Bockstaller, M.R.; Akgun, B.; Satija, S.; Karim, A. Nanoparticle-Driven Orientation Transition an Soft-Shear Alignment in Diblock Copolymer Films via Dynamic Thermal Gradient Field; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013. [Google Scholar]
- Chipman, R.A. Polarimetry Handbook of Optics, 2nd ed.; McGraw-Hill: New York, NY, USA, 2010; Volume 2, p. 22. [Google Scholar]
- Shell, J.R., II; Brown, S.D.; Gartley, M.G.; Schott, J.R. Fundamentals of Polarimetric Remote Sensing; SPIE Press: Bellingham, WA, USA, 2009. [Google Scholar]
- Lu, S.-Y.; Chipman, R.A. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Giakos, G.C.; Picard, R.H.; Dao, P.D.; Crabtree, P.N.; McNicholl, P.J. Polarimetric Wavelet Phenomenology of Space Materials. In Proceedings of the IEEE International Conference on Imaging Systems and Techniques, Batu Ferringhi, Malaysia, 17–18 May 2011; pp. 1–6. [Google Scholar]
- Giakos, G.; Picard, R.; Dao, P.; Crabtree, P. Object detection and characterization by monostatic ladar Bidirectional Reflectance Distribution Function (BRDF) using polarimetric discriminants. In Electro-Optical Remote Sensing, Photonic Technologies, and Applications III; SPIE: Bellingham, WA, USA, 2009; Volume 7482, pp. 84–93. [Google Scholar]
- Goldstein, D.H.; Chenault, D.B. Near Infrared Imaging Polarimetry. Proc. SPIE 2001, 4481, 30–31. [Google Scholar]
- Goldstein, D.H.; Collett, E. Polarized Light; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Giakos, G.; Picard, R.; Dao, P. Superresolution multispectral imaging polarimetric space surveillance LADAR sensor design architectures. In Remote Sensing of Clouds and the Atmosphere XIII; SPIE: Bellingham, WA, USA, 2008; Volume 7107, pp. 95–106. [Google Scholar] [CrossRef]
- Giakos, G.C.; Valluru, K.; Adya, V.; Ambadipudi, K.; Paturi, S.; Bathini, P.; Becker, M.; Farajipour, P.; Marotta, S.; Paxitzis, J.; et al. Stokes parameter imaging of multi-index of refraction biological phantoms utilizing optically active molecular contrast agents. Measuement Sci. Technol. 2009, 20, 11. [Google Scholar] [CrossRef]
- Giakos, G.C.; Marotta, S.; Narayan, C.; Petermann, J.; Shrestha, S.; Baluch, J.; Pingili, D.; Sheffer, D.B.; Zhang, L.; Zervakis, M.; et al. Polarimetric phenomenology of photons with lung cancer tissue. Measuement Sci. Technol. 2011, 22, 114081. [Google Scholar] [CrossRef]
- Giakos, G.C. Advanced Detection, Surveillance, and Reconnaissance Principles. In Proceedings of the IEEE International Workshop on Measurement Systems for Homeland Security, Orlando, FL, USA, 29–30 March 2005; pp. 6–10. [Google Scholar]
- Wang, X.; Lai, J.; Li, Z. Polarization studies for backscattering of RBC suspensions based on Mueller matrix decomposition. Opt. Express. 2012, 20, 20771–20782. [Google Scholar] [CrossRef]
- Lee, K.; Yun, H.; Mun, S.-E.; Lee, G.-Y.; Sung, J.; Lee, B. Ultracompact broadband plasmonic polarimeter. Laser Photonics Rev. 2018, 12, 1700297. [Google Scholar] [CrossRef]
- Wen, D.; Chen, S.; Yue, F.; Chan, K.; Chen, M.; Ardron, M.; Li, K.F.; Wong, P.W.H.; Cheah, K.W.; Pun, E.Y.B.; et al. Metasurface device with helicity dependent functionality. Adv. Opt. Mater. 2016, 4, 321–327. [Google Scholar] [CrossRef]
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar]
- Mueller, J.P.B.; Rubin, N.A.; Devlin, R.C.; Groever, B.; Capasso, F. Metasurface polarization optics: Independent phase control of arbitrary orthogonal states of polarization. Phys. Rev. Lett. 2017, 118, 113901. [Google Scholar] [CrossRef] [PubMed]
- Rubin, N.; Shi, Z.; Capasso, F. Polarization in diffractive optics and metasurfaces. Adv. Opt. Photonics 2021, 13, 836. [Google Scholar] [CrossRef]
- Wen, D.; Yue, F.; Kumar, S.; Ma, Y.; Chen, M.; Ren, X.; Kremer, P.E.; Gerardot, B.D.; Taghizadeh, M.R.; Buller, G.S.; et al. Metasurface for characterization of the polarization state of light. Opt. Express 2015, 23, 10272–10281. [Google Scholar] [CrossRef]
- Balthasar Mueller, J.P.; Leosson, K.; Capasso, F. Ultracompact metasurface in-line polarimeter. Optica 2016, 3, 42–47. [Google Scholar] [CrossRef]
- Feng, Z.; Tang, T.; Wu, T.; Yu, X.; Zhang, Y.; Wang, M.; Zheng, J.; Ying, Y.; Chen, S.; Zhou, J.; et al. Perfecting and extending the near-infrared imaging window. J. Light Sci. Appl. 2021, 10, 197. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Gao, J. 3D Janus plasmonic helical nanoapertures for polarization-encrypted data Storage. Light Sci. Appl. 2019, 8, 45. [Google Scholar] [CrossRef]
- Li, L.; Zhao, H.; Liu, C.; Li, L.; Cui, T.J. Intelligent metasurfaces: Control, communication and computing. Elight 2022, 2, 7. [Google Scholar] [CrossRef]
- Farshchi, R.; Ramsteiner, M.; Herfort, J.; Tahraoui, A.; Grahn, H.T. Optical communication of spin information between light emitting diodes. Appl. Phys. Lett. 2011, 98, 162508. [Google Scholar] [CrossRef]
- Sherson, J.F.; Krauter, H.; Olsson, R.K.; Julsgaard, B.; Hammerer, K.; Cirac, I.; Polzik, E.S. Quantum teleportation between light and matter. Nature 2006, 443, 557–560. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wen, S.; Deng, Z.-L.; Li, X.; Yang, Y. Metasurface-Based Solid Poincaré Sphere Polarizer. Phys. Rev. Lett. 2023, 130, 123801. [Google Scholar] [CrossRef]
- Shen, Z.; Zhao, F.; Jin, C.; Wang, S.; Cao, L.; Yang, Y. Monocular metasurface camera for passive single-shot 4D imaging. Nat. Commun. 2023, 14, 1035. [Google Scholar] [CrossRef] [PubMed]
- Hurley, D.; Ohler, B. Improved Surface Characterization with AFM Imaging, Tech Briefs. Photonics/Optics, 1 November 2017. [Google Scholar]
- Khan, P.; Brennan, G.; Li, Z.; Al Hassan, L.; Rice, D.; Gleeson, M.; Mani, A.A.; Tofail, S.A.M.; Xu, H.; Liu, N.; et al. Circular Polarization Conversion in Single Plasmonic Spherical Particle. Nano Lett. 2022, 22, 1504–1510. [Google Scholar] [CrossRef]
- Namgung, S.D.; Kim, R.M.; Lim, Y.C.; Lee, J.W.; Cho, N.H.; Kim, H.; Huh, J.-S.; Rhee, H.; Nah, S.; Song, M.-K.; et al. Circularly polarized light-sensitive, hot electron transistor with chiral plasmonic nanoparticles. Nat. Commun. 2022, 13, 5081. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Xu, X.; Sun, X.W.; Liang, X.; Valuckas, V.; Zheng, Y.; Paniagua-Domínguez, R.; Kuznetsov, A.I. Efficient visible light modulation based on electrically tunable all dielectric metasurfaces embedded in thin-layer nematic liquid crystals. Sci. Rep. 2019, 9, 8673. [Google Scholar] [CrossRef] [PubMed]
- Sakhare, P.A.; Atmakuri, M.; Dontabhaktuni, J. Tailoring the resonant modes in liquid crystal based all-dielectric metasurfaces. Sci. Rep. 2023, 13, 6780. [Google Scholar] [CrossRef] [PubMed]
- Modi, K.S.; Singh, S.P.; Kaur, J.; Tiwari, U.; Sinha, R.K. All dielectric metasurface based tunable optical modulator: Design and analysis. Photonics Nanostructures—Fundam. Appl. 2021, 43, 100881. [Google Scholar] [CrossRef]















| Element | Measured Muller Matrix | Ideal Muller Matrix | Element Variance | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Air | LHP | LVP | Air | LHP | LVP | Air | LHP | LVP | |
| m11 | 1.000 | 1.000 | 1.000 | 1 | 1 | 1 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| m12 | 0.014 | 0.974 | −0.992 | 0 | 1 | −1 | 2.07 × 10−4 | 6.84 × 10−4 | 5.79× 10−5 |
| m13 | −0.005 | 0.023 | −0.066 | 0 | 0 | 0 | 2.55 × 10−5 | 5.42 × 10−4 | 4.36 × 10−3 |
| m14 | 0.028 | −0.058 | 0.043 | 0 | 0 | 0 | 8.09 × 10−4 | 3.38 × 10−3 | 1.83 × 10−3 |
| m21 | 0.030 | 0.947 | −0.974 | 0 | 1 | −1 | 9.13 × 10−4 | 2.79 × 10−3 | 6.89 × 10−4 |
| m22 | 0.940 | 0.923 | 0.968 | 1 | 1 | 1 | 3.55 × 10−3 | 5.91 × 10−3 | 9.97 × 10−4 |
| m23 | 0.257 | 0.024 | 0.060 | 0 | 0 | 0 | 6.60 × 10−2 | 6.00 × 10−4 | 3.64 × 10−3 |
| m24 | 0.023 | −0.053 | −0.044 | 0 | 0 | 0 | 5.43 × 10−4 | 2.82 × 10−3 | 1.97 × 10−3 |
| m31 | 0.048 | −0.041 | −0.021 | 0 | 0 | 0 | 2.31 × 10−3 | 1.69 × 10−3 | 4.30 × 10−4 |
| m32 | −0.089 | −0.038 | 0.020 | 0 | 0 | 0 | 7.94 × 10−3 | 1.44 × 10−3 | 3.99 × 10−4 |
| m33 | 0.926 | 0.001 | 0.003 | 1 | 0 | 0 | 5.51 × 10−3 | 3.73 × 10−7 | 7.09 × 10−6 |
| m34 | −0.335 | 0.001 | 0.000 | 0 | 0 | 0 | 1.12 × 10−1 | 6.15 × 10−7 | 1.06 × 10−13 |
| m41 | 0.001 | −0.094 | 0.058 | 0 | 0 | 0 | 4.46 × 10−7 | 8.81 × 10−3 | 3.37 × 10−3 |
| m42 | −0.053 | −0.089 | −0.059 | 0 | 0 | 0 | 2.83 × 10−3 | 7.86 × 10−3 | 3.46 × 10−3 |
| m43 | 0.067 | −0.002 | −0.003 | 0 | 0 | 0 | 4.55 × 10−3 | 2.74 × 10−6 | 9.27 × 10−6 |
| m44 | 0.972 | 0.007 | 0.003 | 1 | 0 | 0 | 7.63 × 10−4 | 4.27 × 10−5 | 7.09× 10−6 |
| Standard Deviation | 1.14 × 10−1 | 4.78 × 10−2 | 3.64 × 10−2 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farrahi, T.; Giakos, G.K. Next-Generation Reconfigurable Nanoantennas and Polarization of Light. Micromachines 2023, 14, 1132. https://doi.org/10.3390/mi14061132
Farrahi T, Giakos GK. Next-Generation Reconfigurable Nanoantennas and Polarization of Light. Micromachines. 2023; 14(6):1132. https://doi.org/10.3390/mi14061132
Chicago/Turabian StyleFarrahi, Tannaz, and George K. Giakos. 2023. "Next-Generation Reconfigurable Nanoantennas and Polarization of Light" Micromachines 14, no. 6: 1132. https://doi.org/10.3390/mi14061132
APA StyleFarrahi, T., & Giakos, G. K. (2023). Next-Generation Reconfigurable Nanoantennas and Polarization of Light. Micromachines, 14(6), 1132. https://doi.org/10.3390/mi14061132








