Weak Capacitance Detection Circuit of Micro-Hemispherical Gyroscope Based on Common-Mode Feedback Fusion Modulation and Demodulation
Abstract
:1. Introduction
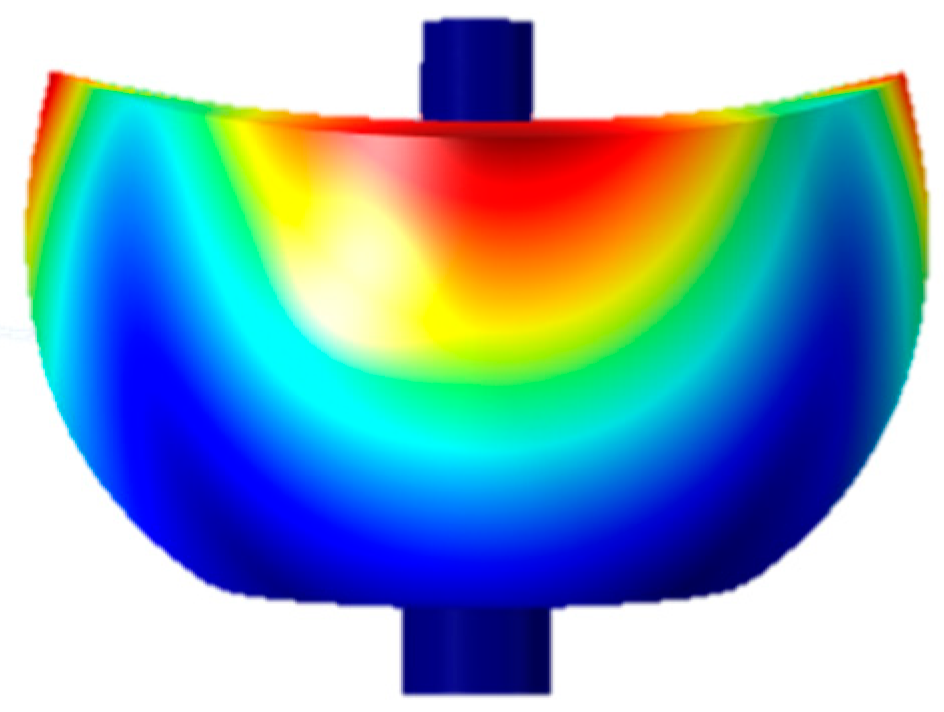
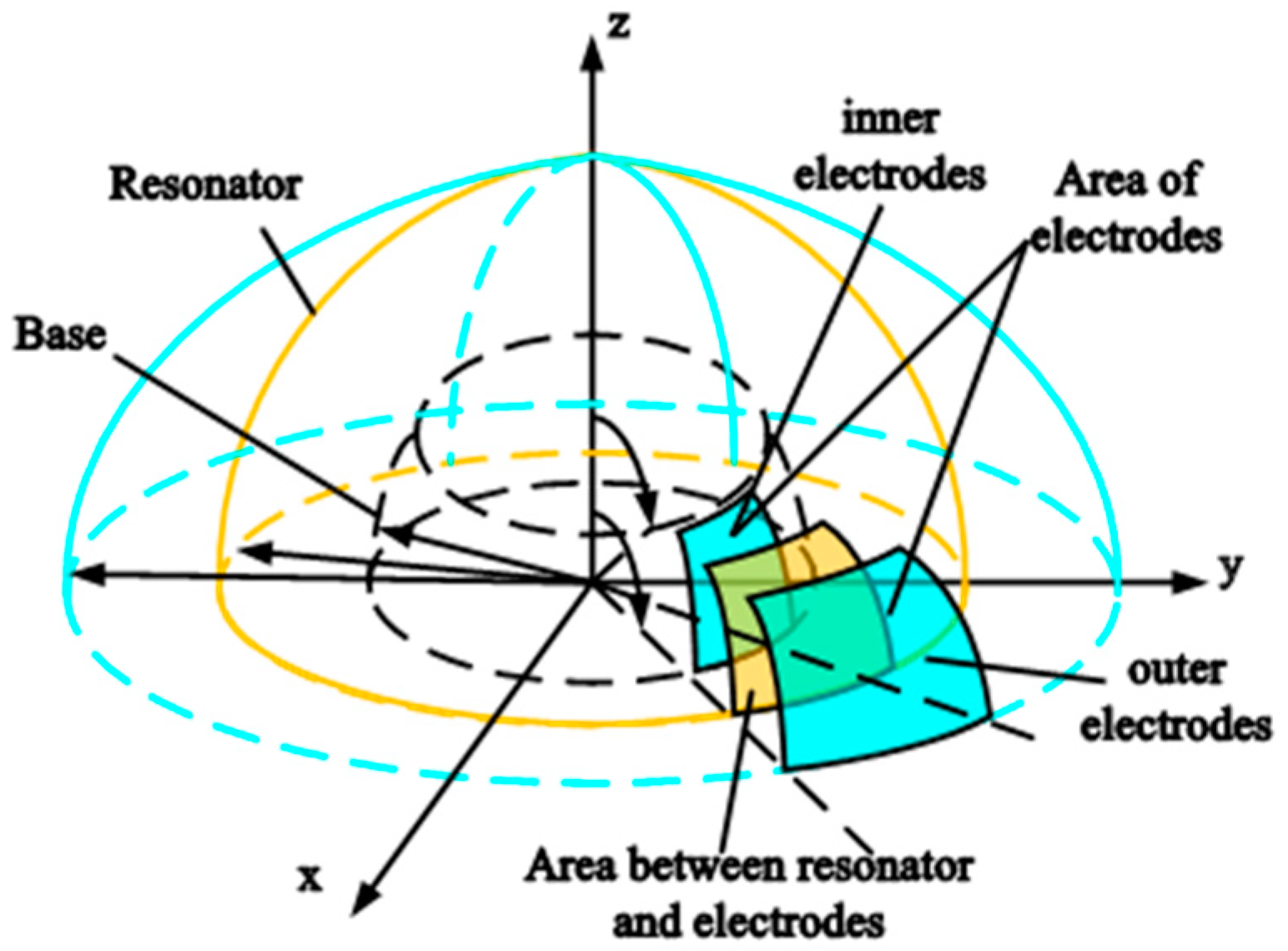
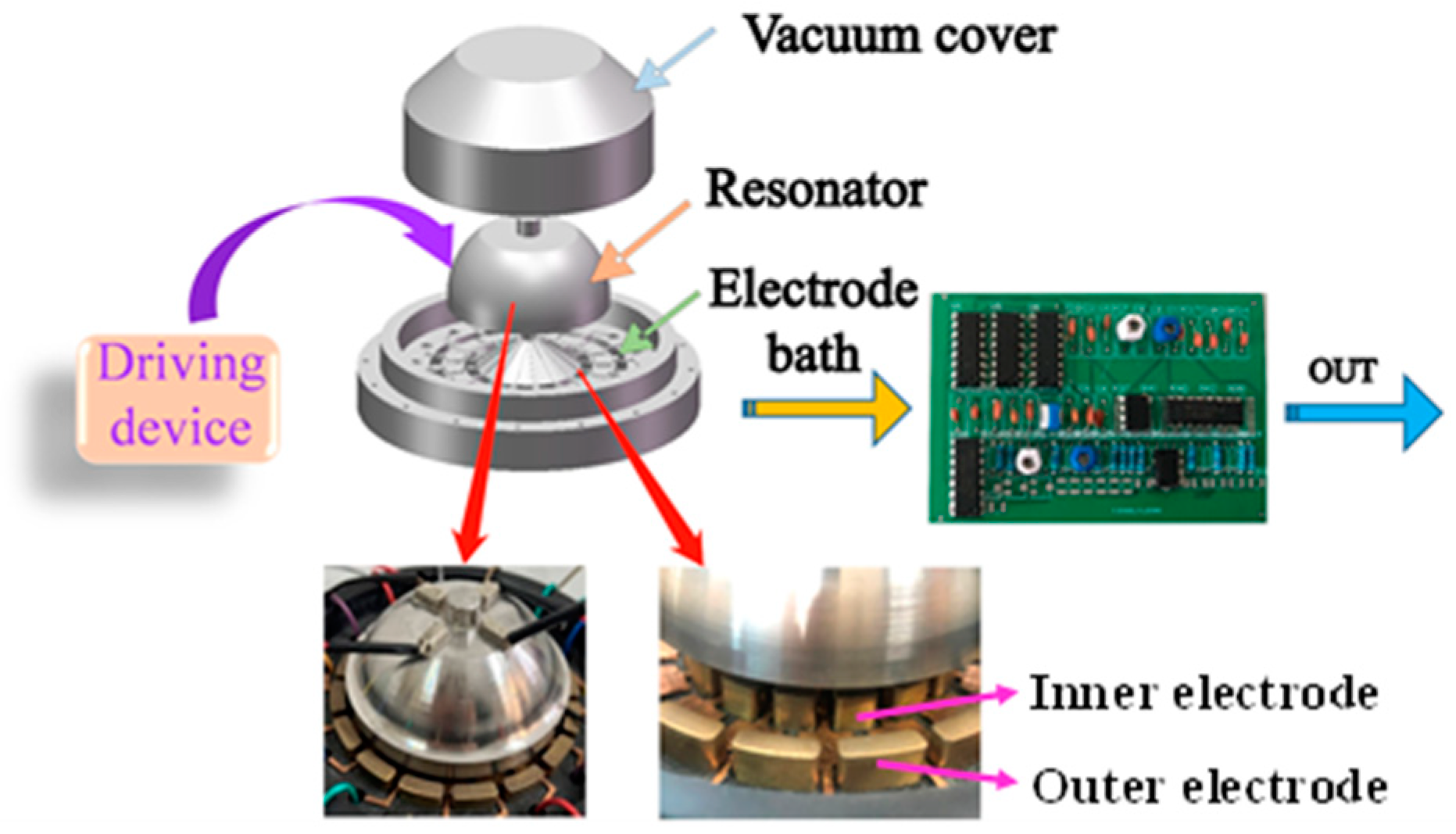
2. Device Architecture of Capacitive Displacement Detection
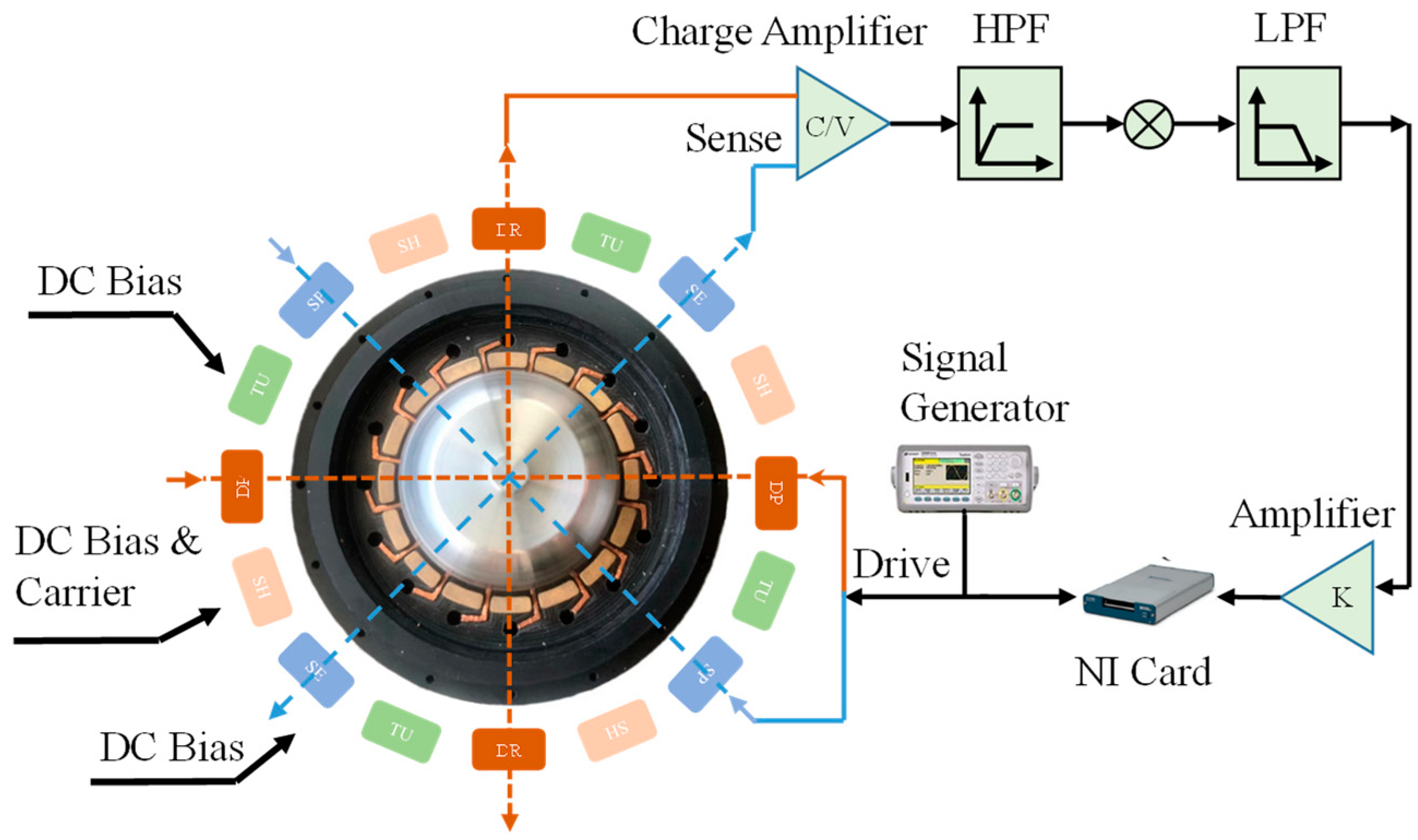
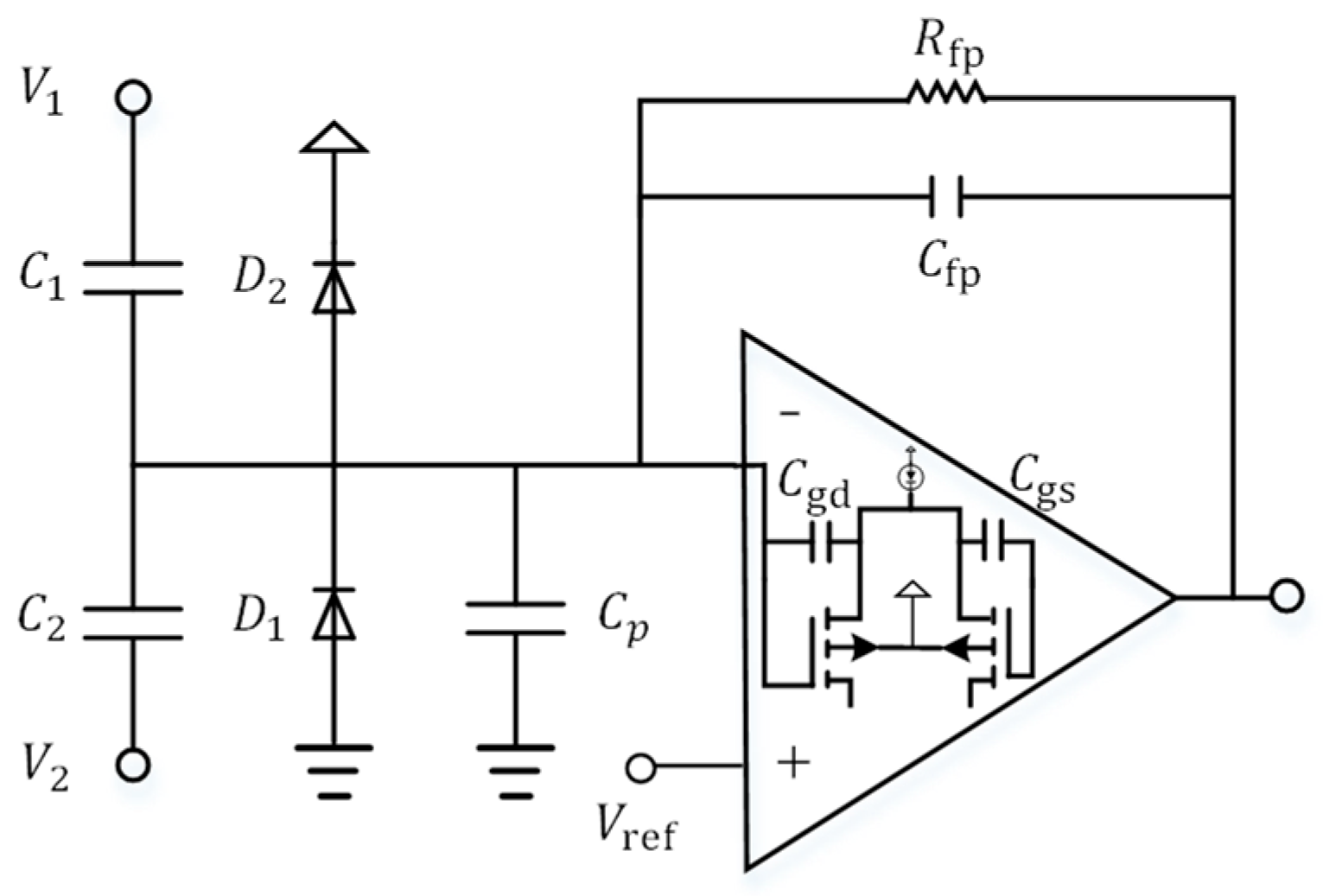
3. Circuit Design
3.1. Noise Analysis
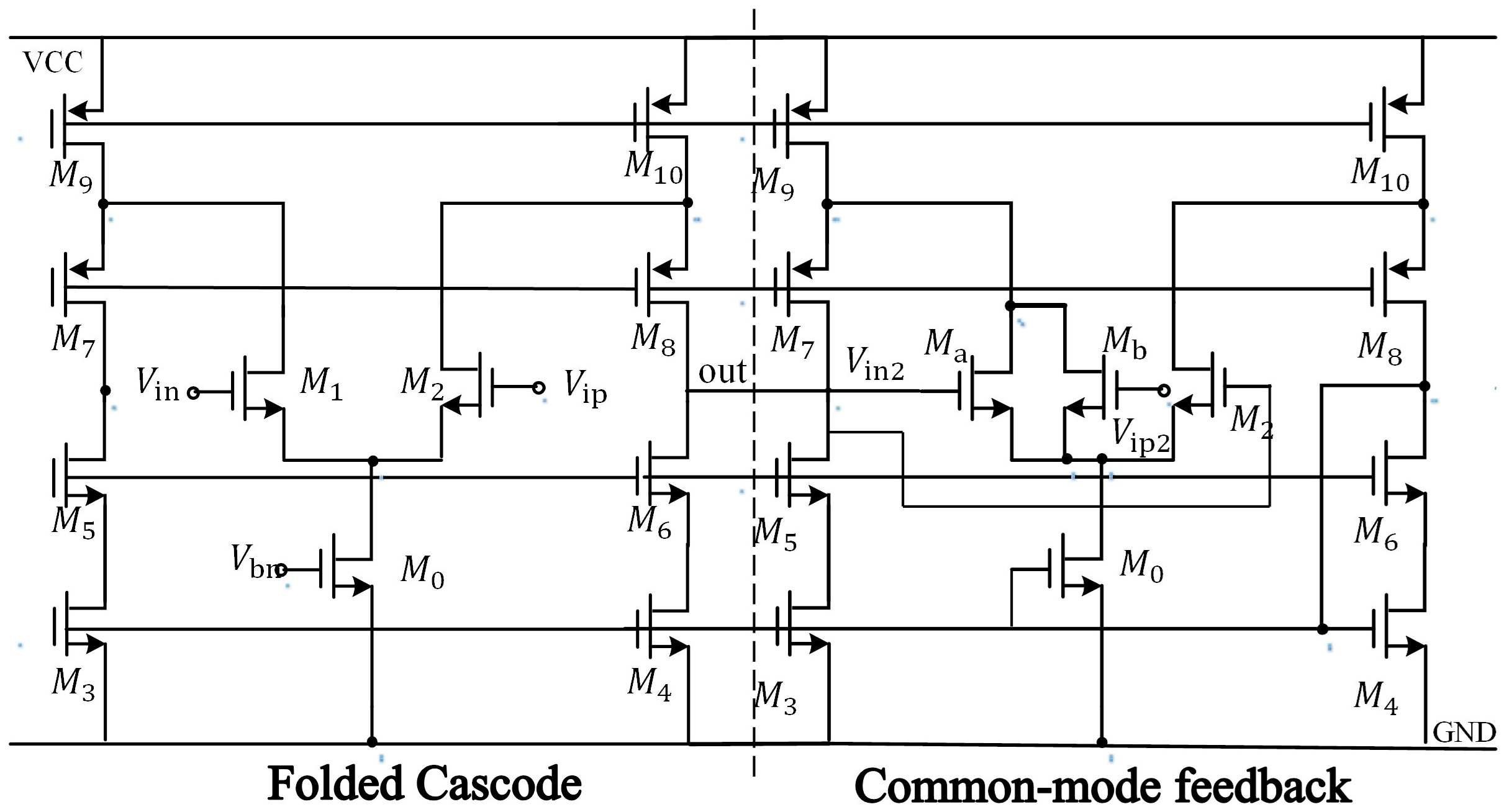
3.2. Operational Amplifier Design
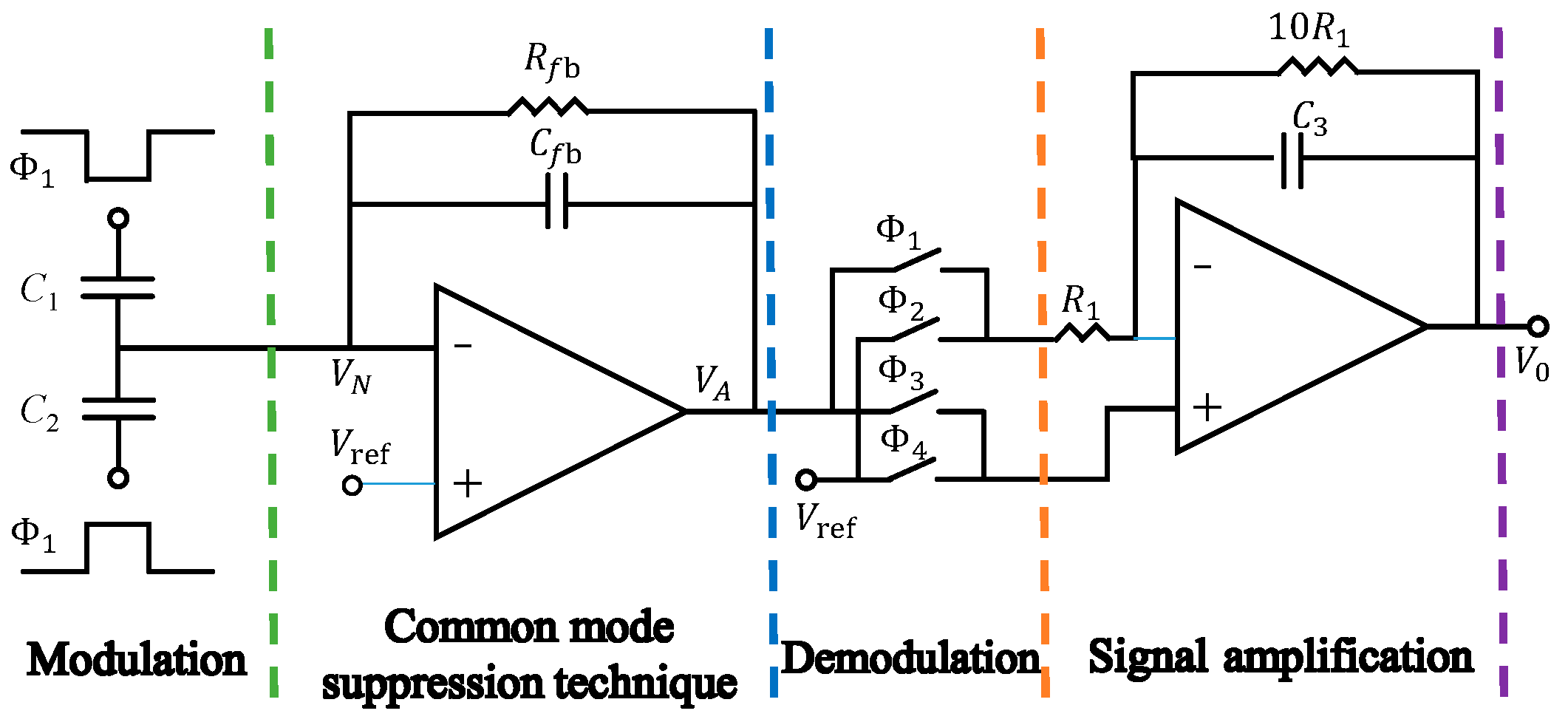
4. Modulation–Demodulation Techniques
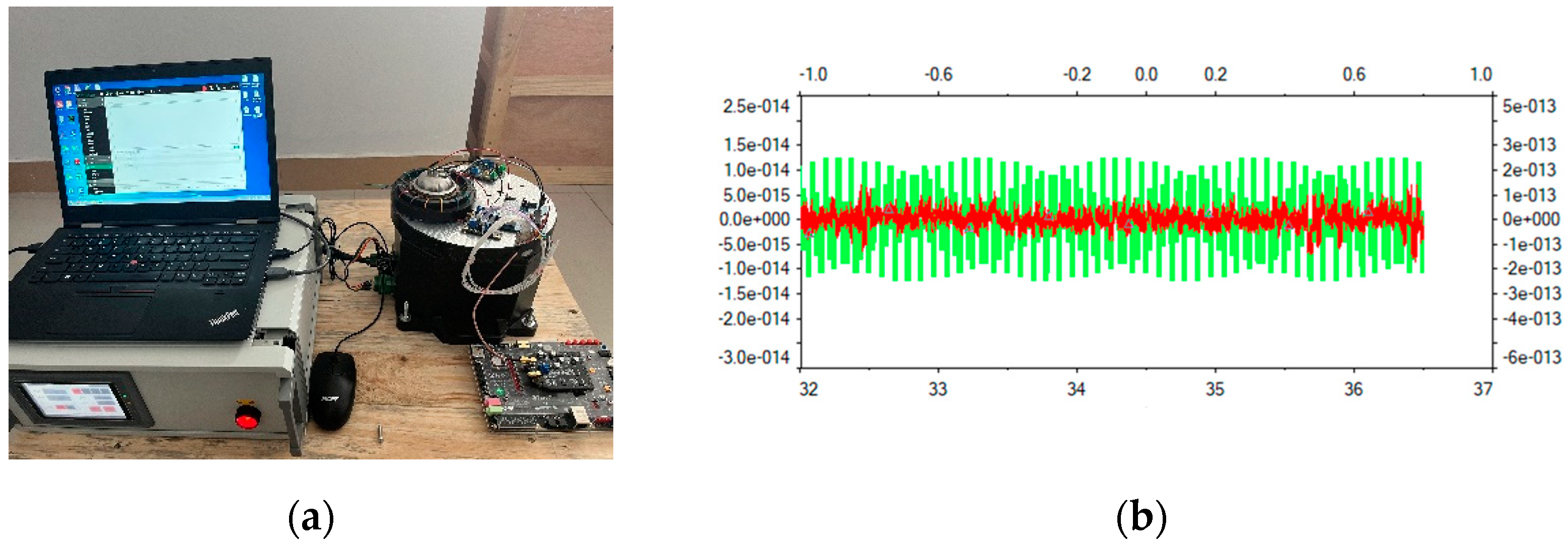
5. Analysis of Test Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, W.; Xiao, D.; Pu, J.; Li, K. Design and Implementation of Signal Detection Circuit for MEMS Vibration Sensor. J. Sens. Microsyst. 2021, 40, 63–66. [Google Scholar]
- Zhang, J.; Li, P.; Zhuang, X.; Zhang, X.; Liu, J. Analysis of temperature drift error Compensation method for hemispherical resonant gyro. Navig. Control 2022, 21, 1–7+55. [Google Scholar]
- Li, Z.M.; Lan, Z.; Jin, K.; Zhang, J.; Zhang, H. Parasitic capacitance adaptive suppression for fly-by-wire capacitive sensor readout circuits. J. Xi’an Jiaotong Univ. 2021, 55, 154–161. [Google Scholar]
- Liu, S.; Li, M.; Meng, F.; Ma, A.; Su, M. Design of micro-capacitive sensor signal detection circuit. Electron. Devices 2020, 43, 613–619. [Google Scholar]
- Qian, M. Research on Principle and Test Method of MEMS Gyroscope. Integr. Circuit Appl. 2017, 34, 72–77. [Google Scholar]
- Zhuang, X.; Ding, J.; Cao, W.; Wu, M. Nondestructive testing of Silicon Hemisphere deep Cavity Structures. Navig. Control 2019, 18, 89–95. [Google Scholar]
- Ataman, C.; Urey, H. Modeling and characterization of comb-actuated resonant microscanners. J. Micromech. Microeng. 2006, 16, 9. [Google Scholar] [CrossRef]
- Gao, S.; Wu, J. Multi-electrode based hemispherical resonant gyro signal detection. J. Harbin Eng. Univ. 2008, 29, 475–477. [Google Scholar]
- Yi, Y.; Song, A.; Li, H.; Leng, M. Design of micro-capacitive detection circuit for capacitive tactile sensors. Instrum. Technol. Sens. 2020, 5, 6–10. [Google Scholar]
- Wu, Q.; Yang, H.; Zhang, C. A high-performance capacitive readout circuit for MEMS gyroscopes. J. Instrum. 2010, 31, 937–943. [Google Scholar]
- Li, X.; Zheng, Y.B. Research on hemispherical resonant gyro signal detection and dynamic performance improvement method. Navig. Control 2015, 14, 32–33. [Google Scholar]
- Zhang, M.; Wang, H.; Lv, D. Analysis and modeling of random errors in MEMS gyroscopes. Electro-Opt. Control 2022, 29, 68–71. [Google Scholar]
- Zhang, W.; Chen, W.; Yin, L.; Di, X.; Chen, D.; Fu, Q.; Zhang, Y.; Liu, X. Study of the Influence of Phase Noise on the MEMS Disk Resonator Gyroscope Interface Circuit. Sensors 2020, 20, 5470. [Google Scholar] [CrossRef] [PubMed]
- Tan, Q.; Li, L. Development history and key technologies of hemispherical resonant gyroscope. Proc. Symp. Inert. Technol. Intell. Navig. 2019, 91–95. [Google Scholar]
- Norouzpour-Shirazi, A.; Zaman, M.F.; Ayazi, F. A digital phase demodulation technique for resonant MEMS gyroscopes. IEEE Sens. J. 2014, 14, 3260–3266. [Google Scholar] [CrossRef]
- Tang, X.; Long, S.; Liu, Y. High-precision low-noise MEMS gyroscope capacitive readout circuit. J. Sens. Technol. 2014, 27, 1191–1195. [Google Scholar]
- Jiang, R.; Kong, D.; Li, Z.; Bao, L.; Lin, B.; Guo, P. Fully differential amplifier for MEMS micro capacitor detection. Semicond. Technol. 2009, 34, 181–184. [Google Scholar]
- Tian, M. Low-Noise Interface Circuit Design for Micro-Multi-Loop Resonant Gyroscopes; Shanghai Jiaotong University: Shanghai, China, 2020. [Google Scholar]
- Zargari, S.; Moezzi, M. A New Readout Circuit with Robust Quadrature Error Compensation for MEMS Vibratory Gyroscopes. Circuits Syst. Signal Process. 2022, 41, 3050–3065. [Google Scholar] [CrossRef]
- Zhang, H.; Tong, Z.; Long, S.; He, K. A novel low-noise silicon micromechanical gyro-capacitor readout circuit. Navig. Control 2019, 18, 100–106. [Google Scholar]




| Performance Parameters | Indicators | Unit |
|---|---|---|
| Open-loop gain | 102 | dB |
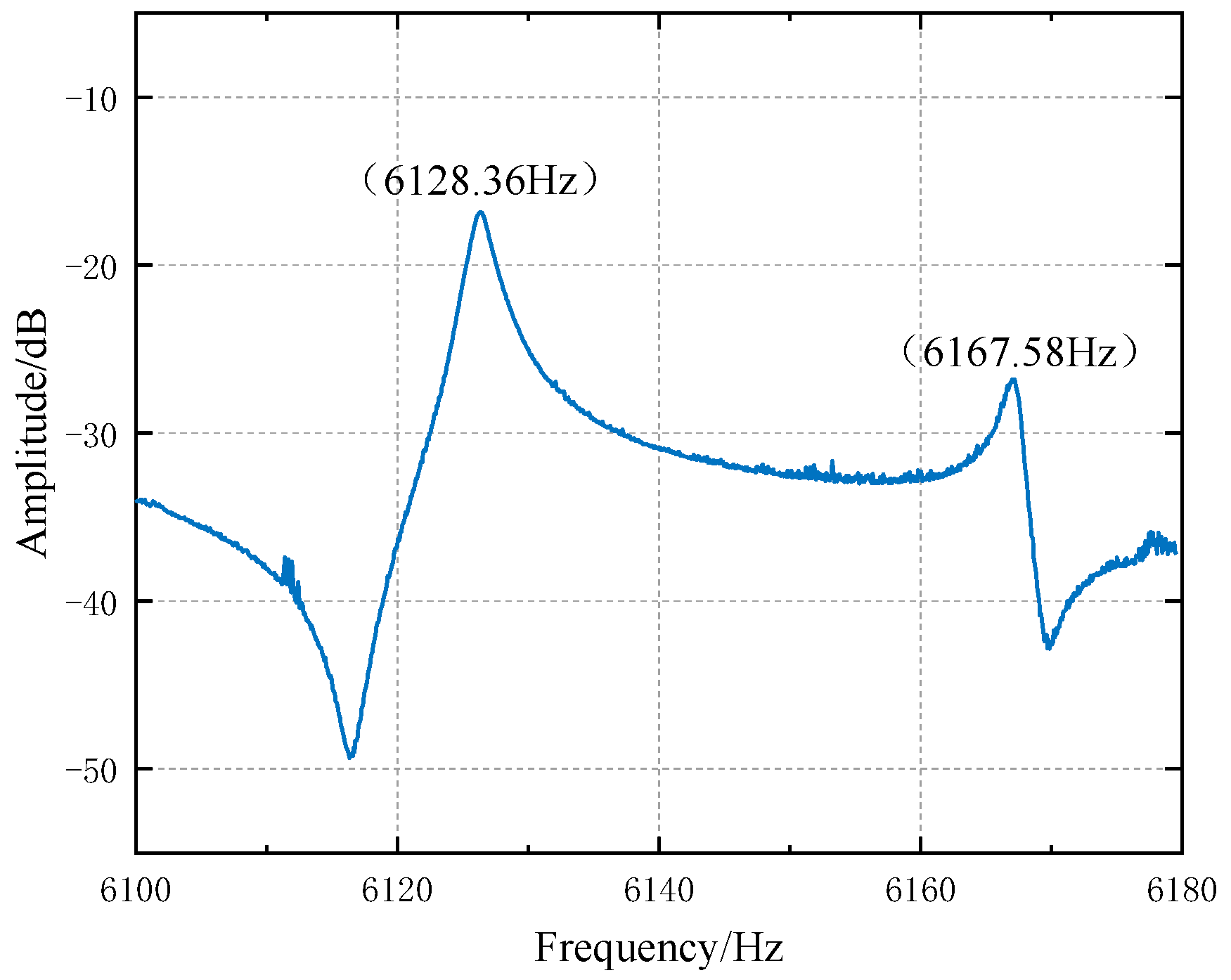
| Gain bandwidth | 18 | MHz |
| Phase margin | 45 | ° |
| Supply voltage | 6 | V |
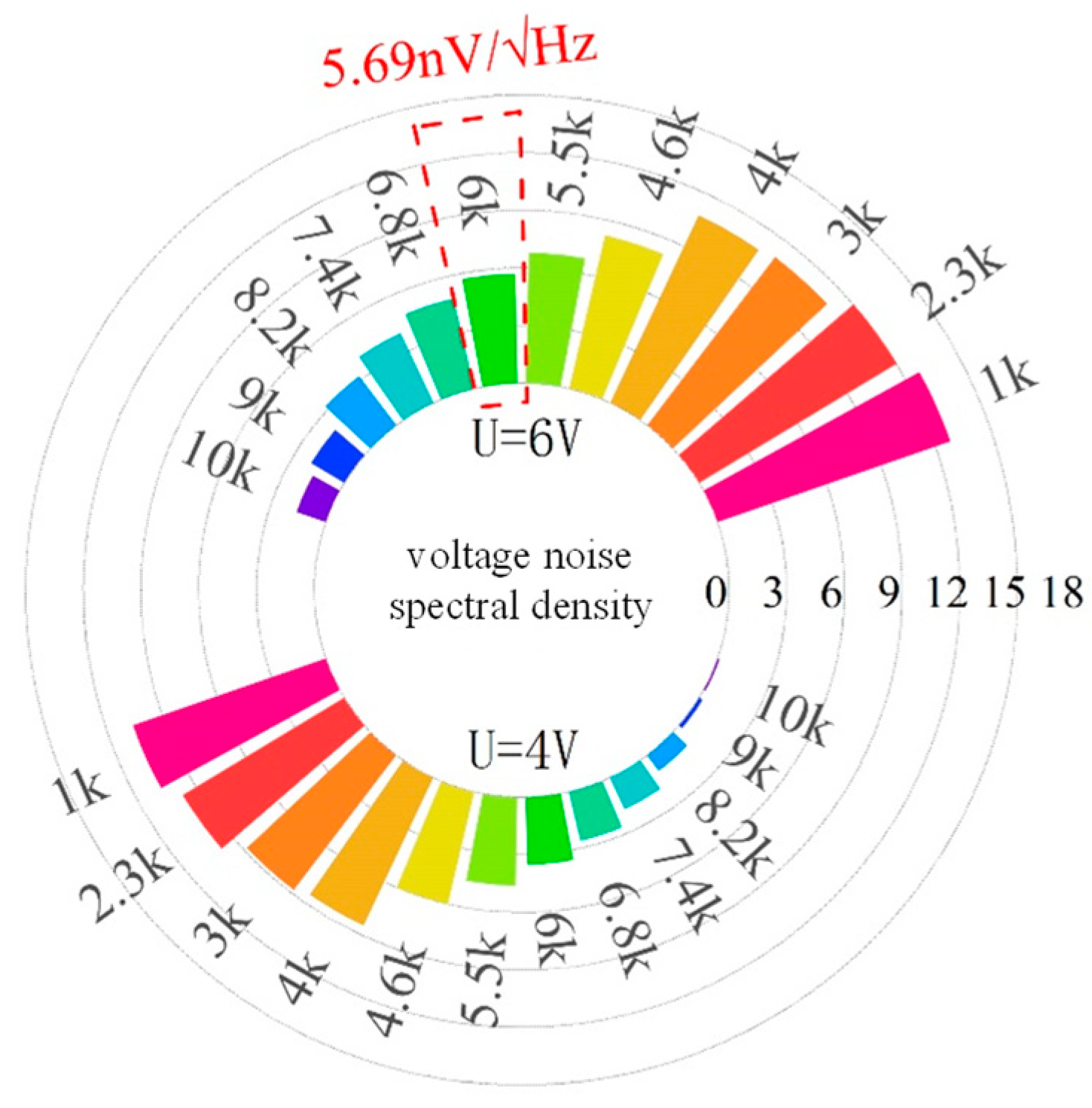
| Equivalent input noise | 6 | nV/√Hz |
| Output amplitude | 1~3 | V |
| Output Voltage Noise (nV/√Hz) | Capacitive Resolution (aF/√Hz) | Sensitivity (V/pF) | Remarks | |
|---|---|---|---|---|
| Institute of Electronics, Chinese Academy of Sciences | / | 1.5 | 16.7 | Reference [10] |
| East China Institute of Optoelectronic Integrated Devices | / | 0.06 | 12.58 | Reference [20] |
| Northern General Electronics Group Limited | 7.82 | 0.116 | / | Reference [16] |
| Amirkabir University of Technology | / | 1.7 | / | Reference [19] |
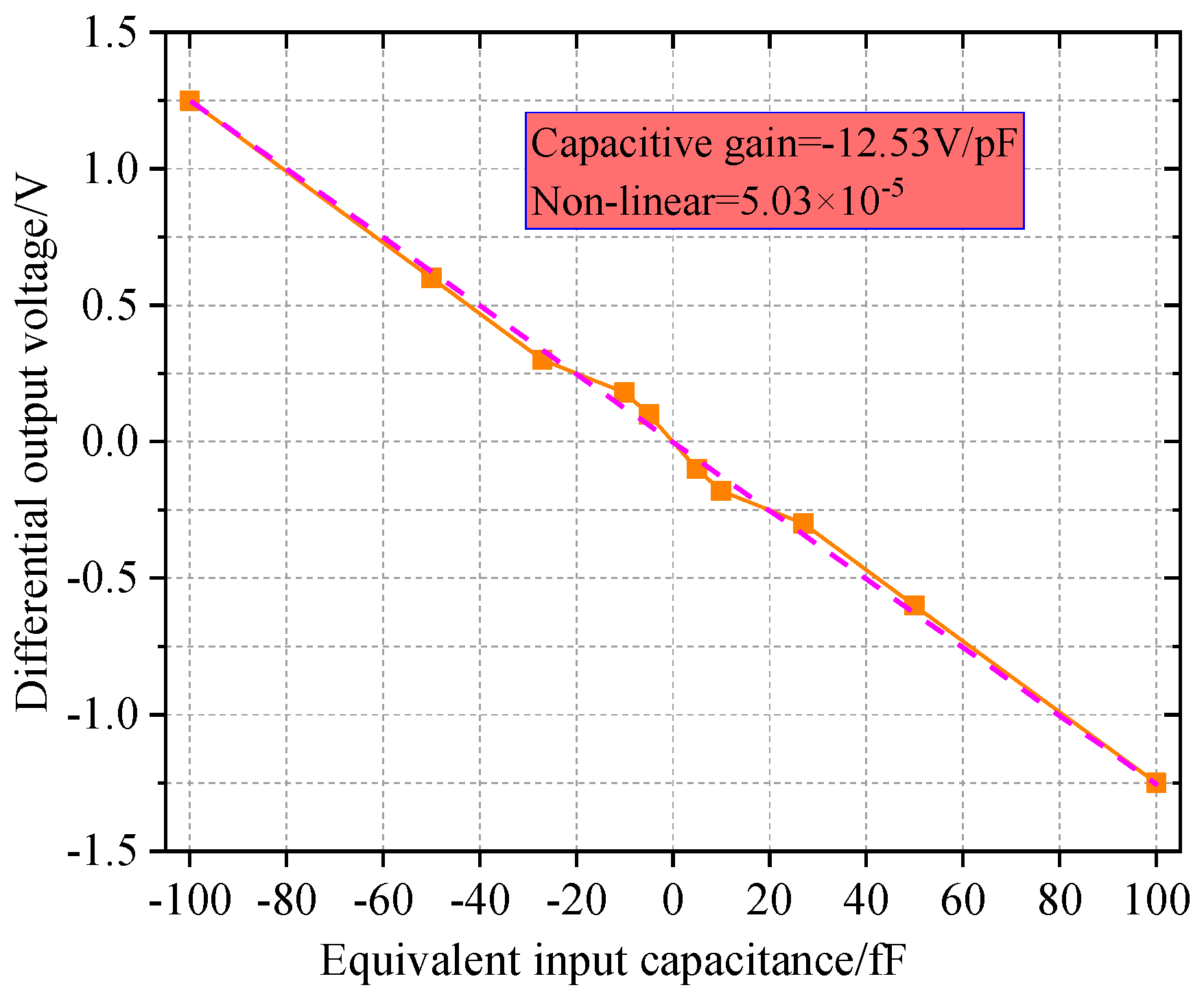
| This article | 5.69 | 0.1 | 12.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, P.; Zhuang, X.; Sheng, Y.; Liu, J.; Gao, Z.; Yu, Z. Weak Capacitance Detection Circuit of Micro-Hemispherical Gyroscope Based on Common-Mode Feedback Fusion Modulation and Demodulation. Micromachines 2023, 14, 1161. https://doi.org/10.3390/mi14061161
Zhang X, Li P, Zhuang X, Sheng Y, Liu J, Gao Z, Yu Z. Weak Capacitance Detection Circuit of Micro-Hemispherical Gyroscope Based on Common-Mode Feedback Fusion Modulation and Demodulation. Micromachines. 2023; 14(6):1161. https://doi.org/10.3390/mi14061161
Chicago/Turabian StyleZhang, Xiaoyang, Pinghua Li, Xuye Zhuang, Yunlong Sheng, Jinghao Liu, Zhongfeng Gao, and Zhiyu Yu. 2023. "Weak Capacitance Detection Circuit of Micro-Hemispherical Gyroscope Based on Common-Mode Feedback Fusion Modulation and Demodulation" Micromachines 14, no. 6: 1161. https://doi.org/10.3390/mi14061161
APA StyleZhang, X., Li, P., Zhuang, X., Sheng, Y., Liu, J., Gao, Z., & Yu, Z. (2023). Weak Capacitance Detection Circuit of Micro-Hemispherical Gyroscope Based on Common-Mode Feedback Fusion Modulation and Demodulation. Micromachines, 14(6), 1161. https://doi.org/10.3390/mi14061161








