Development and Analysis of Graphene-Sheet-Based GaAs Schottky Solar Cell for Enriched Efficiency
Abstract
1. Introduction
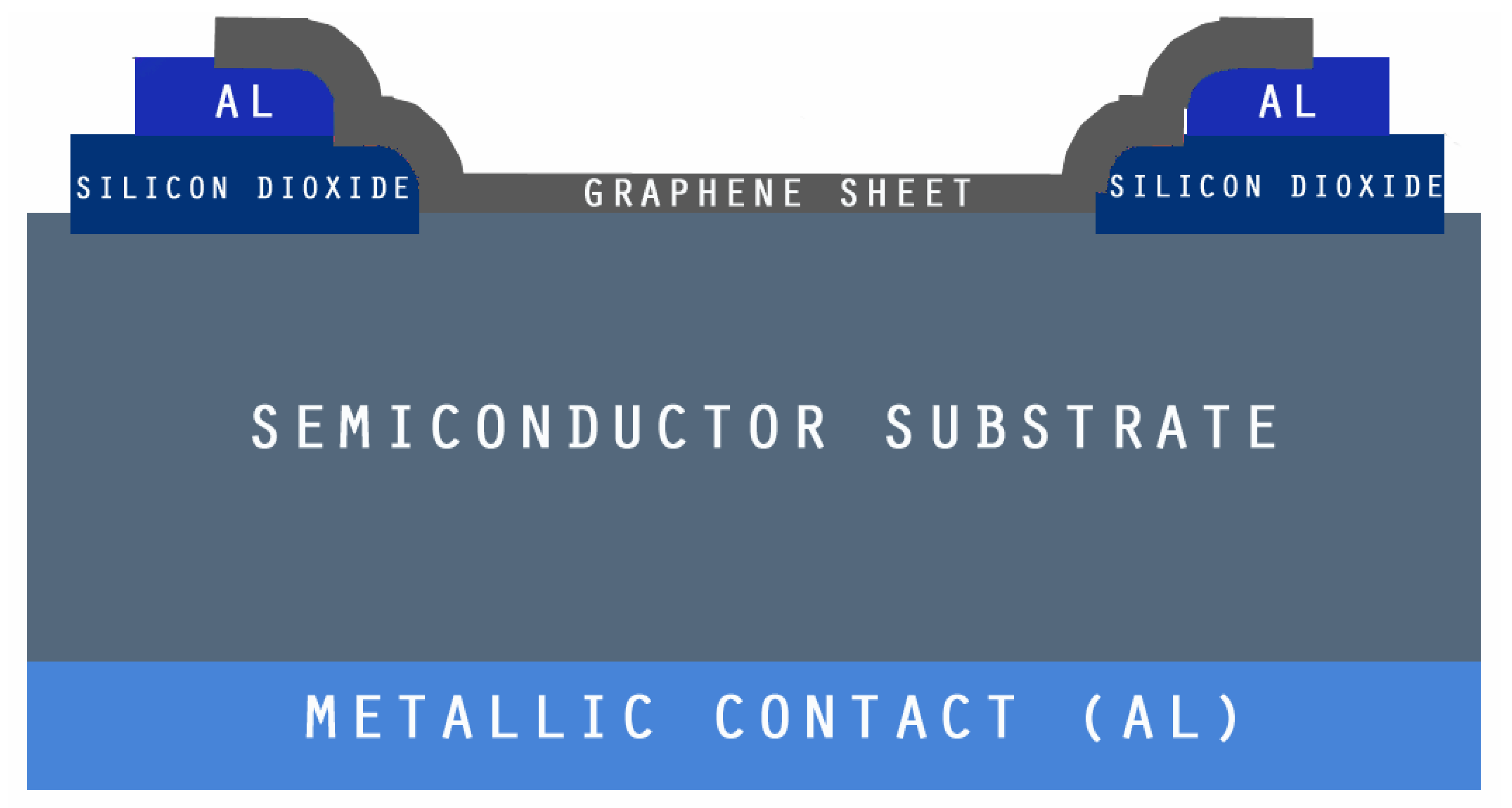
2. Modelling Semi-Transparent Top-Layer Graphene in Atlas
3. Modelling Graphene-Based Solar Cells
4. Results and Discussion
4.1. GaAs and Si Thickness Effect
4.2. Graphene Work Function Effect
4.3. GaAs and Silicon n-Type Doping Effect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Avouris, P.; Freitag, M. Graphene photonics, plasmonics, and optoelectronics. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 6000112. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, H.; Liu, Y.; Li, J. Graphene and its derivatives for the development of solar cells, photoelectrochemical, and photocatalytic applications. Energy Environ. Sci. 2013, 6, 1362–1387. [Google Scholar] [CrossRef]
- Gao, P.; Ding, K.; Wang, Y.; Ruan, K.; Diao, S.; Zhang, Q.; Sun, B.; Jie, J. Crystalline Si/graphene quantum dots heterojunction solar cells. J. Phys. Chem. C 2014, 118, 5164–5171. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, T.; Lv, R.; Zhu, H.; Wang, K.; Wu, D.; Kang, F. Improved efficiency of Graphene/Si heterojunction solar cells by optimizing hydrocarbon feed rate. J. Nanomater. 2014, 2014, 359305. [Google Scholar] [CrossRef]
- Miao, X.; Tongay, S.; Petterson, M.K.; Berke, K.; Rinzler, A.G.; Appleton, B.R.; Hebard, A.F. High Efficiency Graphene Solar Cells by Chemical Doping. Nano Lett. 2012, 12, 2745–2750. [Google Scholar] [CrossRef]
- Lei, Y.; Li, R.; Chen, F.; Xu, J. Hydrothermal synthesis of graphene-CdS composites with improved photoelectric characteristics. J. Mater. Sci. Mater. Electron. 2014, 25, 3057–3061. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, L.; Wang, K. Graphene CdSe nanobelt solar cells with tunable configurations. Nano Res. 2011, 9, 891–900. [Google Scholar] [CrossRef]
- Luo, L.B.; Chen, J.J.; Wang, M.Z.; Hu, H.; Wu, C.Y.; Li, Q.; Wang, L.; Huang, J.-A.; Liang, F.-X. Near-infrared light photovoltaic detector based on GaAs naocone array/monolayer graphene Schottky junction. Adv. Junctional Mater. 2014, 24, 2794–2800. [Google Scholar] [CrossRef]
- Jie, W.; Zheng, F.; Hao, J. Graphene/gallium arsenide-based Schottky junction solar cells. Appl. Phys. Lett. 2013, 103, 233111. [Google Scholar] [CrossRef]
- Aukerman, L.W.; Dvis, P.W.; Graft, R.D.; Shilliday, T.S. Radiation effects in GaAs. J. Appl. Phys. 1963, 34, 3590–3599. [Google Scholar] [CrossRef]
- Dohler, G.H.; Kunzel, H.; Olego, D.; Ploog, K.; Ruden, P.; Stolz, H.J.; Abstreiter, G. Observation of tunable band gap and two-dimensioanl subbands in a novel GaAs superlattice. Pysics Rev. Lett. 1981, 47, 864. [Google Scholar] [CrossRef]
- Tingting, F. Graphene based schottky junction solar cells on patterned silicon pillar array substrate. Appl. Phys. Lett. 2011, 99, 23505. [Google Scholar]
- Behura, S.K.; Nayak, S.; Mukhopadhyay, I.; Jani, O. Junction characteristics of chemically-derived graphene/p-Si heterojunction solar cell. Carbon 2014, 67, 766–774. [Google Scholar] [CrossRef]
- Li, X. Graphene on silicon schottky junction solar cells. Adv. Mater. 2010, 22, 2743–2748. [Google Scholar] [CrossRef] [PubMed]
- Xie, C.; Jie, J.; Nie, B.; Yan, T.; Li, Q.; Lv, P.; Li, F.; Wang, M.; Wu, C.; Wang, L.; et al. Schottky solar cells based on graphene nanoribbon/multiple silicon nanowires junctions. Appl. Phys. Lett. 2012, 100, 193103. [Google Scholar] [CrossRef]
- Zhang, X. High efficiency graphene/Si nanoarray schottky junction solar cells via surface modification and graphene doping. J. Mater. Chem. A 2013, 1, 6593–6601. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef]
- Weber, J.W.; Calado, V.E.; Van De Sanden, M.C.M. Optical constants of graphene measured by spectroscopic ellipsometry. Appl. Phys. Lett. 2010, 97, 091904. [Google Scholar] [CrossRef]
- Arefinia, Z.; Asgari, A. A new modeling approach for graphene based silicon nanowire Schottky junction solar cells. J. Renew. Sustain. Energy 2014, 6, 043132. [Google Scholar] [CrossRef]
- Silvaco. Atlas User’s Manual; Silvaco: Santa Clara, CA, USA, 2014; pp. 163–165. [Google Scholar]
- Lancellotti, L.; Polichetti, T.; Ricciardella, F.; Tari, O.; Gnanapragasam, S.; Daliento, S.; Di Francia, G. Graphene applications in Schottky barrier solar cells. Thin Solid Film. 2012, 522, 390–394. [Google Scholar] [CrossRef]
- Cui, T. Enhanced efficiency of graphene/silicon heterojunction solar cells by molecular doping. J. Mater. Chem. A 2013, 1, 5736–5740. [Google Scholar] [CrossRef]
- Sze, S.M.; Li, Y.; Ng, K.K. Physics of Semiconductor Devices; John Wiley & Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Singh, K.J.; Chettri, D.; Singh, T.J.; Thingujam, T.; Sarkar, S.K. A performance optimization and analysis of graphene based Schottky barrier GaAs solar cell. In Proceedings of the International Conference on Aerospace, Mechanical and Mechatronic Engineering, Bangkok, Thailand, 21–23 April 2017; IOP Publishing: Bristol, UK, 2017; Volume 211, p. 012024. [Google Scholar]
- Li, Y.F.; Yang, W.; Tu, Z.Q.; Liu, Z.C.; Yang, F.; Zhang, L.Q.; Hatakeyama, R. Schottky junction solar cells based on graphene with different numbers of layers. Appl. Phys. Lett. 2014, 104, 043903. [Google Scholar] [CrossRef]
- Kaung, Y. Modeling and design of graphene GaAs junction solar cell. Hindawi. Adv. Condens. Matter Phys. 2015, 2015, 326384. [Google Scholar] [CrossRef]
- Kaung, Y.; Lui, Y.; Ma, Y.; Xu, J.; Yang, X.; Feng, J. TCAD analysis of graphene silicon Schottky junction solar cell. In Proceedings of the International Symposium on Photonics and Optoelectronics, Shanghai, China, 22–24 August 2015; Volume s9656. [Google Scholar]















| Essential Layer Properties | ATLAS Identifier | Material Layer | ||
|---|---|---|---|---|
| Graphene | Substrate | |||
| 4H-SiC | GaAs | Silicon | ||
| Band gap layer Eg (eV) | EG | 0.0 | 1.42 | 1.08 |
| Relative permittivity, εr (F cm−1) | Permittivity | 25 | 13.1 | 13.5 |
| Electron affinity Xe (eV) | Affinity | 5.8 | 4.07 | 4.17 |
| Mobility, µp (cm2/V s) | MUP | 15,000 | 400 | 500 |
| Mobility, µn (cm2/V s) | MUN | 15,000 | 8000 | 1000 |
| Effective density of states Nc (cm−3) | NC300 | 3 × 1017 | 4 × 1017 | 2.8 × 1019 |
| Effective density of states Nv (cm−3) | NV300 | 3 × 1017 | 7 × 1018 | 1.0 × 1019 |
| Thickness (µm) | JSC (mA/cm2) | VOC (V) | FF (%) | Efficiency (%) | ||||
|---|---|---|---|---|---|---|---|---|
| GaAs | Si | GaAs | Si | GaAs | Si | GaAs | Si | |
| 1 | 6.10 | 2.76 | 1.00 | 0.29 | 51 | 28.69 | 3.29 | 2.37 |
| 2 | 6.80 | 3.26 | 0.97 | 0.29 | 51 | 31.88 | 5.03 | 3.11 |
| 5 | 7.90 | 4.14 | 0.94 | 0.18 | 49 | 58.08 | 4.74 | 4.51 |
| 10 | 8.40 | 4.72 | 0.93 | 0.19 | 45 | 60.21 | 4.58 | 5.47 |
| 20 | 9.00 | 5.05 | 0.91 | 0.19 | 45 | 60.95 | 4.58 | 5.99 |
| Graphene Work Function | JSC (mA/cm2) | VOC (V) | FF (%) | Efficiency (%) | ||||
|---|---|---|---|---|---|---|---|---|
| GaAs | Si | GaAs | Si | GaAs | Si | GaAs | Si | |
| 4.4 | 6.10 | 4.72 | 1.00 | 0.18 | 51 | 50.34 | 3.29 | 4.9 |
| 4.6 | 6.10 | 4.72 | 0.97 | 0.16 | 51 | 48.21 | 5.03 | 5.3 |
| 4.8 | 6.10 | 4.72 | 0.94 | 0.19 | 49 | 60.21 | 4.74 | 5.4 |
| Doping of n-Type Effect (/cm−3) | JSC (mA/cm2) | VOC (V) | FF (%) | Efficiency (%) | ||||
|---|---|---|---|---|---|---|---|---|
| GaAs | Si | GaAs | Si | GaAs | Si | GaAs | Si | |
| 3 × 1014 | 6.10 | 4.7 | 1.38 | 0.20 | 68 | 57.04 | 9.54 | 5.65 |
| 3 × 1015 | 6.10 | 4.7 | 1.37 | 0.19 | 66 | 59.73 | 9.52 | 6.50 |
| 3 × 1016 | 6.10 | 4.3 | 1.36 | 0.18 | 67 | 60.21 | 9.50 | 5.47 |
| GaAs Thickness (µm) | Work Function (ev) | N-Type Doping (/cm3) | JSC (mA/cm2) | VOC (V) | FF (%) | Efficiency (%) | |
| GaAs junction solar cell [26] | 5 | 4.8 | 1 × 1014 | 7.966 | 0.301 | 49 | 1.518 |
| Our proposed work | 5 | 4.8 | 3 × 1016 | 6.10 | 0.94 | 49 | 4.74 |
| Si Thickness (µm) | Work Function (ev) | N-Type Doping (/cm3) | JSC (mA/cm2) | VOC (V) | FF (%) | Efficiency (%) | |
| Si junction solar cell [27] | 20 | 4..8 | 1 × 1017 | 5.72 | 0.158 | 58 | 0.874 |
| Our proposed work | 20 | 4..8 | 3 × 1016 | 5.05 | 0.19 | 60.95 | 5.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phimu, L.K.; Dhar, R.S.; Singh, K.J.; Banerjee, A. Development and Analysis of Graphene-Sheet-Based GaAs Schottky Solar Cell for Enriched Efficiency. Micromachines 2023, 14, 1226. https://doi.org/10.3390/mi14061226
Phimu LK, Dhar RS, Singh KJ, Banerjee A. Development and Analysis of Graphene-Sheet-Based GaAs Schottky Solar Cell for Enriched Efficiency. Micromachines. 2023; 14(6):1226. https://doi.org/10.3390/mi14061226
Chicago/Turabian StylePhimu, L. Kholee, Rudra Sankar Dhar, Khomdram Jolson Singh, and Amit Banerjee. 2023. "Development and Analysis of Graphene-Sheet-Based GaAs Schottky Solar Cell for Enriched Efficiency" Micromachines 14, no. 6: 1226. https://doi.org/10.3390/mi14061226
APA StylePhimu, L. K., Dhar, R. S., Singh, K. J., & Banerjee, A. (2023). Development and Analysis of Graphene-Sheet-Based GaAs Schottky Solar Cell for Enriched Efficiency. Micromachines, 14(6), 1226. https://doi.org/10.3390/mi14061226






