Milling Stability Prediction: A New Approach Based on a Composited Newton–Cotes Formula
Abstract
:1. Introduction
2. Composited Newton–Cotes Formula
3. Mathematical Model
4. Simulation Analysis
4.1. Convergence Rate
4.2. Prediction Accuracy
4.3. Computational Efficiency
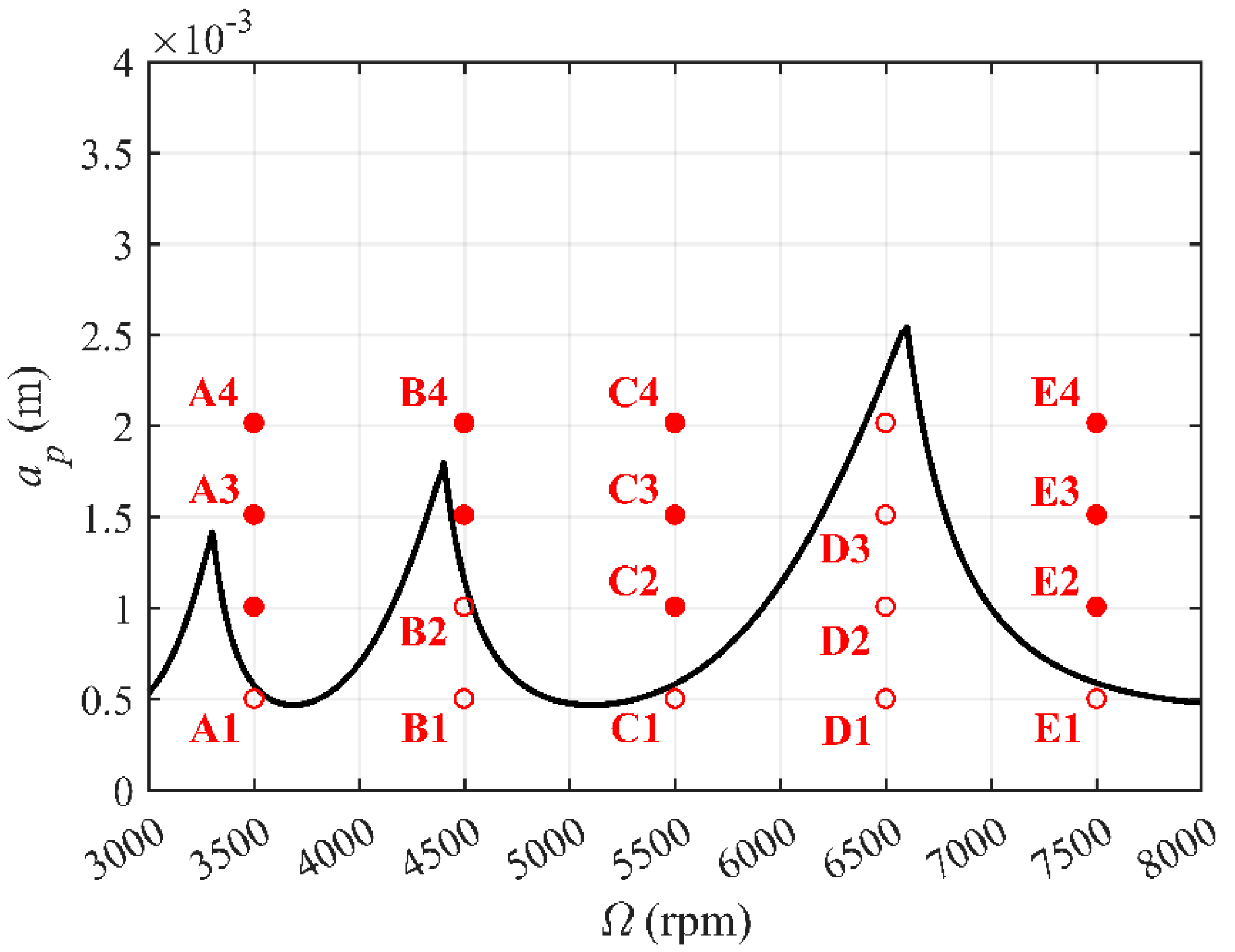
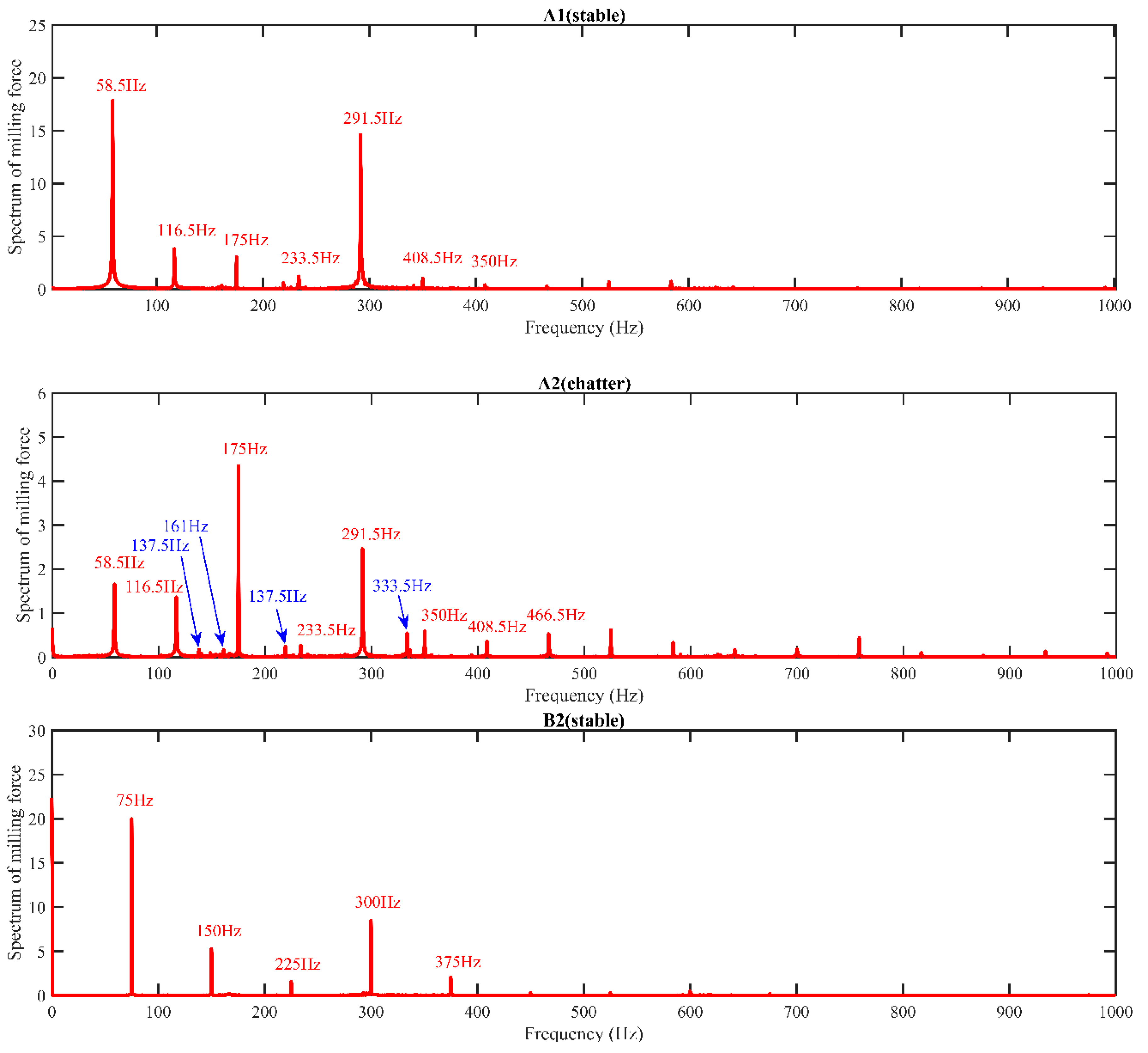
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Li, Y.; Zhang, D.; Zhao, B.; Wang, G.; Pang, X. A Novel Updated Full-Discretization Method for Prediction of Milling Stability. Micromachines 2022, 13, 160. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, J.; Wiercigroch, M. Modelling of regenerative and frictional cutting dynamics. Int. J. Mech. Sci. 2019, 156, 86–93. [Google Scholar] [CrossRef]
- Yue, C.; Gao, H.; Liu, X.; Liang, S.Y.; Wang, L. A review of chatter vibration research in milling. Chin. J. Aeronaut. 2019, 32, 215–242. [Google Scholar] [CrossRef]
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manfacture 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Rafal, R.; Pawel, L.; Krzysztof, K.; Bogdan, K. Chatter identification methods on the basis of time series measured during titanium superalloy milling. Int. J. Mech. Sci. 2015, 99, 196–207. [Google Scholar] [CrossRef]
- Albertelli, P.; Braghieri, L.; Torta, M.; Monno, M. Development of a generalized chatter detection methodogy for variable speed machining. Mech. Syst. Signal Process. 2019, 123, 26–42. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, X.; Liu, Z.; Wang, H.; Jiao, L.; Wang, D.; Leng, S. Early milling chatter identification by improved empirical mode decomposition and multi-indicator synthetic evaluation. J. Sound Vib. 2018, 433, 138–159. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Shi, J.; Song, Q.; Liu, Z.; Wan, Y. Formulating a numerically low-cost method of a constrained layer damper for vibration suppression in thin-walled component milling and experimental validation. Int. J. Mech. Sci. 2017, 128–129, 294–311. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Liu, X.; Zhang, W.; Meng, G. Chatter mitigation for the milling of thin-walled workpiece. Int. J. Mech. Sci. 2018, 138–139, 262–271. [Google Scholar] [CrossRef]
- Song, Q.; Liu, Z.; Wan, Y.; Ju, G.; Shi, J. Application of Sherman-Morrison-Woodbury formulas in instantaneous dynamic of peripheral milling for thin-walled component. Int. J. Mech. Sci. 2015, 96–97, 79–90. [Google Scholar] [CrossRef]
- Altintas, Y.; Weck, M. Chatter stability of metal cutting and grinding. CIRP Ann. 2004, 53, 619–642. [Google Scholar] [CrossRef]
- Wiercigtoch, M.; Budak, E. Sources of nonlinearities, chatter generation and suppression in metal cutting. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2001, 359, 663–693. [Google Scholar] [CrossRef] [Green Version]
- Altintas, Y.; Budak, E. Analytical prediction of stability lobes in milling. CIRP Ann. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Merdol, S.D.; Altintas, Y. Multi frequency solution of chatter stability for low immersion milling. J. Manuf. Sci. Eng. 2004, 126, 459. [Google Scholar] [CrossRef]
- Insperger, T.; Stepan, G. Semi-discretization method for delayed systems. Int. J. Numer. Methods Eng. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Insperger, T.; Stepan, G. Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int. J. Numer. Methods Eng. 2004, 61, 117–141. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, Y.; Yuan, X.; Liu, W. A second-order semi-discretization method for the efficient and accurate stability prediction of milling process. Int. J. Adv. Manuf. Technol. 2017, 92, 583–595. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. A full-discretization method for prediction of milling stability. Int. J. Mach. Tools Manuf. 2010, 50, 502–509. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Second-order full discretization method for milling stability prediction. Int. J. Mach. Tools Manuf. 2010, 50, 926–932. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, X.; Liu, Z.; Wang, D.; Li, J.; Ji, Y. Third-order updated full-discretization method for milling stability prediction. Int. J. Adv. Manuf. Technol. 2017, 92, 2299–2309. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Numerical integration method for prediction of milling stability. J. Manuf. Sci. Eng. 2011, 133, 031005. [Google Scholar] [CrossRef]
- Dong, X.; Qiu, Z. Stability analysis in milling process based on updated numerical integration method. Mech. Sytems Signal Process. 2020, 137, 106435. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Yu, G. An accurate and fast milling stability prediction approach based on the Newton-Cotes rules. Int. J. Mech. Sci. 2020, 177, 105469. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Li, L. An Adams-Moulton-based method for stability prediction of milling processes. Int. J. Adv. Manuf. Technol. 2017, 89, 3049–3058. [Google Scholar] [CrossRef]
- Lehotzky, D.; Insperger, T.; Khasawneh, F.; Stepan, G. Spectral element method for stability analysis of milling processes with discontinuous time-periodicity. Int. J. Adv. Manuf. Technol. 2017, 89, 2503–2514. [Google Scholar] [CrossRef] [Green Version]
- Ramirez, L.F.; Saldivar, B.; Vilchis, J.C.A.; Oca, S.M. Lyapunov-Krasovskii approach to the stability analysis of the milling process. IET Control Theory Appl. 2018, 12, 1332–1339. [Google Scholar] [CrossRef]
- Simos, T.E. Closed Newton—Cotes trigonometrically-fitted formulae of high order for long-time integration of orbital problems. Appl. Math. Lett. 2009, 22, 1616–1621. [Google Scholar] [CrossRef]
- Burg, C.O.E. Derivative-based closed Newton–Cotes numerical quadrature. Appl. Math. Comput. 2012, 218, 7052–7065. [Google Scholar] [CrossRef]
- Odibat, Z.M. Differential transform method for solving Volterra integral equation with separable kernels. Math. Comput. Model. 2008, 48, 1144–1149. [Google Scholar] [CrossRef]
- Qin, C.; Tao, J.; Shi, H.; Xiao, D.; Li, B.; Liu, C. A novel Chebyshev-wavelet-based approach for accurate and fast prediction of milling stability. Precis. Eng. 2020, 62, 244–255. [Google Scholar] [CrossRef]
- Hajdu, D.; Borgioli, F.; Michiels, W.; Insperger, T.; Stepan, G. Robust stability of milling operations based on pseudospectral approach. Int. J. Mach. Tools Manuf. 2020, 149, 103516. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, C.; Jia, J.; Ma, B.; Jiang, X.; Wang, D.; Zhu, T. High-order semi-discretization methods for stability analysis in milling based on precise integration. Precis. Eng. 2022, 73, 71–92. [Google Scholar] [CrossRef]
- Lou, W.; Qin, G.; Zuo, D. Investigation on Cotes-formula-based prediction method and its experimental verification of milling stability. J. Manuf. Process. 2021, 64, 1077–1088. [Google Scholar] [CrossRef]
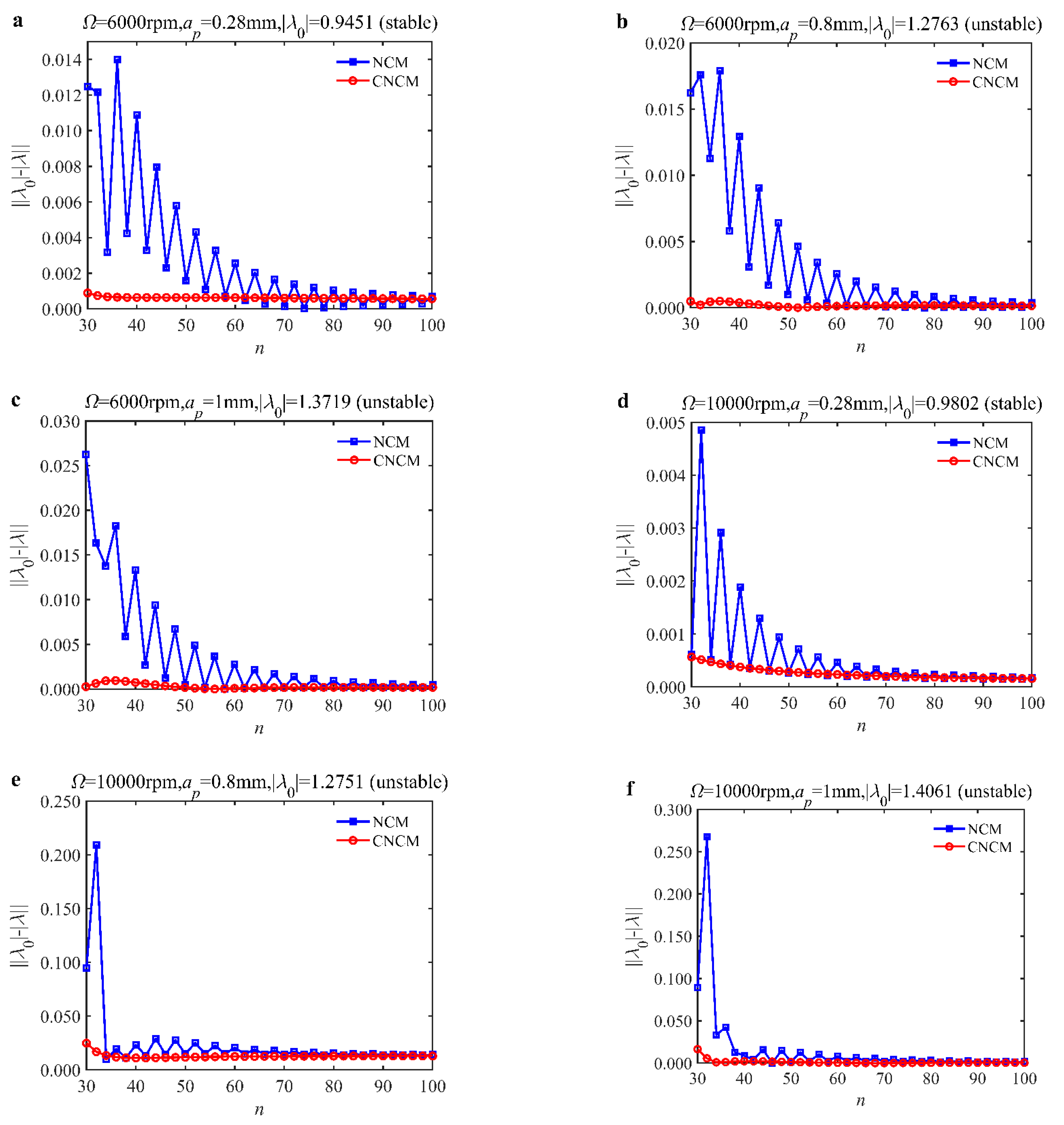
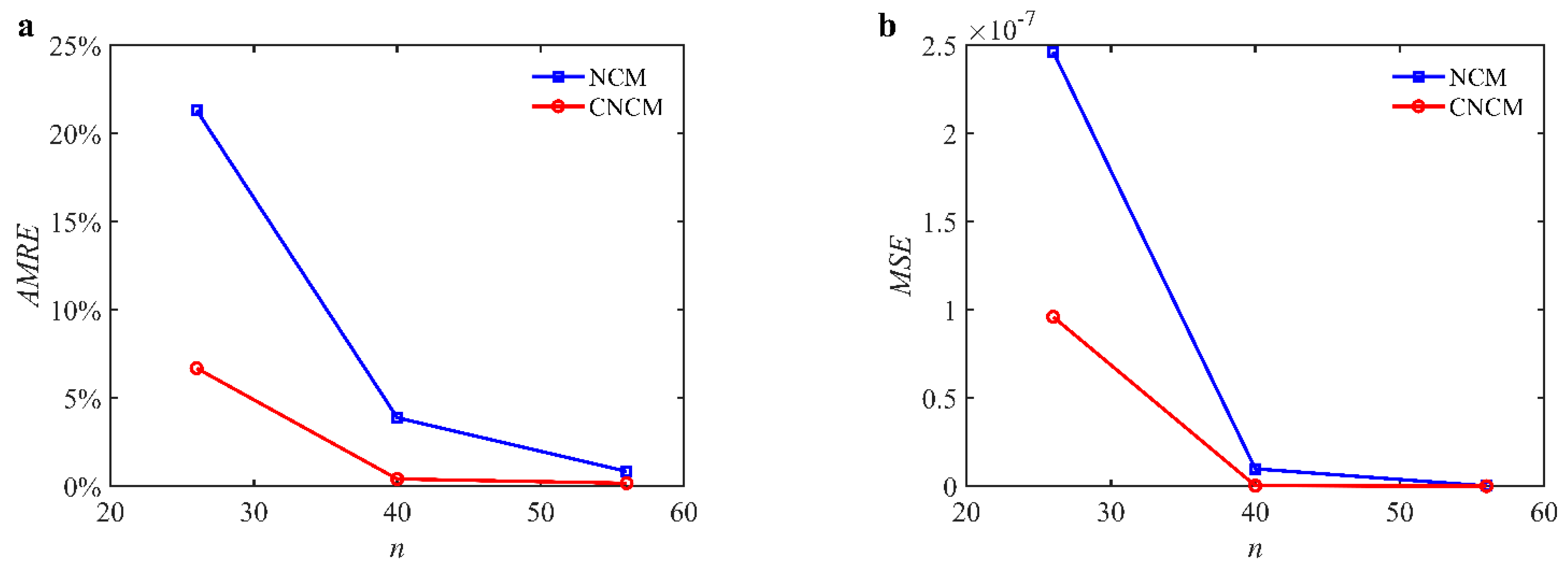
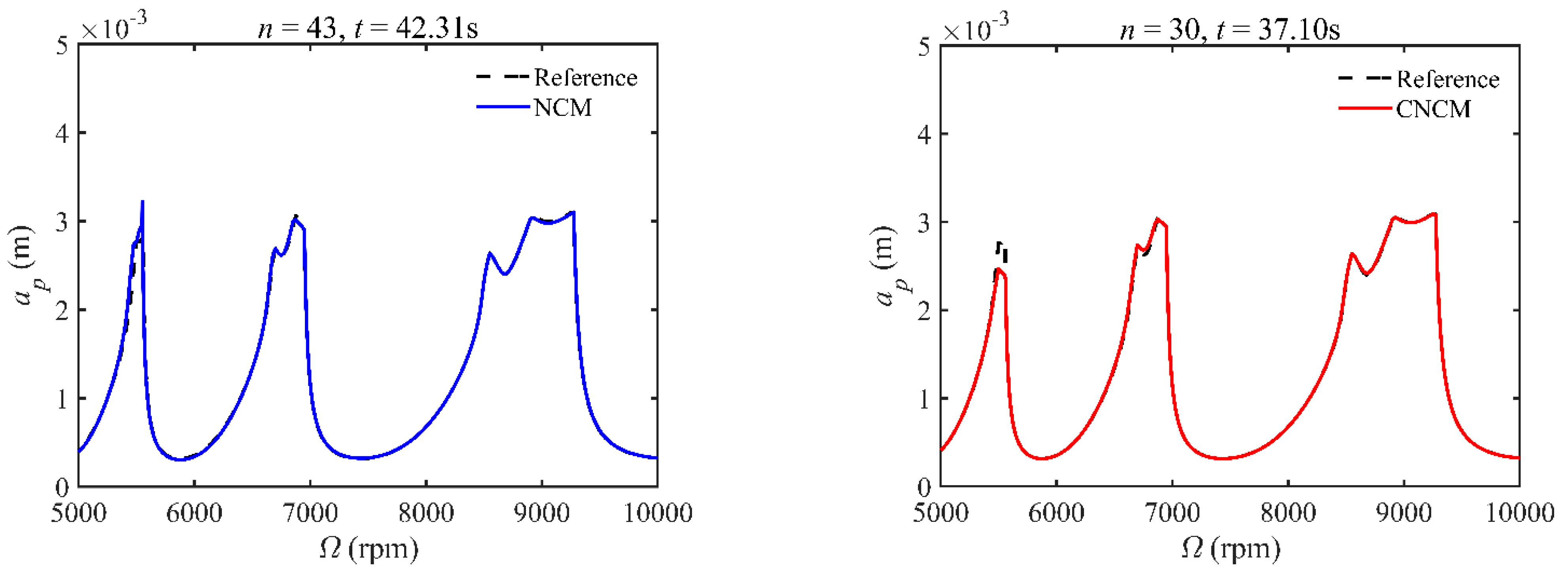
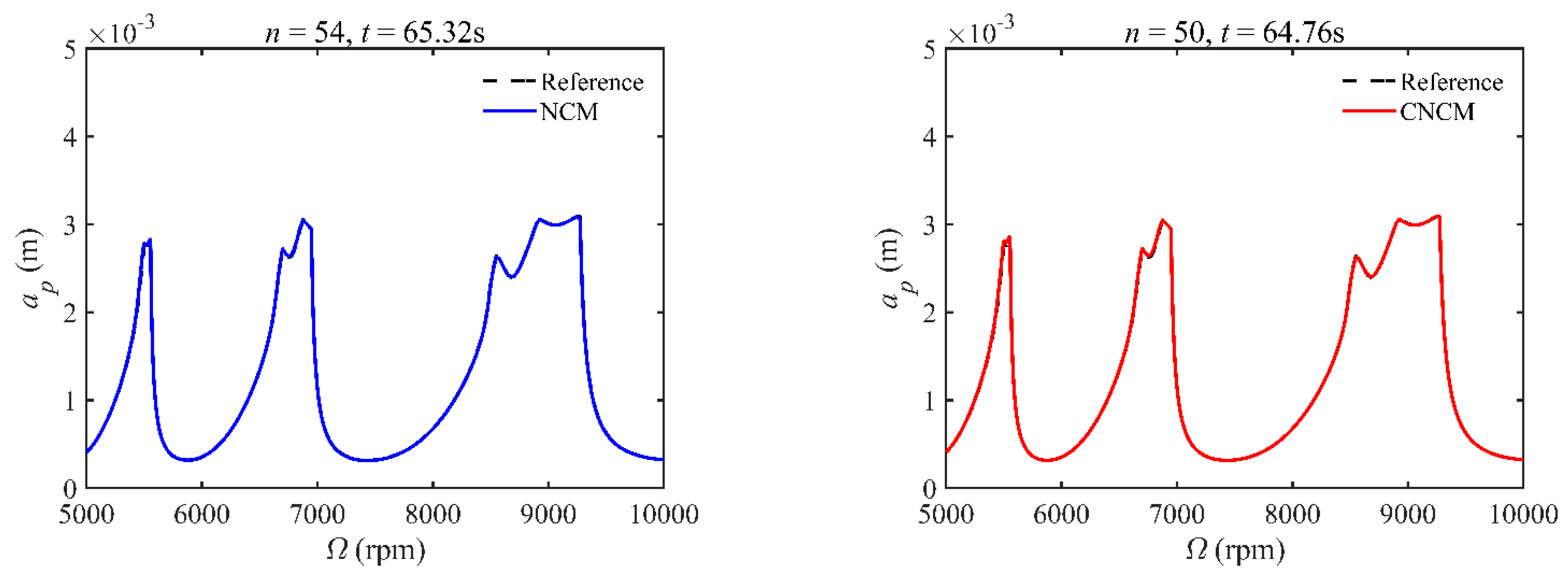




| Parameters | Symbols | Values |
|---|---|---|
| Modal mass (kg) | mt | 0.03993 |
| Damping ratio | ζ | 0.011 |
| Natural frequency (Hz) | ωn | 922 × 2π |
| Tangential linearized cutting force coefficient (N/m) | Kt | 6 × 108 |
| Normal linearized cutting force coefficient (N/m) | Kn | 2 × 108 |
| Number of tool teeth | Nt | 2 |
| Radial immersion ratio | a/D | 1 |
| n | NCM | CNCM |
|---|---|---|
| 26 | 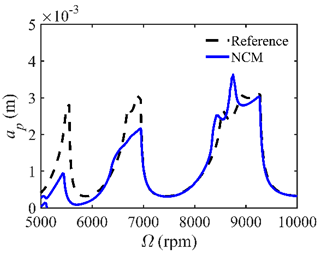 | 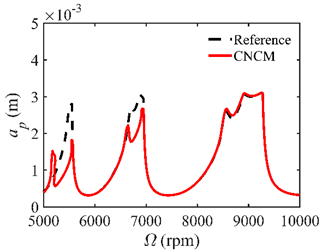 |
| 40 |  | 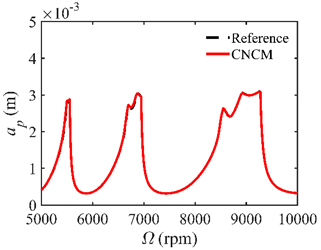 |
| 56 | 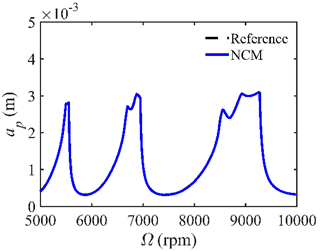 | 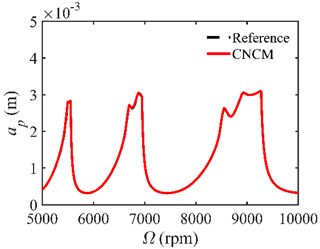 |
| Parameters | Symbols | Values |
|---|---|---|
| Modal mass (kg) | mt | 0.274 |
| Damping ratio | ζ | 0.0338 |
| Natural frequency (Hz) | ωn | 876 × 2π |
| Tangential linearized cutting force coefficient (N/m) | Kt | 5.5 × 108 |
| Normal linearized cutting force coefficient (N/m) | Kn | 3.75 × 108 |
| Number of tool teeth | Nt | 4 |
| Tool diameter (m) | D | 0.012 |
| Radio immersion ratio | a/D | 1 |
| Serial Numbers | Surface Roughness of the Measured Points (μm) | |||
|---|---|---|---|---|
| 1 | 2 | 3 | Average Values | |
| A1 | 1.490 | 1.647 | 1.738 | 1.625 |
| A2 | 2.997 | 2.053 | 2.127 | 2.392 |
| A3 | 2.879 | 2.135 | 2.371 | 2.462 |
| A4 | 2.967 | 2.817 | 2.947 | 2.910 |
| B1 | 1.068 | 1.190 | 1.286 | 1.181 |
| B2 | 1.496 | 1.447 | 1.561 | 1.501 |
| B3 | 2.287 | 2.332 | 2.317 | 2.312 |
| B4 | 2.242 | 2.294 | 2.143 | 2.226 |
| C1 | 1.089 | 1.594 | 1.407 | 1.363 |
| C2 | 2.335 | 2.486 | 2.358 | 2.393 |
| C3 | 2.423 | 2.506 | 2.712 | 2.547 |
| C4 | 2.673 | 2.685 | 2.837 | 2.732 |
| D1 | 1.265 | 1.330 | 1.340 | 1.312 |
| D2 | 1.563 | 1.453 | 1.526 | 1.514 |
| D3 | 1.744 | 1.475 | 1.745 | 1.655 |
| D4 | 1.997 | 1.945 | 1.868 | 1.937 |
| E1 | 1.374 | 1.269 | 1.273 | 1.305 |
| E2 | 3.286 | 2.881 | 3.066 | 3.078 |
| E3 | 3.293 | 3.792 | 2.775 | 3.287 |
| E4 | 3.609 | 3.360 | 3.379 | 3.449 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Ren, P.; Zhou, C.; Du, X. Milling Stability Prediction: A New Approach Based on a Composited Newton–Cotes Formula. Micromachines 2023, 14, 1304. https://doi.org/10.3390/mi14071304
Zheng J, Ren P, Zhou C, Du X. Milling Stability Prediction: A New Approach Based on a Composited Newton–Cotes Formula. Micromachines. 2023; 14(7):1304. https://doi.org/10.3390/mi14071304
Chicago/Turabian StyleZheng, Junqiang, Pengfei Ren, Chaofeng Zhou, and Xu Du. 2023. "Milling Stability Prediction: A New Approach Based on a Composited Newton–Cotes Formula" Micromachines 14, no. 7: 1304. https://doi.org/10.3390/mi14071304
APA StyleZheng, J., Ren, P., Zhou, C., & Du, X. (2023). Milling Stability Prediction: A New Approach Based on a Composited Newton–Cotes Formula. Micromachines, 14(7), 1304. https://doi.org/10.3390/mi14071304







