Implementation of Field-Programmable Gate Array Platform for Object Classification Tasks Using Spike-Based Backpropagated Deep Convolutional Spiking Neural Networks
Abstract
1. Introduction
1.1. Motivation
1.2. Purpose of Study
2. Literature Review
- We hosted deeper convolutions alongside SNNs with very few parameters compared to [49] and were still able to achieve similar accuracy over the MNIST and CIFAR10 datasets.
- We customized the proposed SGD-BP to fit the low-power needs of several target medium-sized intelligent vehicle industries in the form of FPGA implementation while preserving accuracy.
3. Spiking Schematic Design Framework
3.1. Spiking Neuron Model
3.2. Deep Convolutional Spiking Neural Networks (DCSNNs)
4. Training DCSNNs with Backpropagation
4.1. TSSL-BP for DCSNNs
4.2. SGD-BP for DCSNNs
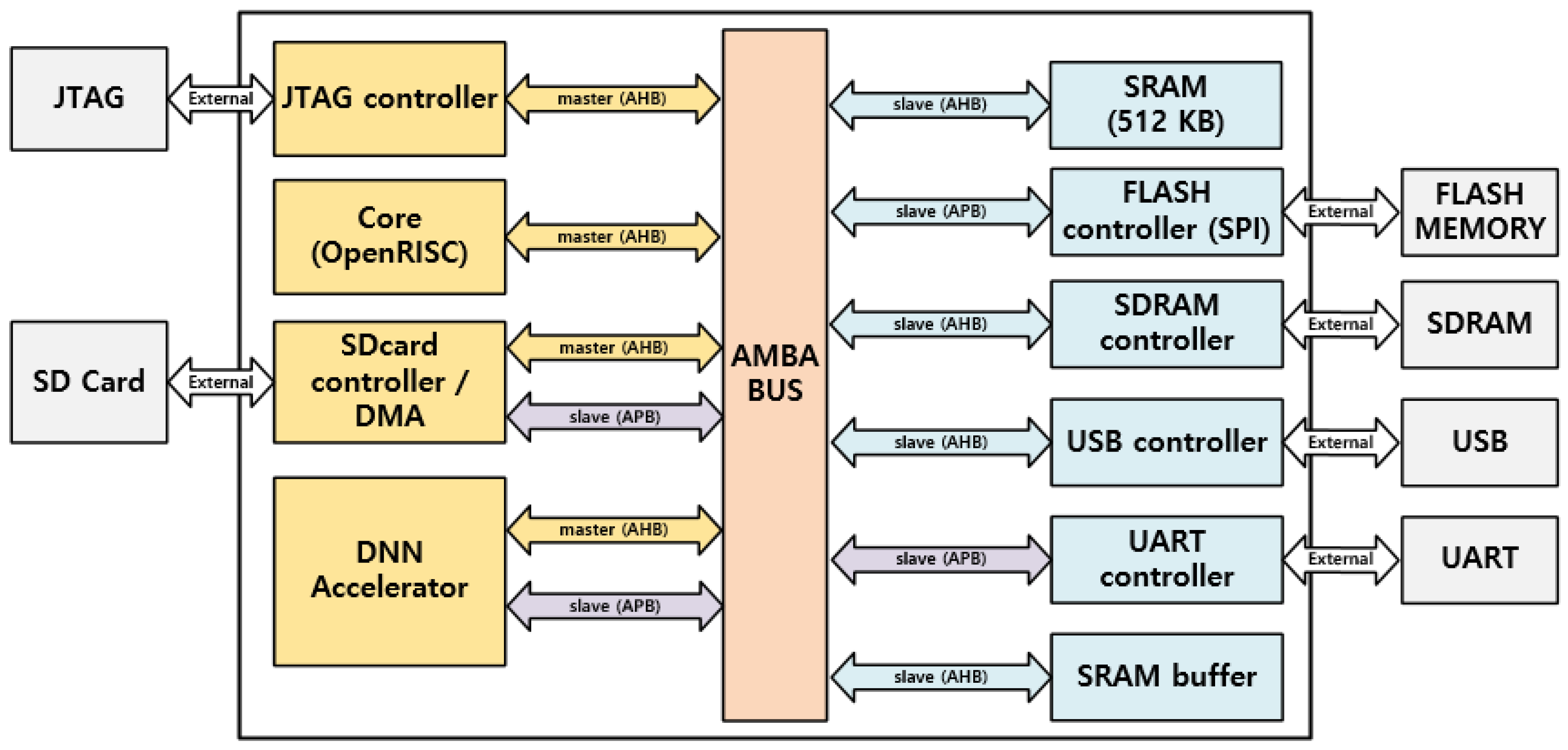
5. FPGA Schematic and Network Architecture
5.1. FPGA Design and Data Processing
5.2. Flow of Data in FPGA Board
5.3. DCSNN Architecture and Network Parameters
6. Experiments and Results
6.1. Public and Private Datasets
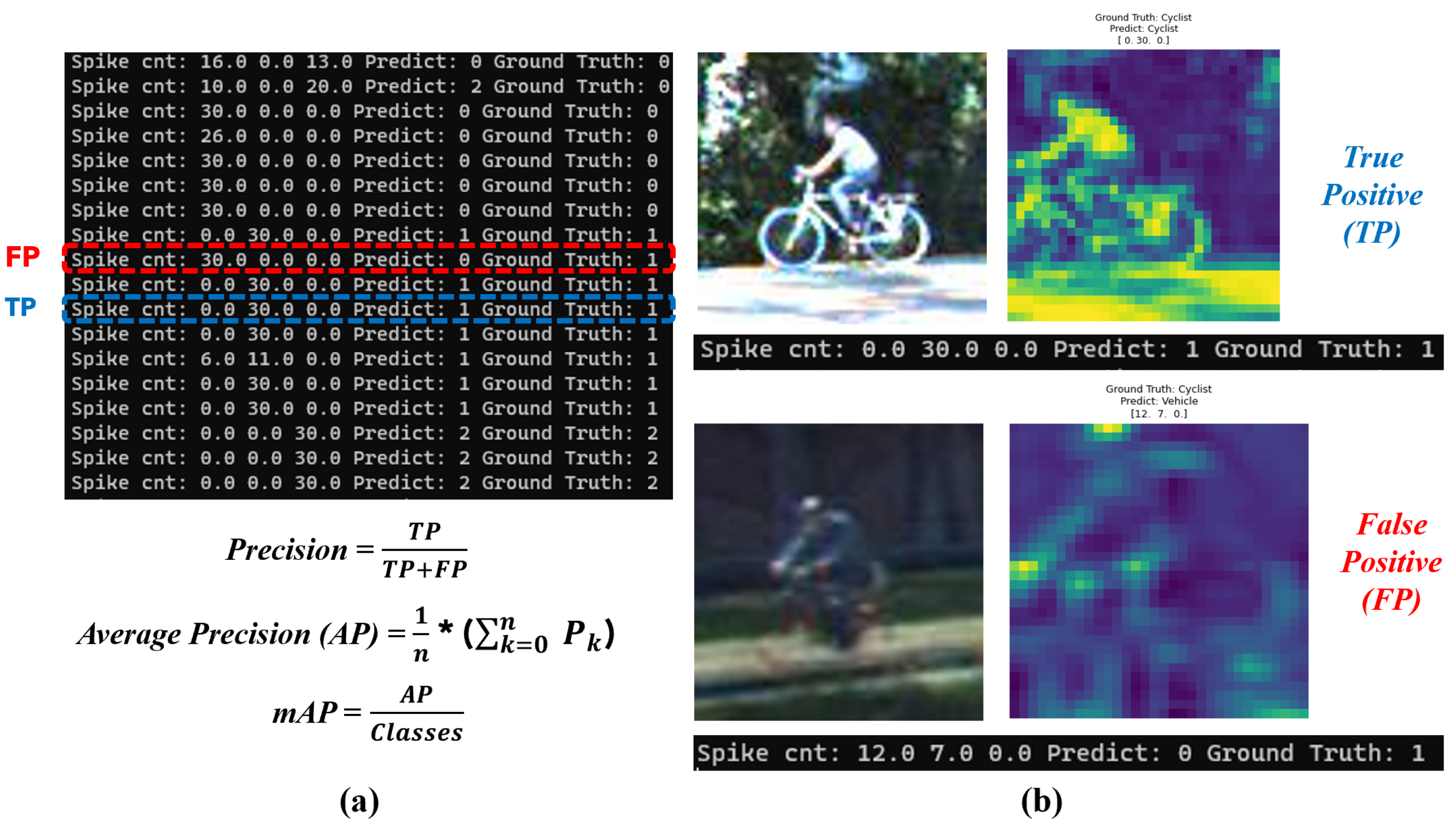
6.2. Performance Evaluations
7. Comparative Study of BP Techniques (TSSL-BP vs. SGD-BP)
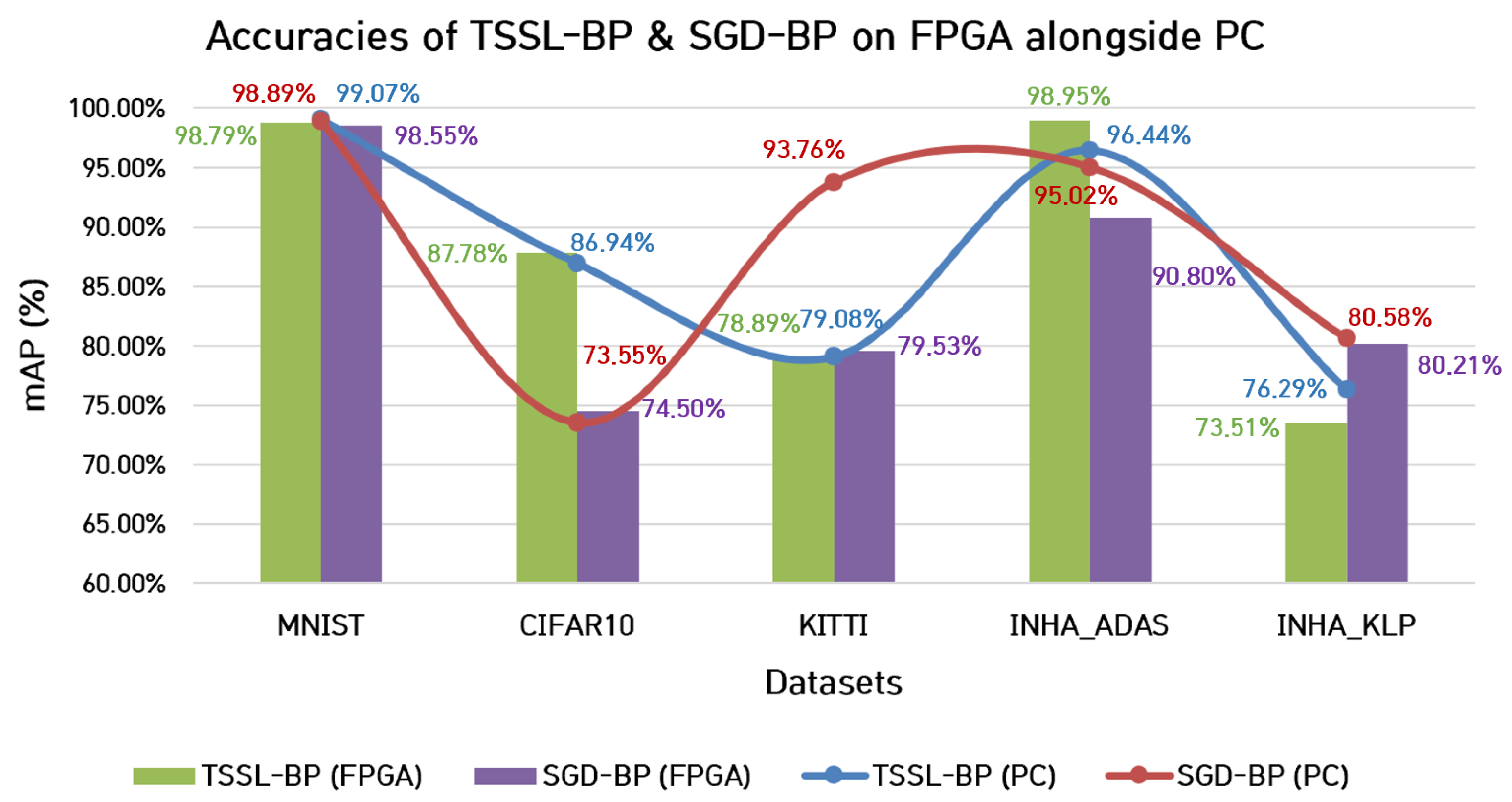
7.1. Classification Accuracy
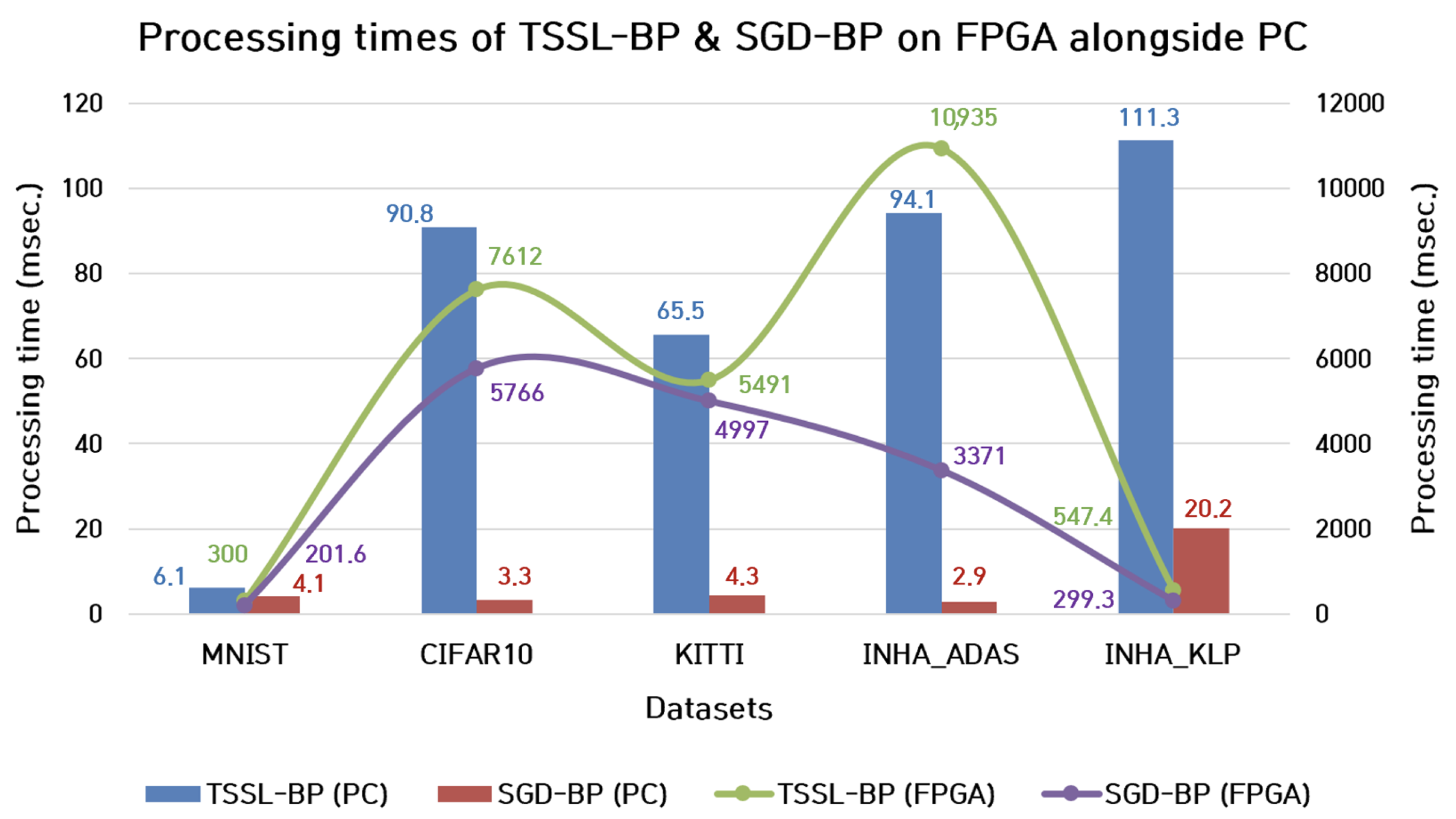
7.1.1. Processing Time
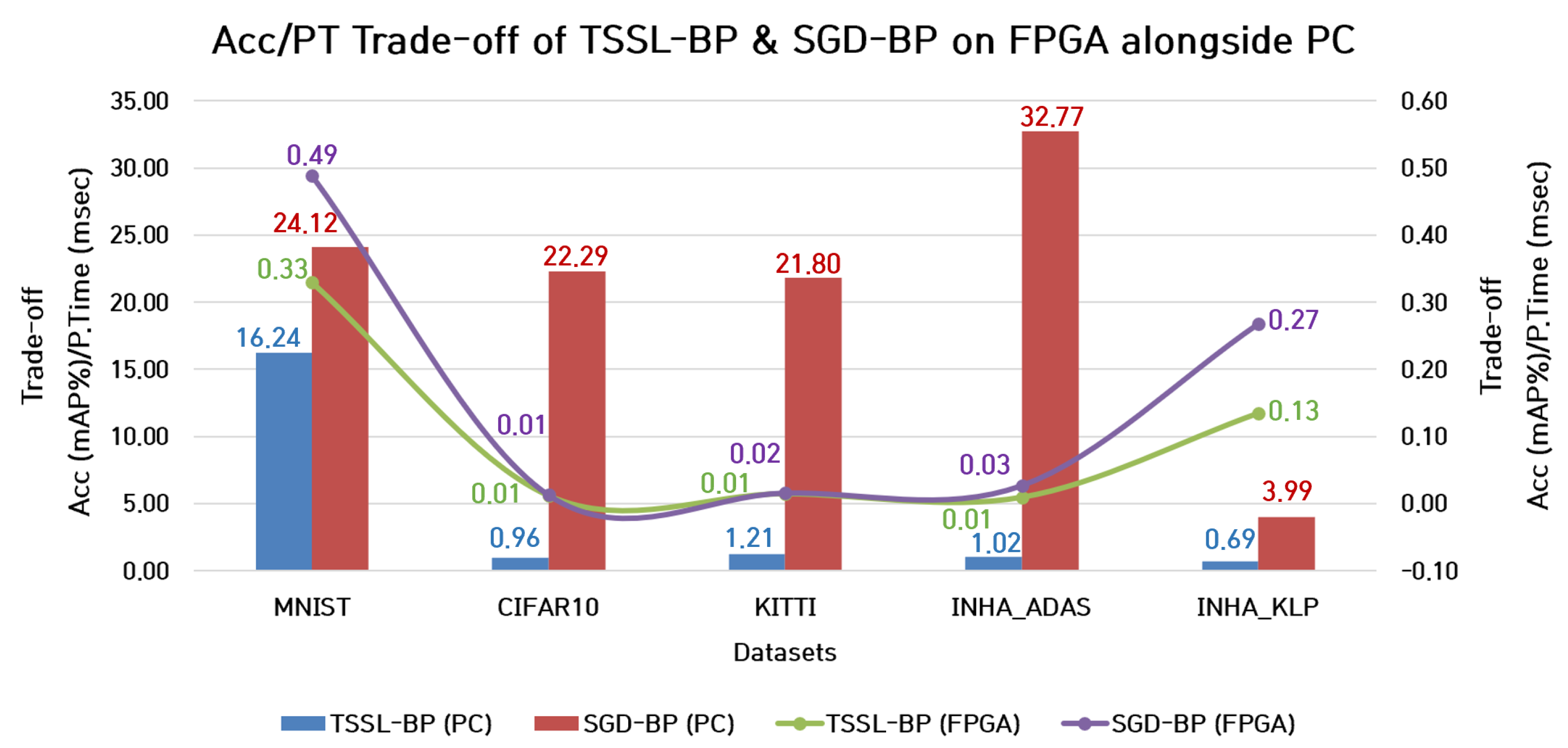
7.1.2. Trade-Off between Accuracy and Processing Time
7.2. Performance Analysis with Respect to Datasets on the FPGA Platform
7.3. Performance Analysis of the Current Study Alongside Other Works
8. Discussions, Limitations, and Future Work
- 1.
- The current work was limited to testing DCSNNs on a single FPGA model, Xilinx Kintex UltraScale. Due to the lack of open-source code, the performance analysis conducted in the study was unable to fully address the pros and cons of the model in comparison to contemporary works carried out on other FPGA models. In the future, this issue could be effectively resolved by contemplating multiple models of FPGA boards with similar on-chip SNN deployment design elements and evaluating various DCSNNs with respect to various datasets.
- 2.
- Experiments must be conducted to ensure that the surrogate gradient descent backpropagation technique is well-tuned to enhance classification accuracy on several ADAS-based private datasets while preserving the shallower network design layers.
- 3.
- Deeper networks (DCSNNs) are currently considered for massive datasets using TSSL-BP and SGD-BP. However, the network design could be expanded to shallow layered networks using the customized parametric surrogate gradient descent backpropagation technique (CPSGD-BP) for greater data size flexibility without compromising performance.
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DCSNN | Deep convolutional spiking neural network |
| TSSL-BP | Temporal spike sequence learning backpropagation |
| SGD-BP | Surrogate gradient descent via backpropagation |
| FPGA | Field-programmable gate array |
| MNIST | MNIST digit classification dataset |
| CIFAR10 | CIFAR object classification dataset with 10 object categories |
| INHA_ADAS | Advanced driver assistance systems vehicle classification dataset collected by INHA University |
| INHA_KLP | Korean license plate alphabet classification dataset collected by INHA University |
| LIF neuron | Leaky integrate firing neuron |
| IF neuron | Integrate firing neuron |
| STDP | Spike-time-dependent plasticity |
| UART | Universal asynchronous receiver–transmitter |
| AMBA | Advanced microcontroller bus architecture |
| CLB | Configurable logic block |
| v | Presynaptic neuron |
| u | Postsynaptic neuron |
| Input spike train | |
| Firing time of presynaptic neuron | |
| Postsynaptic current | |
| Membrane potential voltage | |
| Leaky resistance of the LIF neuron | |
| Membrane potential time constant | |
| Synaptic time constant | |
| Weight of the synaptic connection | |
| Reset mechanism in the spiking activity | |
| Response mechanism kernel | |
| Reset mechanism kernel | |
| Firing equilibrium | |
| Step function | |
| Distance between desired spikes | |
| Distance between produced (actual) spikes | |
| Firing events for desired spikes | |
| Firing events for produced (actual) spikes | |
| Total time steps | |
| Temporal spike loss function | |
| TSSL error at time t | |
| Van Rossum distance function | |
| SGD error at time t | |
| Ground-truth classification labels | |
| Z | Actual output of the network |
| Hyperparameter | |
| c | Gradient thickness |
References
- Tsai, H.F.; Podder, S.; Chen, P.Y. Microsystem Advances through Integration with Artificial Intelligence. Micromachines 2023, 14, 826. [Google Scholar] [CrossRef]
- Rahman, M.A.; Saleh, T.; Jahan, M.P.; McGarry, C.; Chaudhari, A.; Huang, R.; Tauhiduzzaman, M.; Ahmed, A.; Mahmud, A.A.; Bhuiyan, M.S.; et al. Review of Intelligence for Additive and Subtractive Manufacturing: Current Status and Future Prospects. Micromachines 2023, 14, 508. [Google Scholar] [CrossRef] [PubMed]
- Kakani, V.; Kim, H.; Lee, J.; Ryu, C.; Kumbham, M. Automatic Distortion Rectification of Wide-Angle Images Using Outlier Refinement for Streamlining Vision Tasks. Sensors 2020, 20, 894. [Google Scholar] [CrossRef] [PubMed]
- Kakani, V.; Kim, H.; Kumbham, M.; Park, D.; Jin, C.B.; Nguyen, V.H. Feasible Self-Calibration of Larger Field-of-View (FOV) Camera Sensors for the Advanced Driver-Assistance System (ADAS). Sensors 2019, 19, 3369. [Google Scholar] [CrossRef] [PubMed]
- Miraliev, S.; Abdigapporov, S.; Kakani, V.; Kim, H. Real-Time Memory Efficient Multitask Learning Model for Autonomous Driving. IEEE Trans. Intell. Veh. 2023; early access. [Google Scholar] [CrossRef]
- Kakani, V.; Cui, X.; Ma, M.; Kim, H. Vision-based tactile sensor mechanism for the estimation of contact position and force distribution using deep learning. Sensors 2021, 21, 1920. [Google Scholar] [CrossRef]
- Kakani, V.; Nguyen, V.H.; Kumar, B.P.; Kim, H.; Pasupuleti, V.R. A critical review on computer vision and artificial intelligence in food industry. J. Agric. Food Res. 2020, 2, 100033. [Google Scholar] [CrossRef]
- Abdigapporov, S.; Miraliev, S.; Alikhanov, J.; Kakani, V.; Kim, H. Performance Comparison of Backbone Networks for Multi-Tasking in Self-Driving Operations. In Proceedings of the 2022 22nd International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 27 November–1 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 819–824. [Google Scholar]
- Abdigapporov, S.; Miraliev, S.; Kakani, V.; Kim, H. Joint Multiclass Object Detection and Semantic Segmentation for Autonomous Driving. IEEE Access 2023, 11, 37637–37649. [Google Scholar] [CrossRef]
- Ghimire, A.; Kakani, V.; Kim, H. SSRT: A Sequential Skeleton RGB Transformer to Recognize Fine-grained Human-Object Interactions and Action Recognition. IEEE Access 2023, 11, 51930–51948. [Google Scholar] [CrossRef]
- Juraev, S.; Ghimire, A.; Alikhanov, J.; Kakani, V.; Kim, H. Exploring Human Pose Estimation and the Usage of Synthetic Data for Elderly Fall Detection in Real-World Surveillance. IEEE Access 2022, 10, 94249–94261. [Google Scholar] [CrossRef]
- Pagoli, A.; Chapelle, F.; Corrales-Ramon, J.A.; Mezouar, Y.; Lapusta, Y. Large-Area and Low-Cost Force/Tactile Capacitive Sensor for Soft Robotic Applications. Sensors 2022, 22, 4083. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Ponulak, F.; Kasinski, A. Introduction to spiking neural networks: Information processing, learning and applications. Acta Neurobiol. Exp. 2011, 71, 409–433. [Google Scholar]
- Indiveri, G.; Horiuchi, T.K. Frontiers in neuromorphic engineering. Front. Neurosci. 2011, 5, 118. [Google Scholar] [CrossRef] [PubMed]
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Abbott, L.F. Theoretical neuroscience rising. Neuron 2008, 60, 489–495. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 1952, 116, 449. [Google Scholar] [CrossRef]
- Brette, R.; Gerstner, W. Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 2005, 94, 3637–3642. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Akopyan, F.; Sawada, J.; Cassidy, A.; Alvarez-Icaza, R.; Arthur, J.; Merolla, P.; Imam, N.; Nakamura, Y.; Datta, P.; Nam, G.J.; et al. Truenorth: Design and tool flow of a 65 mw 1 million neuron programmable neurosynaptic chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2015, 34, 1537–1557. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A neuromorphic manycore processor with on-chip learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Fang, H.; Mei, Z.; Shrestha, A.; Zhao, Z.; Li, Y.; Qiu, Q. Encoding, model, and architecture: Systematic optimization for spiking neural network in FPGAs. In Proceedings of the 2020 IEEE/ACM International Conference on Computer Aided Design (ICCAD), San Diego, CA, USA, 2–5 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–9. [Google Scholar]
- Lent, R. Evaluating the cognitive network controller with an SNN on FPGA. In Proceedings of the 2020 IEEE International Conference on Wireless for Space and Extreme Environments (WiSEE), Vicenza, Italy, 12–14 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 106–111. [Google Scholar]
- Pham, Q.T.; Nguyen, T.Q.; Hoang, P.C.; Dang, Q.H.; Nguyen, D.M.; Nguyen, H.H. A review of SNN implementation on FPGA. In Proceedings of the 2021 International Conference on Multimedia Analysis and Pattern Recognition (MAPR), Hanoi, Vietnam, 15–16 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Abdelsalam, A.M.; Boulet, F.; Demers, G.; Langlois, J.P.; Cheriet, F. An efficient FPGA-based overlay inference architecture for fully connected DNNs. In Proceedings of the 2018 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 3–5 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Khodamoradi, A.; Denolf, K.; Kastner, R. S2n2: A fpga accelerator for streaming spiking neural networks. In Proceedings of the 2021 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Virtual, 28 February–2 March 2021; pp. 194–205. [Google Scholar]
- Li, S.; Zhang, Z.; Mao, R.; Xiao, J.; Chang, L.; Zhou, J. A fast and energy-efficient snn processor with adaptive clock/event-driven computation scheme and online learning. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1543–1552. [Google Scholar] [CrossRef]
- Cardenas, A.; Guzman, C.; Agbossou, K. Development of a FPGA based real-time power analysis and control for distributed generation interface. IEEE Trans. Power Syst. 2012, 27, 1343–1353. [Google Scholar] [CrossRef]
- Fotis, G.; Vita, V.; Ekonomou, L. Machine learning techniques for the prediction of the magnetic and electric field of electrostatic discharges. Electronics 2022, 11, 1858. [Google Scholar] [CrossRef]
- Pavlatos, C.; Makris, E.; Fotis, G.; Vita, V.; Mladenov, V. Utilization of Artificial Neural Networks for Precise Electrical Load Prediction. Technologies 2023, 11, 70. [Google Scholar] [CrossRef]
- Zhang, W.; Li, P. Spike-train level backpropagation for training deep recurrent spiking neural networks. Adv. Neural Inf. Process. Syst. 2019, 32, 7800–7811. [Google Scholar]
- Jin, Y.; Zhang, W.; Li, P. Hybrid macro/micro level backpropagation for training deep spiking neural networks. Adv. Neural Inf. Process. Syst. 2018, 31, 7005–7015. [Google Scholar]
- Bohte, S.M.; Kok, J.N.; La Poutre, H. Error-backpropagation in temporally encoded networks of spiking neurons. Neurocomputing 2002, 48, 17–37. [Google Scholar] [CrossRef]
- Shrestha, S.B.; Orchard, G. Slayer: Spike layer error reassignment in time. Adv. Neural Inf. Process. Syst. 2018, 31, 1419–1428. [Google Scholar]
- Bellec, G.; Salaj, D.; Subramoney, A.; Legenstein, R.; Maass, W. Long short-term memory and learning-to-learn in networks of spiking neurons. Adv. Neural Inf. Process. Syst. 2018, 31, 795–805. [Google Scholar]
- Huh, D.; Sejnowski, T.J. Gradient descent for spiking neural networks. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Zenke, F.; Ganguli, S. Superspike: Supervised learning in multilayer spiking neural networks. Neural Comput. 2018, 30, 1514–1541. [Google Scholar] [CrossRef]
- Lee, J.H.; Delbruck, T.; Pfeiffer, M. Training deep spiking neural networks using backpropagation. Front. Neurosci. 2016, 10, 508. [Google Scholar] [CrossRef]
- Wu, Y.; Deng, L.; Li, G.; Zhu, J.; Shi, L. Spatio-temporal backpropagation for training high-performance spiking neural networks. Front. Neurosci. 2018, 12, 331. [Google Scholar] [CrossRef]
- Mostafa, H. Supervised learning based on temporal coding in spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 3227–3235. [Google Scholar] [CrossRef]
- Mozafari, M.; Ganjtabesh, M.; Nowzari-Dalini, A.; Thorpe, S.J.; Masquelier, T. Bio-inspired digit recognition using reward-modulated spike-timing-dependent plasticity in deep convolutional networks. Pattern Recognit. 2019, 94, 87–95. [Google Scholar] [CrossRef]
- Lu, H.; Liu, J.; Luo, Y.; Hua, Y.; Qiu, S.; Huang, Y. An autonomous learning mobile robot using biological reward modulate STDP. Neurocomputing 2021, 458, 308–318. [Google Scholar] [CrossRef]
- Kheradpisheh, S.R.; Ganjtabesh, M.; Thorpe, S.J.; Masquelier, T. STDP-based spiking deep convolutional neural networks for object recognition. Neural Netw. 2018, 99, 56–67. [Google Scholar] [CrossRef]
- Bing, Z.; Baumann, I.; Jiang, Z.; Huang, K.; Cai, C.; Knoll, A. Supervised learning in SNN via reward-modulated spike-timing-dependent plasticity for a target reaching vehicle. Front. Neurorobotics 2019, 13, 18. [Google Scholar] [CrossRef]
- Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate gradient learning in spiking neural networks: Bringing the power of gradient-based optimization to spiking neural networks. IEEE Signal Process. Mag. 2019, 36, 51–63. [Google Scholar] [CrossRef]
- Syed, T.; Kakani, V.; Cui, X.; Kim, H. Exploring optimized spiking neural network architectures for classification tasks on embedded platforms. Sensors 2021, 21, 3240. [Google Scholar] [CrossRef] [PubMed]
- Tehreem, S.; Kakani, V.; Cui, X.; Kim, H. Spiking Neural Networks Using Backpropagation. In Proceedings of the 2021 IEEE Region 10 Symposium (TENSYMP), Jeju, Republic of Korea, 23–25 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Zhang, W.; Li, P. Temporal spike sequence learning via backpropagation for deep spiking neural networks. Adv. Neural Inf. Process. Syst. 2020, 33, 12022–12033. [Google Scholar]
- Kakani, V.; Lee, S.; Cui, X.; Kim, H. Performance Analysis of Spiking Neural Network using Temporal Spike-based Backpropagation on Field Programmable Gate Array (FPGA) platform. In Proceedings of the 2022 IEEE Region 10 Symposium (TENSYMP), Mumbai, India, 1–3 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Huang, X.; Jones, E.; Zhang, S.; Xie, S.; Furber, S.; Goulermas, Y.; Marsden, E.; Baistow, I.; Mitra, S.; Hamilton, A. An FPGA implementation of convolutional spiking neural networks for radioisotope identification. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 22–28 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Wang, S.Q.; Wang, L.; Deng, Y.; Yang, Z.J.; Guo, S.S.; Kang, Z.Y.; Guo, Y.F.; Xu, W.X. Sies: A novel implementation of spiking convolutional neural network inference engine on field-programmable gate array. J. Comput. Sci. Technol. 2020, 35, 475–489. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Y.; Khosla, D. Spiking deep convolutional neural networks for energy-efficient object recognition. Int. J. Comput. Vis. 2015, 113, 54–66. [Google Scholar] [CrossRef]
- Sommer, J.; Özkan, M.A.; Keszocze, O.; Teich, J. Efficient Hardware Acceleration of Sparsely Active Convolutional Spiking Neural Networks. arXiv 2022, arXiv:2203.12437. [Google Scholar] [CrossRef]
- Aung, M.T.L.; Qu, C.; Yang, L.; Luo, T.; Goh, R.S.M.; Wong, W.F. DeepFire: Acceleration of convolutional spiking neural network on modern field programmable gate arrays. In Proceedings of the 2021 31st International Conference on Field-Programmable Logic and Applications (FPL), Dresden, Germany, 30 August–3 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 28–32. [Google Scholar]
- Irmak, H.; Corradi, F.; Detterer, P.; Alachiotis, N.; Ziener, D. A dynamic reconfigurable architecture for hybrid spiking and convolutional fpga-based neural network designs. J. Low Power Electron. Appl. 2021, 11, 32. [Google Scholar] [CrossRef]
- Panchapakesan, S.; Fang, Z.; Chandrachoodan, N. EASpiNN: Effective Automated Spiking Neural Network Evaluation on FPGA. In Proceedings of the 2020 IEEE 28th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Fayetteville, AR, USA, 3–6 May 2020; IEEE: Piscataway, NJ, USA, 2020; p. 242. [Google Scholar]
- Diehl, P.U.; Neil, D.; Binas, J.; Cook, M.; Liu, S.C.; Pfeiffer, M. Fast-classifying, high-accuracy spiking deep networks through weight and threshold balancing. In Proceedings of the 2015 International Joint Conference on Neural Networks (IJCNN), Killarney, Ireland, 12–17 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–8. [Google Scholar]
- Rueckauer, B.; Lungu, I.A.; Hu, Y.; Pfeiffer, M.; Liu, S.C. Conversion of continuous-valued deep networks to efficient event-driven networks for image classification. Front. Neurosci. 2017, 11, 682. [Google Scholar] [CrossRef]
- Ma, C.; Xu, J.; Yu, Q. Temporal dependent local learning for deep spiking neural networks. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18 June–2 July 2022; IEEE: Piscataway, NJ, USA, 2021; pp. 1–7. [Google Scholar]
- LeCun, Y.; Haffner, P.; Bottou, L.; Bengio, Y. Object recognition with gradient-based learning. In Shape, Contour and Grouping in Computer Vision; Springer: Berlin/Heidelberg, Germany, 1999; pp. 319–345. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 84–90. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3354–3361. [Google Scholar]










| Network Type | Hybrid [51] | Hybrid [52] | Hybrid [53] | Hybrid [54] | SNN [57] | SNN [55] | Hybrid [56] | Hybrid [49] | Hybrid (This Work) |
|---|---|---|---|---|---|---|---|---|---|
| FPGA Model | Xilinx Artix-7 | XCVU440 | Xilinx Virtex-6 ML605 | Xilinx Zynq UltraScale +XCZU7EV | Xilinx ZCU104 | Xilinx VC707 Xilinx ZCU102 Xilinx VCU118 | Xilinx Zynq Ultrascale+ | Xilinx Kintex UltraScale FPGA | Xilinx Kintex UltraScale FPGA xcku115-flvf1924-2-i |
| Datasets | Synthetic | MNIST SVHN CIFAR10 | DARPA CIFAR10 | MNIST CIFAR10 ImageNet | MNIST CIFAR10 | MNIST SVHN CIFAR10 | MNIST | MNIST CIFAR10 | MNIST CIFAR10 KITTI INHA_ADAS INHA_KLP |
| Encoding Scheme | Real-value spike | Real-value spike | Real-value spike | m-TTFS | Real-value spike | Real-value spike | Rate encoding | Real-value spike | Real-value and Poisson spike |
| Neuron Model | IF | IF | IF | LIF | IF | Izhikevich | LIF | LIF | LIF |
| Convolution Filter Optimization | Time division multiplexing (TDM) | None | None | None | None | None | Unrolling | None | None |
| Design Aspect | Value |
|---|---|
| Device model | Xilinx Kintex UltraScale FPGA (xcku115-flvf1924-2-i) |
| Maximum frequency | 80 Mhz |
| Quantization | 16-bit fixed point |
| Synchronization | Clock-based synchronization |
| CLB LUTs | 196,043 |
| CLB Registers | 172,011 |
| CLB | 32,102 |
| DSP | 415 |
| BRAM | 112 KB |
| SDRAM | 256 MB |
| Spike timing per fixed window | 12.5 ms |
| Input encoding scheme | Real-value spike encoding |
| Average latency to first spike | 303 ms |
| Input | Output | Layer | [Kernel, Stride] | Parameters |
|---|---|---|---|---|
| (32, 32, 3) | (32, 32, 96) | conv3-96 | [3 × 3, 1] | 2592 |
| (32, 32, 96) | (16, 16, 256) | conv3-256 | [3 × 3, 1] | 221,440 |
| (32, 32, 256) | (32, 32, 256) | pooling | [2 × 2, 3] | 0 |
| (16, 16, 256) | (8, 8, 384) | conv3-384 | [3 × 3, 1] | 885,120 |
| (16, 16, 384) | (16, 16, 384) | pooling | [2 × 2, 3] | 0 |
| (8, 8, 384) | (8, 8, 384) | conv3-384 | [3 × 3, 1] | 1,327,488 |
| (8, 8, 384) | (8, 8, 16,384) | conv3-256 | [3 × 3, 1] | 884,992 |
| (1, 1, 16,384) | (1, 1, 1024) | fc | [1 × 1, 0] | 16,777,216 |
| (1, 1, 1024) | (1, 1, 1024) | fc | [1 × 1, 0] | 1,048,576 |
| (1, 1, 1024) | (1, 1, 3) | fc | [1 × 1, 0] | 3072 |
| Input | Output | Layer | [Kernel, Stride] | Parameters |
|---|---|---|---|---|
| (32, 32, 3) | (32, 32, 32) | conv3-32 | [3 × 3, 1] | 864 |
| (32, 32, 32) | (32, 32, 32) | LIF-neuron | none | 0 |
| (32, 32, 32) | (32, 32, 64) | conv3-64 | [3 × 3, 1] | 18,432 |
| (32, 32, 64) | (32, 32, 64) | LIF-neuron | none | 0 |
| (32, 32, 64) | (16, 16, 64) | Avg.pooling | [2 × 2, 2] | 0 |
| (16, 16, 64) | (16, 16, 128) | conv3-128 | [3 × 3, 1] | 73,728 |
| (16, 16, 128) | (16, 16, 128) | LIF-neuron | none | 0 |
| (16, 16, 128) | (16, 16, 128) | conv3-128 | [3 × 3, 1] | 147,456 |
| (16, 16, 128) | (16, 16, 128) | LIF-neuron | none | 0 |
| (16, 16, 128) | (8, 8, 128) | Avg.pooling | [2 × 2, 2] | 0 |
| (8, 8, 128) | (8, 8, 256) | conv3-256 | [3 × 3, 1] | 294,912 |
| (8, 8, 256) | (8, 8, 256) | LIF-neuron | none | 0 |
| (8, 8, 256) | (8, 8, 256) | conv3-256 | [3 × 3, 1] | 589,824 |
| (8, 8, 256) | (8, 8, 256) | LIF-neuron | none | 0 |
| (8, 8, 256) | (4, 4, 256) | Avg.pooling | [2 × 2, 2] | 0 |
| (4, 4, 256) | (1, 1, 4096) | flatten | none | 0 |
| (1, 1, 4096) | (1, 1, 1024) | fc | [1 × 1, 0] | 4,194,304 |
| (1, 1, 1024) | (1, 1, 1024) | LIF-neuron | none | 0 |
| (1, 1, 1024) | (1, 1, 1024) | dropout | none | 0 |
| (1, 1, 1024) | (1, 1, 3) | fc | [1 × 1, 0] | 3072 |
| Dataset | Category | Classes | No. of Samples |
|---|---|---|---|
| MNIST | Public | 10 | 70,000 |
| CIFAR10 | Public | 10 | 60,000 |
| KITTI | Public | 3 | 48,100 |
| INHA_ADAS | Private | 3 | 30,722 |
| INHA_KLP | Private | 50 | 48,100 |
| Platform | Mean (%) | Best (%) | mAP (%) | Processing Time (ms) | Power Consumption (W) |
|---|---|---|---|---|---|
| CPU (Intel i7-12700) | 99.10 | 99.30 | 99.07 | 6.1 | 13.6 |
| FPGA (xcku115-flvf1924-2-i) | 98.50 | 98.80 | 98.79 | 300 | 0.74 |
| CPU (Intel i7-12700) | 99.1 | 99.15 | 98.89 | 4.1 | 12.91 |
| FPGA (xcku115-flvf1924-2-i) | 98.5 | 98.80 | 98.55 | 201.6 | 0.74 |
| Latency of TSSL-BP on FPGA with respect to MNIST dataset | 49× | ||||
| Latency of SGD-BP on FPGA with respect to MNIST dataset | 50× | ||||
| Average power efficiency of TSSL-BP on FPGA with respect to MNIST dataset | 18× | ||||
| Average power efficiency of SGD-BP on FPGA with respect to MNIST dataset | 18× | ||||
| Platform | Mean (%) | Best (%) | mAP (%) | Processing Time (ms) | Power Consumption (W) |
|---|---|---|---|---|---|
| CPU (Intel i7-12700) | 86.90 | 87.00 | 86.94 | 90.8 | 13.6 |
| FPGA (xcku115-flvf1924-2-i) | 87.00 | 87.80 | 87.78 | 7612 | 0.74 |
| CPU (Intel i7-12700) | 73.72 | 74.82 | 73.55 | 3.3 | 12.91 |
| FPGA (xcku115-flvf1924-2-i) | 74.51 | 75.02 | 74.50 | 5766 | 0.74 |
| Latency of TSSL-BP on FPGA with respect to CIFAR10 dataset | 83× | ||||
| Latency of SGD-BP on FPGA with respect to CIFAR10 dataset | 1747× | ||||
| Average power efficiency of TSSL-BP on FPGA with respect to CIFAR10 dataset | 18× | ||||
| Average power efficiency of SGD-BP on FPGA with respect to CIFAR10 dataset | 18× | ||||
| Platform | Mean (%) | Best (%) | mAP (%) | Processing Time (ms) | Power Consumption (W) |
|---|---|---|---|---|---|
| CPU (Intel i7-12700) | 86.17 | 86.52 | 79.2 | 65.5 | 13.6 |
| FPGA (xcku115-flvf1924-2-i) | 85.72 | 86.80 | 78.89 | 5491 | 0.74 |
| CPU (Intel i7-12700) | 97.31 | 97.45 | 80.58 | 4.3 | 12.91 |
| FPGA (xcku115-flvf1924-2-i) | 79.4 | 79.82 | 79.53 | 4997 | 0.74 |
| Latency of TSSL-BP on FPGA with respect to KITTI dataset | 83× | ||||
| Latency of SGD-BP on FPGA with respect to KITTI dataset | 1162× | ||||
| Average power efficiency of TSSL-BP on FPGA with respect to KITTI dataset | 18× | ||||
| Average power efficiency of SGD-BP on FPGA with respect to KITTI dataset | 18× | ||||
| Platform | Mean (%) | Best (%) | mAP (%) | Processing Time (ms) | Power Consumption (W) |
|---|---|---|---|---|---|
| CPU (Intel i7-12700) | 97.44 | 97.89 | 96.5 | 94.1 | 13.6 |
| FPGA (xcku115-flvf1924-2-i) | 97.8 | 98.3 | 98.95 | 10,935 | 0.74 |
| CPU (Intel i7-12700) | 99.18 | 99.15 | 95.02 | 2.9 | 12.91 |
| FPGA (xcku115-flvf1924-2-i) | 95.4 | 96.01 | 90.8 | 3771 | 0.74 |
| Latency of TSSL-BP on FPGA with respect to INHA_ADAS dataset | 115× | ||||
| Latency of SGD-BP on FPGA with respect to INHA_ADAS dataset | 1300× | ||||
| Average power efficiency of TSSL-BP on FPGA with respect to INHA_ADAS dataset | 18× | ||||
| Average power efficiency of SGD-BP on FPGA with respect to INHA_ADAS dataset | 18× | ||||
| Platform | Mean (%) | Best (%) | mAP (%) | Processing Time (ms) | Power Consumption (W) |
|---|---|---|---|---|---|
| CPU (Intel i7-12700) | 88.21 | 88.27 | 74.06 | 111.3 | 13.6 |
| FPGA (xcku115-flvf1924-2-i) | 87.00 | 88.27 | 73.51 | 547.4 | 0.74 |
| CPU (Intel i7-12700) | 98.24 | 98.46 | 80.58 | 20.2 | 12.91 |
| FPGA (xcku115-flvf1924-2-i) | 80.51 | 81.33 | 80.21 | 299.3 | 0.74 |
| Latency of TSSL-BP on FPGA with respect to INHA_KLP dataset | 5× | ||||
| Latency of SGD-BP on FPGA with respect to INHA_KLP dataset | 14× | ||||
| Average power efficiency of TSSL-BP on FPGA with respect to INHA_KLP dataset | 18× | ||||
| Average power efficiency of SGD-BP on FPGA with respect to INHA_KLP dataset | 18× | ||||
| Technique | MNIST | CIFAR10 | KITTI | INHA_ADAS | INHA_KLP |
|---|---|---|---|---|---|
| TSSL-BP | + | + | − | + | − |
| SGD-BP | + | − | + | − | + |
| Technique | MNIST | CIFAR10 | KITTI | INHA_ADAS | INHA_KLP |
|---|---|---|---|---|---|
| TSSL-BP | − | − | + | − | − |
| SGD-BP | + | + | + | + | + |
| Technique | MNIST | CIFAR10 | KITTI | INHA_ADAS | INHA_KLP |
|---|---|---|---|---|---|
| TSSL-BP | − | + | − | − | − |
| SGD-BP | + | + | + | + | + |
| Category | Sommer et al. [54] | Aung et al. [55] | TSSL-BP [49] | SGD-BP [47] |
|---|---|---|---|---|
| Model | Xilinx Zynq UltraScale +XCZU7EV | Xilinx VC707 | Xilinx Kintex UltraScale | Xilinx Kintex UltraScale |
| Quantization | 16 bits | 8 bits | 16 bits | 16 bits |
| Weight | None | 1.17M | 21.1M | 1.38M |
| Accuracy | 98.2% | 98.1% | 98.7% | 97.8% |
| Throughput | 21 FPS | 33 FPS | 3.3 FPS | 3.5 FPS |
| Category | Aung et al. [55] | TSSL-BP [49] | SGD-BP [47] |
|---|---|---|---|
| Model | Xilinx VCU118 | Xilinx Kintex UltraScale | Xilinx Kintex UltraScale |
| Quantization | 8 bits | 16 bits | 16 bits |
| Weight | 12M | 21.1M | 1.38M |
| Accuracy | 81.8% | 87.7% | 78.8% |
| Throughput | 4.04 FPS | 0.13 FPS | 0.17 FPS |
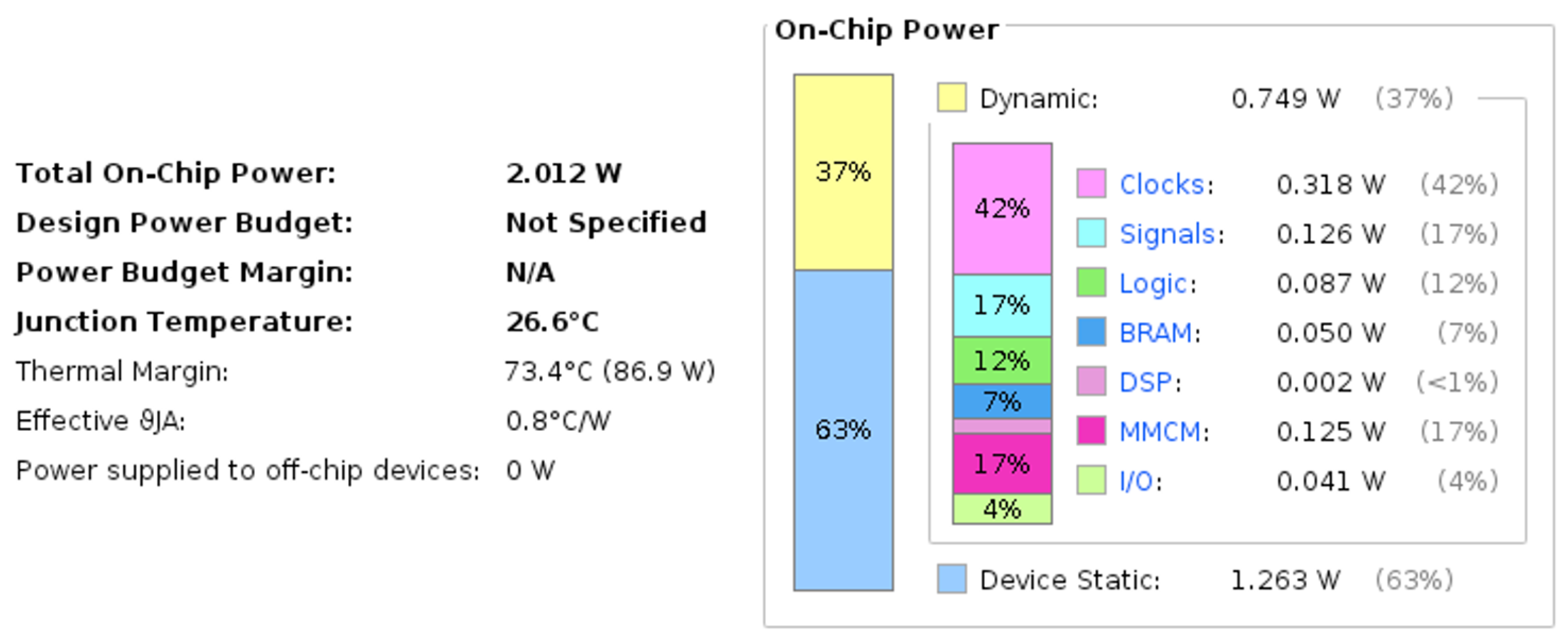
| Computation Device (Type and Model) | Precision (Bits) | Input Image Size (Pixel) | Average Power Consumption (W) | |
|---|---|---|---|---|
| TSSL-BP | SGD-BP | |||
| CPU (Intel i7-12700) | 16 (same for all datasets) | 32 × 32 (same for all datasets) | 13.6 | 12.91 |
| FPGA | 0.74 | 0.74 | ||
| (xcku115-flvf1924-2-i) | ||||
| The average power efficiency of FPGA was 18× | that of CPU across all the datasets | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kakani, V.; Li, X.; Cui, X.; Kim, H.; Kim, B.-S.; Kim, H. Implementation of Field-Programmable Gate Array Platform for Object Classification Tasks Using Spike-Based Backpropagated Deep Convolutional Spiking Neural Networks. Micromachines 2023, 14, 1353. https://doi.org/10.3390/mi14071353
Kakani V, Li X, Cui X, Kim H, Kim B-S, Kim H. Implementation of Field-Programmable Gate Array Platform for Object Classification Tasks Using Spike-Based Backpropagated Deep Convolutional Spiking Neural Networks. Micromachines. 2023; 14(7):1353. https://doi.org/10.3390/mi14071353
Chicago/Turabian StyleKakani, Vijay, Xingyou Li, Xuenan Cui, Heetak Kim, Byung-Soo Kim, and Hakil Kim. 2023. "Implementation of Field-Programmable Gate Array Platform for Object Classification Tasks Using Spike-Based Backpropagated Deep Convolutional Spiking Neural Networks" Micromachines 14, no. 7: 1353. https://doi.org/10.3390/mi14071353
APA StyleKakani, V., Li, X., Cui, X., Kim, H., Kim, B.-S., & Kim, H. (2023). Implementation of Field-Programmable Gate Array Platform for Object Classification Tasks Using Spike-Based Backpropagated Deep Convolutional Spiking Neural Networks. Micromachines, 14(7), 1353. https://doi.org/10.3390/mi14071353








