Cutting-Force Modeling Study on Vibration-Assisted Micro-Milling of Bone Materials
Abstract
:1. Introduction
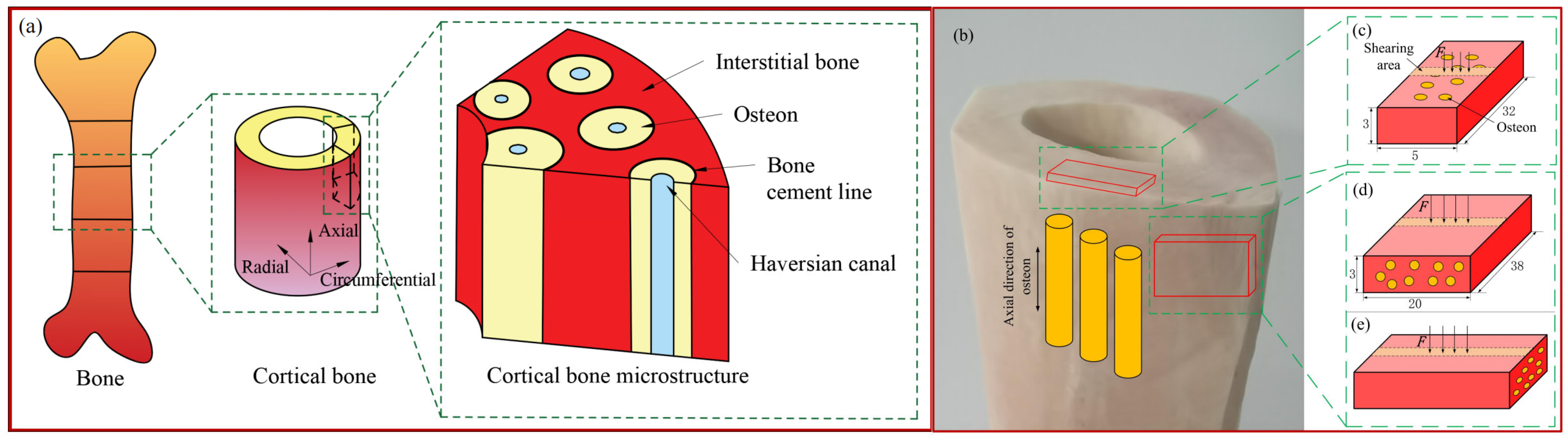
2. Mechanical Properties of Bone Materials
3. Vibration-Assisted Micro-Milling Force Modeling
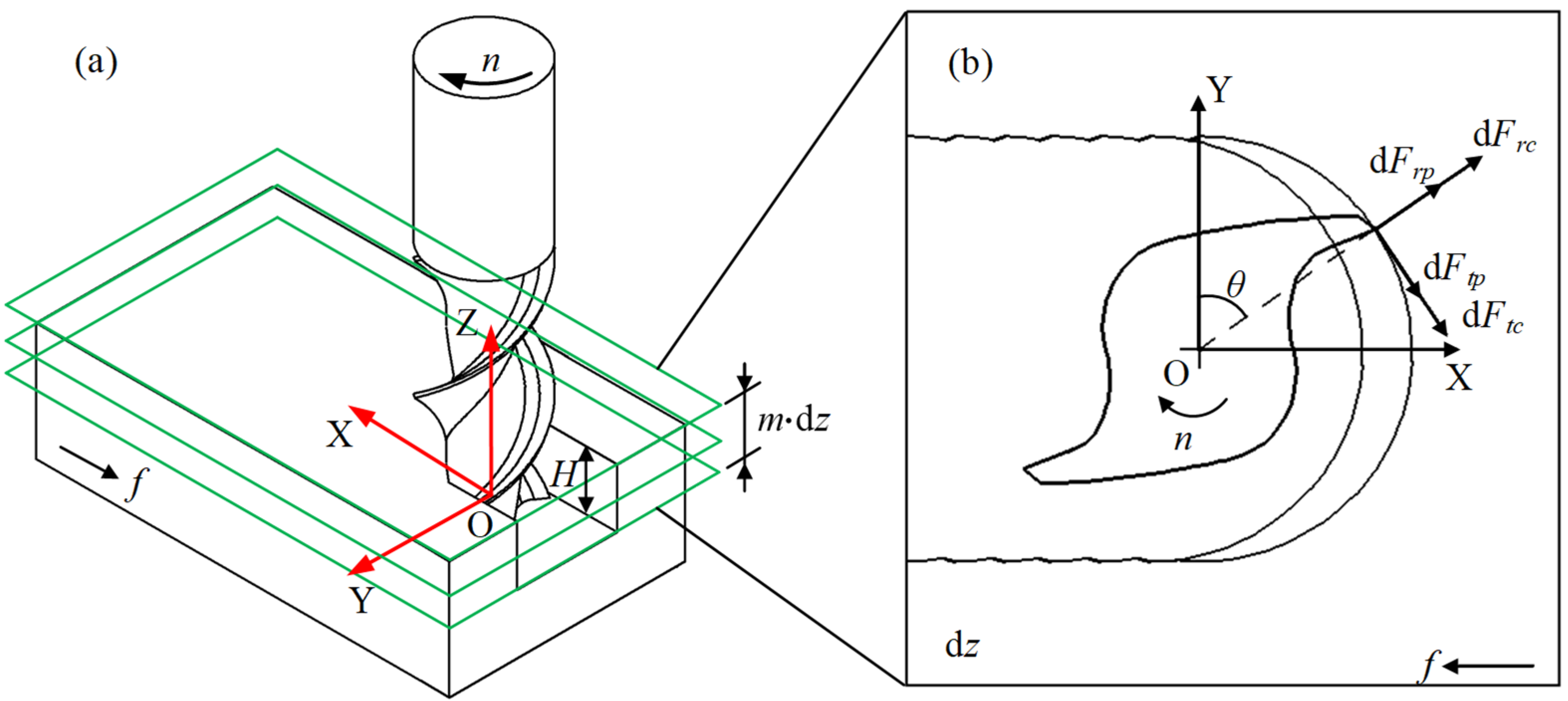
3.1. Anisotropic Cutting-Force Modeling of Bone Materials
3.2. Shear Force Coefficient Model
3.3. Ploughing Force Coefficient Model
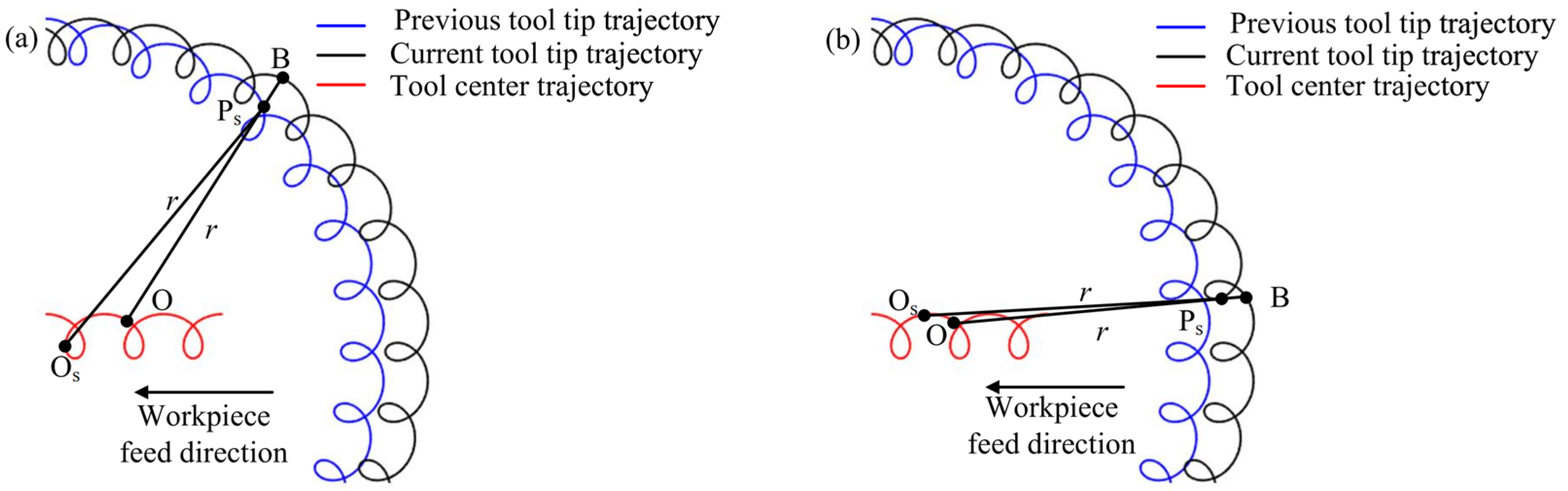
3.4. Instantaneous Cutting Thickness Model
- (1)
- Different cutting edges lead to empty cutting: when the tool center is located in O1 position, the current tool tip position B1 falls within the cutting trajectory already formed by the previous tool tip. Currently, the cutting edge is not involved in cutting and the cutting thickness is zero;
- (2)
- Chip formed by different cutting edges: when the tool center is located in O2 position, the current tool tip position B2 falls outside the cutting trajectory already formed by the previous tool tip and the instantaneous cutting thickness is A2B2;
- (3)
- The same cutting edge leads to empty cutting: when the tool center is located in the O3 position, the current tip position B4 falls within the cutting trajectory already formed by the tip. Currently, the cutting edge does not participate in cutting and the cutting thickness is zero;
- (4)
- Chip formed by the same cutting edge: when the tool center is located in O4 position, the current tool tip position B6 falls outside the cutting trajectory already formed by the tool tip and the instantaneous cutting thickness is B5B6.
4. Experimental Verification
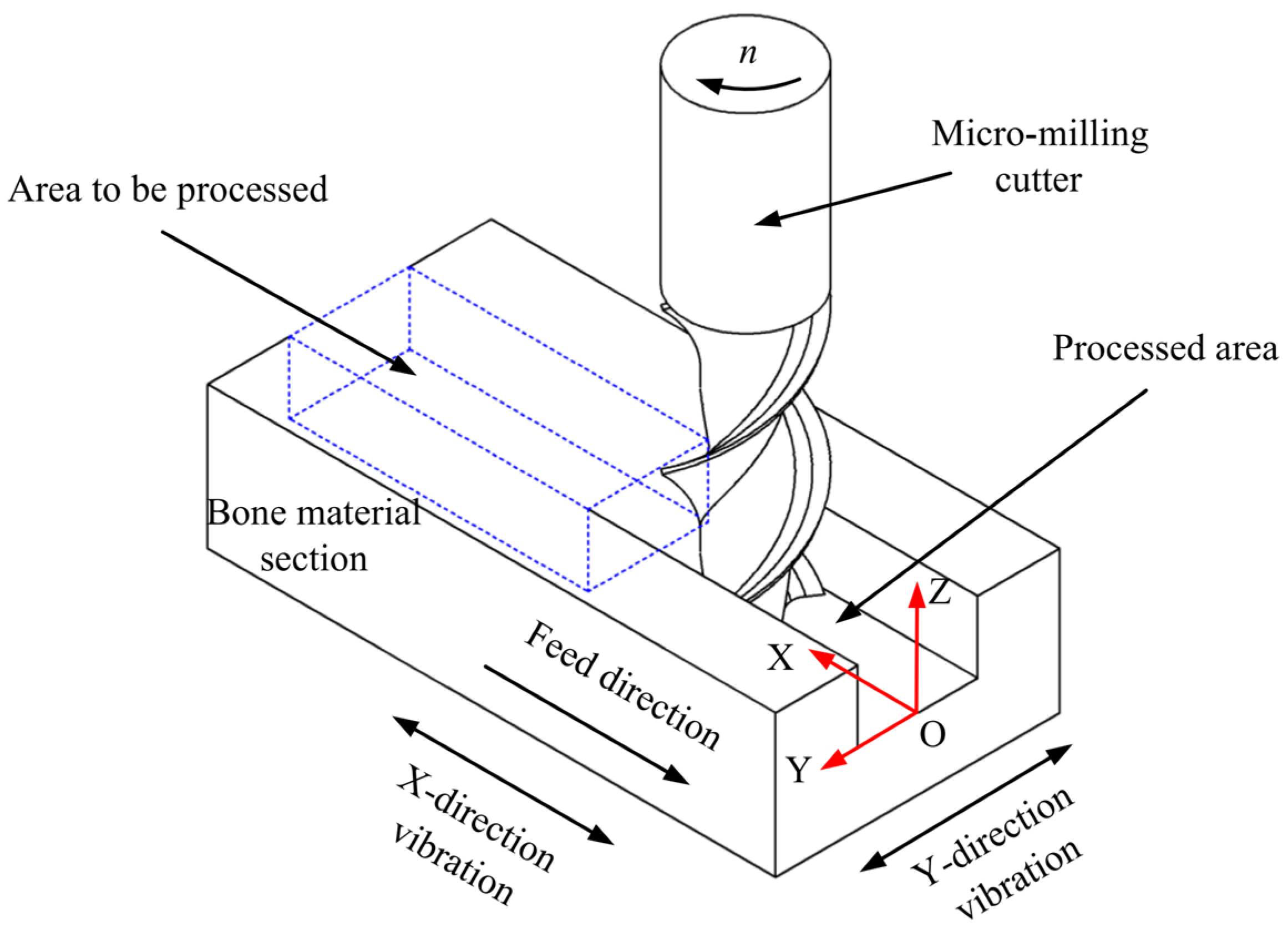
4.1. Vibration-Assisted Micro-Milling System
4.2. Analysis of Experimental Results
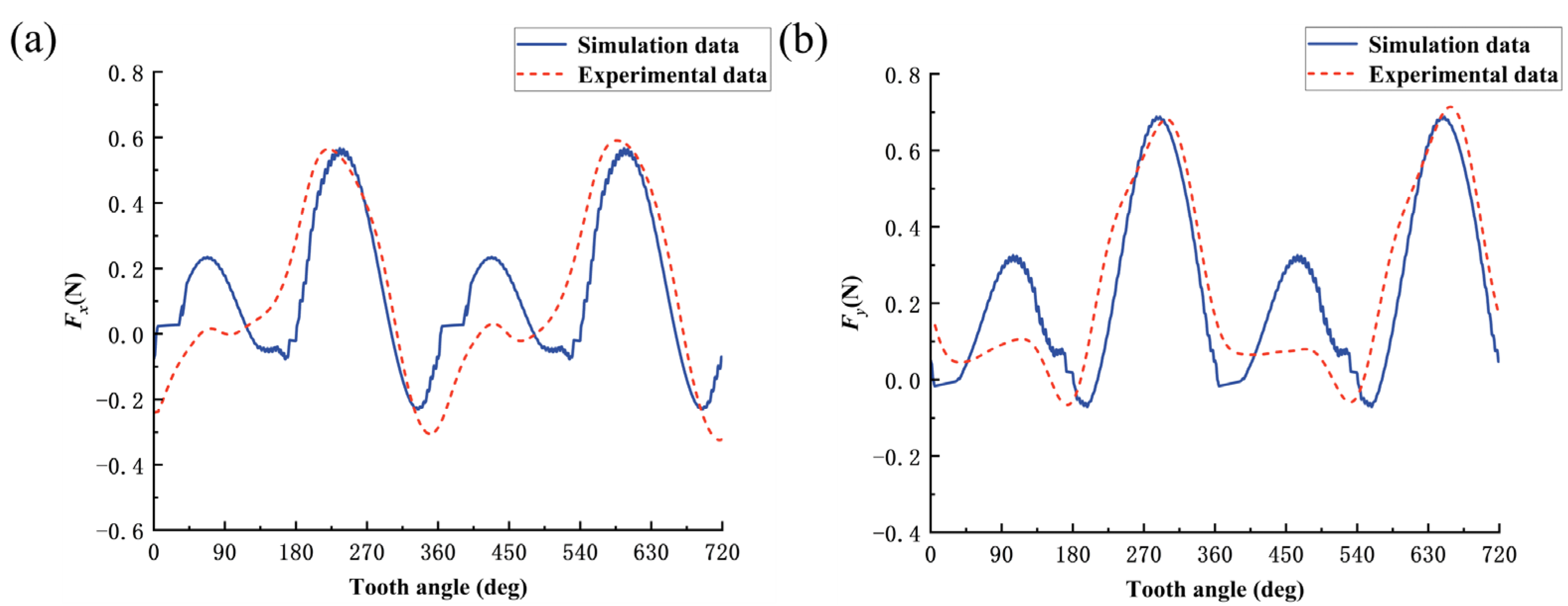
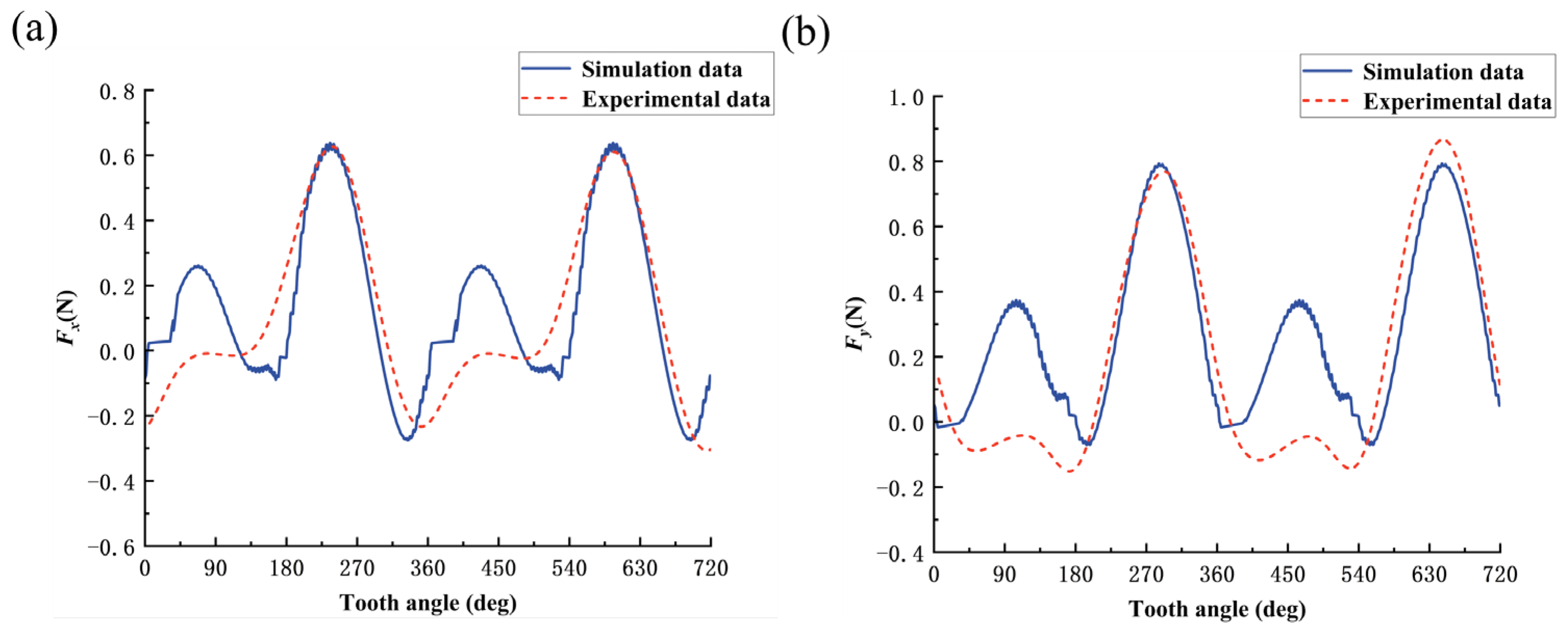
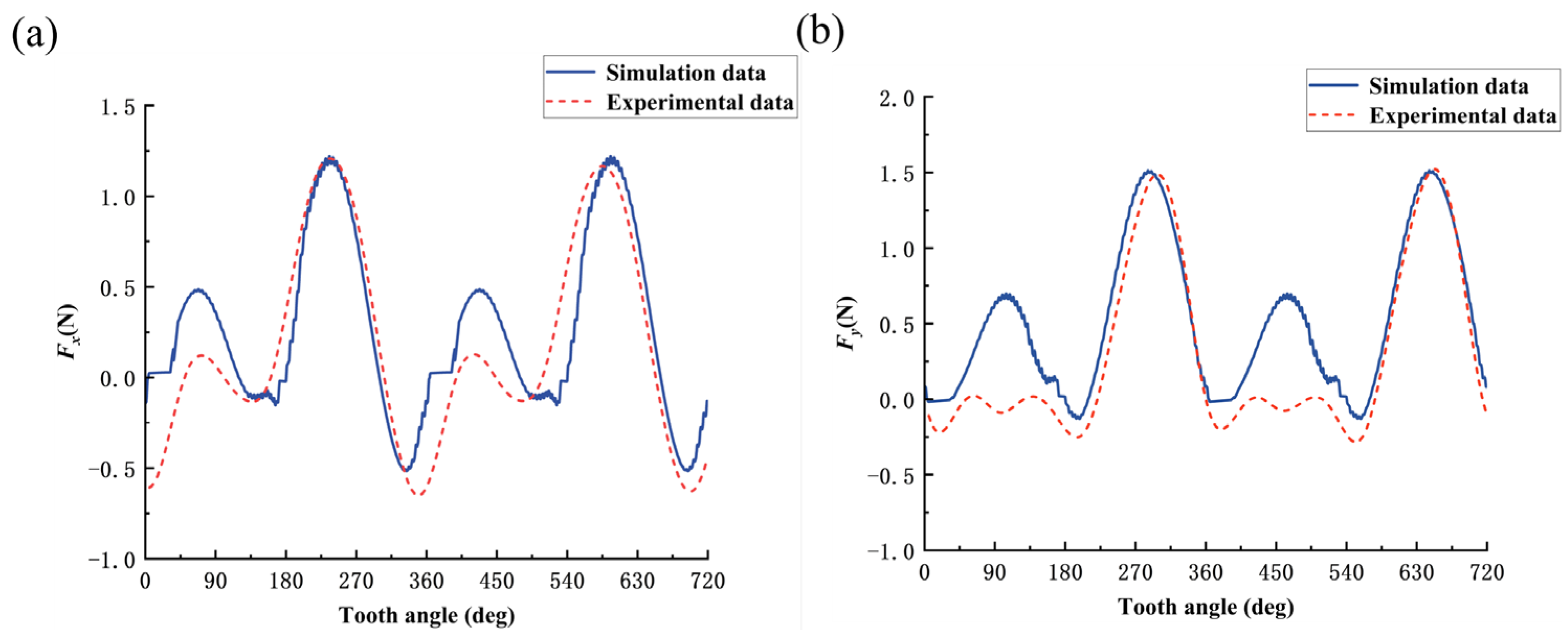
4.2.1. Cutting-Force Model Validation
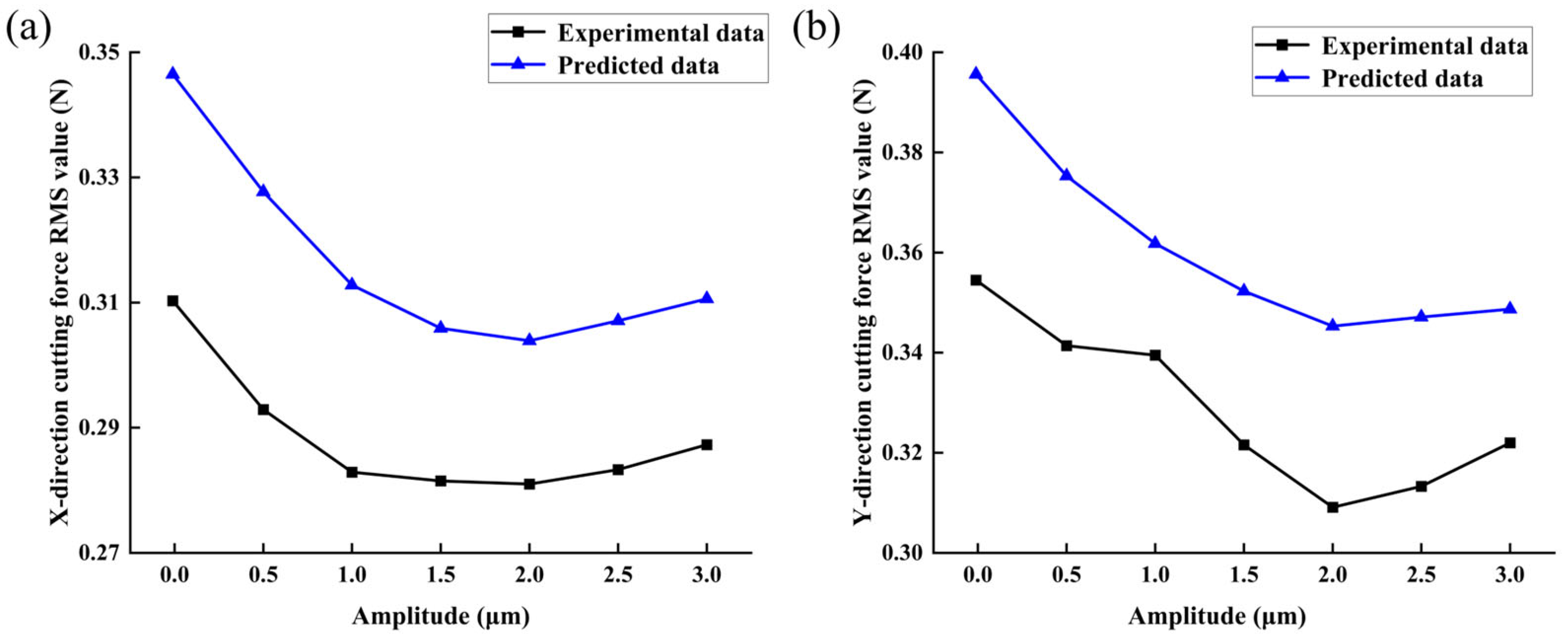
4.2.2. Effect of Amplitude on Cutting Force
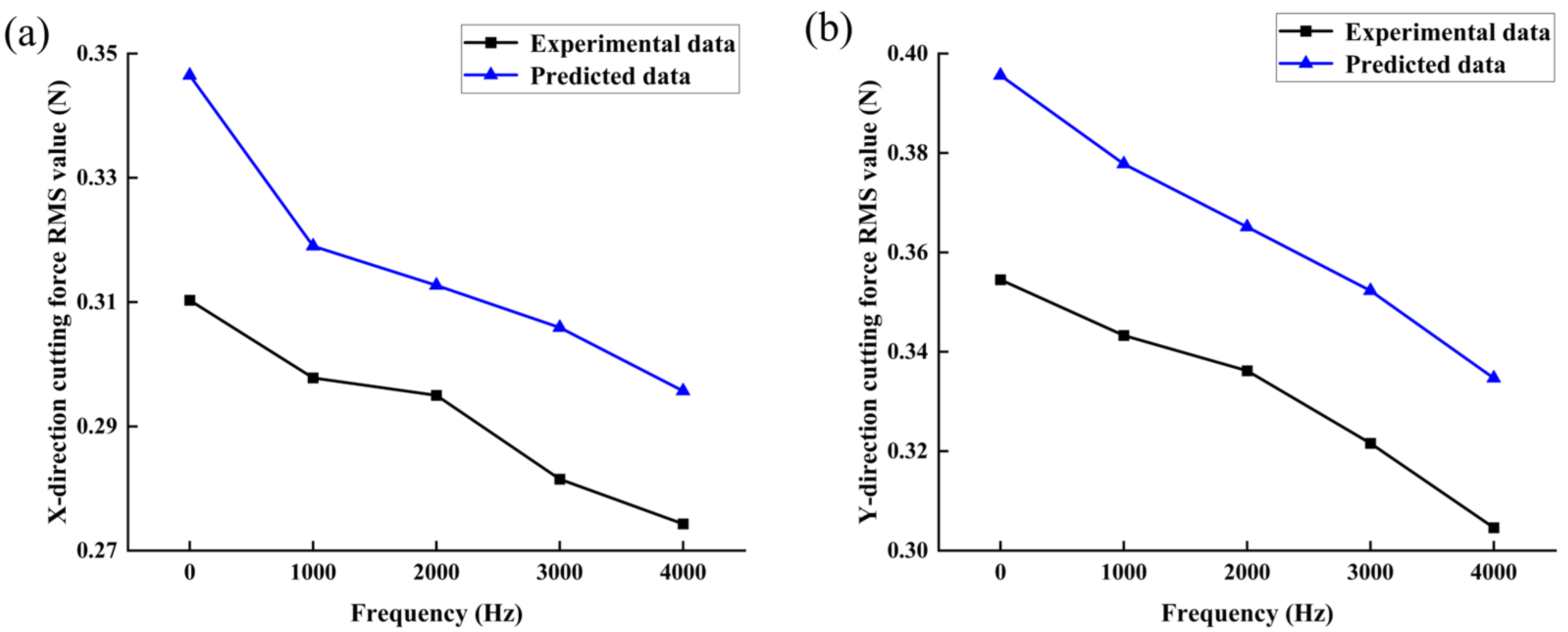
4.2.3. Effect of Frequency on Cutting Force
5. Conclusions
- (1)
- The mechanical properties of bone materials were analyzed. The stress–strain curves of bovine cortical bone samples were obtained by shear tests in vertical, parallel, and cross directions, and the shear strength of bone materials in different directions was calculated according to the test results. The analysis results show that the mechanical properties of bone materials in the three directions are different, and the shear strength in the parallel and cross directions is small. In the vertical direction, the bone material exhibits linear elasticity and elastoplasticity, and the shear strength is large. Therefore, bone materials have obvious anisotropy;
- (2)
- Based on the mechanical analysis method and the oblique cutting micro-element model, the cutting-force model of vibration-assisted micro-milling bone material with multiple processing parameters is established by considering the mechanical properties of bone material anisotropy, tool geometric parameters, ploughing effect, and the kinematics characteristics of the tool in the two-dimensional vibration-assisted micro-milling process. The variation law of cutting force is simulated by MATLAB. It can be seen that after vibration is applied, the change of cutting force with tooth-position angle is a constantly oscillating curve. Because the shear strength is the largest when cutting along the vertical direction, the cutting force in this direction is also the largest; due to the radial runout of the tool, the peak cutting force generated by the two cutting edges is different;
- (3)
- The vibration-assisted micro-milling experiment of bone materials was completed, and the correctness of the cutting-force prediction model was verified. The effects of cutting direction and vibration parameters on cutting force were studied. The results show that among the three cutting directions, the cutting force generated by bone materials in the vertical cutting direction is the largest, and the cutting force of bone materials in the parallel cutting direction and the cross-cutting direction is close. After the vibration effect is applied, the cutting force decreases first and then increases with the increase in the amplitude. With the increase in frequency, the cutting force decreases gradually. In the process of vibration-assisted micro-milling of bone materials, selecting the appropriate cutting direction and vibration parameters can achieve the effect of reducing the cutting force.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Christie, J. Surgical heat injury of bone. Injury 1981, 13, 188–190. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, B.; Li, A. Fracture Mechanical Properties and Fractal Analysis of Fracture Surfaces of Cortical Bone. J. Biomater. Tissue Eng. 2019, 9, 443–449. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, Z.; Fang, B.; Gao, L.; Chen, Z.; Su, G. Study on the Mechanism of Burr Formation by Simulation and Experiment in Ultrasonic Vibration-Assisted Micromilling. Micromachines 2023, 14, 625. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, Q.S.; Dong, Q.S. Temperature Prediction Model of Bone Material Micro-milling Cutting Edges. J. Northeast. Univ. (Nat. Sci.) 2020, 41, 1615. [Google Scholar]
- Tsai, M.-D.; Hsieh, M.-S.; Tsai, C.-H. Bone drilling haptic interaction for orthopedic surgical simulator. Comput. Biol. Med. 2007, 37, 1709–1718. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Gozen, B.A.; Ozdoganlar, O.B. Modeling and experimentation of bone drilling forces. J. Biomech. 2012, 45, 1076–1083. [Google Scholar] [CrossRef]
- Mitsuishi, M.; Warisawa, S.; Sugita, N.; Suzuki, M.; Moriya, H.; Hashizume, H.; Fujiwara, K.; Abe, N.; Inoue, H.; Kuramoto, K.; et al. A Study of Bone Micro-Cutting Characteristics Using a Newly Developed Advanced Bone Cutting Machine Tool for Total Knee Arthroplasty. CIRP Ann. 2005, 54, 41–46. [Google Scholar] [CrossRef]
- Liao, Z.; Axinte, D.; Gao, D. On modelling of cutting force and temperature in bone milling. J. Mater. Process. Technol. 2018, 266, 627–638. [Google Scholar] [CrossRef]
- Liu, S.; Wu, D.M.; Zhao, J. The Study of Bone Cutting Force with FEM. Adv. Mater. Res. 2014, 974, 389–393. [Google Scholar] [CrossRef]
- Li, G.; Xie, W.; Wang, H.; Chai, Y.; Zhang, S.; Yang, L. Optimizing Processing Parameters and Surface Quality of TC18 via Ultrasonic-Assisted Milling (UAM): An Experimental Study. Micromachines 2023, 14, 1111. [Google Scholar] [CrossRef]
- Alam, K.; Ghafoor, A.; Mitrofanov, A.V.; Silberschmidt, V. Experimental Investigation of the Mechanics of Conventional and Ultrasonically-Assisted Drilling of Cortical Bone. In Proceedings of the 6th IASTED International Conference on Biomechanics, BioMech 2011, Pittsburgh, PA, USA, 7–9 November 2011; pp. 55–60. [Google Scholar]
- Sugita, N.; Osa, T.; Aoki, R.; Mitsuishi, M. A new cutting method for bone based on its crack propagation characteristics. CIRP Ann. 2009, 58, 113–118. [Google Scholar] [CrossRef]
- Sui, J.; Sugita, N.; Ishii, K.; Harada, K.; Mitsuishi, M. Mechanistic modeling of bone-drilling process with experimental validation. J. Mater. Process. Technol. 2014, 214, 1018–1026. [Google Scholar] [CrossRef]
- Sugita, N.; Shu, L.; Shimada, T.; Oshima, M.; Kizaki, T.; Mitsuishi, M. Novel surgical machining via an impact cutting method based on fracture analysis with a discontinuum bone model. CIRP Ann. 2017, 66, 65–68. [Google Scholar] [CrossRef]
- Bai, W.; Sun, R.; Gao, Y.; Leopold, J. Analysis and modeling of force in orthogonal elliptical vibration cutting. Int. J. Adv. Manuf. Technol. 2015, 83, 1025–1036. [Google Scholar] [CrossRef]
- Bai, W.; Zhai, Y.; Zhao, J.; Han, G.; Ye, L.; Zhu, X.; Shu, L.; Wang, D. Experimental Investigation of Material Removal in Elliptical Vibration Cutting of Cortical Bone. Chin. J. Mech. Eng. 2023, 36, 52. [Google Scholar] [CrossRef]
- Reilly, D.T.; Burstein, A.H.; Frankel, V.H. The elastic modulus for bone. J. Biomech. 1974, 7, 271–275. [Google Scholar] [CrossRef]
- Burstein, A.H.; Reilly, D.T.; Martens, M. Aging of bone tissue: Mechanical properties. J. Bone Jt. Surg. 1976, 58, 82–86. [Google Scholar] [CrossRef]
- Burstein, A.H.; Currey, J.D.; Frankel, V.H.; Reilly, D.T. The ultimate properties of bone tissue: The effects of yielding. J. Biomech. 1972, 5, 35–44. [Google Scholar] [CrossRef]
- Burstein, A.; Zika, J.; Heiple, K.; Klein, L. Contribution of collagen and mineral to the elastic-plastic properties of bone. J. Bone Jt. Surg. 1975, 57, 956–961. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, K.; Ding, H.; Chen, S.; Zhao, L. An investigation of the influence of phases’ removal ways on surface quality in micro milling SiCp/Al composites. Procedia CIRP 2018, 71, 59–64. [Google Scholar] [CrossRef]
- Kiswanto, G.; Putri, S.K.; Christiand; Fitriawan, M.R.; Hiltansyah, F.; Putra, R.G. Modeling, Simulation, and Analysis of Cutting Force in Micro End Milling Process of Mild Steel Using Mechanistic Model. In Proceedings of the 2021 7th International Conference on Mechatronics and Robotics Engineering (ICMRE), Budapest, Hungary, 3–5 February 2021; pp. 142–149. [Google Scholar] [CrossRef]
- Teimouri, R.; Amini, S. Analytical modeling of ultrasonic burnishing process: Evaluation of active forces. Measurement 2018, 131, 654–663. [Google Scholar] [CrossRef]
- Armarego, E.; Brown, R.H. The Machining of Metals; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1969; 437p. [Google Scholar]
- Liao, Z.; Axinte, D.A. On chip formation mechanism in orthogonal cutting of bone. Int. J. Mach. Tools Manuf. 2016, 102, 41–55. [Google Scholar] [CrossRef]
- Vipindas, K.; Anand, K.; Mathew, J. Effect of cutting edge radius on micro end milling: Force analysis, surface roughness, and chip formation. Int. J. Adv. Manuf. Technol. 2018, 97, 711–722. [Google Scholar] [CrossRef]
- Srinivasa, Y.; Shunmugam, M. Mechanistic model for prediction of cutting forces in micro end-milling and experimental comparison. Int. J. Mach. Tools Manuf. 2013, 67, 18–27. [Google Scholar] [CrossRef]
- Câmara, M.; Rubio, J.C.; Abrão, A.; Davim, J. State of the art on micromilling of materials, a review. J. Mater. Sci. Technol. 2012, 28, 673–685. [Google Scholar] [CrossRef]
- Bin, F.; Zhonghang, Y.; Depeng, L.; Liying, G. Effect of ultrasonic vibration on finished quality in ultrasonic vibration assisted micromilling of Inconel718. Chin. J. Aeronaut. 2021, 34, 209–219. [Google Scholar]
- Ding, H.; Chen, S.-J.; Cheng, K. Two-dimensional vibration-assisted micro end milling: Cutting force modelling and machining process dynamics. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 1775–1783. [Google Scholar] [CrossRef]
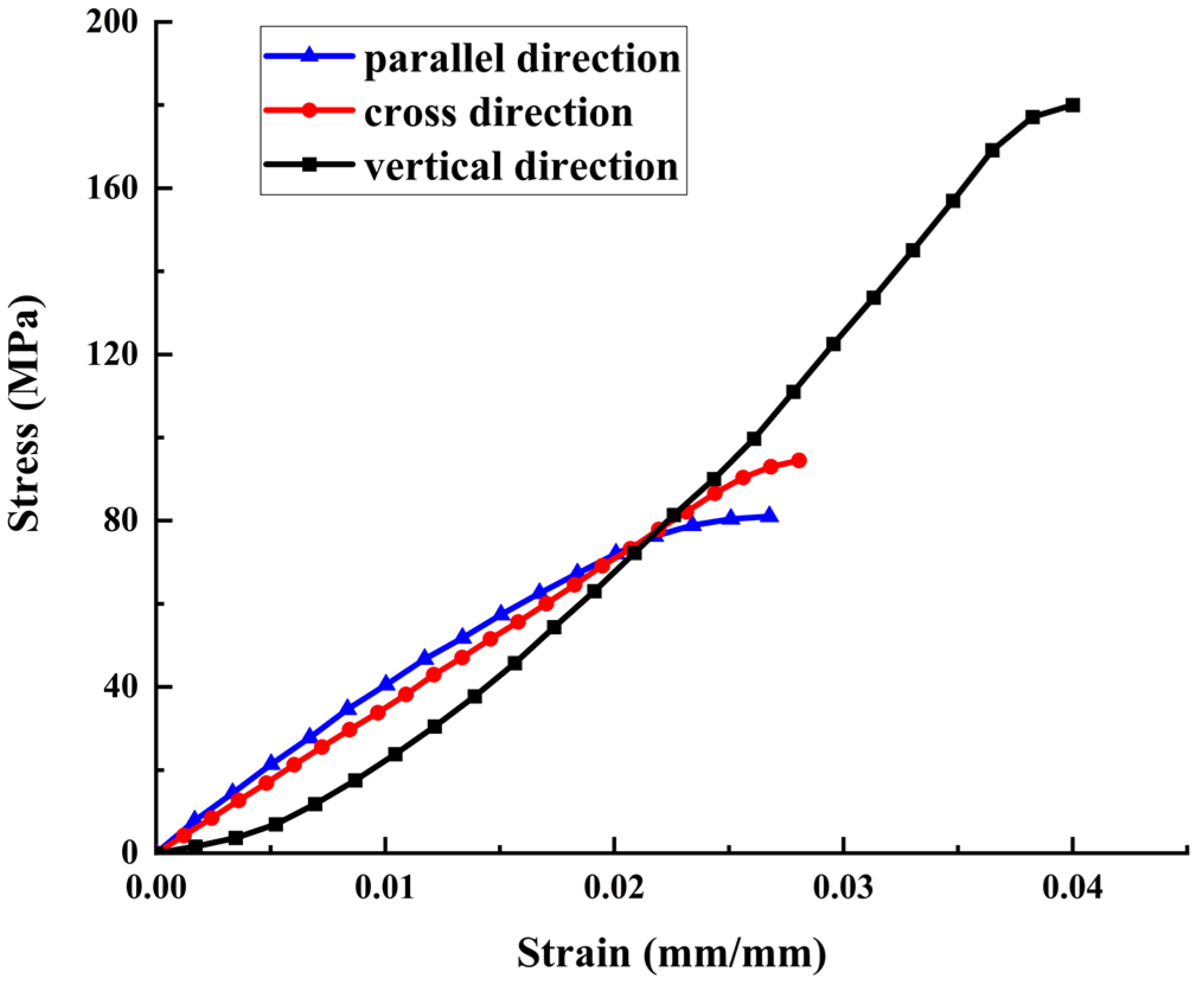




| Load Direction | Shearing Strength (MPa) |
|---|---|
| parallel direction | 81.03 |
| cross direction | 94.48 |
| vertical direction | 180.12 |
| Cutting Area | Rotation Angle | Point Range | |
|---|---|---|---|
| Lower Limit Angle θst | Upper Limit Angle θex | ||
| access to cutting | 0 ≤ θ ≤ θz | 0 | θ |
| continuous cutting | θz < θ ≤ θd | θ–θz | θ |
| exit cutting | θd < θ ≤ θd + θz | θ–θz | θd |
| Cutting Direction i | Friction Coefficient μi |
|---|---|
| 1 | 0.82 |
| 2 | 0.98 |
| 3 | 0.85 |
| Micro- Milling Cutter Type | Spiral Milling Cutter Geometry Parameters | |||||
|---|---|---|---|---|---|---|
| Diameter d (μm) | Rake Angle (deg) | Back Angle (deg) | Spiral Angle λ (deg) | Radius of Obtuse Circle (μm) | Tool Eccentricity (μm) | |
| SGOS550 0.8 × 2.4 C × 4 D × 50 L | 800 | 5 | 10 | 35 | 5 | 2 |
| Experiment Number | Cutting Direction i | Amplitude A (μm) | Frequency f (Hz) |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 2 | 2 | 0 | 0 |
| 3 | 3 | 0 | 0 |
| 4 | 1 | 1 | 3000 |
| 5 | 2 | 1 | 3000 |
| 6 | 3 | 1 | 3000 |
| 7 | 1 | 0.5 | 3000 |
| 8 | 1 | 1.5 | 3000 |
| 9 | 1 | 2 | 3000 |
| 10 | 1 | 2.5 | 3000 |
| 11 | 1 | 3 | 3000 |
| 12 | 1 | 1.5 | 1000 |
| 13 | 1 | 1.5 | 2000 |
| 14 | 1 | 1.5 | 4000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, P.; Zhang, H.; Liu, X.; Yang, Z.; Liu, B.; Liu, T. Cutting-Force Modeling Study on Vibration-Assisted Micro-Milling of Bone Materials. Micromachines 2023, 14, 1422. https://doi.org/10.3390/mi14071422
Shang P, Zhang H, Liu X, Yang Z, Liu B, Liu T. Cutting-Force Modeling Study on Vibration-Assisted Micro-Milling of Bone Materials. Micromachines. 2023; 14(7):1422. https://doi.org/10.3390/mi14071422
Chicago/Turabian StyleShang, Peng, Huaiqing Zhang, Xiaopeng Liu, Zhuang Yang, Bingfeng Liu, and Teng Liu. 2023. "Cutting-Force Modeling Study on Vibration-Assisted Micro-Milling of Bone Materials" Micromachines 14, no. 7: 1422. https://doi.org/10.3390/mi14071422
APA StyleShang, P., Zhang, H., Liu, X., Yang, Z., Liu, B., & Liu, T. (2023). Cutting-Force Modeling Study on Vibration-Assisted Micro-Milling of Bone Materials. Micromachines, 14(7), 1422. https://doi.org/10.3390/mi14071422





