Uncertainty Estimation for the Brillouin Frequency Shift Measurement Using a Scanning Tandem Fabry–Pérot Interferometer
Abstract
:1. Introduction
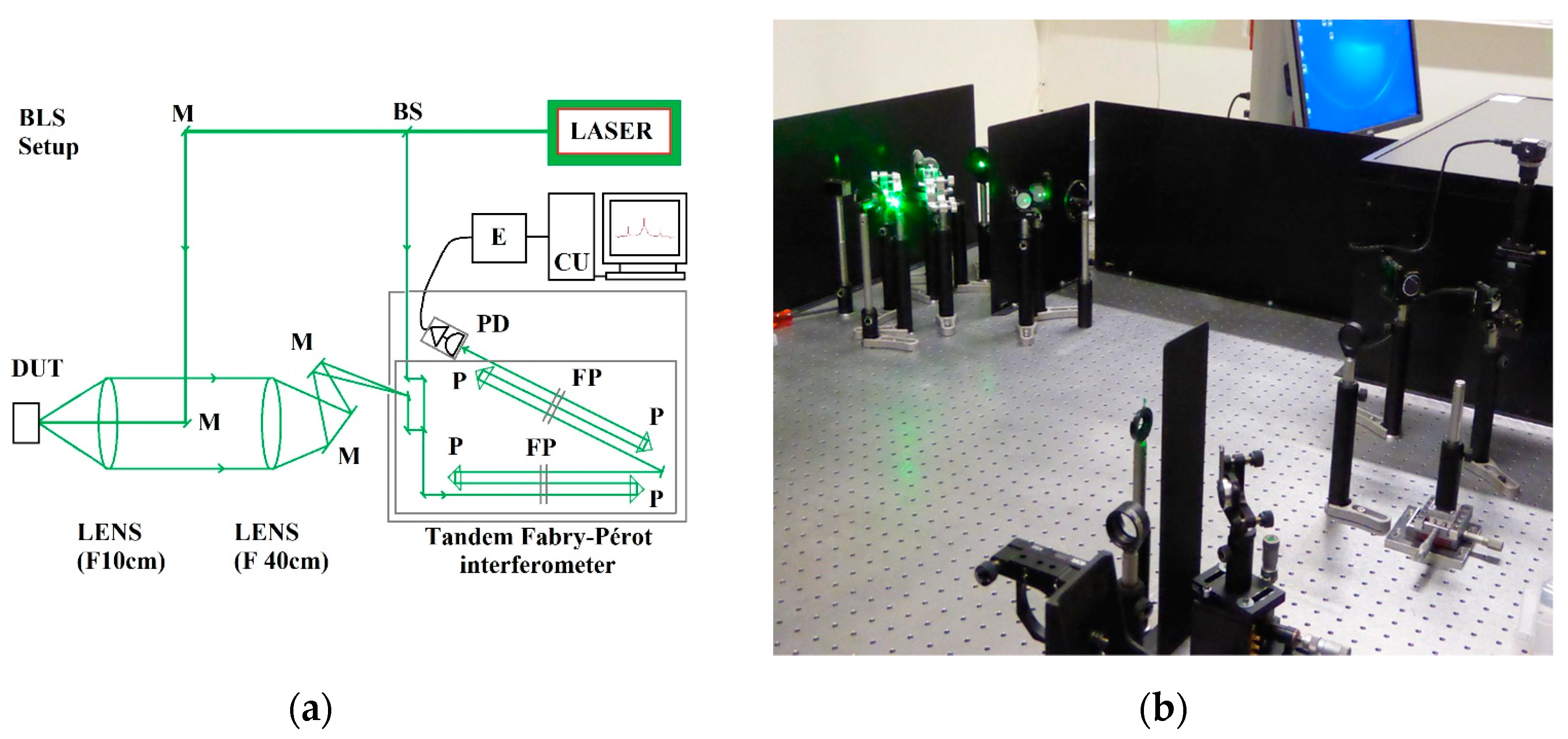
2. Materials and Methods
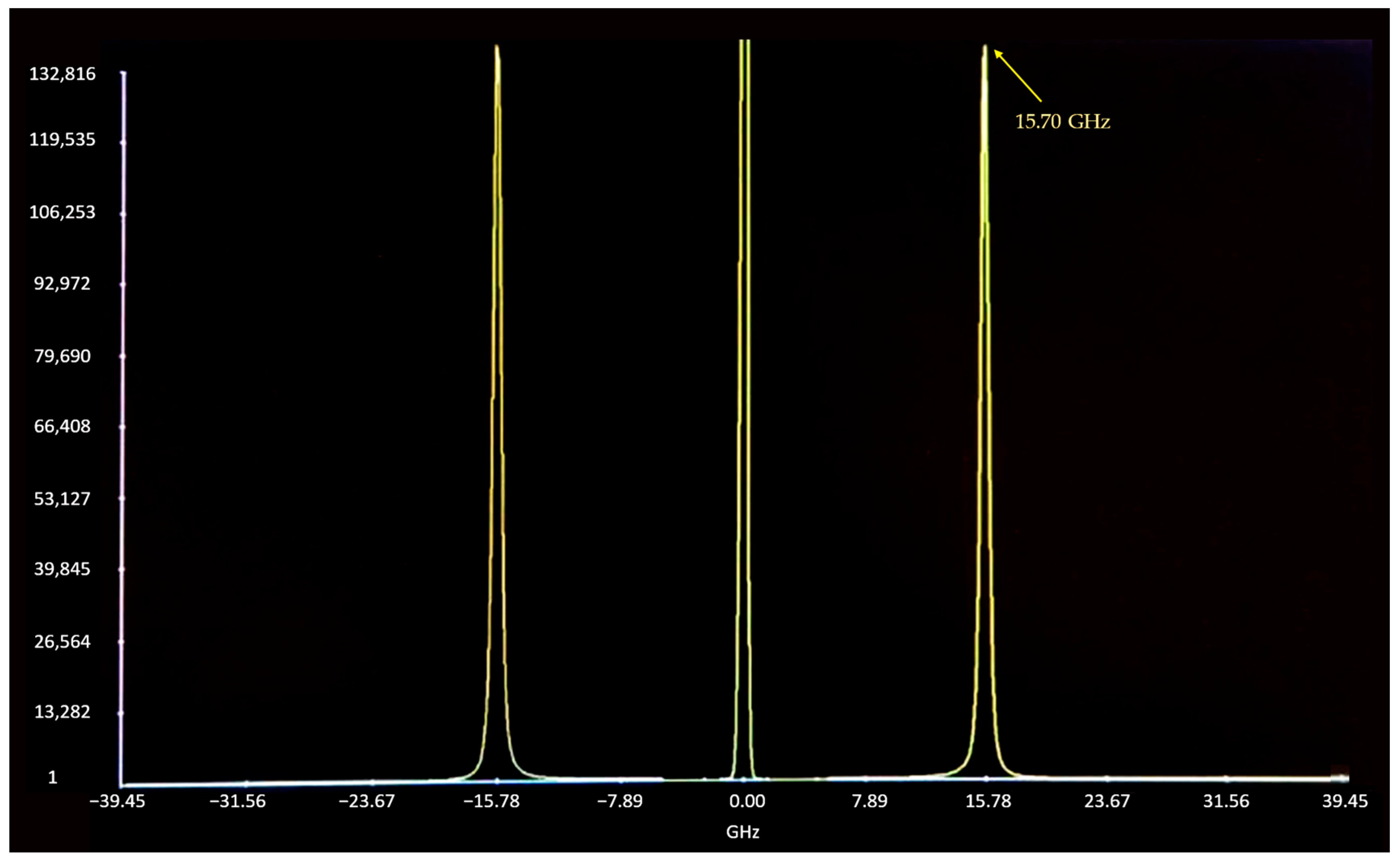
3. Measurement Results
4. Measurement Uncertainty of the Brillouin Frequency Shift
4.1. Contributions Evaluated by Statistical Methods
4.2. Contributions Evaluated by Other Means
4.3. Estimation of the Expanded Measurement Uncertainty
5. Comparison with Calculated Brillouin Frequency Shift
5.1. Uncertainty of the Calculated Frequency Shift
5.2. Comparison of Measured and Calculated Brillouin Frequency Shift
5.3. Uncertainty in the Longitudinal Modulus Derived by BLS Spectrometer
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brillouin, L. Diffusion de La Lumière et Des Rayons X Par Un Corps Transparent Homogène. Ann. Phys. 1922, 9, 88–122. [Google Scholar] [CrossRef]
- Mandelstam, L. Light Scattering by Inhomogeneous Media. Zh. Russ. Fiz. Khim. Ova. 1926, 58, 381. [Google Scholar]
- Blachowicz, T.; Grimsditch, M. Scattering, Inelastic: Brillouin. Encycl. Condens. Matter Phys. 2005, 199–205. [Google Scholar] [CrossRef]
- Curie, J.; Curie, P. Développement Par Compression de l’électricité Polaire Dans Les Cristaux Hémièdres à Faces Inclinées. Bull. Minéral. 1880, 3, 90–93. [Google Scholar] [CrossRef]
- Gross, E. Change of Wave-Length of Light Due to Elastic Heat Waves at Scattering in Liquids. Nature 1930, 126, 201–202. [Google Scholar] [CrossRef]
- Gross, E. The Splitting of Spectral Lines at Scattering of Light by Liquids. Nature 1930, 126, 400. [Google Scholar] [CrossRef]
- Gross, E. Über Änderung der WellenlÄnge Bei Lichtzerstreuung in Kristallen. Z. Phys. 1930, 63, 685–687. [Google Scholar] [CrossRef]
- Gross, E. Modification of Light Quanta by Elastic Heat Oscillations in Scattering Media. Nature 1932, 129, 722–723. [Google Scholar] [CrossRef]
- Raghavendra Rao, B.V. Examination of Molecularly Scattered Light with a Fabry-Perot Etalon—Part I. Liquid Benzene. Proc. Indian Acad. Sci.-Sect. A 1934, 1, 261–268. [Google Scholar] [CrossRef]
- Raghavendra Rao, B.V. Examination of Molecularly Scattered Light with a Fabry-Perot Etalon—Part II. Liquids: Toluene and Carbon Tetrachloride. Proc. Indian Acad. Sci.-Sect. A 1935, 1, 473–483. [Google Scholar] [CrossRef]
- Grimsditch, M.H.; Ramdas, A.K. Brillouin Scattering in Diamond. Phys. Rev. B 1975, 11, 3139–3148. [Google Scholar] [CrossRef]
- Kojima, S. 100th Anniversary of Brillouin Scattering: Impact on Materials Science. Materials 2022, 15, 3518. [Google Scholar] [CrossRef] [PubMed]
- Borovik-Romanov, A.S.; Kreines, N.M. Brillouin-Mandelstam Scattering from Thermal and Excited Magnons. Phys. Rep. 1982, 81, 351–408. [Google Scholar] [CrossRef]
- Kargar, F.; Balandin, A.A. Advances in Brillouin–Mandelstam Light-Scattering Spectroscopy. Nat. Photonics 2021, 15, 720–731. [Google Scholar] [CrossRef]
- Merklein, M.; Kabakova, I.V.; Zarifi, A.; Eggleton, B.J. 100 Years of Brillouin Scattering: Historical and Future Perspectives. Appl. Phys. Rev. 2022, 9, 041306. [Google Scholar] [CrossRef]
- Singaraju, A.B.; Bahl, D.; Stevens, L.L. Brillouin Light Scattering: Development of a Near Century-Old Technique for Characterizing the Mechanical Properties of Materials. AAPS PharmSciTech 2019, 20, 109. [Google Scholar] [CrossRef]
- Palombo, F.; Fioretto, D. Brillouin Light Scattering: Applications in Biomedical Sciences. Chem. Rev. 2019, 119, 7833–7847. [Google Scholar] [CrossRef] [Green Version]
- Prevedel, R.; Diz-Muñoz, A.; Ruocco, G.; Antonacci, G. Brillouin Microscopy: An Emerging Tool for Mechanobiology. Nat. Methods 2019, 16, 969–977. [Google Scholar] [CrossRef]
- Meng, Z.; Traverso, A.J.; Ballmann, C.W.; Troyanova-Wood, M.A.; Yakovlev, V. V Seeing Cells in a New Light: A Renaissance of Brillouin Spectroscopy. Adv. Opt. Photon. 2016, 8, 300–327. [Google Scholar] [CrossRef]
- Antonacci, G.; Beck, T.; Bilenca, A.; Czarske, J.; Elsayad, K.; Guck, J.; Kim, K.; Krug, B.; Palombo, F.; Prevedel, R.; et al. Recent Progress and Current Opinions in Brillouin Microscopy for Life Science Applications. Biophys. Rev. 2020, 12, 615–624. [Google Scholar] [CrossRef]
- Chitanvis, S.M.; Cantrell, C.D. Simple Approach to Stimulated Brillouin Scattering in Glass Aerosols. J. Opt. Soc. Am. B 1989, 6, 1326–1331. [Google Scholar] [CrossRef]
- Boyarchuk, K.A.; Lyakhov, G.A.; Svirko, Y.P. Microwave Driven Anti-Stokes Brillouin Scattering in an Ionized Medium. The Method of Remote Sensing of Atmospheric Aerosols. J. Phys. D. Appl. Phys. 1993, 26, 1561–1565. [Google Scholar] [CrossRef]
- Hair, J.W.; Hostetler, C.A.; Cook, A.L.; Harper, D.B.; Ferrare, R.A.; Mack, T.L.; Welch, W.; Izquierdo, L.R.; Hovis, F.E. Airborne High Spectral Resolution Lidar for Profiling Aerosol Optical Properties. Appl. Opt. 2008, 47, 6734–6753. [Google Scholar] [CrossRef] [Green Version]
- Esselborn, M.; Wirth, M.; Fix, A.; Tesche, M.; Ehret, G. Airborne High Spectral Resolution Lidar for Measuring Aerosol Extinction and Backscatter Coefficients. Appl. Opt. 2008, 47, 346–358. [Google Scholar] [CrossRef]
- Gu, Z.; Witschas, B.; Van De Water, W.; Ubachs, W. Rayleigh-Brillouin Scattering Profiles of Air at Different Temperatures and Pressures. Appl. Opt. 2013, 52, 4640–4651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Witschas, B. Light Scattering on Molecules in the Atmosphere. In Atmospheric Physics, Research Topics in Aerospace; Springer: Berlin/Heidelberg, Germany, 2012; pp. 69–83. [Google Scholar]
- Gu, Z.; Witschas, B.; Ubachs, W. Temperature Retrieval from Rayleigh-Brillouin Scattering Profiles Measured in Air. Opt. Express 2014, 22, 29655–29667. [Google Scholar] [CrossRef] [Green Version]
- Rank, D.H.; Wiggins, T.A.; Wick, R.V.; Eastman, D.P.; Guenther, A.H. Stimulated Brillouin Effect in High-Pressure Gases. J. Opt. Soc. Am. 1966, 56, 174. [Google Scholar] [CrossRef]
- Raman, C.V.; Krishnan, K.S. A New Type of Secondary Radiation. Nature 1928, 121, 501–502. [Google Scholar] [CrossRef]
- Raman, C.V. A New Radiation. Indian J. Phys. 1928, 2, 387–398. [Google Scholar] [CrossRef]
- Hendra, P.J.; Stratton, P.M. Laser-Raman Spectroscopy. Chem. Rev. 1969, 69, 325–344. [Google Scholar] [CrossRef]
- Sandercock, J.R. Some Recent Developments in Brillouin Scattering. RCA Rev. 1975, 36, 89–107. [Google Scholar]
- Sandercock, J.R. Brillouin Scattering Study of SbSI Using a Double-Passed, Stabilised Scanning Interferometer. Opt. Commun. 1970, 2, 73–76. [Google Scholar] [CrossRef]
- Sandercock, J.R. Light Scattering from Thermally Excited Surface Phonons and Magnons. In 7th International Conference on Raman Spectroscopy; Murphy, W.F., Ed.; North-Holland: Amsterdam, The Netherlands, 1980; pp. 364–367. [Google Scholar]
- Sandercock, J.R. Trends in Brillouin Scattering: Studies of Opaque Materials, Supported Films, and Central Modes. In Topics in Applied Physics; Springer: Berlin, Germany, 1982; Volume 51, pp. 173–206. [Google Scholar]
- Vacher, R.; Boyer, L.; Boissier, M. Measurement of the Elastic Constants of Lithium Acetate by Means of the Brillouin Effect. Phys. Rev. B 1972, 6, 674. [Google Scholar] [CrossRef]
- Sussner, H.; Vacher, R. High-Precision Measurements of Brillouin Scattering Frequencies. Appl. Opt. 1979, 18, 3815. [Google Scholar] [CrossRef]
- Vacher, R.; Sussner, H.; Schickfus, M.V. A Fully Stabilized Brillouin Spectrometer with High Contrast and High Resolution. Rev. Sci. Instrum. 1980, 51, 288–291. [Google Scholar] [CrossRef]
- Traverso, A.J.; Thompson, J.V.; Steelman, Z.A.; Meng, Z.; Scully, M.O.; Yakovlev, V.V. Dual Raman-Brillouin Microscope for Chemical and Mechanical Characterization and Imaging. Anal. Chem. 2015, 87, 7519–7523. [Google Scholar] [CrossRef] [PubMed]
- Mattana, S.; Alunni Cardinali, M.; Caponi, S.; Casagrande Pierantoni, D.; Corte, L.; Roscini, L.; Cardinali, G.; Fioretto, D. High-Contrast Brillouin and Raman Micro-Spectroscopy for Simultaneous Mechanical and Chemical Investigation of Microbial Biofilms. Biophys. Chem. 2017, 229, 123–129. [Google Scholar] [CrossRef]
- Meng, Z.; Bustamante Lopez, S.C.; Meissner, K.E.; Yakovlev, V.V. Subcellular Measurements of Mechanical and Chemical Properties Using Dual Raman-Brillouin Microspectroscopy. J. Biophotonics 2016, 9, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Scarponi, F.; Mattana, S.; Corezzi, S.; Caponi, S.; Comez, L.; Sassi, P.; Morresi, A.; Paolantoni, M.; Urbanelli, L.; Emiliani, C.; et al. High-Performance Versatile Setup for Simultaneous Brillouin-Raman Microspectroscopy. Phys. Rev. X 2017, 7, 31015. [Google Scholar] [CrossRef] [Green Version]
- Aschauer, R.; Asenbaum, A.; Geri, H. Fabry-Perot Interferometer with Personal Computer Control. Appl. Opt. 1990, 29, 953. [Google Scholar] [CrossRef]
- Błachowicz, T.; Bukowski, R.; Kleszczewski, Z. Fabry-Perot Interferometer in Brillouin Scattering Experiments. Rev. Sci. Instrum. 1996, 67, 4057–4060. [Google Scholar] [CrossRef]
- Hernandez, G. Fabry-Perot Interferometers; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Perot, A.; Fabry, C. On the Application of Interference Phenomena to the Solution of Various Problems of Spectroscopy and Metrology. Astrophys. J. 1899, 9, 87. [Google Scholar] [CrossRef]
- Fabry, C.; Pérot, A. Théorie et Applications d’une Nouvelle Méthode de Spectroscopie Interférentielle. Ann. Chim. Phys. 1899, 16, 115–144. [Google Scholar]
- Heiman, D.; Hamilton, D.S.; Hellwarth, R.W. Brillouin Scattering Measurements on Optical Glasses. Phys. Rev. B 1979, 19, 6583–6592. [Google Scholar] [CrossRef]
- Asenbaum, A. Computer-Controlled Fabry-Perot Interferometer for Brillouin Spectroscopy. Appl. Opt. 1979, 18, 540. [Google Scholar] [CrossRef]
- Salvato, G.; Ponterio, R.C.; Aliotta, F. New Automatic System for Multipass Fabry-Ṕrot Alignment and Stabilization. Rev. Sci. Instrum. 2006, 77, 113104. [Google Scholar] [CrossRef]
- Błachowicz, T. The Use of Pressure Controlled Fabry-Pérot Interferometer with Linear Scanning of Data for Brillouin-Type Experiments. Rev. Sci. Instrum. 2000, 71, 2988–2991. [Google Scholar] [CrossRef]
- Lindsay, S.M.; Anderson, M.W.; Sandercock, J.R. Construction and Alignment of a High Performance Multipass Vernier Tandem Fabry-Perot Interferometer. Rev. Sci. Instrum. 1981, 52, 1478–1486. [Google Scholar] [CrossRef]
- Dil, J.G.; van Hijningen, N.C.J.A.; van Dorst, F.; Aarts, R.M. Tandem Multipass Fabry-Perot Interferometer for Brillouin Scattering. Appl. Opt. 1981, 20, 1374. [Google Scholar] [CrossRef] [Green Version]
- Mock, R.; Hillebrands, B.; Sandercock, R. Construction and Performance of a Brillouin Scattering Set-up Using a Triple-Pass Tandem Fabry-Perot Interferometer. J. Phys. E 1987, 20, 656. [Google Scholar] [CrossRef]
- Hillebrands, B. Progress in Multipass Tandem Fabry-Perot Interferometry: I. A Fully Automated, Easy to Use, Self-Aligning Spectrometer with Increased Stability and Flexibility. Rev. Sci. Instrum. 1999, 70, 1589–1598. [Google Scholar] [CrossRef] [Green Version]
- Itoh, S.I.; Yamana, T.; Kojima, S. Quick Measurement of Brillouin Spectra of Glass-Forming Material Trimethylene Glycol by Angular Dispersion-Type Fabry-Perot Interferometer System. Jpn. J. Appl. Phys. Part 1 Regul. Pap. Short Notes Rev. Pap. 1996, 35, 2879–2881. [Google Scholar] [CrossRef]
- Ko, J.H.; Kojima, S. Nonscanning Brillouin Spectroscopy Applied to Solid Materials. Rev. Sci. Instrum. 2002, 73, 4390–4392. [Google Scholar] [CrossRef]
- Ike, Y.; Tsukada, S.; Kojima, S. High-Resolution Brillouin Spectroscopy with Angular Dispersion-Type Fabry-Perot Interferometer and Its Application to a Quartz Crystal. Rev. Sci. Instrum. 2007, 78, 3–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shirasaki, M. Large Angular Dispersion by a Virtually Imaged Phased Array and Its Application to a Wavelength Demultiplexer. Opt. Lett. 1996, 21, 366. [Google Scholar] [CrossRef] [PubMed]
- Scarcelli, G.; Yun, S.H. Confocal Brillouin Microscopy for Three-Dimensional Mechanical Imaging. Nat. Photonics 2008, 2, 39–43. [Google Scholar] [CrossRef]
- Scarcelli, G.; Yun, S.H. Multistage VIPA Etalons for High-Extinction Parallel Brillouin Spectroscopy. Opt. Express 2011, 19, 10913–10922. [Google Scholar] [CrossRef] [Green Version]
- Meng, Z.; Traverso, A.J.; Yakovlev, V.V. Background Clean-up in Brillouin Microspectroscopy of Scattering Medium. Opt. Express 2014, 22, 5410. [Google Scholar] [CrossRef] [Green Version]
- Meng, Z.; Yakovlev, V.V. Precise Determination of Brillouin Scattering Spectrum Using a Virtually Imaged Phase Array (VIPA) Spectrometer and Charge-Coupled Device (CCD) Camera. Appl. Spectrosc. 2016, 70, 1356–1363. [Google Scholar] [CrossRef]
- Coker, Z.; Troyanova-Wood, M.; Traverso, A.J.; Yakupov, T.; Utegulov, Z.N.; Yakovlev, V.V. Assessing Performance of Modern Brillouin Spectrometers. Opt. Express 2018, 26, 2400. [Google Scholar] [CrossRef]
- Cotter, D. Stimulated Brillouin Scattering in Monomode Optical Fiber. J. Opt. Commun. 1983, 4, 10–19. [Google Scholar] [CrossRef]
- Garmire, E. Stimulated Brillouin Review: Invented 50 Years Ago and Applied Today. Int. J. Opt. 2018, 2018, 2459501. [Google Scholar] [CrossRef]
- Bai, Z.; Yuan, H.; Liu, Z.; Xu, P.; Gao, Q.; Williams, R.J.; Kitzler, O.; Mildren, R.P.; Wang, Y.; Lu, Z. Stimulated Brillouin Scattering Materials, Experimental Design and Applications: A Review. Opt. Mater. 2018, 75, 626–645. [Google Scholar] [CrossRef]
- Agrawal, G.P. Stimulated Brillouin Scattering. In Nonlinear Fiber Optics; Elsevier: Amsterdam, The Netherlands, 2019; pp. 355–399. [Google Scholar]
- Ballmann, C.W.; Thompson, J.V.; Traverso, A.J.; Meng, Z.; Scully, M.O.; Yakovlev, V.V. Stimulated Brillouin Scattering Microscopic Imaging. Sci. Rep. 2015, 5, 18139. [Google Scholar] [CrossRef] [Green Version]
- Krug, B.; Koukourakis, N.; Czarske, J.W. Impulsive Stimulated Brillouin Microscopy for Non-Contact, Fast Mechanical Investigations of Hydrogels. Opt. Express 2019, 27, 26910. [Google Scholar] [CrossRef] [PubMed]
- Ballmann, C.W.; Meng, Z.; Traverso, A.J.; Scully, M.O.; Yakovlev, V.V. Impulsive Brillouin Microscopy. Optica 2017, 4, 124. [Google Scholar] [CrossRef]
- Remer, I.; Shaashoua, R.; Shemesh, N.; Ben-Zvi, A.; Bilenca, A. High-Sensitivity and High-Specificity Biomechanical Imaging by Stimulated Brillouin Scattering Microscopy. Nat. Methods 2020, 17, 913–916. [Google Scholar] [CrossRef] [PubMed]
- Ballmann, C.W.; Meng, Z.; Yakovlev, V.V. Nonlinear Brillouin Spectroscopy: What Makes It a Better Tool for Biological Viscoelastic Measurements. Biomed. Opt. Express 2019, 10, 1750. [Google Scholar] [CrossRef] [PubMed]
- JRS. Brillouin Scattering by Means of the JRS TFP-1 Tandem Multi-Pass Fabry-Pérot Interferometer; JRS Scientific Instruments: Mettmenstetten, Switzerland, 2023; Available online: http://tablestable.com/uploads/ckeditor/TFP-1/Brillouin%20spectroscopy%20with%20JRS%20TFP-1.pdf (accessed on 15 May 2023).
- Table Stable. Tandem Fabry-Pérot Spectrometers TFP-1 and TFP-2 HC (Operator Manual); The Table Stable Ltd.: Mettmenstetten, Switzerland, 2023; Available online: http://www.tablestable.com/uploads/ckeditor/TFP-2/Manual%20TFP%20unified.pdf (accessed on 15 May 2023).
- Beadie, G.; Brindza, M.; Flynn, R.A.; Rosenberg, A.; Shirk, J.S. Refractive Index Measurements of Poly(Methyl Meth-Acrylate) (PMMA) from 0.4–1.6 μm. Appl. Opt. 2015, 54, 139–143. [Google Scholar] [CrossRef]
- Von Clarmann, T.; Compernolle, S.; Hase, F. Truth and Uncertainty. A Critical Discussion of the Error Concept versus the Uncertainty Concept. Atmos. Meas. Tech. 2022, 15, 1145–1157. [Google Scholar] [CrossRef]
- Lee, J.W.; Hwang, E.; Kacker, R.N. True Value, Error, and Measurement Uncertainty: Two Views. Accredit. Qual. Assur. 2022, 27, 235–242. [Google Scholar] [CrossRef]
- ISO/IEC Guide 98-3:2008; Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995). ISO: Geneva, Switzerland, 2008.
- Kacker, R.; Sommer, K.D.; Kessel, R. Evolution of Modern Approaches to Express Uncertainty in Measurement. Metrologia 2007, 44, 513–529. [Google Scholar] [CrossRef]
- Salzenstein, P.; Pavlyuchenko, E.; Hmima, A.; Cholley, N.; Zarubin, M.; Galliou, S.; Chembo, Y.K.; Larger, L. Estimation of the Uncertainty for a Phase Noise Optoelectronic Metrology System. Phys. Scr. 2012, T149, 14025. [Google Scholar] [CrossRef] [Green Version]
- Pavlyuchenko, E.; Salzenstein, P. Application of Modern Method of Calculating Uncertainty to Microwaves and Opto-Electronics. In Proceedings of the 2014 International Conference Laser Optics, St. Petersburg, Russia, 30 June–4 July 2014; p. 6886449. [Google Scholar] [CrossRef]
- Salzenstein, P.; Pavlyuchenko, E. Uncertainty Evaluation on a 10.52 GHz (5 dBm) Optoelectronic Oscillator Phase Noise Performance. Micromachines 2021, 12, 474. [Google Scholar] [CrossRef]
- Lee, W.K.; Yu, D.H.; Park, C.Y.; Mun, J. The Uncertainty Associated with the Weighted Mean Frequency of a Phase-Stabilized Signal with White Phase Noise. Metrologia 2010, 47, 24–32. [Google Scholar] [CrossRef]
- Salzenstein, P.; Wu, T.Y. Uncertainty Analysis for a Phase-Detector Based Phase Noise Measurement System. Meas. J. Int. Meas. Confed. 2016, 85, 118–123. [Google Scholar] [CrossRef]
- Wu, T.Y.; Murashima, Y.; Sakurai, H.; Iida, K. A Bilateral Comparison of Particle Number Concentration Standards via Calibration of an Optical Particle Counter for Number Concentration up to ~1000 cm−3. Measurement 2022, 189, 110446. [Google Scholar] [CrossRef]
- Wu, T.Y.; Horender, S.; Tancev, G.; Vasilatou, K. Evaluation of Aerosol-Spectrometer Based PM2.5 and PM10 Mass Concentration Measurement Using Ambient-like Model Aerosols in the Laboratory. Measurement 2022, 201, 111761. [Google Scholar] [CrossRef]
- Salzenstein, P.; Kuna, A.; Sojdr, L.; Chauvin, J. Significant Step in Ultra-High Stability Quartz Crystal Oscillators. Electron. Lett. 2010, 46, 1433–1434. [Google Scholar] [CrossRef]
- Salzenstein, P.; Cholley, N.; Kuna, A.; Abbé, P.; Lardet-Vieudrin, F.; Šojdr, L.; Chauvin, J. Distributed Amplified Ultra-Stable Signal Quartz Oscillator Based. Meas. J. Int. Meas. Confed. 2012, 45, 1937–1939. [Google Scholar] [CrossRef]
- Gough, W. The Graphical Analysis of a Lorentzian Function and a Differentiated Lorentzian Function. J. Phys. A Gen. Phys. 1968, 1, 704–709. [Google Scholar] [CrossRef]
- Köning, R.; Flügge, J.; Bosse, H. A Method for the in Situ Determination of Abbe Errors and Their Correction. Meas. Sci. Technol. 2007, 18, 476–481. [Google Scholar] [CrossRef]
- Leach, R. Abbe Error/Offset. CIRP Encycl. Prod. Eng. 2014, 1–4. [Google Scholar] [CrossRef]
- Howard, L.; Stone, J.; Fu, J. Real-Time Displacement Measurements with a Fabry-Perot Cavity and a Diode Laser. Precis. Eng. 2001, 25, 321–335. [Google Scholar] [CrossRef]
- Joo, K.N.; Ellis, J.D.; Spronck, J.W.; Munnig Schmidt, R.H. Design of a Folded, Multi-Pass Fabry-Perot Cavity for Displacement Metrology. Meas. Sci. Technol. 2009, 20, 107001. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.; Wei, H.; Wu, X.; Li, Y. Fabry–Perot Interferometer with Picometer Resolution Referenced to an Optical Frequency Comb. Opt. Lasers Eng. 2015, 67, 128–134. [Google Scholar] [CrossRef]
- Frach, T.; Prescher, G.; Degenhardt, C.; De Gruyter, R.; Schmitz, A.; Ballizany, R. The Digital Silicon Photomultiplier—Principle of Operation and Intrinsic Detector Performance. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Orlando, FL, USA, 24 October–1 November 2009; pp. 1959–1965. [Google Scholar]
- Atherton, P.D. The Scanning Fabry-Perot Spectrometer. Int. Astron. Union Colloq. 1995, 149, 50–59. [Google Scholar] [CrossRef]
- Lindsay, S.M.; Shepherd, I.W. Linear Scanning Circuit for a Piezoelectrically Controlled Fabry-Perot Etalon. Rev. Sci. Instrum. 1977, 48, 1228–1229. [Google Scholar] [CrossRef]
- Afifi, H.A. Ultrasonic Pulse Echo Studies of the Physical Properties of PMMA, PS, and PVC. Polym.-Plast. Technol. Eng. 2003, 42, 193–205. [Google Scholar] [CrossRef]
- Root, S.E.; Gao, R.; Abrahamsson, C.K.; Kodaimati, M.S.; Ge, S.; Whitesides, G.M. Estimating the Density of Thin Polymeric Films Using Magnetic Levitation. ACS Nano 2021, 15, 15676–15686. [Google Scholar] [CrossRef]
- Polyanskiy, M.N. Refractive Index Database. Available online: https://refractiveindex.info/?shelf=organic&book=poly(methyl_methacrylate) (accessed on 14 May 2023).
- ISO/IEC ISO/IEC 17043; Conformity Assessment—General Requirements for Proficiency Testing. ISO: Geneva, Switzerland, 2010.
- Caves, C.M. Quantum-Mechanical Noise in an Interferometer. Phys. Rev. D 1981, 23, 1693–1708. [Google Scholar] [CrossRef]
- Slusher, R.E.; Hollberg, L.W.; Yurke, B.; Mertz, J.C.; Valley, J.F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 1985, 55, 2409–2412. [Google Scholar] [CrossRef] [PubMed]
- Lawrie, B.J.; Lett, P.D.; Marino, A.M.; Pooser, R.C. Quantum Sensing with Squeezed Light. ACS Photonics 2019, 6, 1307–1318. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vahlbruch, H.; Mehmet, M.; Danzmann, K.; Schnabel, R. Detection of 15 dB Squeezed States of Light and Their Application for the Absolute Calibration of Photoelectric Quantum Efficiency. Phys. Rev. Lett. 2016, 117, 110801. [Google Scholar] [CrossRef] [Green Version]
- Polzik, E.S.; Carri, J.; Kimble, H.J. Spectroscopy with Squeezed Light. Phys. Rev. Lett. 1992, 68, 3020–3023. [Google Scholar] [CrossRef] [Green Version]
- Casacio, C.A.; Madsen, L.S.; Terrasson, A.; Waleed, M.; Barnscheidt, K.; Hage, B.; Taylor, M.A.; Bowen, W.P. Quantum-Enhanced Nonlinear Microscopy. Nature 2021, 594, 201–206. [Google Scholar] [CrossRef]
- Yu, H.; McCuller, L.; Tse, M.; Kijbunchoo, N.; Barsotti, L.; Mavalvala, N.; Betzwieser, J.; Blair, C.D.; Dwyer, S.E.; Effler, A.; et al. Quantum Correlations between Light and the Kilogram-Mass Mirrors of LIGO. Nature 2020, 583, 43–47. [Google Scholar] [CrossRef]
- Taylor, M.A.; Janousek, J.; Daria, V.; Knittel, J.; Hage, B.; Bachor, H.A.; Bowen, W.P. Biological Measurement beyond the Quantum Limit. Nat. Photonics 2013, 7, 229–233. [Google Scholar] [CrossRef] [Green Version]
- Schnabel, R.; Mavalvala, N.; McClelland, D.E.; Lam, P.K. Quantum Metrology for Gravitational Wave Astronomy. Nat. Commun. 2010, 1, 110–121. [Google Scholar] [CrossRef] [Green Version]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Dwyer, S.E.; Effler, A.; et al. Quantum-Enhanced Advanced LIGO Detectors in the Era of Gravitational-Wave Astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Andrade, R.B.; Kerdoncuff, H.; Berg-Sørensen, K.; Gehring, T.; Lassen, M.; Andersen, U.L. Quantum-Enhanced Continuous-Wave Stimulated Raman Scattering Spectroscopy. Optica 2020, 7, 470. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Li, F.; Liu, X.; Yakovlev, V.V.; Agarwal, G.S. Quantum-Enhanced Stimulated Brillouin Scattering Spectroscopy and Imaging. Optica 2022, 9, 959. [Google Scholar] [CrossRef]
- Danilishin, S.L.; Khalili, F.Y.; Miao, H. Advanced Quantum Techniques for Future Gravitational-Wave Detectors. Living Rev. Relativ. 2019, 22, 2. [Google Scholar] [CrossRef] [Green Version]
- Dorfman, K.E.; Schlawin, F.; Mukamel, S. Nonlinear Optical Signals and Spectroscopy with Quantum Light. Rev. Mod. Phys. 2016, 88, 045008. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Anderson, B.E.; Horrom, T.; Schmittberger, B.L.; Jones, K.M.; Lett, P.D. Improved Measurement of Two-Mode Quantum Correlations Using a Phase-Sensitive Amplifier. Opt. Express 2017, 25, 21301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, M.A.; Bowen, W.P. Quantum Metrology and Its Application in Biology. Phys. Rep. 2016, 615, 1–59. [Google Scholar] [CrossRef] [Green Version]


| Uncertainty Component | Probability Distribution | Standard Relative Uncertainty Contribution |
|---|---|---|
| Repeatability | t-distribution | 6.64 × 10−5 |
| Reproducibility | t-distribution | Negligible |
| Frequency resolution | rectangular | 2.69 × 10−4 |
| Geometrical error in the BLS spectrometer | rectangular | Negligible |
| Abbe error in BLS spectrometer | rectangular | 2.31 × 10−7 |
| Relative intensity noise (RIN) of laser | rectangular | 4.74 × 10−9 |
| Photodetector’s counting sensitivity | rectangular | Negligible |
| Ambient temperature variation | rectangular | 4.86 × 10−4 |
| Ambient pressure and humidity variation | rectangular | Negligible |
| Resolution of voltmeter for power meter | rectangular | 2.89 × 10−7 |
| Linearity error in scanning of TFPI | rectangular | 1.15 × 10−3 |
| Vibration effect | rectangular | Negligible |
| Combined relative uncertainty for frequency shift measurement | 0.13% | |
| Expanded relative uncertainty for frequency shift measurement (k = 2) | 0.26% | |
| Uncertainty Component | Probability Distribution | Standard Relative Uncertainty Contribution |
|---|---|---|
| Repeatability | t-distribution | 0.31% |
| Refractive index of PMMA | rectangular | 0.17% |
| Ultrasonic velocity measurement variation | rectangular | 1.00% |
| Combined relative uncertainty for calculated frequency shift | 1.06% | |
| Expanded relative uncertainty for calculated frequency shift (k = 2) | 2.13% | |
| Measured Frequency Shift, GHz | Expanded Uncertainty of Measured Frequency Shift, (νm Um), GHz | Calculated Frequency Shift, GHz | Expanded Uncertainty of Calculated Frequency Shift (νc Uc), GHz | Deviation of Frequency Shift, GHz | En |
|---|---|---|---|---|---|
| 15.70 | 0.041 | 15.44 | 0.33 | 0.26 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salzenstein, P.; Wu, T.Y. Uncertainty Estimation for the Brillouin Frequency Shift Measurement Using a Scanning Tandem Fabry–Pérot Interferometer. Micromachines 2023, 14, 1429. https://doi.org/10.3390/mi14071429
Salzenstein P, Wu TY. Uncertainty Estimation for the Brillouin Frequency Shift Measurement Using a Scanning Tandem Fabry–Pérot Interferometer. Micromachines. 2023; 14(7):1429. https://doi.org/10.3390/mi14071429
Chicago/Turabian StyleSalzenstein, Patrice, and Thomas Y. Wu. 2023. "Uncertainty Estimation for the Brillouin Frequency Shift Measurement Using a Scanning Tandem Fabry–Pérot Interferometer" Micromachines 14, no. 7: 1429. https://doi.org/10.3390/mi14071429
APA StyleSalzenstein, P., & Wu, T. Y. (2023). Uncertainty Estimation for the Brillouin Frequency Shift Measurement Using a Scanning Tandem Fabry–Pérot Interferometer. Micromachines, 14(7), 1429. https://doi.org/10.3390/mi14071429







