Formation of Paramagnetic Defects in the Synthesis of Silicon Carbide
Abstract
:1. Introduction
2. Experimental
Sample Preparation
3. Analysis
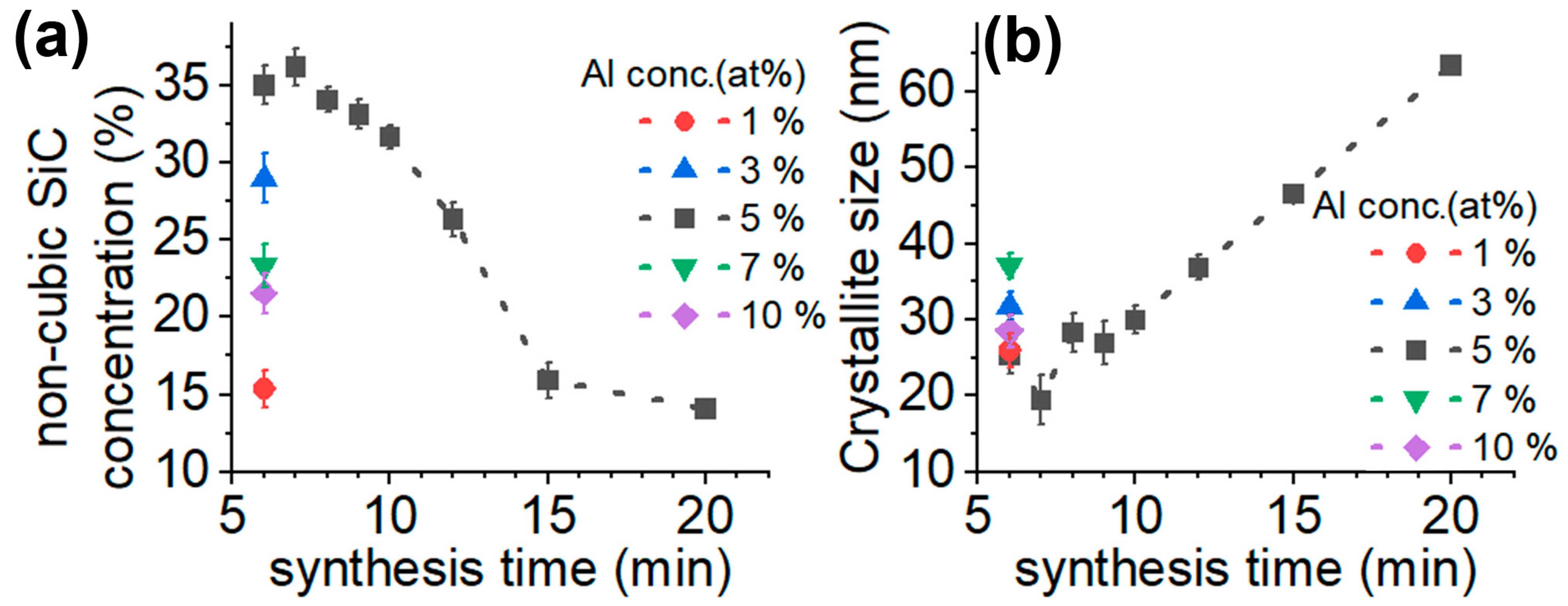
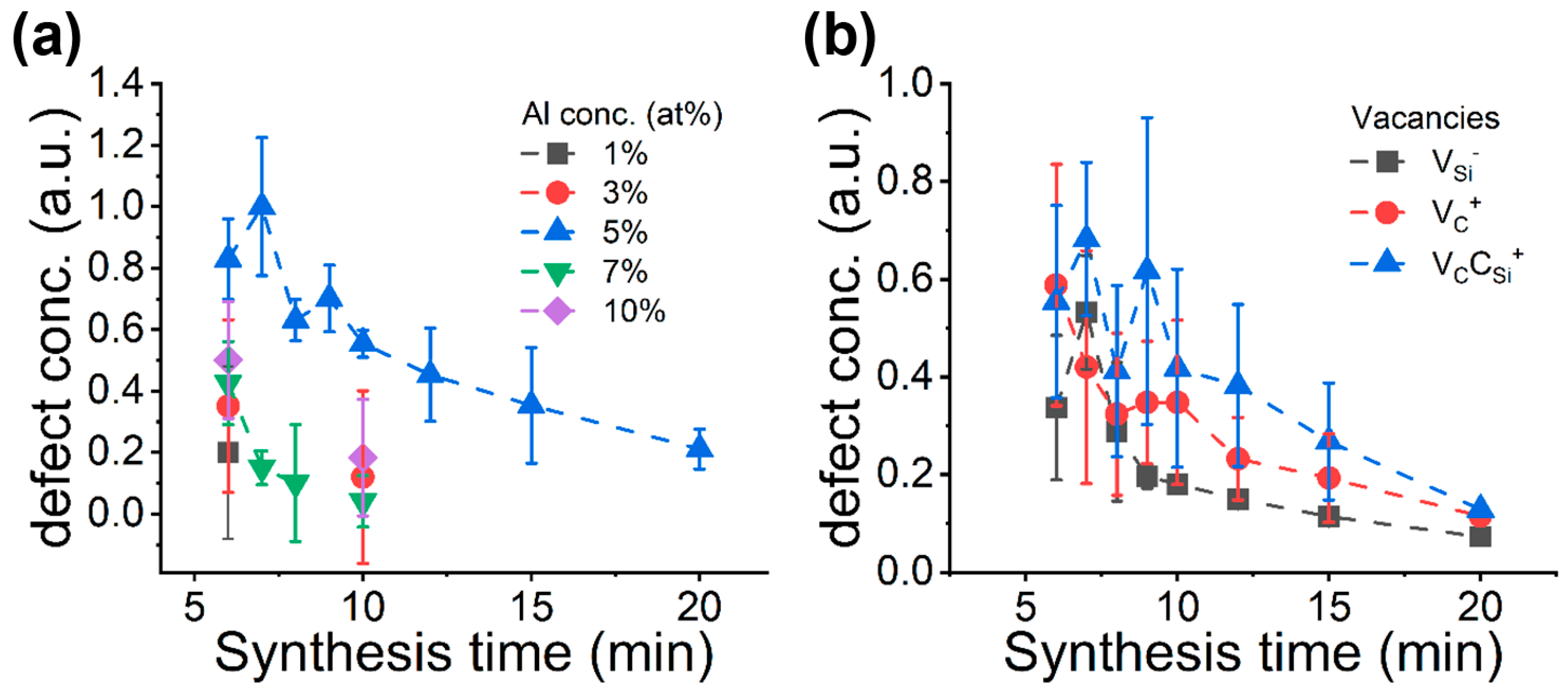
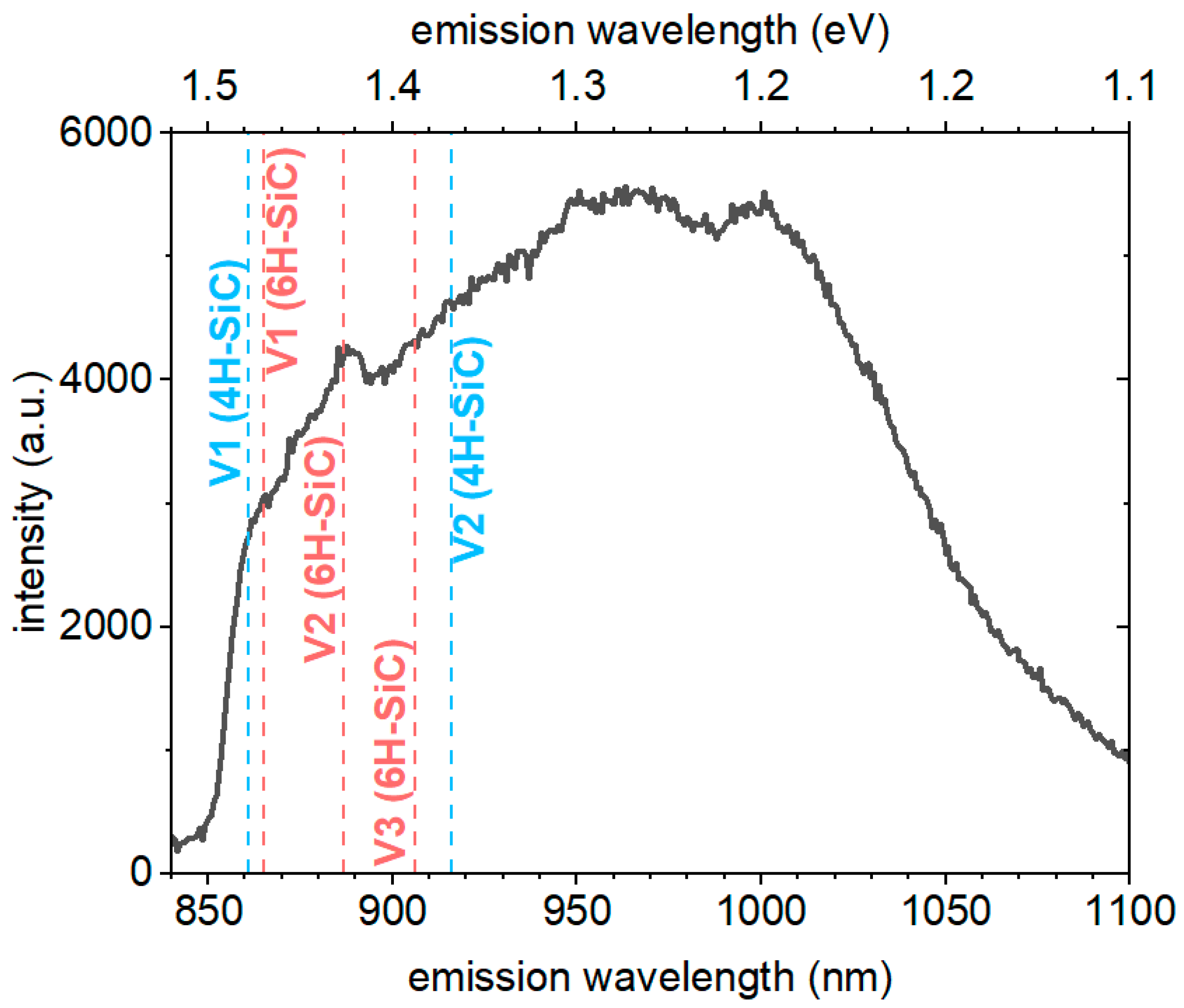
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hemmingsson, C.; Son, N.T.; Kordina, O.; Bergman, J.P.; Janzén, E.; Lindström, J.L.; Savage, S.; Nordell, N. Deep Level Defects in Electron-Irradiated 4H SiC Epitaxial Layers. J. Appl. Phys. 1997, 81, 6155–6159. [Google Scholar] [CrossRef]
- Chakravorty, A.; Singh, B.; Jatav, H.; Meena, R.; Kanjilal, D.; Kabiraj, D. Controlled Generation of Photoemissive Defects in 4H-SiC Using Swift Heavy Ion Irradiation. J. Appl. Phys. 2021, 129, 245905. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.; Song, Y.; Wang, H.; Dong, B.; Li, S.; Ren, J.; Li, Q.; Rommel, M.; Gu, X.; et al. Confocal Photoluminescence Characterization of Silicon-Vacancy Color Centers in 4H-SiC Fabricated by a Femtosecond Laser. Nanotechnol. Precis. Eng. 2020, 3, 218–228. [Google Scholar] [CrossRef]
- Sörman, E.; Son, N.T.; Chen, W.M.; Kordina, O.; Hallin, C.; Janzén, E. Silicon Vacancy Related Defect in 4H and 6H SiC. Phys. Rev. B 2000, 61, 2613–2620. [Google Scholar] [CrossRef]
- Janzén, E.; Gali, A.; Carlsson, P.; Gällström, A.; Magnusson, B.; Son, N.T. The Silicon Vacancy in SiC. Phys. B Condens. Matter 2009, 404, 4354–4358. [Google Scholar] [CrossRef]
- Nagy, R.; Widmann, M.; Niethammer, M.; Dasari, D.B.R.; Gerhardt, I.; Soykal, Ö.O.; Radulaski, M.; Ohshima, T.; Vučković, J.; Son, N.T.; et al. Quantum Properties of Dichroic Silicon Vacancies in Silicon Carbide. Phys. Rev. Appl. 2018, 9, 034022. [Google Scholar] [CrossRef] [Green Version]
- Nagy, R.; Niethammer, M.; Widmann, M.; Chen, Y.-C.; Udvarhelyi, P.; Bonato, C.; Hassan, J.U.; Karhu, R.; Ivanov, I.G.; Son, N.T.; et al. High-Fidelity Spin and Optical Control of Single Silicon-Vacancy Centres in Silicon Carbide. Nat. Commun. 2019, 10, 1954. [Google Scholar] [CrossRef] [Green Version]
- Ivády, V.; Davidsson, J.; Son, N.T.; Ohshima, T.; Abrikosov, I.A.; Gali, Á. Ab Initio Theory of Si-Vacancy Quantum Bits in 4H and 6H-SiC. Mater. Sci. Forum 2018, 924, 895–900. [Google Scholar] [CrossRef]
- Kraus, H.; Soltamov, V.A.; Riedel, D.; Väth, S.; Fuchs, F.; Sperlich, A.; Baranov, P.G.; Dyakonov, V.; Astakhov, G.V. Room-Temperature Quantum Microwave Emitters Based on Spin Defects in Silicon Carbide. Nat. Phys. 2013, 10, 157–162. [Google Scholar] [CrossRef]
- Widmann, M.; Lee, S.-Y.; Rendler, T.; Son, N.T.; Fedder, H.; Paik, S.; Yang, L.-P.; Zhao, N.; Yang, S.; Booker, I.; et al. Coherent Control of Single Spins in Silicon Carbide at Room Temperature. Nat. Mater. 2014, 14, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Echlin, P. Handbook of Sample Preparation for Scanning Electron Microscopy and X-ray Microanalysis, 1st ed.; Springer: New York, NY, USA, 2009; ISBN 978-0-387-85731-2. [Google Scholar]
- Niethammer, M.; Widmann, M.; Rendler, T.; Morioka, N.; Chen, Y.-C.; Stöhr, R.; Hassan, J.U.; Onoda, S.; Ohshima, T.; Lee, S.-Y.; et al. Coherent Electrical Readout of Defect Spins in Silicon Carbide by Photo-Ionization at Ambient Conditions. Nat. Commun. 2019, 10, 5569. [Google Scholar] [CrossRef] [Green Version]
- Carlos, W.E.; Garces, N.Y.; Glaser, E.R.; Fanton, M.A. Annealing of Multivacancy Defects in 4H−SiC. Phys. Rev. B 2006, 74, 235201. [Google Scholar] [CrossRef] [Green Version]
- Son, N.T.; Carlsson, P.; ul Hassan, J.; Janzén, E.; Umeda, T.; Isoya, J.; Gali, A.; Bockstedte, M.; Morishita, N.; Ohshima, T.; et al. Divacancy in 4H-SiC. Phys. Rev. Lett. 2006, 96, 055501. [Google Scholar] [CrossRef]
- Gali, A.; Gällström, A.; Son, N.T.; Janzén, E. Theory of Neutral Divacancy in SiC: A Defect for Spintronics. Mater. Sci. Forum 2010, 645–648, 395–397. [Google Scholar] [CrossRef] [Green Version]
- Falk, A.L.; Buckley, B.B.; Calusine, G.; Koehl, W.F.; Dobrovitski, V.V.; Politi, A.; Zorman, C.A.; Feng, P.X.-L.; Awschalom, D.D. Polytype Control of Spin Qubits in Silicon Carbide. Nat. Commun. 2013, 4, 1819. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivády, V.; Szász, K.; Falk, A.L.; Klimov, P.V.; Janzén, E.; Abrikosov, I.A.; Awschalom, D.D.; Gali, Á. First Principles Identification of Divacancy Related Photoluminescence Lines in 4H and 6H-SiC. Mater. Sci. Forum 2016, 858, 322–325. [Google Scholar] [CrossRef]
- Koehl, W.F.; Buckley, B.B.; Heremans, F.J.; Calusine, G.; Awschalom, D.D. Room Temperature Coherent Control of Defect Spin Qubits in Silicon Carbide. Nature 2011, 479, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Christle, D.J.; Falk, A.L.; Andrich, P.; Klimov, P.V.; Hassan, J.U.; Son, N.T.; Janzén, E.; Ohshima, T.; Awschalom, D.D. Isolated Electron Spins in Silicon Carbide with Millisecond Coherence Times. Nat. Mater. 2014, 14, 160–163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Magnusson, B.; Janzén, E. Optical Characterization of Deep Level Defects in SiC. Mater. Sci. Forum 2005, 483–485, 341–346. [Google Scholar] [CrossRef]
- Somogyi, B.; Gali, A. Computational Design of in Vivo Biomarkers. J. Phys. Condens. Matter 2014, 26, 143202. [Google Scholar] [CrossRef]
- de Vries, M.O.; Sato, S.; Ohshima, T.; Gibson, B.C.; Bluet, J.; Castelletto, S.; Johnson, B.C.; Reineck, P. Fluorescent Silicon Carbide Nanoparticles. Adv. Opt. Mater. 2021, 9, 2100311. [Google Scholar] [CrossRef]
- Castelletto, S.; Johnson, B.C.; Ivády, V.; Stavrias, N.; Umeda, T.; Gali, A.; Ohshima, T. A Silicon Carbide Room-Temperature Single-Photon Source. Nat. Mater. 2013, 13, 151–156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castelletto, S.; Johnson, B.C.; Zachreson, C.; Beke, D.; Balogh, I.; Ohshima, T.; Aharonovich, I.; Gali, A. Room Temperature Quantum Emission from Cubic Silicon Carbide Nanoparticles. ACS Nano 2014, 8, 7938–7947. [Google Scholar] [CrossRef] [PubMed]
- Umeda, T.; Ishoya, J.; Ohshima, T.; Morishita, N.; Itoh, H.; Gali, A. Identification of Positively Charged Carbon Antisite-Vacancy Pairs in 4H-SiC. Phys. Rev. B 2007, 75, 245202. [Google Scholar] [CrossRef]
- von Bardeleben, H.J.; Rauls, E.; Gerstmann, U. Carbon Vacancy-Related Centers in 3C-Silicon Carbide: Negative-U Properties and Structural Transformation. Phys. Rev. B 2020, 101, 184108. [Google Scholar] [CrossRef]
- Rauls, E.; Lingner, T.; Hajnal, Z.; Greulich-Weber, S.; Frauenheim, T.; Spaeth, J.-M. Metastability of the Neutral Silicon Vacancy in 4H-SiC. Phys. Status Solidi B 2000, 217, r1–r3. [Google Scholar] [CrossRef]
- Deák, P.; Aradi, B.; Frauenheim, T.; Gali, A. Challenges for Ab Initio Defect Modeling. Mater. Sci. Eng. B 2008, 154–155, 187–192. [Google Scholar] [CrossRef]
- Umeda, T.; Isoya, J.; Morishita, N.; Ohshima, T.; Kamiya, T.; Gali, A.; Deák, P.; Son, N.T.; Janzén, E. EPR and Theoretical Studies of Positively Charged Carbon Vacancy in 4H-SiC. Phys. Rev. B 2004, 70, 235212. [Google Scholar] [CrossRef] [Green Version]
- Beke, D.; Valenta, J.; Károlyházy, G.; Lenk, S.; Czigány, Z.; Márkus, B.G.; Kamarás, K.; Simon, F.; Gali, A. Room-Temperature Defect Qubits in Ultrasmall Nanocrystals. J. Phys. Chem. Lett. 2020, 11, 1675–1681. [Google Scholar] [CrossRef] [Green Version]
- Beke, D.; Szekrényes, Z.; Czigány, Z.; Kamarás, K.; Gali, Á. Dominant Luminescence Is Not Due to Quantum Confinement in Molecular-Sized Silicon Carbide Nanocrystals. Nanoscale 2015, 7, 10982–10988. [Google Scholar] [CrossRef] [Green Version]
- Viala, J.C.; Bosselet, F.; Laurent, V.; Lepetitcorps, Y. Mechanism and Kinetics of the Chemical Interaction between Liquid Aluminium and Silicon-Carbide Single Crystals. J. Mater. Sci. 1993, 28, 5301–5312. [Google Scholar] [CrossRef]
- Du, H.; Yang, Z.; Libera, M.; Jacobson, D.C.; Wang, Y.C.; Davis, R.F. Chemistry and Structure of Beta Silicon Carbide Implanted with High-Dose Aluminum. J. Am. Ceram. Soc. 1993, 76, 330–335. [Google Scholar] [CrossRef]
- Beke, D.; Károlyházy, G.; Czigány, Z.; Bortel, G.; Kamarás, K.; Gali, A. Harnessing No-Photon Exciton Generation Chemistry to Engineer Semiconductor Nanostructures. Sci. Rep. 2017, 7, 10599. [Google Scholar] [CrossRef] [Green Version]
- Mukasyan, A.S.; Lin, Y.-C.; Rogachev, A.S.; Moskovskikh, D.O. Direct Combustion Synthesis of Silicon Carbide Nanopowder from the Elements. J. Am. Ceram. Soc. 2013, 96, 111–117. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Bockstedte, M.; Heid, M.; Pankratov, O. Signature of Intrinsic Defects in SiC: Ab Initio Calculations of Hyperfine Tensors. Phys. Rev. B 2003, 67, 193102. [Google Scholar] [CrossRef]
- Umeda, T.; Morishita, N.; Ohshima, T.; Itoh, H.; Isoya, J. Electron Paramagnetic Resonance Study of Carbon Antisite-Vacancy Pair in p-Type 4H-SiC. Mater. Sci. Forum 2007, 556–557, 453–456. [Google Scholar] [CrossRef]
- Cantin, J.L.; Von Bardeleben, H.J.; Shishkin, Y.; Ke, Y.; Devaty, R.P.; Choyke, W.J. Identification of the Carbon Dangling Bond Center at the 4H−SiC/SiO2 Interface by an EPR Study in Oxidized Porous SiC. Phys. Rev. Lett. 2004, 92, 015502. [Google Scholar] [CrossRef]
- Umeda, T.; Kobayashi, T.; Sometani, M.; Yano, H.; Matsushita, Y.; Harada, S. Carbon Dangling-Bond Center (Carbon P b Center) at 4H-SiC(0001)/SiO2 Interface. Appl. Phys. Lett. 2020, 116, 071604. [Google Scholar] [CrossRef]
- Umeda, T.; Nakano, Y.; Higa, E.; Okuda, T.; Kimoto, T.; Hosoi, T.; Watanabe, H.; Sometani, M.; Harada, S. Electron-Spin-Resonance and Electrically Detected-Magnetic-Resonance Characterization on P bC Center in Various 4H-SiC(0001)/SiO2 Interfaces. J. Appl. Phys. 2020, 127, 145301. [Google Scholar] [CrossRef]
- Szász, K.; Ivády, V.; Abrikosov, I.A.; Janzén, E.; Bockstedte, M.; Gali, A. Spin and Photophysics of Carbon-Antisite Vacancy Defect in 4 H Silicon Carbide: A Potential Quantum Bit. Phys. Rev. B 2015, 91, 121201. [Google Scholar] [CrossRef] [Green Version]


| Reaction Time | ||||||||
|---|---|---|---|---|---|---|---|---|
| 6 min | 7 min | 8 min | 9 min | 10 min | 12 min | 15 min | ||
| Elements | Concentration [at%], (Error%) | |||||||
| C | 39.3 (12.1) | 44.0 (11.8) | 58.1 (11.5) | 54.5 (11.7) | 58.6 (11.5) | 59.8 (11.4) | 60.2 (11.5) | |
| Si | 58.3 (2.6) | 51.7 (2.7) | 39.2 (2.7) | 42.5 (2.9) | 36.0 (3.0) | 36.4 (2.8) | 38.3 (2.7) | |
| Al | 0.2 (8.9) | 0.2 (8.8) | 0.6 (4.9) | 0.2 (6.7) | 1.3 (4.5) | 0.1 (9.3) | 0.1 (9.2) | |
| O | 1.7 (12.2) | 3.4 (10.8) | 2.1 (11.9) | 2.5 (12.3) | 3.2 (12.1) | 2.6 (12.1) | 0.8 (15.9) | |
| F | 0.2 (15.9) | |||||||
| N | 0.4 (43.1) | 0.5 (28.9) | 0.8 (22.4) | 0.6 (34.0) | ||||
| Na | 0.3 (8.3) | 0.1 (12.3) | ||||||
| K | 0.1 (21.5) | |||||||
| S | 0.2 (5.8) | |||||||
| Fe | 0.4 (14.7) | 0.1 (29.1) | ||||||
| Cu | 0.3 (25.6) | |||||||
| Defect | g-Factor, S | Axx (MHz) | Ayy (MHz) | Azz (MHz) |
|---|---|---|---|---|
| VSi− | 2.0029, 3/2 | |||
| 13C × 4 | 33.0 | 33.0 | 80.0 | |
| 29Si × 12 | 8.2 | 8.2 | 8.2 | |
| VC+ | 2.0027, 1/2 | |||
| 29Si × 4 | 120.0 | 120.0 | 180.0 | |
| VC-CSi+ | 2.0035, 1/2 | |||
| 13C × 1 | 64.0 | 64.0 | 231.0 | |
| 29Si × 3 | 64.0 | 64.0 | 64.0 | |
| VC-VSi | 2.0030, 1 | |||
| 13C × 3 | 50.0 | 50.0 | 110.0 | |
| 29Si × 3 | 12.0 | 12.0 | 12.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukesh, N.; Márkus, B.G.; Jegenyes, N.; Bortel, G.; Bezerra, S.M.; Simon, F.; Beke, D.; Gali, A. Formation of Paramagnetic Defects in the Synthesis of Silicon Carbide. Micromachines 2023, 14, 1517. https://doi.org/10.3390/mi14081517
Mukesh N, Márkus BG, Jegenyes N, Bortel G, Bezerra SM, Simon F, Beke D, Gali A. Formation of Paramagnetic Defects in the Synthesis of Silicon Carbide. Micromachines. 2023; 14(8):1517. https://doi.org/10.3390/mi14081517
Chicago/Turabian StyleMukesh, Nain, Bence G. Márkus, Nikoletta Jegenyes, Gábor Bortel, Sarah M. Bezerra, Ferenc Simon, David Beke, and Adam Gali. 2023. "Formation of Paramagnetic Defects in the Synthesis of Silicon Carbide" Micromachines 14, no. 8: 1517. https://doi.org/10.3390/mi14081517
APA StyleMukesh, N., Márkus, B. G., Jegenyes, N., Bortel, G., Bezerra, S. M., Simon, F., Beke, D., & Gali, A. (2023). Formation of Paramagnetic Defects in the Synthesis of Silicon Carbide. Micromachines, 14(8), 1517. https://doi.org/10.3390/mi14081517






