An RDL Modeling and Thermo-Mechanical Simulation Method of 2.5D/3D Advanced Package Considering the Layout Impact Based on Machine Learning
Abstract
:1. Introduction
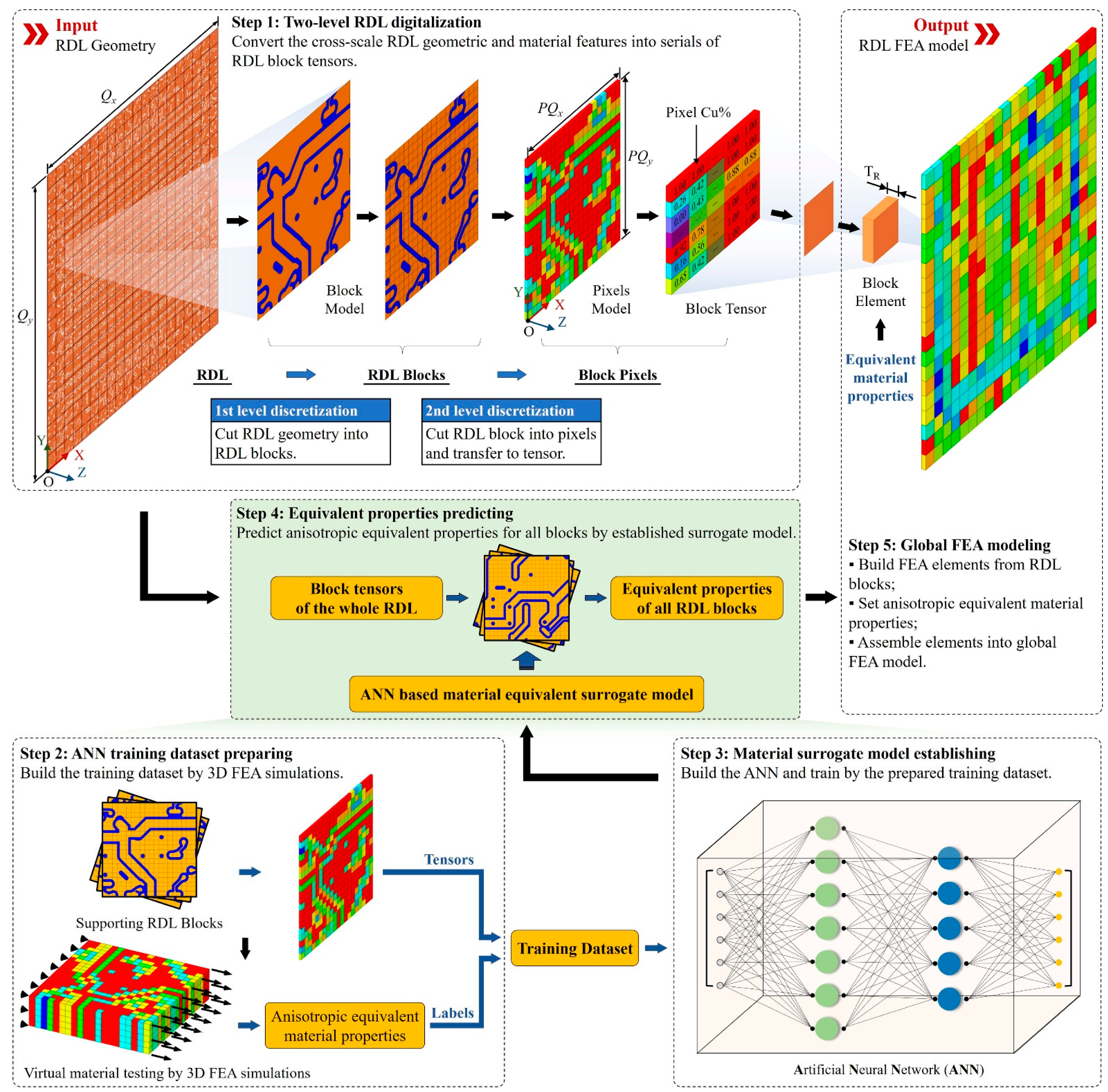
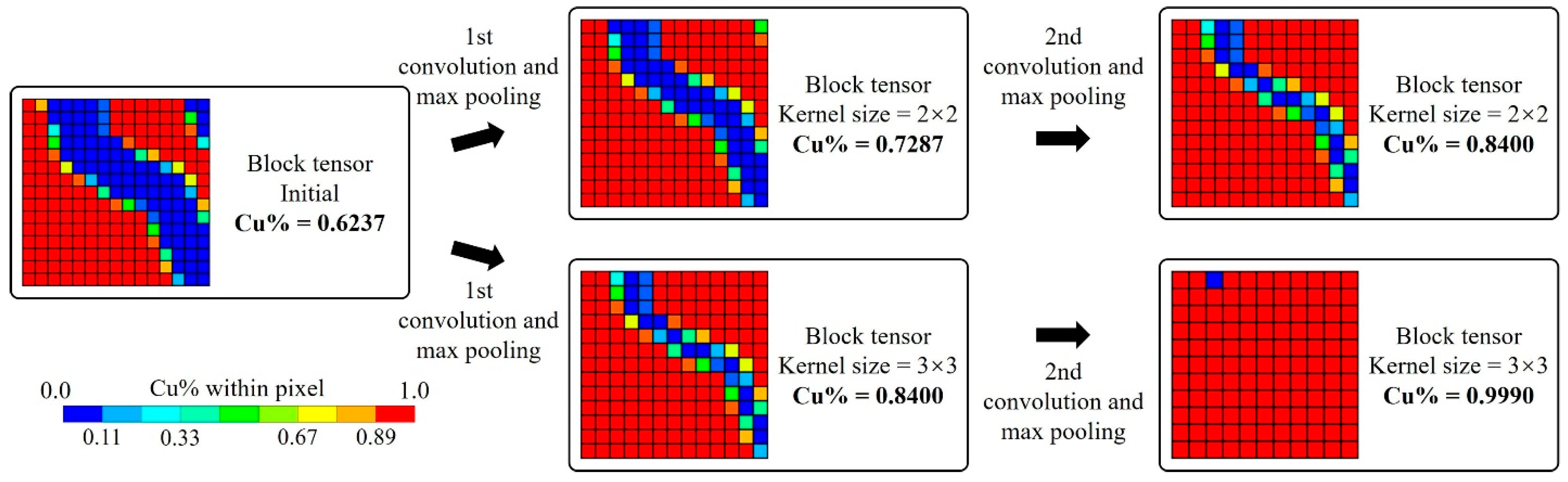
2. Methods
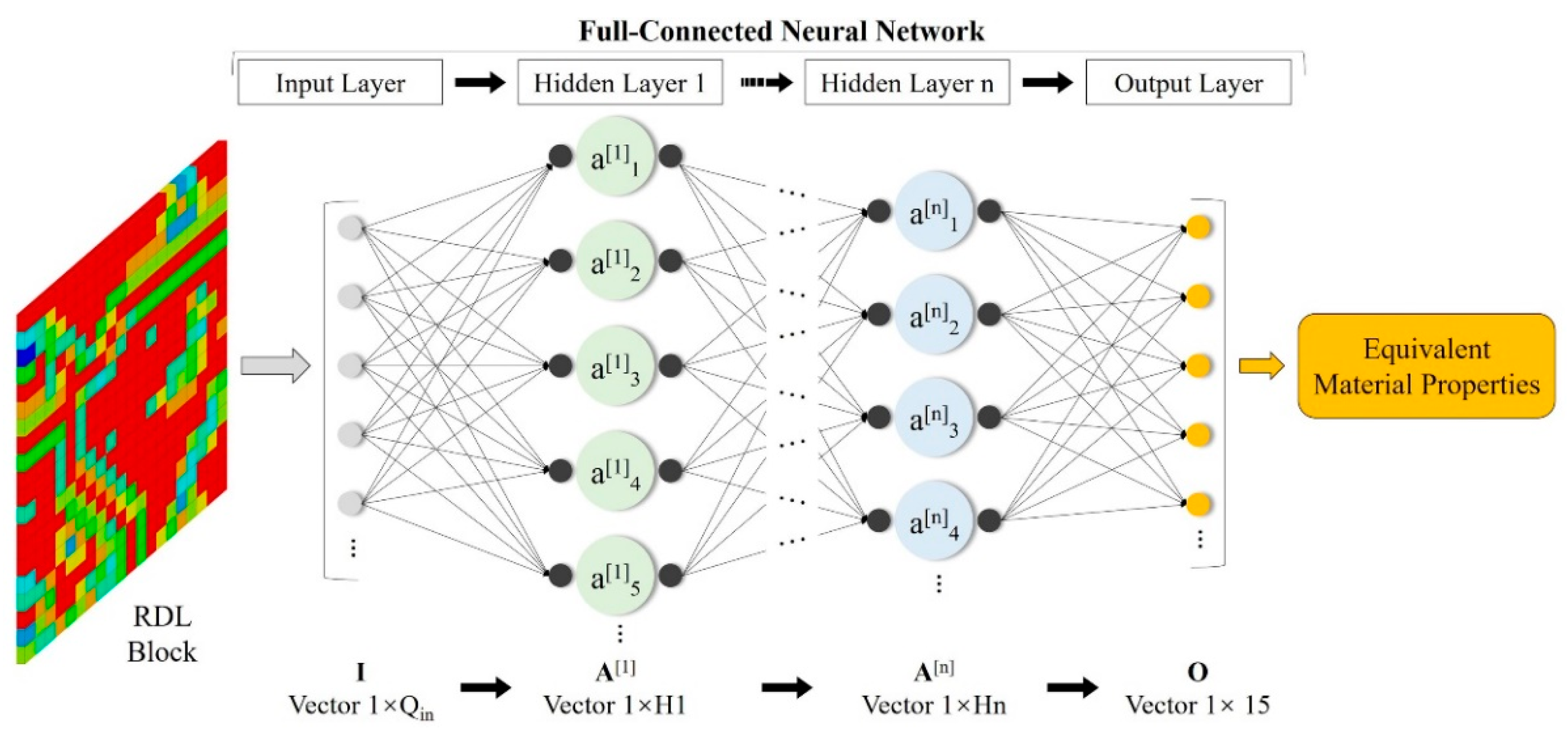
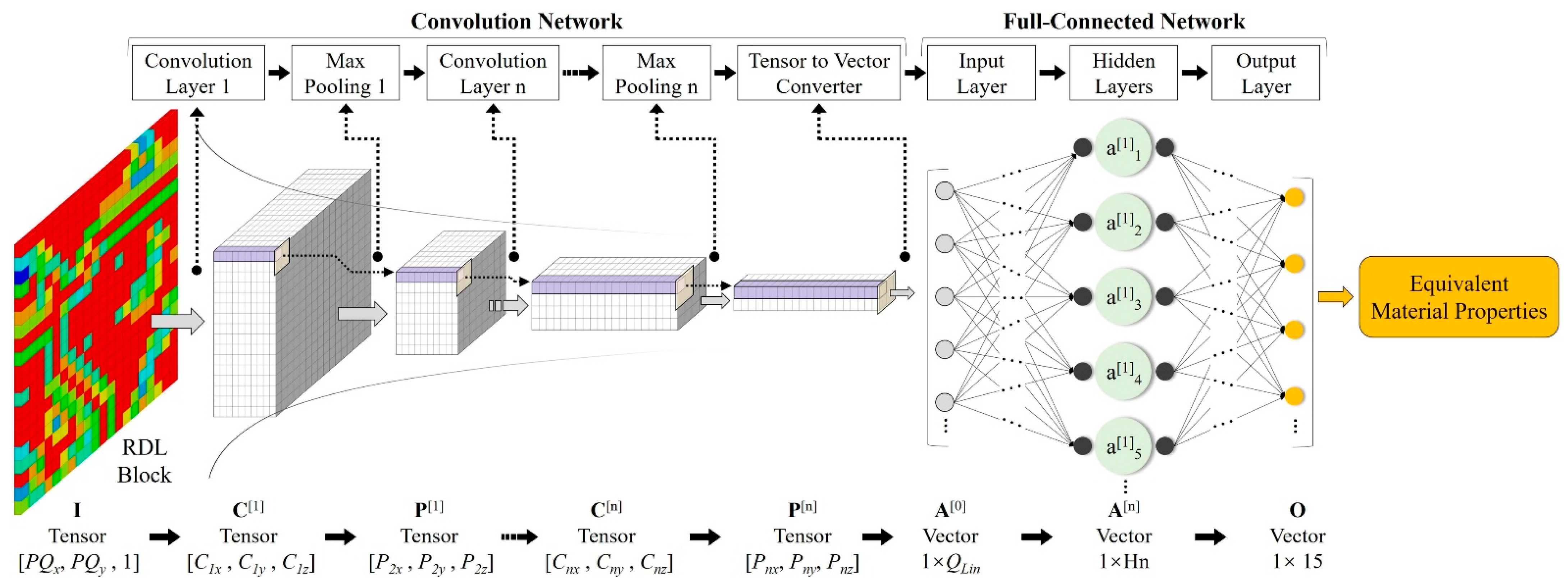
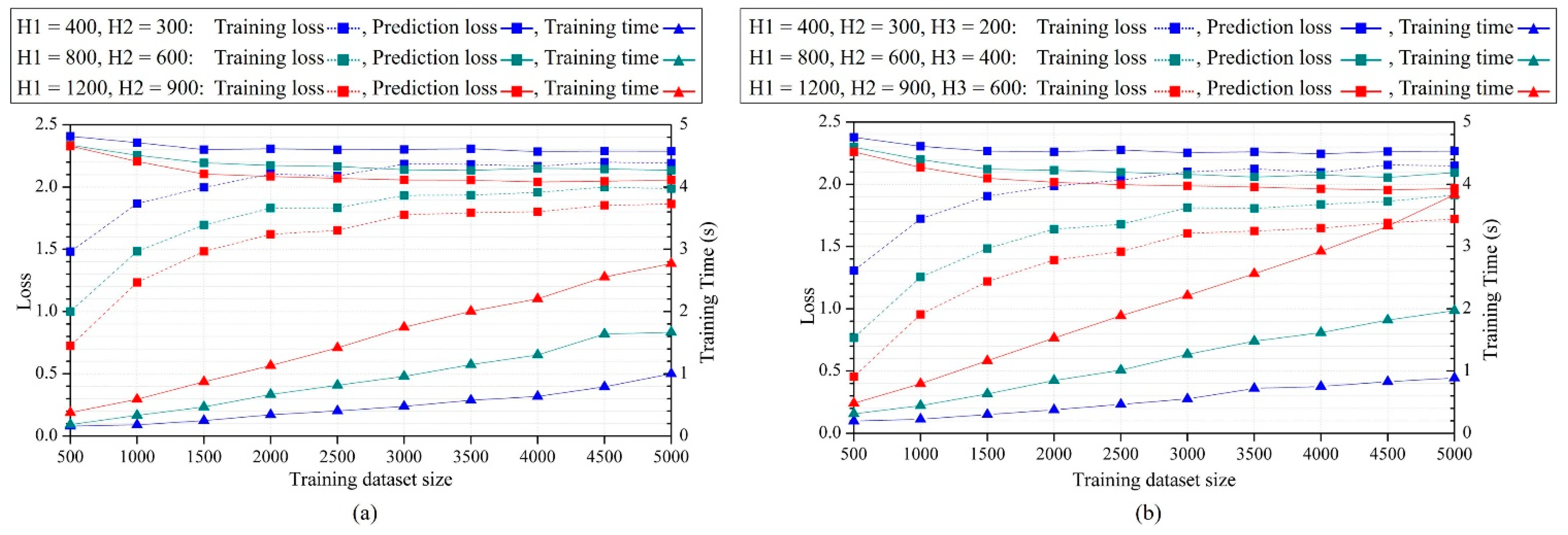
2.1. ANN Architectures
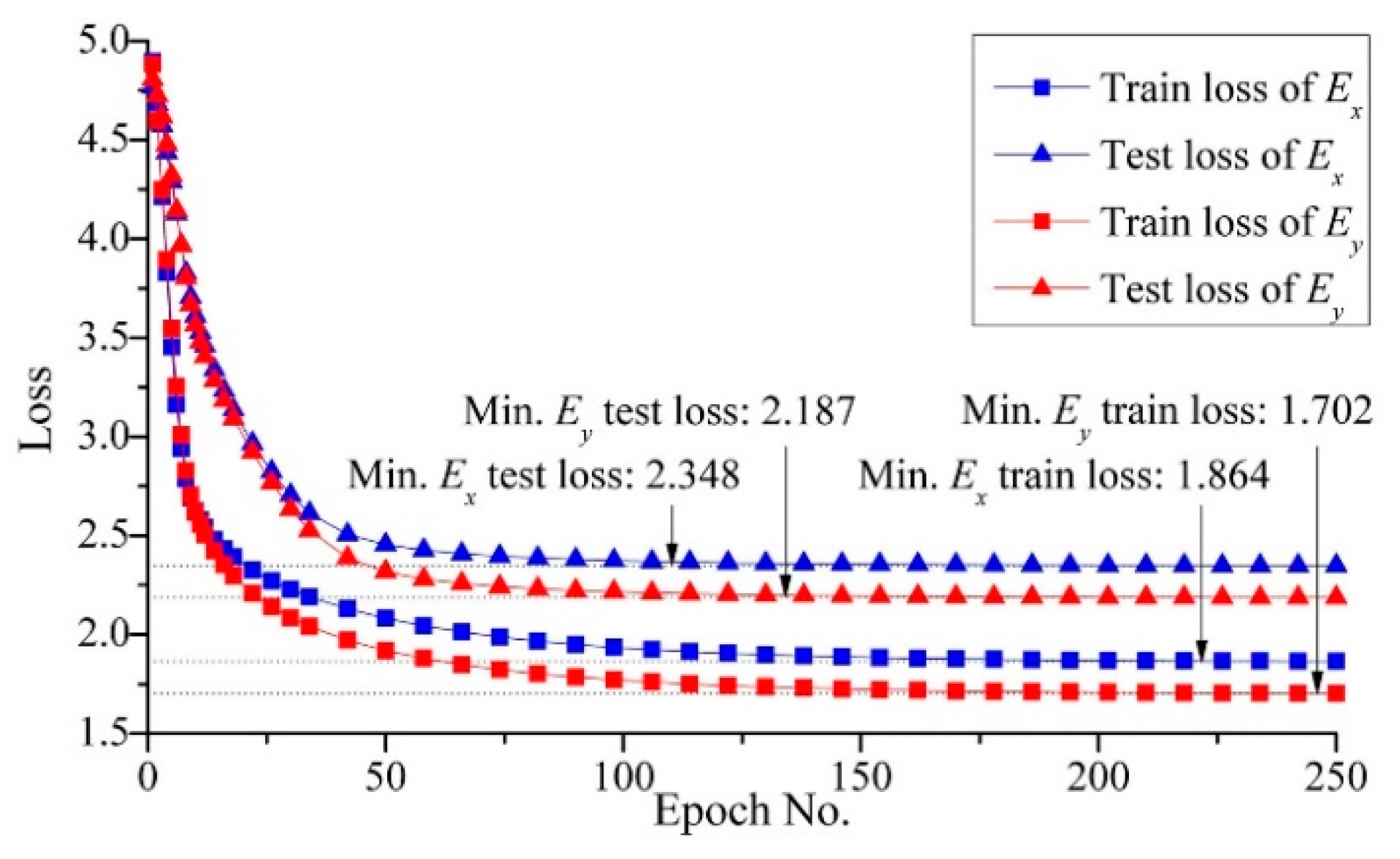
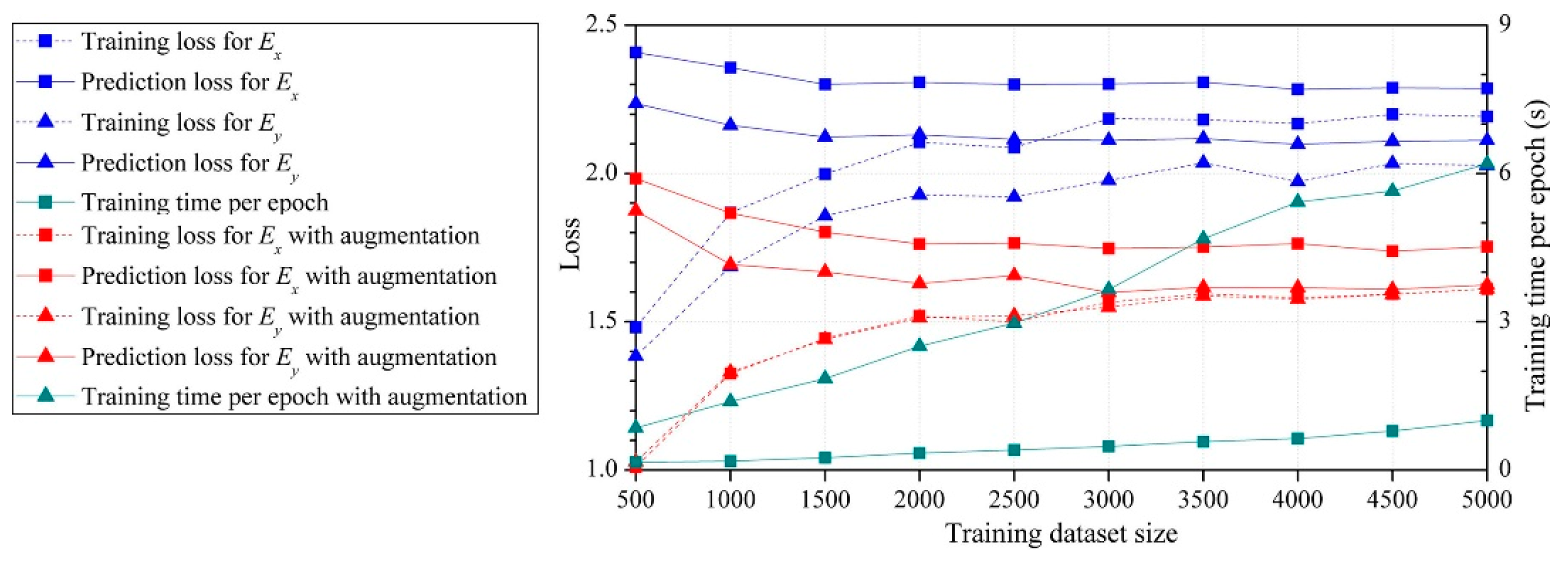
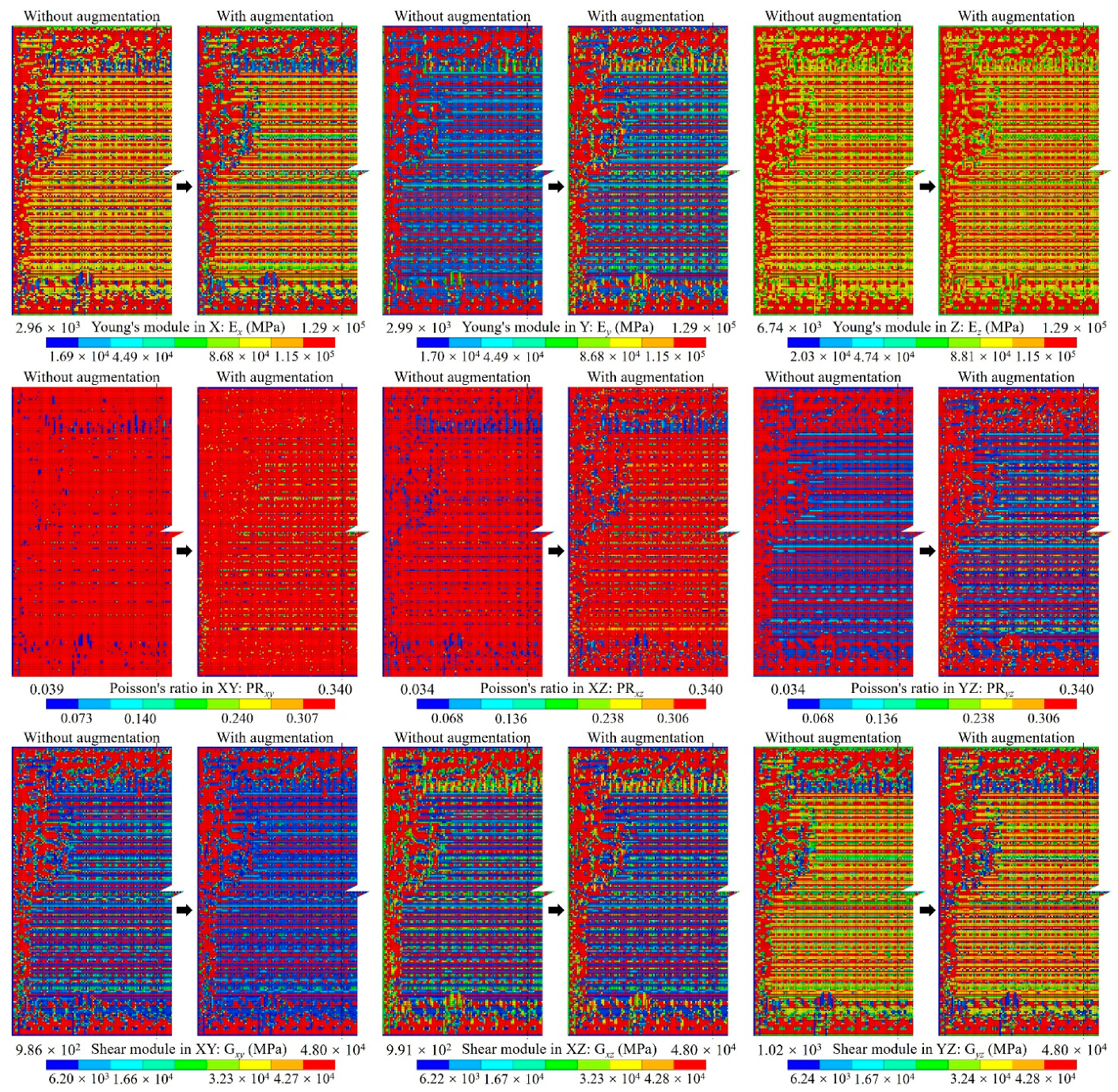
2.2. Training Dataset Augmentation
3. Result and Discussions
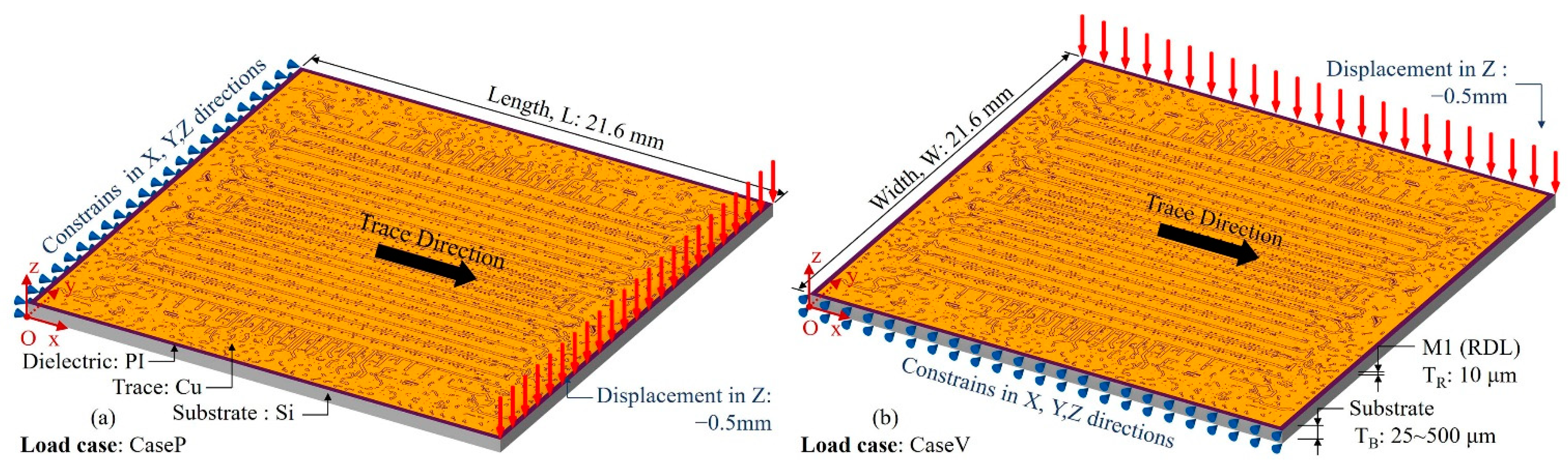
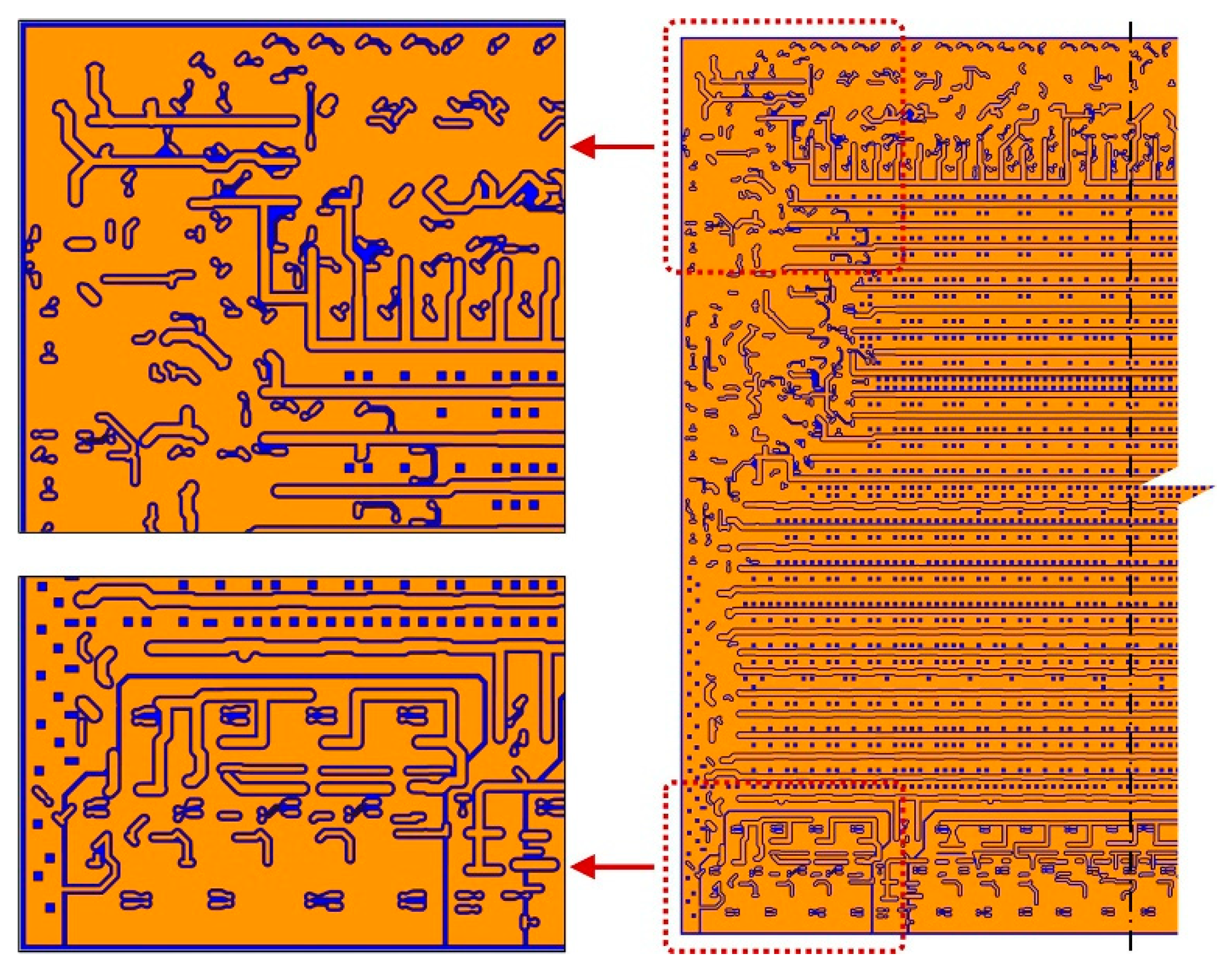
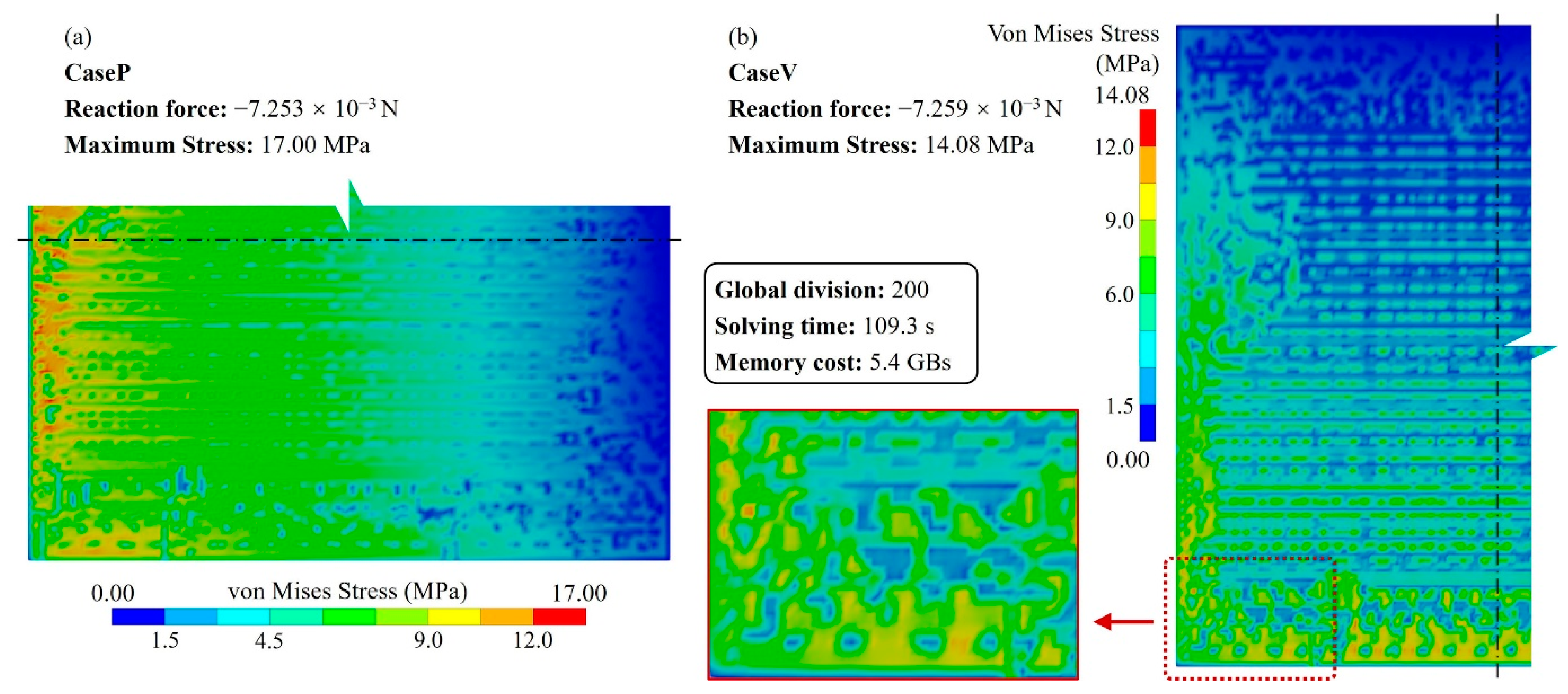
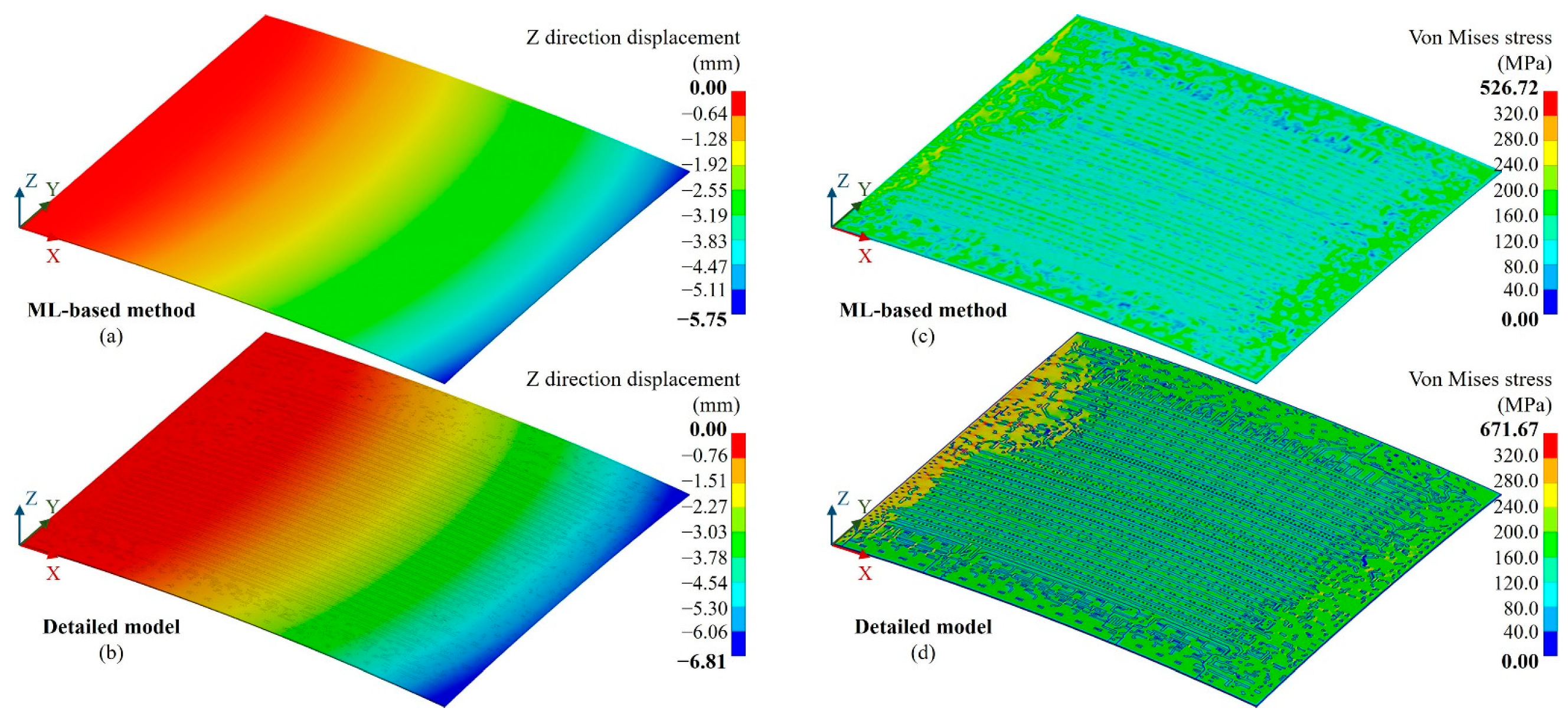
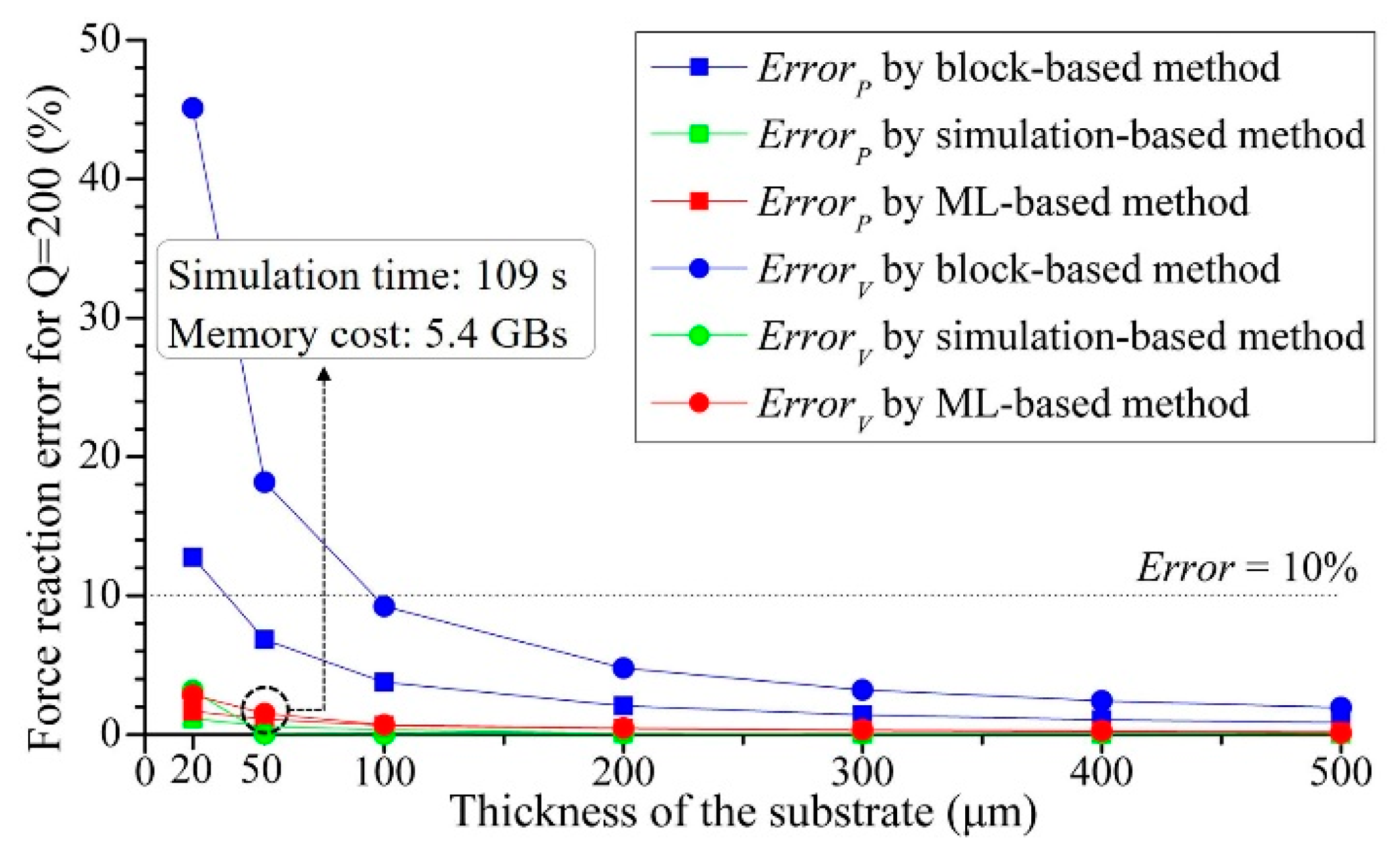
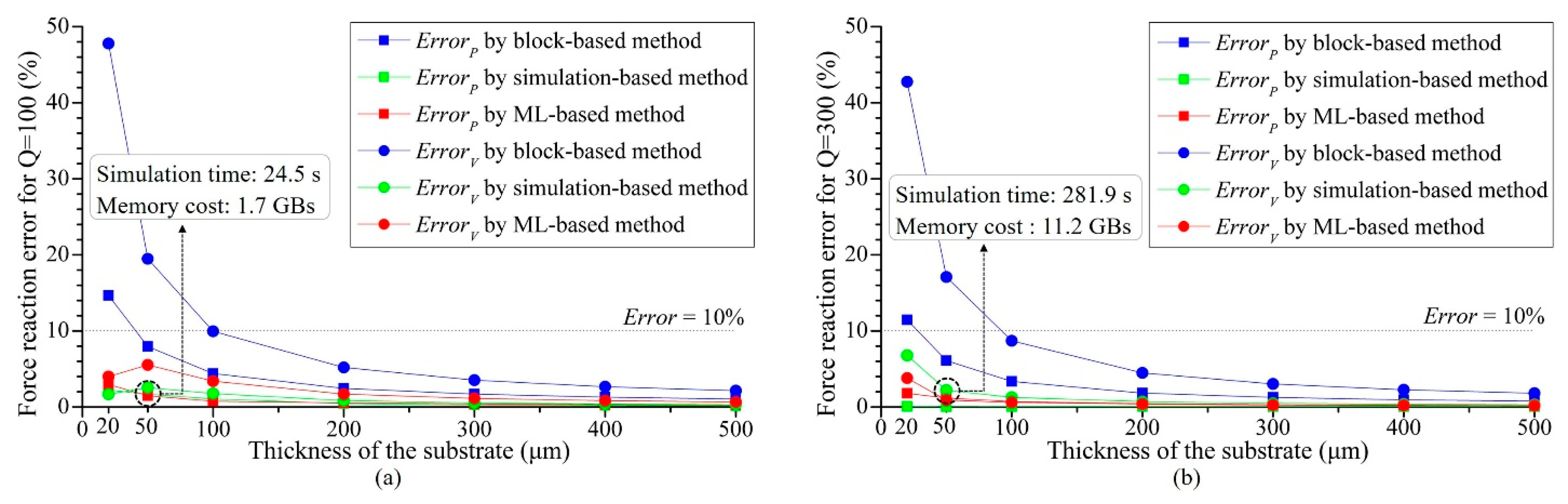
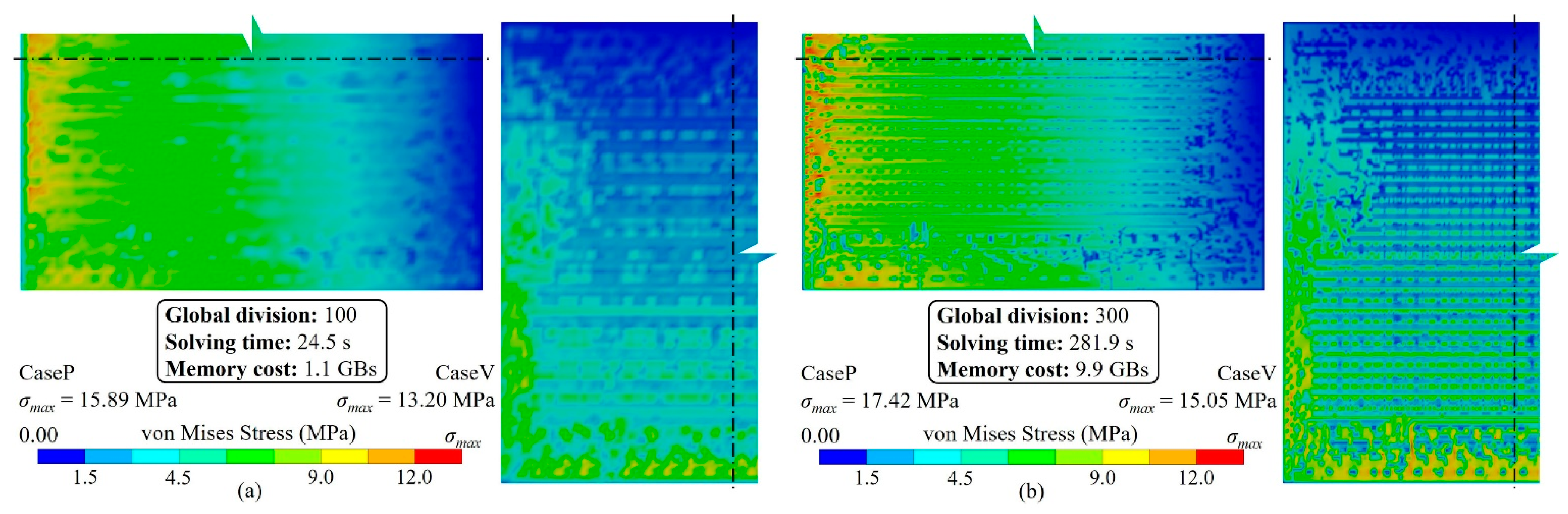
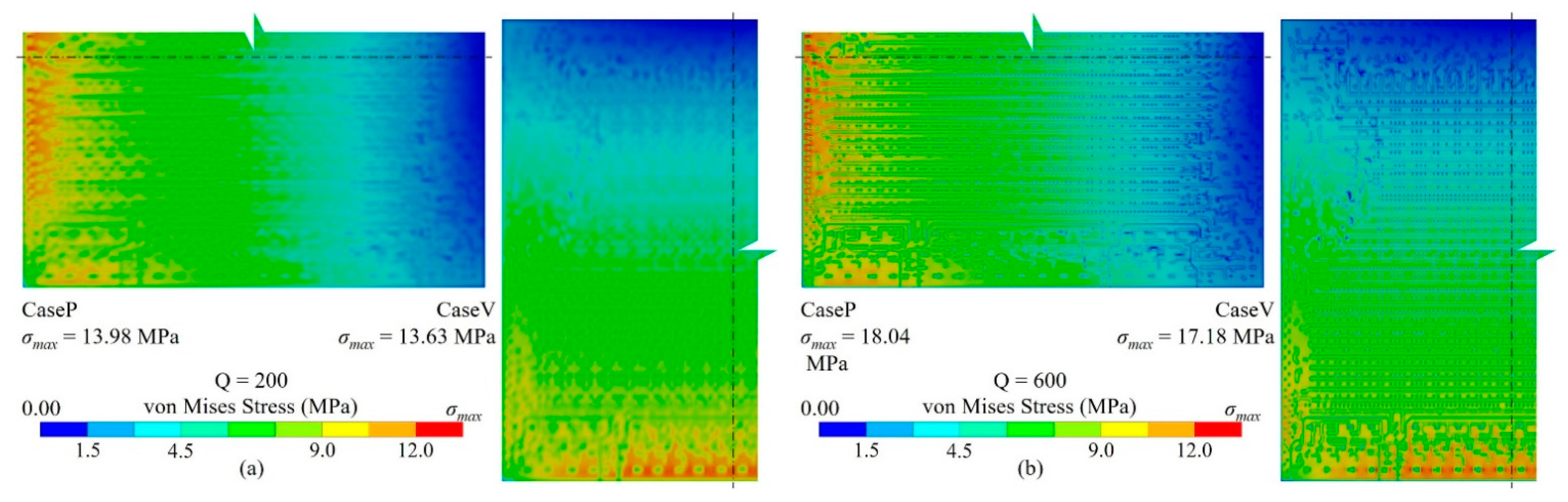
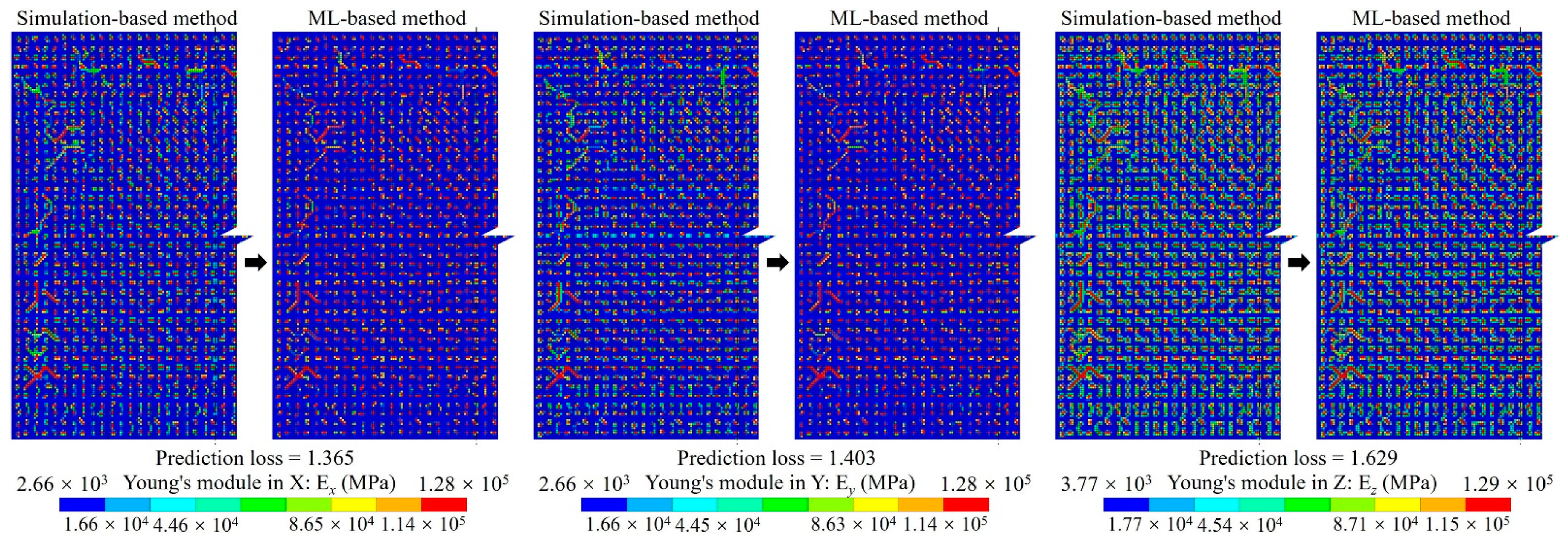
3.1. Method Validation
3.2. Key Factors Influence
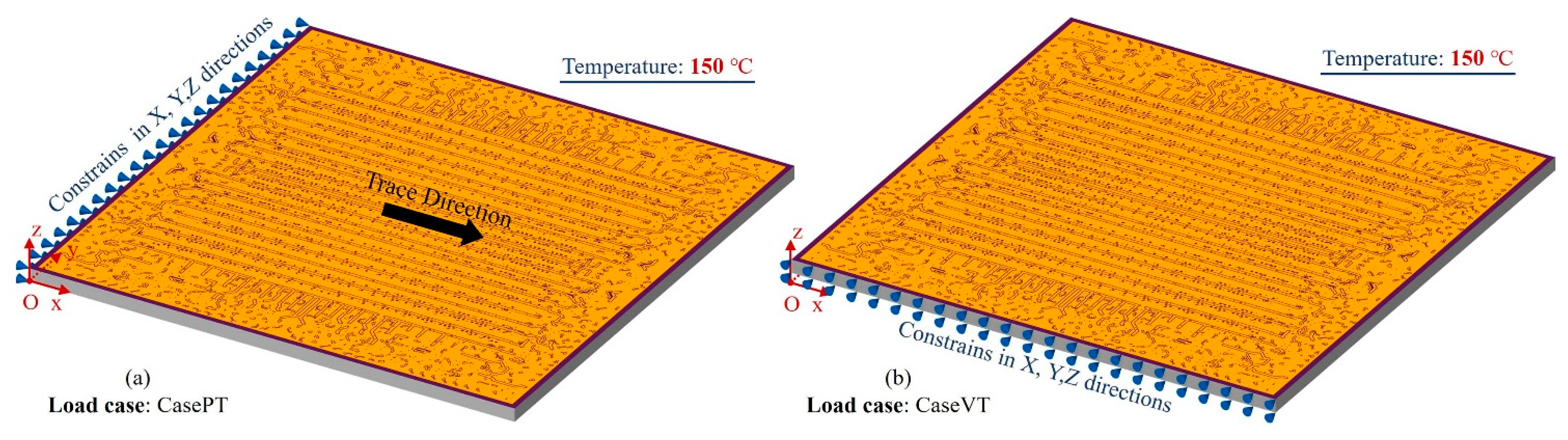
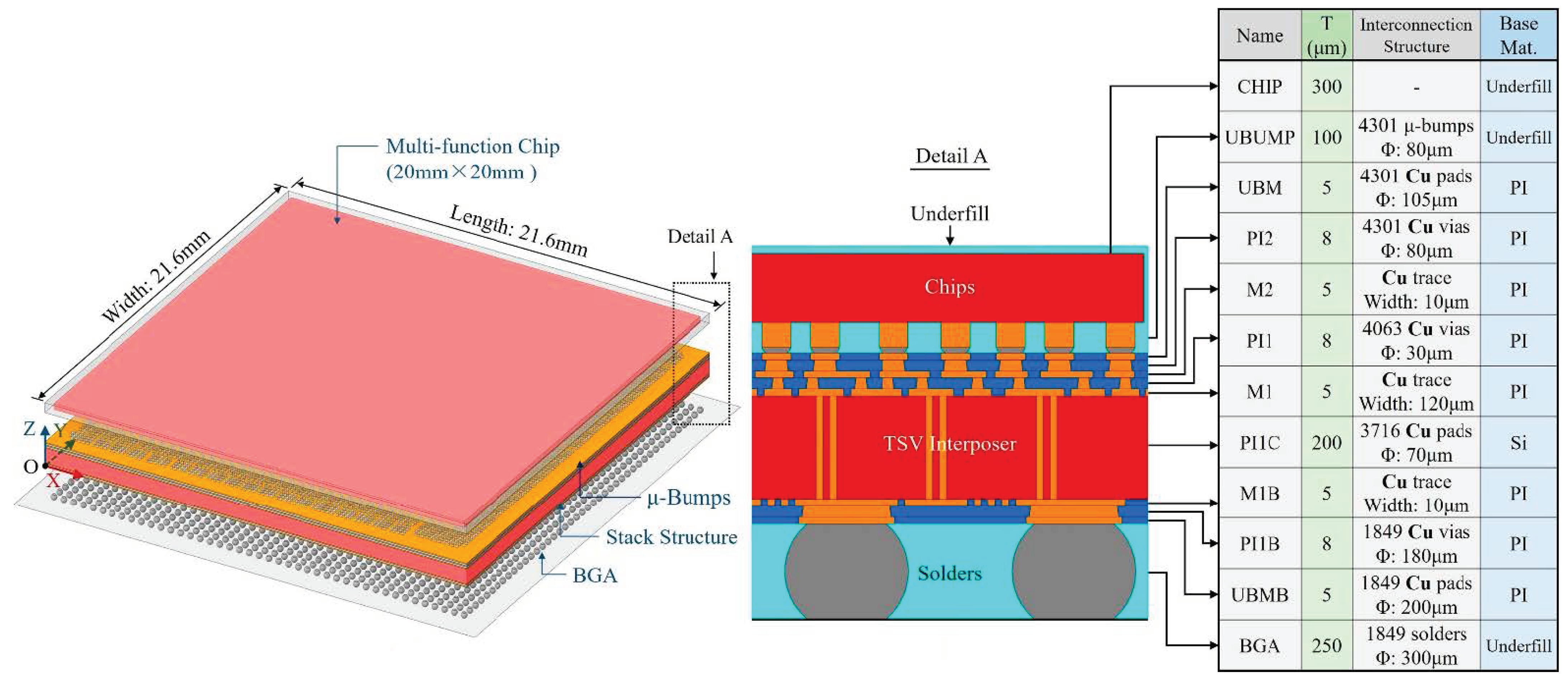
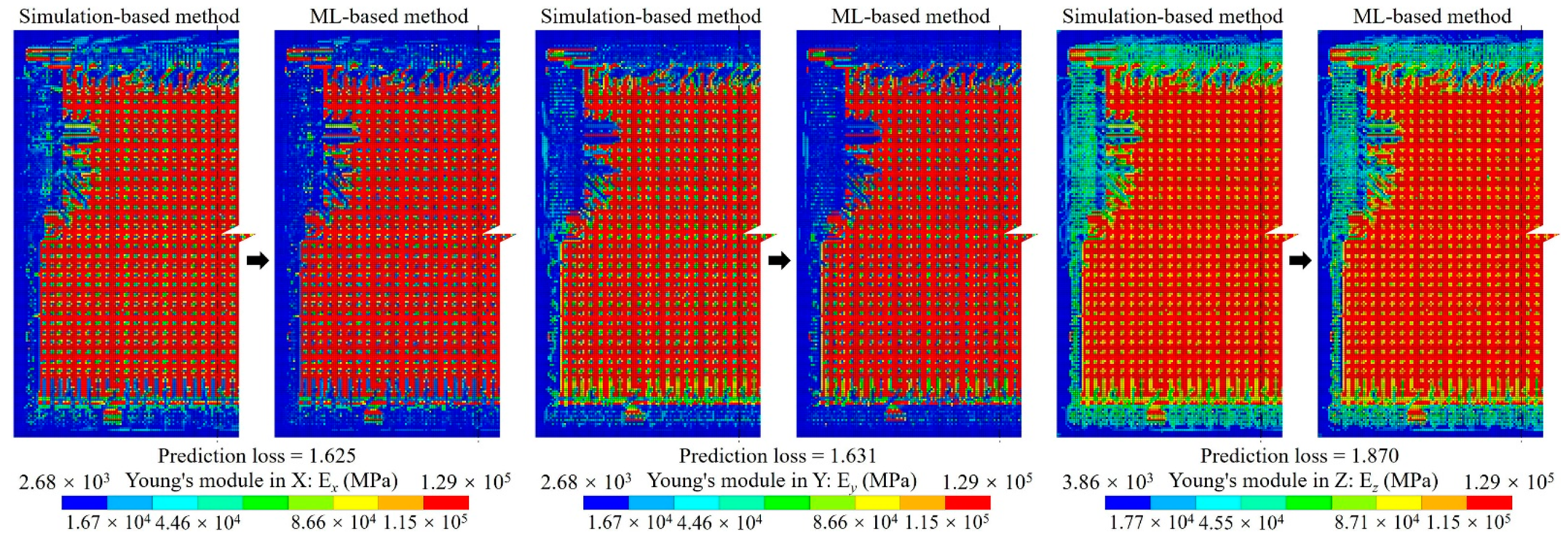
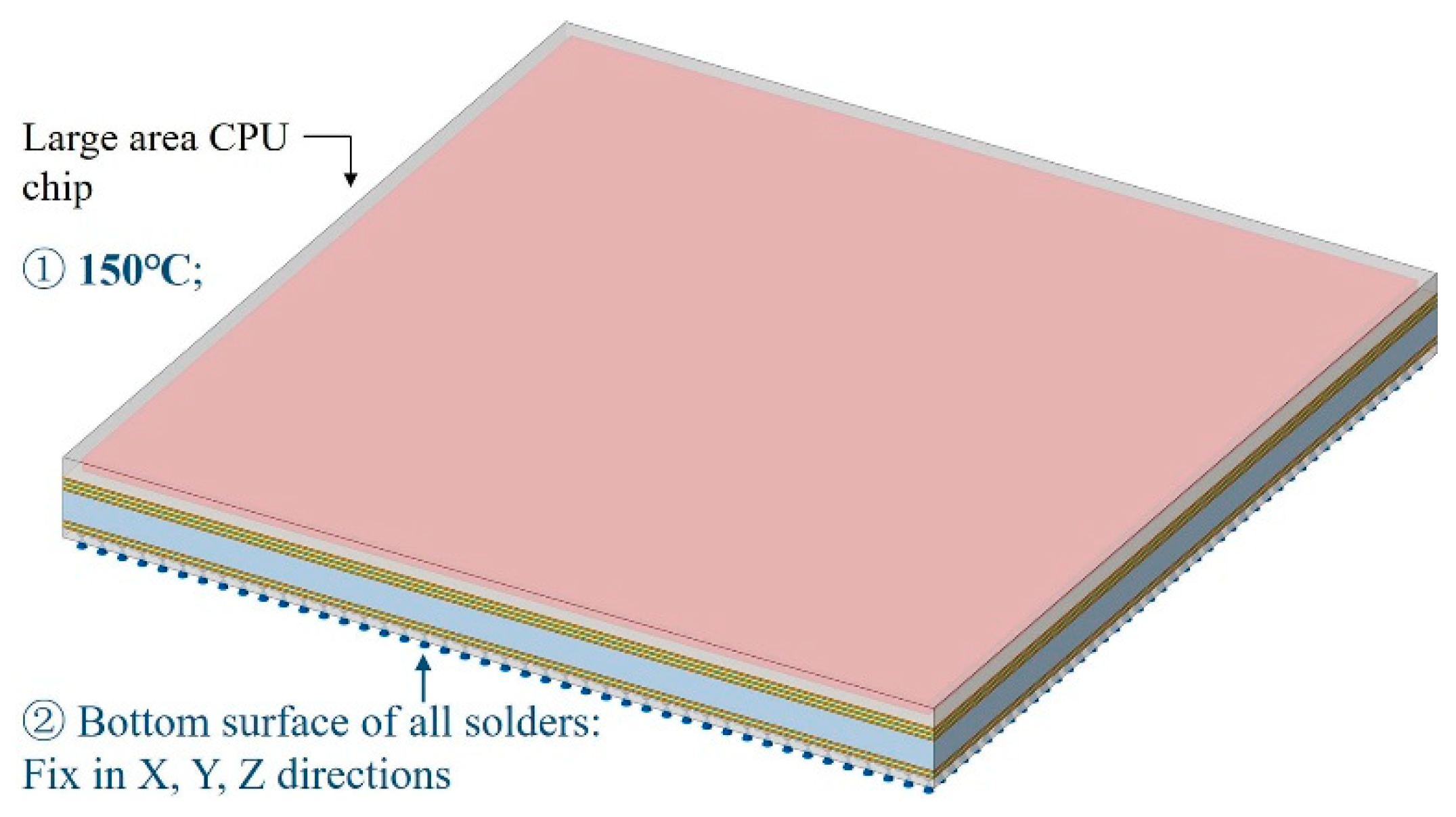
3.3. Large Area 2.5D-Integrated CPU Chip Thermo-Mechanical Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, P.K.; Lu, C.Y.; Wei, W.H.; Chiu, C.; Ting, K.C.; Hu, C.; Tsai, C.H.; Hou, S.Y.; Chiou, W.C.; Wang, C.T.; et al. Wafer Level System Integration of the Fifth Generation CoWoS®-S with High Performance Si Interposer at 2500 Mm2. In Proceedings of the 2021 IEEE 71st Electronic Components and Technology Conference (ECTC), Virtual, 1 June–4 July 2021; IEEE: San Diego, CA, USA, 2021; pp. 101–104. [Google Scholar]
- Ingerly, D.B.; Enamul, K.; Gomes, W.; Jones, D.; Kolluru, K.C.; Kandas, A.; Kim, G.-S.; Ma, H.; Pantuso, D.; Petersburg, C.F.; et al. Foveros: 3D Integration and the Use of Face-to-Face Chip Stacking for Logic Devices. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 9–11 December 2019; IEEE: San Francisco, CA, USA, December 2019; pp. 19.6.1–19.6.4. [Google Scholar]
- SAMSUNG, X-Cube Technology. Available online: https://semiconductor.samsung.com/us/foundry/advanced-package/ (accessed on 28 June 2023).
- Yu, D.C.H.; Wang, C.-T.; Lin, C.-C.; Lu, C.-H.; Wu, G.; Huang, C.-Y.; Chen, W.-T.; Ku, T.; Yee, K.-C.; Tsai, C.-H. SoIC_H Technology for Heterogeneous System Integration. IEEE Trans. Electron. Devices 2022, 69, 7167–7172. [Google Scholar] [CrossRef]
- TSMC-SoIC. Available online: https://3dfabric.tsmc.com/english/dedicatedFoundry/technology/SoIC.htm#SoIC_CoW (accessed on 28 June 2023).
- Lin, M.L.; Liu, M.S.; Chen, H.W.; Chen, S.M.; Yew, M.C.; Chen, C.S.; Jeng, S.-P. Organic Interposer CoWoS-R + (plus) Technology. In Proceedings of the 2022 IEEE 72nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 31 May–3 June 2022; IEEE: San Diego, CA, USA, May 2022; pp. 1–6. [Google Scholar]
- Kim, H.; Co, S.E. Advanced Fan-Out Panel Level Package (FO-PLP) Development for High-End Mobile Application. In Proceedings of the 2023 IEEE 73st Electronic Components and Technology Conference (ECTC), Virtual, 30 May–2 June 2023; IEEE: Orlando, FL, USA, June 2023; pp. 2377–5726. [Google Scholar]
- Ahmad, M.; DeLaCruz, J.; Ramamurthy, A. Heterogeneous Integration of Chiplets: Cost and Yield Tradeoff Analysis. In Proceedings of the 2022 23rd International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), St Julian, Malta, 25–27 April 2022; IEEE: St Julian, Malta, April 2022; pp. 1–9. [Google Scholar]
- Suggs, D.; Subramony, M.; Bouvier, D. The AMD “Zen 2” Processor; IEEE Micro: Los Alamitos, CA, UDA, 2020; Volume 40, pp. 45–52. [Google Scholar] [CrossRef]
- High Bandwidth Memory (HBM) DRAM. Available online: https://www.jedec.org/standards-documents/docs/jesd235a (accessed on 28 June 2023).
- Kudo, H.; Takano, T.; Tanaka, M.; Mawatari, H.; Kitayama, D.; Tai, T.; Tsunoda, T.; Kuramochi, S. Panel-Based Large-Scale RDL Interposer Fabricated Using 2-Μm-Pitch Semi-Additive Process for Chiplet-Based Integration. In Proceedings of the 2022 IEEE 72nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 31 May–3 June 2022; IEEE: San Diego, CA, USA, May 2022; pp. 836–844. [Google Scholar]
- Choi, J.; Jin, J.; Kang, G.; Hwang, H.; Kim, B.; Yun, H.; Park, J.; Lee, C.; Kang, U.-B.; Lee, J. Novel Approach to Highly Robust Fine Pitch RDL Process. In Proceedings of the 2021 IEEE 71st Electronic Components and Technology Conference (ECTC), Virtual, 1 June–4 July 2021; IEEE: San Diego, CA, USA, June 2021; pp. 2246–2251. [Google Scholar]
- Nimbalkar, P.; Bhaskar, P.; Blancher, C.; Kathaperumal, M.; Swaminathan, M.; Tummala, R. Novel Zero Side-Etch Process for <1μm Package Redistribution Layers. In Proceedings of the 2022 IEEE 72nd Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 31 May–3 June 2022; IEEE: San Diego, CA, USA, May 2022; pp. 2168–2173. [Google Scholar]
- Takano, T.; Kudo, H.; Tanaka, M.; Akazawa, M. Submicron-Scale Cu RDL Pattering Based on Semi-Additive Process for Heterogeneous Integration. In Proceedings of the 2019 IEEE 69th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2019; IEEE: Las Vegas, NV, USA, May 2019; pp. 94–100. [Google Scholar]
- Hou, S.Y.; Chen, W.C.; Hu, C.; Chiu, C.; Ting, K.C.; Lin, T.S.; Wei, W.H.; Chiou, W.C.; Lin, V.J.C.; Chang, V.C.Y.; et al. Wafer-Level Integration of an Advanced Logic-Memory System Through the Second-Generation CoWoS Technology. IEEE Trans. Electron. Devices 2017, 64, 4071–4077. [Google Scholar] [CrossRef]
- Jourdain, A.; Schleicher, F.; De Vos, J.; Stucchi, M.; Chery, E.; Miller, A.; Beyer, G.; Van der Plas, G.; Walsby, E.; Roberts, K.; et al. Extreme Wafer Thinning and Nano-TSV Processing for 3D Heterogeneous Integration. In Proceedings of the 2020 IEEE 70th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 3–30 June 2020; IEEE: Orlando, FL, USA, June 2020; pp. 42–48. [Google Scholar]
- Serbulova, K.; Chen, S.-H.; Hellings, G.; Hiblot, G.; Veloso, A.; Jourdain, A.; De Boeck, J.; Groeseneken, G.; Horiguchi, N. Impact of Sub-Μm Wafer Thinning on Latch-up Risk in STCO Scaling Era. In Proceedings of the 2021 43rd Annual EOS/ESD Symposium (EOS/ESD), Tucson, AZ, USA, 26 September–1 October 2021; IEEE: Tucson, AZ, USA, September 2021; pp. 1–6. [Google Scholar]
- Pham, V.-L.; Wang, H.; Xu, J.; Wang, J.; Park, S.; Singh, C. A Study of Substrate Models and Its Effect On Package Warpage Prediction. In Proceedings of the 2019 IEEE 69th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2019; IEEE: Las Vegas, NV, USA, May 2019; pp. 1130–1139. [Google Scholar]
- JESD22-A104C; Temperature Cycling. JEDEC: Arlington County, VA, USA, 2005.
- Lee, C.-C.; Lin, Y.-M.; Liu, H.-C.; Syu, J.-Y.; Huang, Y.-C.; Chang, T.-C. Reliability Evaluation of Ultra Thin 3D-IC Package under the Coupling Load Effects of the Manufacturing Process and Temperature Cycling Test. Microelectron. Eng. 2021, 244–246, 111572. [Google Scholar] [CrossRef]
- Che, F.X.; Lin, J.-K.; Au, K.Y.; Hsiao, H.-Y.; Zhang, X. Stress Analysis and Design Optimization for Low-k Chip with Cu Pillar Interconnection. IEEE Trans. Compon. Packag. Manufact. Technol. 2015, 5, 1273–1283. [Google Scholar] [CrossRef]
- Machani, K.V.; Kuechenmeister, F.; Breuer, D.; Klewer, C.; Cho, J.K.; Young-Fisher, K. Chip Package Interaction (CPI) Risk Assessment of 22FDX® Wafer Level Chip Scale Package (WLCSP) Using 2D Finite Element Analysis Modeling. In Proceedings of the 2020 IEEE 70th Electronic Components and Technology Conference (ECTC), Orlando, FL, USA, 3–30 June 2020; IEEE: Orlando, FL, USA, June 2020; pp. 1100–1105. [Google Scholar]
- Lee, C.-C.; Kao, K.-S.; Liu, H.-C.; Hsieh, C.-P.; Chang, T.-C. Micro Solder Joint Reliability and Warpage Investigations of Extremely Thin Double-Layered Stacked-Chip Packaging. J. Electron. Packag. 2022, 144, 011001. [Google Scholar] [CrossRef]
- Che, F.X.; Pang, J.H.L. Fatigue Reliability Analysis of Sn–Ag–Cu Solder Joints Subject to Thermal Cycling. IEEE Trans. Device Mater. Relib. 2013, 13, 36–49. [Google Scholar] [CrossRef]
- Wang, M.; Wells, B. Substrate Trace Modeling for Package Warpage Simulation. In Proceedings of the 2016 IEEE 66th Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 31 May–3 June 2016; IEEE: Las Vegas, NV, USA, May 2016; pp. 516–523. [Google Scholar]
- McCaslin, L.O.; Yoon, S.; Kim, H.; Sitaraman, S.K. Methodology for Modeling Substrate Warpage Using Copper Trace Pattern Implementation. IEEE Trans. Adv. Packag. 2009, 32, 740–745. [Google Scholar] [CrossRef]
- Valdevit, L.; Khanna, V.; Sharma, A.; Sri-Jayantha, S.; Questad, D.; Sikka, K. Organic Substrates for Flip-Chip Design: A Thermo-Mechanical Model That Accounts for Heterogeneity and Anisotropy. Microelectron. Reliab. 2008, 48, 245–260. [Google Scholar] [CrossRef]
- Lien, C.-Y.; Chuang, Y.-C.; Yao, Y.; Charn, E.; Chen, E. Block-Based Finite Element Modeling, Simulation, and Optimization of the Warpage of Embedded Trace Substrate. In Proceedings of the 2018 IEEE 20th Electronics Packaging Technology Conference (EPTC), Singapore, 4–7 December 2018; IEEE: Singapore, December 2018; pp. 802–806. [Google Scholar]
- Lee, C.-C.; Wang, C.-W.; Chen, C.-Y. Comparison of Mechanical Modeling to Warpage Estimation of RDL-First Fan-Out Panel-Level Packaging. IEEE Trans. Compon., Packag. Manufact. Technol. 2022, 12, 1100–1108. [Google Scholar] [CrossRef]
- Gibson, R.F.; Ganapathy, V.; Jardine, A.K.S.; Tsang, A.H.C.; Thulukkanam, K.; Karnopp, D. Principles of Composite Material Mechanics, 4th ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Yaddanapudi, V.K.; Krishnaswamy, S.; Rath, R.; Gandhi, R. Validation of New Approach of Modelling Traces by Mapping Mechanical Properties for a Printed Circuit Board Mechanical Analysis. In Proceedings of the 2015 IEEE 17th Electronics Packaging and Technology Conference (EPTC), Singapore, 2–4 December 2015; IEEE: Singapore, December 2015; pp. 1–6. [Google Scholar]
- Lee, K.; Nam, S.; Ji, H.; Choi, J.; Jin, J.-E.; Kim, Y.; Na, J.; Ryu, M.-Y.; Cho, Y.-H.; Lee, H.; et al. Multiple Machine Learning Approach to Characterize Two-Dimensional Nanoelectronic Devices via Featurization of Charge Fluctuation. Npj 2D Mater. Appl. 2021, 5, 4. [Google Scholar] [CrossRef]
- Mao, Z.; Asai, Y.; Yamanoi, A.; Seki, Y.; Wiranata, A.; Minaminosono, A. Fluidic Rolling Robot Using Voltage-Driven Oscillating Liquid. Smart Mater. Struct. 2022, 31, 105006. [Google Scholar] [CrossRef]
- Peng, Y.; Yamaguchi, H.; Funabora, Y.; Doki, S. Modeling Fabric-Type Actuator Using Point Clouds by Deep Learning. IEEE Access 2022, 10, 94363–94375. [Google Scholar] [CrossRef]
- Mao, Z.; Peng, Y.; Hu, C.; Ding, R.; Yamada, Y.; Maeda, S. Soft Computing-Based Predictive Modeling of Flexible Electrohydrodynamic Pumps. Biomim. Intell. Robot. 2023, 3, 100114. [Google Scholar] [CrossRef]
- Dai, M.; Demirel, M.F.; Liang, Y.; Hu, J.-M. Graph Neural Networks for an Accurate and Interpretable Prediction of the Properties of Polycrystalline Materials. Npj Comput. Mater. 2021, 7, 103. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, Y.; Xu, B. Transferable, Deep-Learning-Driven Fast Prediction and Design of Thermal Transport in Mechanically Stretched Graphene Flakes. ACS Nano 2021, 15, 16597–16606. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; Huang, W.-Z.; Li, M.; Feng, X.-Q. Deep Learning Method for Determining the Surface Elastic Moduli of Microstructured Solids. Extrem. Mech. Lett. 2021, 44, 101226. [Google Scholar] [CrossRef]
- Gong, Z.; Xu, Z.; Hu, J.; Yan, B.; Ding, X.; Sun, J.; Zhang, P.; Deng, J. Thermal Conductivity Prediction of UO2-BeO Composite Fuels and Related Decisive Features Discovery via Convolutional Neural Network. Acta Mater. 2022, 240, 118352. [Google Scholar] [CrossRef]
- Selvanayagam, C.; Duong, P.L.T.; Raghavan, N. AI-Assisted Package Design for Improved Warpage Control of Ultra-Thin Packages. In Proceedings of the 2020 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE), Cracow, Poland, 5–8 July 2020; IEEE: Cracow, Poland, July 2020; pp. 1–7. [Google Scholar]
- Selvanayagam, C.; Duong, P.L.T.; Wilkerson, B.; Raghavan, N. Global Optimization of Surface Warpage for Inverse Design of Ultra-Thin Electronic Packages Using Tensor Train Decomposition. IEEE Access 2022, 10, 48589–48602. [Google Scholar] [CrossRef]
- Silicon-Si. Available online: https://www.matweb.com/search/DataSheet.aspx?MatGUID=7d1b56e9e0c54ac5bb9cd433a0991e27&ckck=1 (accessed on 28 April 2023).
- Material: Copper—PVD or Electroplated. Available online: https://www.mit.edu/~6.777/matprops/copper.htm (accessed on 28 April 2023).
- McKeen, L.W. Film Properties of Plastics and Elastomers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 978-0-12-813292-0. [Google Scholar]







| Name | Si [42] | Cu [43] | PI [44] |
|---|---|---|---|
| CTE | 2.6 × 10−6 | 1.64 × 10−5 | 2 × 10−5 |
| Young’s Modulus (MPa) | 1.31 × 10−5 | 1.30 × 10−5 | 2.5 × 10−3 |
| Poisson Ratio | 0.28 | 0.34 | 0.34 |
| Probe Nodes | X Normal Stress (MPa) | Y Normal Stress (MPa) | Z Normal Stress (MPa) | XY Shear Stress (MPa) | YZ Shear Stress (MPa) | XZ Shear Stress (MPa) | Location |
|---|---|---|---|---|---|---|---|
| N1 | −392.25 | −394.70 | 101.78 | −1.31 | −0.66 | −8.05 | Metal under ubump |
| N2 | −250.24 | −230.09 | 1.77 | 0.10 | −3.08 | 3.39 | Metal beside small dielectric region |
| N3 | −109.31 | −103.23 | 32.40 | 0.18 | −1.74 | 1.36 | Inside local dielectric region |
| N4 | −180.49 | −117.92 | −3.94 | 0.40 | −6.37 | 1.17 | Metal beside local dielectric region |
| N5 | −188.31 | −46.89 | 84.21 | 0.18 | −5.46 | 0.97 | Metal beside dielectric region in X direction, under ubump |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wang, Z.; Ma, S.; Chu, X.; Li, C.; Wang, W.; Jin, Y.; Wu, D. An RDL Modeling and Thermo-Mechanical Simulation Method of 2.5D/3D Advanced Package Considering the Layout Impact Based on Machine Learning. Micromachines 2023, 14, 1531. https://doi.org/10.3390/mi14081531
Wu X, Wang Z, Ma S, Chu X, Li C, Wang W, Jin Y, Wu D. An RDL Modeling and Thermo-Mechanical Simulation Method of 2.5D/3D Advanced Package Considering the Layout Impact Based on Machine Learning. Micromachines. 2023; 14(8):1531. https://doi.org/10.3390/mi14081531
Chicago/Turabian StyleWu, Xiaodong, Zhizhen Wang, Shenglin Ma, Xianglong Chu, Chunlei Li, Wei Wang, Yufeng Jin, and Daowei Wu. 2023. "An RDL Modeling and Thermo-Mechanical Simulation Method of 2.5D/3D Advanced Package Considering the Layout Impact Based on Machine Learning" Micromachines 14, no. 8: 1531. https://doi.org/10.3390/mi14081531
APA StyleWu, X., Wang, Z., Ma, S., Chu, X., Li, C., Wang, W., Jin, Y., & Wu, D. (2023). An RDL Modeling and Thermo-Mechanical Simulation Method of 2.5D/3D Advanced Package Considering the Layout Impact Based on Machine Learning. Micromachines, 14(8), 1531. https://doi.org/10.3390/mi14081531








