Subthreshold Conduction of Disordered ZnO-Based Thin-Film Transistors
Abstract
1. Introduction
2. Materials and Methods
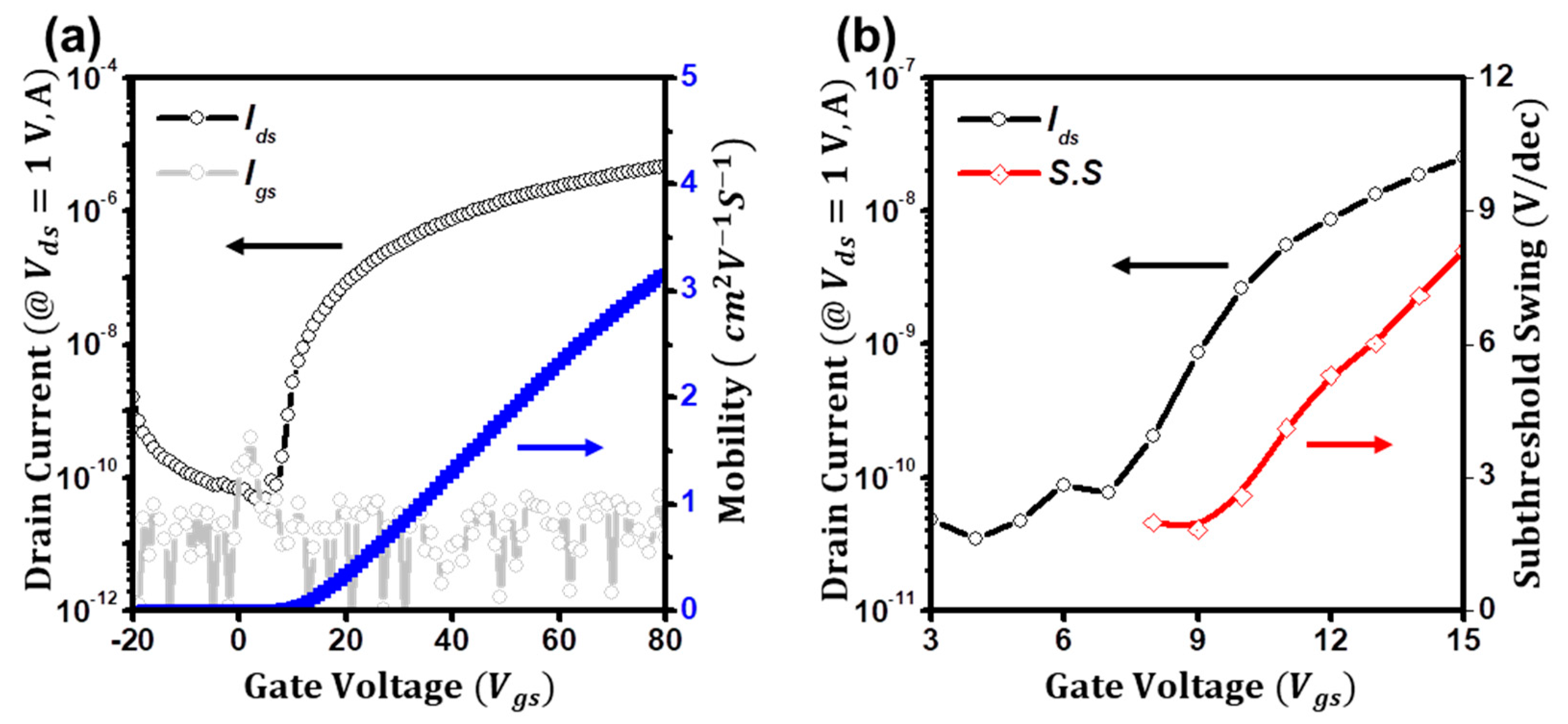
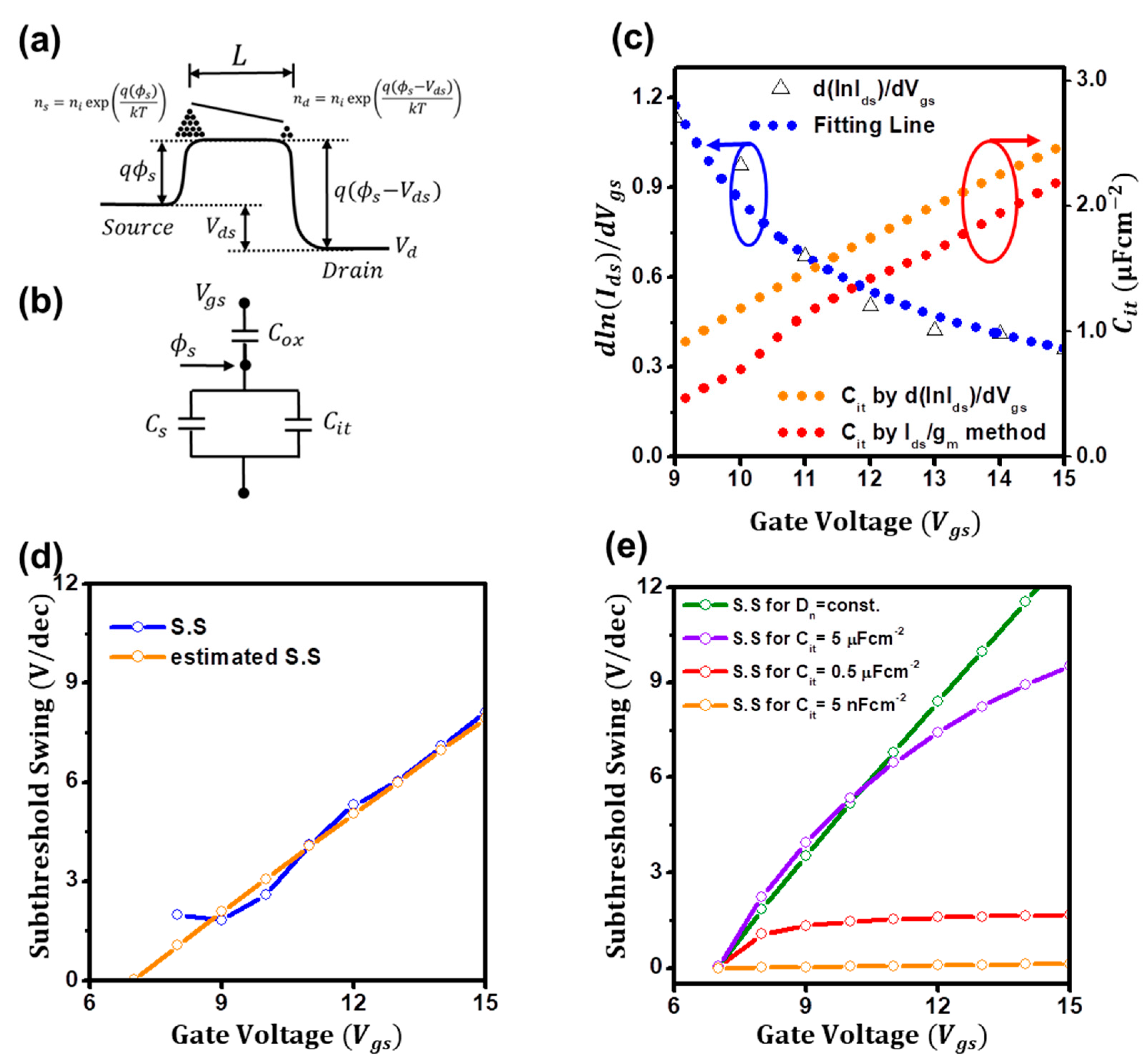
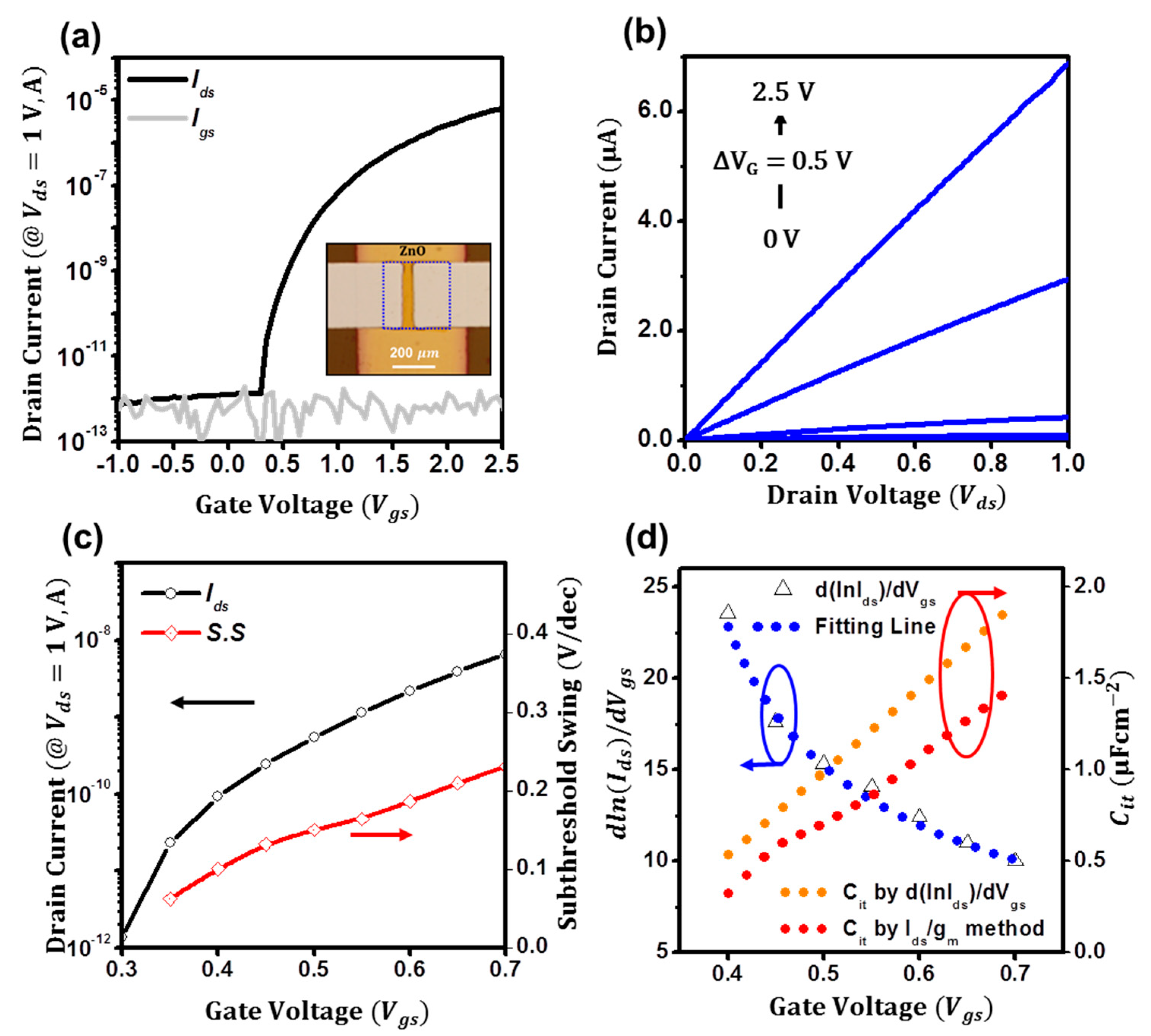
3. Results
4. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Kim, S.; Kwon, H.J.; Lee, S.; Shim, H.; Chun, Y.; Choi, W.; Kwack, J.; Han, D.; Song, M.; Kim, S.; et al. Low-Power Flexible Organic Light-Emitting Diode Display Device. Adv. Mater. 2011, 23, 3511–3516. [Google Scholar] [CrossRef]
- Rogers, J.A.; Someya, T.; Huang, Y. Materials and Mechanics for Stretchable Electronics. Science 2010, 327, 1603–1607. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.P.; Li, Y.Q.; Tang, J.X. Recent Advances in Flexible Organic Light-Emitting Diodes. J. Mater. Chem. C 2016, 4, 9116–9142. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Zhang, B.; Wang, H.; Xin, Q.; Song, A. Flexible Indium-Gallium-Zinc-Oxide Schottky Diode Operating beyond 2.45 GHz. Nat. Commun. 2015, 6, 7561. [Google Scholar] [CrossRef]
- Liang, K.; Xu, X.; Zhou, Y.; Wang, X.; McCulley, C.M.; Wang, L.; Kulkarni, J.; Dodabalapur, A. Nanospike Electrodes and Charge Nanoribbons: A New Design for Nanoscale Thin-Film Transistors. Sci. Adv. 2022, 8, eabm1154. [Google Scholar] [CrossRef] [PubMed]
- Barua, A.; Leedy, K.D.; Jha, R. Deep-Subthreshold Schottky Barrier IGZO TFT for Ultra Low-Power Applications. Solid State Electron. Lett. 2020, 2, 59–66. [Google Scholar] [CrossRef]
- Samanta, S.; Chand, U.; Xu, S.; Han, K.; Wu, Y.; Wang, C.; Kumar, A.; Velluri, H.; Li, Y.; Fong, X.; et al. Low Subthreshold Swing and High Mobility Amorphous Indium-Gallium-Zinc-Oxide Thin-Film Transistor with Thin HfO2 Gate Dielectric and Excellent Uniformity. IEEE Electron. Device Lett. 2020, 41, 856–859. [Google Scholar] [CrossRef]
- Newsom, T.L.; Allemang, C.R.; Cho, T.H.; Dasgupta, N.P.; Peterson, R.L. 59.9 MV·dec Subthreshold Swing Achieved in Zinc Tin Oxide TFTs with In Situ Atomic Layer Deposited AlO Gate Insulator. IEEE Electron. Device Lett. 2023, 44, 72–75. [Google Scholar] [CrossRef]
- Shur, M.; Hack, M. Physics of Amorphous Silicon Based Alloy Field-Effect Transistors. J. Appl. Phys. 1984, 55, 3831–3842. [Google Scholar] [CrossRef]
- Tang, Z.; Wie, C.R. Capacitance-Voltage Characteristics and Device Simulation of Bias Temperature Stressed a-Si:H TFTs. Solid State. Electron. 2010, 54, 259–267. [Google Scholar] [CrossRef]
- Arkhipov, I.V.; Heremans, P.; Emelianova, E.V.; Adriaenssens, G.J.; Bässler, H. Weak-Field Carrier Hopping in Disordered Organic Semiconductors: The Effects of Deep Traps and Partly Filled Density-of-States Distribution. J. Phys. Condens. Matter 2002, 14, 9899–9911. [Google Scholar] [CrossRef]
- Dasgupta, S.; Brock, R.; Kaplar, R.; Marinella, M.; Smith, M.; Atcitty, S. Extraction of Trapped Charge in 4H-SiC Metal Oxide Semiconductor Field Effect Transistors from Subthreshold Characteristics. Appl. Phys. Lett. 2011, 99, 97–100. [Google Scholar] [CrossRef]
- Sharroush, S.M.; Abdalla, Y.S.; Dessouki, A.A.; El-Badawy, E.S.A. Subthreshold MOSFET Transistor Amplifier Operation. In Proceedings of the 2009 4th International Design and Test Workshop (IDT), Riyadh, Saudi Arabia, 15–17 November 2009; pp. 1–6. [Google Scholar]
- Taylor, G.W. Subthreshold Conduction in Mosfet’s. IEEE Trans. Electron. Devices 1978, 25, 337–350. [Google Scholar] [CrossRef]
- Fahrner, W.R.; Löffler, S.; Chan, Y.; Kwong, S.; Man, K. Determination of the Trap Density in Amorphous Silicon by Quasi-Static Capacitance-Voltage Measurements. J. Electrochem. Soc. 1998, 145, 1786–1790. [Google Scholar] [CrossRef]
- Frutuoso, T.M.; Garros, X.; Lugo-Alvarez, J.; Kammeugne, R.K.; Zouknak, L.D.M.; Viey, A.; Vandendeale, W.; Ferrari, P.; Gaillard, F. Ultra-Fast CV Methods (<10 μs) for Interface Trap Spectroscopy and BTI Reliability Characterization Using MOS Capacitors. In Proceedings of the 2022 IEEE International Reliability Physics Symposium (IRPS), Dallas, TX, USA, 27–31 March 2022; pp. 3A21–3A26. [Google Scholar]
- Fiorenza, P.; Giannazzo, F.; Roccaforte, F. Characterization of SiO2/4H-SiC Interfaces in 4H-SiC MOSFETs: A Review. Energies 2019, 12, 2310. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, Z.; Si, M.; Ye, P.D. Characterization of Interface and Bulk Traps in Ultrathin Atomic Layer-Deposited Oxide Semiconductor MOS Capacitors with HfO2/In2O3 Gate Stack by C-V and Conductance Method. Front. Mater. 2022, 9, 850451. [Google Scholar] [CrossRef]
- Yoon, M.; Park, J.; Tran, D.C.; Sung, M.M. Fermi-Level Engineering of Atomic Layer-Deposited Zinc Oxide Thin Films for a Vertically Stacked Inverter. ACS Appl. Electron. Mater. 2020, 2, 537–544. [Google Scholar] [CrossRef]
- Jan, T.; Azmat, S.; Rahman, A.U.; Ilyas, S.Z.; Mehmood, A. Experimental and DFT Study of Al Doped ZnO Nanoparticles with Enhanced Antibacterial Activity. Ceram. Int. 2022, 48, 20838–20847. [Google Scholar] [CrossRef]
- Janotti, A.; Van De Walle, C.G. Fundamentals of Zinc Oxide as a Semiconductor. Rep. Prog. Phys. 2009, 72, 126501. [Google Scholar] [CrossRef]
- Yoon, M.; Hyun, D.; Kim, H.-S. Subgap States in Aluminum- and Hydrogen-Doped Zinc-Oxide Thin-Film Transistors. J. Mater. Chem. C 2023, 11, 9952–9959. [Google Scholar] [CrossRef]
- Lee, S.; Jeon, S.; Nathan, A. Modeling Sub-Threshold Current-Voltage Characteristics in Thin Film Transistors. IEEE/OSA J. Disp. Technol. 2013, 9, 883–889. [Google Scholar]
- Yoon, M.; Lee, J. Intrinsic Device Parameter Extraction Method for Zinc Oxide-Based Thin-Film Transistors. Appl. Phys. Express 2021, 14, 124003. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, D.H.; Jeong, H.S.; Hwang, S.H.; Lee, S.; Kim, M.H.; Lim, J.H.; Kwon, H.I. Comparative Study on the Separate Extraction of Interface and Bulk Trap Densities in Indium Gallium Zinc Oxide Thin-Film Transistors Using Capacitance–Voltage and Current–Voltage Characteristics. Coatings 2021, 11, 1135. [Google Scholar] [CrossRef]
- Kim, Y.; Bae, M.; Kim, W.; Kong, D.; Choi, S.; Jung, H.K.; Kim, H.; Kim, S.; Kim, D.M.; Kim, D.H. Amorphous InGaZnO Thin-Film Transistors-Part I: Complete Extraction of Density of States over the Full Subband-Gap Energy Range. IEEE Trans. Electron. Devices 2012, 59, 2689–2698. [Google Scholar] [CrossRef]
- Schmitz, J.; Kaleli, B.; Kuipers, P.; Van Den Berg, N.; Smits, S.M.; Hueting, R.J.E. Interface Trap Density Estimation in FinFETs from the Subthreshold Current. In Proceedings of the 2016 International Conference on Microelectronic Test Structures (ICMTS), Yokohama, Japan, 28–31 March 2016; pp. 164–167. [Google Scholar]
- Fleetwood, D.M.; Winokur, P.S.; Reber, R.A.; Meisenheimer, T.L.; Schwank, J.R.; Shaneyfelt, M.R.; Riewe, L.C. Effects of Oxide Traps, Interface Traps, and “Border Traps” on Metal-Oxide-Semiconductor Devices. J. Appl. Phys. 1993, 73, 5058–5074. [Google Scholar] [CrossRef]
- Wang, Y.; Kang, K.M.; Kim, M.; Park, H.H. Effective Oxygen-Defect Passivation in Zno Thin Films Prepared by Atomic Layer Deposition Using Hydrogen Peroxide. J. Korean Ceram. Soc. 2019, 56, 302–307. [Google Scholar] [CrossRef]
- Cervantes-López, J.L.; Rangel, R.; Espino, J.; Martínez, E.; García-Gutiérrez, R.; Bartolo-Pérez, P.; Alvarado-Gil, J.J.; Contreras, O.E. Photoluminescence on Cerium-Doped ZnO Nanorods Produced under Sequential Atomic Layer Deposition—Hydrothermal Processes. Appl. Phys. A Mater. Sci. Process. 2017, 123, 86. [Google Scholar] [CrossRef]
- Chen, C.Y.; Kanicki, J. Gated-Four-Probe a-Si:H TFT Structure: A New Technique to Measure the Intrinsic Performance of a-Si:H TFT. IEEE Electron. Device Lett. 1997, 18, 340–342. [Google Scholar] [CrossRef]
- Pesavento, P.V.; Chesterfield, R.J.; Newman, C.R.; Frisble, C.D. Gated Four-Probe Measurements on Pentacene Thin-Film Transistors: Contact Resistance as a Function of Gate Voltage and Temperature. J. Appl. Phys. 2004, 96, 7312–7324. [Google Scholar] [CrossRef]
- Cheng, X.; Lee, S.; Nathan, A. Deep Subthreshold TFT Operation and Design Window for Analog Gain Stages. IEEE J. Electron. Devices Soc. 2018, 6, 195–200. [Google Scholar] [CrossRef]
- Li, L.; Lu, N.; Liu, M.; Bässler, H. General Einstein Relation Model in Disordered Organic Semiconductors under Quasiequilibrium. Phys. Rev. B—Condens. Matter Mater. Phys. 2014, 90, 214107. [Google Scholar] [CrossRef]
- Nguyen, T.H.; O’Leary, S.K. Einstein Relation for Disordered Semiconductors: A Dimensionless Analysis. J. Appl. Phys. 2005, 98, 2003–2006. [Google Scholar] [CrossRef]
- Geiger, M.; Schwarz, L.; Zschieschang, U.; Manske, D.; Pflaum, J.; Weis, J.; Klauk, H.; Weitz, R.T. Quantitative Analysis of the Density of Trap States in Semiconductors by Electrical Transport Measurements on Low-Voltage Field-Effect Transistors. Phys. Rev. Appl. 2018, 10, 044023. [Google Scholar] [CrossRef]
- Stallings, K.; Smith, J.; Chen, Y.; Zeng, L.; Wang, B.; Di Carlo, G.; Bedzyk, M.J.; Facchetti, A.; Marks, T.J. Self-Assembled Nanodielectrics for Solution-Processed Top-Gate Amorphous IGZO Thin-Film Transistors. ACS Appl. Mater. Interfaces 2021, 13, 15399–15408. [Google Scholar] [CrossRef]
- Kong, L.A.; Sun, J.; Qian, C.; Gou, G.; He, Y.; Yang, J.; Gao, Y. Ion-Gel Gated Field-Effect Transistors with Solution-Processed Oxide Semiconductors for Bioinspired Artificial Synapses. Org. Electron. 2016, 39, 64–70. [Google Scholar] [CrossRef]
- Yoon, M. Threshold-Voltage Extraction Methods for Atomically Deposited Disordered ZnO Thin-Film Transistors. Materials 2023, 16, 2940. [Google Scholar] [CrossRef]
- Yoon, M.; Lee, J. Charge Transfer Doping with an Organic Layer to Achieve a High-Performance p-Type WSe2transistor. J. Mater. Chem. C 2021, 9, 9592–9598. [Google Scholar] [CrossRef]
- Kalb, W.L.; Batlogg, B. Calculating the Trap Density of States in Organic Field-Effect Transistors from Experiment: A Comparison of Different Methods. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 81, 035327. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, M. Subthreshold Conduction of Disordered ZnO-Based Thin-Film Transistors. Micromachines 2023, 14, 1596. https://doi.org/10.3390/mi14081596
Yoon M. Subthreshold Conduction of Disordered ZnO-Based Thin-Film Transistors. Micromachines. 2023; 14(8):1596. https://doi.org/10.3390/mi14081596
Chicago/Turabian StyleYoon, Minho. 2023. "Subthreshold Conduction of Disordered ZnO-Based Thin-Film Transistors" Micromachines 14, no. 8: 1596. https://doi.org/10.3390/mi14081596
APA StyleYoon, M. (2023). Subthreshold Conduction of Disordered ZnO-Based Thin-Film Transistors. Micromachines, 14(8), 1596. https://doi.org/10.3390/mi14081596




