Variable-Structure Proportional–Integral–Derivative Laser Solder Joint Temperature Intelligent Control Method with Adjustable Power Upper Limit
Abstract
:1. Introduction
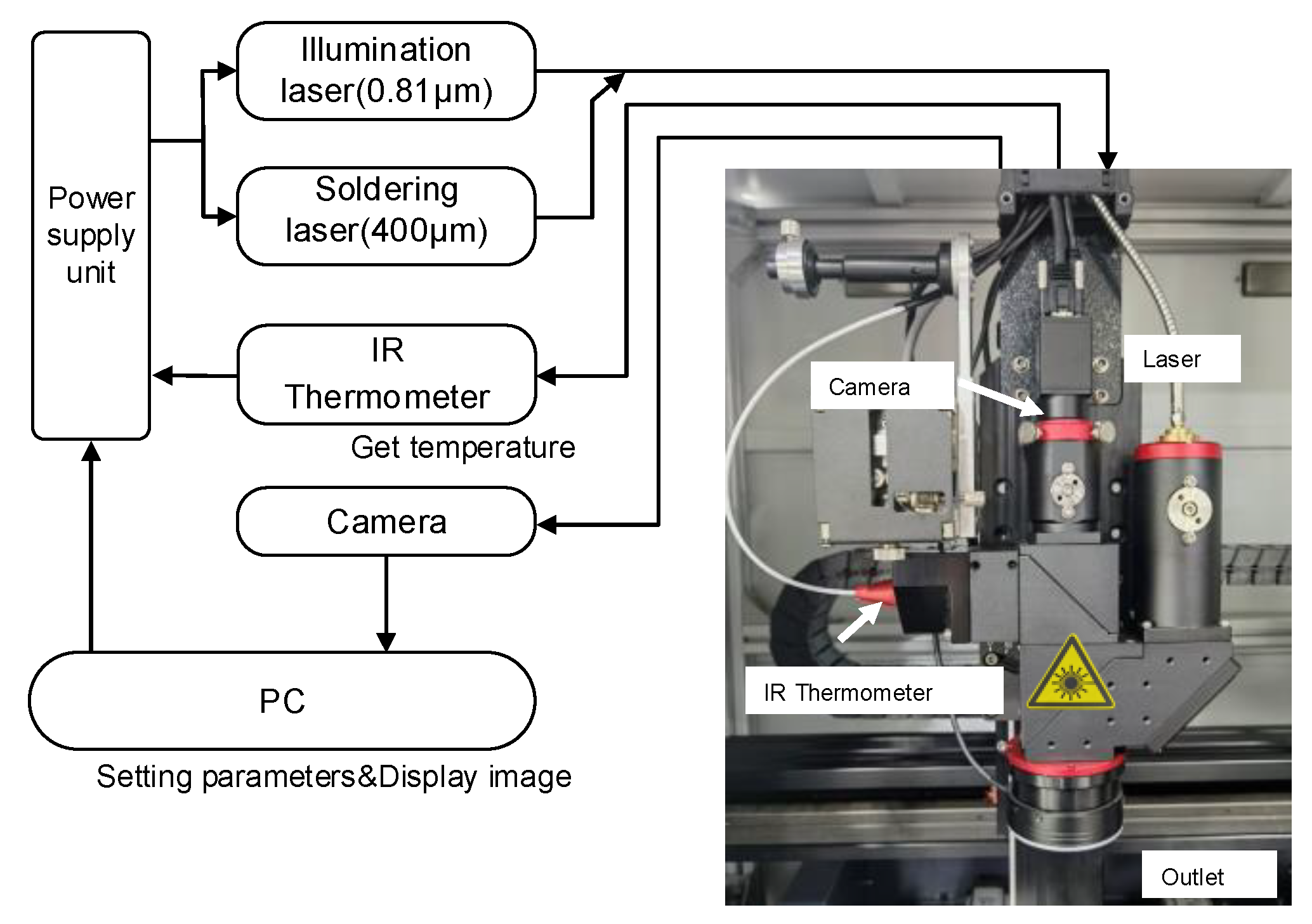
2. Experimental Setup
2.1. Task Analysis
2.2. Control System of Laser Soldering
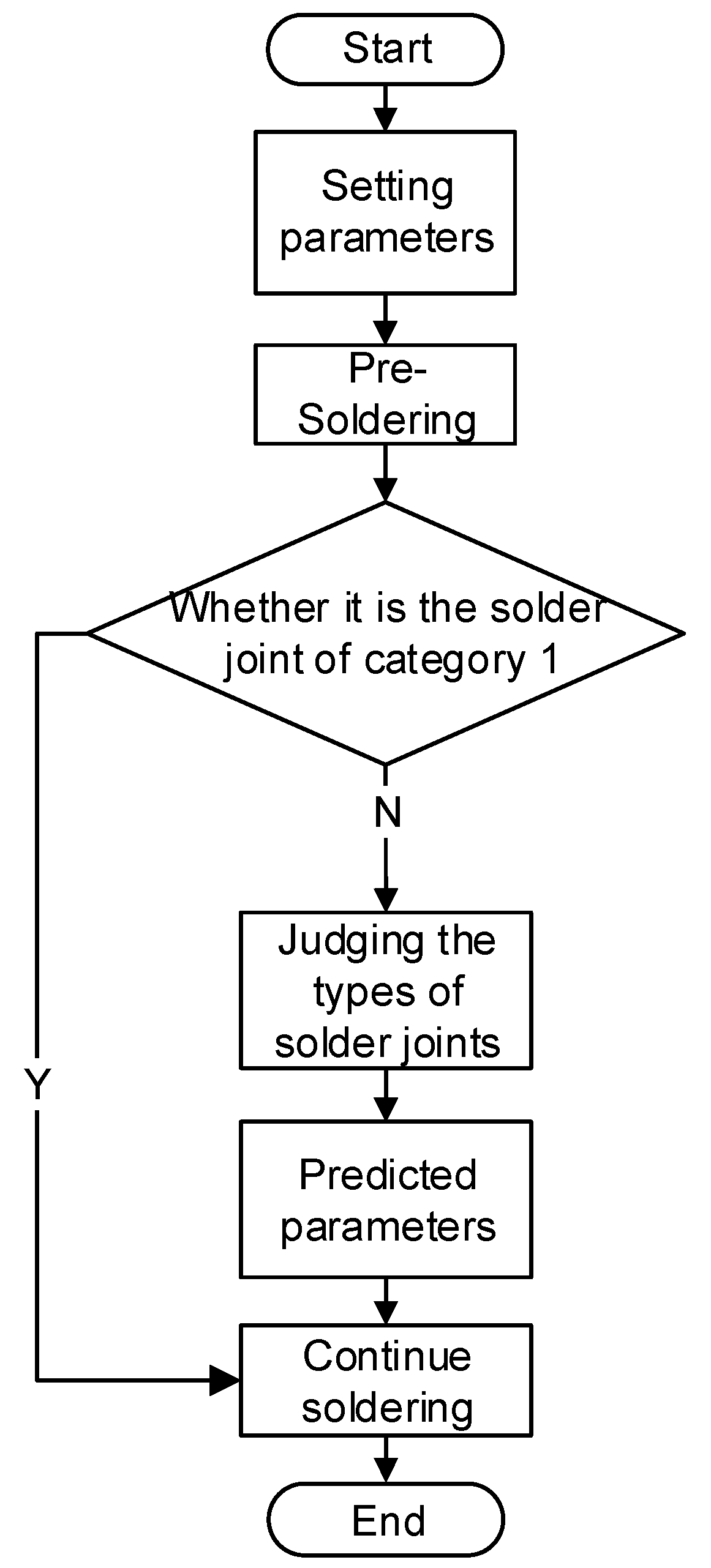
3. Strategies for Controlling Solder Joint Temperature
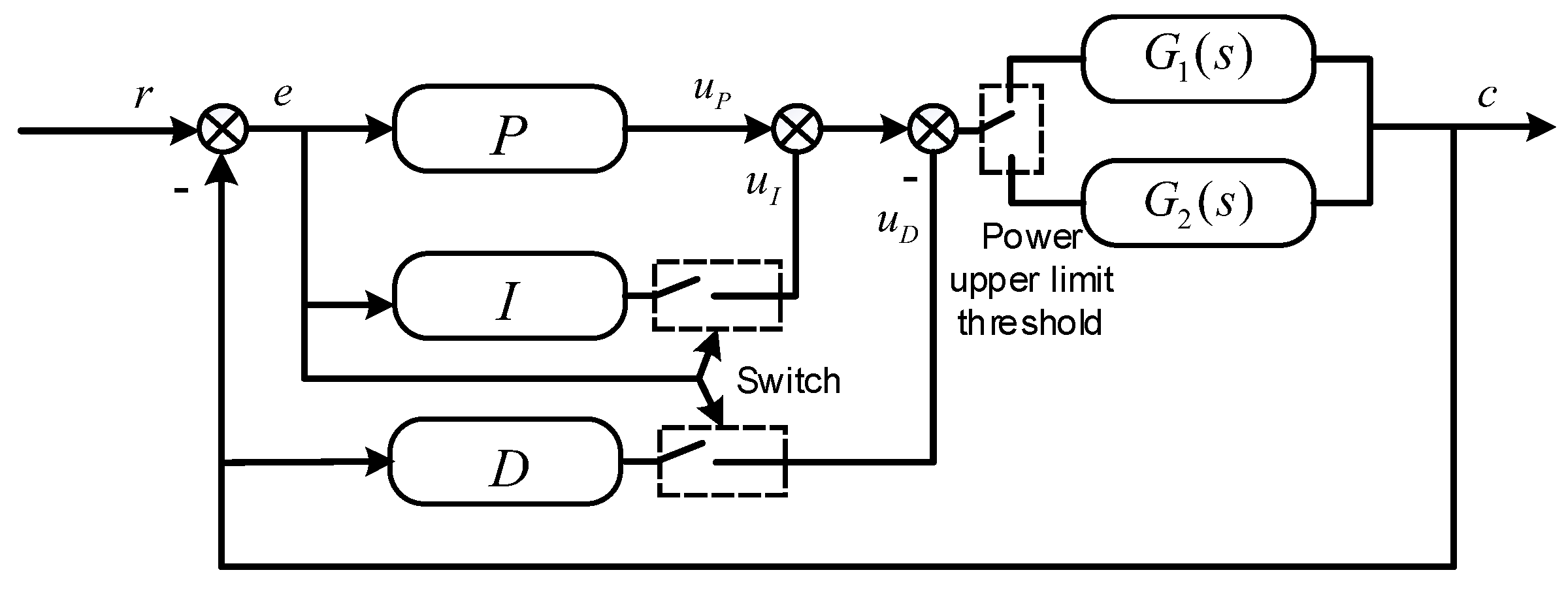
3.1. Variable-Structure PID with Adjustable Upper Limit of Power
3.1.1. Improved PID Algorithm
- For the most significant errors, P control accelerates the response speed.
- For significant errors, PD mode mitigates overshoot.
- For minor errors, PID mode eliminates steady-state deviation.
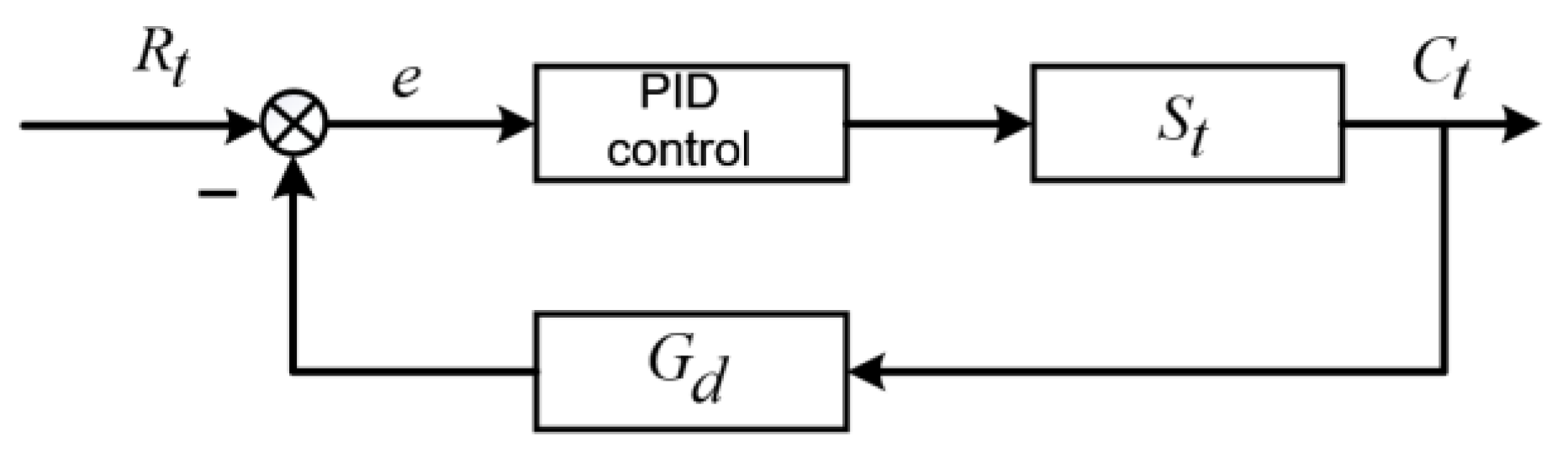
3.1.2. Stability Analysis
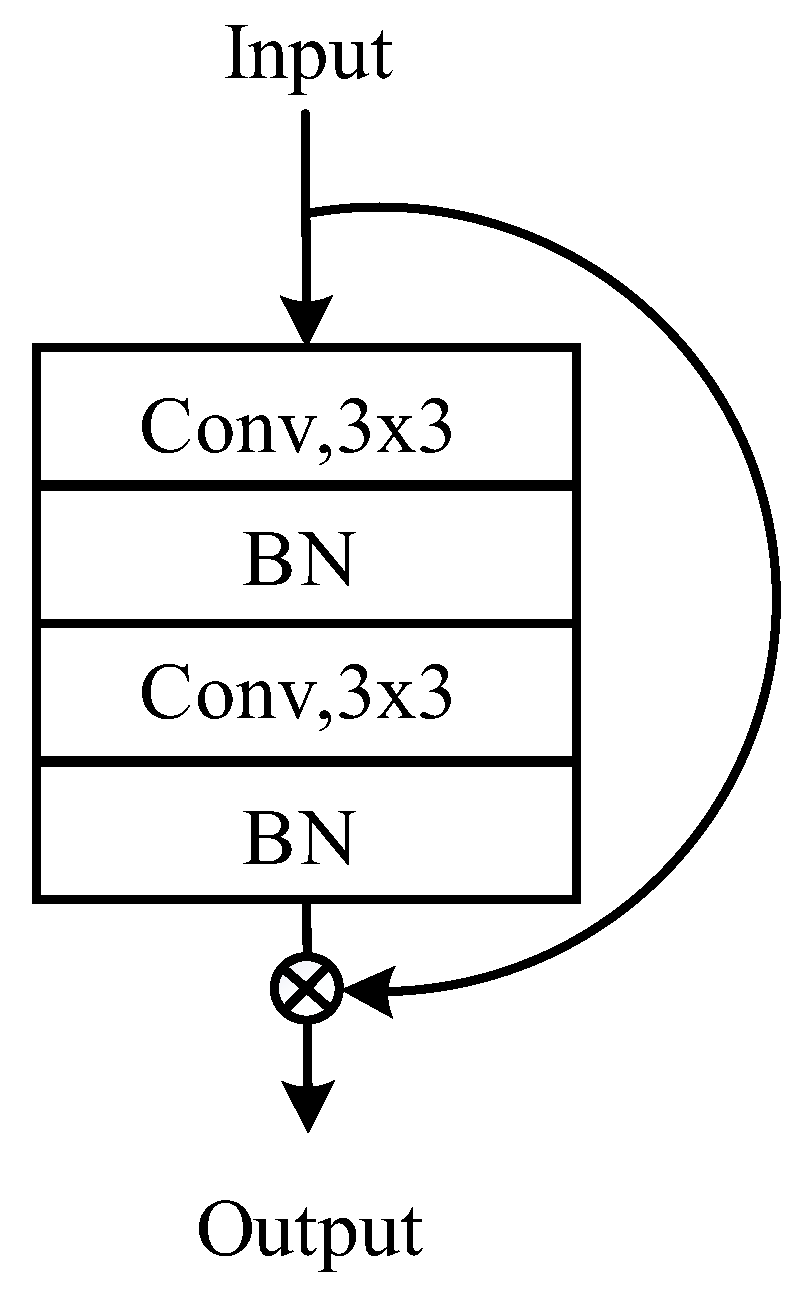
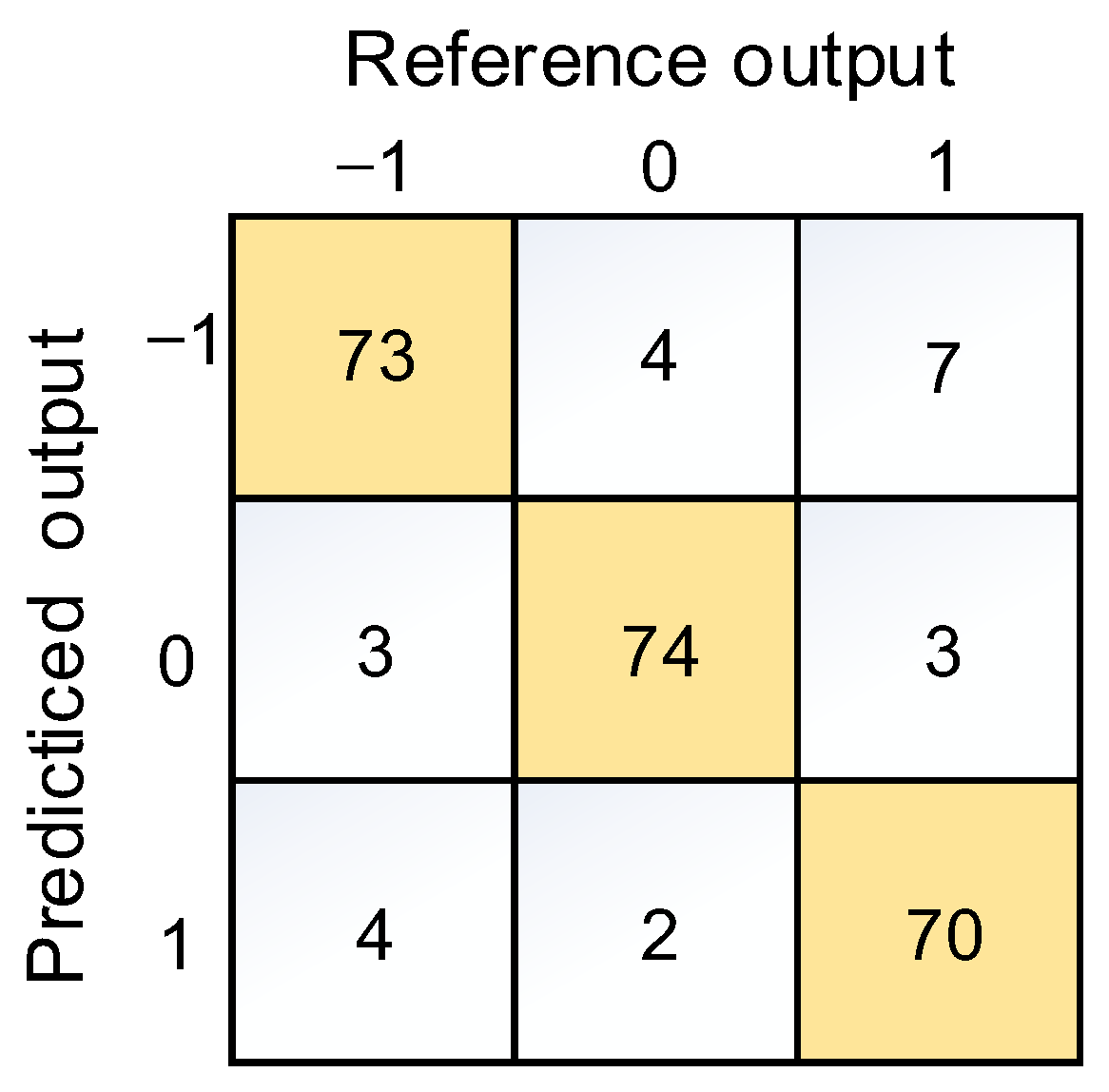
3.2. Optimization Model of Process Parameters Based on ResNet
3.2.1. Neural Network
3.2.2. Transfer Learning
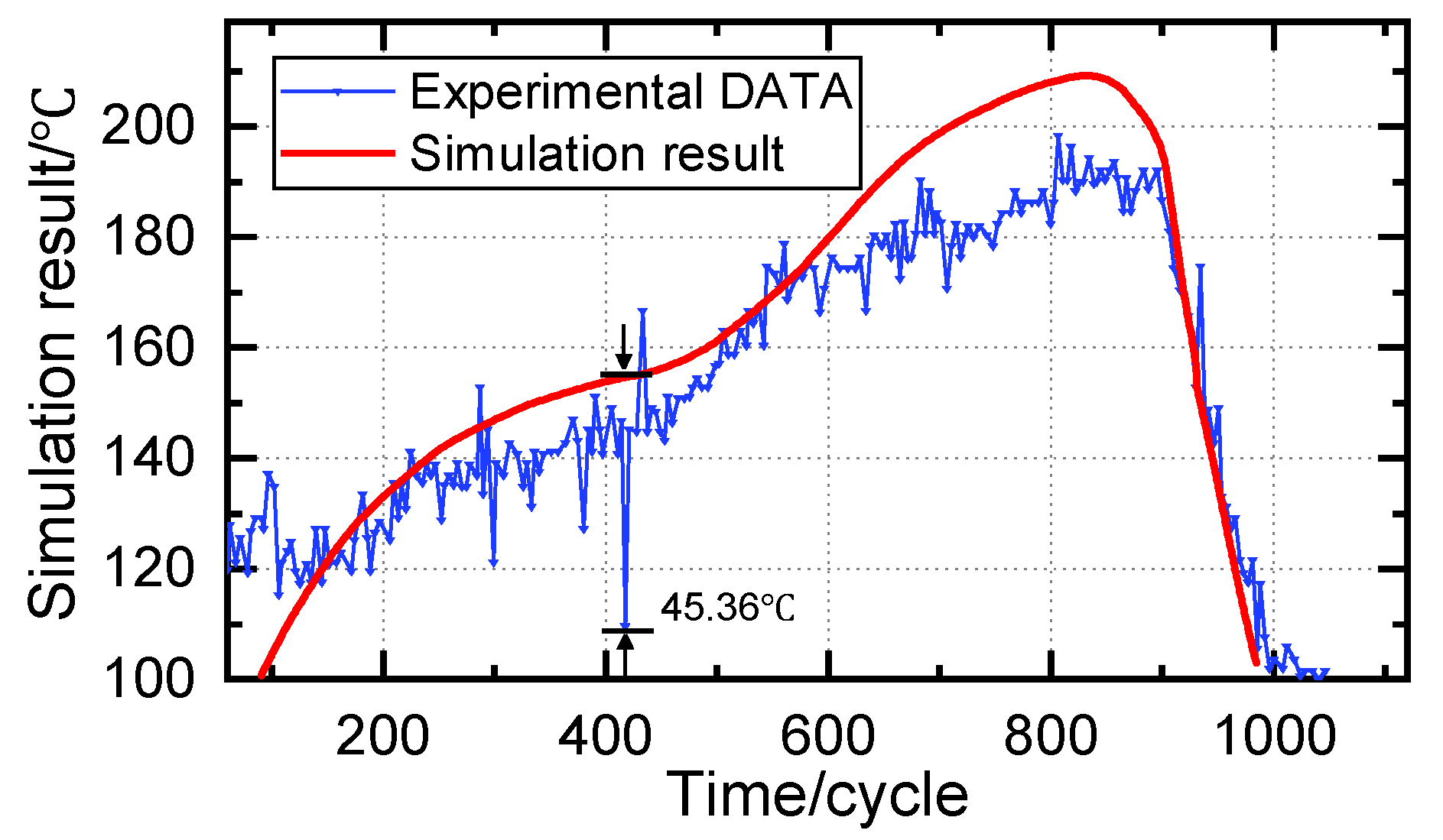
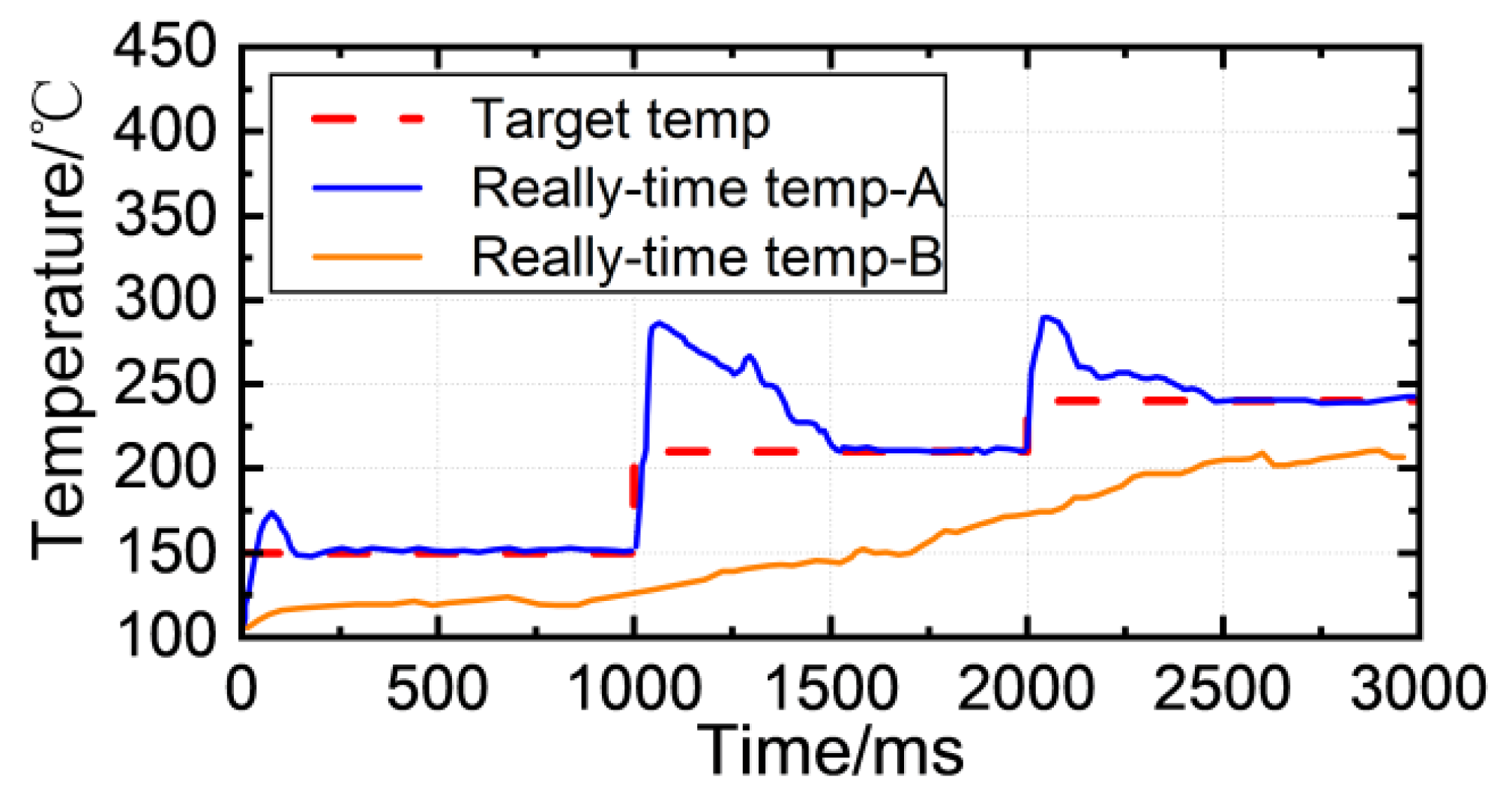
4. Experimental Results and Analysis
4.1. Experimental Scheme
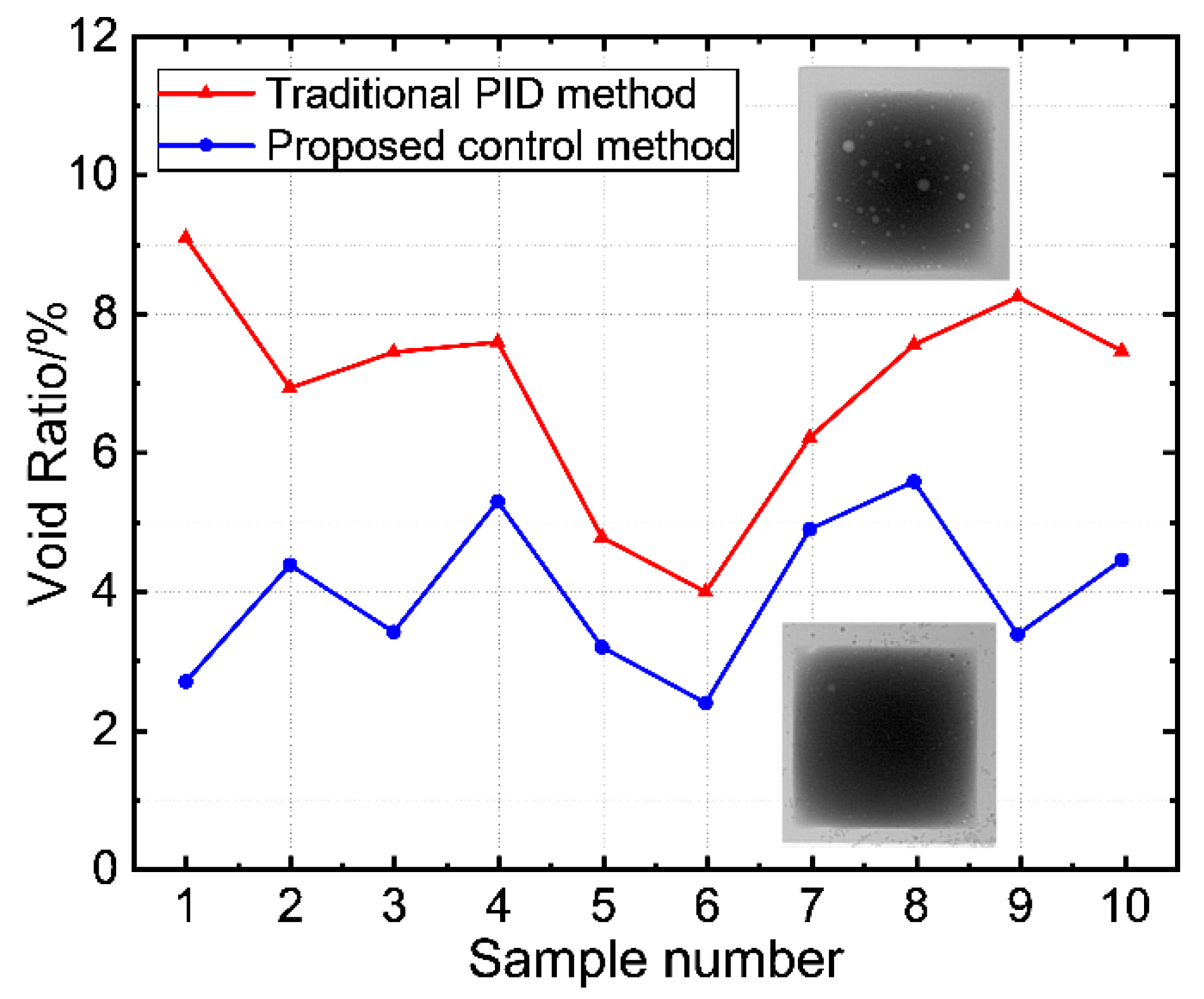
4.2. Sodering Experiments
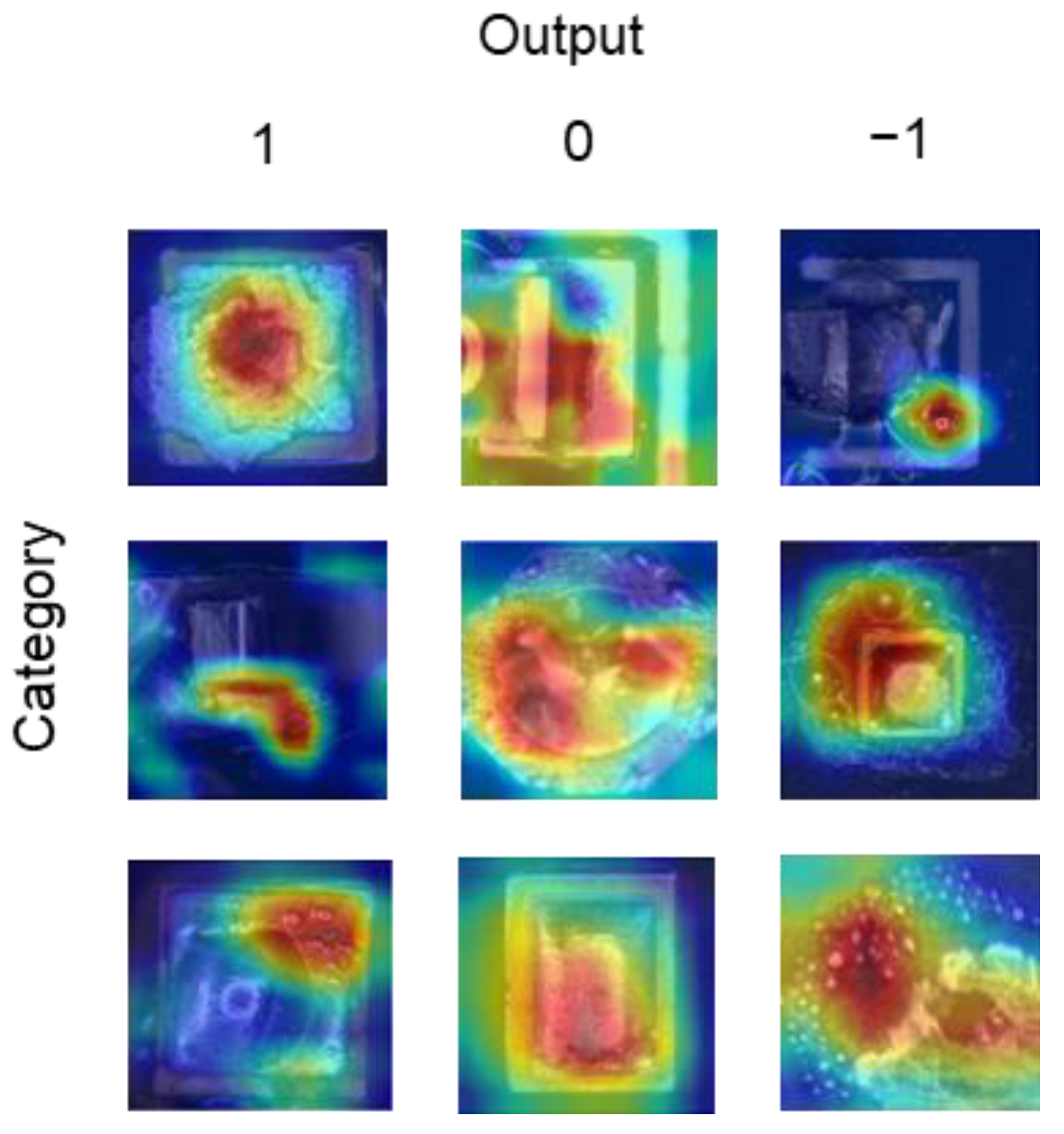
4.3. Exploration of Soldering Quality Factors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Web Exclusive: Laser Soldering Compression Method for Fine-Pitch, Thin-Die Applications. Available online: https://www.laserfocusworld.com/industrial-laser-solutions/article/14221584/laser-soldering-compression-method-for-finepitch-thindie-applications (accessed on 7 June 2023).
- Xin, Z.; Xue, S.; Han, Z. Review on Application of Laser Soldering Technology to Join High Density Packaging Device with Lead-Free Solder. Weld. Join. 2007, 11, 21–26. [Google Scholar] [CrossRef]
- Appan, R.M.; Ismail, A.B.; Ahmad, Z.A.; Ariga, T.; Hussain, L.B. Wetting Properties of Sn–Pb, Sn–Zn and Sn–Zn–Bi Lead–Free Solders. J. Teknol. 2008, 46, 1–14. [Google Scholar] [CrossRef]
- Xu, Z.; Sharma, A.; Lee, S.J.; Jung, J.P. Effect of Soldering Temperature on Wetting and Optical Density of Dip Coated Sn and Sn-3.5Ag Solders. Mater. Manuf. Process. 2015, 30, 127–132. [Google Scholar] [CrossRef]
- Yuan, J.; Huang, C.; Chen, J.; Liu, F.; Qiu, Y. Investigation on Laser Direct Welding of Quad Flat Pack Components. J. Electron. Packag. 2013, 135, 044501. [Google Scholar] [CrossRef]
- Lee, J. Finite Element Models of Laser Welding. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1992. [Google Scholar]
- Beckett, P.M.; Fleming, A.R.; Gilbert, J.M.; Whitehead, D.G. The Finite Element Modelling of Laser Soldering for Electronic Assemblies. Int. J. Numer. Model. Electron. Netw. Devices Fields 2002, 15, 265–281. [Google Scholar] [CrossRef]
- Tian, D.; Wang, C.; Tian, Y. Modeling of Micropitch Shift of a Magnetoelectrical Sensor During Laser Solder Ball Bonding Process. IEEE Trans. Adv. Packag. 2009, 32, 136–145. [Google Scholar] [CrossRef]
- Chen, Z.; He, C.; Zheng, Y.; Shi, X.; Song, T. A Novel Thermodynamic Model and Temperature Control Method of Laser Soldering Systems. Math. Probl. Eng. 2015, 2015, 509031. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N.; Arya, Y.; Ocak, C. (1 + PD)-PID Cascade Controller Design for Performance Betterment of Load Frequency Control in Diverse Electric Power Systems. Neural Comput. Applic. 2021, 33, 15433–15456. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N. Novel Fuzzy 1PD-TI Controller for AGC of Interconnected Electric Power Systems with Renewable Power Generation and Energy Storage Devices. Eng. Sci. Technol. Int. J. 2022, 35, 101166. [Google Scholar] [CrossRef]
- Çelik, E. Performance Analysis of SSA Optimized Fuzzy 1PD-PI Controller on AGC of Renewable Energy Assisted Thermal and Hydro-Thermal Power Systems. J. Ambient Intell. Humaniz. Comput. 2022, 13, 4103–4122. [Google Scholar] [CrossRef]
- Fathi, A.; Khajepour, A.; Toyserkani, E.; Durali, M. Clad Height Control in Laser Solid Freeform Fabrication Using a Feedforward PID Controller. Int. J. Adv. Manuf. Technol. 2007, 35, 280–292. [Google Scholar] [CrossRef]
- Çelik, E.; Öztürk, N. First Application of Symbiotic Organisms Search Algorithm to Off-Line Optimization of PI Parameters for DSP-Based DC Motor Drives. Neural Comput. Applic. 2018, 30, 1689–1699. [Google Scholar] [CrossRef]
- Celik, E.; Gor, H. Enhanced Speed Control of a DC Servo System Using PI + DF Controller Tuned by Stochastic Fractal Search Technique. J. Frankl. Inst. 2019, 356, 1333–1359. [Google Scholar] [CrossRef]
- Huang, Y.; Li, G.; Shao, W.; Gong, S.; Zhang, X. A Novel Dual-Channel Weld Seam Tracking System for Aircraft T-Joint Welds. Int. J. Adv. Manuf. Technol. 2017, 91, 751–761. [Google Scholar] [CrossRef]
- Prabhakar, G.; Selvaperumal, S.; Nedumal Pugazhenthi, P. Fuzzy, P.D. Plus I Control-Based Adaptive Cruise Control System in Simulation and Real-Time Environment. IETE J. Res. 2018, 65, 69–79. [Google Scholar] [CrossRef]
- Hoo, C.L.; Wong, J. Integration of Derivative Control on SIPIC in Motor Speed Control: SIPIC+D in Motor Speed Control. Asian J. Control 2020, 22, 706–715. [Google Scholar] [CrossRef]
- Günther, J.; Pilarski, P.M.; Helfrich, G.; Shen, H.; Diepold, K. Intelligent Laser Welding through Representation, Prediction, and Control Learning: An Architecture with Deep Neural Networks and Reinforcement Learning. Mechatronics 2016, 34, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, X.; Katayama, S. Weld Appearance Prediction with BP Neural Network Improved by Genetic Algorithm during Disk Laser Welding. J. Manuf. Syst. 2015, 34, 53–59. [Google Scholar] [CrossRef]
- Kwon, O.; Kim, H.G.; Kim, W.; Kim, G.-H.; Kim, K. A Convolutional Neural Network for Prediction of Laser Power Using Melt-Pool Images in Laser Powder Bed Fusion. IEEE Access 2020, 8, 23255–23263. [Google Scholar] [CrossRef]
- Božič, A.; Kos, M.; Jezeršek, M. Power Control during Remote Laser Welding Using a Convolutional Neural Network. Sensors 2020, 20, 6658. [Google Scholar] [CrossRef]
- Yuguang, Z.; Kai, X.; Dongyan, S. An Improved Artificial Neural Network for Laser Welding Parameter Selection and Prediction. Int. J. Adv. Manuf. Technol. 2013, 68, 755–762. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 770–778. [Google Scholar]
- Xuepin, T.; Shijin, L.; Cheng, Q. Study on the Identification Methods of Typical Cultured Fish Based on ResNet. Fish. Mod. 2022, 49, 81–88. [Google Scholar] [CrossRef]
- Xia, C.; Pan, Z.; Li, Y.; Chen, J.; Li, H. Vision-Based Melt Pool Monitoring for Wire-Arc Additive Manufacturing Using Deep Learning Method. Int. J. Adv. Manuf. Technol. 2022, 120, 551–562. [Google Scholar] [CrossRef]
- Jang, J.; Van, D.; Jang, H.; Baik, D.H.; Yoo, S.D.; Park, J.; Mhin, S.; Mazumder, J.; Lee, S.H. Residual Neural Network-Based Fully Convolutional Network for Microstructure Segmentation. Sci. Technol. Weld. Join. 2020, 25, 282–289. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.; Wang, R.; Li, M. Numerical Modeling and Optimization of Laser Soldering for Micro-USB Electric Connector: Modeling of Laser Soldering. Int. J. Numer. Model. 2015, 28, 175–188. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–23 October 2017. [Google Scholar]
- Ho, M.-P.; Ngai, W.-K.; Chan, T.-W.; Wai, H. An Artificial Neural Network Approach for Parametric Study on Welding Defect Classification. Int. J. Adv. Manuf. Technol. 2022, 120, 527–535. [Google Scholar] [CrossRef]
- Liping, Y. Mask-FGSM Adversarial Samples Attack Base on Grad-CAM. Comput. Appl. Softw. 2022, 39, 39. [Google Scholar] [CrossRef]
- Busek, D.; Dusek, K.; Ruzicka, D.; Placek, M.; Mach, P.; Urbanek, J.; Stary, J. Flux Effect on Void Quantity and Size in Soldered Joints. Microelectron. Reliab. 2016, 60, 135–140. [Google Scholar] [CrossRef]






| Symbol | Value |
|---|---|
| Absorptivity | |
| Laser output power | |
| Laser beam radius | |
| Distance from laser beam center |
| Symbol | Value |
|---|---|
| Proportional coefficient | |
| Integral coefficient | |
| Differential coefficient | |
| Error function | |
| Output function | |
| Subtractive function of error | |
| Increasing function of error | |
| , | Error value |
| Material | Proportion |
|---|---|
| Sn | 96% |
| Ag | 3% |
| Cu | 0.5% |
| Parameter | Value |
|---|---|
| Preheating temperature | 140 °C |
| Soaking temperature | 180 °C |
| Reflow temperature | 230 °C |
| Soldering temperature Per segment | 1000 ms |
| Power upper limit Per segment | 30% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Cao, P.; Zhang, C.; Yan, K.; Zhang, Y. Variable-Structure Proportional–Integral–Derivative Laser Solder Joint Temperature Intelligent Control Method with Adjustable Power Upper Limit. Micromachines 2023, 14, 1618. https://doi.org/10.3390/mi14081618
Li M, Cao P, Zhang C, Yan K, Zhang Y. Variable-Structure Proportional–Integral–Derivative Laser Solder Joint Temperature Intelligent Control Method with Adjustable Power Upper Limit. Micromachines. 2023; 14(8):1618. https://doi.org/10.3390/mi14081618
Chicago/Turabian StyleLi, Mingchao, Pengbin Cao, Cong Zhang, Kuan Yan, and Yuquan Zhang. 2023. "Variable-Structure Proportional–Integral–Derivative Laser Solder Joint Temperature Intelligent Control Method with Adjustable Power Upper Limit" Micromachines 14, no. 8: 1618. https://doi.org/10.3390/mi14081618
APA StyleLi, M., Cao, P., Zhang, C., Yan, K., & Zhang, Y. (2023). Variable-Structure Proportional–Integral–Derivative Laser Solder Joint Temperature Intelligent Control Method with Adjustable Power Upper Limit. Micromachines, 14(8), 1618. https://doi.org/10.3390/mi14081618







