An Analytical Model of Dynamic Power Losses in eGaN HEMT Power Devices

Abstract

In this work, we present an analytical model of dynamic power losses for enhancement-mode AlGaN/GaN high-electron-mobility transistor power devices (eGaN HEMTs). To build this new model, the dynamic on-resistance (R_dson) is first accurately extracted via our extraction circuit based on a double-diode isolation (DDI) method using a high operating frequency of up to 1 MHz and a large drain voltage of up to 600 V; thus, the unique problem of an increase in the dynamic R_dson is presented. Then, the impact of the current operation mode on the on/off transition time is evaluated via a dual-pulse-current-mode test (DPCT), including a discontinuous conduction mode (DCM) and a continuous conduction mode (CCM); thus, the transition time is revised for different current modes. Afterward, the discrepancy between the drain current and the real channel current is qualitative investigated using an external shunt capacitance (ESC) method; thus, the losses due to device parasitic capacitance are also taken into account. After these improvements, the dynamic model will be more compatible for eGaN HEMTs. Finally, the dynamic power losses calculated via this model are found to be in good agreement with the experimental results. Based on this model, we propose a superior solution with a quasi-resonant mode (QRM) to achieve lossless switching and accelerated switching speeds.

1. Introduction

Enhancement-mode AlGaN/GaN high-electron mobility transistor power devices (eGaN HEMTs) are the most promising candidates for use as next-generation power devices. In such devices, III–V materials have several merits due to their wide bandgap energy, high critical breakdown electric field, high electron mobility and capability [1,2], and polarization effect [3]. Due to these advantages, a high-frequency (high-fs) converter operating in the range of 1–5 MHz based on eGaN HEMTs can be readily realized. Although high-fs operation can help to reduce the converter size, it will generate more challenges with respect to dynamic power loss. Thus, building an analytical dynamic power loss model for an eGaN-based high-fs switch becomes important for prototype application in circuit design.

Recently, some state-of-the-art dynamic power loss models for eGaN HEMTs have been proposed. Wang et al. developed two analytical loss models based on detailed parasitic parameters for high-voltage and low-voltage GaN eHEMTs [4,5]. In these models, the gate charge (Q_g) and output charge (Q_oss), instead of the voltage-dependent capacitance, were used to improve the non-linear characteristics. However, the loss caused by output capacitance is not separately discussed in terms of a hard switch and soft switch. Shen et al. fully accounted for the effects of parasitic parameters and transconductance [6]. Hou et al. and Guacci et al. investigated the loss caused by the output capacitance in a hard switch and soft switch using simulation methods rather than experimental methods [7,8]. However, these models did not take into account the impact on device loss from some aspects, instead of fully evaluating it; thus, the results accuracy is affected. For example, the problem of increased losses caused by dynamic on-resistance (R_dson) is not discussed.

Chen et al. presented a complete analytical loss model for low-voltage eGaN HEMTs, for which a piecewise model was employed [9]. Piecewise models are also usually used to evaluate the dynamic power losses for Si- and SiC-based metal-oxide-semiconductor field-effect transistors (MOSFETs) [10,11,12,13,14,15]. These models are carefully considered and allow accurate evaluation of device power losses. However, these models fail to include sufficient consideration of the parasitic elements and merely focus on Si-based MOSFETs, but not on GaN HEMTs. In addition, the effect of current operation mode on device transition time and loss is not considered in all known device loss models. Therefore, these analytical models need to be modified for use on eGaN HEMTs to make a more comprehensive and accurate model.

To improve the dynamic power loss model of eGaN HEMTs, we propose three experimental methods according to the practical application of devices in high-fs circuits, such as the double-diode isolation (DDI) method, the dual-pulse-current-mode test (DPCT) method, and the external shunt capacitance (ESC) method. Then, the dynamic R_dson is accurately extracted in a high operating frequency (fs) of up to 1 MHz and a high drain voltage up to 600 V; the effect of current operation mode on the transition time is revealed, and the effect of current operation mode on the device loss is discussed from the shape of operating waveforms in the circuit. As the real channel current (Ich) is qualitatively modified compared to the drain current (I_drain), we can directly test in the device drain side. Afterward, the dynamic power loss of eGaN HEMTs is carefully described via a modified 12-segment piecewise model. Finally, we propose a quasi-resonant mode (QRM) with a low off-state drain voltage (V_{ds_off}), a zero turn-on current, and a relatively large on-state peak current for a lossless design and fast transit speed in power switches.

2. Background and Methodology

2.1. Traditional Power Loss Model

In the piecewise model, the operating sequence of the device is shown in Figure 1. In particular, the device was usually connected in series using a choke or transformer in power switches; thus, the value of I_sta indicated the current mode of the device. (I_sta = 0) denoted the device operating in discontinuous conduction mode (DCM), while (I_sta > 0) denoted the device operating in continuous conduction mode (CCM). Whether the device operated in CCM or DCM depends on the choke in series. As we know, in a high-frequency circuit, chokes follow the volt-second balance principle, that is, the starting current of the choke in each cycle must be equal to the end current. During the t_on time when the device was switched on, the choke current rose under an applied forward voltage V1, the rise slope was V1/L, and L was the inductance of the choke; during the t_off time when the device was switched off, the choke current fell under an applied reverse voltage V2, and the fall slope was V2/L. Therefore, the peak value of the choke current in each cycle was V1·t_on/L, and the end current value was (V1·t_on − V2·t_off)/L. Then, according to the known values of V1 and V2, we could design the required L to make the device operate in CCM or DCM.

A traditional calculation formula for high-f_s power losses of device is given as follows [16]:

$${\mathrm{P}}_{\mathrm{sw}}=\frac{1}{2}{I}_{ds}{V}_{ds}(t_{on}+t_{off})f_s+\frac{1}{2}{C}_{oss}{V}_{ds}{}^2{f}_s+K_{th}{I}_{dson\_rms}{}^2{R}_{dson}+Q_g{V}_{gs}{f}_s$$

(1)

where I_{dson_rms} is the on-state drain-source current in the root mean square (RMS) value, and K_th is the temperature coefficients related to R_dson. The first term in Equation (1) occurs in the crossing area of I_ds and the V_ds, while the second term is the output capacitor energy dissipated in the device during the turn-on transition. Then, the third and fourth terms are the conductive loss and driving loss, respectively. Equation (1) is approximate, as it does not take into account the problem of a dynamic R_dson increase, the impact of I_drain on the transition time, or the discrepancy between I_drain and the real channel current.

2.2. Experimental Circuit and Method

A switching circuit with a floating buck–boost topology was employed to analyze the switching processes, as shown in Figure 2a. In this circuit, an HEMT device was used and shown with a simple three-capacitor model that included the parasitic capacitors C_gs, C_gd and C_ds. The pulse width modulation (PWM) was produced via a pulse generator (81150A, Keysight Technologies, Inc., Santa Rosa, CA, USA) with a maximum PWM of 120 MH, and amplified using a gate driver (SI8271GB), which had a 1.8-ampere peak source current and a 4.0-ampere peak sink current, and D₁ was selected as a SiC diode (C3D10065E) rated at 15 A/650 V, which was used to reduce the reverse recovery problem. The parasitic resistor and parasitic inductor were ignored to simply study the important role of the parasitic capacitors at a relatively high-f_s that is smaller than 30 MHz. Then, various voltages and PWM in DCM and CCM were applied to elucidate the switching processes and the production of dynamic power losses.

The part of Figure 2b marked with the light-yellow area shows our novel dynamic R_dson extraction circuit based on a double-diode isolation (DDI) method; the details on how to configure, test and calculate this circuit can be obtained from Refs. [17,18,19]. In this design, the model of the gate driver was SI8271GB, and D₁ and D₂ (1 A/1 kV UF4007) were used in series to isolate the high off-state voltage of the eGaN HEMTs. Then, the dynamic R_dson of the eGaN HEMTs could be easily extracted. Diodes in series made it possible to test the real-time forward voltage drop (V_F) of D₂ in a low-voltage range and precisely estimate the V_F of D₁ in the same forward current. In addition, the diodes in series reduced the parasitic capacitor by half, which was very helpful to the high-f_s response of the extraction circuit. We called this method the DDI method. Moreover, ZD₁ and D₃ were free-wheeling diodes, and ZD₁ was also a positive clamping diode. These two diodes were a general 5-volt Zener ZD₁ and a general small signal diode D₃ (1N4148) with 75 V/150 mA. All of the functional diodes, including D₁, D₂, ZD₁ and D₃, were specially selected to have a very low parasitic capacitance, which improved the high-f_s response of the extraction circuit to several MHz. I₁ was a constant-current source of only several mA, meaning that it could not produce a temperature problem and have an extra self-heating effect. I₁ consisted of a constant-current diode, which was actually a junction field transistor with a gate-source short connection. Therefore, I₁ could achieve an excellent constant current over a wide operating voltage range. R_t provided a minimum load for I₁ and suppressed the voltage spike at point B. An isolated low-voltage probe (P2221 from Keysight Inc.) with a 1:1 attenuation could be used to test the V_F of D₂ and the voltage at point B. The low-voltage probe with a 1:1 attenuation did not amplify the background noise and operate in a low-voltage range, meaning that it could obtain an improved test accuracy.

We built the above switching circuit and extraction circuit using one printed circuit board (PCB), as shown in Figure 2b.

2.3. Qualitative Method Used to Discover the Channel Behavior

Since we could not directly perform the measurements inside of the HEMT device, we proposed an evaluation method that employed an extended parallel capacitor C_ds, as shown in Figure 3, which we called the “external shunt capacitance (ESC)” method. In this lumped circuit, the intrinsic capacitor C_ds was assumed not to exist, and the extended capacitor C_ds outside of the device was assumed to be the intrinsic capacitor. Therefore, the channel current (I_channel) and I_drain could be directly and separately measured using an oscilloscope and current probes. This method was different to the traditional simulation method [20], and the discrepancy between I_channel and I_drain could be visually observed. Although an extra parallel capacitor led to an increase in the measured I_drain and I_channel, this qualitative method could be used to assess the difference between these two currents, and, thereby, the cause of the discrepancy could be located. After understanding this reason, the resulting loss effect on the eGaN HEMT device could be further quantified via an analytical method. Using the analytical method, the additional C_ds was no longer required; therefore, the C_ds did not materially affect the device’s losses.

3. Extraction of the Dynamic R_dson

It is well known that a high V_{ds_off} will cause surface- and buffer-related trapping processes, which will lead to a larger dynamic R_dson compared to the direct current (DC) R_dson (R_{dson_DC}) [21,22]. Figure 4 illustrates the mechanism of the increase in the dynamic R_dson induced via the trapping effect. The high electric field helps the electrons to escape from the GaN well, and these electrons are then captured by traps or some of the surface states that are activated via a high electric field. When removing the electric field, these trapped electrons cannot be instantaneously released to the well. The reason for the slow return of electrons is that the trapping time of electrons in the off-state is in the order of ns, whereas the detrapping time of electrons in the on-state is in the order of second [23,24]. Thus, trapped electrons accumulate and worsen the device’s performance at a high f_s. Meanwhile, electrons migrate from the gate to the gate-drain side’s adjacent surface to form a virtue gate; hence, the number of electrons in the access region decreases. The decreasing number of electrons in the drift region will result in a large dynamic R_dson [25,26].

In the circuit of Figure 2a, the current I₁ flows partly through R_t and partly through the HEMT device, and the voltage of point B (V_B) can be directly tested using the voltage probe P2221. Then, the dynamic R_dson can be calculated as follows:

$$R_{dson}=({\overline{V}}_B-2{\overline{V}}_{F\_D2})/({\overline{I}}_{drain}-I_1+{\overline{V}}_B/R_t)$$

(2)

where ${\overline{V}}_B$, ${\overline{V}}_{F\_D2}$, ${\overline{I}}_{drain}$, ${\overline{I}}_{D2}$, and I₁ are the average voltages of point B and D₂, the average currents through a resistive load and D₂, and the current of the constant-current supply, respectively. I_drain, the voltage of point A (V_drain), and V_{F_D2} of D₂ are tested using a current probe (TCP0020), a high-voltage differential probe (THDP0200), and a low-voltage differential probe with a 1:1 attenuation (TIVH02) and displayed using an oscilloscope (MDO3104). Finally, the calculated dynamic R_dson is normalized by R_{dson_DC}, which is 200 $\mathrm{m}\Omega$, derived from an eGaN HEMT (GS66502B from GaN Systems Inc., Ottawa, Canada) [27].

Figure 5b–f show the results of the dynamic R_dson of the eGaN HEMT for various V_{ds_off}, f_s, duty cycles, I_drain, and operating temperatures, which are extracted in the on-state by taking average values in the stable region marked in Figure 5a. Figure 5b shows that the dynamic R_dson increases as V_drain increases under the conditions of an 80% duty cycle and an f_s of 100 kHz, meaning that the dynamic R_dson is voltage dependent. Figure 5c,d shows the dynamic R_dson increases as f_s increases and duty cycle decreases, respectively, for a 500-volt V_drain condition, meaning that the dynamic R_dson is also time dependent. Considering that the dynamic R_dson is not only affected by the trapping effect, we further test the relationship between the dynamic R_dson and I_drain and temperature, as shown in Figure 5e,f, respectively. These two tests will help us to isolate the trapping effect caused by the increase in the dynamic R_dson in a particular complex test condition.

In conclusion, the trend regarding the results of the extracted dynamic R_dson of the eGaN HEMT is consistent with the mechanism of the trapping-effect-induced increase in the dynamic R_dson. In Figure 6, we can obtain the real conduction resistance of the eGaN HEMT device under a certain working condition, and the conduction loss can then be corrected.

4. Discussion on the Effect of the Drain Current using a Double-Mode Test Technique

Based on the test circuit in Figure 1, a double-mode test technique, which included a DCM and a CCM, is proposed. In general, the electrical performance of a GaN device is characterized by either single-pulse or double-pulse mode. The typical “double-pulse” test is performed in three steps. The first step, which is represented by the turn-on pulse, is the initial adjusted pulse width. This pulse is adjusted to find the desired test current. The second step is to turn off the first pulse. The turnoff period is short to keep the load current as close as possible to a constant value. The third step is represented by the second turn-on pulse. The pulse width is shorter than the first pulse, meaning that that the device is not overheated, but it needs to be long enough for the measurements to be taken. Turn-off and turn-on timing measurements are then captured at the turning off of the first pulse and the turning on of the second pulse. This “double-pulse” technique only sends two pulses to the device, which is not periodically sustained, and the current in the third step is always higher than 0 A [28,29,30]. In order to fully obtain the characteristics of the periodic operation of the device in the high-frequency circuit, we make the device continuously work periodically and stably in the CCM or DCM state by controlling the L value and the V_{ds_off} [31,32]. With the “double-pulse-current-mode” technique, we are able to focus on the impact of the starting current and peak current on the transition time of the device, which is not easy to do with the conventional “double-pulse” technique. Then, the tested waveforms during the turn-on and turn-off transitions for various voltage and PWM conditions are illustrated in the Figure 6. To ensure that the switching circuit operates in open-loop CCM and DCM, V_Bulk is set to 400 V, and the V_Load is set to 80 V in DCM and 20 V in CCM, meaning that the V_{ds_off} values of the devices in the two modes are different.

The current I_drain in DCM only exhibits one resonant waveform when the drain voltage decreases, as shown in Figure 6a, while I_drain in CCM has an extra linear increase before the resonant waveform occurs, as shown in Figure 6b. The corresponding voltage fall time is approximately 14 ns in Figure 6a and approximately 42 ns in Figure 6b, meaning that that the extra linear increase in the current will increase the turn-on time and cause a high dynamic power loss. This linear increase in the current is caused by the high start current and the linear conduction of the eGaN HEM at this time. This finding means that DCM is a superior operating mode in terms of reducing the turn-on time.

In addition, the rise time of the drain voltage during the turn-off transition, which is approximately 10 ns, as shown in Figure 6d, is faster than that of approximately 30 ns shown in Figure 6c. This observation is true because I_drain in Figure 6d is higher than that in Figure 6c, and the rise time of the drain voltage during the turn-off transition mainly depends on the charge time of C_oss. Moreover, the peak current in DCM during the turn-off transition will be higher than that in CCM under the same output power conditions. This observation means that DCM is a superior operating mode in terms of reducing the turn-off time.

In conclusion, the drain current will significantly affect the turn-on and turn-off times, and DCM is better than CCM at reducing the crossover power losses.

5. Investigation of the Real Channel Current

According to the qualitative method shown in Figure 2, we can study the discrepancy between I_drain and I_channel. Figure 7a shows the tested I_drain, I_channel, V_drain, and V_drive values of the AlGaN/GaN HEMT in the turn-on transition for a V_{ds_off} of 500 V, an f_s of 100 kHz, and a duty cycle of 16.5%. It is shown that I_channel is larger than I_drain, while the drain voltage decreases. The current path in this time interval is shown in Figure 7b, where the channel current partially results from the discharging current of the parasitic output capacitor.

Figure 7c shows the tested I_drain, I_channel, V_drain, and V_drive values of the AlGaN/GaN HEMT during the turn-off transition for a V_{ds_off} of 500 V, an f_s of 100 kHz, and a duty cycle of 16.5%. It is shown that I_channel is smaller than I_drain, while the drain voltage increases. The current path in this time interval is shown in Figure 7d, where the channel current is partially diverted to the branch of the output capacitor.

In conclusion, I_channel is not exactly equal to I_drain, and, unfortunately, I_channel cannot be directly tested. However, with the above test results and the current path analysis, we can acquire the reason for the discrepancy between I_channel and I_drain, meaning that the real I_channel value can be obtained via a test of I_drain and an analytical method, and the power losses of eGaN HEMTs can be correctly evaluated.

6. Modeling of Switching Power Losses

Figure 8 shows a detailed timing diagram of the switching period [33] for eGaN HEMTs in DCM or CCM. The operating period of the power devices can be divided into 12-time intervals from t₀ to t₁₂ based on the status of the drain voltage and I_drain in the off-state, on-state, turn-on transition, and turn-off transition. To investigate the detailed dynamic power loss, we reclassified the 12-time intervals into four stages (S1–S4) based on their different contributions to the dynamic power loss.

6.1. Stage 1 (S1)—Off-State with a High V_ds

During the t₀–t₁ and t₁₀–t₁₁ time intervals and the time of the off-state, the device sustains a high V_ds. Thus, the voltage-dependent leakage current (I_lk) will lead to an off-state power loss (P_off). We can no longer ignore this power loss, especially at a very high drain voltage and very high frequency. In general, the t₀–t₁ and t₁₀–t₁₁ time intervals can be neglected in comparison to the off-state time, meaning that P_off can be written as follows:

$$P_{off}=I_{lk}{V}_{ds}[t_{t_0-t_1}+t_{t_{11}-t_{12}}+(1-D)T]f_s\approx I_{lk}{V}_{ds}(1-D)$$

(3)

where T and D are the period and duty cycle, respectively. In addition, eGaN HEMTs have no reverse recovery problem because the 2DEG in the channel is naturally formed via the polarization effect. This outcome will reduce the power loss and mitigate the electromagnetic interference (EMI) problem, which is produced via the reverse recovery caused by ringing.

6.2. Stage 2 (S2)—On-State in Saturation Region

During the t₄–t₇ time intervals, the device is in the on-state. The RMS value of the drain current (I_{drain_rms}) can be written as follows:

$$I_{drain\_rms}=\sqrt{f_s{\displaystyle \underset{0}{\overset{1/f_s}{\int }}{I}_{drain}{}^2(t)dt}}$$

(4)

To take the problem of the increase in the dynamic R_dson into account, the traditional conductive power loss (P_con) can be modified as follows:

$$P_{con}=I_{drain\_rms}{}^2{R}_{dson\_DC}{k}_{dv}{k}_{df}{k}_{dd}{k}_{th\_R}{k}_{cu}$$

(5)

where $k_{dv}$, $k_{df}$, $k_{dd}$, $k_{cu}$, and $k_{th\_R}$ are the dynamic coefficients of R_dson related to the voltage, f_s, the duty cycle, the current, and the temperature, respectively.

6.3. Stage 3 (S3)—Turn-on Transition

During the t₁–t₄ time interval, the device is in the turn-on transition. In the t₁–t₂ time interval, I_drain increases, while V_drain decreases slightly in CCM, but this time interval does not exist in DCM; in the t₂–t₃ time interval, V_drain decreases and leads to a resonant I_drain. In the t₃–t₄ time intervals, V_drain decreases to a very low voltage, and the device starts to operate in an ohmic conducting state. These crossovers of V_drain and I_drain will cause power losses during the turn-on transition (P_{turn_on}):

$$P_{turn\_on}={\displaystyle \underset{t_1-t_4}{\int }{V}_{ds}(t)I_{drain}(t)f_s}dt+\frac{1}{2}{C}_{oss}{V}_{ds}{}^2{f}_s$$

(6)

1.

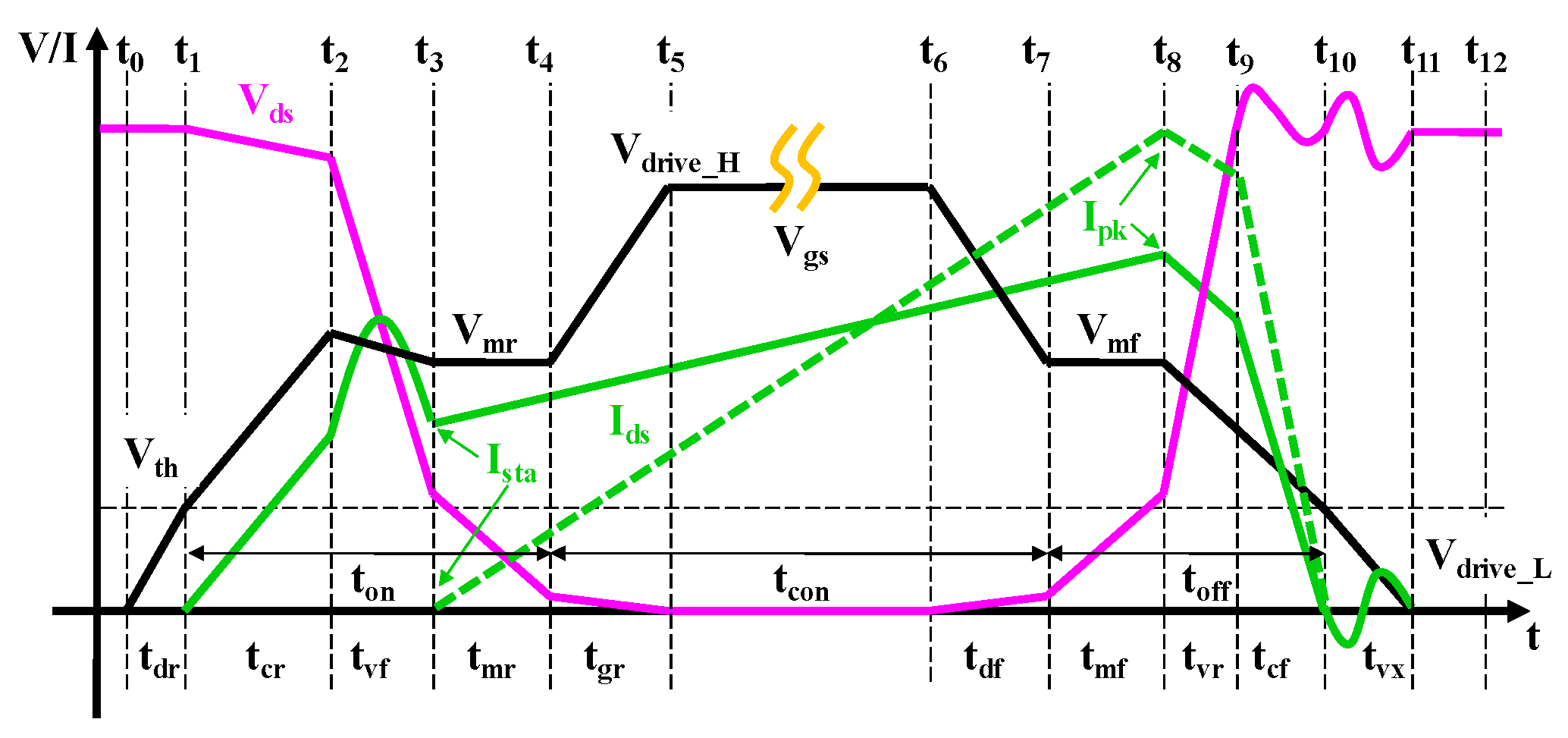
In the t₁–t₂ time interval, I_drain increases almost linearly from 0 to the I_sta at t₂, which is similar to a Si-based MOSFET [13,34], while V_drain decreases slightly from V_ds to V_r due to the result of the parasitic inductance voltage drop caused by a high di/dt in the circuit. At t₂, the current of the freewheeling diode D₁ decreases to zero. In this time interval, the gate voltage of the device slightly exceeds V_th, meaning that the device is operating in a linear region. Meanwhile, the trapping effect of a high electric field will also lead to a large dynamic R_dson in the linear region (R_{turn_on_cr}), which is similar to that in the on-state, as well as an extra gate lag. Thus, the coefficients of the dynamic R_dson should be the same as those in Figure 4. Assuming that the heatsink is large enough and the self-heating effect is ignored, the t₁–t₂ time interval, V_r, and the power losses in this time interval (P_{turn_on_cr}) can be written as follows:

$$R_{turn\_on\_cr}=\frac{\Delta V_{ds}}{\Delta I_{channel}}\approx \frac{k_{dv}{k}_{df}{k}_{dd}{k}_{th\_R}{k}_{cu}{L}_{eff\_Gate}}{W_{eff\_Gate}{\mu }_s{C}_{gs}(V_{drive\_H}-V_{th})}$$

(7)

$$t_1-t_2=\frac{C_{gs}{R}_{g\_on}{i}_{sta}+L_s{i}_{sta}{g}_m}{[V_{drive\_H}-0.5(V_{mr}+V_{th})]g_m}{k}_{lag}$$

(8)

$$V_r=V_{ds}-L_s\frac{i_{sta}}{t_1-t_2}-R_{turn\_on\_cr}\frac{i_{sta}}{2}$$

(9)

$$P_{turn\_on\_cr}=\frac{1}{2}{i}_{sta}{V}_r(t_1-t_2)f_s$$

(10)

where L_{eff_Gate} and W_{eff_Gate} are the effective channel length and width, respectively. L_s is the source inductor, which is in series with and between the source terminal and the ground. The coefficient of the gate lag(k_lag) is a fitting parameter, which can be obtained by measuring the turn-on delay for various V_{ds_off}, f_s and duty cycles.

2.

In the t₂–t₃ time interval, the HEMT device takes over the total inductive load current, and V_ds decreases to a boundary voltage of (V_mr − V_th) at t₃ due to the discharging of C_oss. The stray inductors in series around the circuit are resonant with C_oss and the stray capacitors (C_stray) in this time interval. The current path through the device is illustrated in Figure 5b. It is assumed that V_gs and i_sta remain unchanged, and the reverse recovery of the D₁ is zero. In addition, the current in this time interval is usually large enough; hence, the charging time of C_oss can be ignored. Moreover, voltage-dependent C_oss is not suitable for the calculation of power losses in this time interval because V_drain is always changing. Therefore, Q_gd is used to replace C_oss, and the time interval of t₂–t₃ can then be written as follows:

$$C_{gd\_vf}=\frac{Q_{gd}}{\Delta V}=\frac{Q_{gd}}{V_r-V_{mr}+V_{th}}$$

(11)

$$t_2\text{–}{t}_3=\frac{Q_{gd}{R}_{g\_on}+C_{stray}(V_r-V_{mr}+V_{th})/g_m}{V_{drive\_H}-V_{mr}}$$

(12)

Then, the power losses in this time interval (P_{turn_on_vf}) can be written as follows [35]:

$${\overline{I}}_v{}_f\approx 0.5(\frac{V_r}{R_{turn\_on\_cr}}+\frac{V_{mr}-V_{th}}{R_{dson}})$$

(13)

$$\begin{array}{rr}{P}_{turn\_on\_vf}& =\frac{1}{2}(i_{sta}+{\overline{I}}_v{}_f)(V_r-V_{mr}+V_{th})(t_2-t_3)f_s\\ & +\frac{1}{2}{C}_{stray}[{V_r}^2-{(V_r-V_{mr}+V_{th})}^2]f_s\hfill \end{array}$$

(14)

where ${\overline{I}}_{vf}$ is the average channel current during the t₂–t₃ time interval.

3.

During the t₃–t₄ time interval, the HEMT device operates in an ohmic conducting state. Then, V_drain continues to decrease until it reaches a low on-voltage (V_on) from (V_mr − V_th). Assuming that i_sta and the Miller voltage V_mr do not change, the t₃–t₄ time interval, V_{on_r}, and the power losses in this time interval (P_{turn_on_mr}) can be written as follows [36]:

$$t_3-t_4=\frac{Q_{gd}{R}_{g\_on}}{V_{drive\_H}-V_{mr}}$$

(15)

$$V_{on\_r}=i_{sta}{R}_{dson}{k}_{dv}{k}_{df}{k}_{dd}{k}_{th\_R}{k}_{cu}$$

(16)

$$\begin{array}{ll}{P}_{turn\_on\_mr}& =\frac{1}{2}{i}_{sta}(V_{mr}-V_{th}-V_{on\_r})(t_3-t_4)f_s\\ & +\frac{1}{2}{C}_{stray}[{(V_{mr}-V_{th}-V_{on\_r})}^2-{V_{on\_r}}^2]f_s\end{array}$$

(17)

From the above analysis, Equation (6) can be modified as follows:

$$P_{turn\_on}(\mathrm{measured})=P_{turn\_on\_cr}+P_{turn\_on\_vf}+P_{turn\_on\_mr}$$

(18)

We noticed that at this stage, i_sta is a tested drain current instead of a real channel current, and they are actually different in the t₂–t₃ time interval, as shown in Figure 5a. However, I_channel is the real factor that results in the power losses in this stage, and the real I_channel is the combined current of I_drain and the discharging current of C_oss:

$$I_{channel}=I_{drain}+I_{Cds}+I_{Cgd}\approx I_{drain}+I_{Cds}$$

(19)

Thus, Equation (18) can be finally modified as follows [12]:

$$P_{turn\_on\_act}=P_{turn\_on\_mea}+P_{turn\_on}{}_{\_dis}$$

(20)

where

$$P_{turn\_on}{}_{\_dis}=\frac{1}{2}{C}_{oss}{V}_{ds\_\mathit{off}}{}^2{f}_s$$

(21)

Thus,

$$\begin{array}{ll}{P}_{turn\_on}{}_{\_act}& =P_{turn\_on\_cr}+P_{turn\_on\_vf}\\ & +P_{turn\_on\_mr}+\frac{1}{2}{C}_{oss}{V}_{dsf}{}^2{f}_s\end{array}$$

(22)

6.4. Stage 4 (S4)—Turn-off Transition

During the t₇–t₁₁ time intervals, the device is in a turn-off transition. In the t₇–t₈ time intervals, the drain voltage increases, while I_drain stays almost constant; in the t₈–t₉ time intervals, the drain voltage continuously increases, while I_drain slightly decreases. In the t₉–t₁₀ time intervals, I_drain decreases, while the drain voltage stays almost constant. Finally, I_drain decreases to zero, and the drain voltage becomes resonant in the t₁₀–t₁₁ time intervals. These crossovers of V_drain and I_drain will cause power losses during the turn-off transition (P_{turn_off}) as follows:

$$P_{turn\_off}={\displaystyle \underset{t_7-t_{10}}{\int }{V}_{ds}(t)I_{drain}(t)f_s}dt$$

(23)

4.

In the t₇–t₈ time interval, the observations are very similar to those in the t₃–t₄ time interval. The HEMT device moves into a linear region from an ohmic conducting state. V_drain increases to a boundary voltage of $V_{mf}-V_{th}$. Assuming that the peak current is unchanged, and $V_{mf}=V_{mr}$, the t₇–t₈ time interval, V_{on_f}, and the power losses in this time interval (P_{turn_on_mf}) can be written as follows:

$$t_7-t_8=\frac{Q_{gd}{R}_{g\_off}}{V_{mf}-V_{drive\_L}}$$

(24)

$$V_{on\_f}=I_{pk}{R}_{dson}{k}_{dv}{k}_{df}{k}_{dd}{k}_{th\_R}{k}_{cu}$$

(25)

$$P_{turn\_off\_mf}=\frac{1}{2}{i}_{pk}(t_7-t_8)(V_{mf}-V_{th}-V_{on\_f})f_s$$

(26)

5.

In the t₈–t₉ time interval, the observations are very similar to those in the t₂–t₃ time intervals. V_drain continues to increase more quickly towards the off-state V_{ds_off}, while I_drain decreases slightly to i_r. This current drop is caused by a charging shunt to other peripheral devices [33], and the current path through the device is illustrated in Figure 5d. Assuming that the Miller voltage (V_mf) remains unchanged and the current-dependent charging time of C_oss can no longer be ignored, we have the following equation:

$$\begin{array}{l}{t}_8-t_9\approx \frac{Q_{gd}{R}_{g\_off}+C_{stray}(V_{ds}-V_{mf}+V_{th})/(2g_m)}{V_{mf}-V_{drive\_L}}\\ +\frac{C_{oss}(V_{ds}-V_{mf}+V_{th})}{i_{pk}}\end{array}$$

(27)

$$i_r=i_{pk}-C_{stray}\frac{d{V}_{ds}}{dt}=i_{pk}-C_{stray}\frac{V_{ds}-V_{mf}+V_{th}}{t_8-t_9}$$

(28)

$$P_{turn\_off\_vr}=\frac{i_{pk}+i_r}{2}(V_{ds}+V_{mr}-V_{th})(t_8-t_9)f_s$$

(29)

6.

In the t₉–t₁₀ time interval, the observations are similar to those in the t₁–t₂ time interval. I_drain decreases from i_r to a low value because the current begins to divert from the HEMT device to D₁. In this time interval, the drain voltage is in a state of resonance, while V_gs decreases to (V_mr − V_th), and the device channel current reaches zero at t₁₀ [20]. Then, the t₉–t₁₀ time interval and the power losses at this time interval (P_{turn_off_cf}) can be written as follows:

$$t_9-t_{10}=\frac{(C_{gs}{R}_{g\_off}+L_s{g}_m)i_r}{[0.5(V_{mf}+V_{th})-V_{drive\_L}]g_m}$$

(30)

$$P_{turn\_off\_cf}=\frac{1}{2}{i}_r{V}_{ds\_off}(t_9-t_{10})f_s+\frac{L_{stray}{i}_r{}^2}{2}$$

(31)

7.

During the t₁₀–t₁₁ time interval, the device is turned off, but V_drain ringing occurs due to the resonance between C_oss and L_stray. These fluctuations of the drain voltage will lead to a slight power loss, which depends on the ringing peak voltage (V_{ds_pk}). Assuming that the reverse recovery of D₁ is zero, we have the following equation:

$$\frac{L_{stray}{i}_r{}^2}{2}=\frac{C_{oss}\Delta V^2}{2}\to \Delta V=\sqrt{\frac{L_{stray}{i}_r{}^2}{C_{oss}}}\to V_{ds\_pk}=V_{ds\_off}+\Delta V$$

(32)

$$P_{turn\_off\_vx}\approx \frac{1}{2}{C}_{oss}(V_{ds\_pk}{}^2-V_{ds\_off}{}^2)f_s$$

(33)

From the above analysis, Equation (23) can be modified as follows:

$$P_{turn\_off}(\mathrm{measured})=P_{turn\_off\_mf}+P_{turn\_off\_vr}+P_{turn\_off\_cf}+P_{turn\_off\_vx}$$

(34)

Instead of real channel currents, they are actually different in the t₈–t₉ time interval, as shown in Figure 5c. However, I_channel is the real factor that results in the power losses in this stage, and the real I_channel is the diverted current of I_drain and the charging current of C_oss

$$I_{channel}=I_{drain}-I_{Cds}-I_{Cgd}\approx I_{drain}-I_{Cds}$$

(35)

Therefore, Equation (34) can be finally modified as follows [12]:

$$P_{turn\_off}(\mathrm{actual})=P_{turn\_off}(\mathrm{measured})-P_{turn\_off}(\mathrm{charge})$$

(36)

where

$$P_{turn\_off\_char}=\frac{1}{2}{C}_{oss}{V}_{ds\_off}{}^2{f}_s$$

(37)

Thus,

$$\begin{array}{l}{P}_{turn\_off\_act}=P_{turn\_off\_mf}+P_{turn\_off\_vr}+P_{turn\_off\_cf}\\ +P_{turn\_off\_vx}-\frac{1}{2}{C}_{oss}{V}_{ds\_off}{}^2{f}_s\end{array}$$

(38)

Finally, the total power loss (P_total) should be described based on the sum of Equations (3)–(38):

$$P_{total}=P_{off}+P_{con}+P_{turn\_on}{}_{\_act}+P_{turn\_off}{}_{\_act}$$

(39)

In particular, the effects of I_channel and I_drain on P_total can finally cancel out for a hard switch. However, in a soft switch application, such as a zero-voltage switch (ZVS), $P_{turn\_on}{}_{\_dis}$ is zero; hence,$P_{turn\_off}{}_{\_char}$ can no longer cancel out. This correction becomes very meaningful to the universality of the dynamic power loss model for eGaN HEMTs.

As can be seen, P_total in Equation (39) is very different to that in Equation (1). Equation (39) has no power loss of reverse recovery, but it takes the trapping effect-induced dynamic R_dson and the impacts of the I_drain and the real I_channel into account.

7. Model Verification via Experiments

To verify our dynamic power loss model, we adopt a floating buck–boost power converter with a light-emitting diodes (LEDs) operating in DCM and CCM. To maintain the operation mode and the output current (I_o) in an open-loop control system, some key parameters are adjusted (such as L₁) or tested (such as the output voltage V_o, the peak operating current I_pk, and the output power P_o) in the circuit, as shown in Figure 9, for an input voltage (V_Bulk) of 400 V, a duty cycle of 10%, and various f_s and I_o values.

The power losses are then tested using a power analyzer (PW6001-03 from HIOKI Inc., Ueda, Nagano Prefecture, Japan). Figure 10a–c reveal that the analytical results of the total dynamic power losses generated via the proposed model are in good agreement with experimental results in both CCM and DCM, even for various I_o, f_s and V_Bulk values. The experimental results are slightly different from the analytical results, which may be because of the measurement accuracy of the power meter reduced at a high f_s.

Figure 11a shows the relationship between the total dynamic power losses and I_o in CCM and DCM. In the case of a small I_o, the switching loss is dominant, while in the case of a large I_o, the conduction loss is dominant. In addition, the dynamic power loss increases faster with the increase in I_o in DCM than in CCM, indicating that DCM is not suitable for high current conditions.

Figure 11b shows the switching loss during the turn-on and turn-off transitions in CCM and DCM. The results reveal that the switching loss is lower in DCM than in CCM during the turn-on transition, but larger during the turn-off transition when I_o is larger than 1.25 A. This finding means that DCM is more suitable for a relatively small I_o. In this case, according to Figure 10b and Figure 11a, a 1.25-ampere I_o is a moderate output current that is acceptable.

It also can be seen that all calculated results are a little bit higher than the experimental results, especially in a higher than 2-ampere I_o condition and CCM mode. According to the analysis, the calculation model is not accurate enough to evaluate the self-heating effect of the device. Of course, in a high-frequency circuit, the peak current and the operating temperature of the device should be controlled by designing a suitable heat sink. In this case, when the I_o is 2 A, the device peak current is as high as 10 A, which is higher than the rated device continuous operating current of 7.5 A. Generally, our design should ensure that the operating current of the device does not exceed the rated 7.5 A, a certain margin should be designed, and the operating temperature of the device should not exceed 120 °C. Although the high operating temperature may not have any effect on the GaN device, it will have a bad effect on other surrounding devices.

To restrain the peak current and obtain a high operating efficiency, the QRM is, thus, proposed. The reason for this proposal is that QRM works at the DCM boundary, where V_drain will decrease to a minimum value at the beginning of the turn-on transition, while I_drain decreases to zero. In addition, the peak on-state current in DCM is usually larger than that in CCM, and the current will be at a controllable high level, meaning that the turn-off time is fast in QRM. Therefore, QRM is more suitable for the achievement of a lossless switch and even for the reduction in the turn-off transition time.

8. Conclusions

An improved 12-time-interval piecewise dynamic power loss model for eGaN HEMTs is developed by specially quantifying the effects of the increase in the dynamic R_dson, the impact of I_drain on the turn-on and turn-off times, and the real I_channel; good agreement with some experimental results is proven.

In this work, three methods or techniques are proposed, which are DDI method, the double-mode test technique and qualitative method. Then, the dynamic R_dson is obtained by our new extraction circuit at a high operating fs of up to 1 MHz and high drain voltage of up to 600 V, the drain current is found to significantly affect the turn-on and turn-off times via a switching circuit operating in DCM and CCM, and the real channel current is accurately calculated to distinguish it from the measured drain current. All of these parameters are included in the power loss model.

Moreover, the QRM has a low V_{ds_off}, zero turn-on current, and relatively large peak current. Therefore, on the basis of the model, we propose the QRM to obtain a high efficiency and decrease the turn-off switching time required for the application of eGaN HEMTs.