Abstract
The viscosity of fluid plays a major role in the flow dynamics of microchannels. Viscous drag and shear forces are the primary tractions for microfluidic fluid flow. Capillary blood vessels with a few microns diameter are impacted by the rheology of blood flowing through their conduits. Hence, regenerated capillaries should be able to withstand such impacts. Consequently, there is a need to understand the flow physics of culture media through the lumen of the substrate as it is one of the vital promoting factors for vasculogenesis under optimal shear conditions at the endothelial lining of the regenerated vessel. Simultaneously, considering the diffusive role of capillaries for ion exchange with the surrounding tissue, capillaries have been found to reorient themselves in serpentine form for modulating the flow conditions while developing sustainable shear stress. In the current study, S-shaped (S1) and delta-shaped (S2) serpentine models of capillaries were considered to evaluate the shear stress distribution and the oscillatory shear index (OSI) and relative residual time (RRT) of the derivatives throughout the channel (due to the phenomena of near-wall stress fluctuation), along with the influence of culture media rheology on wall stress parameters. The non-Newtonian power-law formulation was implemented for defining rheological viscosity of the culture media. The flow actuation of the media was considered to be sinusoidal and physiological, realizing the pulsatile blood flow behavior in the circulatory network. A distinct difference in shear stress distributions was observed in both the serpentine models. The S1 model showed higher change in shear stress in comparison to the S2 model. Furthermore, the non-Newtonian viscosity formulation was found to produce more sustainable shear stress near the serpentine walls compared to the Newtonian formulation fluid, emphasizing the influence of rheology on stress generation. Further, cell viability improved in the bending regions of serpentine channels compared to the long run section of the same channel.
1. Introduction
Transfusion of blood in the circulatory network of the human physiological circulatory system addresses multiple metabolic phenomena. Along with the mass transport phenomena, energy transfer is also a crucial feature of circulating blood. Focus on capillary blood transport and rate of fluxes of radial species is significant in comparison to axial mass flux. Further enhancement in the radial transport of chemical species can be achieved by increasing the hydraulic length of capillaries. Radial transport of chemical species is achieved by the natural serpentine arrangement of capillaries [1]. At the same time, the elastic wall of serpentine vascular geometry facilitates vascular regeneration [2]. Hence, a systematic evaluation of the related mechanical properties of blood vessels yields useful markers for analyzing the state of vascular diseases [3,4,5]. However, studies considering the serpentine shape of capillaries and their influence on radial dispersion of species is limited in the literature. Thus, the successful developmental regeneration of vascular capillaries demands a comprehensive mapping of stress distribution on the walls of different serpentine geometry capillaries having micron-dimension radius.
Regenerative materials for vascular capillary play a typical role in sustaining the mechanical properties of vessels while supporting their biological activities. Hydrogel is considered a successful candidate for vascular regenerative devices due to its enhanced transport capabilities, cellular proliferation, and differentiation in its microniche environment [6]. With its superior mixing capabilities [7], it promotes cell functionality over scaffold-based niches [8]. Natural GelMA has inherent stimulating species, which promote cell functionality. Synthetic GelMa lacks mechanical stability and therefore cannot support cell adhesion and attachment [9]. On the other hand, natural biomaterials have the potential to replicate the structure of extracellular matrices to promote cell growth, differentiation, and proliferation [10,11]. Being a gelatin-based bioink, GelMA can intrinsically resolve intricate vascular networks and channels while offering an endothelial cell microniche with the essential properties of native niches.
In addition to media rheology, the transient influx of culture media in the form of physiological flow has also been found to support media transport of chemical species while modulating compliance of the capillary wall [12,13,14,15]. These influx velocity profiles can generate optimized values of shear stress on the inner wall of the capillary vessel structure, thereby supporting cell growth [16,17]. Some studies have evaluated the effect of generic hemodynamic stress on the annular surface of straight and bifurcated tubular channels in the presence of physiological and sinusoidal flow [18,19]. These influx profiles have the capability to develop an adequate amount of stress on the luminal wall containing endothelial cells. Shear stress near the wall of a serpentine model can moderate the viability of cells. The proliferation rate of endothelial cells over a regenerative substrate (hydrogel) is more sensitive to stress distributive patterns [20]. It has been reported that regulated wall shear stress can enhance the growth of endothelial cells and their migration [21]. The interconnected points between the cytoskeleton and the topographical extracellular substrate are also influenced by distributed shear stress. It has been observed that vessel wall compliance of capillaries in the presence of stress enhances the migration properties of seeded cells. Thus, bioprinted serpentine structures with an elastic wall can be an ideal model for enhancing cell viability in the presence of transient influx of culture media.
The cumulative influence of media material properties (rheological), along with the transient influx, makes the assessment process of shear stress in serpentine models complicated [22,23]. Considering a non-Newtonian rheology of working media, the shear rate is elevated [24] at the bending phase (referring to the sine-wave pattern) of the serpentine structure [25]. This leads to a decrease in the driving pressure [26] and results in elevation of upstream pressure, damaging the smaller arterial blood vessels [27]. Hence, a corrective working pressure of 70 to 100 mmHg can be obtained for implementing pressure boundary conditions for serpentine flow. Blood viscosity increases when the shear rates decrease with increasing vascular diameter or with low flow.
In the present study, two different serpentine models (S1 and S2) were considered for capillary vessels. A numerical study was conducted to evaluate shear stress mapping on these serpentine models at the physiological boundary condition. Axial velocity pressure and shear rate were evaluated for these serpentine geometries. The material properties of GelMa hydrogels have been previously considered for their structured material properties in order to support cell proliferation [28]. Fluctuation in shear stress with time was evaluated in the form of oscillatory shear index (OSI), which captures the time integral functional form of shear stress near the wall. The OSI quantifies the endothelium’s directional preference to flow-induced shear stress. Hence, temporospatial patterns of the strain rate can be derived from OSI magnitudes. The higher magnitude of OSI at any point of the model contributes to a higher magnitude of executive pressure at that point. The residence period of OSI magnitude can be used to derive the relative residence time (RRT). RRT measures a particle’s residence time on the channel wall. It represents an inverse functionality to that of OSI, i.e., with an increase in OSI value, RRT magnitude decreases, attenuating the promotion of the particle–surface interaction site. Thus, RRT was also evaluated to quantize the regions of lower magnitudes of OSI.
2. Methodology
A two-dimensional CAD model of two different serpentine blood vessels was designed. The influence of fluid on the serpentine wall was realized by a fluid–solid interaction (FSI) module in COMSOL Multiphysics 5.5. Different hemodynamic parameters, namely, axial velocity and shear rate, OSI, RRT, and pressure gradient, were evaluated for two distinct inlet flow boundary conditions.
2.1. Numerical Analysis
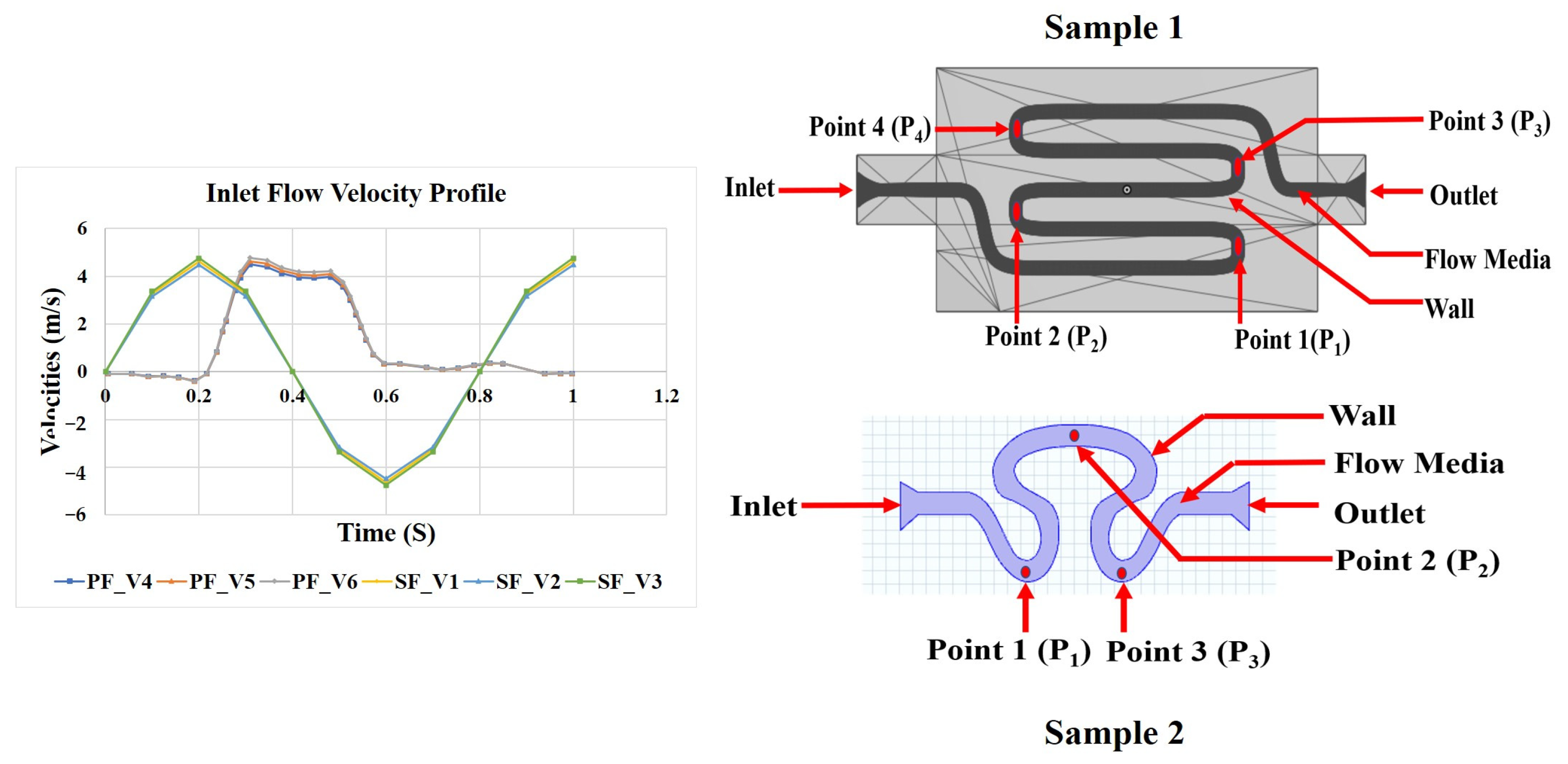
A schematic representation of two different serpentine channels is shown in Figure 1: S-shaped serpentine (model S1) and delta-shaped serpentine (model S2). It also shows the inlet flow boundary conditions, namely, pulsatile and sinusoidal. Mean arterial pressures of 80, 85, and 90 mmHg were considered for this study [29,30]. These pressure values were converted into their corresponding inlet velocities for serpentine geometries 1 and 2. Three different flow rates (corresponding to systolic, diastolic, and mean arterial pressure) based on the transient inlet velocity functions of sinusoidal (SF; V1, V2, and V3) and physiological (PF; V4, V5, and V6) were considered in the study [31]. The physiological functions (waveform) were derived from 4D Laser Doppler data of blood flow across the cross section of the subclavicular artery of a healthy subject. The study was approved by the Institute Ethical Committee (NITRR/IEC/2021/12). The obtained temporospatial functions were interpolated thereafter using the curve-fitting MATLAB 2021a toolbox. Further, the interpolated function with the lowest root mean square error (RMSE) value was selected for the study. The functions corresponding to the inlet flow velocity conditions for V1 to V6 are given in Table 1. One complete cycle of both sinusoidal and physiological flows is equivalent to the required simulation time, as represented by T [31]. Different study models were formulated for S1 and S2 as tabulated in Table 2.
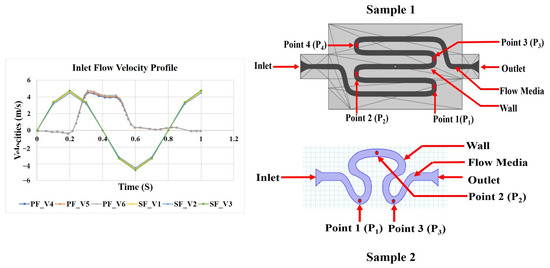
Figure 1.
Schematic diagram of the proposed serpentine model of 1 (length is not as per scale; Y1: 5 mm, Y2: 32 mm, Y3: 0.8 mm, Y4: 3 mm, Y5: 5 mm, Y6: 14 mm) and 2 (length is not as per scale; X1: 2.75 mm, X2: 2.75 mm, X3: 2.75 mm, X4: 0.8 mm, X5: 5 mm, X6: 9 mm) with different inlet velocity profiles.

Table 1.
Inlet flow velocity function for V1 to V6.

Table 2.
Different boundary conditions for the numerical study.
Fluid flow (with Newtonian and non-Newtonian viscosity formulations for blood equivalent) was evaluated for no-slip boundary conditions near the wall. The following properties of working fluid were used for numerical analysis at 300 K: density = 1066 kg/m3 and dynamic viscosity = 3.5 × 10−3 Pa·s. The wall of the serpentine channel was modeled using GelMA material properties (density = 1020 kg/m3, viscosity = 4.2 × 10−3 Pa·s, Young’s modulus = 3.18 KPa) and by considering the Newtonian viscosity formulation. The entire structure was filled with fluid.
The Navier–Stokes Equations (1) and (2) for non-Newtonian fluids are an extension of the classical equation and include additional parameters to accurately describe the non-Newtonian characteristics of the fluid. The parameters encompass the viscosity coefficient, which is now dependent on the shear rate or stress, and power-law indices, which quantify the fluid’s shear-thinning or shear-thickening characteristics. The viscosity coefficient quantifies the fluid’s opposition to flow, where larger values correspond to greater resistance. Meanwhile, the power-law indices govern the speed at which viscosity alters in response to applied stress. The parameters have physical significance as they are used to quantify the intricate flow characteristics of non-Newtonian fluids. They enable us to create models and gain insights into how these fluids react to external forces and shearing conditions. This is especially critical in other intricate fluids where precise forecasts are vital for optimizing flow patterns and the transport phenomena.
The Navier–Stokes equation was used to represent the momentum of the fluid model. Time-dependent partial differential equation of incompressible Navier–Stokes (Equation (1)) was used for the simulation [31,32]:
where is the fluid density, is the velocity vector, and is the dynamic viscosity. The non-Newtonian power-law formulation was also considered for evaluating the viscosity of the culture medium. The power-law viscosity model was represented by Equation (3), where η is the viscosity, n is the power-law constant, K is the flow consistency index, and is the shear strain rate (s−1). The n and K were selected as 0.66 [33] and 1, respectively, in the present study [34]:
Four different points corresponding to positions P1 (on rear region 1), P2 (on neck region 1), P3 (on rear region 2), and P4 (on neck region 2) were identified on sample 1. Similarly, for sample 2, three different points, P1, P2, and P3, were identified on the neck, abdominal, and rear region, respectively (as shown in Figure 1). These regions of samples 1 and 2 are the downstream region immediately after curvilinear orientation of the ascending and descending phases of the serpentine structure, and they are likely to be sensitive to vortex formation within the serpentine model. The pressure, axial velocity, and shear rate over an entire cardiac cycle (T) were evaluated at distinct set points of T/3, T/2, and T cycles.
One of the key factors affecting OSI is wall shear stress (WSS). A high OSI can result when the direction of WSS varies quickly over time as it does in oscillatory flows [35]. The WSS was calculated near the wall of the serpentine vascular channels using Equation (4):
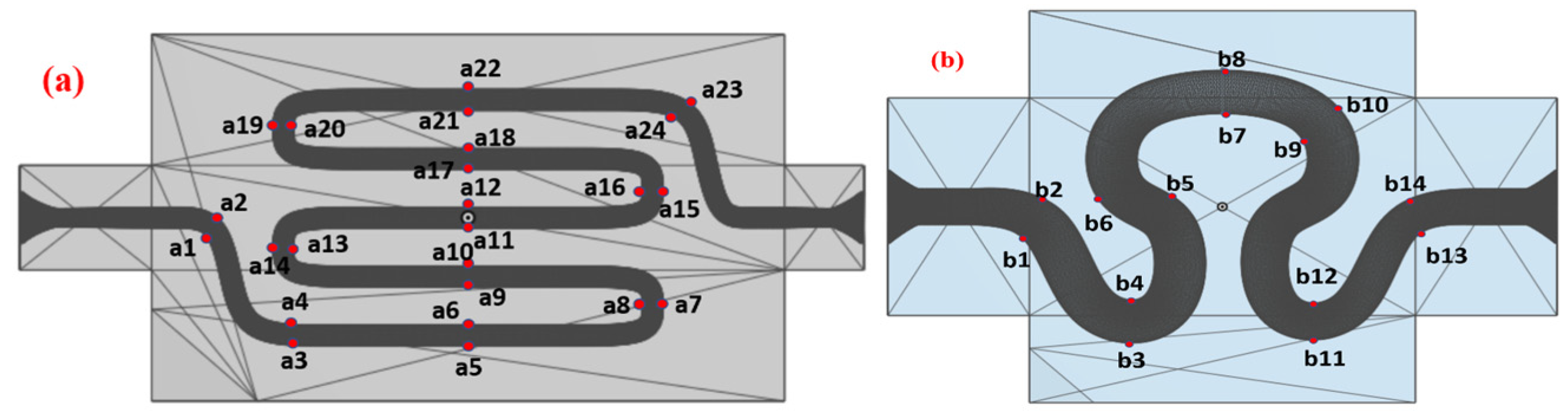
where = stress magnitude at all 24 and 13 points for samples 1 and 2, respectively.
The WSS was calculated for the no-slip wall boundary condition for both samples 1 and 2 for physiological flow for velocity model V6. The typical reason for selecting V6 was higher velocity magnitude compared to other velocity models as it leads to a higher velocity gradient near the wall, which in turn leads to maximum variation in the wall shear stress value. The time integral of WSS was calculated at different study points, as indicated in Figure 2. The WSS was measured at all 24 and 14 ROI points for samples 1 and 2, respectively, as the maximum WSS variation was observed at those points.
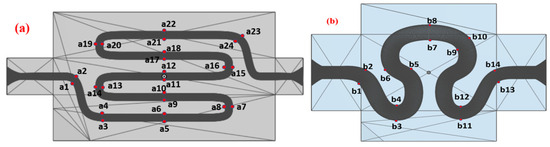
Figure 2.
Different points for WSS, OSI, and RRT calculation of (a) model S1 and (b) model S2.
The WSS plays a critical role in the development of OSI and can be a useful indicator of the hemodynamic forces. Significant variation of the WSS magnitude was used to evaluate the behavior of oscillatory shear index (OSI) [36]. In the present study, OSI was evaluated using Equation (5):
where T = total time cycle of cardiac impulse (or simulation duration).
The value of OSI at different study points for serpentine geometries 1 and 2 were computed using Equation (5).
The magnitude of WSS was influenced by the coaxial variation (curl) of the serpentine model. Unsteady flow behavior within the vascular structure was used to evaluate computational analysis time. The particle spent time [37] within the serpentine channel was estimated by relative residence time (RRT) using Equation (6):
From Equation (6), it can be observed that the RRT parameter includes the effects of both OSI and WSS [38].
Fluid flow and hemodynamic parameters were solved by COMSOL Multiphysics. Laminar flow and solid mechanics modules were used to evaluate these parameters. Fluid-Structure Interaction Multiphysics was used to establish the relationship between two physics. Fine element size was used for meshing the entire geometry with 0.2293 minimum element quality. The fluid–solid contact equation was solved using the Multifrontal Massively Parallel Solver (MUMPS) in COMSOL Multiphysics 5.5 [39]. The linearity of a system with real nonsymmetrical and symmetrical positive attributes can be analyzed using MUMPS [40]. MUMPS uses Gaussian elimination to resolve a linear equation based on sparse data used in a distributed memory system [41]. The following methods and termination parameters were used—nonlinear method: constant (Newton), termination technique: iteration or tolerance, and termination criteria: solution and residual. Sensitivity and uncertainty analyses were performed to observe the variability of the output parameters for different input parameters following previously used methods [31].
2.2. Grid Convergence Index
A grid convergence test was performed in order to establish the ideal grid size for the study, ensuring that the results were not influenced by the grid resolution. The grid convergence index (GCI) is a quantitative metric used to assess the level of convergence in a grid refinement study [42]. Both the serpentine models S1 and S2 were discretized using three distinct element sizes. This discretization was carried out for a sinusoidal flow with velocity V3. The pressure at point P1 was assessed for a duration of one complete cycle considering various sizes of elements. The order of convergence was evaluated using Equation (7).
The variables f1, f2, and f3 represent the parameter values of pressure at P1 for three distinct grid sizes. Based on the analysis of Equation (7), the variable p was determined and the refinement ratio ‘r’ was computed based on the grid spacing. Upon performing necessary calculations for the relevant parameters, the grid convergence index (GCI) was determined. The GCI was calculated using the Richardson extrapolation method, which relies on the estimation of the fractional error [42]. The GCI was calculated using Equation (8), and the results are listed in Table 3.

Table 3.
Order of accuracy and grid convergence index for the pressure variable.
3. Results
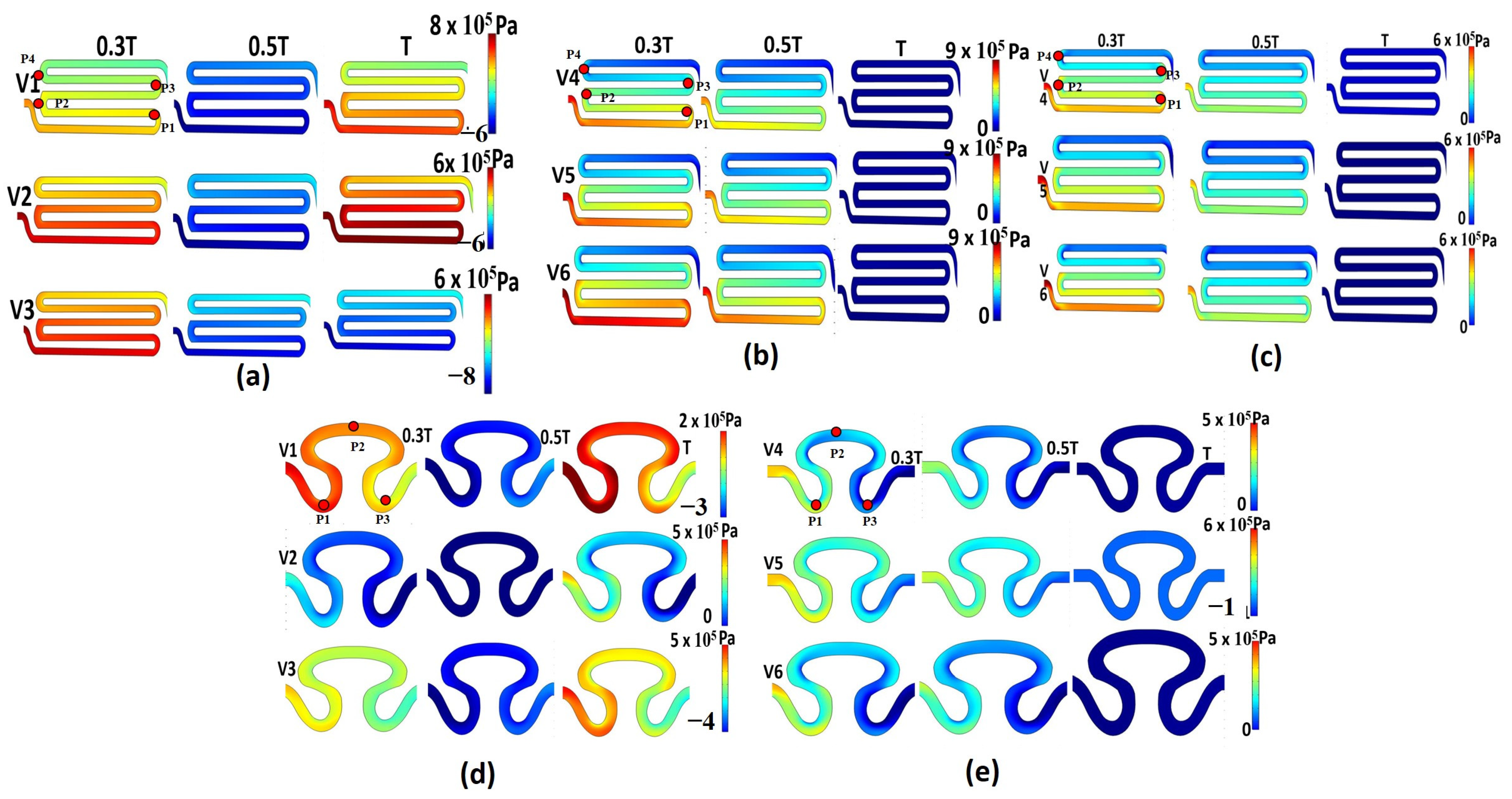
Hemodynamic parameters, including pressure, axial velocity, and shear rate, are important regulators that can impact cell growth. All S-shaped serpentine model analyses for the S1 model were grouped as I, II, and III, while the delta-shaped serpentine model analyses for the S2 model was grouped as conditions IV and V. No Newtonian study was added for the S2 model because the Newtonian model had shown significantly lower spatial variation for strain rate in comparison to non-Newtonian models in the S1 model. Hence, this model was not considered further in the study. Figure 3 represents the contour plot of pressure for all groups. For the non-Newtonian viscosity formulation with sinusoidal flow (model I, Table 2), maximum pressure of Pa and minimum pressure of were developed for inlet flow velocity condition V1 on its rear region 1 (P1) and neck region 2 (P2), respectively (refer to Figure 3a). It was observed that for all inlet velocity conditions in the S1 model, the pressure decreased as fluid flowed from the rear region 1 (P1) to the neck region 2 (P4) by the end of the complete cycle. This can be attributed to the development of localized Coriolis vortex formation due to the occurrence of abrupt angle of inclination on the downstream of the flow path. The contour plot of pressure for the non-Newtonian viscosity formulation with physiological flow (model II) is shown in Figure 3b. It was observed that in due course of time, the localized pressure value decreased with respect to space directed from the inlet to the outlet for inlet flow velocity conditions V4 and V5. For the Newtonian viscosity formulation with physiological flow (model III, Table 2), the magnitude of pressure was constant for all flow velocity conditions at the end of the study cycle. Maximum pressure of Pa was observed for all flow velocity conditions for model III (physiological flow with Newtonian viscosity of serpentine model 1, see Table 2). At the edge of neck region 1 (P2) of serpentine model S1 at the T/3 cycle, maximum pressures were identified, as shown in Figure 3c. The pressure contour of non-Newtonian viscosity formulation for sinusoidal flow of serpentine model S2 (model IV, refer Table 2) is shown in Figure 3d. It was observed that the maximum pressure gradient was obtained in the neck region P1 for inlet flow velocity conditions V2 and V3. Similarly, for inlet flow velocity condition V1, maximum pressure gradient of Pa was recorded in between the neck region (P1) and abdominal region (P2) of sample S2 at the end of the T cycle. For model V (physiological flow with non-Newtonian viscosity of serpentine model S2, refer Table 2), the contour plot showed pressure values ranging from Pa for inlet flow velocity condition V5 in the neck region P1, as shown in Figure 3e. For the other two flow velocities V4 and V6, the maximum pressure gradient was observed near the neck region P1. Overall, the results showed that for all flow boundary conditions, Newtonian fluid had a small pressure gradient, so it could easily flow through the channel. However, the pressure drop considering the non-Newtonian fluid flow formulation was substantially larger (Figure 3a,c). In contrast, the curvature of the fluid interface was maximum in the serpentine model S1, which produced a greater maximum pressure gradient compared to serpentine model S2, as shown in Figure 3a,d.
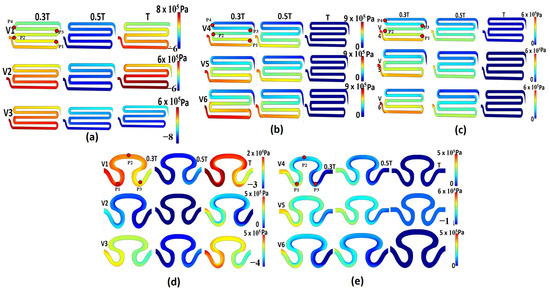
Figure 3.
Contour plot of pressure for different models: (a) model S1, non-Newtonian viscosity with sinusoidal flow; (b) model S1, non-Newtonian viscosity with physiological flow; (c) model S1, Newtonian viscosity with sinusoidal flow; (d) model S2, non-Newtonian viscosity with sinusoidal flow; (e) model S2, non-Newtonian viscosity with physiological flow.
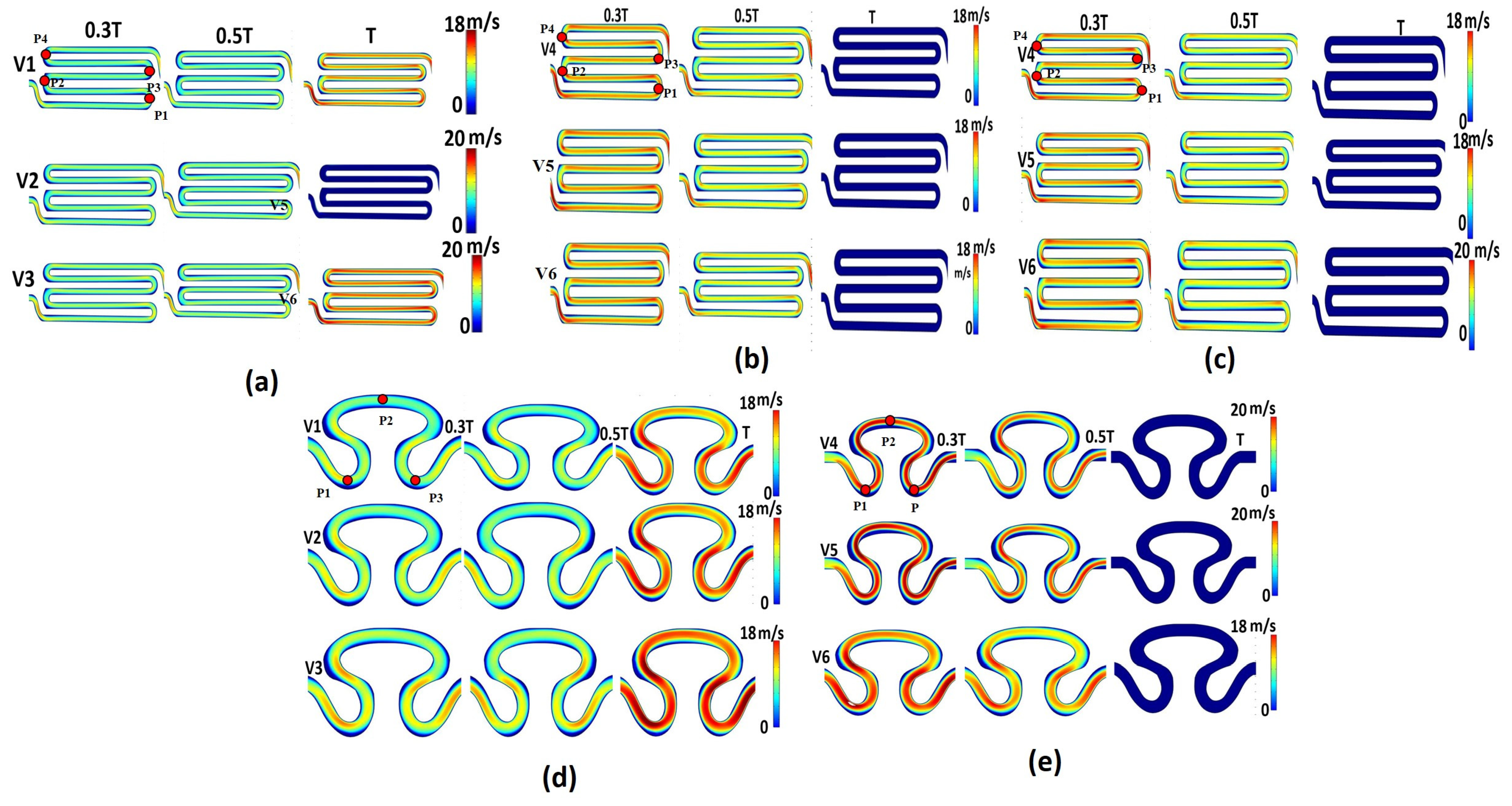
The flow pattern in a serpentine channel is not uniform, with areas of higher and lower pressure along its length. The channel geometry can influence the flow pattern, generating eddies or vortices, and change the axial velocity of fluid. The axial velocity contour profiles for all five models are shown in Figure 4. The magnitude of axial velocity for the non-Newtonian viscosity formulation with sinusoidal flow of sample S1 (model I, Table 2) was found to be maximum (20 mm/min) on the rear region (P1 and P2) and neck region (P1 and P2) for inlet flow velocity conditions V1 and V3 at the T cycle (Figure 4a). Similarly, the maximum (18 mm/min) velocity was observed at rear region P1 and the outlet region for inlet flow velocity V2. The contour profile of axial velocity of the non-Newtonian viscosity formulation with physiological flow of sample S1 (model II) had maximum axial velocity on the rear region (P1 and P2) and neck region (P1 and P2) at the T/3 time cycle, as shown in Figure 4b. From Figure 4c, it can be observed that the contour plot of axial velocity for the Newtonian viscosity formulation with physiological flow of serpentine model S1 (model III) was similar to the axial velocity obtained for the non-Newtonian viscosity formulation with physiological flow of serpentine model 2 (model V). Such observation might be due to the serpentine channel orientation effect, irrespective of the hematocrit model of the working fluid flowing through the serpentine channels. The maximum velocity (20 mm/min) for both models was developed for the V6 condition on the periphery of point P1 of both serpentine models at T/3 s. For the non-Newtonian viscosity formulation with sinusoidal flow of serpentine model S2, the local maximum axial velocity (18 mm/min) was recorded on the periphery of the neck region (P1) and the periphery of the rear region (P3 at the T cycle, as shown in Figure 4d). Similarly, for the non-Newtonian viscosity formulation with physiological flow of serpentine model S2, it was observed that variations in axial velocity were measured at T/3 and T/2 s for inlet flow velocity conditions V4, V5, and V6. As depicted in Figure 4e, the maximum axial velocity was generated on the periphery of the neck region (P1), abdominal region (P2), and rear region (P3) at T/3 for inlet flow velocity conditions V4 and V5. From Figure 4b,e, it can be seen that the serpentine model S1 tended to have lower axial velocities than serpentine model S2 due to the larger radius of the curvature. Similarly, it was observed that the non-Newtonian viscosity produced a greater maximum axial velocity compared to the Newtonian viscosity formulation, as shown in Figure 4b,c.
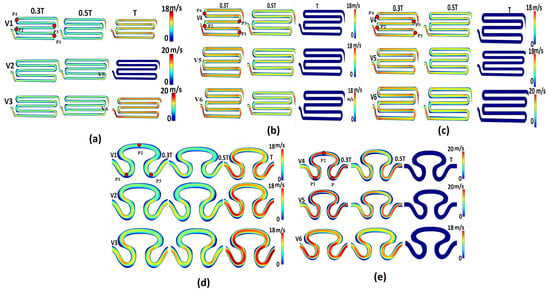
Figure 4.
Contour plot of axial velocity for different models: (a) model S1, non-Newtonian viscosity with sinusoidal flow; (b) model S1, non-Newtonian viscosity with physiological flow; (c) model S1, Newtonian viscosity with sinusoidal flow; (d) model S2, non-Newtonian viscosity with sinusoidal flow; (e) model S2, non-Newtonian viscosity with physiological flow.
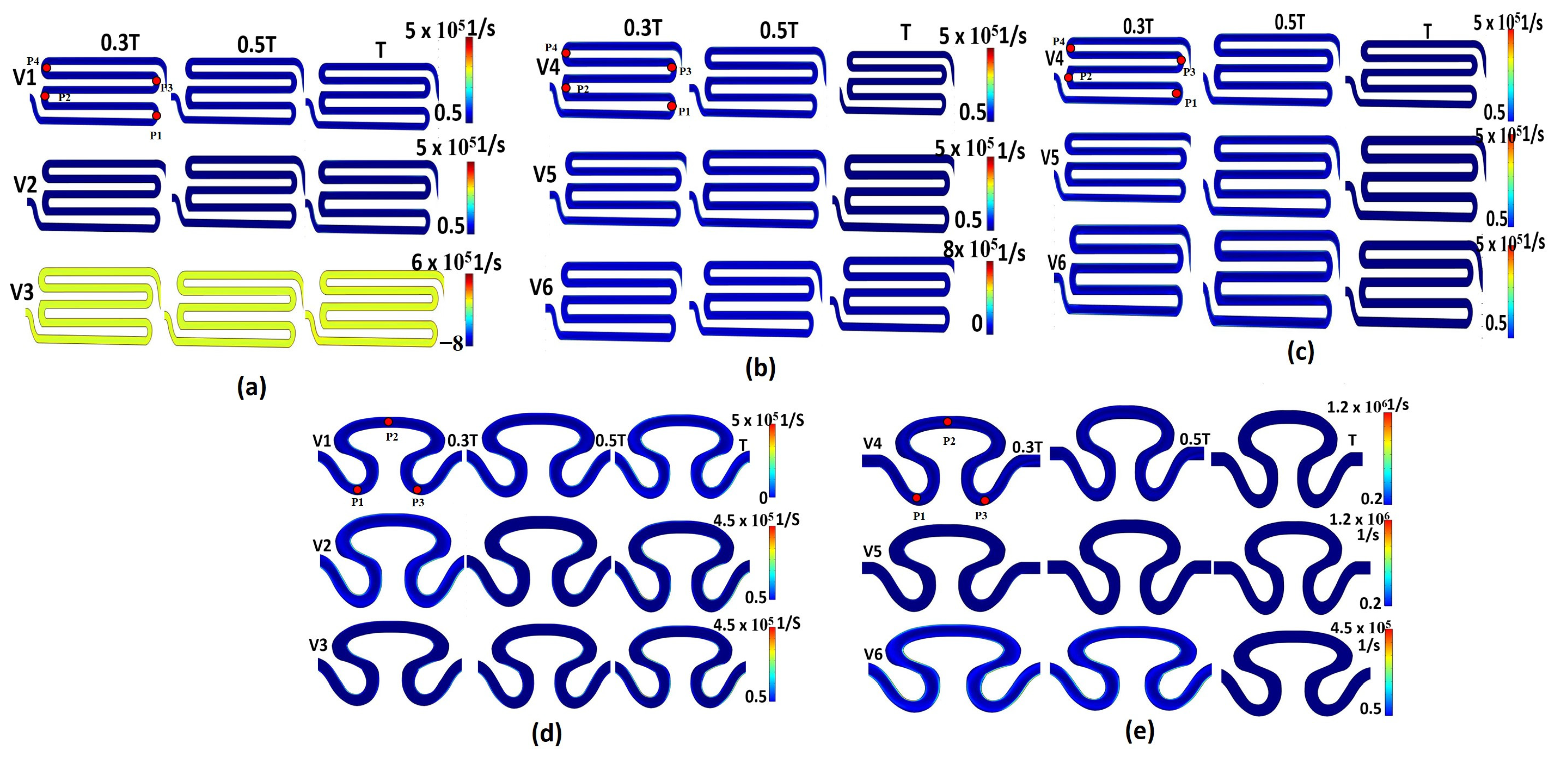
The gradients in axial velocity were also evaluated in the form of shear rate. The variation of axial velocity for the Newtonian and non-Newtonian viscosity formulations induced a significant fluctuation in the shear rate. Evaluation of the shear rate close to the wall of the lumen is crucial for many physiological processes. Changes in the shear rate close to a wall can influence how well cells adhere to that surface. Figure 5a shows the contour plots of the shear rate for all models. The non-Newtonian viscosity formulation with sinusoidal flow of serpentine model S1 (model I, Table 2) resulted in a greater maximum shear rate (6 ) for inlet flow velocity condition V3 compared to inlet flow conditions V1 and V2. This maximum (6 ) shear rate was obtained in the rear region P1 for the T/3, T/2, and T cycles. A contour plot of shear rate of the non-Newtonian viscosity formulation with physiological flow of serpentine model S2 is shown in Figure 5b. Local minima and maxima shear rate magnitude were observed for inlet flow velocity condition V6 (0.5 and 8 ) near the wall of the rear region 1 of serpentine model S1 after one complete cycle. The contour plot of the Newtonian viscosity formulation with physiological flow of serpentine model S1 showed the maximum shear rate () in the neck region 2 and rear region 1 at the T/3 and T/2 cycles for inlet flow boundary condition V5 (Figure 5c). For the non-Newtonian viscosity formulation with sinusoidal flow of serpentine model S2, the maximum shear rate () was observed for inlet flow velocity condition V1 near the rear region (P3) at the T cycle, as shown in Figure 5d. The contour plot of shear rate for the non-Newtonian viscosity formulation of physiological flow of serpentine model S2 is shown in Figure 5e. It was observed that there was significant variation in the shear rate contour profile for inlet flow condition V6 in the periphery of the abdominal region (P2) at the T/2 cycle. From Figure 5b,c, it can be observed that the non-Newtonian formulation exhibited a greater maximum shear rate at the end of the T cycle compared to the Newtonian viscosity formulation. In comparison to serpentine model S2, the maximum shear rate was produced by serpentine model S1 due to the formation of eddies.

Figure 5.
Contour plot of shear rate for different models: (a) model S1, non-Newtonian viscosity with sinusoidal flow; (b) model S1, non-Newtonian viscosity with physiological flow; (c) model S1, Newtonian viscosity with sinusoidal flow; (d) model S2, non-Newtonian viscosity with sinusoidal flow; (e) model S2, non-Newtonian viscosity with physiological flow.
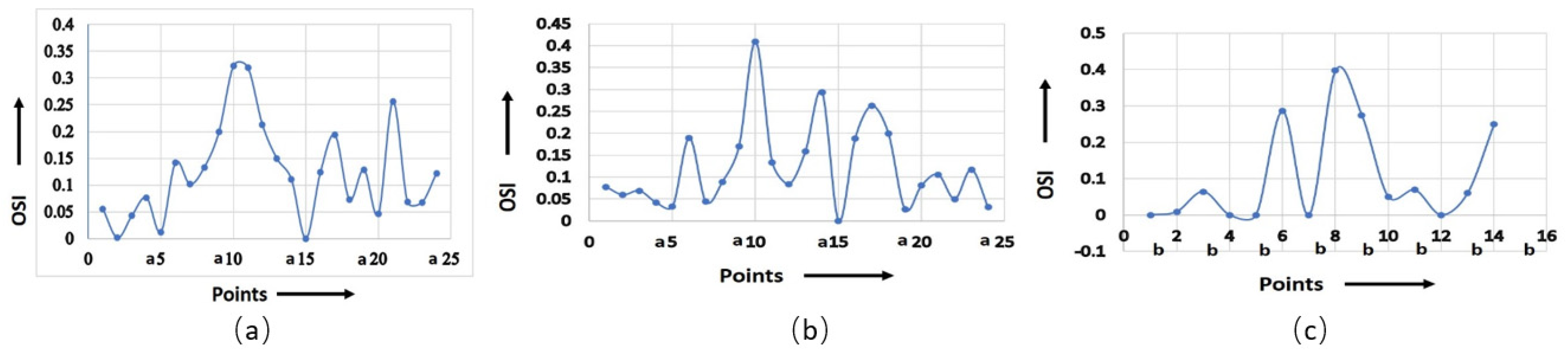
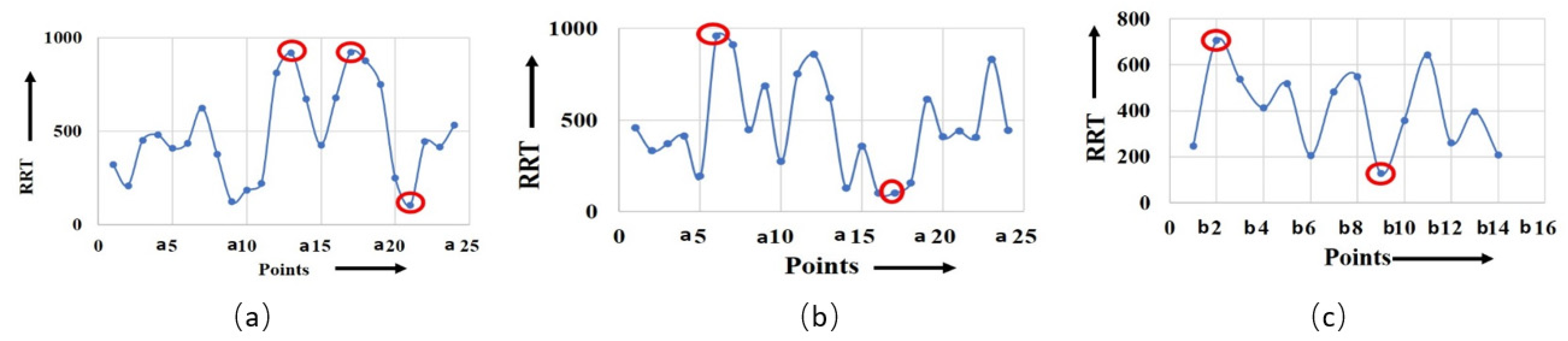
The shear rate is a crucial factor that influences the OSI value. As the shear rate increases, the material experiences higher deformation and viscous dissipation, resulting in higher flow asymmetry as well as OSI value. However, the relationship between the shear rate and OSI value is dependent on various material properties, i.e., viscoelasticity, atomic weight, concentration, and temperature of the working fluid. It was observed that the maximum OSI was obtained at point a10 for the non-Newtonian viscosity formulation of serpentine model S1, as shown in Figure 6a,b. Figure 6c shows the maximum OSI (0.4) at point b8 for the non-Newtonian viscosity formulation for serpentine model S2. The rate of change in OSI was maximum for point a10 for the non-Newtonian and Newtonian viscosity formulations in serpentine model S1, whereas the maximum rate of change in OSI was observed for point b8 for the non-Newtonian viscosity formulation in serpentine model S2. There was a positive correlation between OSI and RRT. The regions with low OSI tended to have longer RRTs, indicating that fluid elements reside longer in these regions prior to leaving. This is due to the fact that low OSI regions are typically associated with regions of flow separation and recirculation, where fluid is confined and complex flow patterns occur. Figure 7a demonstrates that the maximum (910) and minimum (100) magnitudes of RRT were measured for the Newtonian viscosity of serpentine model S1 at points a17 and a21, respectively. Similarly, for the non-Newtonian viscosity formulation of serpentine model S1, the maximum (950) and minimum (100) magnitudes of RRT were measured for points a6 and a17, respectively (Figure 7b). For serpentine model S2, the maximum (700) and minimum (110) magnitude of RRT were produced at b2 and b9 points, respectively, as shown in Figure 7c. From Figure 7b,c, it can be seen that the maximum RRT magnitude of serpentine model S1 was higher in comparison to serpentine model S2 due to surface tension, which caused particles to adhere to the wall of the channel. The RRT values for serpentine model S1 was higher in the regions for ¼ length of the channel from the inlet and outlet. In addition to that, the RRT curve of the non-Newtonian viscosity formulation of serpentine model S1 showed maximum negative gradient, while the serpentine model S2 had the maximum positive gradient. A big difference in RRT between the upper and lower walls was observed at points a11 and a12 for the Newtonian viscosity formulation in serpentine model S1. Similarly, the maximum RRT difference was observed at points a5 and a6 for a non-Newtonian viscosity formulation of serpentine model S1. Serpentine model S2 showed the maximum RRT difference at points b1 and b2 for non-Newtonian viscosity.
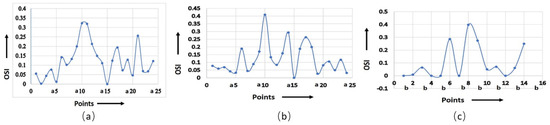
Figure 6.
Calculated OSI for (a) model S1, Newtonian; (b) model S1, non-Newtonian; (c) model S2, non-Newtonian.
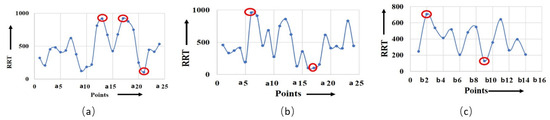
Figure 7.
Calculated RRT for (a) model S1, Newtonian; (b) model S1, non-Newtonian; (c) model S2, non-Newtonian. The highlighted points show the maximum and minimum magnitude of RRT for respective models.
Deviations in hemodynamic parameters, including pressure, axial velocity, and shear rate, are presented in Table 3. The maximum and minimum deviation of pressure was reported for V4 and V6 inlet flow conditions at points P1 and P2, respectively, at the end of one complete flow cycle in the S2 model. Maximum deviation in axial velocity was observed for the V6 inlet flow condition at point P2 during the T/2 flow cycle in model II (as shown in Table 4). From the above observation, it was found that the maximum deviations of pressure (39.98%), axial velocity (25.8%), and shear rate (70.15%) were obtained for the non-Newtonian viscosity formulation with physiological flow for serpentine model S2 near point P2 at the T and T/2 cycles.

Table 4.
Calculated deviation for pressure, shear rate, and velocity.
4. Discussion
Variations in working fluid rheology, orientation of serpentine geometry, and the flow architecture of the working fluid at different regions of the serpentine vascular channel significantly affected the distribution of pressure, axial velocity, and shear rate of the flowing fluid. Dean number was employed to develop a relationship between the flow rate and the fluctuating fluid pressure in a curved channel [43,44]. For models I and III, the maximum downstream pressure was developed at the end of one complete cycle due to fully developed flow [45,46]. In microchannels [47,48], the flow restriction parameter R depended on the channel length, which caused maximum pressure to be generated at the inlet region for the case of the non-Newtonian viscosity formulation with sinusoidal and physiological flows in serpentine models S1 and S2. For the non-Newtonian formulation with physiological flow of serpentine model 2, minimal variations in the magnitude of the flow parameters were found due to insignificant variation of the pressure gradient at different flow fluxes.
Variations in the pressure gradient influenced the axial velocity for different study configurations. In the case of transient analysis, the maximum variations in axial velocity distribution were observed at the end of the complete cycle in models II and V. Serpentine structure, along with the rheology of the media, could be the cause of such a phenomenon [49]. For the non-Newtonian formulation with physiological flow in serpentine model S2 (model V), axial velocity near the wall stopped [50]. It was observed that for most of the conditions, the velocity variation was maximum at the T/3 flow cycle because the curvilinear shape of the proposed serpentine structures reduced the kinetic energy of the flowing particles with the development of the flow. Due to specific orientation of the serpentine conduits, fluid particles obtained higher kinetic energy at the initial flow phase T/3, and the particles therefore had higher velocity in the presence of maximum magnitude of pressure gradient in both the Newtonian and non-Newtonian viscosity formulations with physiological flow in the serpentine model S2 [51,52].
Variations in the axial velocity of fluid influenced the shear rate distribution inside the channel. For the non-Newtonian viscosity model with sinusoidal flow in serpentine model S1, the parabolic profile of the velocity distribution promoted particles to have prolonged attachment on the walls, resulting in higher magnitude of localized shear rate [53]. For models II, III, IV, and V, a minimal variation in shear rate was found due to a nominal variation in axial velocity with respect to the luminal radius of the serpentine channel [54,55].
Pressure gradient profiles were found to be heterogeneous in serpentine models. It resulted in the generation of distinct localized discrete axial vorticity (as shown in Table 4). The development of localized vortices due to the serpentine model was responsible for maximum velocity deviation, leading to the development of radial pressure gradient [56,57]. Furthermore, elevated radial pressure gradient influenced the radial flow of the media, thereby enhancing deviation in the shear rate of adjacent regions. Different flow waveforms (sinusoidal and physiological) altered the distribution of fluid particles in dynamic flow. It resulted in generation of maximum shear rate variation [58,59]. Narrow conduits of flow channel in between two adjacent serpentine structures promoted the development of uniform shear rate [60] with minimal variation. Corners and bending structures complicated fluid flow structures through the microchannel. It resulted in recirculation or flow separation. These complex flow patterns caused variations in the residence time of the fluid [61,62]. Since, the power-law model was used to represent the non-Newtonian nature of the fluid flow, the flow rate was not linear in relation to the applied shear stress, thereby affecting the RRT distribution.
Higher values of OSI in the non-Newtonian fluid formulation was due to the presence of nonlinearity in the rheological behavior of the non-Newtonian viscosity fluid. At point a10 for the non-Newtonian viscosity formulation of serpentine model S2, the shear rate was higher, which enhanced the power-law index, causing an increase in the OSI magnitude. In the case of Newtonian fluid, the shear stress and shear rate were in phase, which restricted the fluctuation of OSI [14,63]. In serpentine model S1, the central axis had greater degree of curvature in comparison to serpentine model S2. Hence, the direction of the flow changed gradually. Minute changes in flow direction made it less likely for the flow profile to split and create eddies. Hence, it had smoother flow with lower OSI values. In addition to the serpentine model S2, the flow path was also divided into multiple channels. The flow then recombined in the downstream region. Formation of multiple channels disturbed the flow patterns [64] and flow separation, leading to increased flow variation and elevated OSI values. The fluid’s surface tension was responsible for the creation of menisci at the corners of serpentine model S1, resulting in a change in the flow pattern and velocity of the fluid, which increased the RRT value [65,66].
5. Conclusions
Hemodynamic properties of biofluid, such as pressure, axial velocity, and shear rate, were found to play an essential role in inducing physiological behavior and promoting cell adhesion properties under in vitro conditions on the inner lining of a serpentine plane. Fluid in the serpentine channel generated longitudinal stress, which in turn influenced cellular functionality. This numerical analysis evaluated the impact of Newtonian and non-Newtonian viscosity models on various fluid dynamic parameters of the culture media–serpentine wall interaction. Simultaneously, the local maxima and minima of different hemodynamic parameters were identified at specified regions of the serpentine models (model S1: points P1 to P4; model S2: points P1 to P3) as potential slots of effective cellular proliferative zones over the inner lining of the serpentine channel. It was observed that the non-Newtonian viscosity formulation possessed maximum variation in rheological properties compared to the Newtonian viscosity model. In comparison to serpentine model S2, the formation of eddies within serpentine model S1 was more frequent. It produced maximum variation in pressure, axial velocity, and shear rate. OSI and RRT distribution mapping also provided suitable marked regions in serpentine model S1 and S2, which could support maximum growth of cells.
Author Contributions
Writing—original draft, K.D.; Writing—review & editing, K.M. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
The author would like to acknowledge partial funding from NASA Florida Space Grant Program and “SPARC [SPARC/2018-2019/140/SL (IN)]” for this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kittler, H.; Riedl, E.; Rosendahl CAnd Cameron, A. Dermatoscopy of unpigmented lesions of the skin: A new classification of vessel morphology based on pattern analysis. Dermatopathol. Pract. Concept. 2008, 14, 3. [Google Scholar]
- Tomasina, C.; Bodet, T.; Mota, C.; Moroni, L.; Camarero-Espinosa, S. Bioprinting vasculature: Materials, cells and emergent techniques. Materials 2019, 12, 2701. [Google Scholar] [CrossRef] [PubMed]
- Camasão, D.B.; Mantovani, D.J.M.T.B. The mechanical characterization of blood vessels and their substitutes in the continuous quest for physiological-relevant performances. A critical review. Mater. Today Bio 2021, 10, 100106. [Google Scholar] [CrossRef] [PubMed]
- Bit, A.; Alblawi, A.; Chattopadhyay, H.; Quais, Q.A.; Benim, A.C.; Rahimi-Gorji, M.; Do, H.T. Three dimensional numerical analysis of hemodynamic of stenosed artery considering realistic outlet boundary conditions. Comput. Methods Programs Biomed. 2020, 185, 105163. [Google Scholar] [CrossRef]
- Wang, D.; Xu, Y.; Li, Q.; Turng, L.S. Artificial small-diameter blood vessels: Materials, fabrication, surface modification, mechanical properties, and bioactive functionalities. J. Mater. Chem. B 2020, 8, 1801–1822. [Google Scholar] [CrossRef]
- Bertassoni, L.E.; Cecconi, M.; Manoharan, V.; Nikkhah, M.; Hjortnaes, J.; Cristino, A.L.; Barabaschi, G.; Demarchi, D.; Dokmeci, M.R.; Yang, Y.; et al. Hydrogel bioprinted microchannel networks for vascularization of tissue engineering constructs. Lab Chip 2014, 14, 2202–2211. [Google Scholar] [CrossRef] [PubMed]
- Nie, J.; Gao, Q.; Wang, Y.; Zeng, J.; Zhao, H.; Sun, Y.; Shen, J.; Ramezani, H.; Fu, Z.; Liu, Z.; et al. Vessel-on-a-chip with hydrogel-based microfluidics. Small 2018, 14, 1802368. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, M.; Zhang, Y.; Yin, J.; Pei, R. Nanocomposite hydrogels for tissue engineering applications. Nanoscale 2020, 12, 14976–14995. [Google Scholar] [CrossRef]
- Shukla, P.; Mitruka, M.; Pati, F. The effect of the synthetic route on the biophysiochemical properties of methacrylated gelatin (GelMA) based hydrogel for development of GelMA-based bioinks for 3D bioprinting applications. Materialia 2022, 25, 101542. [Google Scholar] [CrossRef]
- Ahmed, E.M. Hydrogel: Preparation, characterization, and applications: A review. J. Adv. Res. 2015, 6, 105–121. [Google Scholar] [CrossRef]
- Sun, W.; Gregory, D.A.; Tomeh, M.A.; Zhao, X. Silk fibroin as a functional biomaterial for tissue engineering. Int. J. Mol. Sci. 2021, 22, 1499. [Google Scholar] [CrossRef] [PubMed]
- Miah, M.; Karim, A. Computational Investigation of Pulsatile Blood Flow in the Models of Arterial Stenosis and Aneurysm. Ph.D. Dissertation, Department of Mechanical and Production Engineering (MPE), Islamic University of Technology (IUT), Gazipur, Bangladesh, 2018. [Google Scholar]
- Tiwari, A.; Chauhan, S.S. Effect of varying viscosity on two-layer model of pulsatile flow through blood vessels with porous region near walls. Transp. Porous Media 2019, 129, 721–741. [Google Scholar] [CrossRef]
- Dincau, B.; Dressaire, E.; Sauret, A. Pulsatile flow in microfluidic systems. Small 2020, 16, 1904032. [Google Scholar] [CrossRef] [PubMed]
- Zamir, M.; Budwig, R.S. Physics of pulsatile flow. Appl. Mech. Rev. 2002, 55, B35. [Google Scholar] [CrossRef]
- Hsiai, T.K.; Cho, S.K.; Honda, H.M.; Hama, S.; Navab, M.; Demer, L.L.; Ho, C.M. Endothelial cell dynamics under pulsating flows: Significance of high versus low shear stress slew rates (∂ τ/∂ τ). Ann. Biomed. Eng. 2002, 30, 646–656. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.W.; Kim, D.H.; Lee, J.H.; Youn, Y.N. The effect of pulsatile flow on bmsc-derived endothelial-like cells in a small-sized artificial vessel made by 3-dimensional bioprinting. Stem Cells Int. 2018, 2018, 7823830. [Google Scholar] [CrossRef] [PubMed]
- Hendriks, M.; Ramasamy, S.K. Blood vessels and vascular niches in bone development and physiological remodeling. Front. Cell Dev. Biol. 2020, 8, 602278. [Google Scholar] [CrossRef]
- Dessalles, C.A.; Leclech, C.; Castagnino, A.; Barakat, A.I. Integration of substrate-and flow-derived stresses in endothelial cell mechanobiology. Commun. Biol. 2021, 4, 764. [Google Scholar] [CrossRef]
- Buchanan, C.F.; Verbridge, S.S.; Vlachos, P.P.; Rylander, M.N. Flow shear stress regulates endothelial barrier function and expression of angiogenic factors in a 3D microfluidic tumor vascular model. Cell Adhes. Migr. 2014, 8, 517–524. [Google Scholar] [CrossRef]
- Souilhol, C.; Serbanovic-Canic, J.; Fragiadaki, M.; Chico, T.J.; Ridger, V.; Roddie HAnd Evans, P.C. Endothelial responses to shear stress in atherosclerosis: A novel role for developmental genes. Nat. Rev. Cardiol. 2020, 17, 52–63. [Google Scholar] [CrossRef]
- Tokas, S. Performance Analysis of Simple-t and 3dhelical Passive Micromixers with Newtonian and Non-Newtonian Fluid. Ph.D. Dissertation, Delhi Technological University, Delhi, India, 2020. [Google Scholar]
- Lee, E.; Kim BAnd Choi, S. Hand-held, automatic capillary viscometer for analysis of Newtonian and non-Newtonian fluids. Sens. Actuators A Phys. 2020, 313, 112176. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Tiwari, A. Solute dispersion in non-Newtonian fluids flow through small blood vessels: A varying viscosity approach. Eur. J. Mech.-B/Fluids 2022, 94, 200–211. [Google Scholar] [CrossRef]
- Mehri, R.; Mavriplis, C.; Fenech, M. Red blood cell aggregates and their effect on non-Newtonian blood viscosity at low hematocrit in a two-fluid low shear rate microfluidic system. PLoS ONE 2018, 13, e0199911. [Google Scholar] [CrossRef]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef] [PubMed]
- Leone, M.; Asfar, P.; Radermacher, P.; Vincent, J.L.; Martin, C. Optimizing mean arterial pressure in septic shock: A critical reappraisal of the literature. Crit. Care 2015, 19, 101. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Han, S.H.; Kook, Y.M.; Lee, K.M.; Jin, Y.Z.; Koh, W.G.; Lee, J.H.; Lee, K. A novel 3D indirect co-culture system based on a collagen hydrogel scaffold for enhancing the osteogenesis of stem cells. J. Mater. Chem. B 2020, 8, 9481–9491. [Google Scholar] [CrossRef] [PubMed]
- Demers, D.; Wachs, D. Physiology, mean arterial pressure. In Statpearls [Internet]; Statpearls Publishing: St. Petersburg, FL, USA, 2019. [Google Scholar]
- Papaioannou, T.G.; Protogerou, A.D.; Vrachatis, D.; Konstantonis, G.; Aissopou, E.; Argyris, A.; Nasothimiou, E.; Gialafos, E.J.; Karamanou, M.; Tousoulis, D.; et al. Mean arterial pressure values calculated using seven different methods and their associations with target organ deterioration in a single-center study of 1878 individuals. Hypertens. Res. 2016, 39, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, K.; Gupta, S.; Mitra, K.; Bit, A. Numerical and Experimental Analysis of Shear Stress Influence on Cellular Viability in Serpentine Vascular Channels. Micromachines 2022, 13, 1766. [Google Scholar] [CrossRef]
- Guo, B.; Guo, C. The convergence of non-Newtonian fluids to Navier–Stokes equations. J. Math. Anal. Appl. 2009, 357, 468–478. [Google Scholar] [CrossRef][Green Version]
- Gangawane, K.M.; Manikandan, B. Laminar natural convection characteristics in an enclosure with heated hexagonal block for non-Newtonian power law fluids. Chin. J. Chem. Eng. 2017, 25, 555–571. [Google Scholar] [CrossRef]
- Dejam, M. Dispersion in non-Newtonian fluid flows in a conduit with porous walls. Chem. Eng. Sci. 2018, 189, 296–310. [Google Scholar] [CrossRef]
- Basavaraja, P.; Surendran, A.; Gupta, A.; Saba, L.; Laird, J.R.; Nicolaides, A.; Mtui, E.E.; Baradaran, H.; Lavra, F.; Suri, J.S. Wall shear stress and oscillatory shear index distribution in carotid artery with varying degree of stenosis: A hemodynamic study. J. Mech. Med. Biol. 2017, 17, 1750037. [Google Scholar] [CrossRef]
- Sotelo Parraguez, J.A.; Urbina, J.; Valverde, I.; Tejos Nunez, C.A.; Irarrázaval Mena, P.; Andia Kohnenkampf, M.E.; Uribe Arancibia, S.A.; Hurtado Sepulveda, D.E. 3D Quantification of Wall Shear Stress and Oscillatory Shear Index Using a Finite-Element Method in 3D CINE PC-MRI Data of the Thoracic Aorta. IEEE Trans. Med. Imaging 2016, 35, 1475–1487. [Google Scholar] [CrossRef]
- Soulis, J.V.; Lampri, O.P.; Fytanidis, D.K.; Giannoglou, G.D. Relative residence time and oscillatory shear index of non-Newtonian flow models in aorta. In Proceedings of the 2011 10th International Workshop on Biomedical Engineering, Kos, Greece, 5–7 October 2011; pp. 1–4. [Google Scholar]
- Mutlu, O.; Salman, H.E.; Al-Thani, H.; El-Menyar, A.; Qidwai, U.A.; Yalcin, H.C. How does hemodynamics affect rupture tissue mechanics in abdominal aortic aneurysm: Focus on wall shear stress derived parameters, time-averaged wall shear stress, oscillatory shear index, endothelial cell activation potential, and relative residence time. Comput. Biol. Med. 2023, 154, 106609. [Google Scholar] [CrossRef] [PubMed]
- Braga da Costa Campos, L.M. Steady Heat Conduction. Complex Anal. Appl. Flows Fields 2020, 388, 607–634. [Google Scholar] [CrossRef]
- Sterling, T.; Brodowicz, M.; Anderson, M. High Performance Computing: Modern Systems and Practices; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar]
- Amestoy, P.; Buttari, A.; Duff, I.; Guermouche, A.; L’Excellent, J.Y.; Uçar, B. Encyclopedia of Parallel Computing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–15. [Google Scholar] [CrossRef]
- Bit, A.; Chattopadhyay, H. Numerical investigations of pulsatile flow in stenosed artery. Acta Bioeng. Biomech. 2014, 16, 33–44. [Google Scholar] [PubMed]
- Hoque, M.M.; Alam, M.M. Effects of Dean number and curvature on fluid flow through a curved pipe with magnetic field. Procedia Eng. 2013, 56, 245–253. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Cai, Y.; Wang, B.; Luo, X. A cost-effective serpentine micromixer utilizing ellipse curve. Anal. Chim. Acta 2021, 1155, 338355. [Google Scholar] [CrossRef]
- Shen, F.; Ai, M.; Ma, J.; Li, Z.; Xue, S. An easy method for pressure measurement in microchannels using trapped air compression in a one-end-sealed capillary. Micromachines 2020, 11, 914. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X. Numerical analysis of the flow and heat transfer characteristics in serpentine microchannel with variable bend amplitude. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2022–2041. [Google Scholar] [CrossRef]
- Andersson, M. Microfluidics at High Pressures: Understanding, Sensing, and Control. Ph.D. Dissertation, Acta Universitatis Upsaliensis, Uppsala, Sweden, 2018. [Google Scholar]
- Hazar, H.; Yilmaz, M.; Sevinc, H. A comparative analysis of a novel flow field pattern with different channel size configurations. Fuel 2022, 319, 123867. [Google Scholar] [CrossRef]
- Jha, B.K.; Malgwi, P.B. Computational analysis on unsteady hydromagnetic Couette flow of fluid—Particle suspension in an accelerated porous channel. Partial. Differ. Equ. Appl. Math. 2022, 5, 100370. [Google Scholar] [CrossRef]
- Rahmati, A.R.; Akbari, O.A.; Marzban, A.; Toghraie, D.; Karimi, R.; Pourfattah, F. Simultaneous investigations the effects of non-Newtonian nanofluid flow in different volume fractions of solid nanoparticles with slip and no-slip boundary conditions. Therm. Sci. Eng. Prog. 2018, 5, 263–277. [Google Scholar] [CrossRef]
- Qin, R.; Duan, C. The principle and applications of Bernoulli equation. J. Phys. Conf. Ser. 2017, 916, 012038. [Google Scholar] [CrossRef]
- Quetzeri-Santiago, M.A.; Hunter, I.W.; van der Meer, D.; Rivas, D.F. Impact of a microfluidic jet onto a pendant droplet. arXiv 2021, arXiv:2105.12361. [Google Scholar]
- Benoit, C. Re: Why is the Shear Stress Maximum at the Walls of a Microfluidic Device? Available online: https://www.researchgate.net/post/Why-is-the-shear-stress-maximum-at-the-walls-of-a-microfluidic-device/59f6fe9d404854506c67f2a3/citation/download (accessed on 22 August 2023).
- Sun, P.; Zhou, L.; Wang, Z.; Shi, J. Influences of geometric parameters on serpentine nozzles for turbofan. Aerosp. Sci. Technol. 2023, 136, 108224. [Google Scholar] [CrossRef]
- Abed, W.M.; Whalley, R.D.; Dennis, D.J.; Poole, R.J. Experimental investigation of the impact of elastic turbulence on heat transfer in a serpentine channel. J. Non-Newton. Fluid Mech. 2016, 231, 68–78. [Google Scholar] [CrossRef]
- Dutta, P.; Nandi, N. Effect of bend curvature on velocity & pressure distribution from straight to a 90° pipe bend-A Numerical Study. REST J. Emerg. Trends Model. Manuf. 2016, 2, 103–108. Available online: www.restpublisher.com/journals/jemm (accessed on 22 August 2023).
- Ionescu, V. Numerical modeling of centrifugal microfluidic flow in rectangular channels for Lab-on-a-CD platform applications. In Advanced Topics in Optoelectronics, Microelectronics and Nanotechnologies X (Vol. 11718, 289-299); SPIE: Washington, DC, USA, 2020. [Google Scholar]
- Amaratunga, M.; Rabenjafimanantsoa, H.A.; Time, R.W. Estimation of shear rate change in vertically oscillating non-Newtonian fluids: Predictions on particle settling. J. Non-Newton. Fluid Mech. 2020, 277, 104236. [Google Scholar] [CrossRef]
- Yang, H.; Yao, G.; Wen, D. Experimental investigation on convective heat transfer of Shear-thinning fluids by elastic turbulence in a serpentine channel. Exp. Therm. Fluid Sci. 2020, 112, 109997. [Google Scholar] [CrossRef]
- Hamedi, N.; Revstedt, J.; Tornberg, E.; Innings, F. Application of CFD-based correction factors to increase the accuracy of flow curve determination in a couette rheometer. Appl. Rheol. 2016, 26, 35341. [Google Scholar] [CrossRef]
- Ducloué, L.; Casanellas, L.; Haward, S.J.; Poole, R.J.; Alves, M.A.; Lerouge, S.; Shen, A.Q.; Lindner, A. Secondary flows of viscoelastic fluids in serpentine microchannels. Microfluid. Nanofluidics 2019, 23, 33. [Google Scholar] [CrossRef]
- Poole, R.J.; Lindner, A.; Alves, M.A. Viscoelastic secondary flows in serpentine channels. J. Non-Newton. Fluid Mech. 2013, 201, 10–16. [Google Scholar] [CrossRef]
- Del Giudice, F. A review of microfluidic devices for rheological characterisation. Micromachines 2022, 13, 167. [Google Scholar] [CrossRef]
- Thurgood, P.; Suarez, S.A.; Pirogova, E.; Jex, A.R.; Peter, K.; Baratchi, S.; Khoshmanesh, K. Tunable harmonic flow patterns in microfluidic systems through simple tube oscillation. Small 2020, 16, 2003612. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Liu, X.; Zhang, Y.; Zhang, N.; Ye, X.; Deng, X. Hemodynamic impact of stenting on carotid bifurcation: A potential role of the stented segment and external carotid artery. Comput. Math. Methods Med. 2021, 2021, 7604532. [Google Scholar] [CrossRef]
- Pietrasanta, L.; Mameli, M.; Mangini, D.; Georgoulas, A.; Michè, N.; Filippeschi, S.; Marengo, M. Developing flow pattern maps for accelerated two-phase capillary flows. Exp. Therm. Fluid Sci. 2020, 112, 109981. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).