Flow Boiling of Liquid n-Heptane in Microtube with Various Fuel Flow Rate: Experimental and Numerical Study
Abstract
1. Introduction
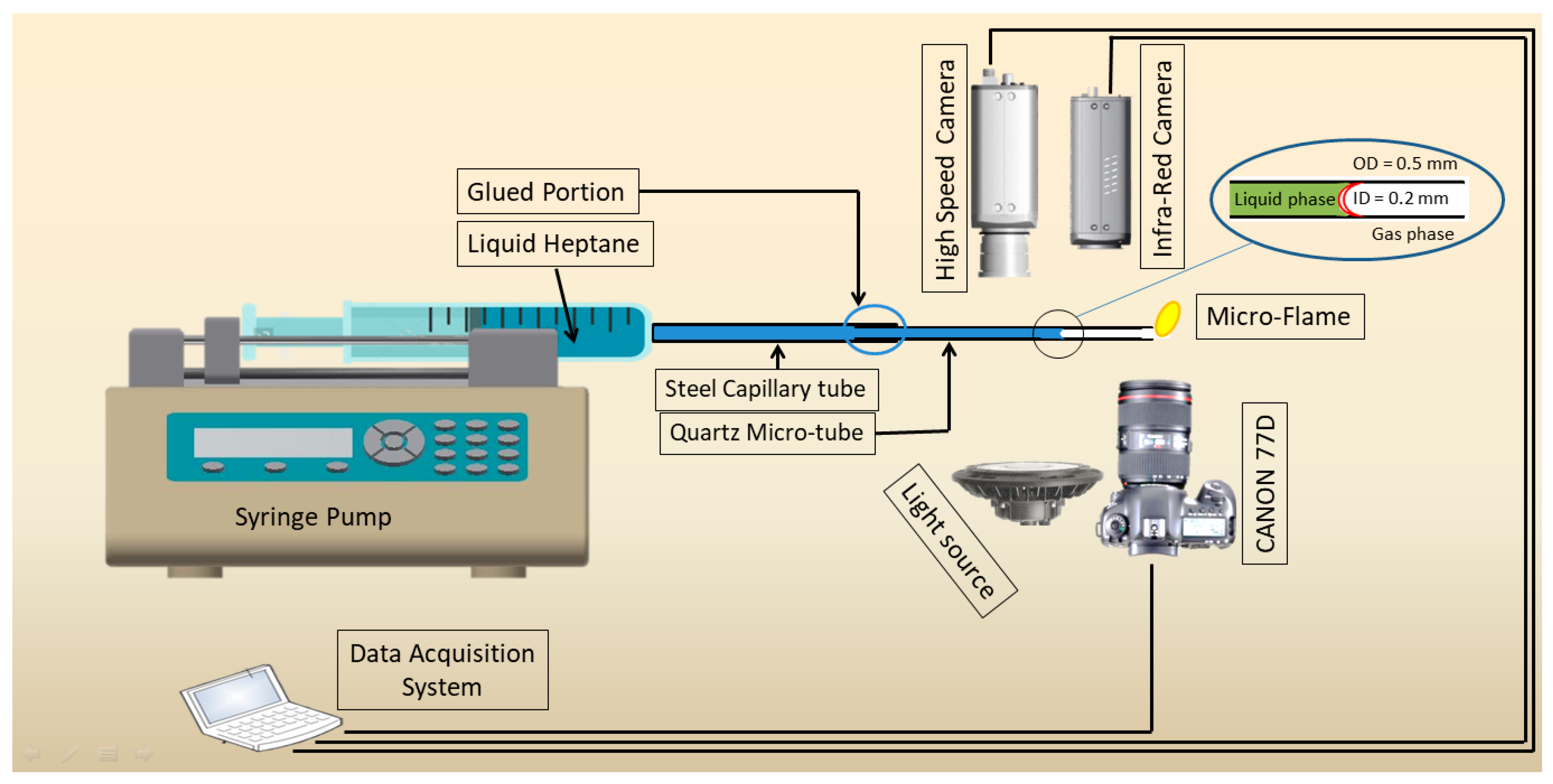
2. Experimental Setup
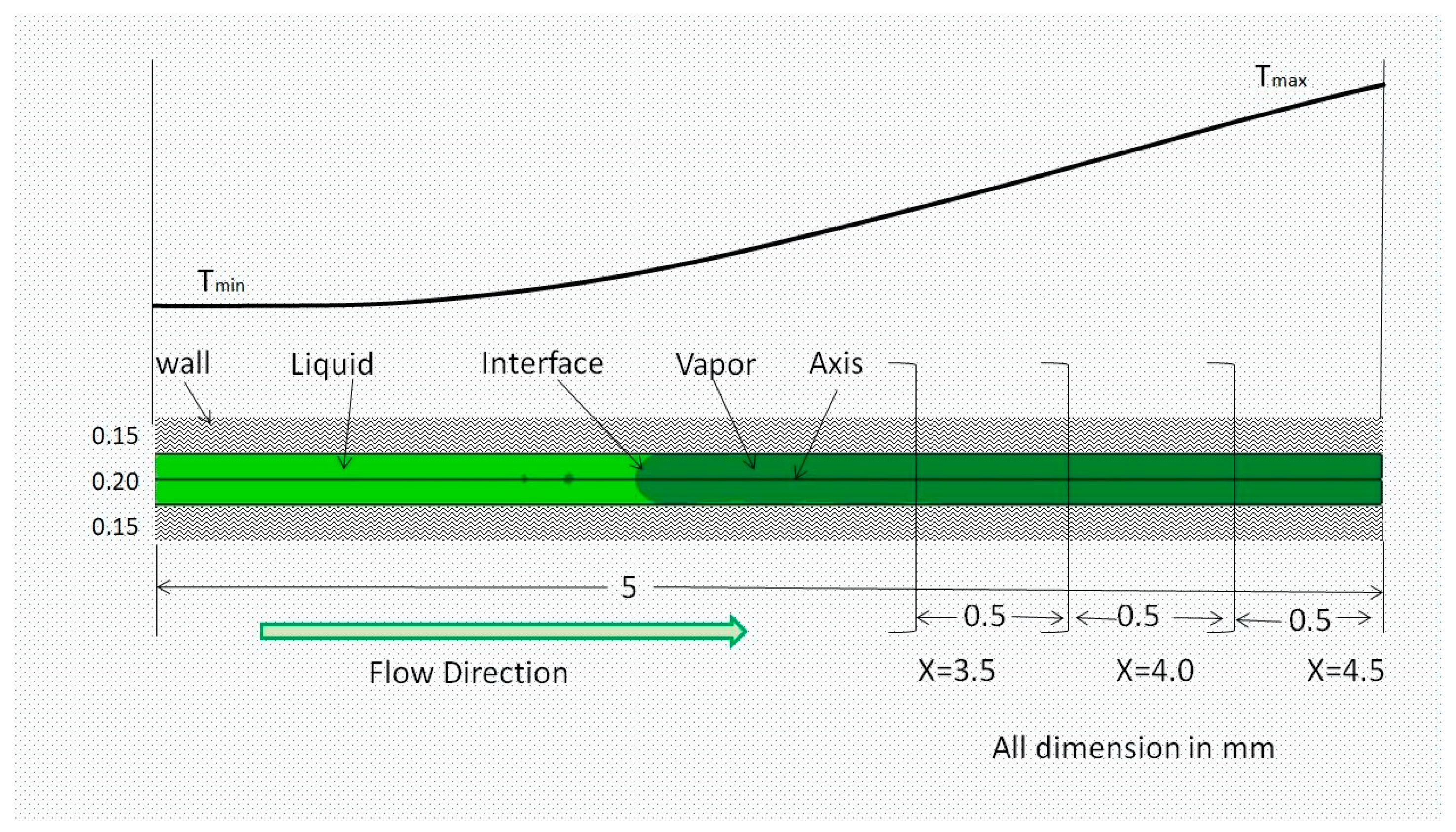
3. Observation
4. Mathematical Modeling
- In the microtube, the gravity effect is dominated by the surface tension force.
- The physical properties like surface tension, latent heat, and density are constant for each phase.
- The liquid n-heptane boiling point is assumed to be 373.15 K.
4.1. VOF Model
4.2. Heat and Mass Transfer Due to Evaporation at the Interface
4.3. Simulation Condition and Grid System
4.4. Data Reduction
5. Results and Discussion
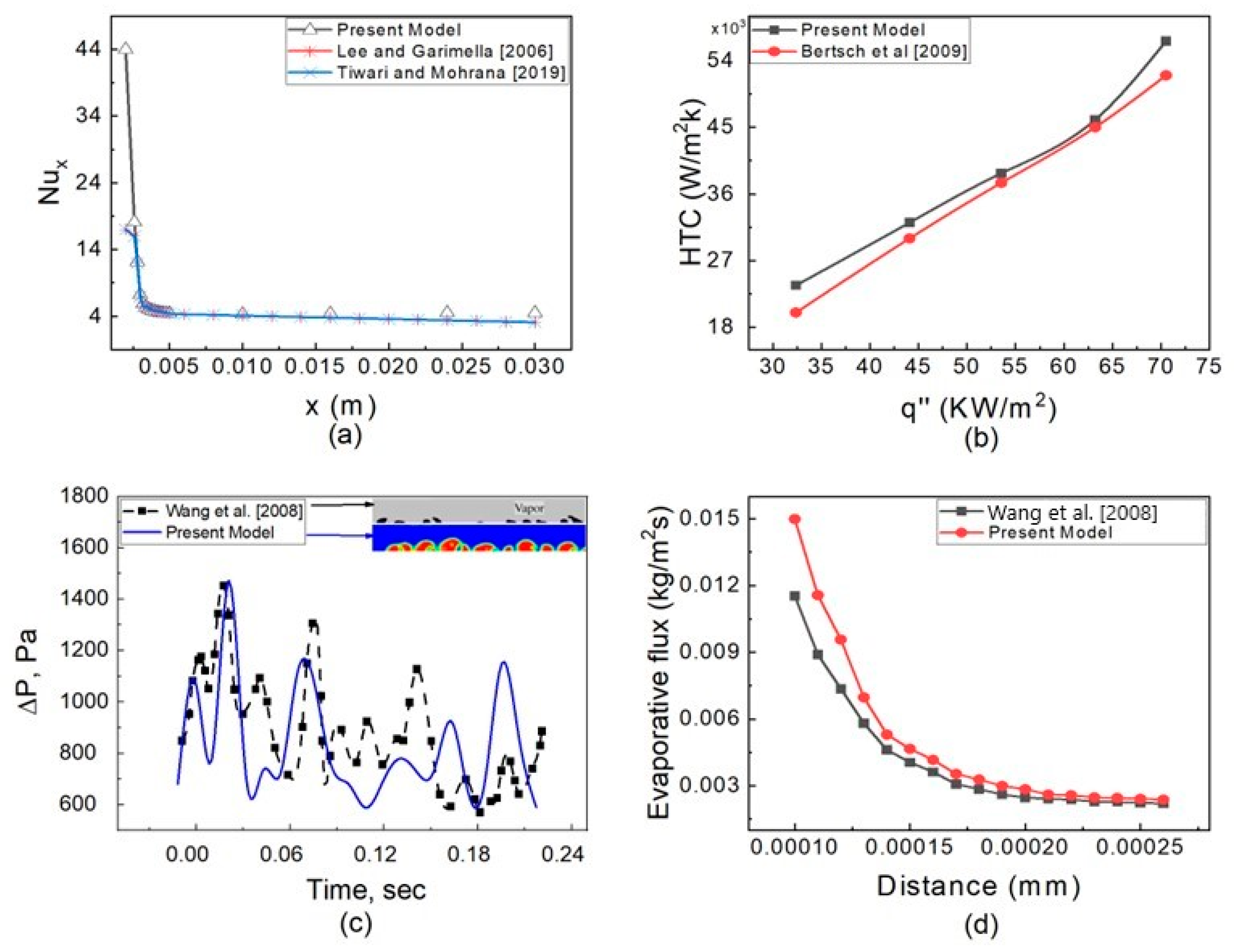
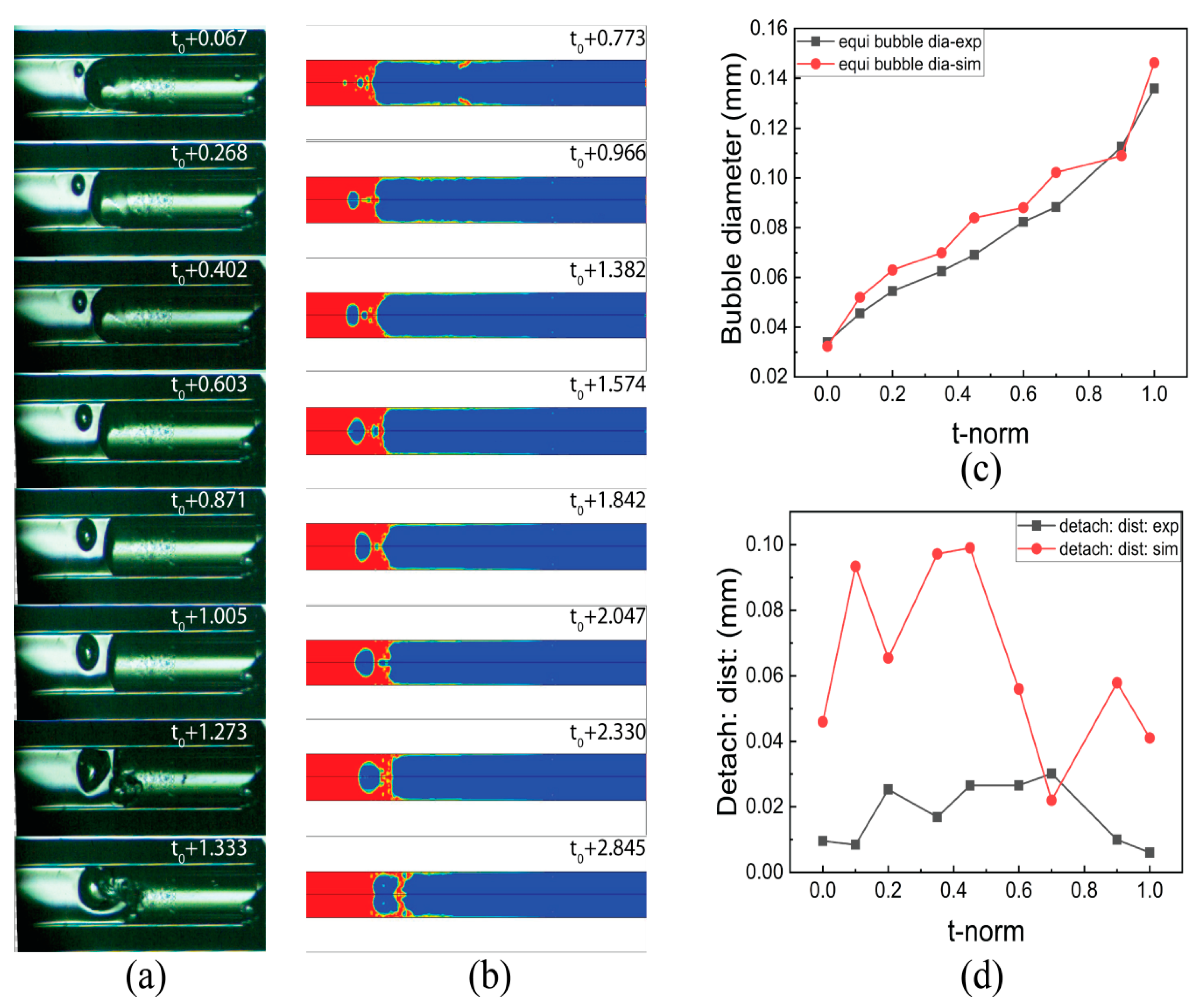
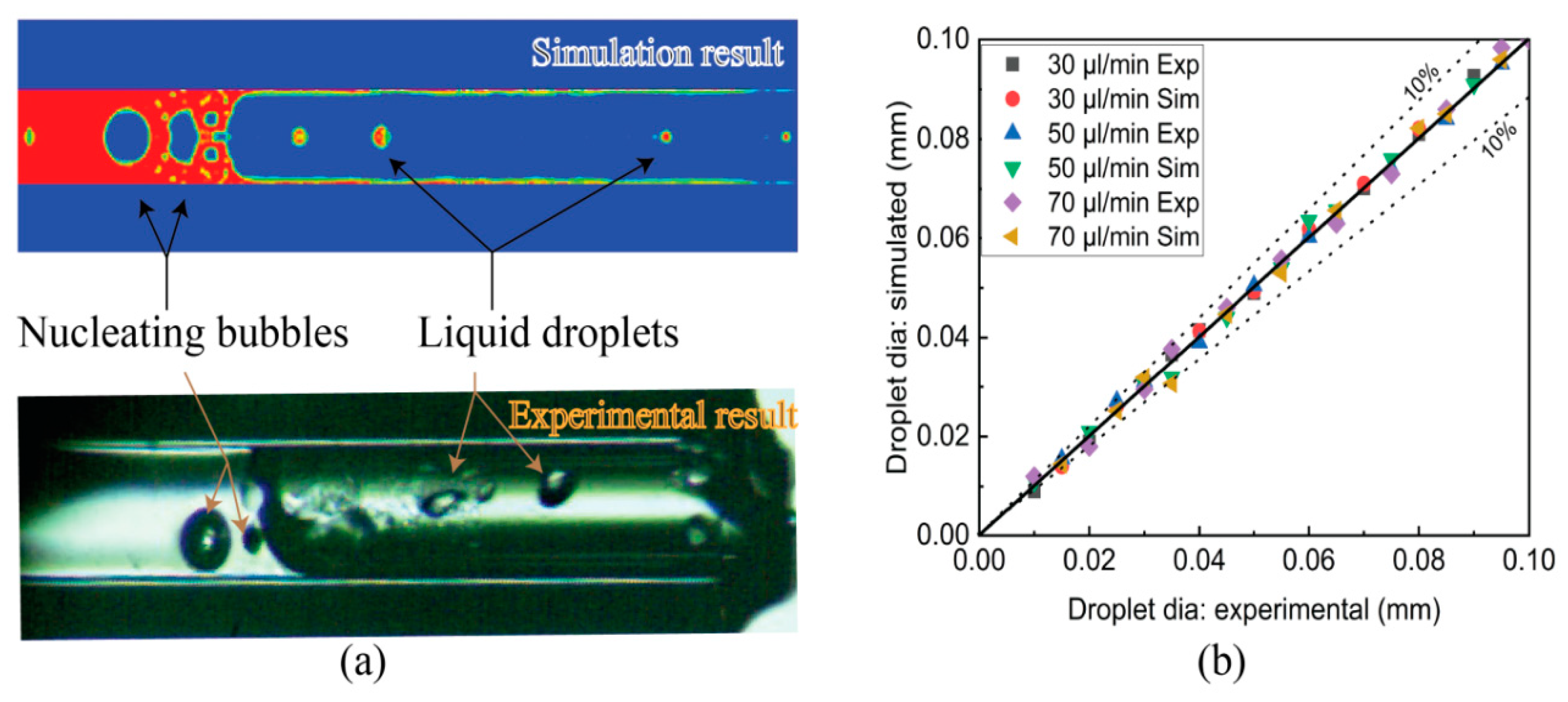
5.1. Validation
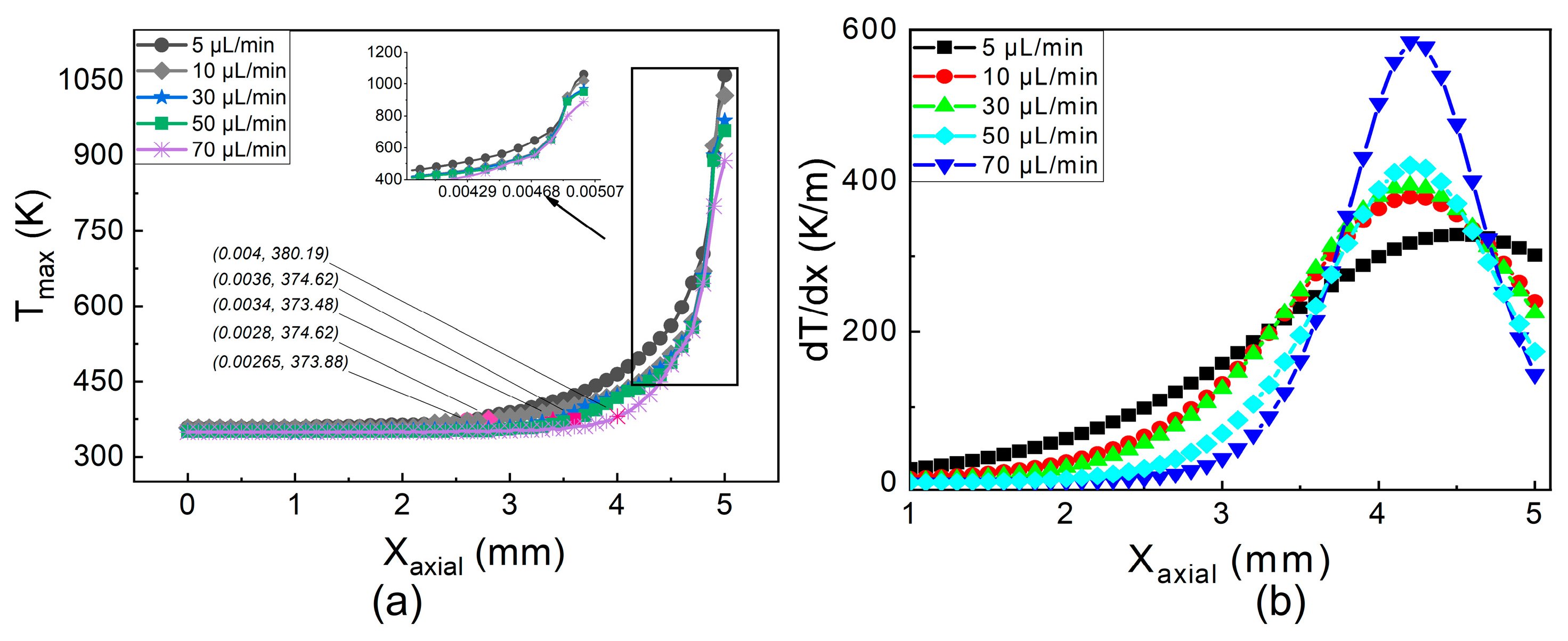
5.2. Mass Flow Rate Effect on Two-Phase Flow and Evaporation Rate
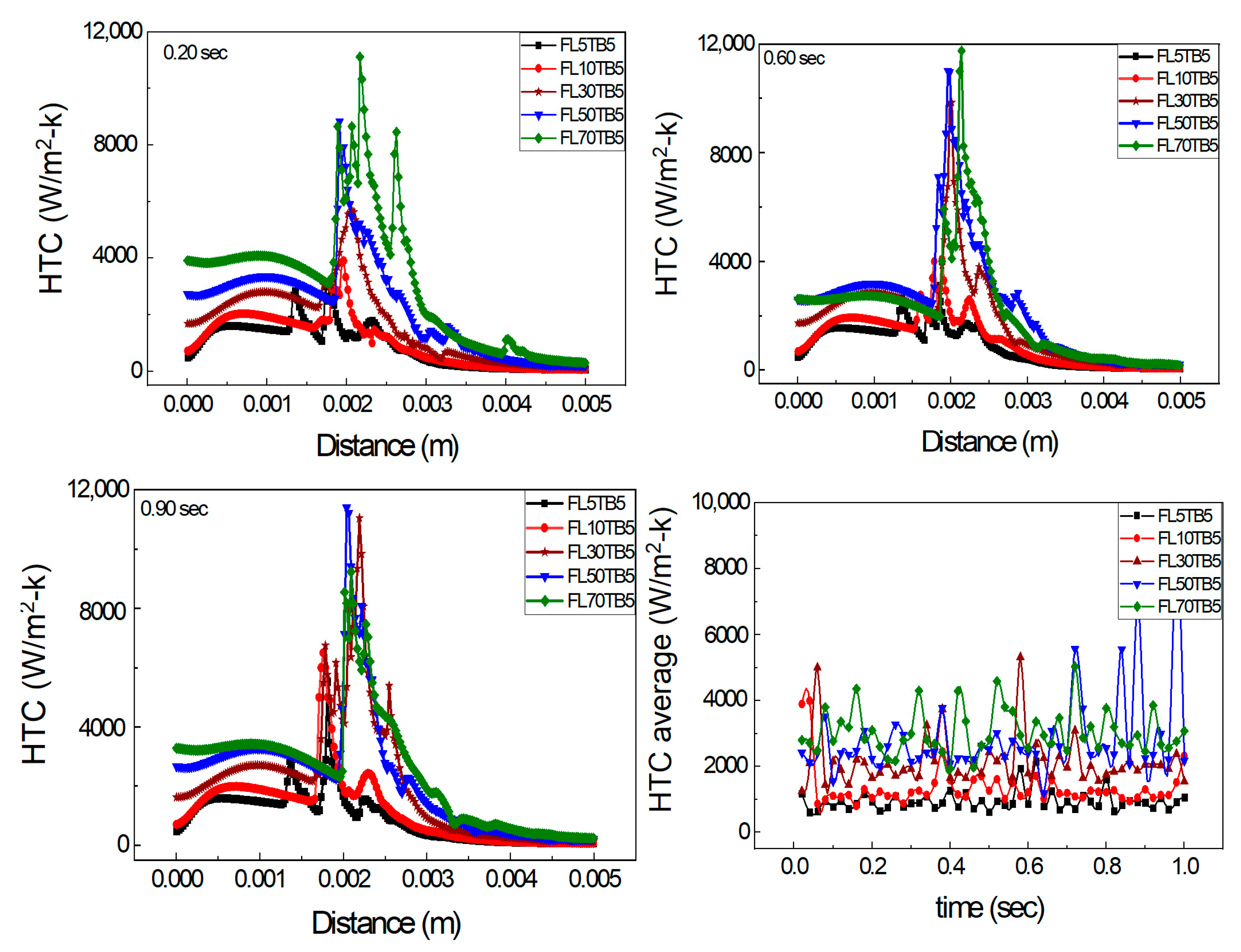
5.3. Mass Flow Rate Effect on Heat Transfer
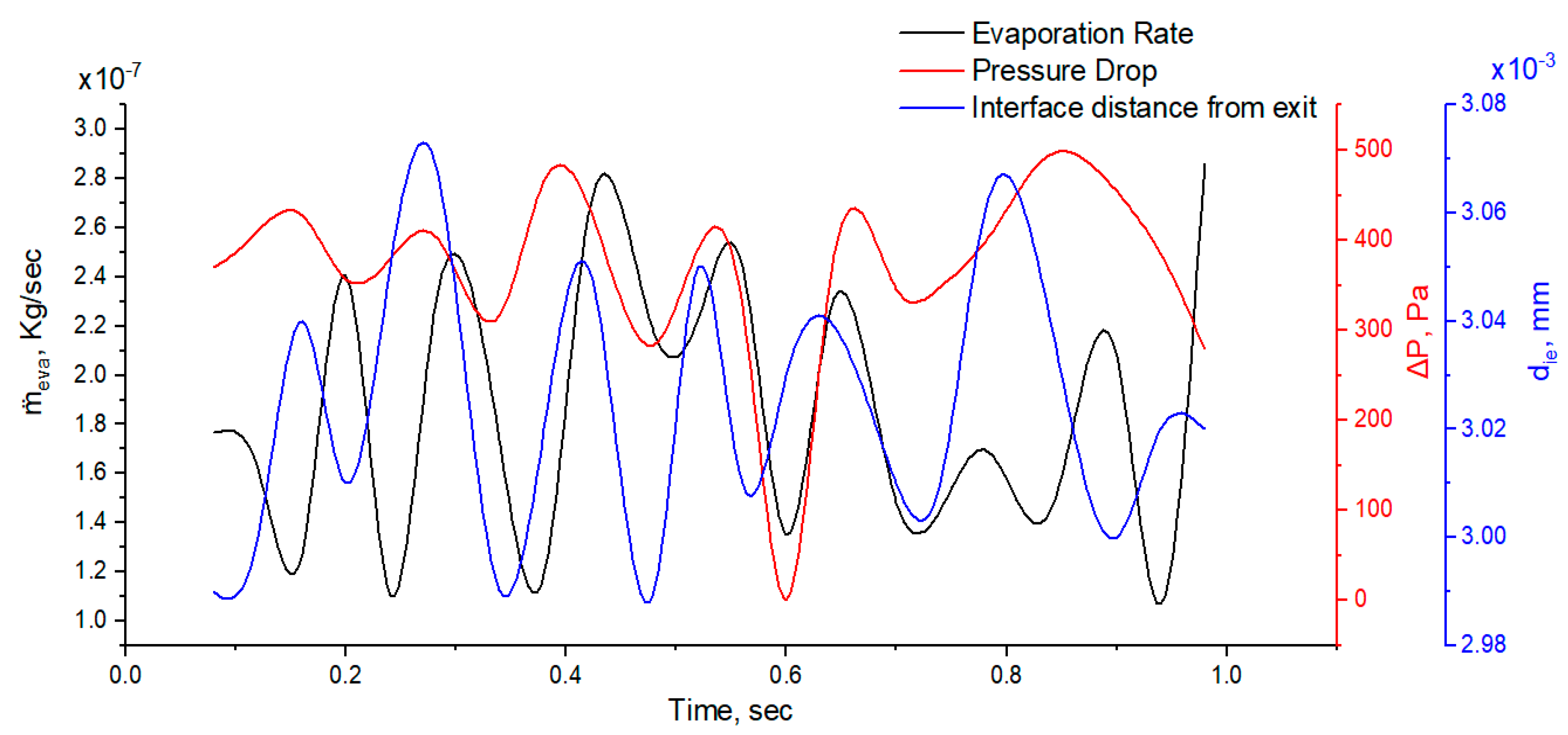
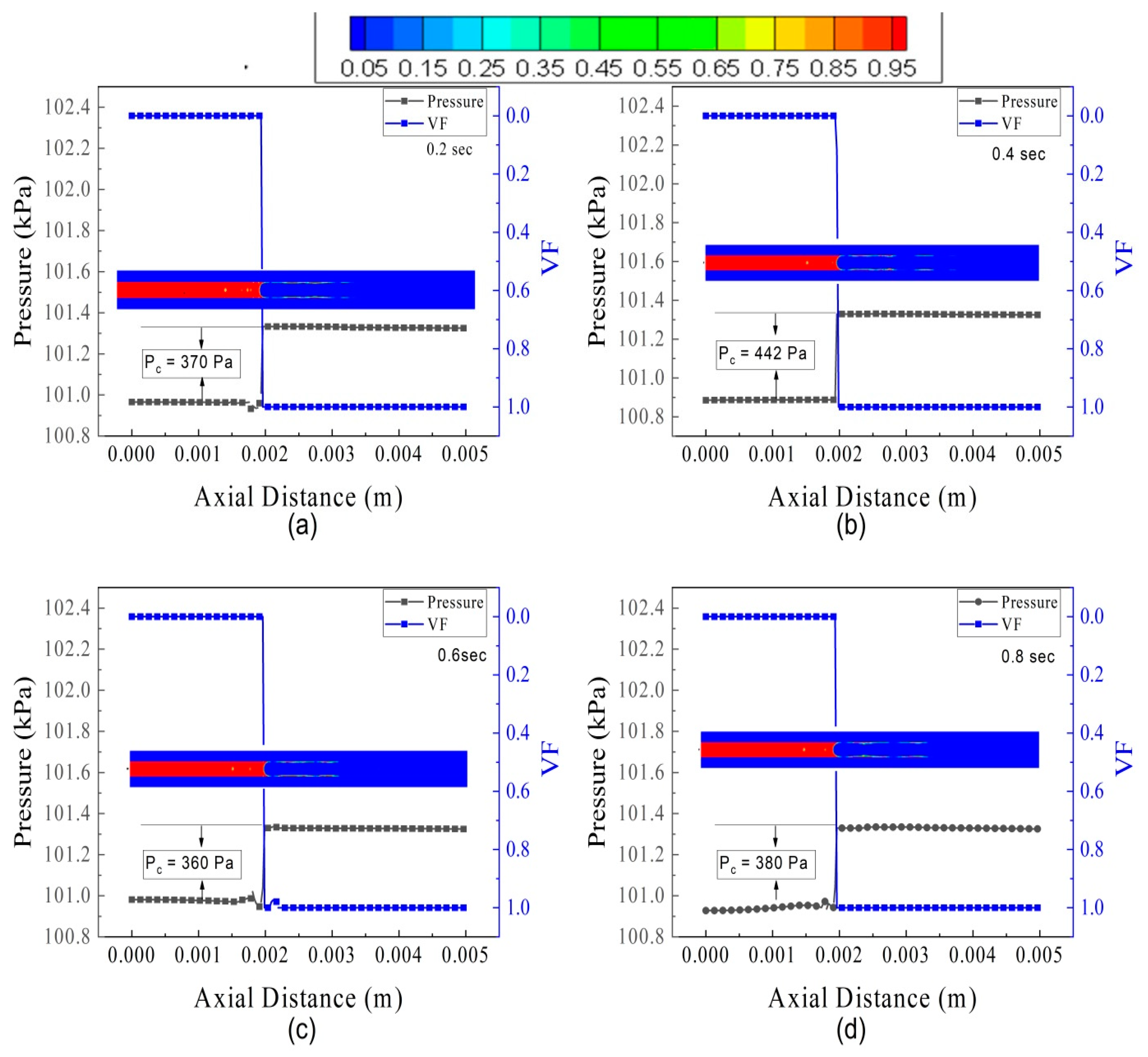
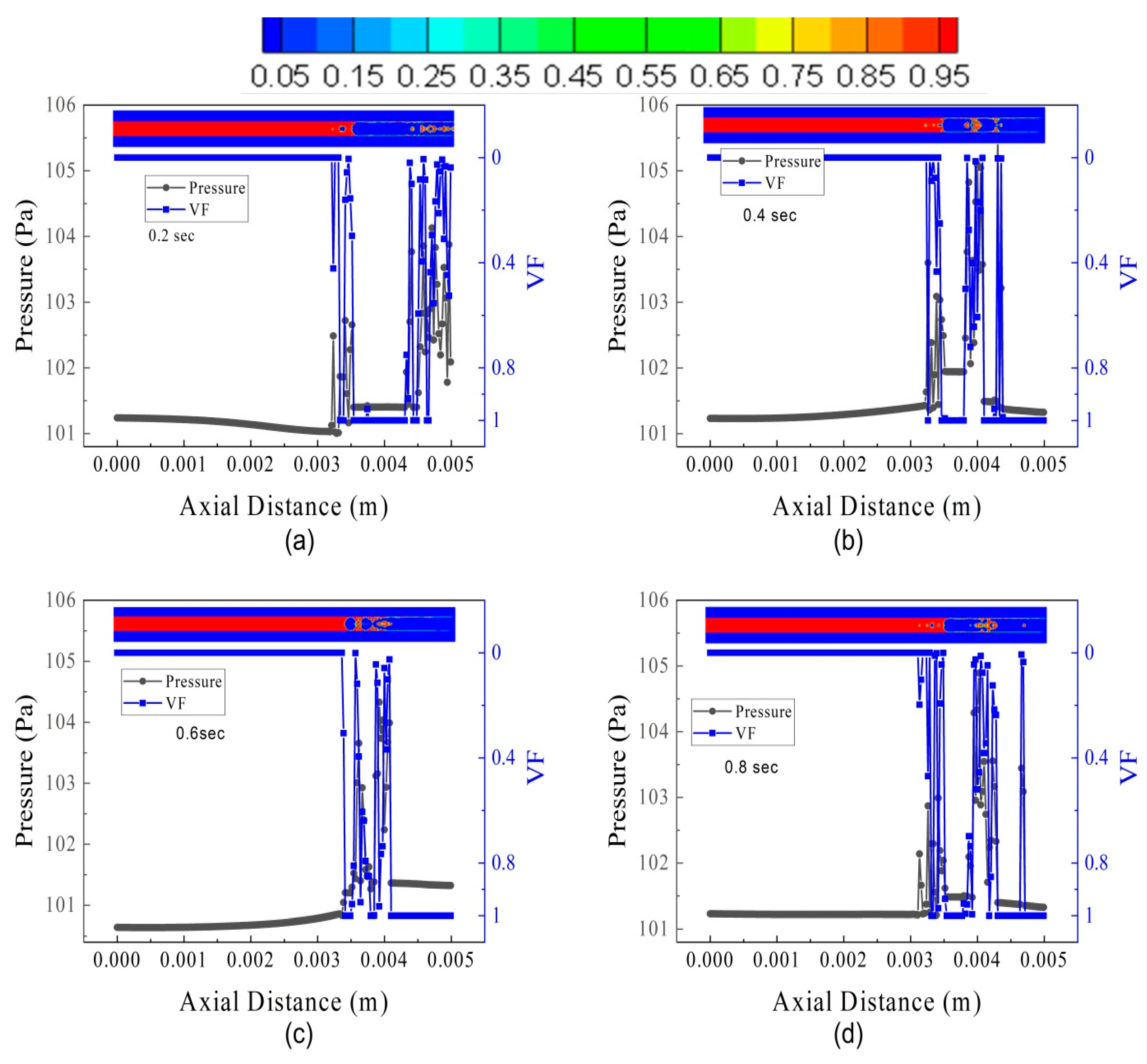
5.4. Mass Flow Rate Effect on Pressure Oscillation and Volume Fraction
5.5. Fuel Flow Rate Effect on Ressure Drop
6. Conclusions
- The steady flow with a dynamic meniscus was obtained at FFR < 10 µL/min and the highest wall temperature was 1050 K. In the microtube, an unstable flow with nucleate bubbles and liquid droplets predominates at an FFR of 30 to 70 µL/min.
- It is found that the pressure drop across the meniscus and the interface distance of the meniscus from the exit of the microtube affect the evaporative flux at the meniscus.
- One peak of HTC was obtained when the FFR was less than 10 µL/min, but at high fuel flow rates of 30 to 70 µL/min, numerous peaks of HTC were obtained at various time steps. The location of the peak was determined based on the temperature boundary condition, whereas the peak of HTC is dependent on the fuel flow rate.
- At a low fuel flow rate of 10 µL/min, the capillary force was found to be dynamic. The pressure oscillation was found at 30–70 µL/min. In the liquid regime, the axial pressure tends to rise during nucleating bubble breakup and decrease during bubble growth.
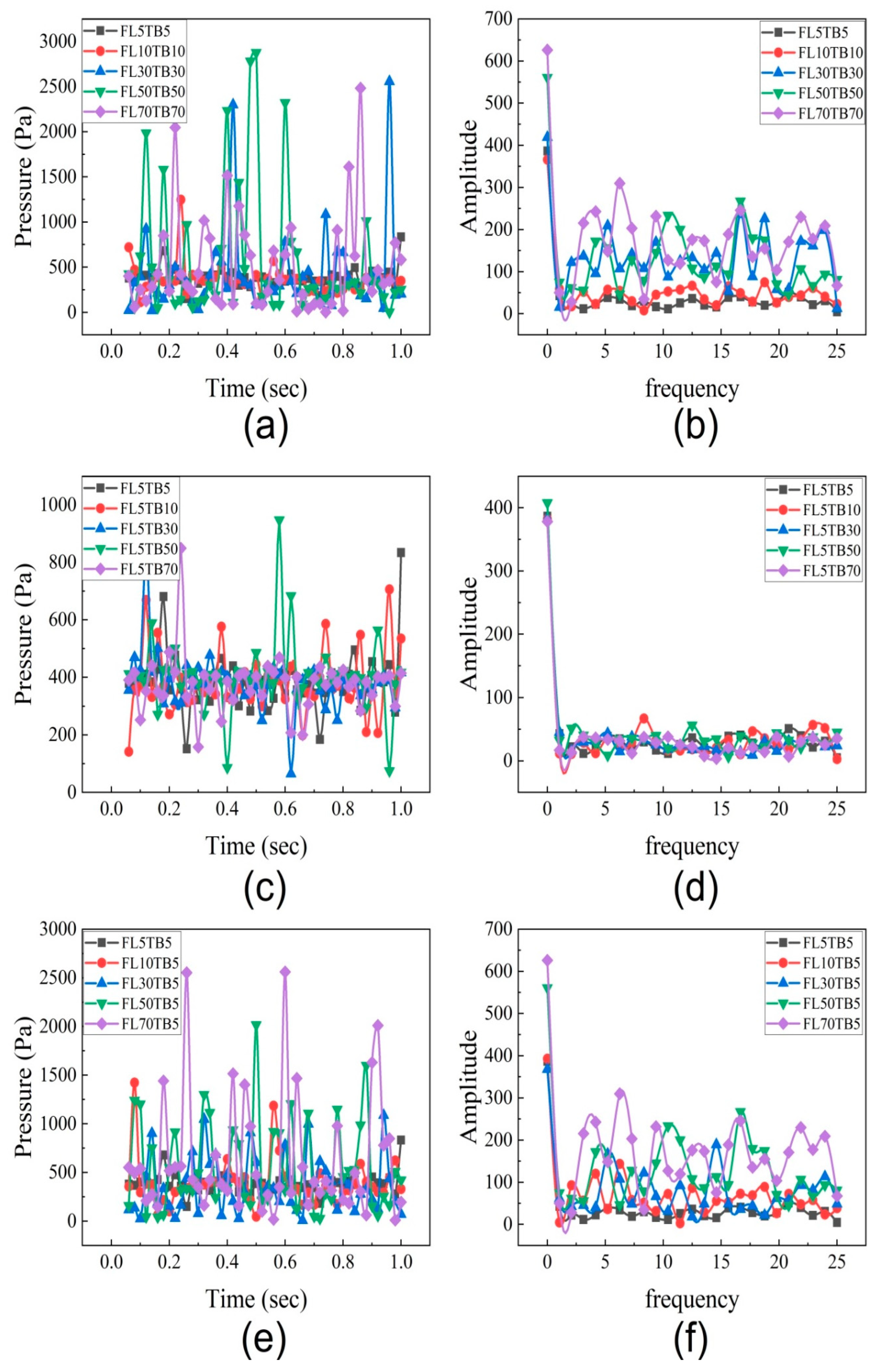
- At various fuel flow rates, the oscillation of the pressure drop was also obtained in the microtube. At all flow rates, both high-frequency low-amplitude and low-frequency high-amplitude pressure fluctuations were observed. The liquid n-heptane fuel flow rate is mostly responsible for the large amplitude.
- The fuel flow rate remained constant while the temperature boundary changed, or it remained constant while the fuel flow rate changed, although the slope of the fitted curve was larger in the latter instance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ju, Y.; Maruta, K. Microscale combustion: Technology development and fundamental research. Prog. Energy Combust. Sci. 2011, 37, 669–715. [Google Scholar] [CrossRef]
- Maruta, K. Micro and mesoscale combustion. Proc. Combust. Inst. 2011, 33, 125–150. [Google Scholar] [CrossRef]
- Epstein, A.H. Millimeter-Scale, Micro-Electro-Mechanical Systems Gas Turbine Engines. J. Eng. Gas Turbines Power 2004, 126, 205–226. [Google Scholar] [CrossRef]
- Gu, Y. Gasdynamic Modeling and Parametric Study of Mesoscale Internal Combustion Swing Engine/Generator Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2006. [Google Scholar]
- Dahm, W.; Mijit, J.; Mayor, R.; Qiao, G.; Benajmin, A.; Gu, Y.; Lei, Y.; Papke, M.; Wu, S. Micro internal combustion swing engine (MICSE) for portable power generation systems. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar]
- Liu, Q.; Jiang, L.; Yang, W.; Zhao, D. Experimental study of flame propagation in single chamber of MICSE. In Proceedings of the 10th Asia-Pacific Conference on Combustion, ASPACC, Beijing, China, 19–22 July 2015. [Google Scholar]
- Zhou, X.; Zhang, Z.; Kong, W.; Du, N. Investigations of leakage mechanisms and its influences on a micro swing engine considering rarefaction effects. Appl. Therm. Eng. 2016, 106, 674–680. [Google Scholar] [CrossRef]
- Kim, N.I.; Kato, S.; Kataoka, T.; Yokomori, T.; Maruyama, S.; Fujimori, T.; Maruta, K. Flame stabilization and emission of small Swiss-roll combustors as heaters. Combust. Flame 2005, 141, 229–240. [Google Scholar] [CrossRef]
- Kim, N.I.; Aizumi, S.; Yokomori, T.; Kato, S.; Fujimori, T.; Maruta, K. Development and scale effects of small Swiss-roll combustors. Proc. Combust. Inst. 2007, 31, 3243–3250. [Google Scholar] [CrossRef]
- Chou, S.K.; Yang, W.M.; Chua, K.J.; Li, J.; Zhang, K.L. Development of micro power generators—A review. Appl. Energy 2011, 88, 1–16. [Google Scholar] [CrossRef]
- Jiang, D.; Yang, W.; Chua, K.J.; Ouyang, J. Thermal performance of micro-combustors with baffles for thermophotovoltaic system. Appl. Therm. Eng. 2013, 61, 670–677. [Google Scholar] [CrossRef]
- Dunn-Rankin, D.; Leal, E.M.; Walther, D.C. Personal power systems. Prog. Energy Combust. Sci. 2005, 31, 422–465. [Google Scholar] [CrossRef]
- Hussain, T.; Markides, C.N.; Balachandran, R. Flame dynamics in a micro-channeled combustor. AIP Conf. Proc. 2015, 1642, 130–137. [Google Scholar] [CrossRef]
- Loire, S.; Fonoberov, V.A. Combustion of methane in microchannels. In Proceedings of the ASME 2009 International Mechanical Engineering Congress and Exposition, Lake Buena Vista, FL, USA, 13–19 November 2009; American Society of Mechanical Engineers Digital Collection; American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Maruta, K. Flame Chromatography: Toward Fuel Indexing Based on Multiple Weak Flames in a Meso-Scale Channel with a Prescribed Temperature Profile. In Proceedings of the ASME 2011 9th International Conference on Nanochannels, Microchannels, and Minichannels, Edmonton, AB, Canada, 19–22 June 2011; American Society of Mechanical Engineers Digital Collection; Canada. American Society of Mechanical Engineers: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Kinoshita, K.; Yoshimoto, T.; Kato, Y.; Kubo, N.; Takagi, T. Stability Limits, Behaviors and Characteristics of the Diffusion Flame. Proc. Conf. Kansai Branch 2004, 79, 5–15. [Google Scholar] [CrossRef]
- Rashid, M.T.; Li, J.; Chen, X.; Wang, N. Flow Boiling and Heat Transfer of N-heptane Flow in a Microtube Heated by Concurrent Microflame. Combust. Sci. Technol. 2021, 195, 265–293. [Google Scholar] [CrossRef]
- Leong, K.; Ho, J.; Wong, K. A critical review of pool and flow boiling heat transfer of dielectric fluids on enhanced surfaces. Appl. Therm. Eng. 2016, 112, 999–1019. [Google Scholar] [CrossRef]
- Prajapati, Y.K.; Bhandari, P. Flow boiling instabilities in microchannels and their promising solutions—A review. Exp. Therm. Fluid Sci. 2017, 88, 576–593. [Google Scholar] [CrossRef]
- Dalkilic, A.S. A review of flow boiling in mini and microchannel for enhanced geometries. J. Therm. Eng. 2018, 4, 2037–2074. [Google Scholar] [CrossRef]
- Zhou, X.; Li, J.; Chen, X.; Wang, N. Effects of pulse power on evaporation characteristics of an n-heptane droplet in a microtube. Appl. Therm. Eng. 2023, 231, 120895. [Google Scholar] [CrossRef]
- Nebuloni, S.; Thome, J.R. Numerical modeling of laminar annular film condensation for different channel shapes. Int. J. Heat Mass Transf. 2010, 53, 2615–2627. [Google Scholar] [CrossRef]
- Rashid, M.T.; Li, J.; Chen, X.; Song, A.; Wang, N. Numerical simulation of evaporation phenomena and heat transfer of liquid Hydrocarbon in a microtube. Int. J. Heat Mass Transf. 2021, 179, 121734. [Google Scholar] [CrossRef]
- Zhao, T.; Liao, Q. Theoretical analysis of film condensation heat transfer inside vertical mini triangular channels. Int. J. Heat Mass Transf. 2002, 45, 2829–2842. [Google Scholar] [CrossRef]
- Wang, H.S.; Rose, J.W. A Theory of Film Condensation in Horizontal Noncircular Section Microchannels. J. Heat Transf. 2005, 127, 1096–1105. [Google Scholar] [CrossRef]
- Wang, H.S.; Rose, J.W. Film condensation in horizontal microchannels: Effect of channel shape. Int. J. Therm. Sci. 2006, 45, 1205–1212. [Google Scholar] [CrossRef]
- Ferrari, A.; Magnini, M.; Thome, J.R. Numerical analysis of slug flow boiling in square microchannels. Int. J. Heat Mass Transf. 2018, 123, 928–944. [Google Scholar] [CrossRef]
- Guo, Z.; Haynes, B.; Fletcher, D. Numerical simulation of annular flow boiling in microchannels. J. Comput. Multiph. Flows 2016, 8, 61–82. [Google Scholar] [CrossRef]
- Tiwari, N.; Moharana, M.K. Conjugate heat transfer analysis of liquid-vapor two phase flow in a microtube: A numerical investigation. Int. J. Heat Mass Transf. 2019, 142, 118427. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Zhou, S.; Tsegay, S.; Ahmad, N.; Zhu, Y. Effects of hydrogen-enriched biogas on combustion and emission of a dual-fuel diesel engine. Energy Sources Part A Recover. Util. Environ. Eff. 2020, 1–16. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Zhou, S.; Tsegay, A.S.; Zhu, Y.; Malik, A.; Ahmad, N.; Legese, Z. Effects of CO2 ratio in biogas on performance, combustion and emissions of a dual-fuel diesel engine. Int. Energy J. 2020, 15–38. [Google Scholar]
- Müller-Steinhagen, H.; Epstein, N.; Watkinson, A.P. Subcooled-boiling and convective heat transfer for heptane flowing inside an annulus and past a coiled wire: Part II—Correlation of data. J. Heat Transfer. 1986, 108, 928–933. [Google Scholar] [CrossRef]
- Müller-Steinhagen, H.; Watkinson, A.; Epstein, N. Subcooled-boiling and convective heat transfer to heptane flowing inside an annulus and past a coiled wire: Part I—Experimental results. J. Heat Transfer. 1986, 108, 922–927. [Google Scholar] [CrossRef]
- Hapke, I.; Boye, H.; Schmidt, J. Flow boiling of water and n-heptane in micro channels. Microscale Thermophys. Eng. 2002, 6, 99–115. [Google Scholar] [CrossRef]
- Dhavaleswarapu, H.K.; Murthy, J.Y.; Garimella, S.V. Numerical investigation of an evaporating meniscus in a channel. Int. J. Heat Mass Transf. 2012, 55, 915–924. [Google Scholar] [CrossRef][Green Version]
- Ahmed, S.A.; Zhou, S.; Zhu, Y.; Feng, Y.; Malik, A.; Ahmad, N. Influence of Injection Timing on Performance and Exhaust Emission of CI Engine Fuelled with Butanol-Diesel Using a 1D GT-Power Model. Processes 2019, 7, 299. [Google Scholar] [CrossRef]
- Lee, W.H. Multiphase Trabsport Fundamentals, Reator Saftey, Applications; Hemisphere Publishing: Washington, DC, USA, 1980; Volume 1. [Google Scholar]
- Khan, Z.A.; Ahmad, N.; Sattar, M.; Haq, M.A.; Khan, I.; Ganie, A.H. Cell alternation algorithm for simulating bubble growth in boiling flows through volume of fluid (VOF) method in fluent. Alex. Eng. J. 2022, 61, 13051–13066. [Google Scholar] [CrossRef]
- Fang, C.; David, M.; Rogacs, A.; Goodson, K. Volume of fluid simulation of boiling two-phase flow in a vapor-venting microchannel. Front. Heat Mass Transf. 2010, 1, 013002. [Google Scholar] [CrossRef]
- Schrage, R.W. A Theoretical Study of Interphase Mass Transfer; Columbia University Press: New York, NY, USA, 1953. [Google Scholar]
- Wu, C.; Li, J. Numerical simulation of flow patterns and the effect on heat flux during R32 condensation in microtube. Int. J. Heat Mass Transf. 2018, 121, 265–274. [Google Scholar] [CrossRef]
- Lee, P.-S.; Garimella, S.V. Thermally developing flow and heat transfer in rectangular microchannels of different aspect ratios. Int. J. Heat Mass Transf. 2006, 49, 3060–3067. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. A composite heat transfer correlation for saturated flow boiling in small channels. Int. J. Heat Mass Transf. 2009, 52, 2110–2118. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, X.; Ye, P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube. Int. J. Heat Mass Transf. 2008, 51, 1003–1016. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. REFPROP: Reference Fluid Thermodynamic and Transport Properties; NIST Standard Reference Database; Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2007; Volume 23.
- Wang, H.; Murthy, J.Y.; Garimella, S.V. Transport from a volatile meniscus inside an open microtube. Int. J. Heat Mass Transf. 2008, 51, 3007–3017. [Google Scholar] [CrossRef][Green Version]
- Polansky, J.; Kaya, T. Stability of an evaporating meniscus: Part I–Theoretical analysis. Int. J. Therm. Sci. 2016, 107, 209–219. [Google Scholar] [CrossRef]
- Lie, Y.; Su, F.; Lai, R.; Lin, T. Experimental study of evaporation heat transfer characteristics of refrigerants R-134a and R-407C in horizontal small tubes. Int. J. Heat Mass Transf. 2006, 49, 207–218. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. Effects of heat flux, mass flux, vapor quality, and saturation temperature on flow boiling heat transfer in microchannels. Int. J. Multiph. Flow 2008, 35, 142–154. [Google Scholar] [CrossRef]
- Basu, S.; Ndao, S.; Michna, G.J.; Peles, Y.; Jensen, M.K. Flow Boiling of R134a in Circular Microtubes—Part I: Study of Heat Transfer Characteristics. J. Heat Transf. 2011, 133, 051502. [Google Scholar] [CrossRef]
- Huang, S.-C.; Kawanami, O.; Kawakami, K.; Honda, I.; Kawashima, Y.; Ohta, H. Experimental Study of the Relation Between Heat Transfer and Flow Behavior in a Single Microtube. Microgravity Sci. Technol. 2008, 20, 193–197. [Google Scholar] [CrossRef]
- Yen, T.-H.; Kasagi, N.; Suzuki, Y. Forced convective boiling heat transfer in microtubes at low mass and heat fluxes. Int. J. Multiph. Flow 2003, 29, 1771–1792. [Google Scholar] [CrossRef]
- Wang, S.; Liu, P.; Zhao, H.; Zhang, Y. A novel method for calculating the dynamic capillary force and correcting the pressure error in micro-tube experiment. Sci. Rep. 2017, 7, 16590. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Sefiane, K.; Wang, Z.-G.; Harmand, S. Analysis of two-phase pressure drop fluctuations during micro-channel flow boiling. Int. J. Heat Mass Transf. 2014, 70, 353–362. [Google Scholar] [CrossRef]
- Kawahara, A.; Chung, P.-Y.; Kawaji, M. Investigation of two-phase flow pattern, void fraction and pressure drop in a microchannel. Int. J. Multiph. Flow 2002, 28, 1411–1435. [Google Scholar] [CrossRef]
- Bogojevic, D.; Sefiane, K.; Walton, A.; Lin, H.; Cummins, G. Two-phase flow instabilities in a silicon microchannels heat sink. Int. J. Heat Fluid Flow 2009, 30, 854–867. [Google Scholar] [CrossRef]
- Singh, S.G.; Bhide, R.R.; Duttagupta, S.P.; Puranik, B.P.; Agrawal, A. Two-Phase Flow Pressure Drop Characteristics in Trapezoidal Silicon Microchannels. IEEE Trans. Components Packag. Technol. 2009, 32, 887–900. [Google Scholar] [CrossRef]








| Property | Value |
|---|---|
| Density (kg/m3) | 666.95 at 295.45 K |
| Thermal conductivity (W/m-K) | 0.12746 |
| Thermal capacity (J/kg) | 2298.4 |
| Viscosity (kg/m-s) | 0.000331 |
| Vapor molecular weight | 100 |
| Evaporation latent heat (J/kg) | 3.506 × 105 |
| Saturated vapor pressure (Pa) | 5316 at 295.45 K |
| Accommodation coefficient | 1 |
| Grid No. | Grid Size | Average HTC (W/m2-K) | e% | Evaporative Flux at Meniscus (Kg/m2-s) | e% | ΔP (Pa) | e% |
|---|---|---|---|---|---|---|---|
| 1 | 64,500 | 967 | ----- | 8.63 × 10−9 | ---- | 1324 | ---- |
| 2 | 34,000 | 960 | 0.72 | 8.56 × 10−9 | 0.81 | 1315 | 0.67 |
| 3 | 22,000 | 945 | 2.2 | 8.5 × 10−9 | 1.51 | 1290 | 2.5 |
| FFR (µL/min) | 5 | 10 | 30 | 50 | 70 |
| MFR (mg/s) | 0.056 | 0.113 | 0.343 | 0.58 | 0.797 |
| Case. No | Case Name | Investigation | Remarks |
|---|---|---|---|
| 1 | FL5TB5 | Experiment and Simulation | Boundary condition retrieved from experiment with 5 µL/min of mass flow rate |
| 2 | FL10TB10 | Experiment and Simulation | Boundary condition retrieved from experiment with 10 µL/min of mass flow rate |
| 3 | FL30TB30 | Experiment and Simulation | Boundary condition retrieved from experiment with 30 µL/min of mass flow rate |
| 4 | FL50TB50 | Experiment and Simulation | Boundary condition retrieved from experiment with 50 µL/min of mass flow rate |
| 5 | FL70TB70 | Experiment and Simulation | Boundary condition retrieved from experiment with 70 µL/min of mass flow rate |
| 6 | FL10TB5 | Simulation | Flow rate is 10 µL/min while boundary condition is from case 1 |
| 7 | FL30TB5 | Simulation | Flow rate is 30 µL/min while boundary condition is from case 1 |
| 8 | FL50TB5 | Simulation | Flow rate is 50 µL/min while boundary condition is from case 1 |
| 9 | FL70TB5 | Simulation | Flow rate is 70 µL/min while boundary condition is from case 1 |
| 10 | FL5TB10 | Simulation | Flow rate is 5 µL/min while boundary condition is from case 2 |
| 11 | FL5TB30 | Simulation | Flow rate is 5 µL/min while boundary condition is from case 3 |
| 12 | FL5TB50 | Simulation | Flow rate is 5 µL/min while boundary condition is from case 4 |
| 13 | FL5TB70 | Simulation | Flow rate is 5 µL/min while boundary condition is from case 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, M.T.; Ahmad, N.; Swati, R.F.; Khan, M.B. Flow Boiling of Liquid n-Heptane in Microtube with Various Fuel Flow Rate: Experimental and Numerical Study. Micromachines 2023, 14, 1760. https://doi.org/10.3390/mi14091760
Rashid MT, Ahmad N, Swati RF, Khan MB. Flow Boiling of Liquid n-Heptane in Microtube with Various Fuel Flow Rate: Experimental and Numerical Study. Micromachines. 2023; 14(9):1760. https://doi.org/10.3390/mi14091760
Chicago/Turabian StyleRashid, Muhammad Tahir, Naseem Ahmad, Raees Fida Swati, and Muhammad Bilal Khan. 2023. "Flow Boiling of Liquid n-Heptane in Microtube with Various Fuel Flow Rate: Experimental and Numerical Study" Micromachines 14, no. 9: 1760. https://doi.org/10.3390/mi14091760
APA StyleRashid, M. T., Ahmad, N., Swati, R. F., & Khan, M. B. (2023). Flow Boiling of Liquid n-Heptane in Microtube with Various Fuel Flow Rate: Experimental and Numerical Study. Micromachines, 14(9), 1760. https://doi.org/10.3390/mi14091760






