Theoretical and Experimental Investigation of Surface Textures in Vibration-Assisted Micro Milling
Abstract
1. Introduction
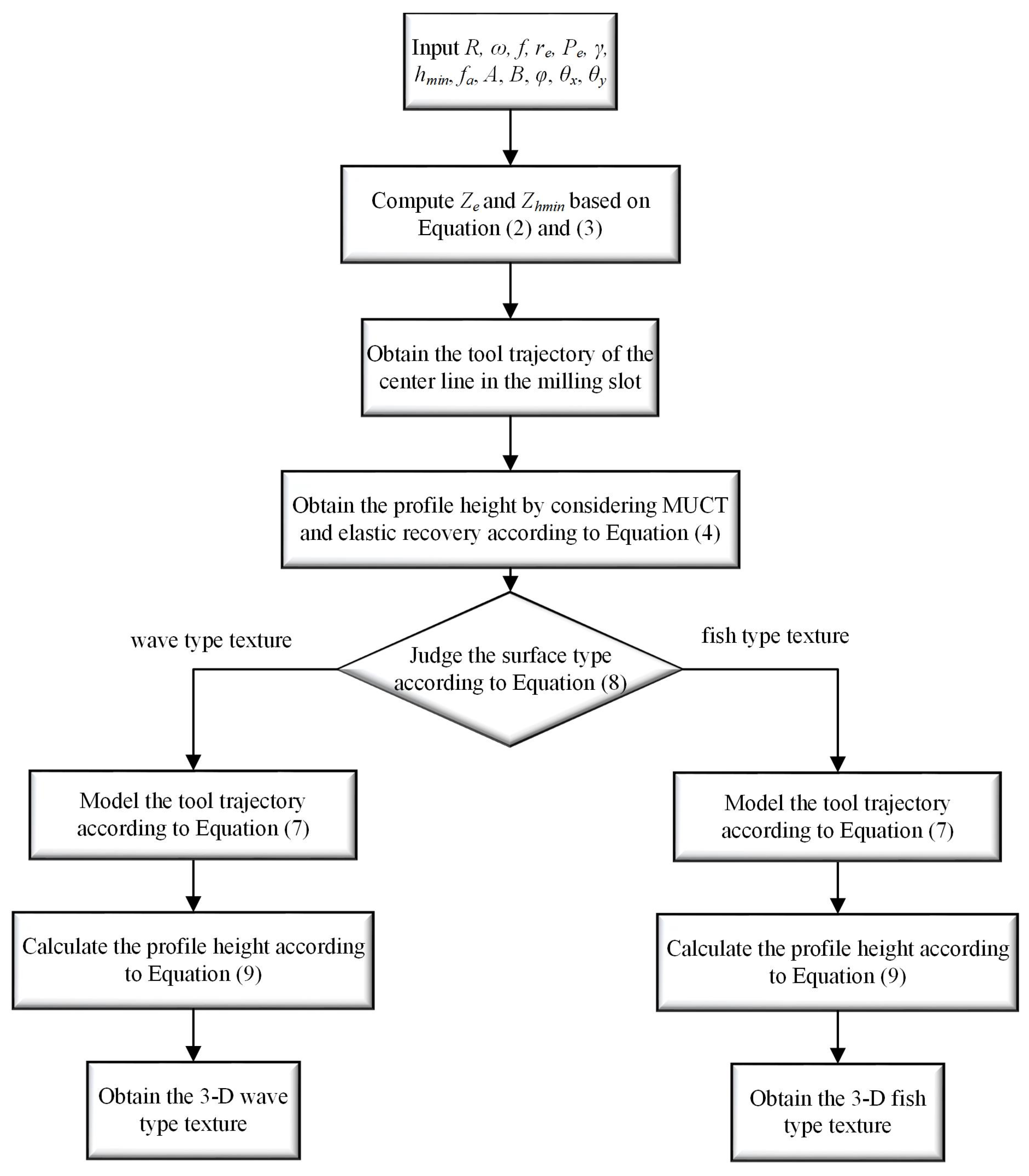
2. Surface Texture Modeling
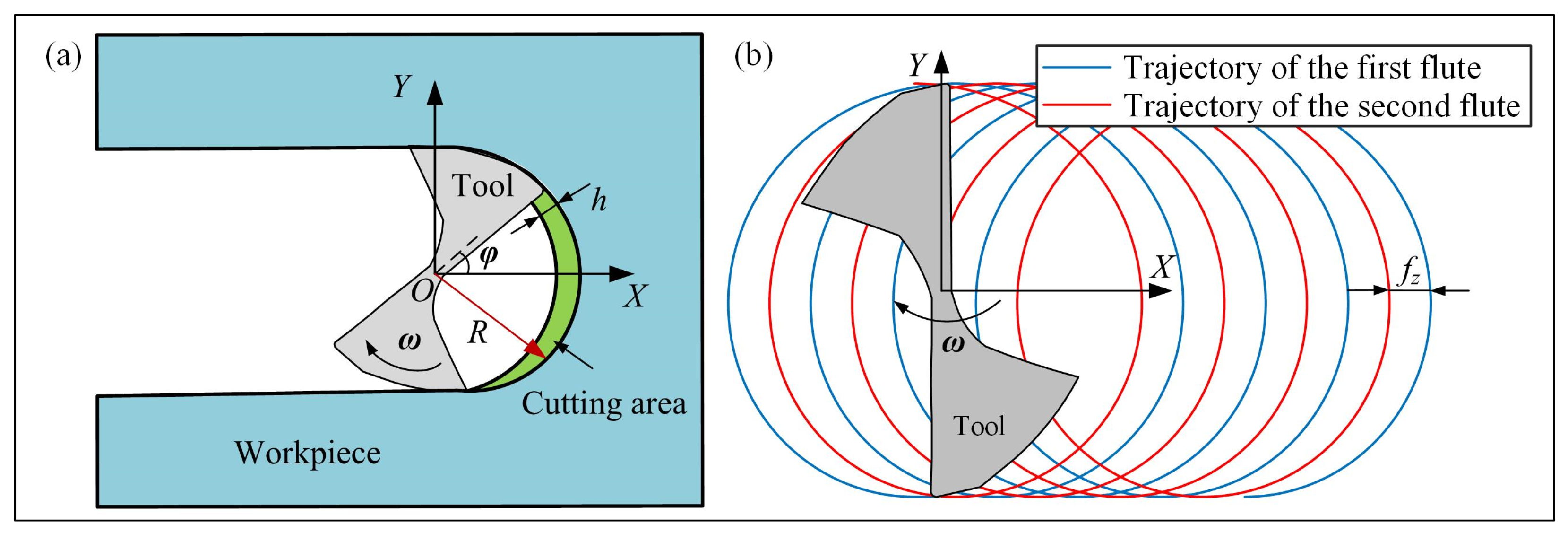
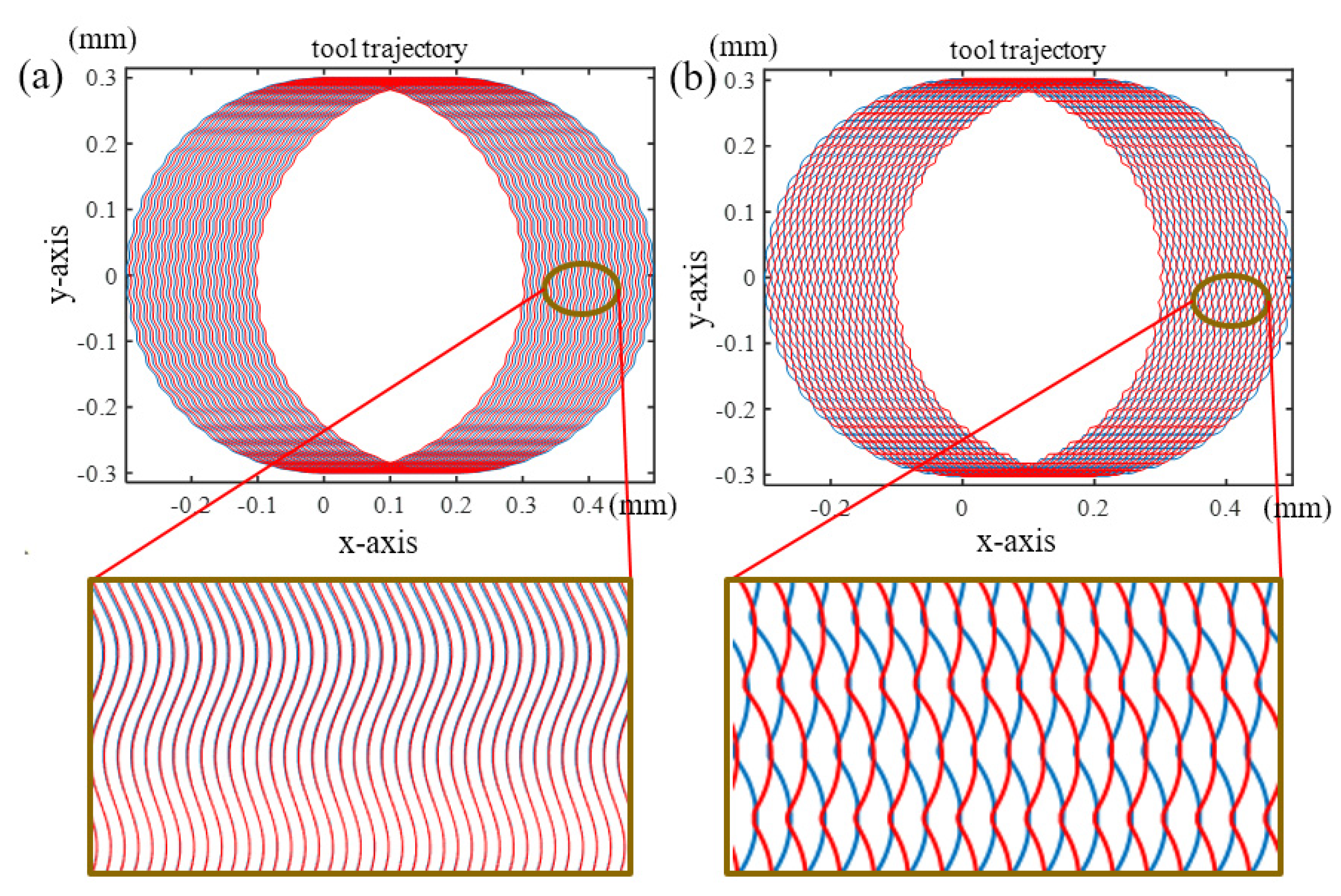
2.1. Tool Trajectory Modeling
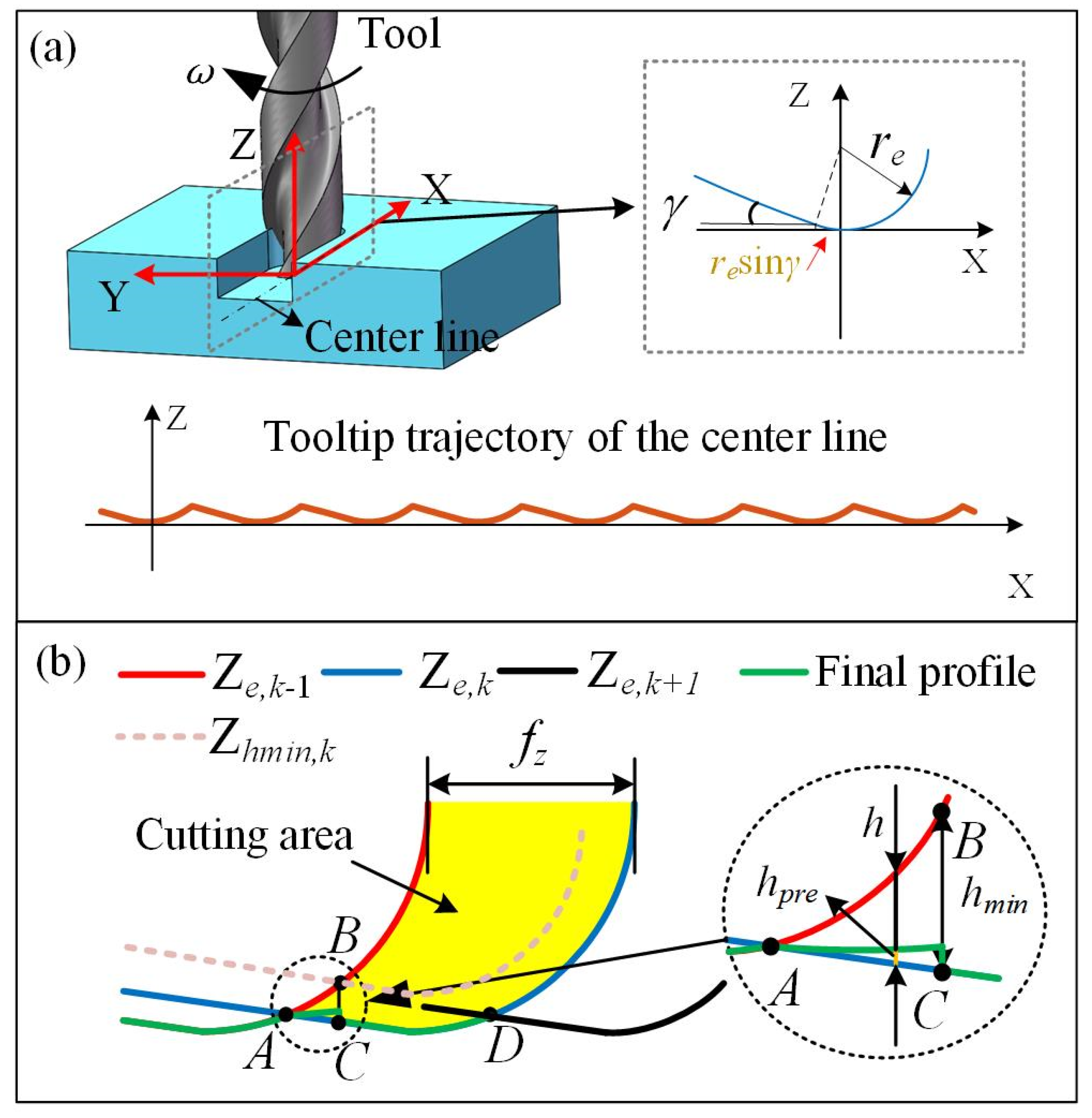
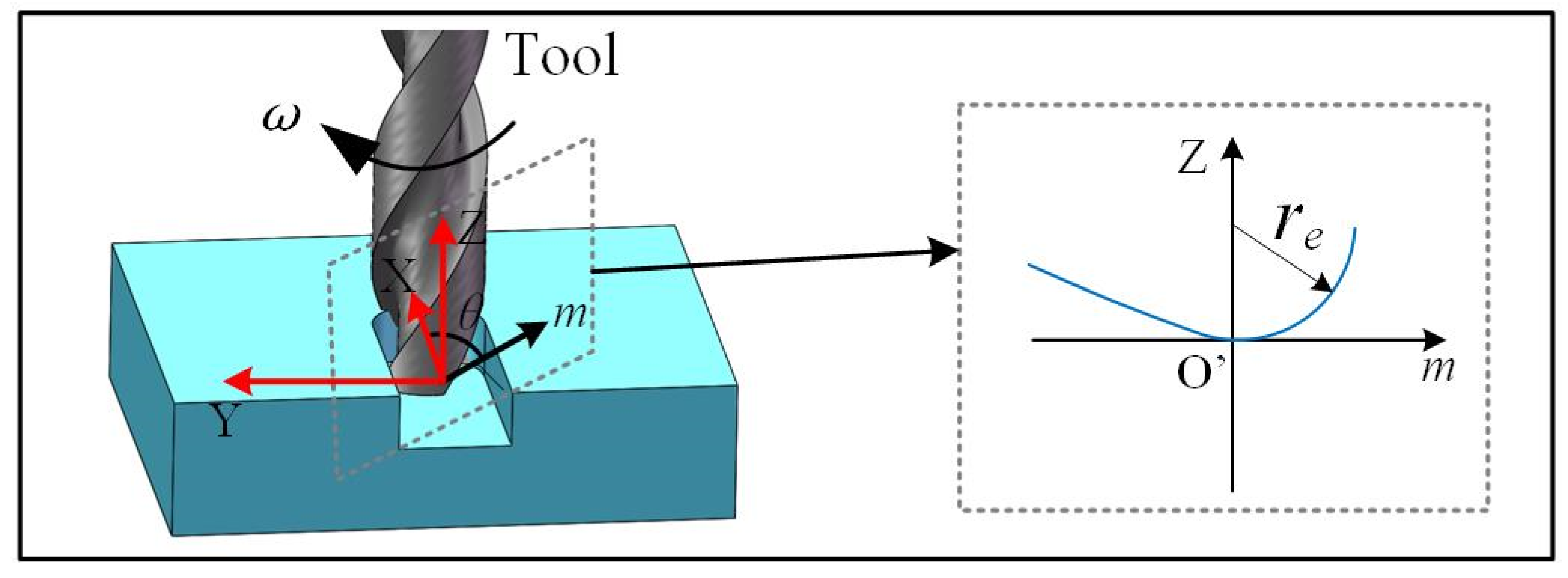
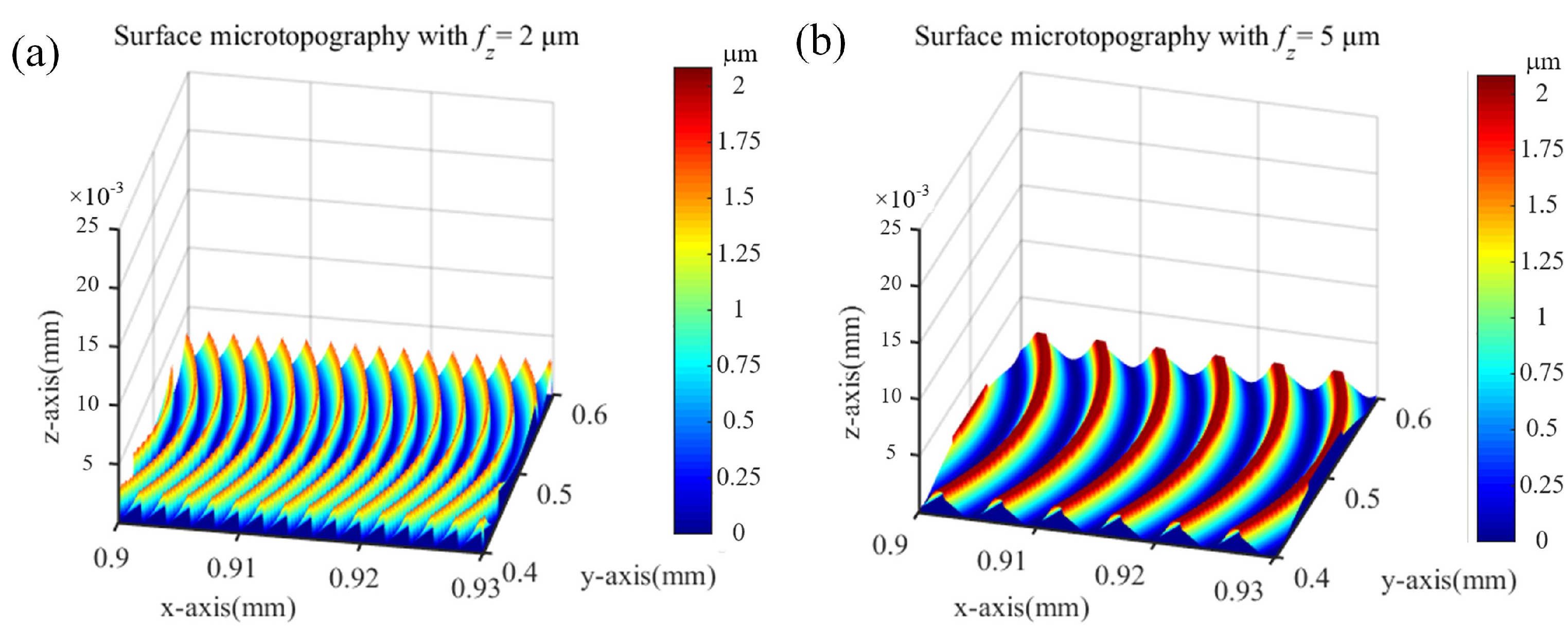
2.2. Three-Dimensional Micro-Milling Surface Modeling
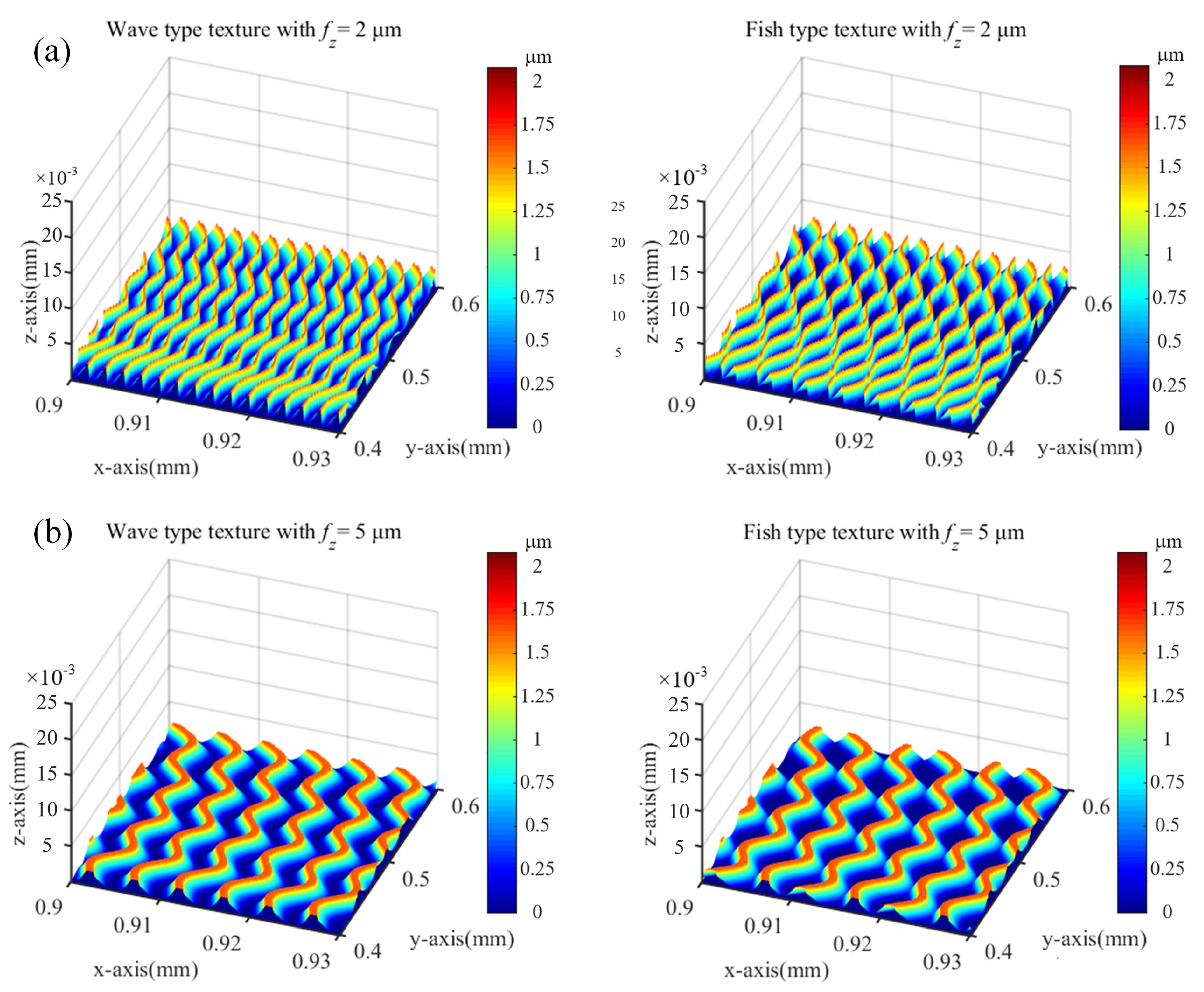
2.3. Vibration-Assisted Micro-Milling Texture Modeling
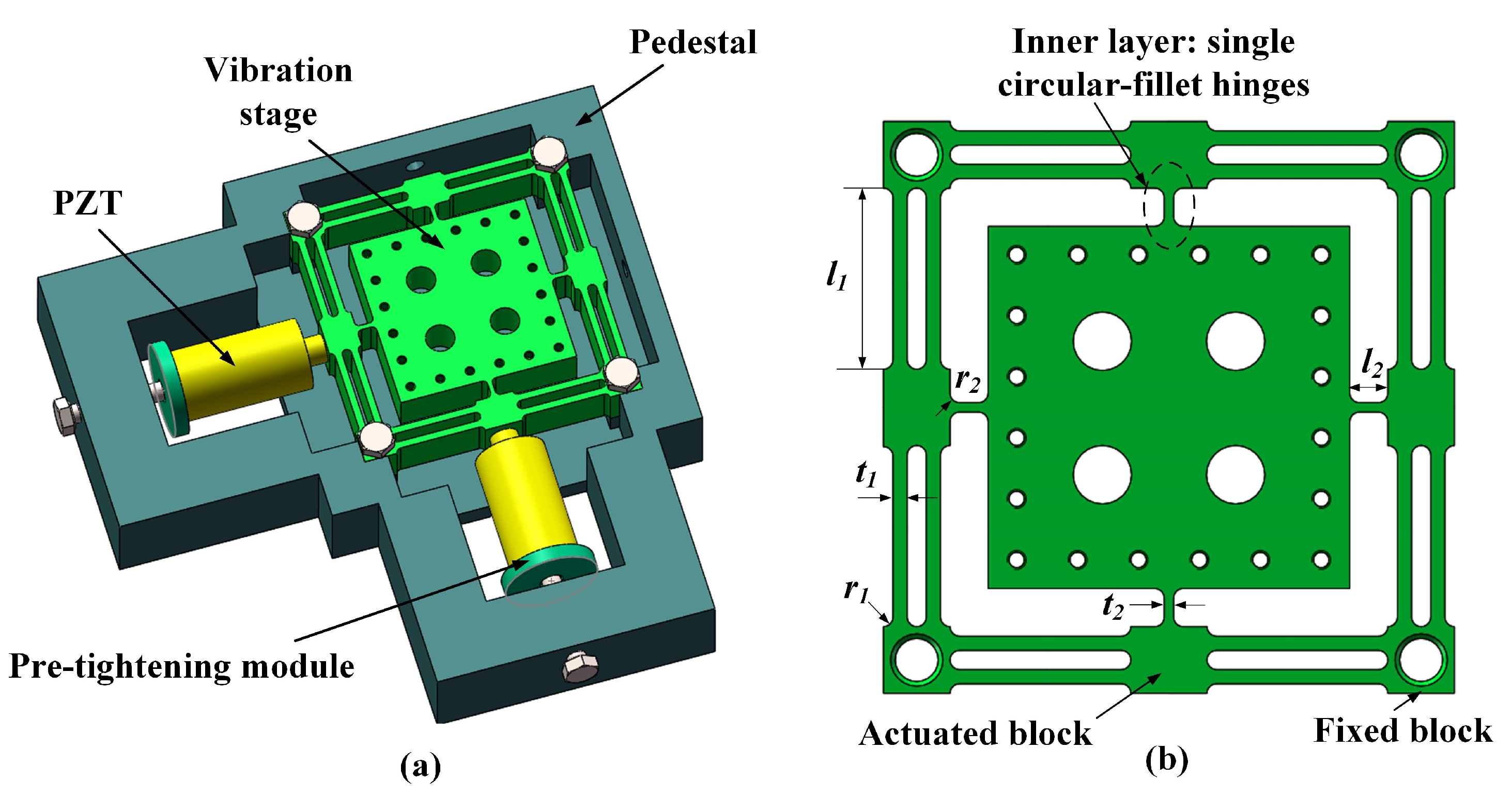
3. Vibration-Stage Design and Optimization
3.1. Vibration-Stage Design
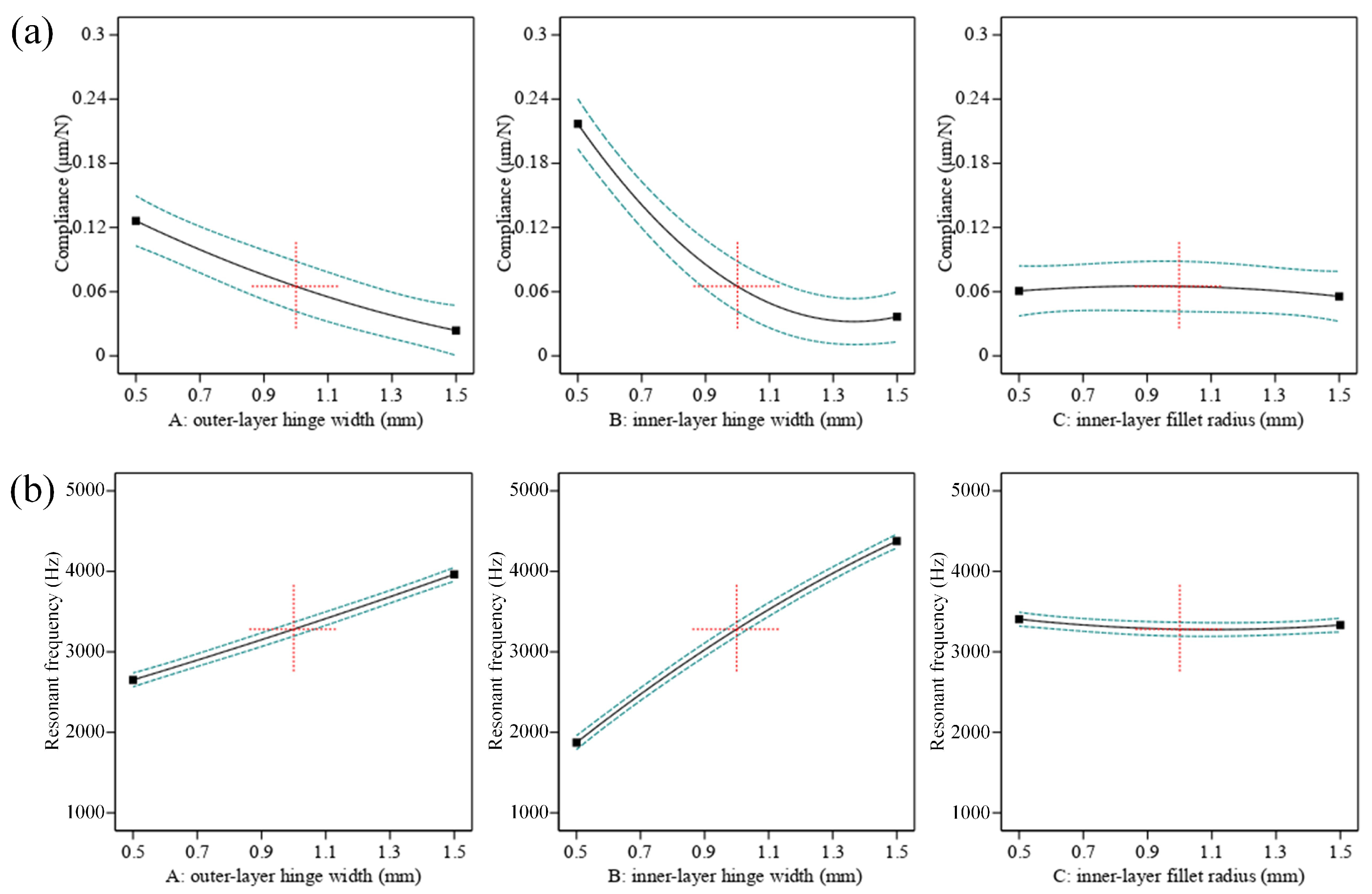
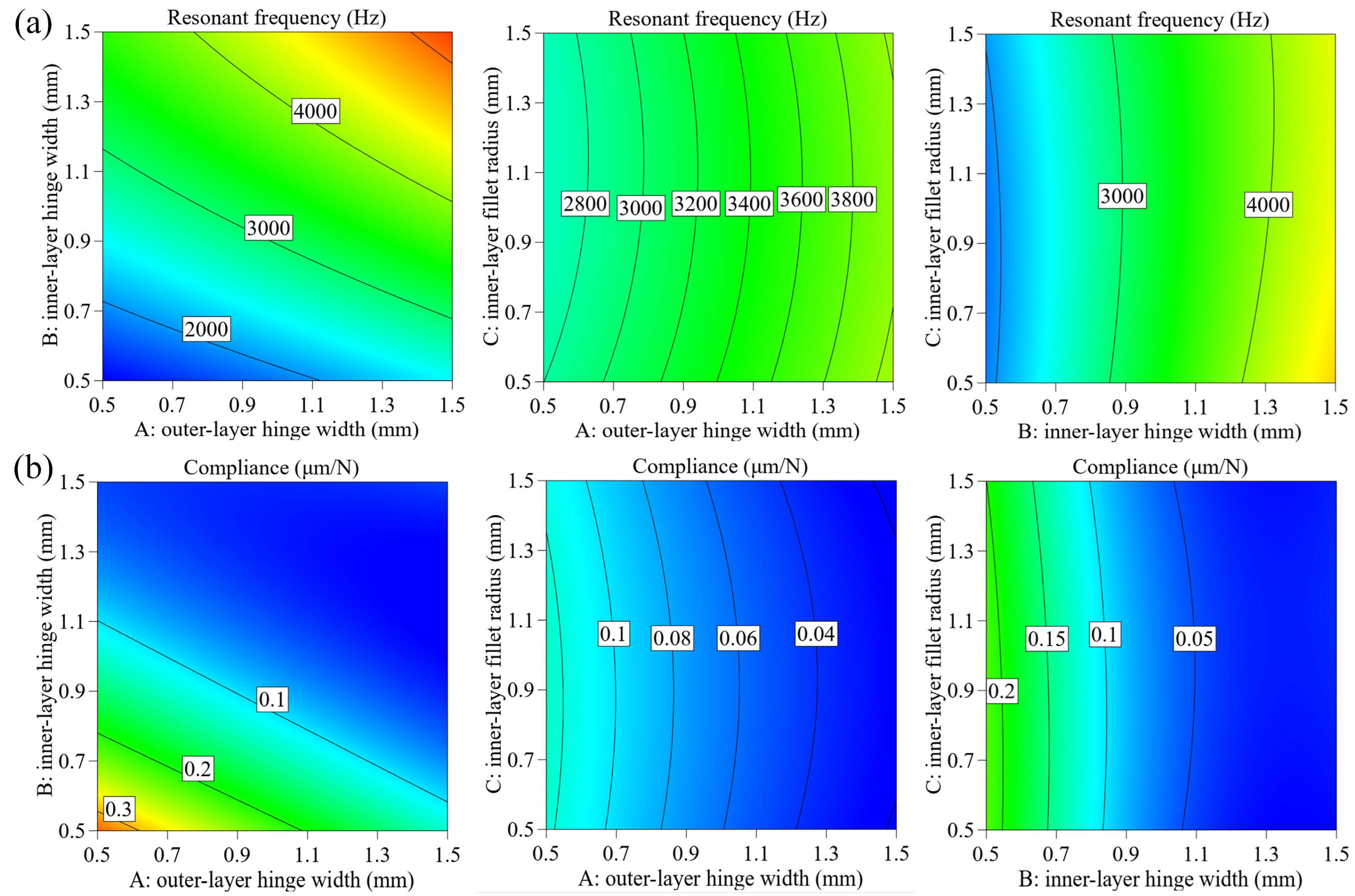
3.2. Parameters Optimization
4. Experimentation
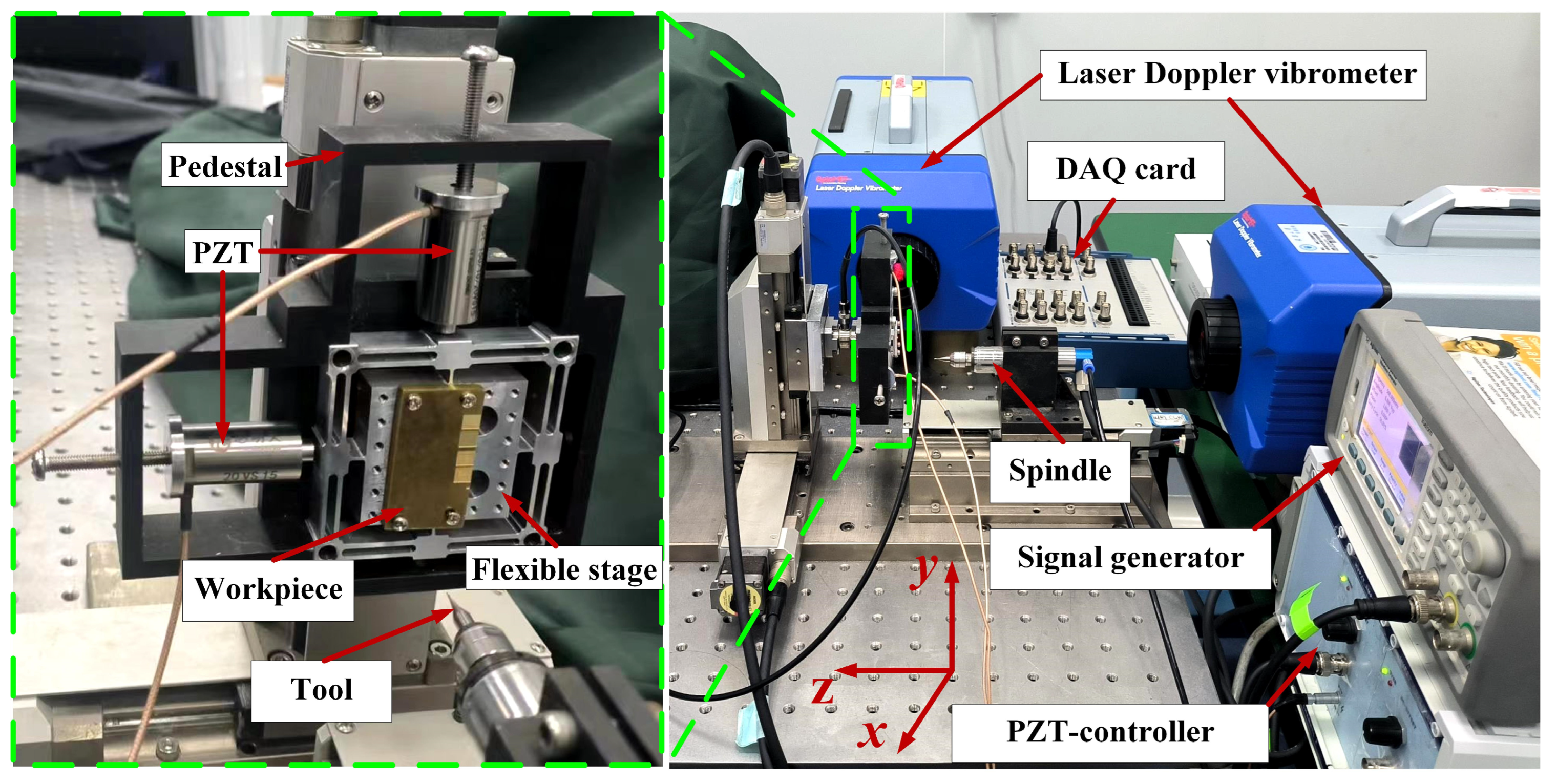
4.1. Experiment Setup
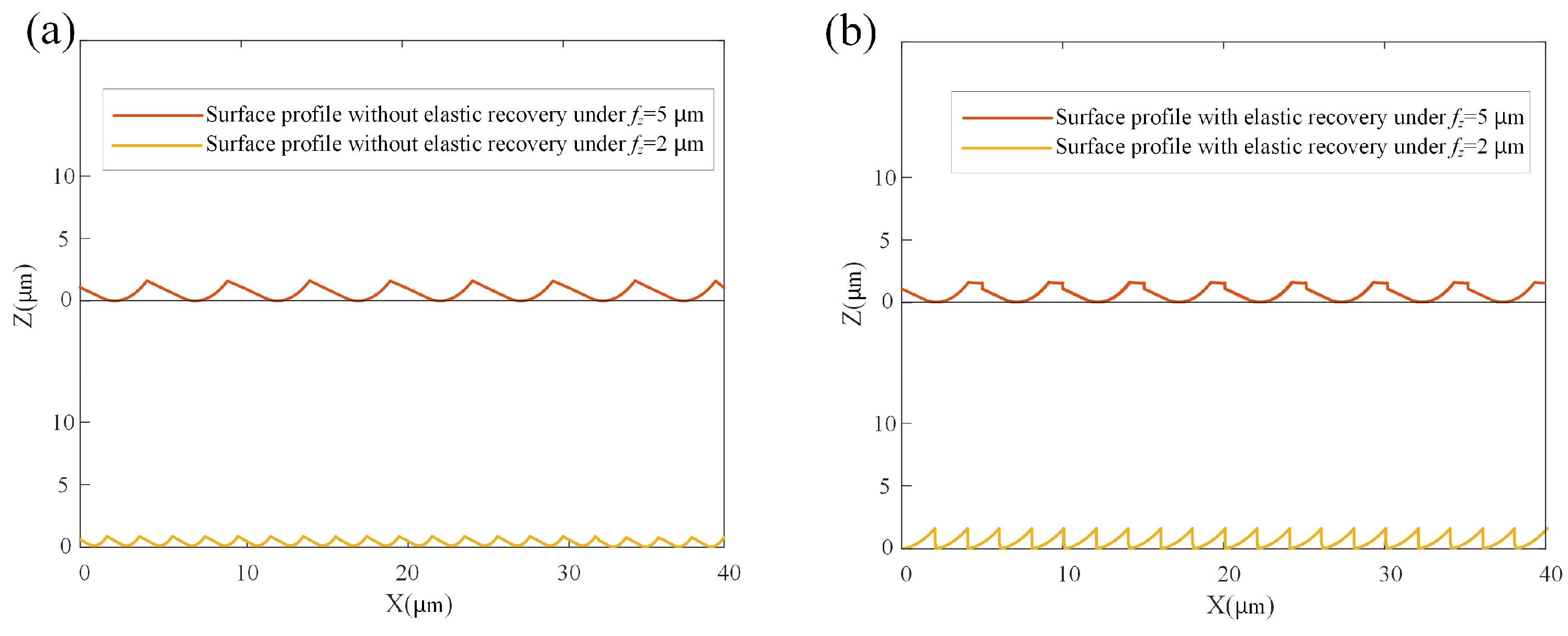
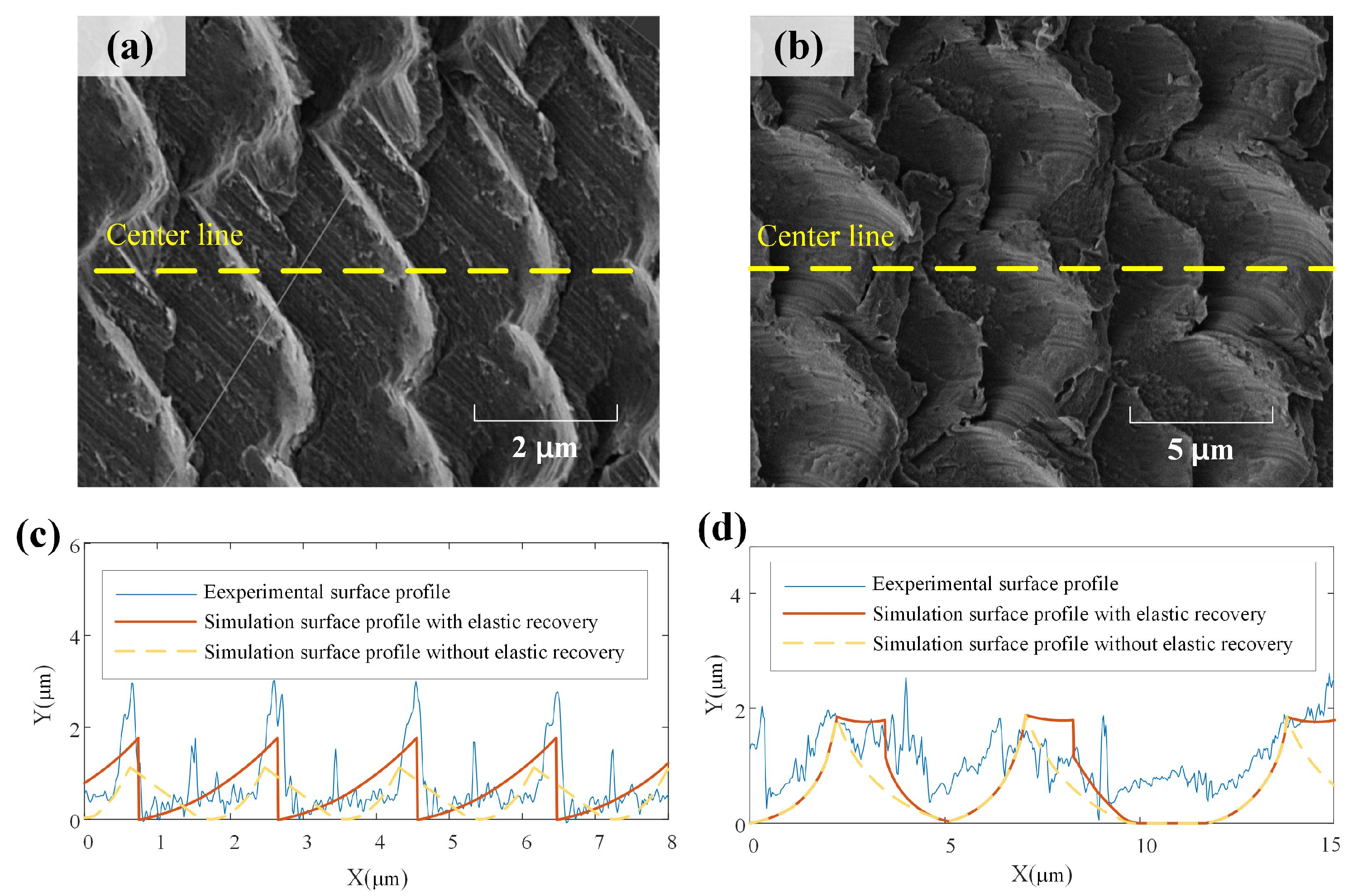
4.2. Results and Discussion
5. Conclusions
- A precise analytical approach was proposed to model the surface generation process in vibration-assisted micro milling. This model incorporates critical size effects, including tool edge geometry, minimum chip thickness, and material elastic recovery, which enables reliable prediction of absolute texture dimensions.
- The modeling approach provides insights into texture formation mechanisms under various machining condition parameters. By controlling the spindle speed and vibration frequency, predictable wave-type and fish scale-type morphologies can be generated, as evidenced by both simulation and experiments.
- A 2-DOF flexible vibration stage was designed and fabricated. The micro-milling experiments demonstrated the feasibility of embedding controlled micro-scale surface patterns onto machined workpieces using this vibration-assisted method. Reasonable consistency was achieved between simulated and experimentally fabricated textures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Order | t1 | t2 | r2 | C | f | Q |
|---|---|---|---|---|---|---|
| 1 | 0.5 | 0.5 | 0.5 | 0.3521 | 1421 | 4.77 × 10−2 |
| 2 | 0.5 | 0.5 | 1 | 0.3598 | 1405 | 5.01 × 10−2 |
| 3 | 0.5 | 0.5 | 1.5 | 0.3111 | 1511 | 3.60 × 10−2 |
| 4 | 0.5 | 1 | 0.5 | 0.0871 | 2857 | 1.10 × 10−3 |
| 5 | 0.5 | 1 | 1 | 0.0957 | 2725 | 1.55 × 10−3 |
| 6 | 0.5 | 1 | 1.5 | 0.0944 | 2744 | 1.48 × 10−3 |
| 7 | 0.5 | 1.5 | 0.5 | 0.0497 | 3783 | 1.48 × 10−5 |
| 8 | 0.5 | 1.5 | 1 | 0.0561 | 3557 | 8.01 × 10−5 |
| 9 | 0.5 | 1.5 | 1.5 | 0.0596 | 3453 | 1.40 × 10−4 |
| 10 | 1 | 0.5 | 0.5 | 0.2126 | 1828 | 1.47 × 10−2 |
| 11 | 1 | 0.5 | 1 | 0.2146 | 1820 | 1.50 × 10−2 |
| 12 | 1 | 0.5 | 1.5 | 0.1918 | 1925 | 1.14 × 10−2 |
| 13 | 1 | 1 | 0.5 | 0.0617 | 3394 | 1.83 × 10−4 |
| 14 | 1 | 1 | 1 | 0.0662 | 3276 | 2.95 × 10−4 |
| 15 | 1 | 1 | 1.5 | 0.0617 | 3393 | 1.84 × 10−4 |
| 16 | 1 | 1.5 | 0.5 | 0.0324 | 4685 | 3.02 × 10−4 |
| 17 | 1 | 1.5 | 1 | 0.0363 | 4425 | 1.50 × 10−4 |
| 18 | 1 | 1.5 | 1.5 | 0.0371 | 4375 | 1.27 × 10−4 |
| 19 | 1.5 | 0.5 | 0.5 | 0.1119 | 2519 | 2.60 × 10−3 |
| 20 | 1.5 | 0.5 | 1 | 0.1123 | 2516 | 2.63 × 10−3 |
| 21 | 1.5 | 0.5 | 1.5 | 0.1050 | 2601 | 2.12 × 10−3 |
| 22 | 1.5 | 1 | 0.5 | 0.0455 | 3953 | 1.10 × 10−5 |
| 23 | 1.5 | 1 | 1 | 0.0479 | 3853 | 9.03 × 10−6 |
| 24 | 1.5 | 1 | 1.5 | 0.0439 | 4023 | 1.87 × 10−5 |
| 25 | 1.5 | 1.5 | 0.5 | 0.0241 | 5431 | 9.76 × 10−4 |
| 26 | 1.5 | 1.5 | 1 | 0.0266 | 5170 | 7.02 × 10−4 |
| 27 | 1.5 | 1.5 | 1.5 | 0.0263 | 5194 | 7.25 × 10−4 |
References
- Maboudian, R.; Howe, R.T. Critical Review: Adhesion in Surface Micromechanical Structures. J. Vac. Sci. Technol. B 1997, 15, 1–20. [Google Scholar] [CrossRef]
- Jung, Y.C.; Bhushan, B. Contact Angle, Adhesion and Friction Properties of Micro-and Nanopatterned Polymers for Superhydrophobicity. Nanotechnology 2006, 17, 4970–4980. [Google Scholar] [CrossRef]
- Moskal, D.; Martan, J.; Honner, M. Scanning Strategies in Laser Surface Texturing: A Review. Micromachines 2023, 14, 1241. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Chen, G.; Liu, Q.; Pan, B.; Chen, W. Investigation on the Micro Cutting Mechanism and Surface Topography Generation in Ultraprecision Diamond Turning. Micromachines 2022, 13, 381. [Google Scholar] [CrossRef] [PubMed]
- Alpas, A.T.; Zhang, J. Effect of Microstructure (Particulate Size and Volume Fraction) and Counterface Material on the Sliding Wear Resistance of Particulate-Reinforced Aluminum Matrix Composites. Metall. Mater. Trans. A 1994, 25, 969–983. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, L.; Fang, Y.; Dun, A.; Zhao, J.; Xu, X.; Zhu, X. Application of Flow Field Analysis in Ion Beam Figuring for Ultra-Smooth Machining of Monocrystalline Silicon Mirror. Micromachines 2022, 13, 318. [Google Scholar] [CrossRef] [PubMed]
- Derevyanko, D.I.; Shelkovnikov, V.V.; Orlova, N.A.; Goldenberg, B.G.; Lemzyakov, A.G.; Korolkov, V.P. Fabrication of High-Aspect-Ratio Microstructures for LIGA-Technology by Sinchrotron Radiation Polymerisation of Thetetraacrylate Monomer. Phys. Procedia 2017, 86, 122–126. [Google Scholar] [CrossRef]
- Takahata, K.; Gianchandani, Y.B. Batch Mode Micro-Electro-Discharge Machining. J. Microelectromech. Syst. 2002, 11, 102–110. [Google Scholar] [CrossRef]
- Scott, S.M.; Ali, Z. Fabrication Methods for Microfluidic Devices: An Overview. Micromachines 2021, 12, 319. [Google Scholar] [CrossRef]
- Axinte, D.; Huang, H.; Yan, J.; Liao, Z. What Micro-Mechanical Testing Can Reveal about Machining Processes. Int. J. Mach. Tools Manuf. 2022, 183, 103964. [Google Scholar] [CrossRef]
- Song, B.; Jing, X.; Yang, H.; Zheng, S.; Zhang, D.; Li, H. On Unsteady-Cutting State Material Separation and Dead Metal Zone Modeling Considering Chip Fracture. J. Manuf. Process 2023, 108, 62–78. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, W.; Huo, D. Review of Vibration Devices for Vibration-Assisted Machining. Int. J. Adv. Manuf. Technol. 2020, 108, 1631–1651. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, L.; Zhang, G.; Ni, C.; Lin, B. Review of Ultrasonic Vibration-Assisted Machining in Advanced Materials. Int. J. Mach. Tools Manuf. 2020, 156, 103594. [Google Scholar] [CrossRef]
- Yang, Z.; Zou, P.; Zhou, L.; Wang, X.; Usman, M.M. Modeling and Experimental Analysis of Surface Topography Generation Mechanism during Ultrasonic Vibration-Assisted Grinding. Precis. Eng. 2023, 80, 30–44. [Google Scholar] [CrossRef]
- Feng, Y.; Hsu, F.C.; Lu, Y.T.; Lin, Y.F.; Lin, C.T.; Lin, C.F.; Lu, Y.C.; Liang, S.Y. Force Prediction in Ultrasonic Vibration-Assisted Milling. Mach. Sci. Technol. 2020, 25, 307–330. [Google Scholar] [CrossRef]
- Zhu, W.L.; Zhu, Z.; He, Y.; Ehmann, K.F.; Ju, B.F.; Li, S. Development of a Novel 2-D Vibration-Assisted Compliant Cutting System for Surface Texturing. IEEE-ASME Trans. Mechatron. 2017, 22, 1796–1806. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, D.; Zhu, H.; Ehmann, K.F. Machining of Micro Grayscale Images on Freeform Surfaces by Vibration-Assisted Cutting. J. Manuf. Process 2020, 58, 660–667. [Google Scholar] [CrossRef]
- Jin, X.; Xie, B. Experimental Study on Surface Generation in Vibration-Assisted Micro-Milling of Glass. Int. J. Adv. Manuf. Technol. 2015, 81, 507–512. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, W.; Chen, X.; Zhang, Y.; Xu, C.; Wang, K.; Wang, W.; Jiang, X. Generation Mechanism of Surface Micro-Texture in Axial Ultrasonic Vibration-Assisted Milling (AUVAM). Int. J. Adv. Manuf. Technol. 2022, 122, 1651–1667. [Google Scholar] [CrossRef]
- Chen, W.; Huo, D.; Shi, Y.; Hale, J.M. State-of-the-Art Review on Vibration-Assisted Milling: Principle, System Design, and Application. Int. J. Adv. Manuf. Technol. 2018, 97, 2033–2049. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, W.; Huo, D. Investigation on the Tool Wear Suppression Mechanism in Non-Resonant Vibration-Assisted Micro Milling. Micromachines 2020, 11, 380. [Google Scholar] [CrossRef]
- Zheng, L.; Fang, M.; Chen, W.; Huo, D.; Li, H. Enhancement Mechanism of Fish-Scale Surface Texture on Flow Switching and Mixing Efficiency in Microfluidic Chips. Langmuir 2023, 39, 7396–7407. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Zhibing, L.; Xibin, W.; Tao, H. Experimental Study on Cutting Force and Surface Quality in Ultrasonic Vibration-Assisted Milling of C/SiC Composites. Int. J. Adv. Manuf. Technol. 2021, 112, 2003–2014. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, W.; Huo, D.; Lyu, X. Design, Analysis, and Control of a Two-Dimensional Vibration Device for Vibration-Assisted Micromilling. IEEE-ASME Trans. Mechatron. 2020, 25, 1510–1518. [Google Scholar] [CrossRef]
- Börner, R.; Winkler, S.; Junge, T.; Titsch, C.; Schubert, A.; Drossel, W.G. Generation of Functional Surfaces by Using a Simulation Tool for Surface Prediction and Micro Structuring of Cold-Working Steel with Ultrasonic Vibration Assisted Face Milling. J. Mater. Process Technol. 2018, 255, 749–759. [Google Scholar] [CrossRef]
- Ding, H.; Chen, S.J.; Ibrahim, R.; Cheng, K. Investigation of the Size Effect on Burr Formation in Two-Dimensional Vibration-Assisted Micro End Milling. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2011, 225, 2032–2039. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, L.; Huo, D.; Chen, Y. Surface Texture Formation by Non-Resonant Vibration Assisted Micro Milling. J. Micromech. Microeng. 2018, 28, 025006. [Google Scholar] [CrossRef]
- Zheng, L.; Chen, W.; Pozzi, M.; Teng, X.; Huo, D. Modulation of Surface Wettability by Vibration Assisted Milling. Precis. Eng. 2019, 55, 179–188. [Google Scholar] [CrossRef]
- Lv, B.; Lin, B.; Cao, Z.; Liu, W.; Wang, G. Numerical Simulation and Experimental Investigation of Structured Surface Generated by 3D Vibration-Assisted Milling. J. Manuf. Process 2023, 89, 371–383. [Google Scholar] [CrossRef]
- Yuan, Y.; Yu, K.; Zhang, C.; Chen, Q.; Yang, W. Generation of Textured Surfaces by Vibration-Assisted Ball-End Milling. Nanomanuf. Metrol. 2023, 6, 19. [Google Scholar] [CrossRef]
- Jing, X.; Song, B.; Xu, J.; Zhang, D. Mathematical Modeling and Experimental Verification of Surface Roughness in Micro-End-Milling. Int. J. Adv. Manuf. Technol. 2022, 120, 7627–7637. [Google Scholar] [CrossRef]
- Song, B.; Jing, X.; Ren, Y.; Ren, Y.; Li, H. Design and Experimentation of a Novel Separable Vibration-Assisted Stage. Nanomanuf. Metrol. 2023, 6, 23. [Google Scholar] [CrossRef]


| Tool Radius (μm) | Spindle Speed (rpm) | Tool Edge Radius (μm) | MUCT (μm) | Material Elastic Recovery Ratio |
|---|---|---|---|---|
| 600 | 5000 | 5 | 2.4 | 0.2 |
| No | Spindle Speed (rpm) | Vibration Frequency (Hz) | Vibration Amplitude (µm) | Phase Difference | Feed Per Tooth (µm) |
|---|---|---|---|---|---|
| Test a | 5000 | 2417 | 2 | 90 | 2 |
| Test b | 5000 | 2500 | 2 | 90 | 2 |
| Parameters | L1 | L2 | b | s1 | s2 |
| Value (mm) | 4 | 17 | 10 | 8 | 7 |
| Material | Density | Young’s Modulus | Poisson’s Ratio | Yield Strength | Tensile Strength |
|---|---|---|---|---|---|
| Al7075-T651 | 2.81 g/cm3 | 71 GPa | 0.33 | 455 MPa | 524 MPa |
| No | Spindle Speed (rpm) | Vibration Frequency (Hz) | Vibration Amplitude (µm) | Feed Per Tooth (µm) |
|---|---|---|---|---|
| Test 1 | 5000 | 0 | 0 | 2 |
| Test 2 | 5000 | 2500 | 2 | 2 |
| Test 3 | 5000 | 2417 | 2 | 2 |
| Test 4 | 5000 | 2500 | 2 | 5 |
| Test 5 | 5000 | 2417 | 2 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.; Zhang, D.; Jing, X.; Ren, Y.; Chen, Y.; Li, H. Theoretical and Experimental Investigation of Surface Textures in Vibration-Assisted Micro Milling. Micromachines 2024, 15, 139. https://doi.org/10.3390/mi15010139
Song B, Zhang D, Jing X, Ren Y, Chen Y, Li H. Theoretical and Experimental Investigation of Surface Textures in Vibration-Assisted Micro Milling. Micromachines. 2024; 15(1):139. https://doi.org/10.3390/mi15010139
Chicago/Turabian StyleSong, Bowen, Dawei Zhang, Xiubing Jing, Yingying Ren, Yun Chen, and Huaizhong Li. 2024. "Theoretical and Experimental Investigation of Surface Textures in Vibration-Assisted Micro Milling" Micromachines 15, no. 1: 139. https://doi.org/10.3390/mi15010139
APA StyleSong, B., Zhang, D., Jing, X., Ren, Y., Chen, Y., & Li, H. (2024). Theoretical and Experimental Investigation of Surface Textures in Vibration-Assisted Micro Milling. Micromachines, 15(1), 139. https://doi.org/10.3390/mi15010139








