A High-Accuracy RC Time Constant Auto-Tuning Scheme for Integrated Continuous-Time Filters
Abstract
:1. Introduction
2. Conventional Master–Slave Tuning Scheme
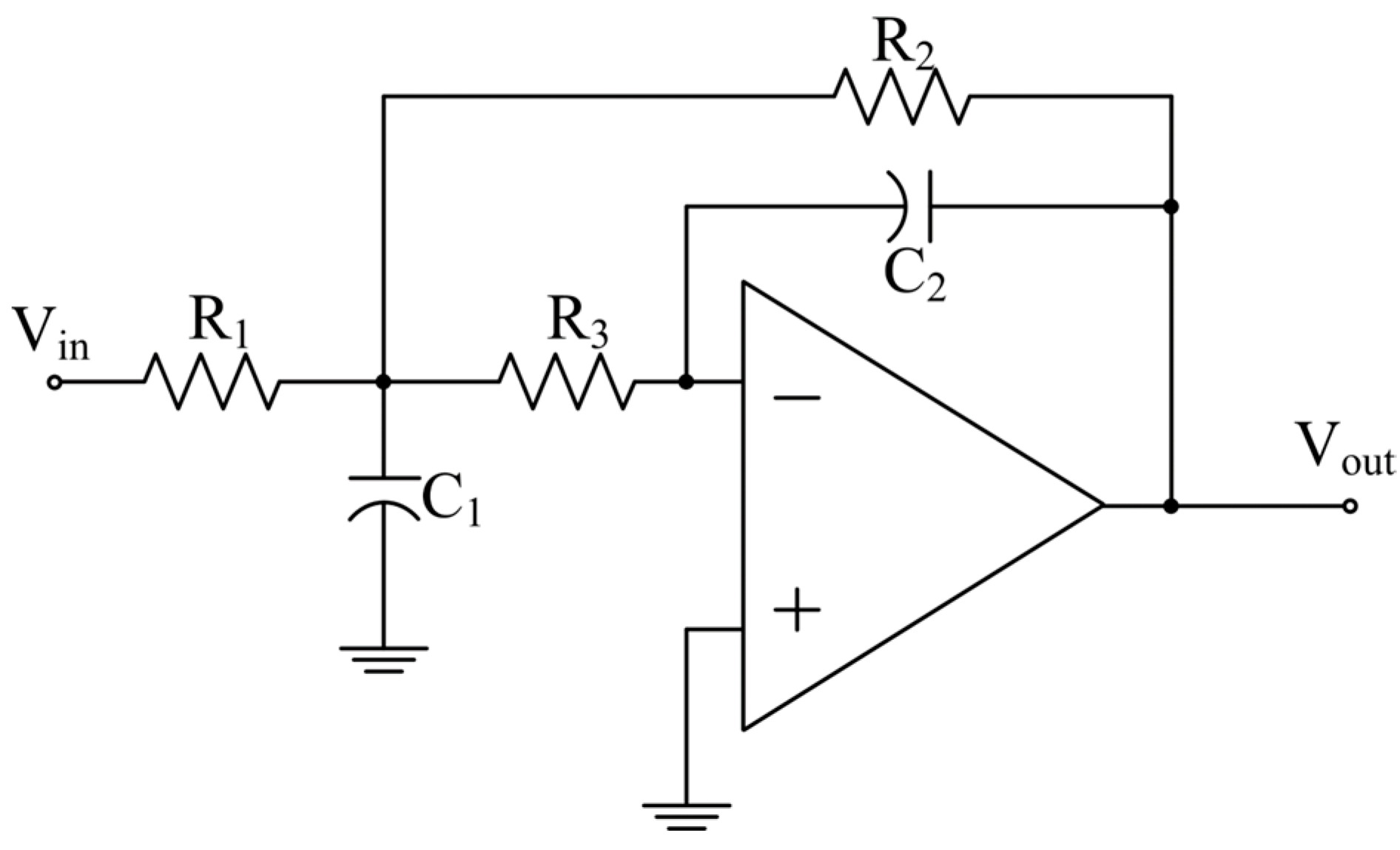
2.1. Active-RC Filter Performance under PVT Variation
2.2. The Classic Master–Slave Auto-Tuning Scheme
2.3. Discussion on Nonidealities
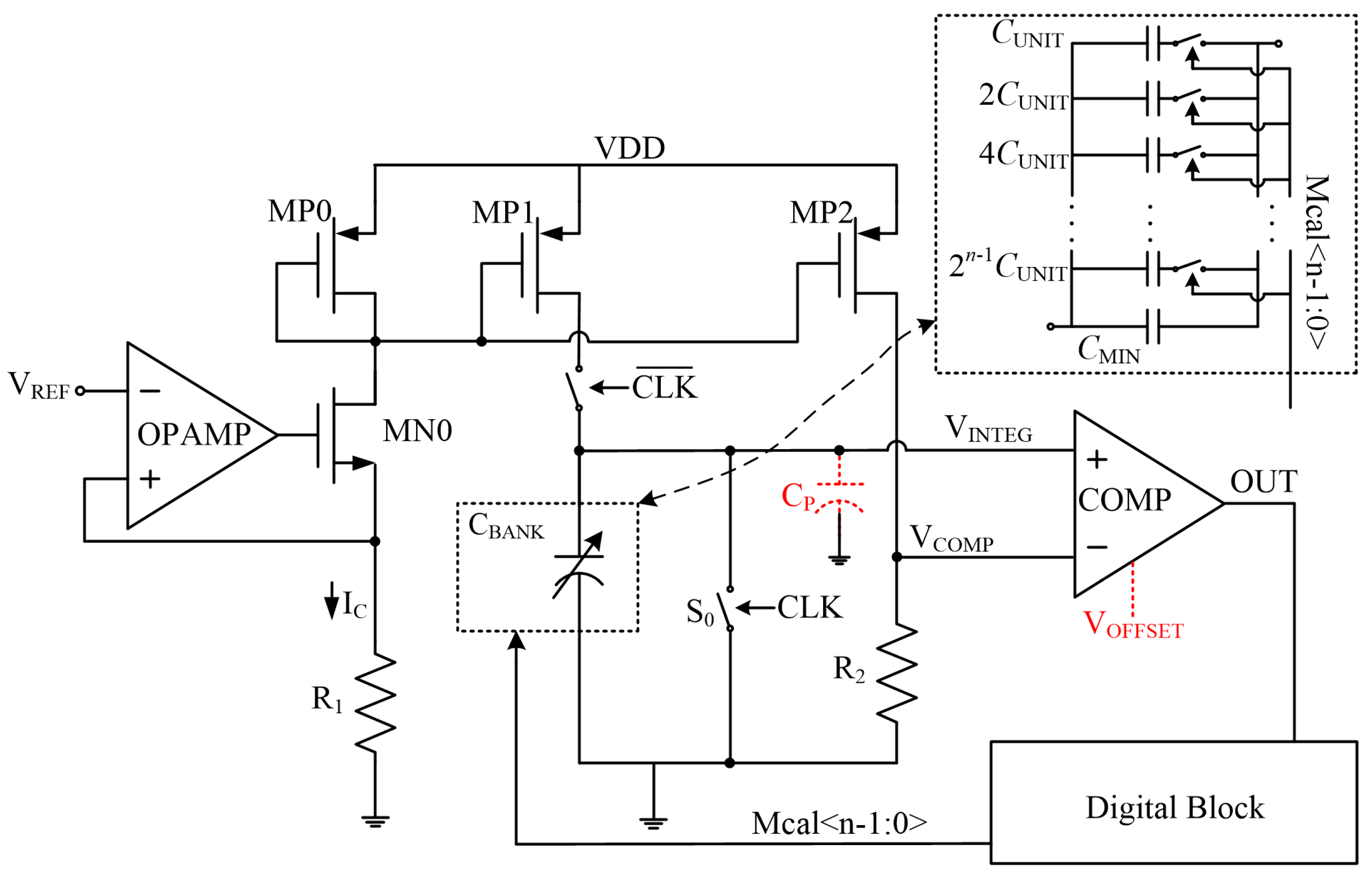
3. Proposed Method
- Parasitic capacitance cancelation technique:
- 2.
- Symmetric comparison technique:
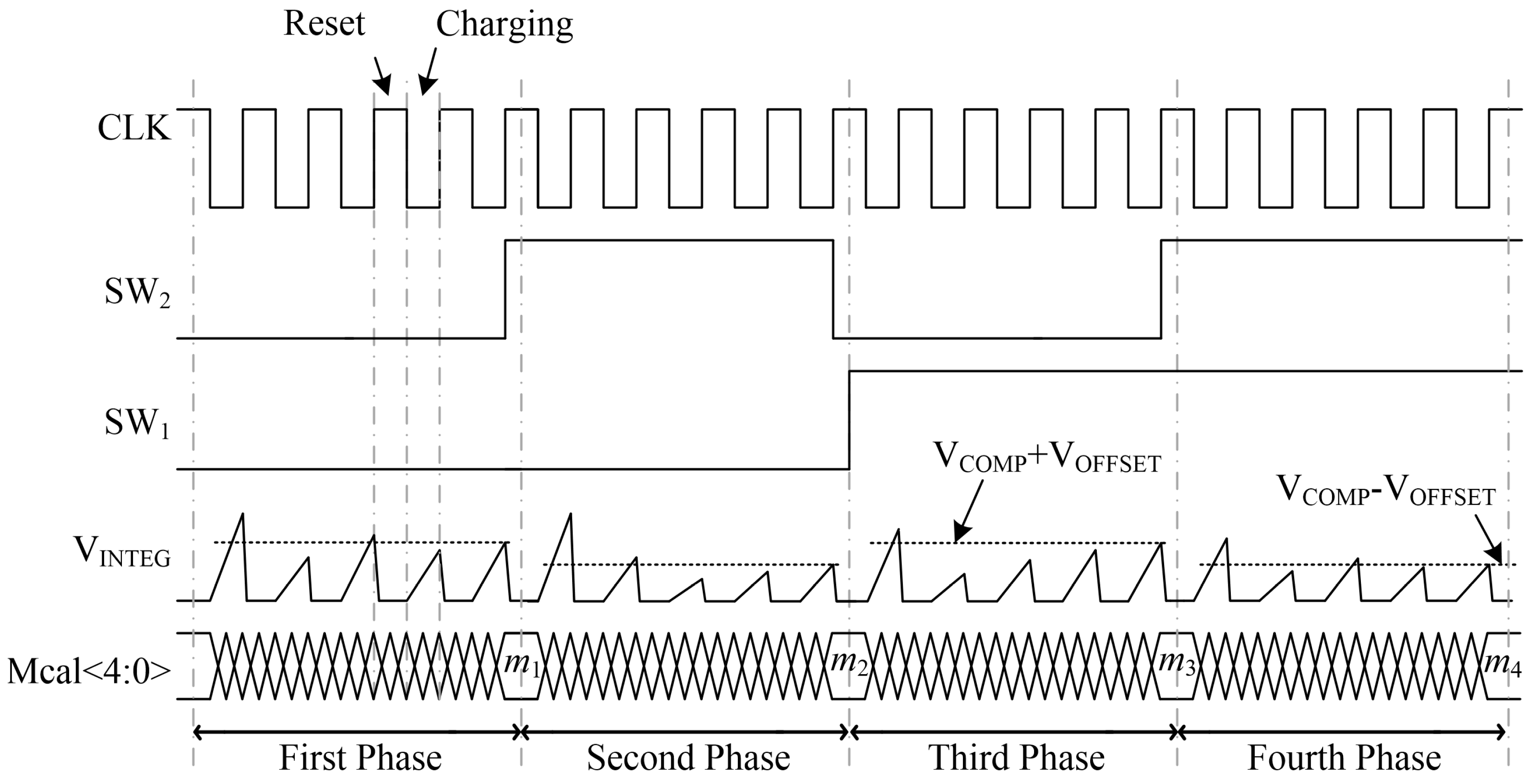
- For the first phase, SW1 and SW2 are both set to 0. The multiplexers pass VCOMP to the negative input of the comparator and VINTEG to the positive input. The positive output of the comparator is sampled as OUT. The redundant CBANK and transistor MP2 are cut off by S1 and S2. The control word is searched by means of the successive approximation procedure. The resultant value of the control word Mcal<4:0> is latched up as m1.
- For the second phase, SW1 stays 0 and SW2 switches to 1. The input ports of the comparator are reversed by the multiplexers, as well as the output ports. The same calibration procedure is repeated for a second time, and the resultant control word is latched up as m2.
- For the third phase, SW1 switches to 1 and SW2 switches to 0. In this phase, MP3 and the redundant CBANK take part in charging VINTEG. Two capacitor banks are charged by 2IC at the same node. The connections of the multiplexers are the same as in phase 1. The control word m3 is obtained by a tuning procedure.
- For the fourth phase, SW1 and SW2 are both 1. VCOMP is passed to the positive input of the comparator and VINTEG is passed to the negative input. The redundant part is involved as in phase 3. The calibration result is m4.
4. Circuit Design and Simulation Results
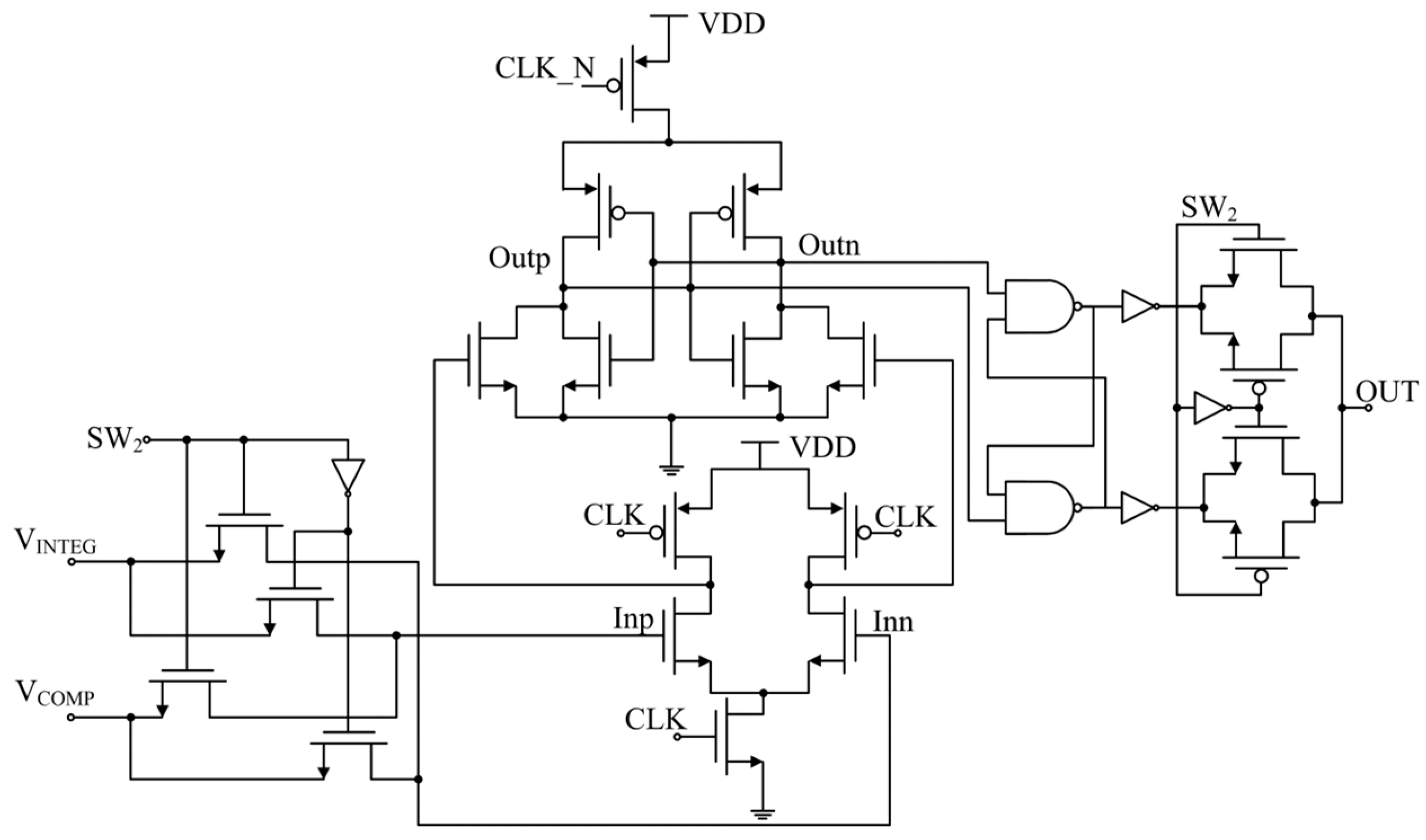
4.1. Circuit Design
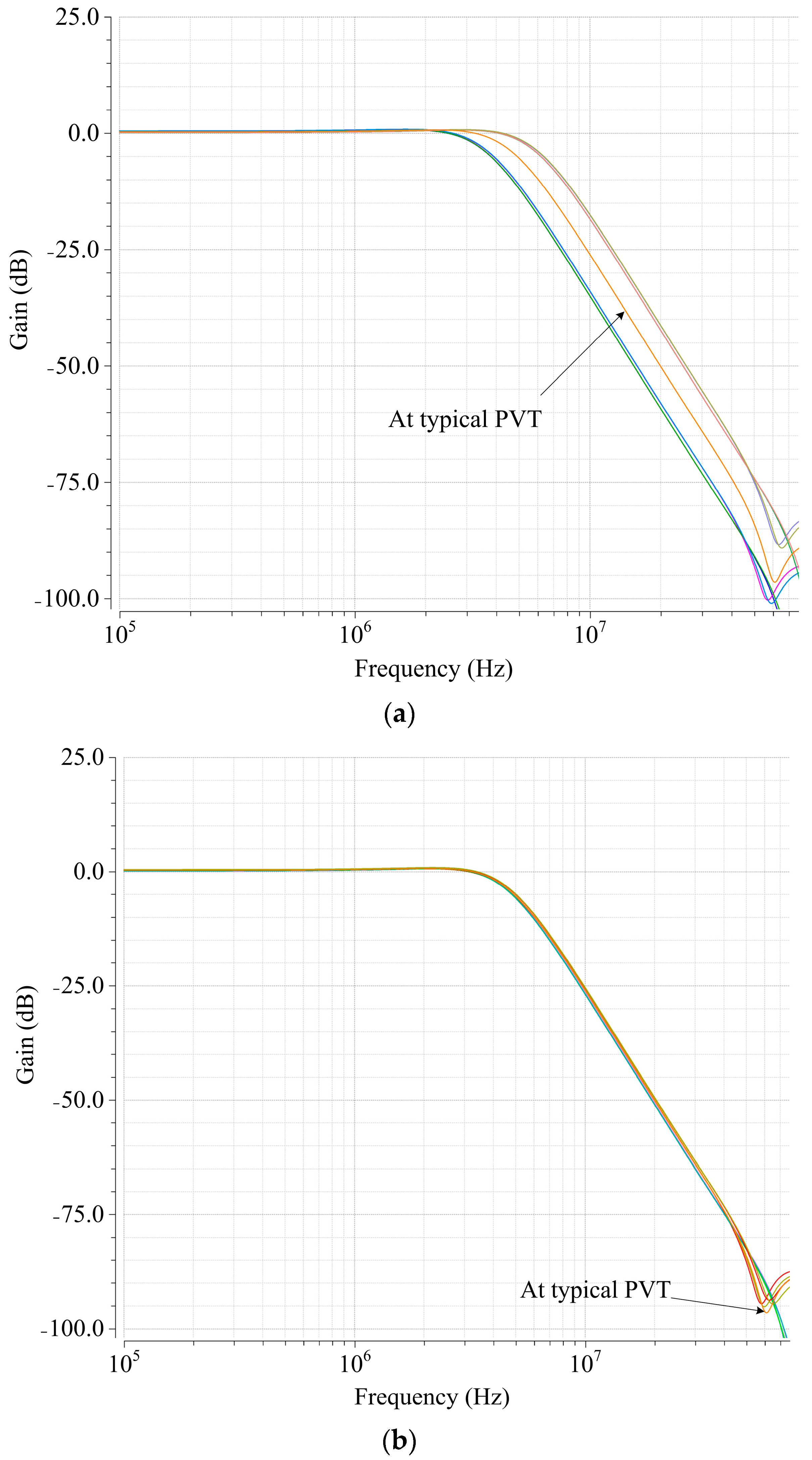
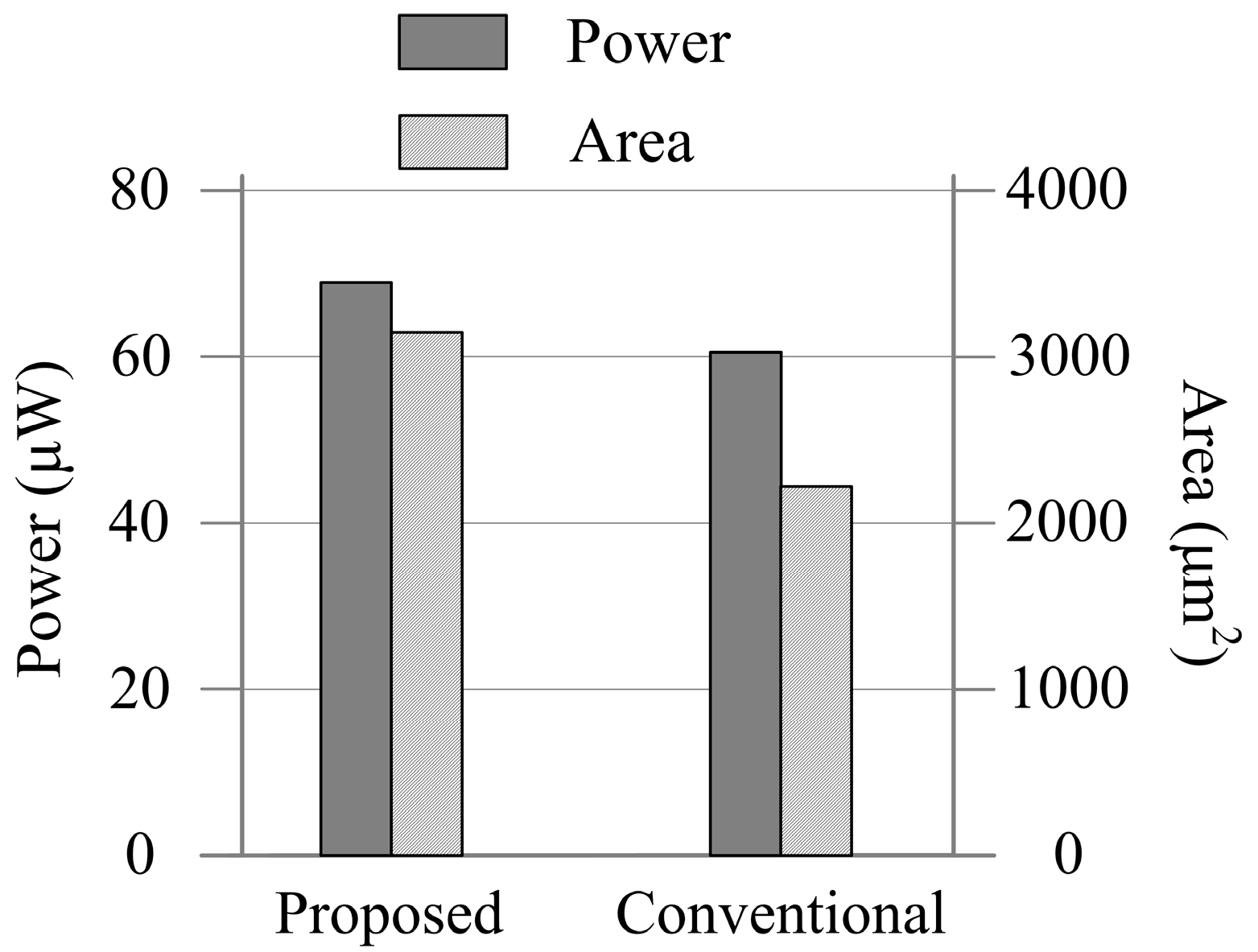
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lavalle-Aviles, F.; Sánchez-Sinencio, E. A 0.6-V Power-Efficient Active-RC Analog Low-Pass Filter with Cutoff Frequency Selection. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 1757–1769. [Google Scholar] [CrossRef]
- Rasekh, A.; Bakhtiar, M.S. Design of Low-Power Low-Area Tunable Active RC Filters. IEEE Trans. Circuits Syst. II: Express Briefs 2018, 65, 6–10. [Google Scholar] [CrossRef]
- Gao, S.; Chen, Z.-J.; Sun, X.; Yang, S.; Li, B.; Lin, X.-L. A Reconfigurable Active-RC Filter with Variable Gain and an RC-Reused Tuning Circuit. In Proceedings of the 2022 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Shenzhen, China, 11–13 November 2022. [Google Scholar]
- Compassi-Severo, L.; Noije, W.V. A 0.4-V 10.9-μW/Pole Third-Order Complex BPF for Low Energy RF Receivers. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 2017–2026. [Google Scholar] [CrossRef]
- Sanabria-Borbón, A.C.; Sánchez-Sinencio, E. Synthesis of High-Order Continuously Tunable Low-Pass Active-R Filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1841–1854. [Google Scholar] [CrossRef]
- Miti, D.; Jovanovi, G.; Stojev, M.; Anti, D. Fast Locking Time Biquadratic Band-Pass Filter Utilizing Nonlinear Sliding-Mode Controller. J. Circuits Syst. Comput. 2021, 30, 2150154. [Google Scholar] [CrossRef]
- Kledrowetz, V.; Haze, J.; Prokop, R.; Fujcik, L. An Active Resistor with a Lower Sensitivity to Process Variations, and its Application in Current Reference. IEEE Access 2020, 8, 197263–197275. [Google Scholar] [CrossRef]
- Zhang, C.; Shang, L.; Wang, Y.; Tang, L. A CMOS Programmable Fourth-Order Butterworth Active-RC Low-Pass Filter. Electronics 2020, 9, 204. [Google Scholar] [CrossRef]
- Osman, H.; Life, E.S.-S. A PVT-Resilient, Highly-Linear Fifth-Order Ring-Oscillator-Based Filter. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4295–4308. [Google Scholar] [CrossRef]
- Karolis, K.; Romualdas, N. A method for continuous tuning of MOSFET–RC filters with extended control range. J. Electr. Eng. 2016, 67, 449–453. [Google Scholar]
- Kumar, V.; Mehra, R.; Islam, A. A 2.5 GHz Low Power, High-Q, Reliable Design of Active Bandpass Filter. IEEE Trans. Device Mater. Reliab. 2017, 17, 229–244. [Google Scholar] [CrossRef]
- Gao, T.; Li, W.; Chen, Y.; Li, N.; Ren, J. A 5.5mW 80-400MHz Gm-C low pass filter with a unique auto-tuning system. IEICE Electron. Express 2011, 8, 1034–1039. [Google Scholar] [CrossRef]
- Abdolmaleki, M.; Dousti, M.; Tavakoli, M.B. Design and simulation of tunable low-pass Gm-C filter with 1 GHz cutoff frequency based on CMOS inventers for high speed telecommunication applications. Analog. Integr. Circuits Signal Process. 2019, 100, 279–286. [Google Scholar] [CrossRef]
- Abdolmaleki, M.; Dousti, M.; Tavakoli, M.B. Design and simulation of fourth order low-pass Gm-C filter with novel auto-tuning circuit in 90 nm CMOS. Analog. Integr. Circuits Signal Process. 2021, 107, 451–461. [Google Scholar] [CrossRef]
- Xia, B.; Yan, S.; Sanchez-Sinencio, E. An RC time constant auto-tuning structure for high linearity continuous-time /spl Sigma//spl Delta/ modulators and active filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2004, 51, 2179–2188. [Google Scholar] [CrossRef]
- Huang, H.Y.; Wu, C.C.; Luo, C.H. An MICS band frequency synthesizer using active inductor and auto-calibration scheme. Int. Microelectron. J. 2021, 43, 592–599. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, Q.; Shi, C.; Zhang, R. A 1.2 GHz bandwidth and 88 dB gain range analog baseband for multi-standard 60 GHz applications. IEICE Electron. Express 2022, 17, 20190742. [Google Scholar] [CrossRef]
- Jin, B.; Chen, Z.; Liu, X.; Shen, Z.; Bao, Y.; Xing, Y.; Wan, P. A SAR-based Fast Automatic Frequency Tuning Circuit in a 3-th Order Active-RC Complex Filter. In Proceedings of the 2021 IEEE 15th International Conference on Anti-counterfeiting, Security, and Identification (ASID), Xiamen, China, 29–31 October 2021. [Google Scholar]
- Guo, Y.; Jin, J.; Liu, X.; Zhou, J. An Inverter-Based Continuous Time Sigma Delta ADC with Latency-Free DAC Calibration. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3630–3642. [Google Scholar] [CrossRef]
- Lee, S.; Shi, C.; Wang, J.; Sanabria, A.; Osman, H.; Hu, J.; Sanchez-Sinencio, E.A. Built-In Self-Test and In Situ Analog Circuit Optimization Platform. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3445–3458. [Google Scholar] [CrossRef]
- Talebzadeh, J.; Kale, I. A novel two-channel continuous-time time-interleaved 3rd-order sigma-delta modulator with integrator-sharing topology. Analog. Integr. Circuits Signal Process 2018, 95, 375–385. [Google Scholar] [CrossRef]
- Ju, C.; Li, X.; Zou, J.; Wei, Q.; Zhou, B.; Zhang, R. An Auto-Tuning Continuous-Time Bandpass Sigma-Delta Modulator with Signal Observation for MEMS Gyroscope Readout Systems. Sensors 2020, 20, 1973. [Google Scholar] [CrossRef]
- Hughes, J.B.; Bird, N.C.; Soin, R.S. Self-tuned RC-active filters for VLSI. Electron. Lett. 1986, 22, 993–994. [Google Scholar] [CrossRef]
- Cunha, M.W.L.; Schneider, M.C.; Dalcastagne, A.L. Automatic tuning of MOSFET-C filters using digitally programmable current attenuators. In Proceedings of the 1997 IEEE International Symposium on Circuits and Systems (ISCAS), Hong Kong, China, 12 June 1997. [Google Scholar]
- Oshima, T.; Maio, K.; Hioe, W.; Hioe, W.; Shibahara, Y. Novel automatic tuning method of RC filters using a digital-DLL technique. IEEE J. Solid-State Circuits 2004, 39, 2052–2054. [Google Scholar] [CrossRef]
- Kiela, K.; Jurgo, M.; Macaitis, V.; Macaitis, V.; Navickas, R. Wideband Reconfigurable Integrated Low-Pass Filter for 5G Compatible Software Defined Radio Solutions. Electronics 2021, 10, 734. [Google Scholar] [CrossRef]
- Wang, R.; Lin, M.; Wang, H.; Sun, S. A widely tunable active-RC complex filter for multi-mode wireless receivers with automatic frequency tuning. IEICE Electron. Express 2016, 13, 20160764. [Google Scholar] [CrossRef]
- Kladovščikov, L.; Navickas, R.; Kiela, K. Self-tuning system for multistandard active RC filters. Microelectron. J. 2019, 90, 260–266. [Google Scholar] [CrossRef]
- Omeni, O.; Rodriguez-Villegas, E.; Toumazou, C. A Micropower CMOS Continuous-Time Filter with On-Chip Automatic Tuning. Int. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 695–705. [Google Scholar] [CrossRef]
- Gandhi, P.P.; Devashrayee, N.M. A novel low offset low power CMOS dynamic comparator. Analog. Integr. Circuits Signal Process. 2018, 96, 147–158. [Google Scholar] [CrossRef]
- Kladovšcikov, L.; Navickas, R. Review of self tuning methods for direct conversion transceivers. In Proceedings of the 2017 Open Conference of Electrical, Electronic and Information Sciences, Vilnius, Lithuania, 27 April 2017. [Google Scholar]
- Zhang, M.; Fan, X. An energy-efficient SAR ADC using a single-phase clocked dynamic comparator with energy and speed enhanced technique. IEICE Electron. Express 2017, 14, 20170219. [Google Scholar] [CrossRef]




| Digital Control Word | Value |
|---|---|
| m1 obtained in phase 1 | 10010 |
| m2 obtained in phase 2 | 10011 |
| m3 obtained in phase 3 | 10111 |
| m4 obtained in phase 1 | 11000 |
| Calculated mTAGT | 11101 |
| Corners | Process Corner | Voltage (V) | Temperature (°C) | fc before Calibration (MHz) | fc after Calibration (MHz) | Tuning Error |
|---|---|---|---|---|---|---|
| Typical Corner | TT | 1.2 | 27 | 3.00 | - | - |
| Corner 1 | FF | 1.1 | −40 | 4.00 | 3.10 | 3.33% |
| Corner 2 | FF | 1.1 | 125 | 3.98 | 3.02 | 0.67% |
| Corner 3 | FF | 1.3 | −40 | 3.95 | 2.97 | 1.00% |
| Corner 4 | FF | 1.3 | 125 | 3.97 | 2.91 | 3.00% |
| Corner 5 | SS | 1.1 | −40 | 2.27 | 2.99 | 0.33% |
| Corner 6 | SS | 1.1 | 125 | 2.27 | 2.90 | 3.33% |
| Corner 7 | SS | 1.3 | −40 | 2.26 | 2.93 | 2.33% |
| Corner 8 | SS | 1.3 | 125 | 2.25 | 2.89 | 3.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, G.; Wu, H.; Yin, Y.; Zheng, L.; Zhuang, Y. A High-Accuracy RC Time Constant Auto-Tuning Scheme for Integrated Continuous-Time Filters. Micromachines 2024, 15, 166. https://doi.org/10.3390/mi15010166
Jin G, Wu H, Yin Y, Zheng L, Zhuang Y. A High-Accuracy RC Time Constant Auto-Tuning Scheme for Integrated Continuous-Time Filters. Micromachines. 2024; 15(1):166. https://doi.org/10.3390/mi15010166
Chicago/Turabian StyleJin, Gang, Hao Wu, Yue Yin, Lei Zheng, and Yiqi Zhuang. 2024. "A High-Accuracy RC Time Constant Auto-Tuning Scheme for Integrated Continuous-Time Filters" Micromachines 15, no. 1: 166. https://doi.org/10.3390/mi15010166
APA StyleJin, G., Wu, H., Yin, Y., Zheng, L., & Zhuang, Y. (2024). A High-Accuracy RC Time Constant Auto-Tuning Scheme for Integrated Continuous-Time Filters. Micromachines, 15(1), 166. https://doi.org/10.3390/mi15010166







