Research on Spatial Localization Method of Magnetic Nanoparticle Samples Based on Second Harmonic Waves
Abstract
:1. Introduction
2. Theoretical Analysis
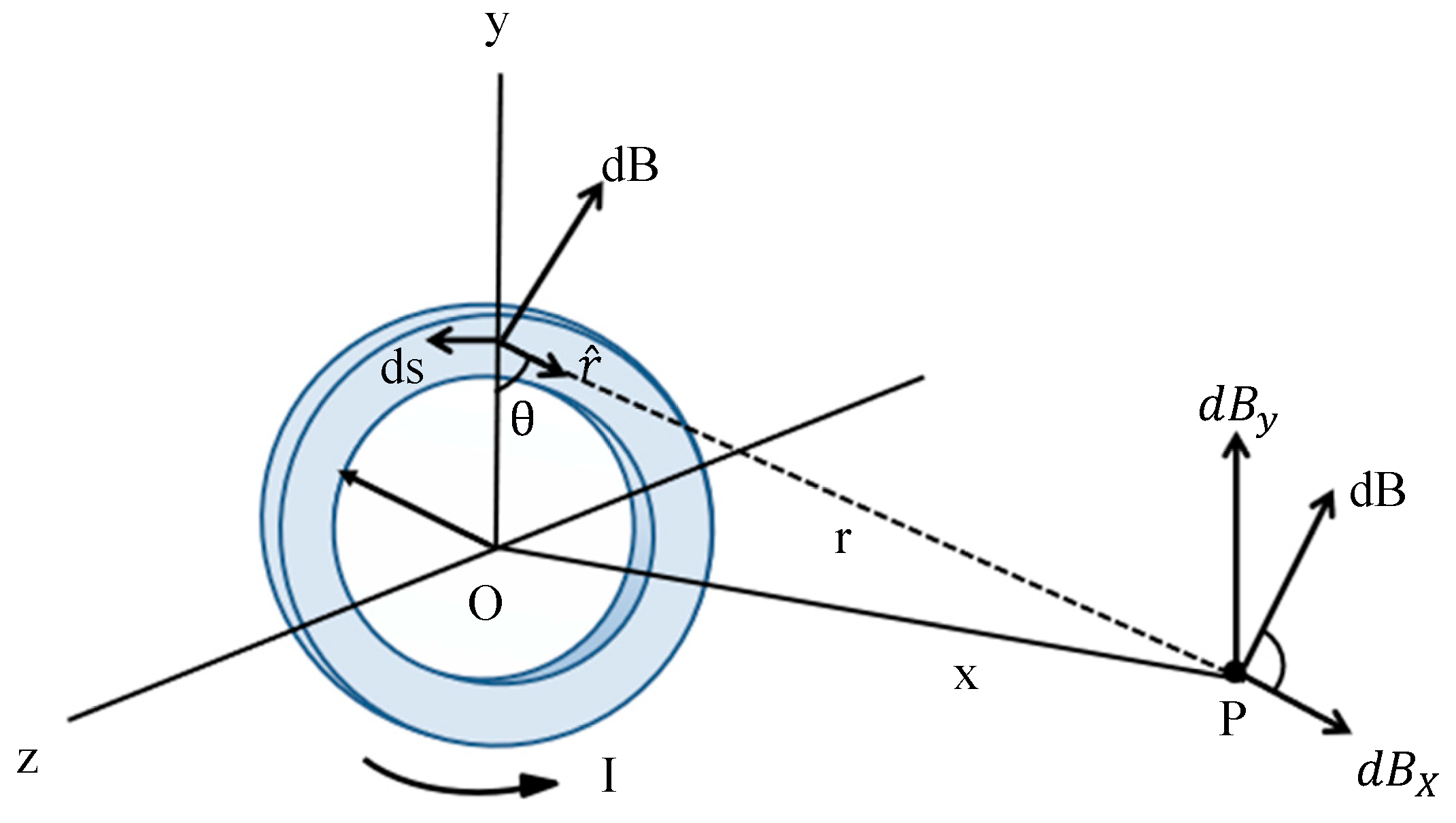
2.1. Second Harmonic Response Analysis of Magnetic Nanoparticles
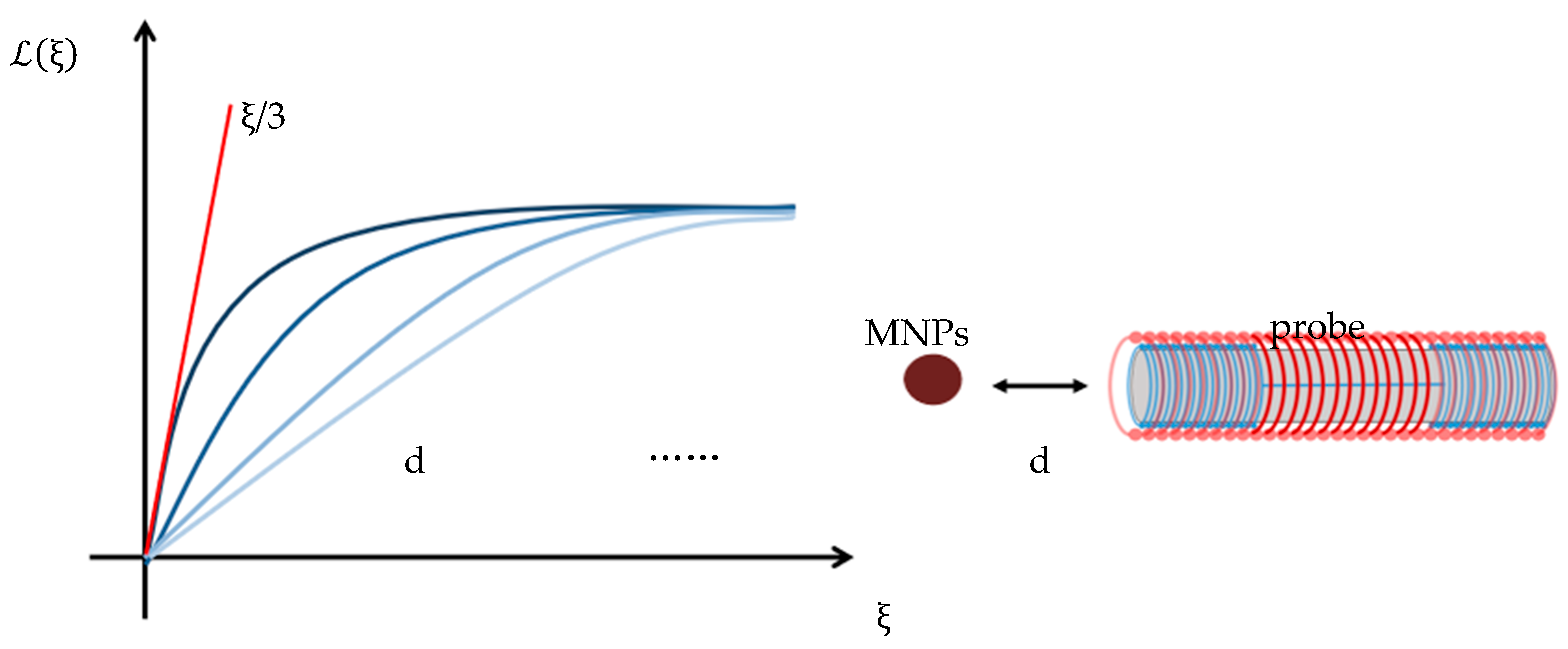
2.2. Establishing the Relationship between Bias Field and Sample Spatial Distance Based on Langevin Equation
2.3. Probe Structure Design
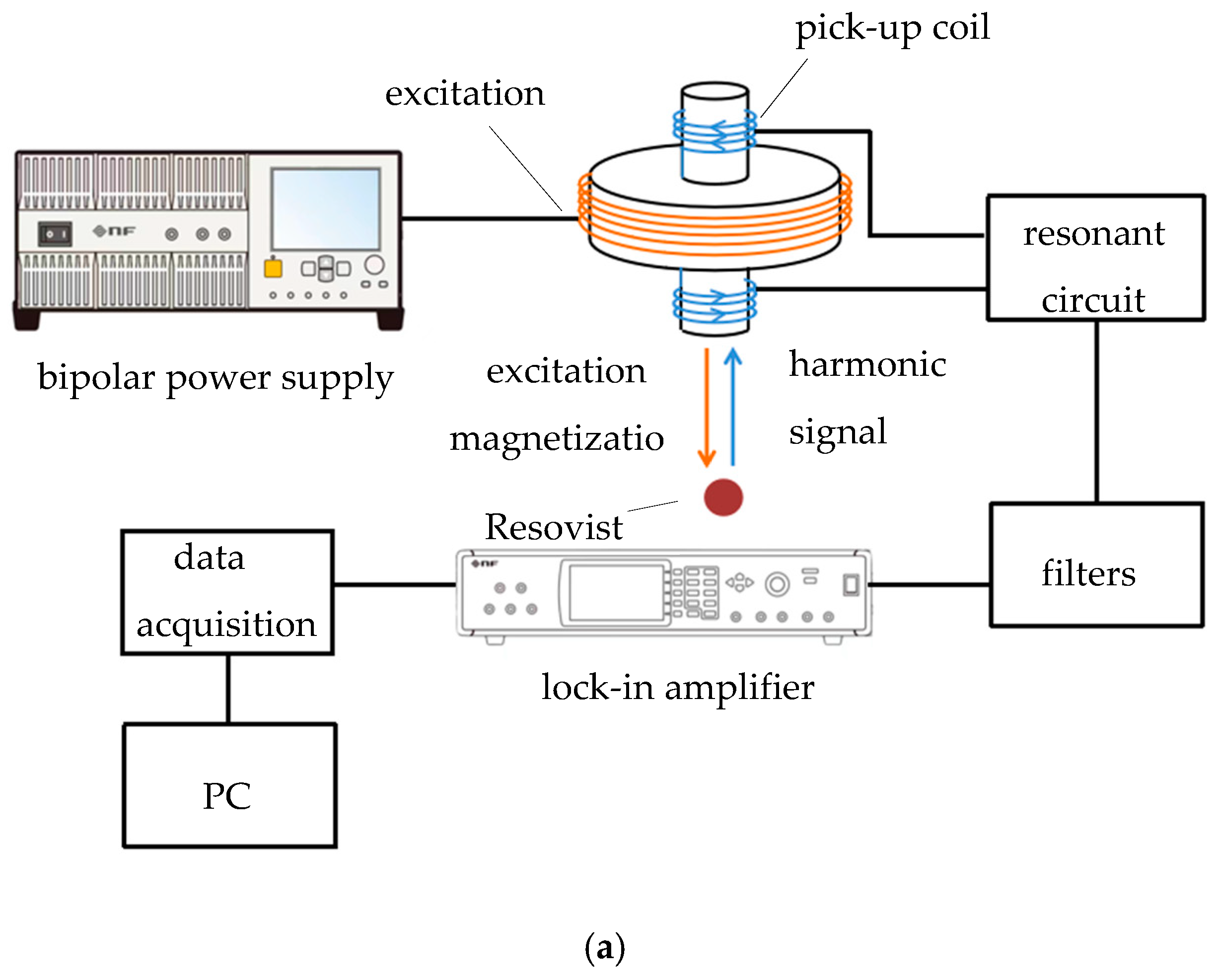
3. Measurement Experiment
3.1. Effect of Sample Concentration on the Second Harmonic Signal of Magnetic Particles
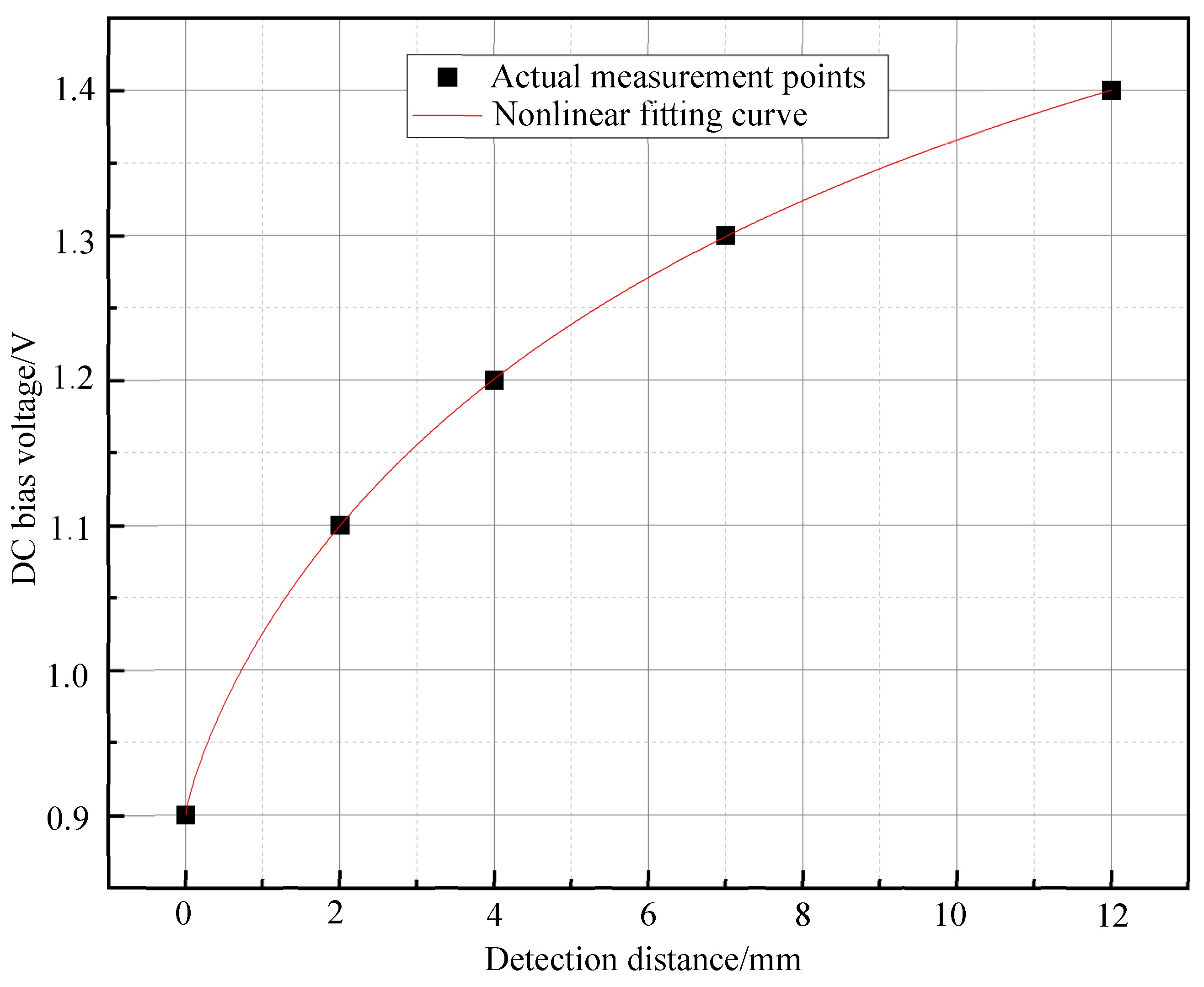
3.2. Effect of Sample Distance on the Second Harmonic Signal of Magnetic Particles
3.3. Experimental Verification
4. Discussion
- (1)
- Improvement of positioning accuracy. Although the gradient-free detection system significantly reduces the volume and energy consumption, there is still a certain decline in spatial resolution compared with traditional MPI. In the next step, we need to continue to optimize the design of the detection coil and the signal measurement processing in order to further improve the positioning accuracy and reach the level required for clinical applications.
- (2)
- Improve the anti-interference ability. Since the gradientless system is more sensitive to environmental magnetic interference, the hardware architecture and signal processing algorithms need to be further optimized to ensure the system’s good working ability in complex environments.
- (3)
- Based on the distance–concentration bivariate analytical model, there is still a certain measurement error, which may originate from the DC source superposition step value being too large, resulting in the saturated DC bias field corresponding to the peak point of the signal being not accurate enough. Therefore, the detection sensitivity can be improved by reducing the DC bias field step size.
- (4)
- Different SPIONs have different saturation magnetization curves due to their material properties, and the correlation model between the DC bias field and the spatial axial distance needs to be further optimized to accurately determine the detection depth and concentration of the magnetic nanoparticle tracer.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mishra, S.; Yadav, M.D. Magnetic Nanoparticles: A Comprehensive Review from Synthesis to Biomedical Frontiers. Langmuir ACS J. Surf. Colloids 2024, 40, 17239–17269. [Google Scholar] [CrossRef] [PubMed]
- Ficko, B.W.; Giacometti, P.; Diamond, S.G. Nonlinear susceptibility magnitude imaging of magnetic nanoparticles. J. Magn. Magn. Mater. 2015, 378, 267–277. [Google Scholar] [CrossRef]
- Sosnovik, D.E.; Nahrendorf, M.; Weissleder, R. Magnetic nanoparticles for MR imaging: Agents, techniques and cardiovascular applications. Basic Res. Cardiol. 2008, 1031, 22–130. [Google Scholar] [CrossRef] [PubMed]
- Gleich, B.; Weizenecker, J. Tomographic imaging using the nonlinear response of magnetic particles. Nature 2005, 435, 1214–1217. [Google Scholar] [CrossRef]
- Saritas, E.U.; Goodwill, P.W.; Croft, L.R.; Konklw, J.J.; Lu, K.; Zheng, B.; Conolly, S.M. Magnetic particle imaging (MPI) for NMR and MRI researchers. J. Magn. Reson. 2013, 229, 116–126. [Google Scholar] [CrossRef] [PubMed]
- Tsujita, Y.; Morishita, M.; Muta, M.; Sasayama, T.; Enpuku, K. Three-Dimensional Magnetic Nanoparticle Imaging Using Multiple Pickup Coils. In Proceedings of the 2016 International Conference of Asian Union of Magnetics Societies (ICAUMS), Tainan, Taiwan, 1–5 August 2016; pp. 144–150. [Google Scholar]
- Shi, B.; Zhiyao, L.; Lingke, G.; Kewen, L. Distance layer analysis of magnetic nanoparticles at non-zero field points based on the half-peak width model of harmonic magnetization response. J. Instrum. 2024, 45, 149–157. [Google Scholar]
- Shiozawa, M.; Lefor, A.T.; Hozumi, Y.; Kurihara, K.; Sata, N.; Yasuda, Y.; Kusakabe, M. Sentinel lymph node biopsy in patients with breast cancer using superparamagnetic iron oxide and a magnetometer. Breast Cancer 2013, 20, 223–229. [Google Scholar] [CrossRef]
- Krag, D.N.; Weaver, D.L.; Alex, J.C.; Fairbank, J.T. Surgical resection and radiolocalization of the sentinel lymph node in breast cancer using a gamma probe. Surg. Oncol. 1993, 2, 335–339. [Google Scholar] [CrossRef]
- Giuliano, A.E.; Kirgan, D.M.; Guenther, J.M.; Morton, D.L. Lymphatic mapping and sentinel lymphadenectomy for breast cancer. Ann. Surg. 1994, 220, 391–401. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Kitajima, M. Sentinel node mapping for gastric cancer: Is the jury still out? Gastric Cancer 2004, 7, 135–137. [Google Scholar] [CrossRef]
- Ahmed, M.; Purushotham, A.D.; Douek, M. Novel techniques for sentinel lymph node biopsy in breast cancer: A systematic review. Lancet Oncol. 2014, 15, e351–e362. [Google Scholar] [CrossRef] [PubMed]
- O’hea, B.J. Sentinel lymph node biopsy in breast cancer: Initial experience at Memorial Sloan Kettering Cancer Center. J. Am. Coll. Surg. 1998, 186, 423–427. [Google Scholar] [CrossRef] [PubMed]
- Bleicher, R.J.; Ruth, K.; Sigurdson, E.R.; Beck, J.R.; Ross, E.; Wong, Y.N.; Patel, S.A.; Boraas, M.; Chang, E.I.; Topham, N.S.; et al. Time to surgery and breast cancer survival in the United States. JAMA Oncol. 2016, 2, 1244. [Google Scholar] [CrossRef]
- Douek, M.; Klaase, J.; Monypenny, I.; Kothari, A.; Zechmeister, K.; Brown, D.; Wyld, L.; Drew, P.; Garmo, H.; Agbaje, O.; et al. Sentinel Node Biopsy Using a Magnetic Tracer versus Standard Technique: The SentiMAG Multicentre Trial. Ann. Surg. Oncol. 2014, 21, 1237–1245. [Google Scholar] [CrossRef]
- Thill, M.; Kurylcio, A.; Welter, R.; van Haasteren, V.; Grosse, B.; Berclaz, G.; Polkowski, W.; Hauser, N. The Central-European SentiMag study: Sentinel lymph node biopsy with superparamagnetic iron oxide (SPIO) vs. radioisotope. Breast 2014, 23, 175–179. [Google Scholar] [CrossRef]
- Houpeau, J. Sentinel Lymph Node identification Using Superparamagnetic Iron Oxide Particles versus Radioisotope: The French Sentimag Feasibility Trial. Surg. Oncol. 2016, 113, 501–507. [Google Scholar] [CrossRef]
- Ghilli, M. Superparamagnetic iron oxide tracer: A valid alternative in sentinel node biopsy for breast cancer treatment. Eur. J. Cancer Care 2017, 26, e12385. [Google Scholar] [CrossRef]
- Bai, S.; Gai, L.; Zhang, Q.; Kang, Y.; Liu, Z.; He, Y.; Liu, W.; Jiang, T.; Du, Z.; Du, S.; et al. Development of a human-size magnetic particle imaging device for sentinel lymph node biopsy of breast cancer. Front. Bioeng. Biotechnol. 2024, 12, 1327521. [Google Scholar] [CrossRef]
- Othman, N.B.; Yoshida, T.; Enpuku, K. Harmonic signal detection based magnetic nanoparticle imaging system for breast cancer diagnosis. ARPN J. Eng. Appl. Sci. 2015, 10, 9934–9940. [Google Scholar]
- Taruno, K.; Kurita, T.; Kuwahata, A.; Yanagihara, K.; Enokido, K.; Katayose, Y.; Nakamura, S.; Takei, H.; Sekino, M.; Kusakabe, M. Multicenter clinical trial on sentinel lymph node biopsy using superparamagnetic iron oxide nanoparticles and a novel handheld magnetic probe. J. Surg. Oncol. 2019, 120, 1391–1396. [Google Scholar] [CrossRef]
- Kuwahata, A.; Tanaka, R.; Matsuda, S.; Amada, E.; Irino, T.; Mayanagi, S.; Chikaki, S.; Saito, I.; Tanabe, N.; Kawakubo, H.; et al. Development of Magnetic Probe for Sentinel Lymph Node Detection in Laparoscopic Navigation for Gastric Cancer Patients. Sci. Rep. 2020, 10, 1798. [Google Scholar] [CrossRef] [PubMed]
- Morishige, T.; Mihaya, T.; Bai, S.; Miyazaki, T.; Yoshida, T.; Matsuo, M.; Enpuku, K. Highly Sensitive Magnetic Nanoparticle Imaging Using Cooled-Cu/HTS-Superconductor Pickup Coils. IEEE Trans. Appl. Supercond. 2014, 24, 1800105. [Google Scholar] [CrossRef]
- Bai, S.; Hirokawa, A.; Tanabe, K.; Sasayama, T.; Yoshida, T.; Enpuku, K. Narrowband Magnetic Particle Imaging Utilizing Electric Scanning of Field Free Point. IEEE Trans. Magn. 2015, 51, 5101404. [Google Scholar] [CrossRef]
- Tanaka, S.; Oishi, T.; Suzuki, T.; Zhang, Y.; Liao, S.H.; Horng, H.E.; Yang, H.C. Magnetic particle imaging with use of second harmonic response of magnetization. In Proceedings of the 2015 5th International Workshop on Magnetic Particle Imaging (IWMPI), Istanbul, Turkey, 26–28 March 2015; pp. 170–174. [Google Scholar]
- Tanaka, S.; Suzuki, T.; Kobayashi, K.; Liao, S.H.; Horng, H.E.; Yang, H.C. Analysis of magnetic nanoparticles using second harmonic responses. J. Magn. Magn. Mater. 2017, 440, 189–191. [Google Scholar] [CrossRef]
- Yoshida, T.; Ogawa, K.; Tsubaki, T.; Othman, N.B.; Enpuku, K. Detection of Magnetic Nanoparticles Using the Second-Harmonic Signal. IEEE Trans. Magn. 2011, 47, 2863–2866. [Google Scholar] [CrossRef]
- Othman, N.A.; Tsubaki, T.; Kitahara, D.; Yoshida, T.; Enpuku, K.; Kandori, A. Magnetic Nanoparticle Imaging Using Second Harmonic Signals for Sentinel Lymph Node Detection. J. Magn. Soc. Jpn. 2013, 37, 295–298. [Google Scholar] [CrossRef]
- Ota, S.; Nishimoto, K.; Yamada, T.; Takemura, Y. Second harmonic response of magnetic nanoparticles under parallel static field and perpendicular oscillating field for magnetic particle imaging. AIP Adv. 2020, 10, 015007. [Google Scholar] [CrossRef]
- Wu, M.; Du, Q.; Ke, L.; Zu, W. Study on the second harmonic detection method of nonlinear magnetization signal in magnetic nanoparticle imaging. J. Electron. Meas. Instrum. 2022, 36, 87–94. [Google Scholar]
- Obaidat, I.M.; Narayanaswamy, V.; Alaabed, S.; Sambasivam, S.; Muralee Gopi, C.V. Principles of Magnetic Hyperthermia: A Focus on Using Multifunctional Hybrid Magnetic Nanoparticles. Magnetochemistry 2019, 5, 67. [Google Scholar] [CrossRef]








| Actual Distance /mm | Extrapolated Distance | Distance Error |
|---|---|---|
| 10 | 9.57 | 4.3% |
| 7.5 | 7.34 | 2.13% |
| 5 | 5.24 | 4.8% |
| 2.5 | 2.71 | 8.4% |
| 1 | 0.96 | 4.0% |
| Actual Concentration | Extrapolated Concentration | Concentration Error |
|---|---|---|
| 44.6 | 42.9 | 3.8% |
| 35.7 | 37.6 | 5.3% |
| 26.8 | 25.9 | 3.34% |
| 17.6 | 18.2 | 3.41% |
| 13.5 | 12.9 | 4.48% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Huang, P.; Zheng, F.; Yu, H.; Li, Y.; Qiu, Z.; Gai, L.; Liu, Z.; Bai, S. Research on Spatial Localization Method of Magnetic Nanoparticle Samples Based on Second Harmonic Waves. Micromachines 2024, 15, 1218. https://doi.org/10.3390/mi15101218
Wang Z, Huang P, Zheng F, Yu H, Li Y, Qiu Z, Gai L, Liu Z, Bai S. Research on Spatial Localization Method of Magnetic Nanoparticle Samples Based on Second Harmonic Waves. Micromachines. 2024; 15(10):1218. https://doi.org/10.3390/mi15101218
Chicago/Turabian StyleWang, Zheyan, Ping Huang, Fuyin Zheng, Hongli Yu, Yue Li, Zhichuan Qiu, Lingke Gai, Zhiyao Liu, and Shi Bai. 2024. "Research on Spatial Localization Method of Magnetic Nanoparticle Samples Based on Second Harmonic Waves" Micromachines 15, no. 10: 1218. https://doi.org/10.3390/mi15101218
APA StyleWang, Z., Huang, P., Zheng, F., Yu, H., Li, Y., Qiu, Z., Gai, L., Liu, Z., & Bai, S. (2024). Research on Spatial Localization Method of Magnetic Nanoparticle Samples Based on Second Harmonic Waves. Micromachines, 15(10), 1218. https://doi.org/10.3390/mi15101218






