Physical Sensors Based on Lamb Wave Resonators
Abstract
1. Introduction
2. Fundamental Principles of LWRs
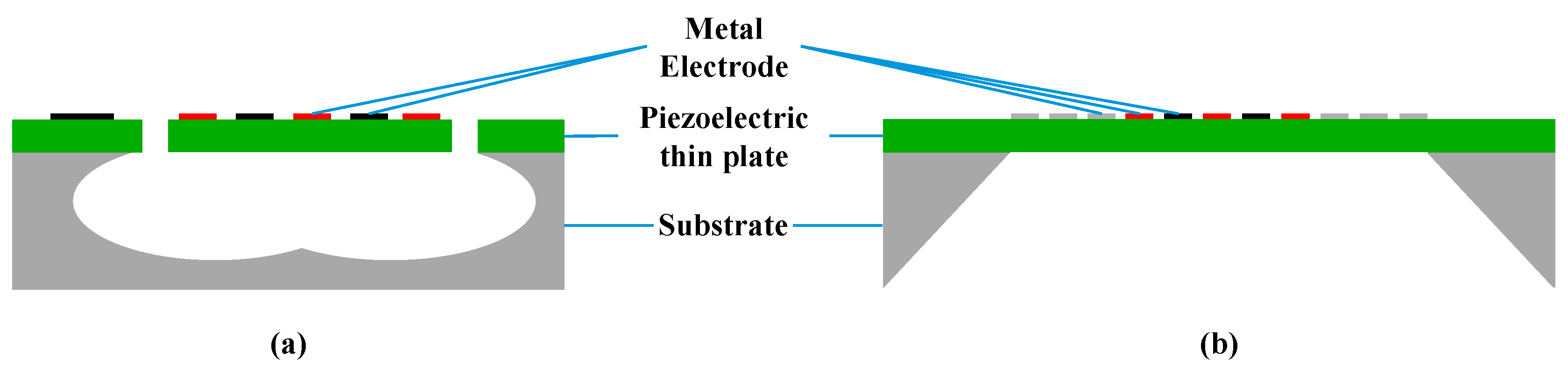
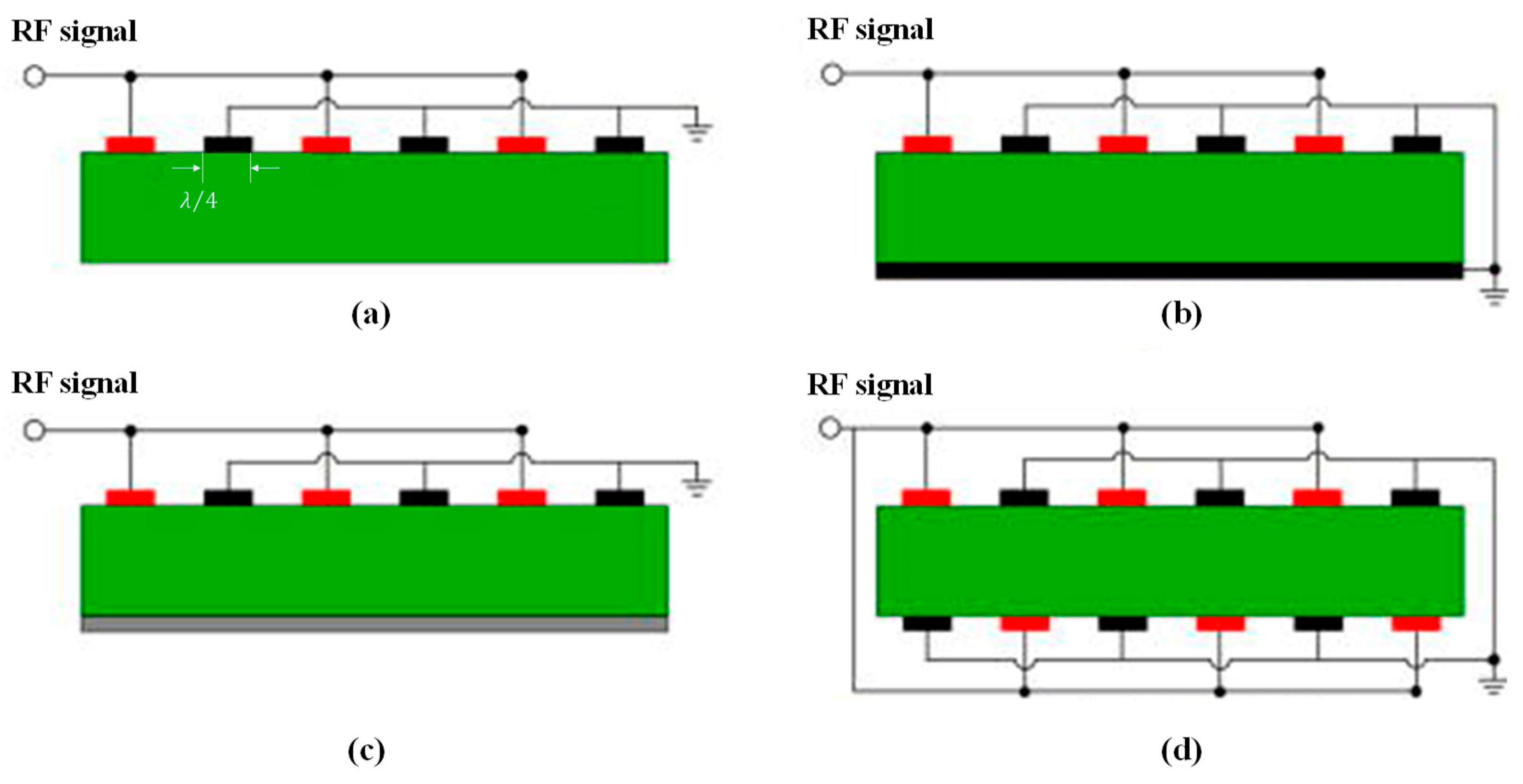
2.1. Structure of the LWR
2.2. Calculation Methods for Lamb Wave Modes
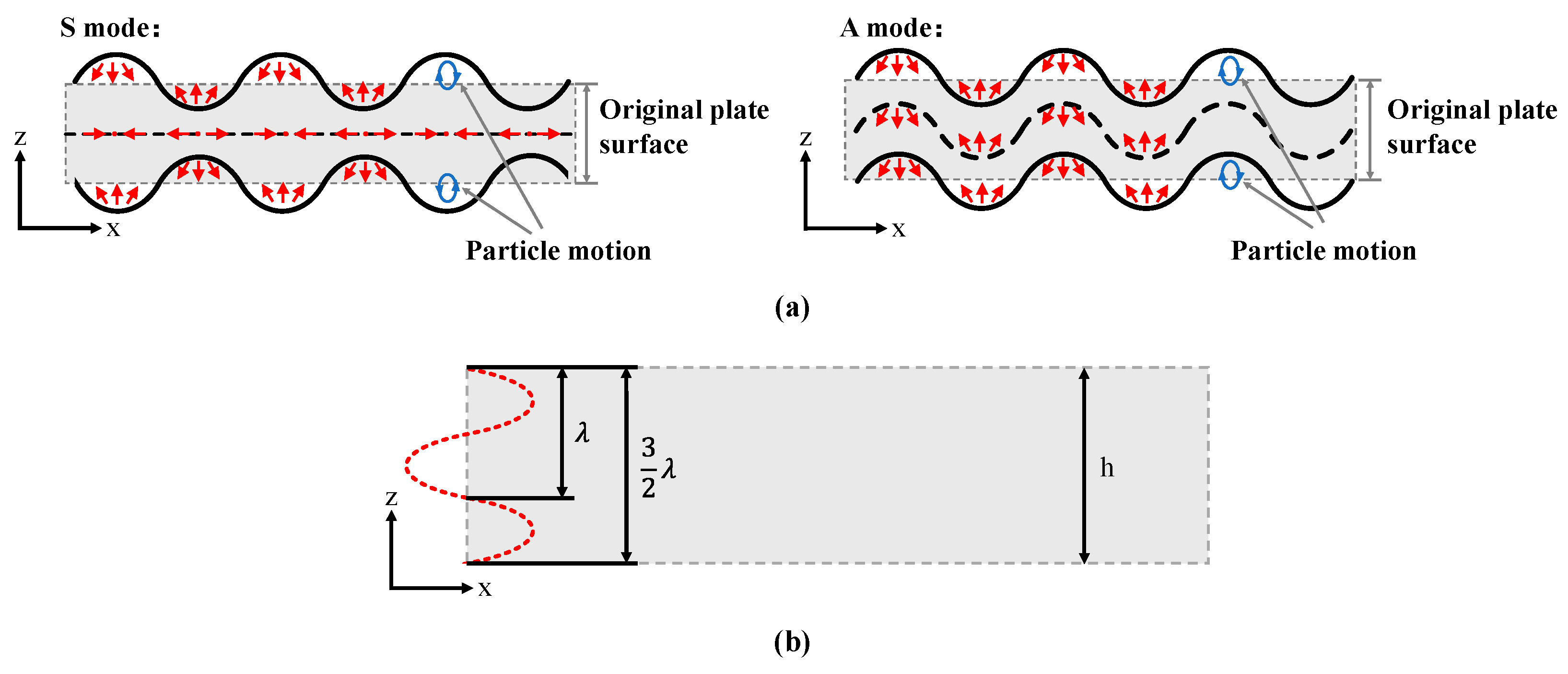
2.3. Dispersion Characteristics of the Lamb Wave
2.4. Key Parameters of Lamb Wave Resonator
2.4.1. Quality Factor
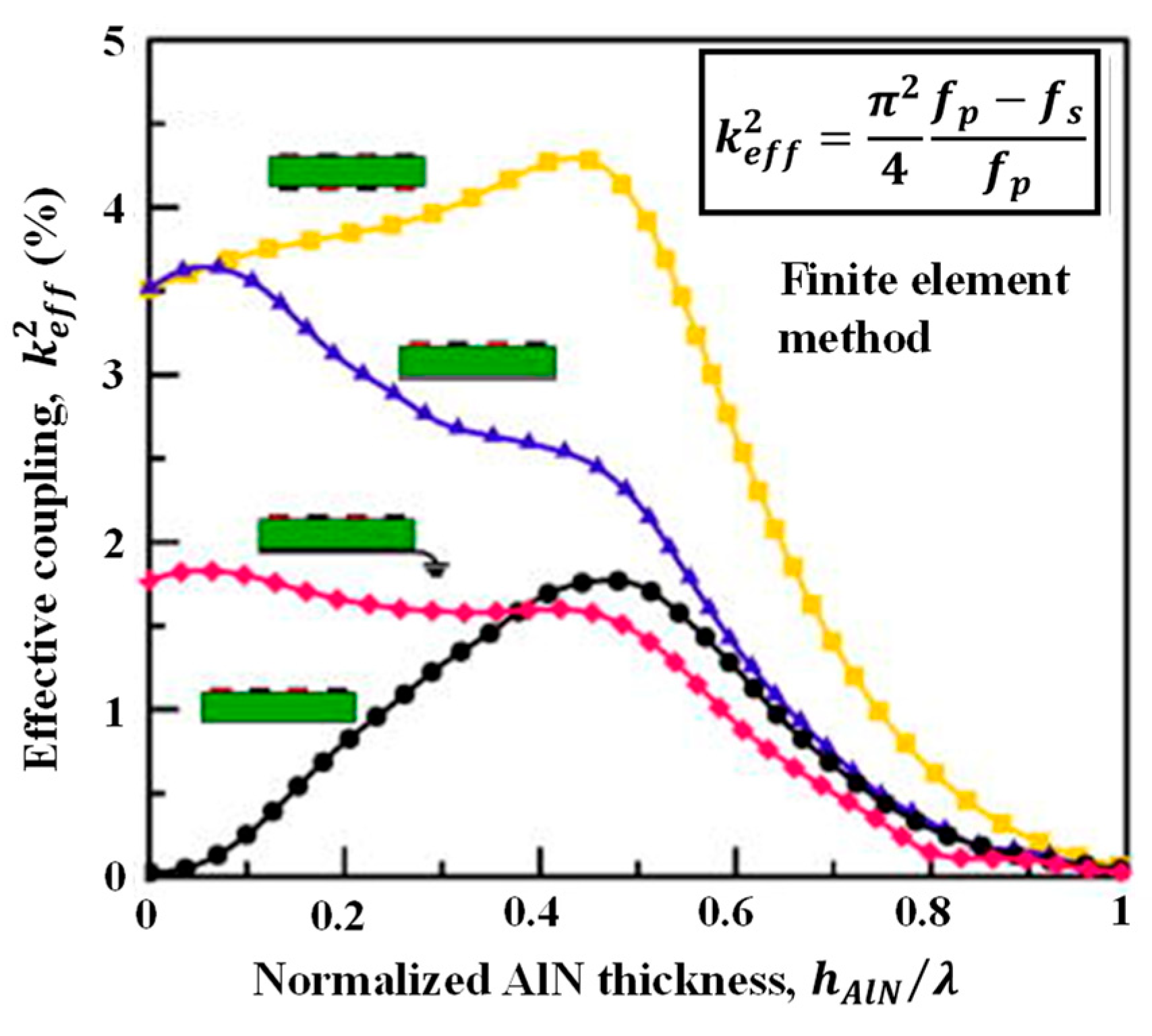
2.4.2. Effective Electromechanical Coupling Coefficient
3. Manufacturing Materials for Sensors
3.1. Piezoelectric Materials
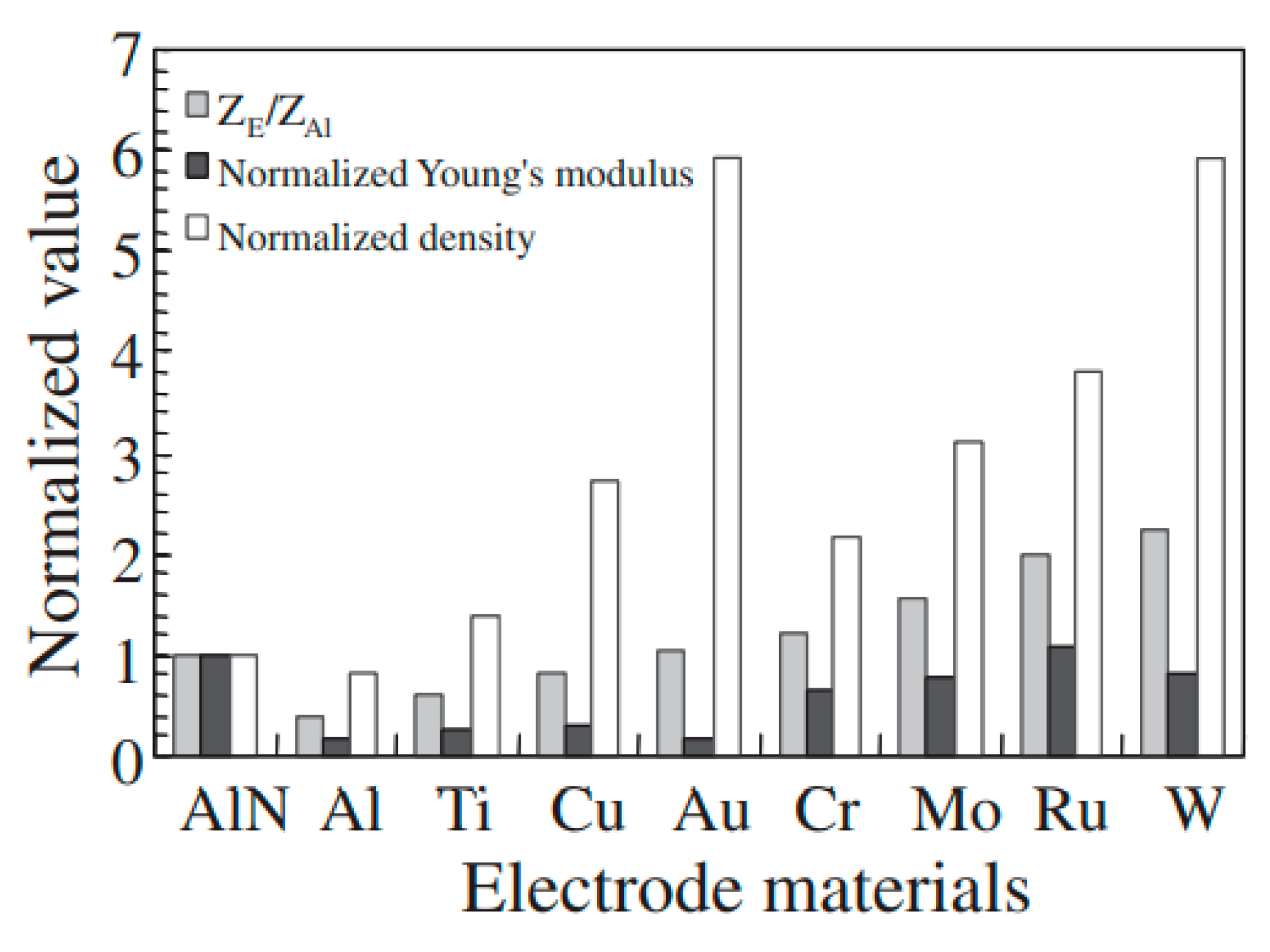
3.2. Electrode Materials
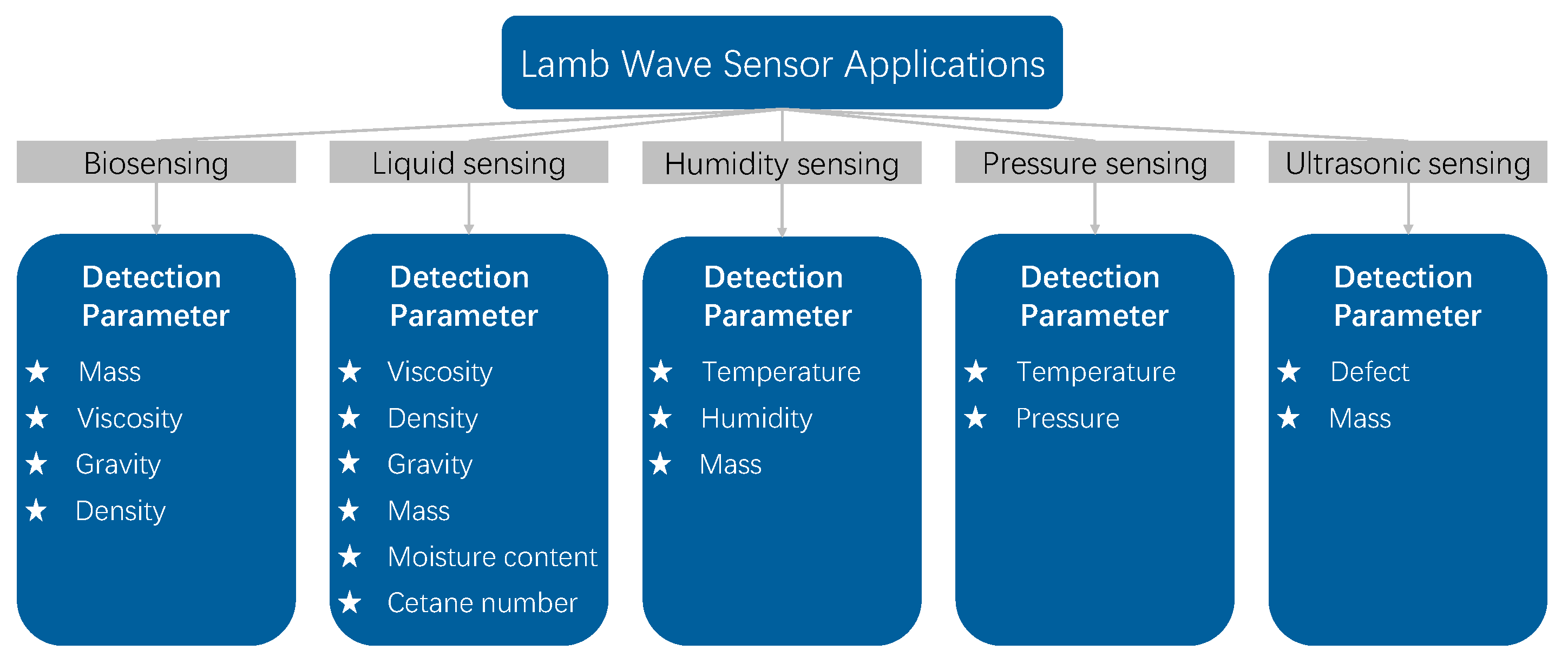
4. LWR as Sensors
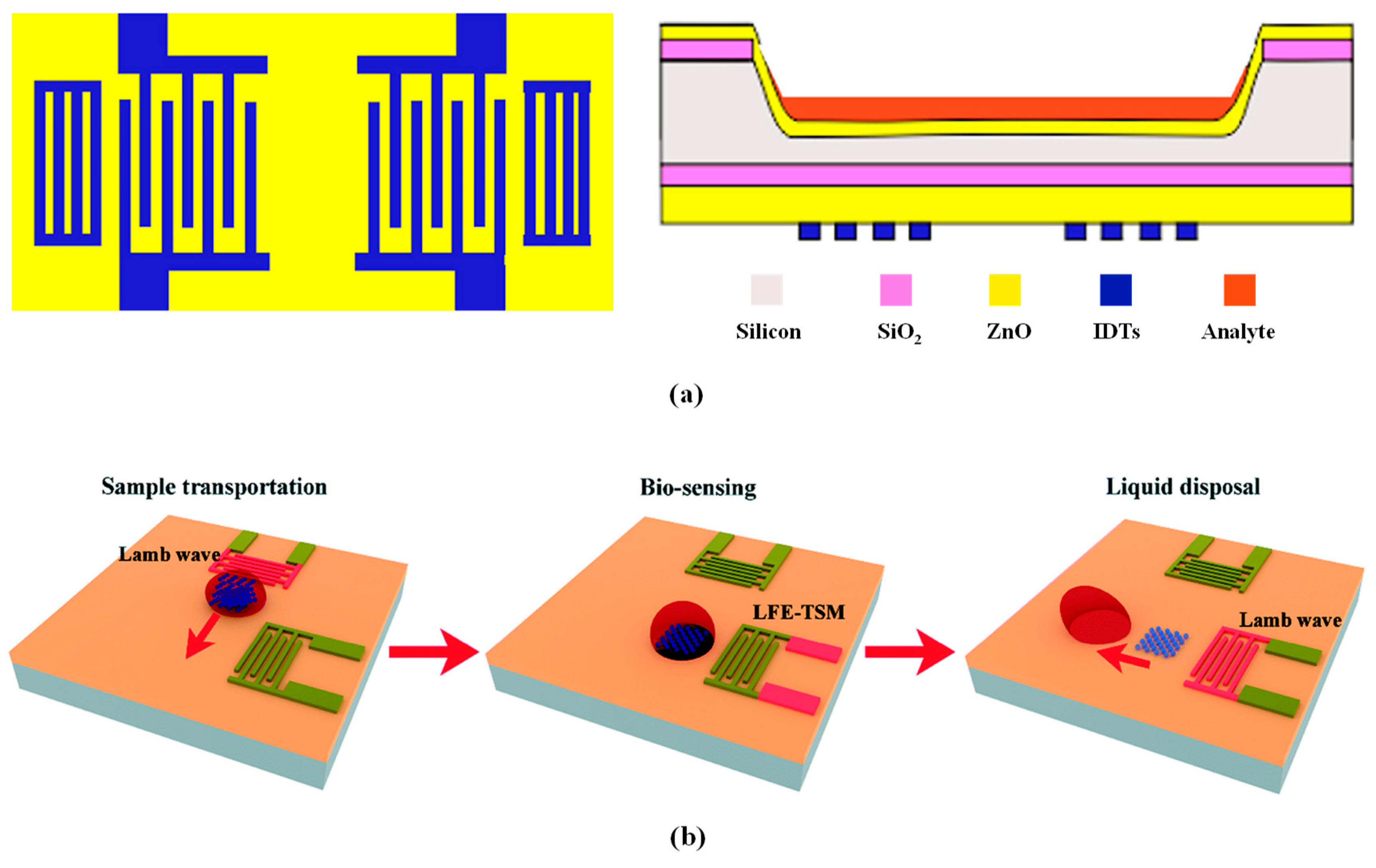
4.1. LWR Biosensors
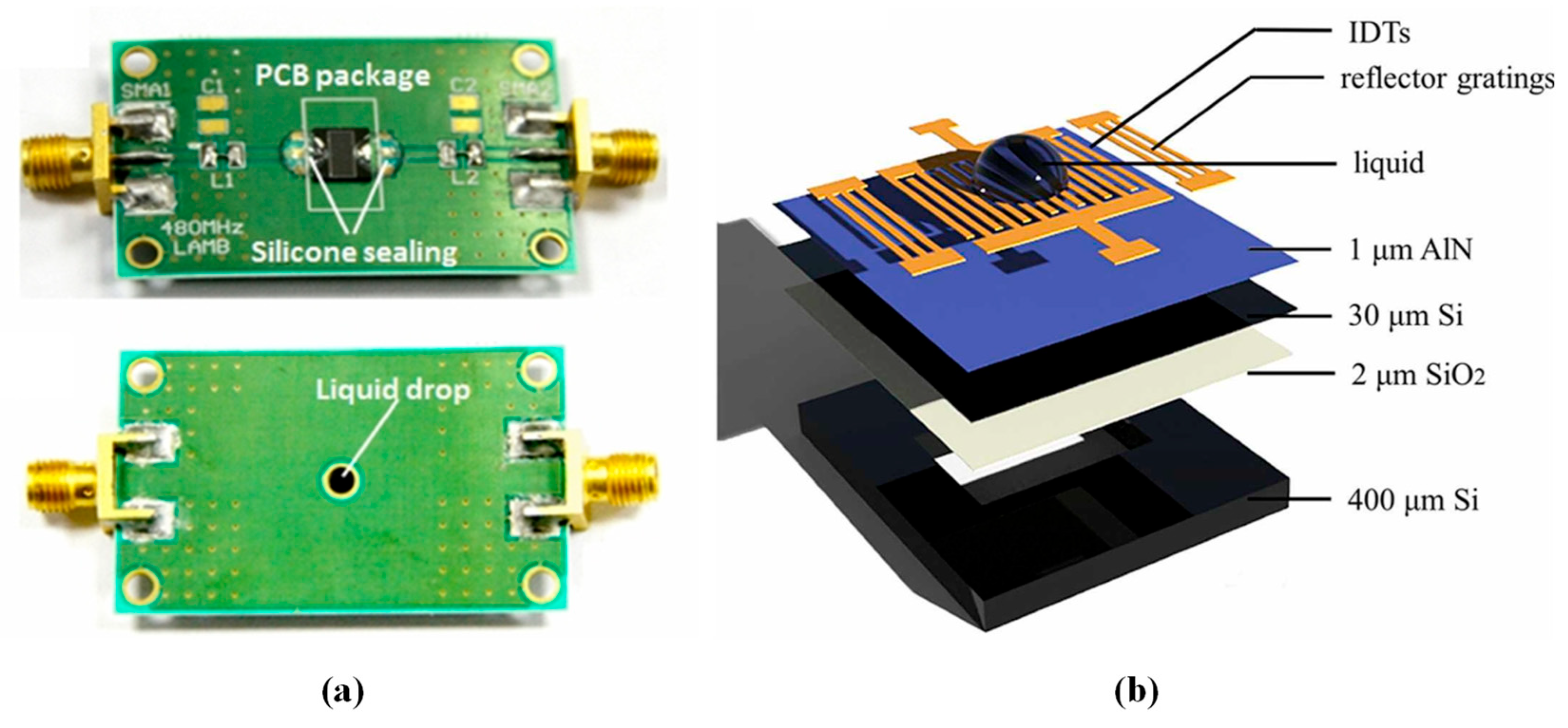
4.2. LWR Liquid Sensors
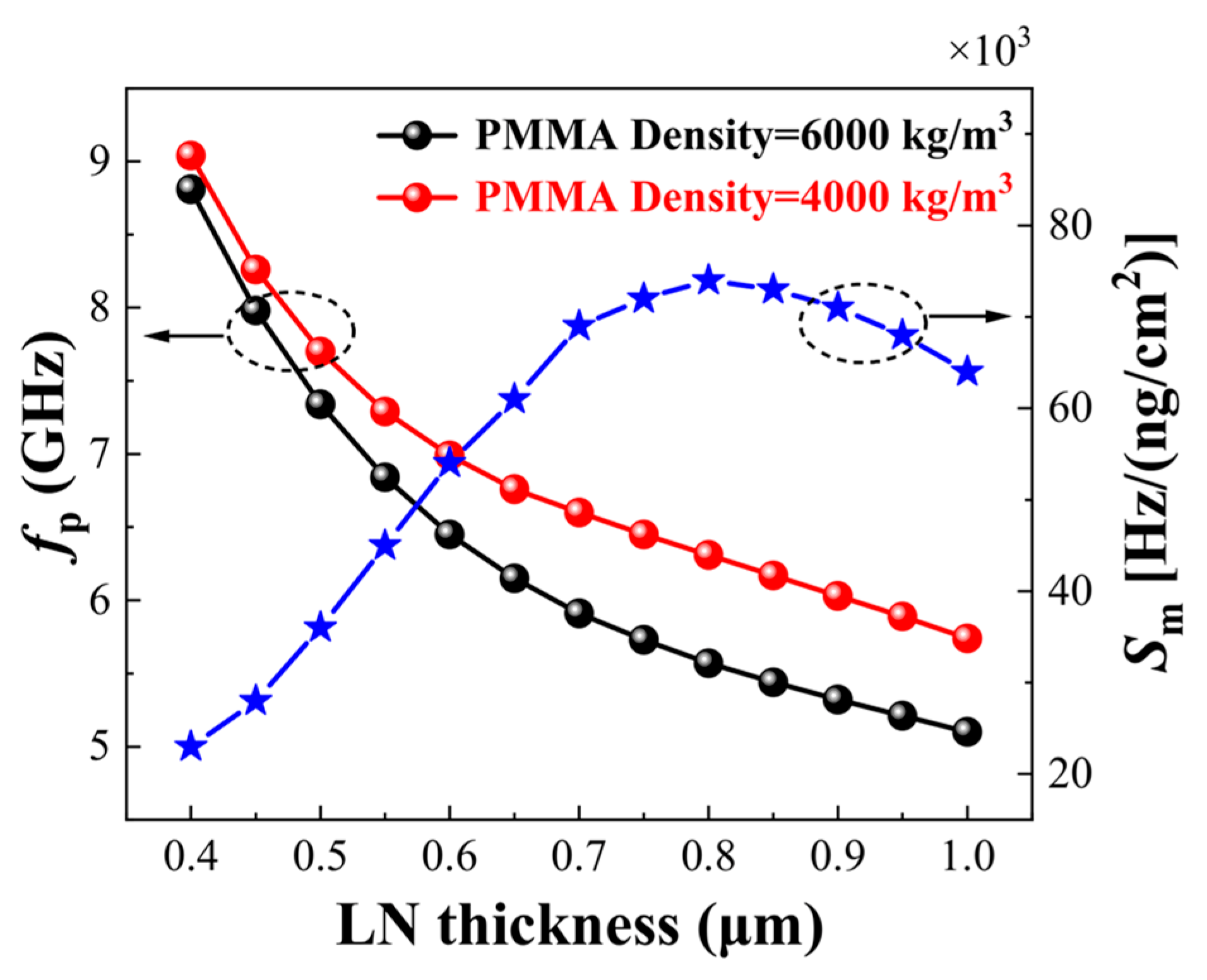
4.3. LWR Pressure Sensors

4.4. LWR Humidity Sensors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, J.; Anurakparadorn, K.; Gu, H.R.; Zhao, M.H.; Wei, X.Y. Design of SAW sensor for longitudinal strain measurement with improved sensitivity. Microsyst. Technol. 2019, 25, 351–359. [Google Scholar] [CrossRef]
- Malocha, D.C.; Humphries, J.; Figueroa, J.A.; Lamothe, M.; Weeks, A. 915 MHz SAW wireless passive sensor system performance. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 3 November 2016. [Google Scholar] [CrossRef]
- Wang, X.Y.; Du, L.L.; Cheng, L.N.; Zhai, S.P.; Chao, Z.; Wang, W.; Liang, Y.; Yang, D.C.; Chen, Q.; Lei, G. Pd/Ni nanowire film coated SAW hydrogen sensor with fast response. Sens. Actuators B Chem. 2022, 351, 130952. [Google Scholar] [CrossRef]
- Nguyen, T.M.H.; Shin, S.G.; Choi, H.W.; Bark, C.W. Recent Advances in Self-Powered and Flexible UVC Photodetectors. Exploration 2022, 2, 20210078. [Google Scholar] [CrossRef]
- Chen, Y.F.; Gao, Z.Q.; Zhang, F.J.; Wen, Z.; Sun, X.H. Recent Progress in Self-Powered Multifunctional E-Skin for Advanced Applications. Exploration 2022, 2, 20210112. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.R.; Zhang, X.L.; Sun, H.B. Exceptional Point Protected Robust On-Chip Optical Logic Gates. Exploration 2022, 2, 20210243. [Google Scholar] [CrossRef] [PubMed]
- Toda, K. Lamb-wave delay lines with interdigital electrodes. J. Appl. Phys. 1973, 44, 56–62. [Google Scholar] [CrossRef]
- White, R.M.; Wenzel, S.W. Fluid loading of a Lamb-wave sensor. Appl. Phys. Lett. 1988, 52, 1653–1655. [Google Scholar] [CrossRef]
- Bjurström, J.; Yantchev, V.; Katardjiev, I. Thin film Lamb wave resonant structures—The first approach. Solid-State Electron. 2006, 50, 322–326. [Google Scholar] [CrossRef]
- Bjurström, J.; Katardjiev, I.; Yantchev, V. Lateral-field-excited thin-film Lamb wave resonator. Appl. Phys. Lett. 2005, 86, 154103. [Google Scholar] [CrossRef]
- Yantchev, V.; Enlund, J.; Biurström, J.; Katardjiev, I. Design of high frequency piezoelectric resonators utilizing laterally propagating fast modes in thin aluminum nitride (AlN) films. Ultrasonics 2006, 45, 208–212. [Google Scholar] [CrossRef]
- Luo, T.C.; Liu, W.J.; Wen, Z.W.; Xie, Y.; Tong, X.; Cai, Y.; Liu, Y.; Sun, C.L. A High-Sensitivity Gravimetric Biosensor Based on S1 Mode Lamb Wave Resonator. Sensors 2022, 22, 5912. [Google Scholar] [CrossRef]
- Bharati, M.; Rana, L.; Gupta, R.; Sharma, A.; Jha, P.K.; Tomar, M. Realization of a DNA biosensor using inverted Lamb wave MEMS resonator based on ZnO/SiO2/Si/ZnO membrane. Anal. Chim. Acta 2023, 1249, 340929. [Google Scholar] [CrossRef] [PubMed]
- Tao, R.; Reboud, J.; Torun, H.; McHale, G.; Dodd, L.E.; Wu, Q.; Tao, K.; Yang, X.; Luo, J.T.; Todryk, S.; et al. Integrating microfluidics and biosensing on a single flexible acoustic device using hybrid modes. Lab Chip 2020, 20, 1002–1011. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Huang, F.; Memon, M.M.; Pan, S.L.; Wang, T.; Peng, B.; Zhang, W.L. Dependence of the Lamb wave viscosity sensor on the liquid morphology. Sens. Actuators A Phys. 2022, 343, 113694. [Google Scholar] [CrossRef]
- Wang, T.; Mu, X.J.; Kropelnicki, P.; Randles, A.B.; Lee, C.K. Viscosity and density decoupling method using a higher order Lamb wave sensor. J. Micromech. Microeng. 2014, 24, 075002. [Google Scholar] [CrossRef]
- Mirea, T.; Yantchev, V.; Olivares, J.; Iborra, E. Influence of liquid properties on the performance of S0-mode Lamb wave sensors II: Experimental validation. Sens. Actuators B Chem. 2016, 229, 331–337. [Google Scholar] [CrossRef]
- Mirea, T.; Iborra, E.; Yantchev, V. S0 Lamb wave resonators for in-liquid sensing: Promising alternative to shear bulk acoustic wave devices. In Proceedings of the 2016 European Frequency and Time Forum (EFTF), York, UK, 4–7 April 2016. [Google Scholar] [CrossRef]
- Xuan, W.P.; He, X.L.; Chen, J.K.; Wang, W.B.; Wang, X.Z.; Xu, Y.; Xu, Z.; Fu, Y.Q.; Luo, J.K. High sensitivity flexible Lamb-wave humidity sensors with a graphene oxide sensing layer. Nanoscale 2015, 7, 7430–7436. [Google Scholar] [CrossRef]
- Pang, J.T.; Le, X.H.; Xu, Z.; Gao, C.; Xie, J. A humidity sensor based on AlN Lamb wave resonator coated with graphene oxide of different concentrations. J. Micromech. Microeng. 2018, 28, 105016. [Google Scholar] [CrossRef]
- Dhillon, A.S.; Mohanan, A.A. A New Multilayered Substrate for Facile Fabrication of Flexible One-Port Lamb Wave Resonator Sensors. IEEE Sens. J. 2023, 23, 25824–25835. [Google Scholar] [CrossRef]
- Mu, X.J.; Kropelnicki, P.; Wang, Y.; Randles, A.B.; Chuan Chai, K.T.; Cai, H.; Gu, Y.D. Dual mode acoustic wave sensor for precise pressure reading. Appl. Phys. Lett. 2014, 105, 113507. [Google Scholar] [CrossRef]
- Wang, T.; Tang, Z.J.; Lin, H.M.; Zhan, K.; Wan, J.; Wu, S.H.; Gu, Y.D.; Luo, W.B.; Zhang, W.L. A Low Temperature Drifting Acoustic Wave Pressure Sensor with an Integrated Vacuum Cavity for Absolute Pressure Sensing. Sensors 2020, 20, 1788. [Google Scholar] [CrossRef] [PubMed]
- Nastro, A.; Bertelli, S.; Ferrari, M.; Rufer, L.; Basrour, S.; Ferrari, V. Flexural Plate Wave Piezoelectric MEMS Pressure Sensor. Proceedings 2024, 97, 185. [Google Scholar] [CrossRef]
- Kim, T.; Kim, J.; Jiang, X.N. AlN Ultrasound Sensor for Photoacoustic Lamb Wave Detection in a High-Temperature Environment. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1444–1451. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Fan, L.; Zhang, S.Y.; Zhang, H. Theoretical research on ultrasonic sensors based on high-order Lamb waves. J. Appl. Phys. 2014, 115, 204513. [Google Scholar] [CrossRef]
- Dou, S.X.; Qi, M.K.; Chen, C.; Zhou, H.; Wang, Y.; Shang, Z.G.; Yang, J.; Wang, D.P.; Mu, X.J. High-temperature high-sensitivity AlN-on-SOI Lamb wave resonant strain sensor. AIP Adv. 2018, 8, 065315. [Google Scholar] [CrossRef]
- Dou, S.X.; Cao, J.; Zhou, H.; Chen, C.; Wang, Y.; Yang, J.; Wang, D.P.; Shang, Z.G.; Mu, X.J. Dual-resonator Lamb wave strain sensor with temperature compensation and enhanced sensitivity. Appl. Phys. Lett. 2018, 113, 093502. [Google Scholar] [CrossRef]
- Rana, L.; Gupta, R.; Sharma, A.; Tomar, M.; Gupta, V. Development of MEMS-Based Lamb Wave Acoustic Devices. IEEE T. Electron Dev. 2018, 65, 1523–1528. [Google Scholar] [CrossRef]
- Lin, C.M.; Chen, Y.Y.; Felmetsger, V.V.; Senesky, D.G.; Pisano, A.P. AlN/3C–SiC Composite Plate Enabling High-Frequency and High-Q Micromechanical Resonators. Adv. Mater. 2012, 24, 2722–2727. [Google Scholar] [CrossRef]
- Xie, Z.W.; Zhu, H.S.; Kang, T.F.; Che, W.Q.; Xue, Q. 1GHz GaN MEMS Oscillator Based on GaN-on-Si MMIC Technology. In Proceedings of the 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Guangzhou, China, 27–29 November 2022. [Google Scholar] [CrossRef]
- Lin, C.M.; Yantchev, V.; Zou, J.; Chen, Y.Y.; Pisano, A.P. Micromachined One-Port Aluminum Nitride Lamb Wave Resonators Utilizing the Lowest-Order Symmetric Mode. J. Microelectromech. S. 2013, 23, 78–91. [Google Scholar] [CrossRef]
- Yantchev, V.; Katardjiev, I. Micromachined thin film plate acoustic resonators utilizing the lowest order symmetric lamb wave mode. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2006, 54, 87–95. [Google Scholar] [CrossRef]
- Anderås, E.; Katardjiev, I.; Yantchev, V. Lamb wave resonant pressure micro-sensor utilizing a thin-film aluminium nitride membrane. J. Micromech. Microeng. 2011, 21, 085010. [Google Scholar] [CrossRef]
- Zou, J.; Gao, A.; Pisano, A.P. Spectrum-clean S1 AlN Lamb wave resonator with damped edge reflectors. Appl. Phys. Lett. 2020, 116, 023505. [Google Scholar] [CrossRef]
- Zou, J.; Lin, C.M.; Lam, C.S.; Pisano, A.P. Transducer design for AlN Lamb wave resonators. J. Appl. Phys. 2017, 121, 154502. [Google Scholar] [CrossRef]
- Campanella, H.; Khine, L.; Tasi, J.M. Aluminum Nitride Lamb-Wave Resonators for High-Power High-Frequency Applications. IEEE Electron Device Lett. 2013, 34, 316–318. [Google Scholar] [CrossRef]
- Piazza, G.; Stephanou, P.J.; Pisano, A.P. One and two port piezoelectric higher order contour-mode MEMS resonators for mechanical signal processing. Solid-State Electron. 2007, 51, 1596–1608. [Google Scholar] [CrossRef]
- Tharpe, T.; Tabrizian, R.A. A 9.4 GHZ Intrinsically Switchable Lamb-Wave Resonator Using Atomic-Layer-Deposited Ferroelectric Hafnia-Zirconia. In Proceedings of the 2022 Solid-State Sensors, Actuators and Microsystems Workshop, Hilton Head, SC, USA, 5–9 June 2022. [Google Scholar] [CrossRef]
- Kuypers, J.H.; Lin, C.M.; Vigevani, G.; Pisano, A.P. Intrinsic temperature compensation of aluminum nitride Lamb wave resonators for multiple-frequency references. In Proceedings of the 2008 IEEE International Frequency Control Symposium, Honolulu, HI, USA, 19–21 May 2008. [Google Scholar] [CrossRef]
- Kadota, M.; Ogami, T. High frequency lamb wave resonator using LiNbO3 crystal thin plate and application to tunable filter. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010. [Google Scholar] [CrossRef]
- Tao, R.; Wang, W.B.; Luo, J.T.; Hasan, S.A.; Torun, H.; Canyelles-Pericas, P.; Zhou, J.; Xuan, W.P.; Cooke, M.D.; Gibson, D.; et al. Thin film flexible/bendable acoustic wave devices: Evolution, hybridization and decoupling of multiple acoustic wave modes. Surf. Coat. Tech. 2019, 357, 587–594. [Google Scholar] [CrossRef]
- Rose, J.L.; Nagy, P.B. Ultrasonic Waves in Solid Media. J. Acoust. Soc. Am. 2000, 107, 1807–1808. [Google Scholar] [CrossRef]
- Zou, J. High-Performance Aluminum Nitride Lamb Wave Resonators for RF Front-End Technology. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2015. [Google Scholar]
- Zou, J.; Lin, C.M.; Gao, A.; Pisano, A.P. The Multi-Mode Resonance in AlN Lamb Wave Resonators. J. Microelectromech. Syst. 2018, 27, 973–984. [Google Scholar] [CrossRef]
- Kropelnicki, P.; Muckensturm, K.M.; Mu, X.J.; Randles, A.B.; Cai, H.; Ang, W.C.; Tsai, J.M.; Vogt, H. CMOS-compatible ruggedized high-temperature Lamb wave pressure sensor. J. Micromech. Microeng. 2013, 23, 085018. [Google Scholar] [CrossRef]
- Lin, C.M.; Yen, T.T.; Lai, Y.J.; Felmetsger, V.V.; Hopcroft, M.A.; Kuypers, J.H.; Pisano, A.P. Temperature-compensated aluminum nitride lamb wave resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 524–532. [Google Scholar] [CrossRef]
- Mebarki, M.; Laidoudi, F.; Boubenider, F. Numerical Study of S0 Lamb Mode Resonator based on c-BN/AlN for 5G Operating Acoustic Devices. Acoust. Phys. 2021, 67, 457–464. [Google Scholar] [CrossRef]
- Assila, N.; Kadota, M.; Tanaka, S. High-Frequency Resonator Using A1 Lamb Wave Mode in LiTaO3 Plate. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1529–1535. [Google Scholar] [CrossRef] [PubMed]
- Lv, S.T.; Zhu, Z.; Long, F.; Sun, H.Y.; Song, C.G.; Zhang, A.Y.; Tan, F.Z.; Zhao, J.C. Characterization analysis of quality factor, electro-mechanical coupling and spurious modes for AlN Lamb-wave resonators with fs > 2 GHz. Microelectron. J. 2022, 125, 105466. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, N.; Sun, C.L.; Merugu, S.; Singh, N.; Gu, Y.D. A High Coupling Coefficient 2.3-GHz AlN Resonator for High Band LTE Filtering Application. IEEE Electron Device Lett. 2016, 37, 1344–1346. [Google Scholar] [CrossRef]
- Zou, J.; Gao, A.; Pisano, A.P. Ultralow Acoustic Loss Micromachined Butterfly Lamb Wave Resonators on AlN Plates. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 67, 671–674. [Google Scholar] [CrossRef]
- Sun, H.Y.; Lv, S.T.; Zhang, A.Y.; Song, C.G.; Sun, X.Y.; Tan, F.Z.; Liang, L.H.; Zhu, Y.F.; Zhao, J.C. High Quality-Factor and Spectrum-Clean AlN Lamb-Wave Resonators with Optimized Lateral Reflection Boundary Conditions and Transducer Design. Micromachines 2022, 13, 779. [Google Scholar] [CrossRef]
- Feld, D.A.; Parker, R.; Ruby, R.; Bradley, P.; Dong, S. After 60 years: A new formula for computing quality factor is warranted. In Proceedings of the 2008 IEEE Ultrasonics Symposium, Beijing, China, 2–5 November 2008. [Google Scholar] [CrossRef]
- Zou, J.; Lin, C.M.; Pisano, A.P. Quality factor enhancement in Lamb wave resonators utilizing butterfly-shaped AlN plates. In Proceedings of the 2014 IEEE International Ultrasonics Symposium, Chicago, IL, USA, 3–6 September 2014. [Google Scholar] [CrossRef]
- Lin, C.M.; Zou, J.; Chen, Y.Y.; Pisano, A.P. High-Q piezoelectric Lamb wave resonators based on AlN plates with chamfered corners. In Proceedings of the 2015 IEEE International Ultrasonics Symposium (IUS), Taipei, Taiwan, 21–24 October 2015. [Google Scholar] [CrossRef]
- Zhu, H.S.; Tu, C.; Lee, J.E.Y. High-Q low impedance UHF-band ALN-ON-SI mems resonators using quasi-symmetrical Lamb wave modes. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016. [Google Scholar] [CrossRef]
- Binci, L.; Tu, C.; Zhu, H.; Lee, J.Y. Planar ring-shaped phononic crystal anchoring boundaries for enhancing the quality factor of Lamb mode resonators. Appl. Phys. Lett. 2016, 109, 203501. [Google Scholar] [CrossRef]
- Zou, J.; Liu, J.S.; Tang, G.B.; Lin, C.M.; Lam, C.S. Transverse mode suppression in the AlN lamb wave resonators by “piston mode”. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar] [CrossRef]
- Liu, J.Y.; Zhou, J.; Zou, Y.; Gao, C.; Xie, Y.; Sun, C.L. AlN Checker-mode Resonators with Routing Structures. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019. [Google Scholar] [CrossRef]
- Song, E.S.; Kang, S.; Kim, H.; Kim, Y.K.; An, J.E.; Baek, C.W. Wafer-Level Fabrication of a Fused-Quartz Double-Ended Tuning Fork Resonator Oscillator Using Quartz-on-Quartz Direct Bonding. IEEE Electron Device Lett. 2013, 34, 692–694. [Google Scholar] [CrossRef]
- Hung, C.H.; Wang, W.S.; Lin, Y.C.; Liu, T.W.; Sun, J.H.; Chen, Y.Y.; Esashi, M.; Wu, T.T. Design and fabrication of an AT-cut quartz phononic Lamb wave resonator. J. Micromech. Microeng. 2013, 23, 065025. [Google Scholar] [CrossRef]
- Lin, C.M.; Yen, T.T.; Lai, Y.J.; Felmetsger, V.V.; Hopcroft, M.A.; Kuypers, J.H.; Pisano, A.P. Experimental study of temperature-compensated aluminum nitride Lamb wave resonators. In Proceedings of the 2009 IEEE International Frequency Control Symposium Joint with the 22nd European Frequency and Time Forum, Besancon, France, 20–24 April 2009. [Google Scholar] [CrossRef]
- Vinita; Singh, J. Bulk acoustic wave (BAW) resonator-based MEMS magnetic field sensor. J. Mater. Sci. Mater. Electron. 2024, 35, 750. [Google Scholar] [CrossRef]
- Singh, J.; Gupta, S.K.; Vinita. Room temperature operating formaldehyde sensor based on n-type ZnO functionalized surface acoustic wave resonator. Sens. Actuators A Phys. 2024, 365, 11481. [Google Scholar] [CrossRef]
- Sui, W.; Sheplak, M.; Feng, P.X.L. Gallium Nitride (GaN) MEMS Lamb Wave Resonators Operating At High Temperature Up To 800 °C. In Proceedings of the 2024 IEEE 37th International Conference on Micro Electro Mechanical Systems (MEMS), Austin, TX, USA, 21–25 January 2024. [Google Scholar] [CrossRef]
- Du, X.Y.; Fu, Y.Q.; Tan, S.C.; Luo, J.K.; Flewitt, A.J.; Milne, W.I.; Lee, D.S.; Park, N.M.; Park, J.; Choi, Y.J.; et al. ZnO film thickness effect on surface acoustic wave modes and acoustic streaming. Appl. Phys. Lett. 2008, 93, 094105. [Google Scholar] [CrossRef]
- Mirpuri, C.; Xu, S.; Long, J.D.; Ostrikov, K. Low-temperature plasma-assisted growth of optically transparent, highly oriented nanocrystalline AlN. J. Appl. Phys. 2007, 101, 024312. [Google Scholar] [CrossRef]
- Loebl, H.P.; Klee, M.; Metzmacher, C.; Brand, W.; Milsom, R.; Lok, P. Piezoelectric thin AlN films for bulk acoustic wave (BAW) resonators. Mater. Chem. Phys. 2003, 79, 143–146. [Google Scholar] [CrossRef]
- Fu, Y.Q.; Luo, J.K.; Nguyen, N.T.; Walton, A.J.; Flewitt, A.J.; Zu, X.T.; Li, Y.; McHale, G.; Matthews, A.; Iborra, E.; et al. Advances in piezoelectric thin films for acoustic biosensors, acoustofluidics and lab-on-chip applications. Prog. Mater. Sci. 2017, 89, 31–91. [Google Scholar] [CrossRef]
- Monroy, E.; Omnès, F.; Calle, F. Wide-bandgap semiconductor ultraviolet photodetectors. Semicond. Sci. Technol. 2003, 18, R33. [Google Scholar] [CrossRef]
- Ichihashi, H.; Yanagitani, T.; Takayanagi, S.; Kawabe, M.; Matsukawa, M. Gigahertz acoustic wave velocity measurement in GaN single crystals considering acousto-electric effect. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1307–1313. [Google Scholar] [CrossRef]
- Klimm, D.; Ganschow, S.; Schulz, D.; Fornari, R. The growth of ZnO crystals from the melt. J. Cryst. Growth 2008, 310, 3009–3013. [Google Scholar] [CrossRef]
- Ruiz, E.; Alvarez, S.; Alemany, P. Electronic structure and properties of AlN. Phys. Rev. B 1994, 49, 7115. [Google Scholar] [CrossRef]
- Bhatt, R.; Bhaumik, I.; Ganesamoorthy, S.; Karnal, A.K.; Swami, M.K.; Patel, H.S.; Gupta, P.K. Urbach tail and bandgap analysis in near stoichiometric LiNbO3 crystals. Phys. Status Solidi A 2011, 209, 176–180. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, H.; Wang, Z.Q.; Zhang, S.Y. Effects of electrodes on performance figures of thin film bulk acoustic resonators. J. Acoust. Soc. Am. 2007, 122, 1646–1651. [Google Scholar] [CrossRef]
- Kirk, K.J.; Hou, R.Z.; Pragada, N.M.; Torbay, L.; Schmarje, N.; Hutson, D. High temperature ultrasonic transducers using lithium niobate piezocomposite. In Proceedings of the 51st Annual Conference of the British Institute of Non-Destructive Testing 2012, Northamptonshire, UK, 11–13 September 2012. [Google Scholar]
- Ohmori, Y.; Yamaguchi, M.; Yoshino, K.; Inuishi, Y. Electron Hall Mobility in Reduced LiNbO3. Jpn. J. Appl. Phys. 1976, 15, 2263. [Google Scholar] [CrossRef]
- Patel, N.; Branch, D.W.; Schamiloglu, E.; Cular, S. Comparative study of 0° X-cut and Y + 36°-cut lithium niobate high-voltage sensing. Rev. Sci. Instrum. 2015, 86, 085001. [Google Scholar] [CrossRef] [PubMed]
- Gao, A.; Zou, J. Extremely High Q AlN Lamb Wave Resonators Implemented by Weighted Electrodes. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019. [Google Scholar] [CrossRef]
- Cao, H.; Lu, X.; Ren, H. An A0 mode Lamb-wave AlN resonator on SOI substrate with vertically arranged double-electrodes. J. Micromech. Microeng. 2022, 32, 095004. [Google Scholar] [CrossRef]
- Zolfaghari, P.; Zadehsafari, M.; Akbari, A.; Ghavifekr, H.B. An acoustic piezoelectric ring-shape Lamb wave MEMS resonator. In Proceedings of the 2017 4th International Conference on Electrical and Electronic Engineering (ICEEE), Ankara, Turkey, 8–10 April 2017. [Google Scholar] [CrossRef]
- Wang, R.Y.; Bhave, S.A.; Bhattacharjee, K. Design and Fabrication of S0 Lamb-Wave Thin-Film Lithium Niobate Micromechanical Resonators. J. Microelectromechanical Syst. 2015, 24, 300–308. [Google Scholar] [CrossRef]
- Sun, H.Y.; Lv, S.T.; Long, F.; Song, C.G.; Sun, X.Y.; Tan, F.Z.; Zhao, J.C. Structural design and experimental analysis for AlN Lamb-wave resonators with different electrical boundary conditions. Solid-State Electron. 2022, 195, 108404. [Google Scholar] [CrossRef]
- Zou, J.; Lam, C.S. Electrode design of AlN Lamb wave resonators. In Proceedings of the 2016 IEEE International Frequency Control Symposium (IFCS), New Orleans, LA, USA, 9–12 May 2016. [Google Scholar] [CrossRef]
- Zhang, H.X.; Tang, Z.F.; Wang, Z.; Pan, S.T.; Han, Z.Y.; Sun, C.L.; Zhang, M.L.; Duan, X.X.; Pang, W. Acoustic Streaming and Microparticle Enrichment within a Microliter Droplet Using a Lamb-Wave Resonator Array. Phys. Rev. Appl. 2018, 9, 064011. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, C.; Dou, S.X.; Zhou, H.; Yang, J.; Wang, D.P.; Chen, Y.; Cheng, Y.H.; Shang, Z.G.; Mu, X.J. Temperature decoupled viscosity-density product measurement in liquid by utilizing a dual-mode AlN-based acoustic wave resonator. Appl. Phys. Lett. 2018, 113, 203502. [Google Scholar] [CrossRef]
- Ueda, M.; Nishihara, T.; Taniguchi, S.; Yokoyama, T.; Tsutsumi, J.; Iwaki, M.; Satoh, Y. Film Bulk Acoustic Resonator using High-Acoustic-Impedance Electrodes. Jpn. J. Appl. Phys. 2007, 46, 4642. [Google Scholar] [CrossRef]
- Li, Y.X.; Hu, A.; Fu, Y.T.; Liu, S.F.; Shen, W.T.; Hu, H.; Nie, X.Y. Al Alloys and Casting Processes for Induction Motor Applications in Battery-Powered Electric Vehicles: A Review. Metals 2022, 12, 216. [Google Scholar] [CrossRef]
- Zahroh, F.F.; Sugihartono, I.; Safitri, E.D. Young’s Modulus Calculation of Some Metals Using Molecular Dynamics Method Based on the Morse Potential. Comput. Exp. Res. Mater. Renew. Energy 2019, 2, 19–34. [Google Scholar] [CrossRef]
- Takaki, S.; Masumura, T.; Tsuchiyama, T. Elastic constants in ideal poly-crystalline metals. J. Soc. Mater. Sci. Jpn. 2020, 69, 657–660. [Google Scholar] [CrossRef]
- Veiga, C.; Davim, J.P.; Loureiro, A.J.R. Properties and Applications of Titanium Alloys: A Brief Review. Rev. Adv. Mater. Sci. 2012, 32, 133–148. [Google Scholar]
- Cimalla, V.; Röhlig, C.C.; Pezoldt, J.; Niebelschütz, M.; Ambacher, O.; Brückner, K.; Hein, M.; Weber, J.; Milenkvoic, S.; Smith, A.J.; et al. Nanomechanics of Single Crystalline Tungsten Nanowires. J. Nanomater. 2008, 2008, 638947. [Google Scholar] [CrossRef]
- Zhang, H.X.; Tang, Z.F.; Wang, Z.; Pan, S.T.; Sun, C.L.; Duan, X.X.; Pang, W. Bioparticle manipulations using lamb wave resonator array. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar] [CrossRef]
- Gao, F.; Al-Qahtani, A.M.; Khelif, A.; Boussaid, F.; Benchabane, S.; Cheng, Y.; Agnaf, Q.E.; Bermak, A. Towards Acoustic Radiation Free Lamb Wave Resonators for High-Resolution Gravimetric Biosensing. IEEE Sens. J. 2020, 21, 2725–2733. [Google Scholar] [CrossRef]
- Zaitsev, B.D.; Kunetsova, V.; Joshi, S.G. Propagation of acoustic waves in plates bordered with viscous liquid. In Proceedings of the 1997 IEEE Ultrasonics Symposium Proceedings. An International Symposium (Cat. No.97CH36118), Toronto, ON, Canada, 5–8 October 1997. [Google Scholar] [CrossRef]
- Kanazawa, K.K.; Gordon II, J.G. The oscillation frequency of a quartz resonator in contact with liquid. Anal. Chim. Acta 1985, 175, 99–105. [Google Scholar] [CrossRef]
- Mirea, T.; Yantchev, V. Influence of liquid properties on the performance of S0-mode Lamb wave sensors: A theoretical analysis. Sens. Actuators B Chem. 2015, 208, 212–219. [Google Scholar] [CrossRef]
- Caliendo, C.; Hamidullah, M. Pressure sensing with zero group velocity lamb modes in self-supported a-SiC/c-ZnO membranes. J. Phys. D Appl. Phys. 2018, 51, 385102. [Google Scholar] [CrossRef]
- Caliendo, C.; D’Amico, A.; Castro, F.L. Lamb Waves Propagation along 3C-SiC/AlN Membranes for Application in Temperature-Compensated, High-Sensitivity Gravimetric Sensors. Sensors 2013, 13, 550–564. [Google Scholar] [CrossRef]
- Caliendo, C.; Hamidullah, M.; Laidoudi, F. Amorphous SiC/c-ZnO-Based Quasi-Lamb Mode Sensor for Liquid Environments. Sensors 2017, 17, 1209. [Google Scholar] [CrossRef]
- Caliendo, C. Theoretical investigation of Lamb wave A0 mode in thin SiC/AlN membranes for sensing application in liquid media. Sens. Actuators B Chem. 2013, 179, 287–292. [Google Scholar] [CrossRef]
- Pantazis, A.K.; Konstantinidis, G.; Gizeli, E. Study of the Effect of the Operating Frequency of a GaN Lamb Wave Device to Viscosity and Protein Sensing. IEEE Sens. J. 2016, 16, 7028–7036. [Google Scholar] [CrossRef]
- Gu, J.W.; He, X.L.; Jin, S.Y.; Zhang, Y.J.; Li, L.F.; Kong, L.H.; Li, P. Single-Crystalline LiNbO3 Film-Based Piezoelectric Sensors for Ultra-Precision Pressure-Sensing Applications. IEEE Sens. J. 2024, 24, 15909–15917. [Google Scholar] [CrossRef]
- Ding, B.; Wang, M.R.; Wang, X.F.; Yu, J.Y.; Sun, G. Electrospun nanomaterials for ultrasensitive sensors. Mater. Today 2010, 13, 16–27. [Google Scholar] [CrossRef] [PubMed]
- Rahman, S.A.; Khan, S.A.; Rehman, M.M.; Kim, W.Y. Highly Sensitive and Stable Humidity Sensor Based on the Bi-Layered PVA/Graphene Flower Composite Film. Nanomaterials 2022, 12, 1026. [Google Scholar] [CrossRef]
- Yu, B.W.; Fu, Y.M.; Wang, P.L.; Zhao, Y.Y.; Xing, L.L.; Xue, X.Y. Enhanced piezo-humidity sensing of a Cd-ZnO nanowire nanogenerator as a self-powered/active gas sensor by coupling the piezoelectric screening effect and dopant displacement. Phys. Chem. Chem. Phys. 2015, 17, 10856–10860. [Google Scholar] [CrossRef]
- Gu, Y.; Jiang, H.; Ye, Z.; Su, N.; Kuang, X.L.; Liu, W.J.; Li, G.F.; Song, X.J.; Zhang, L.; Bai, W.; et al. Impact of Size on Humidity Sensing Property of Copper Oxide Nanoparticles. Electron. Mater. Lett. 2020, 16, 61–71. [Google Scholar] [CrossRef]
- Bodenhöfer, K.; Hierlemann, A.; Noetzel, G.; Weimar, U.; Göpel, W. Performances of Mass-Sensitive Devices for Gas Sensing: Thickness Shear Mode and Surface Acoustic Wave Transducers. Anal. Chem. 1996, 68, 2210–2218. [Google Scholar] [CrossRef]
- Pang, J.T.; Le, X.H.; Huang, W.; Xie, J. A Humidity Sensor Based on Lamb Wave Resonator with Different Graphene Oxide Film. In Proceedings of the 2018 IEEE 13th Annual International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Singapore, 22–26 April 2018. [Google Scholar] [CrossRef]




| Material | LiNbO3 | AlN | ZnO | GaN |
|---|---|---|---|---|
| Crystal structure | Trigonal | Wurtzite | Wurtzite | Wurtzite |
| Bandgap/eV | 3.95 | 6.3 | 3.35 | 3.39 |
| 6500–7365 | 10,150–11,050 | 6340 | 8040 | |
| - | 5800 | 2700–2720 | 4130 | |
| 0.8 | 135 | 200 | 1000 | |
| 4.64 | 5.61–5.72 | 3.25–3.3 | 6.095–6.15 | |
| ) | 85(29) | 8.5 | 8.66 | 8.9 |
| (%) | 5–11.3 | 3.1–8 | 1.5–1.7 | 0.13 |
| ) | 35 | 36.5 | 35.6 | 45 |
| Piezoelectric Material | Sensor Structure | Wave Mode | Operating Frequency/MHz | Detection Target | Sensitivity | Detection Limits/Pgul−1 | Reference |
|---|---|---|---|---|---|---|---|
| LiNbO3 | PMMA/Mo/LN/SiO2/Si | S1 | 8000 | Biomolecule | ) | - | [12] |
| ZnO | ZnO/SiO2/Si/SiO2/ZnO/Al | A0, S0 | 91.55~137.44 | DNA | ) | 82~84 | [13] |
| ZnO | Cr/Au/ZnO/Al | A0, A-TSM, S-TSM | 7.41~14.1 | Imatinib | ) | - | [14] |
| AlN | PMMA/Ni/AlN/SiO2 | A0 | 129.96~139.7 | Biomolecule | ) | - | [95] |
| Piezoelectric Material | Sensor Structure | Operating Frequency/MHz | Detection Target | Q Factor | Sensitivity | Reference |
|---|---|---|---|---|---|---|
| AlN | Al/AlN/Mo/Si | 851~881 | Dielectric permittivity, Viscosity, Density | 1200~1400 | - | [17,18,98] |
| GaN | Cr/Au/GaN/seed layer/Si | 142~458 | Viscosity, Protein-antibody | - | ) | [103] |
| AlN | Al/AlN/SOI | - | Viscosity Density | - | ) ) | [16] |
| AlN | Au/Ti/AlN/SOI | 327.7 | Viscosity | - | - | [15] |
| Piezoelectric Material | Sensor Structure | Wave Mode | Temperature Range/°C | Operating Frequency /MHz | Reference | |||
|---|---|---|---|---|---|---|---|---|
| AlN | Al/AlN/Si/SiO2/Si | LFE | −50~300 | 481.4 | −19.03 | −13.17 | −10.28 | [46] |
| AlN | Al/AlN/SiO2/SoI | LFE, SAW | −50~300 | 478~988 | −21.14~−21.49 | −21.70~−23.53 | −0.612~+0.227 | [22] |
| LiNbO3 | Cr/Au/LN/SiO2/Si/Glue/Si | SH0, SH1, SH2, A1 | −40~100 | 424.2~885.4 | −3.18~−26.57 | - | 6.21~41.38 | [104] |
| AlN | Mo/AlN/Mo/AlN/SOI | - | 20~220 | 819.5 | −14.4 | - | 18.28 | [23] |
| Piezoelectric Material | Sensor Structure | Wave Mode | Operating Frequency /MHz | Sensitivity | Frequency Hysteresis/kHz | Reference | |
|---|---|---|---|---|---|---|---|
| ZnO | GO/Al/ZnO/PI | A0, S0 | 150~395 | ) | - | - | [19] |
| AlN | GO/Cr/Al/PSG/AlN/SOI | A0 | ~390 | ) | −27.2~−28.9 | 12~20 | [110] |
| ZnO | Al/ZnO/Al/SU-8/Si/SU-8 | S0 | 65.82 | ) | - | - | [21] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Yue, Y.; Liang, Z.; Zhao, X.; Li, F.; Peng, W.; Zhu, Q.; He, Y. Physical Sensors Based on Lamb Wave Resonators. Micromachines 2024, 15, 1243. https://doi.org/10.3390/mi15101243
Yu Z, Yue Y, Liang Z, Zhao X, Li F, Peng W, Zhu Q, He Y. Physical Sensors Based on Lamb Wave Resonators. Micromachines. 2024; 15(10):1243. https://doi.org/10.3390/mi15101243
Chicago/Turabian StyleYu, Zixia, Yongqing Yue, Zhaozhao Liang, Xiaolong Zhao, Fangpei Li, Wenbo Peng, Quanzhe Zhu, and Yongning He. 2024. "Physical Sensors Based on Lamb Wave Resonators" Micromachines 15, no. 10: 1243. https://doi.org/10.3390/mi15101243
APA StyleYu, Z., Yue, Y., Liang, Z., Zhao, X., Li, F., Peng, W., Zhu, Q., & He, Y. (2024). Physical Sensors Based on Lamb Wave Resonators. Micromachines, 15(10), 1243. https://doi.org/10.3390/mi15101243








