On the Complex Flow Dynamics of Shear Thickening Fluids Entry Flows
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations
2.2. Geometry, Boundary Conditions, Mesh Analysis and Numerical Methods
3. Results
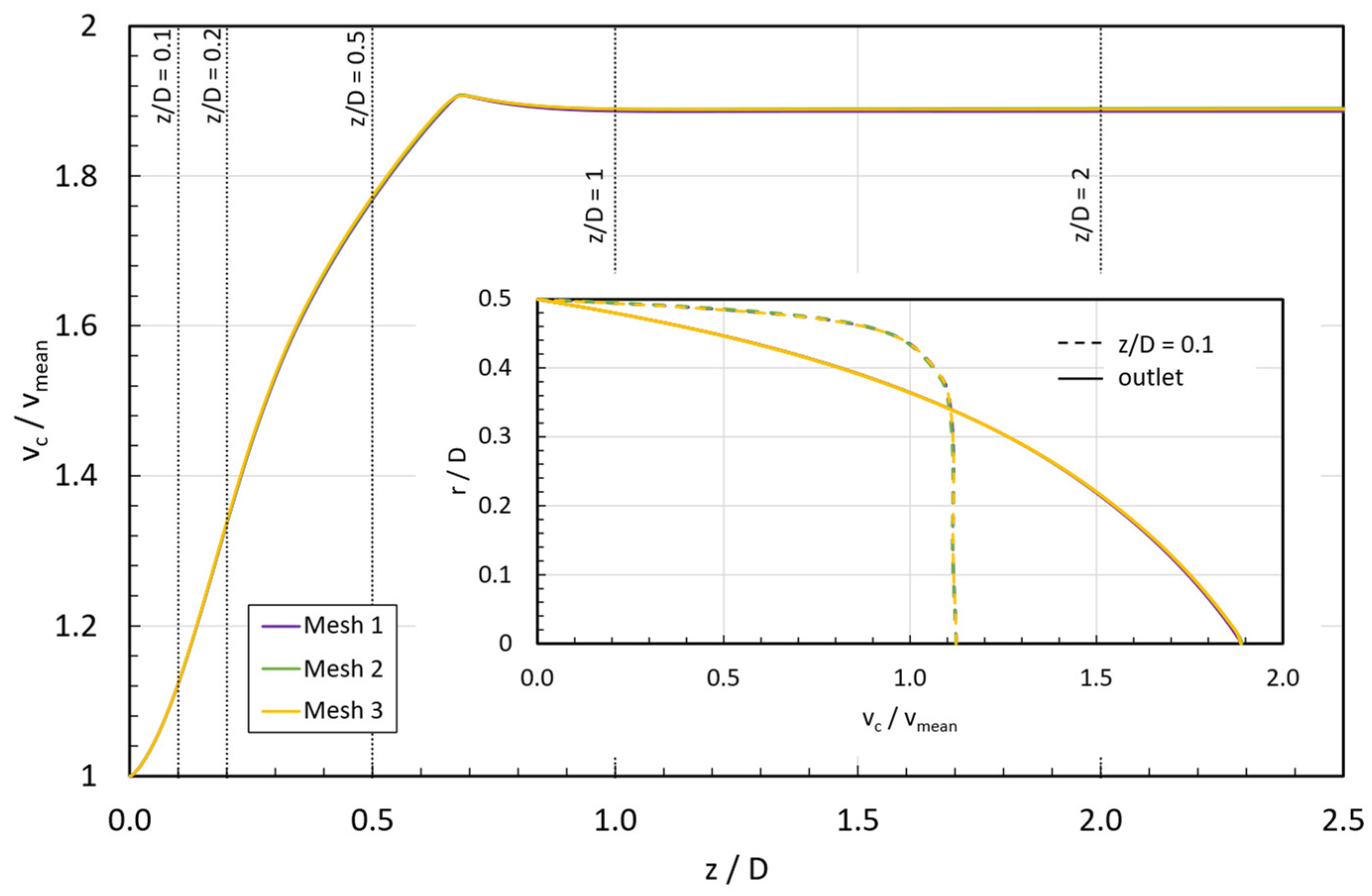
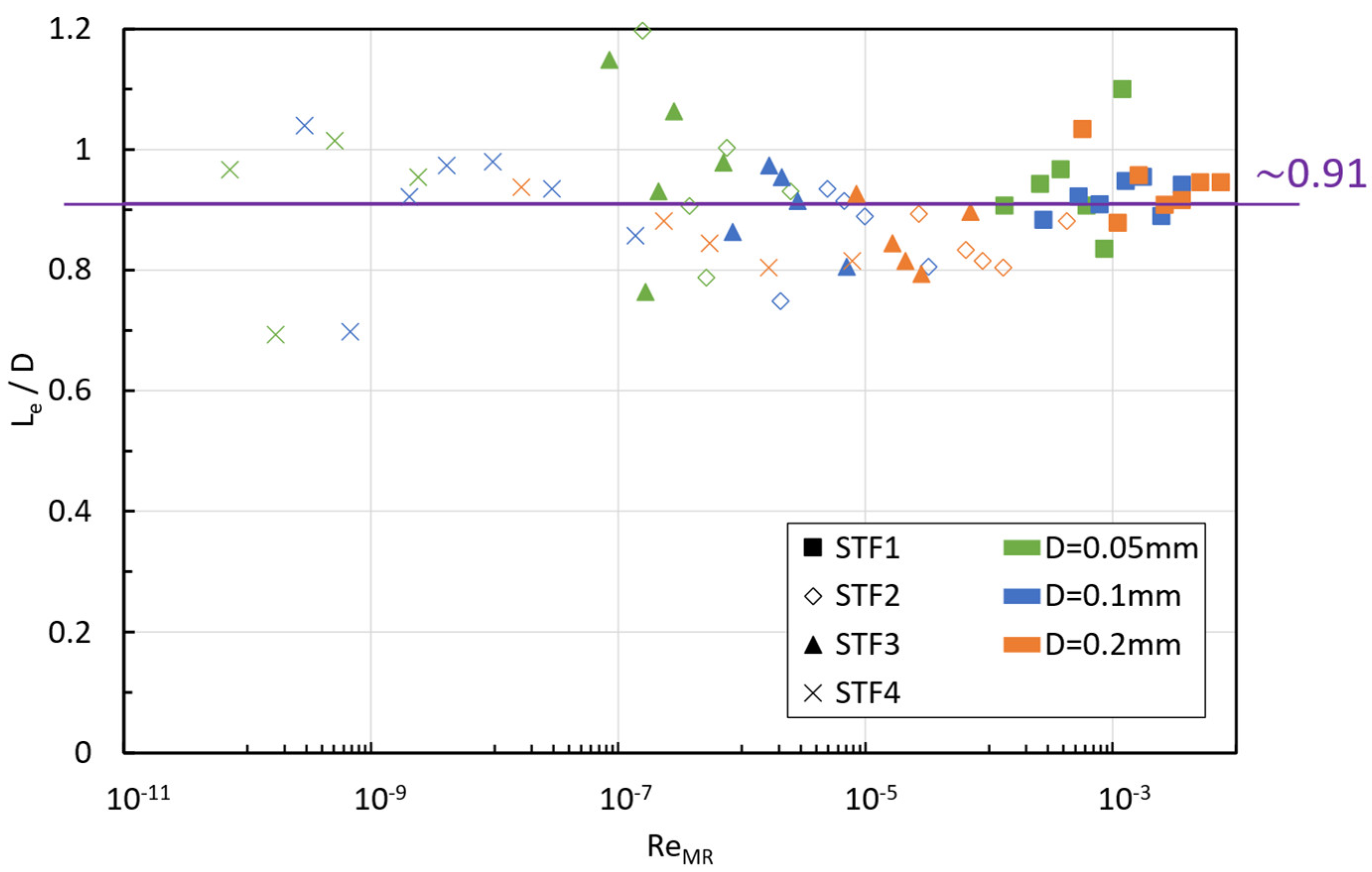
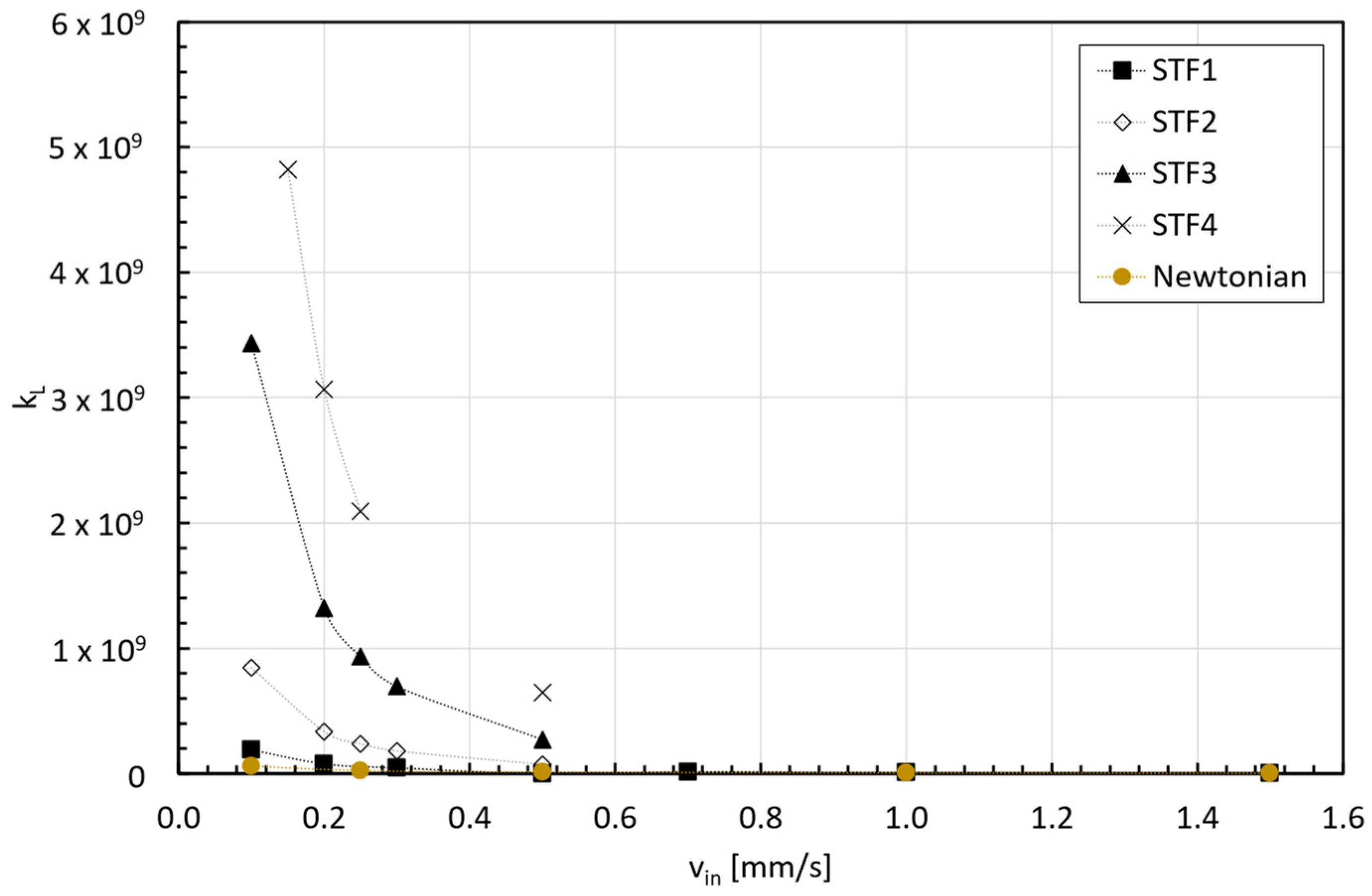
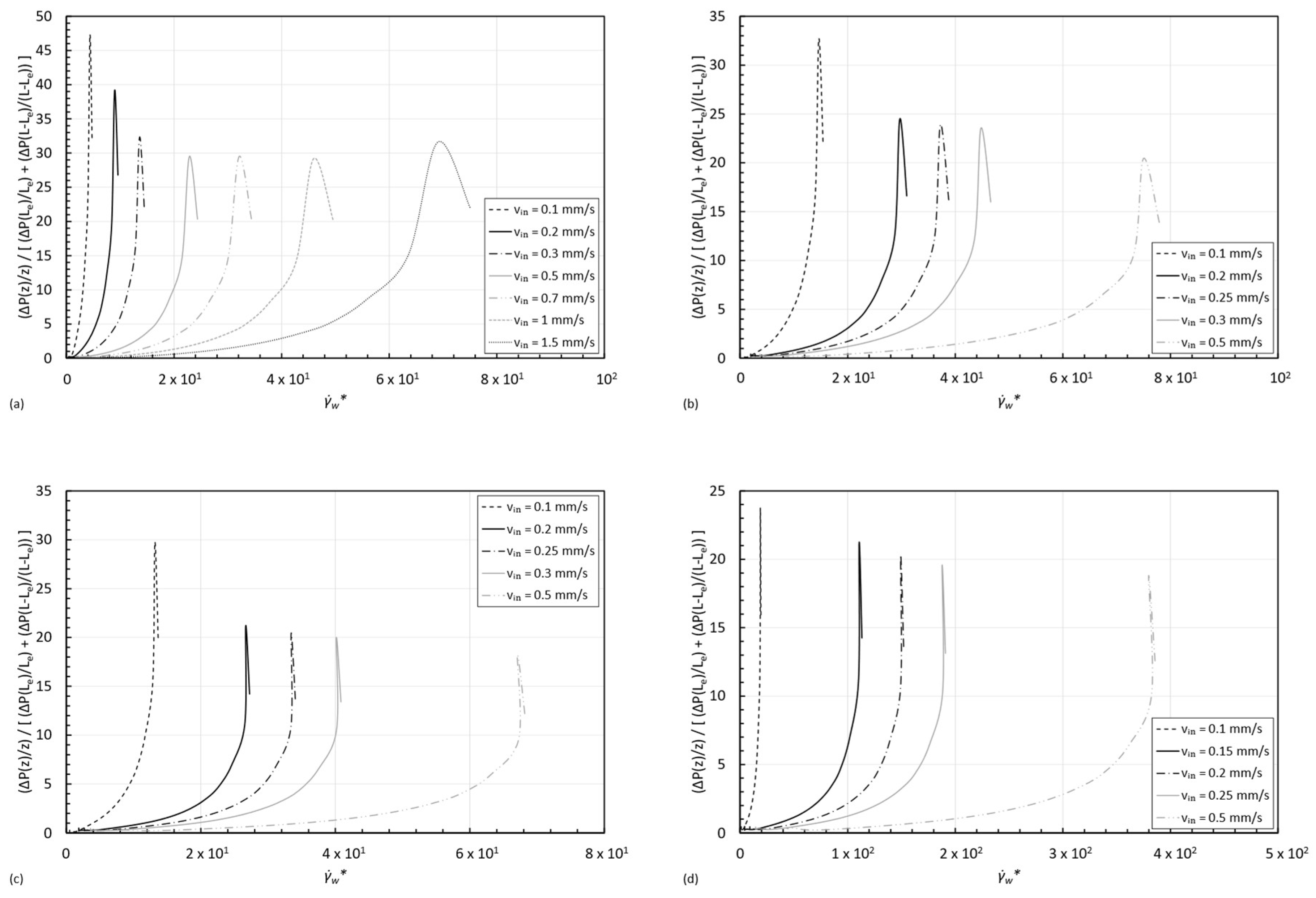
3.1. Entrance Length
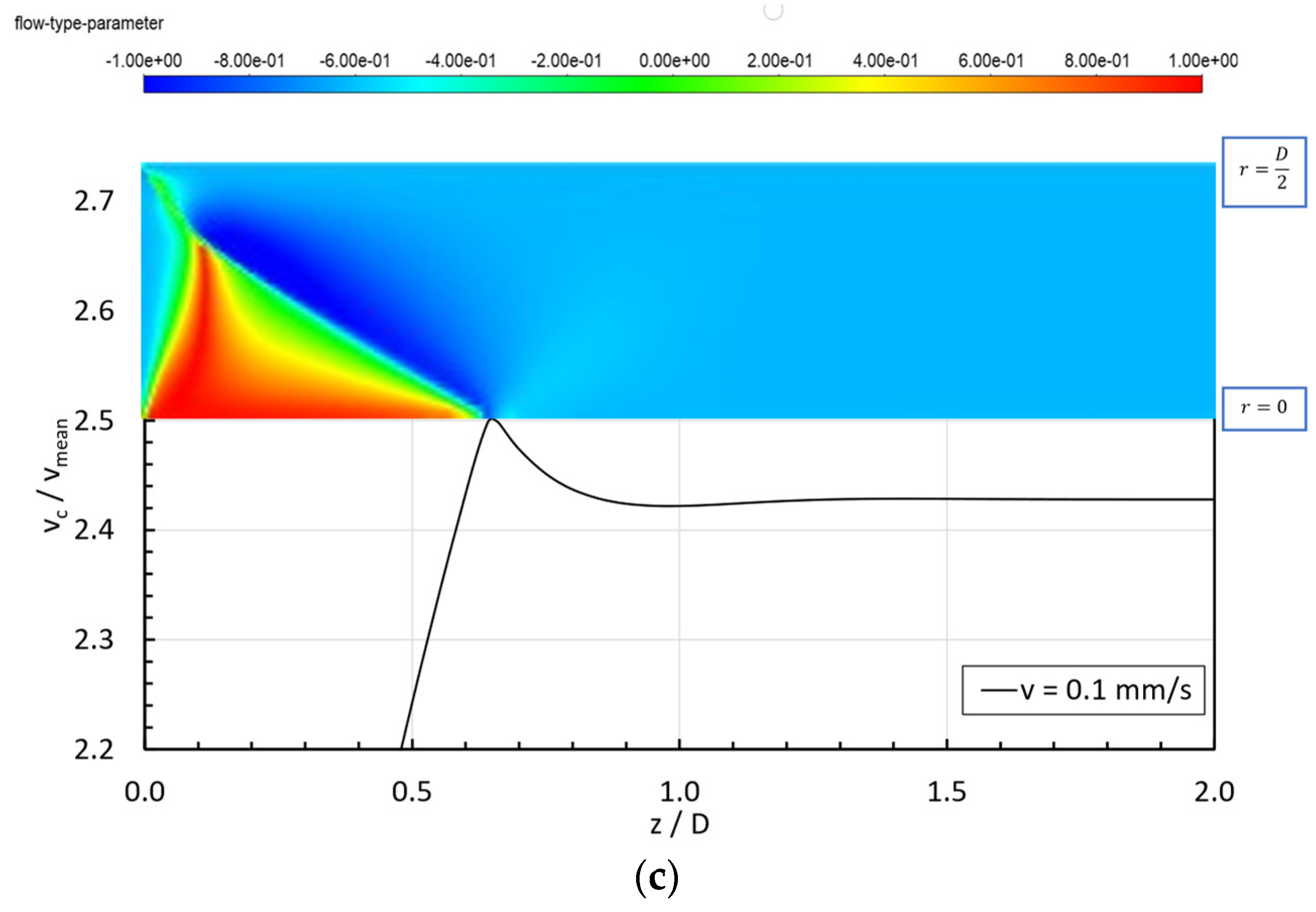
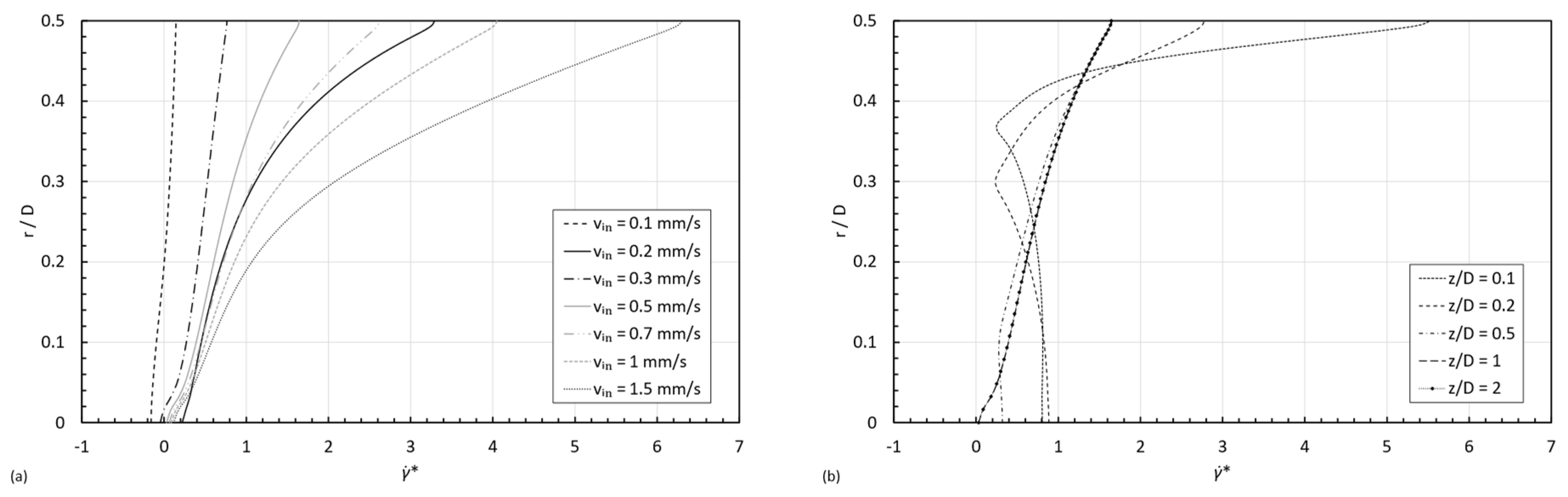
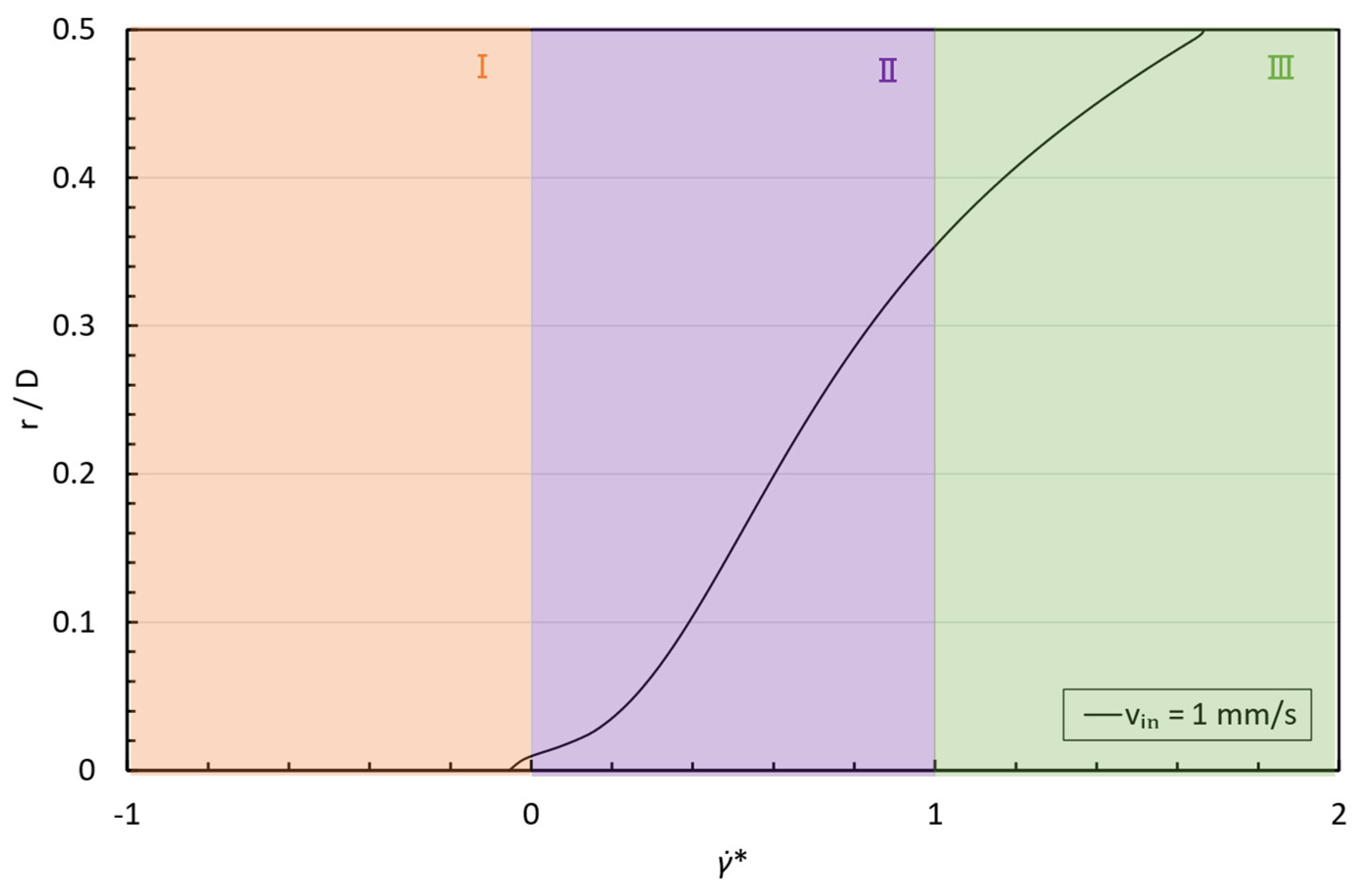
3.2. Flow-Type Parameter
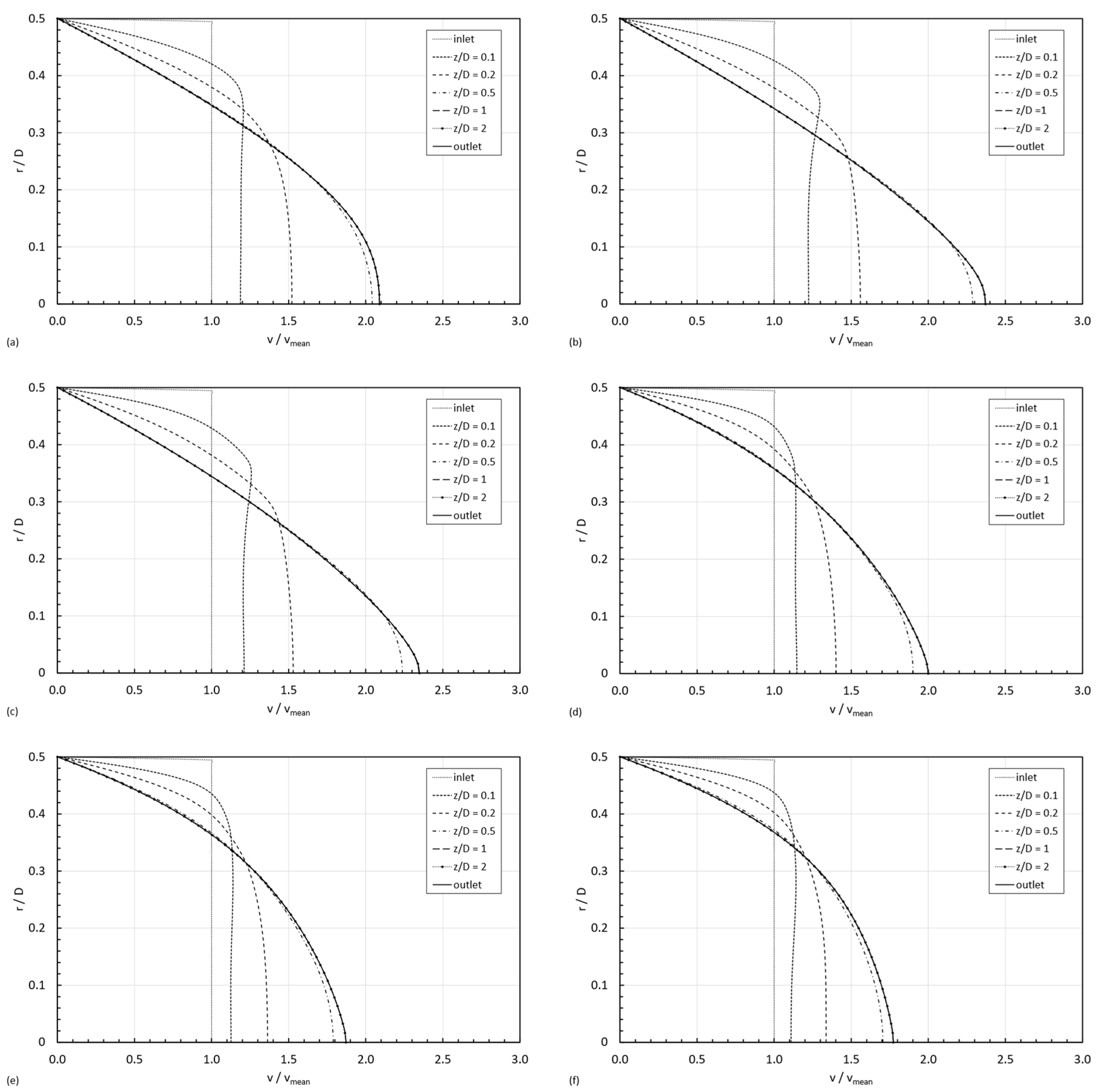
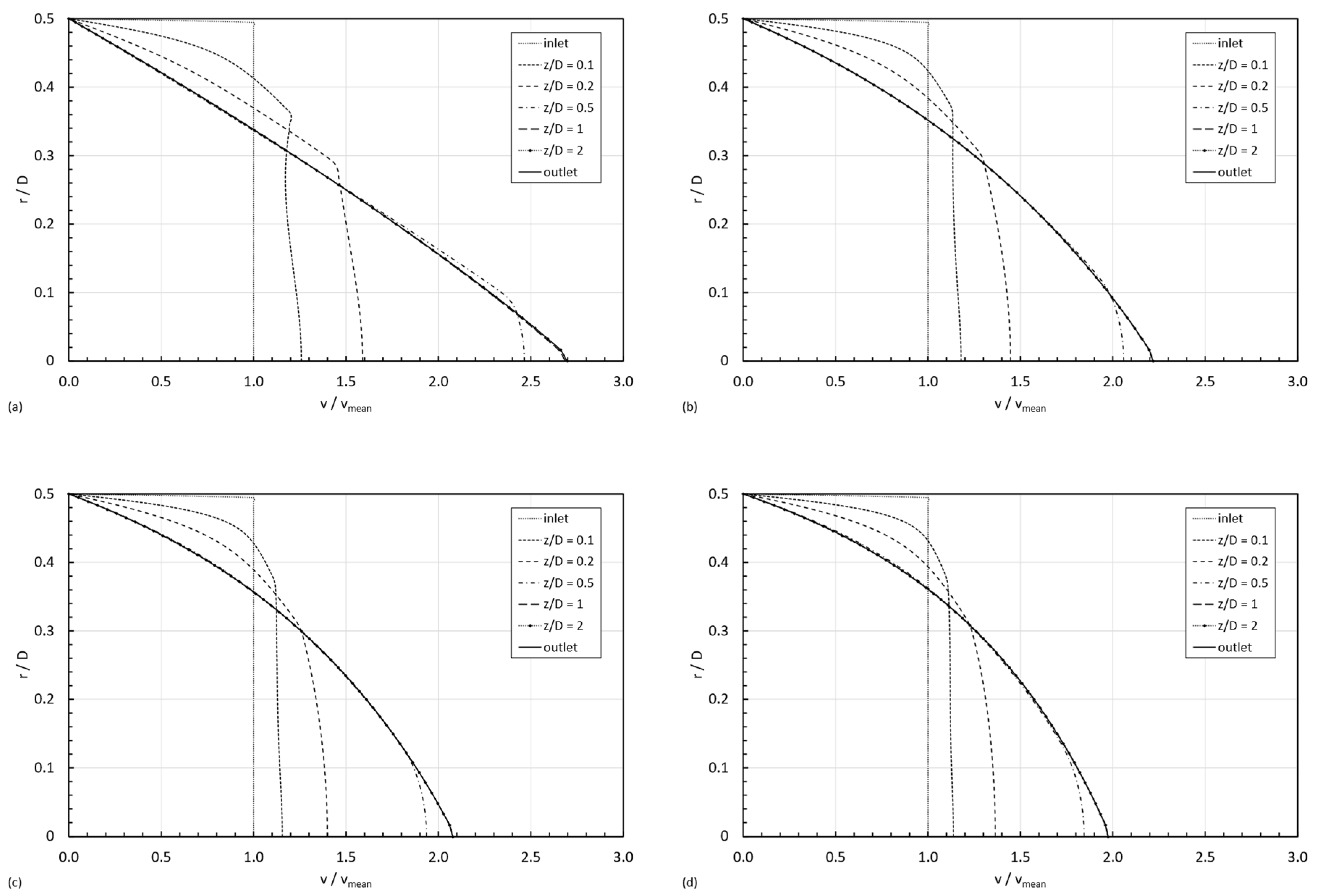
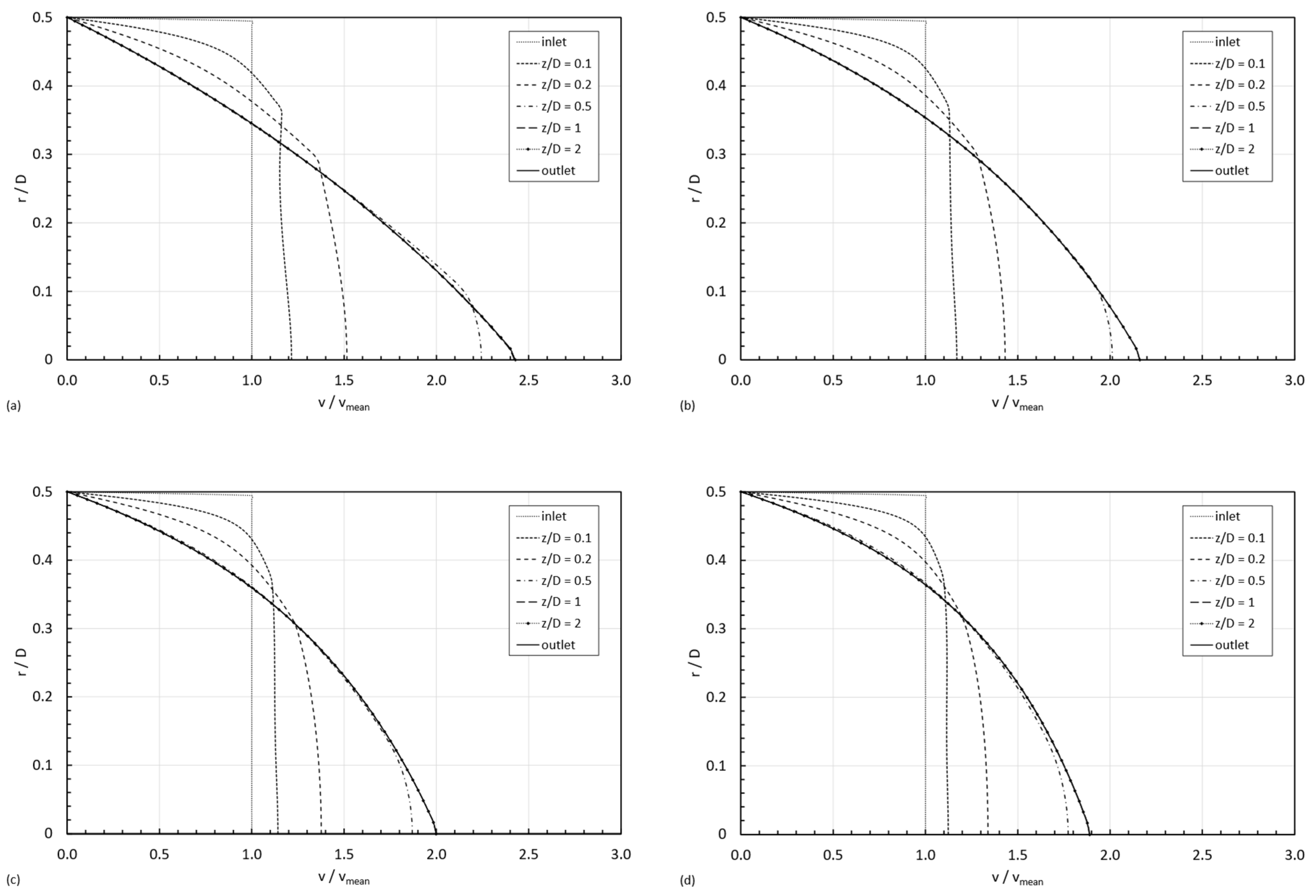
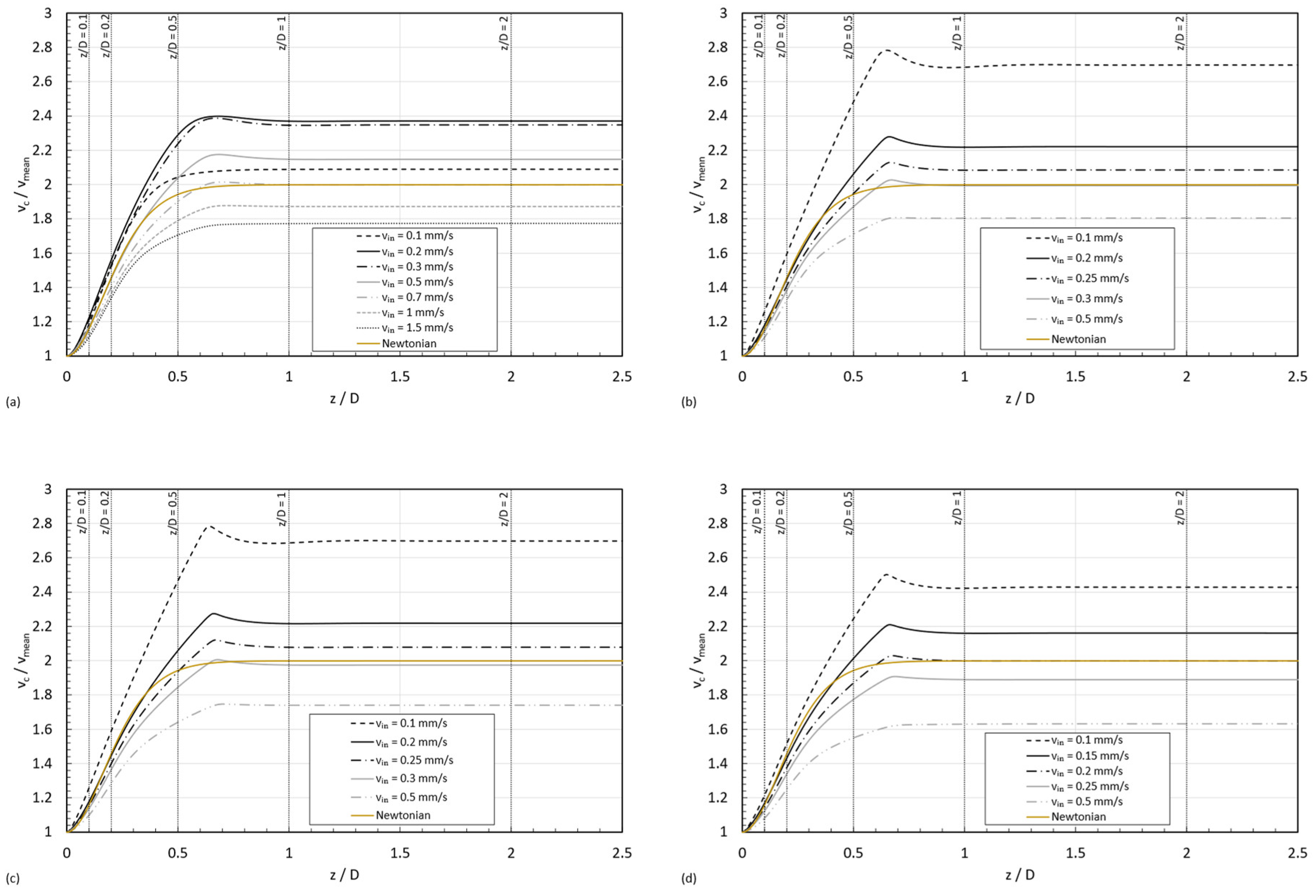
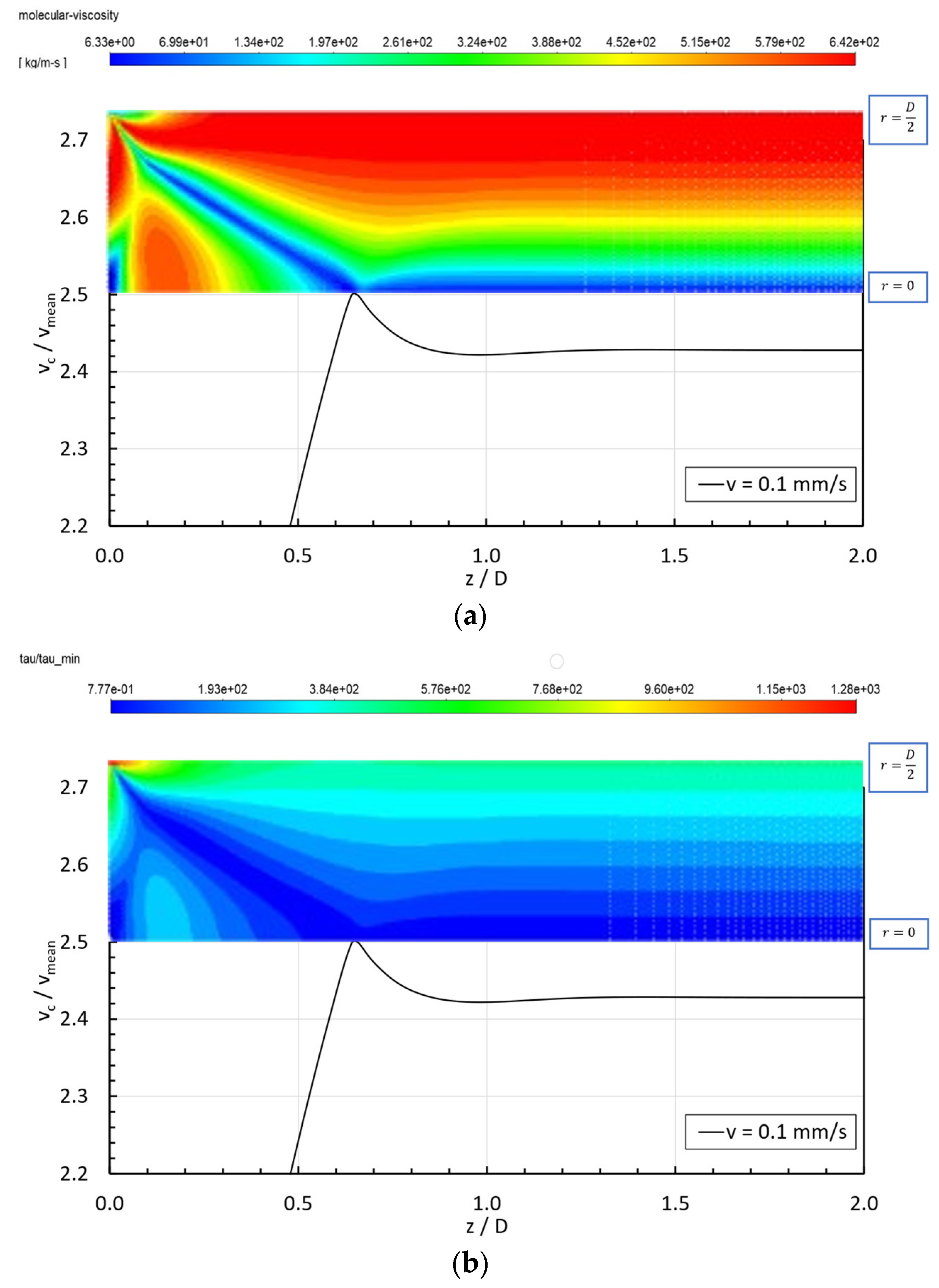
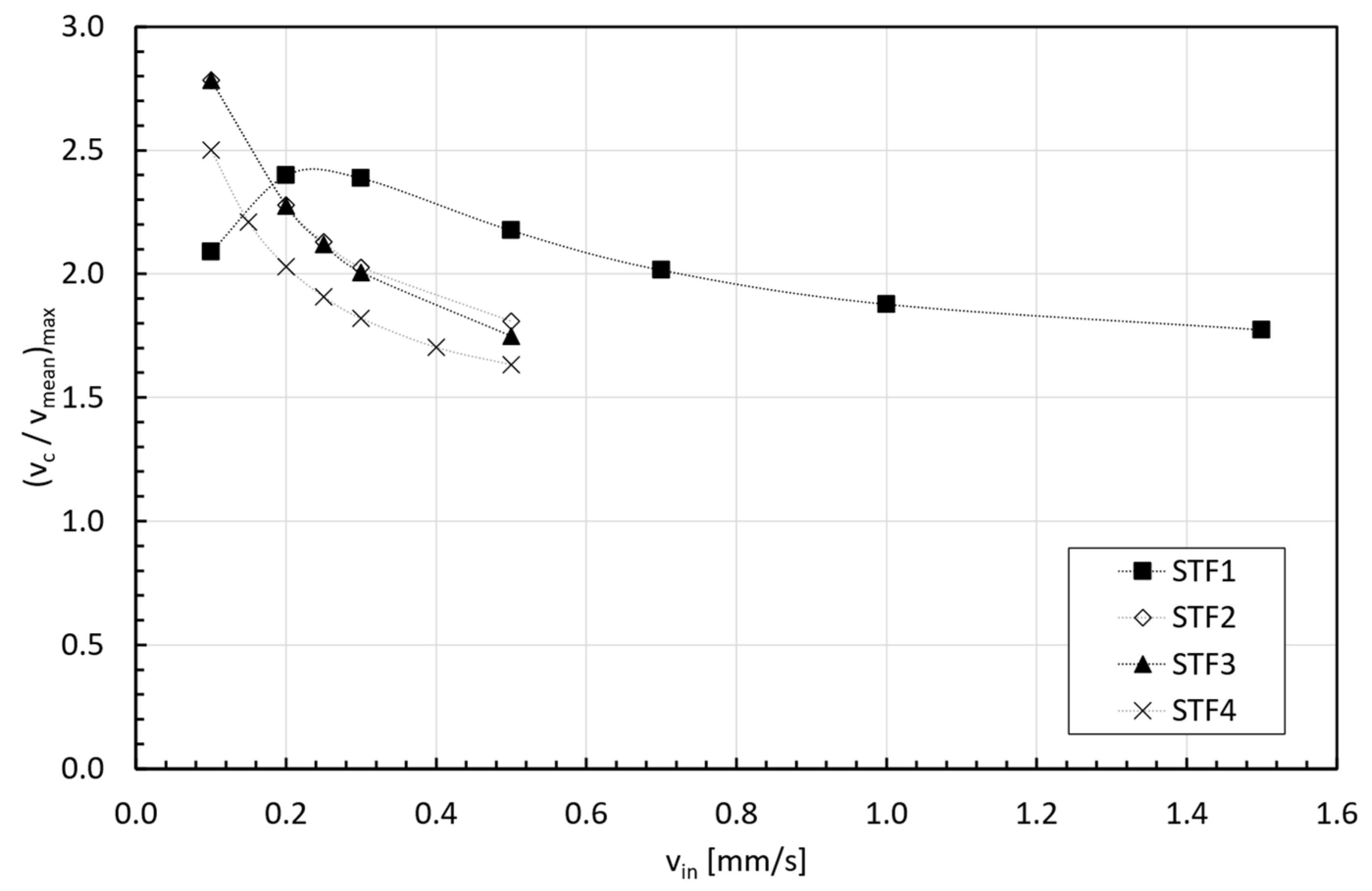
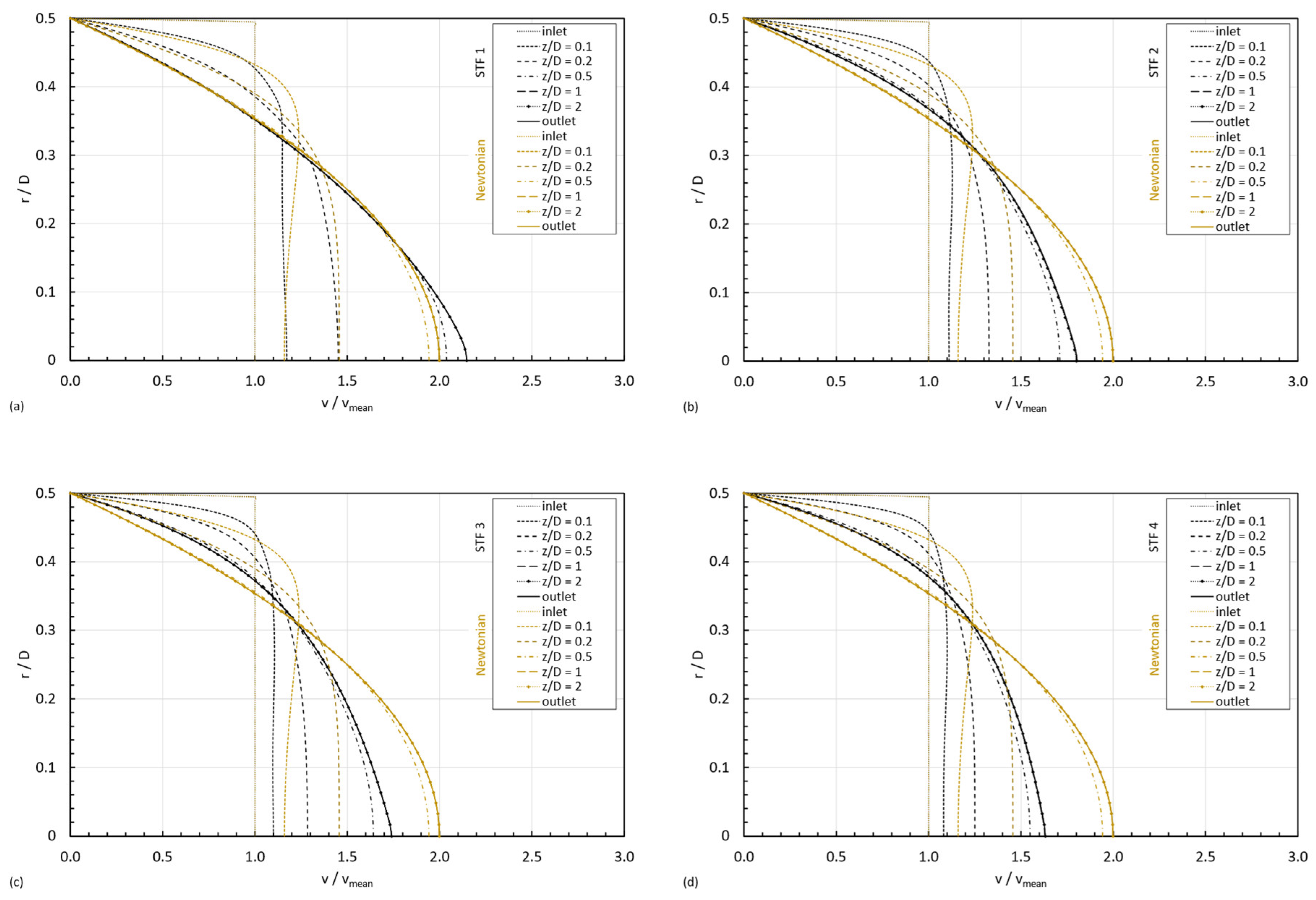
3.3. Velocity Profiles
- Case 1:
- both and are within Region I. The first shear thinning behavior dominates the whole fluid domain, and the viscosity decreases monotonically from the centerline towards the wall in the radial direction.
- Case 2:
- belongs to Region I and is within Region II. The shear thinning behavior is dominating next to the centerline, and the shear thickening does it next to the wall; consequently, there is a non-monotonical variation in viscosities in the radial direction, and there will be a minimum in the viscosity at a certain distance from the centerline when the shear rate reaches the in the viscosity curve.
- Case 3:
- belongs to Region I and is within Region III. The shear thinning behavior is dominating next to the centerline and next to the wall; however, the fact of reaching the two critical shear rates ( and ) in the viscosity curve results in a non-monotonical variation in viscosities in the radial direction. The viscosity will diminish from the centerline towards a minimum at a certain distance from the centerline; then it will increase until the maximum in shear rate, closer to the wall; and, finally, the viscosity will decrease from that maximum until reaching at the wall.
- Case 4:
- both and are within Region II. The shear thickening behavior is dominating the whole fluid domain, and the viscosity increases monotonically from the centerline towards the wall in the radial direction.
- Case 5:
- belongs to Region II and is within Region III. The shear thickening behavior is dominating next to the centerline, and the shear thinning does it next to the wall. Consequently, the viscosity will increase from the centerline to reach a maximum at a certain distance, and, from that position, it will decrease towards the wall of the pipe.
- Case 6:
- both and belong to Region III. This scenario is similar to case 1 in the sense that the viscosity decreases radially from the centerline towards the wall of the pipe, but in this case, it follows the second shear thinning and not the first one in the viscosity curve.
- Case 7:
- both and are within Region I. Since , the viscosity increases from the centerline towards the wall. It is the reversed situation discussed in case 1.
- Case 8:
- belongs to Region I and is within Region II. The shear thinning behavior is dominating next to the wall, and the shear thickening does it next to the centerline, resulting in the reverse situation described in case 2.
- Case 9:
- belongs to Region I and is within Region III. The second shear thinning behavior is dominating next to the centerline, whereas the first shear thinning does it next to the wall, resulting in the reversed case 3.
- Case 10:
- both and are within Region II. The shear thickening behavior is dominating the whole fluid domain, but because , the viscosity decreases monotonically from the centerline towards the wall in the radial direction.
- Case 11:
- belongs to Region II and is within Region III. The shear thickening behavior is dominating next to the wall, and the shear thinning does it next to the centerline. Consequently, the viscosity will increase from the centerline to reach a maximum at a certain distance, and, from that position, it will decrease towards the wall of the pipe.
- Case 12:
- both and belong to Region III. This scenario is similar to case 7 in the sense that the viscosity increases radially from the centerline towards the wall of the pipe, but in this case, it follows the second shear thinning and not the first one in the viscosity curve.
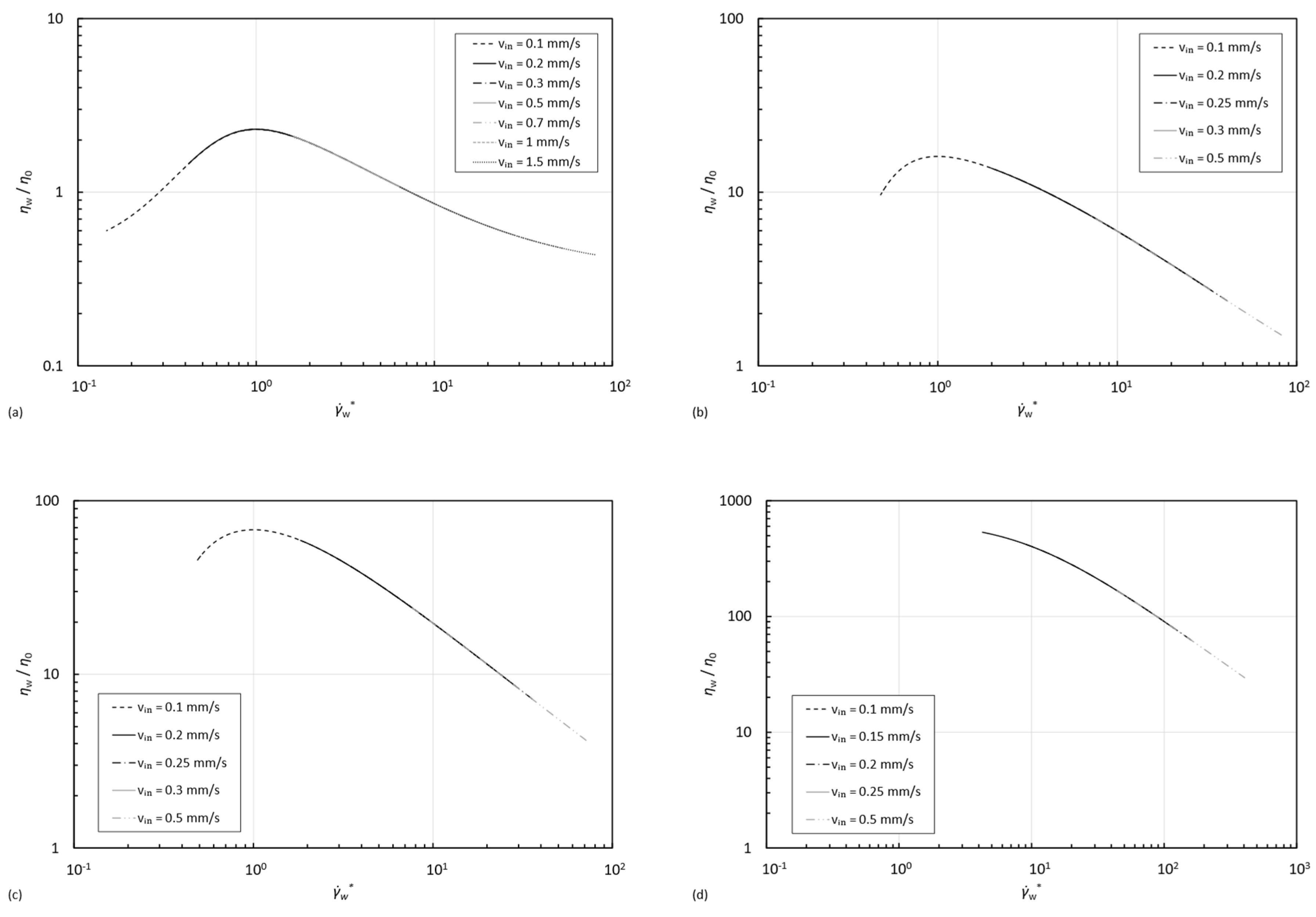
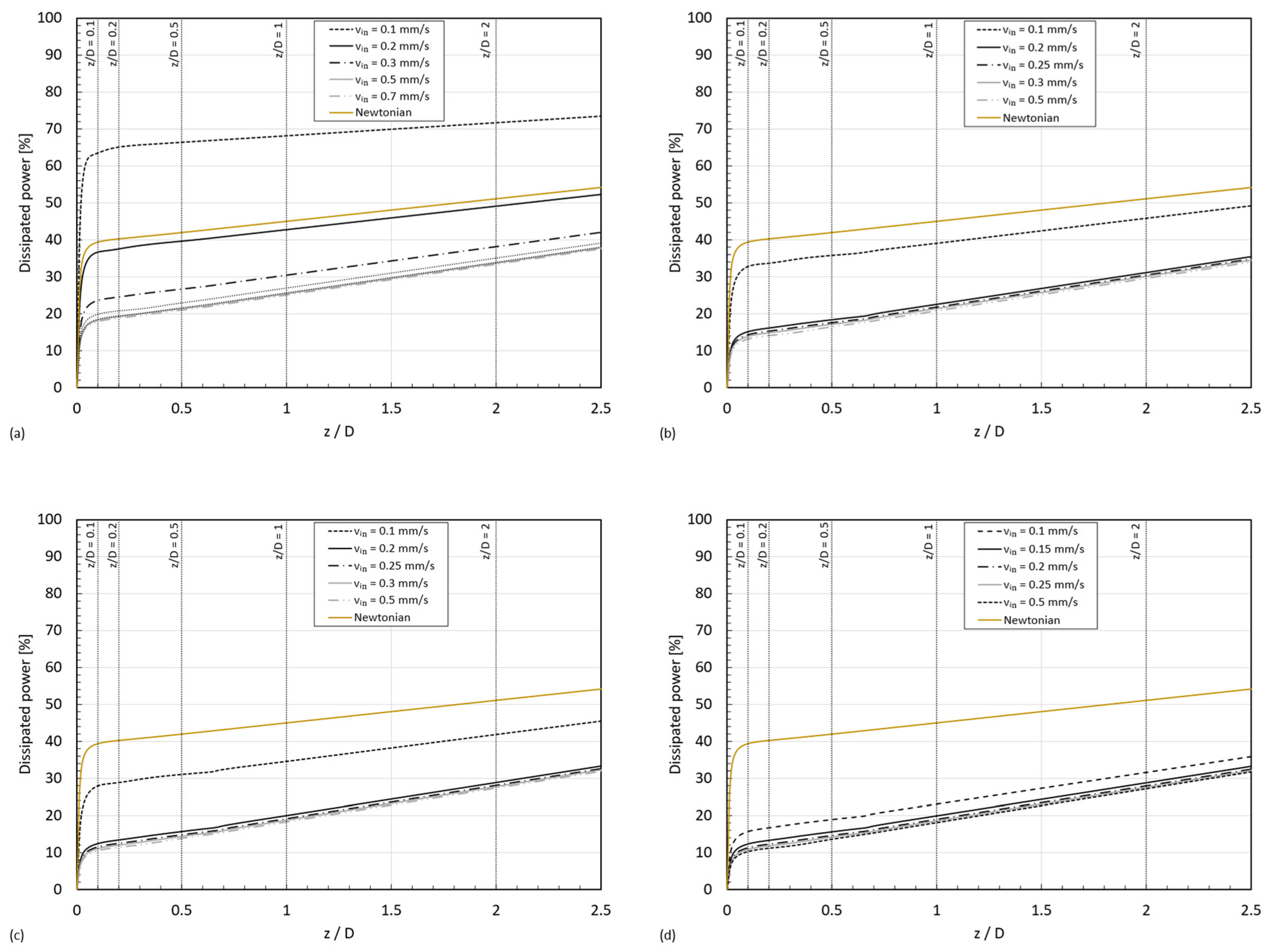
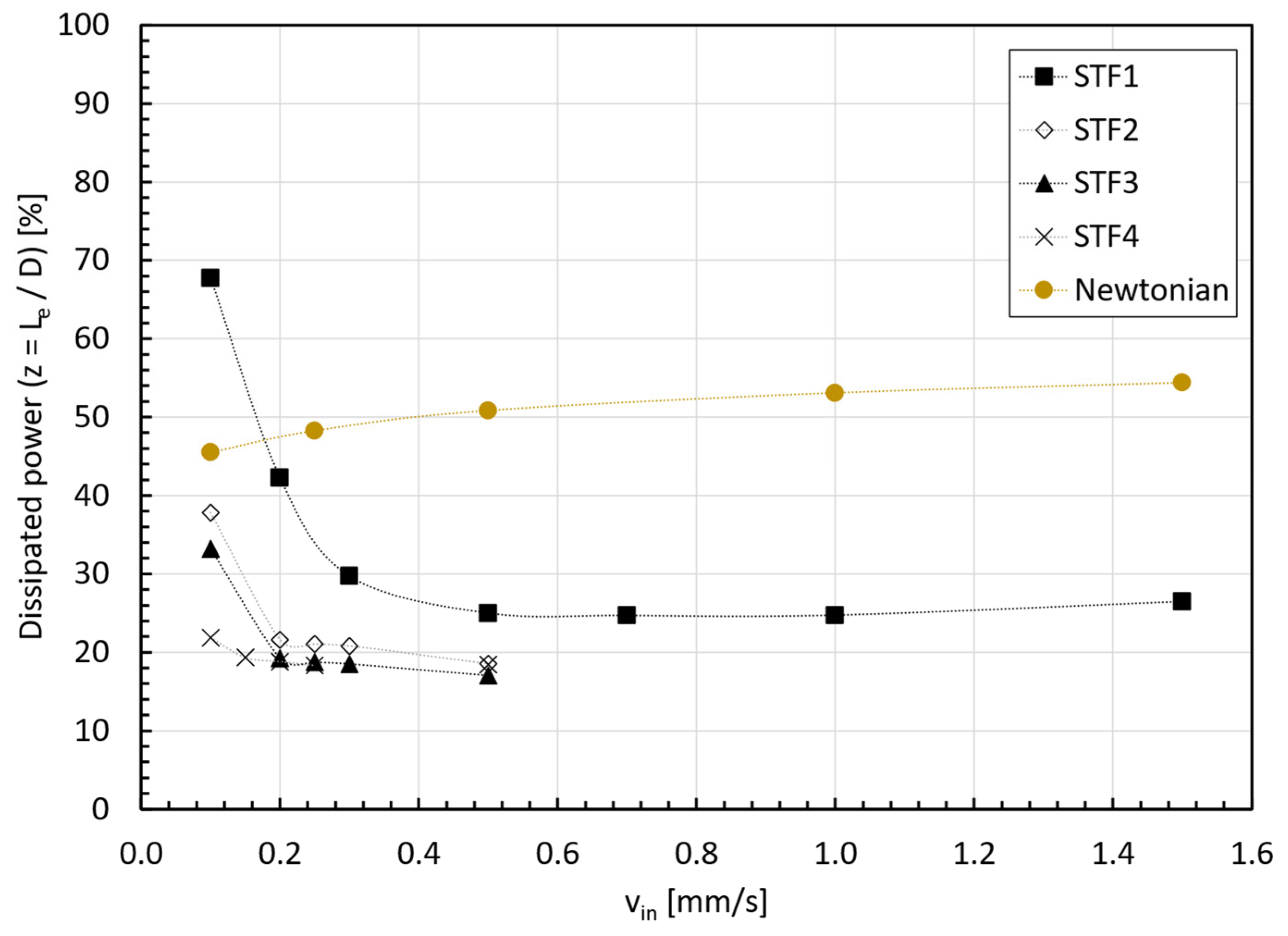
3.4. Dissipated Power
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Gürgen, S.; Kuşhan, M.C.; Li, W. Shear thickening fluids in protective applications: A review. Prog. Polym. Sci. 2017, 75, 48–72. [Google Scholar] [CrossRef]
- Brown, E.; Jaeger, H.M. Shear thickening in concentrated suspensions: Phenomenology, mechanisms and relations to jamming. Rep. Prog. Phys. 2014, 77, 046602. [Google Scholar] [CrossRef] [PubMed]
- Barnes, H.A. Shear-Thickening (“Dilatancy”) in Suspensions of Nonaggregating Solid Particles Dispersed in Newtonian Liquids. J. Rheol. 1989, 33, 329–366. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J. Complex Fluids in Energy Dissipating Systems. Appl. Sci. 2016, 6, 206. [Google Scholar] [CrossRef]
- Mewis, J.; Wagner, N.J. Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Rathee, V.; Blair, D.L.; Urbach, J.S. Dynamics and memory of boundary stresses in discontinuous shear thickening suspensions during oscillatory shear. Soft Matter 2021, 17, 1337–1345. [Google Scholar] [CrossRef]
- Baumgarten, A.S.; Kamrin, K. Modeling stress relaxation in dense, fine-particle suspensions. J. Rheol. 2020, 64, 367–377. [Google Scholar] [CrossRef]
- Cho, J.H.; Griese, A.H.; Peters, I.R.; Bischofberger, I. Lasting effects of discontinuous shear thickening in cornstarch suspensions upon flow cessation. Phys. Rev. Fluids 2022, 7, 063302. [Google Scholar] [CrossRef]
- Gürgen, S.; Kuşhan, M.C. The ballistic performance of aramid based fabrics impregnated with multi-phase shear thickening fluids. Polym. Test. 2017, 64, 296–306. [Google Scholar] [CrossRef]
- Gürgen, S.; Sofuoğlu, M.A. Experimental investigation on vibration characteristics of shear thickening fluid filled CFRP tubes. Compos. Struct. 2019, 226, 111236. [Google Scholar] [CrossRef]
- Gürgen, S.; Fernandes, F.A.O.; de Sousa, R.J.A.; Kuşhan, M.C. Development of Eco-friendly Shock-absorbing Cork Composites Enhanced by a Non-Newtonian Fluid. Appl. Compos. Mater. 2021, 28, 165–179. [Google Scholar] [CrossRef]
- Sheikhi, M.R.; Gürgen, S. Anti-impact design of multi-layer composites enhanced by shear thickening fluid. Compos. Struct. 2022, 279, 114797. [Google Scholar] [CrossRef]
- Sheikhi, M.R.; Gürgen, S.; Kuşhan, M.C. Vibration Damping Systems with Shear Thickening Fluid. In Shear Thickening Fluid: Theory and Applications, Gürgen, S., Ed. Springer International Publishing: Cham, Switzerland, 2023; pp. 77–97.
- Sheikhi, M.R.; Gürgen, S.; Altuntas, O.; Sofuoğlu, M.A. Anti-impact and vibration-damping design of cork-based sandwich structures for low-speed aerial vehicles. Arch. Civ. Mech. Eng. 2023, 23, 71. [Google Scholar] [CrossRef]
- Yay, Ö.; Diltemiz, S.; Kushan, M.; Gürgen, S. Shear Thickening Fluid-Based Vibration Damping Applications. 2024; 10; pp. 59-69.
- Ferreira Serra, G.; Fernandes, F.A.O.; Alves de Sousa, R.J.; Noronha, E.; Ptak, M. New hybrid cork-STF (Shear thickening fluid) polymeric composites to enhance head safety in micro-mobility accidents. Compos. Struct. 2022, 301, 116138. [Google Scholar] [CrossRef]
- Antunes e Sousa, G.J.; Rocha, A.R.S.; Serra, G.F.; Fernandes, F.A.O.; Alves de Sousa, R.J. Shear Thickening Fluids in Cork Agglomerates: An Exploration of Advantages and Drawbacks. Sustainability 2023, 15, 6764. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.; Martínez-Aranda, S.; Campo-Deaño, L. CorkSTFμfluidics—A novel concept for the development of eco-friendly light-weight energy absorbing composites. Mater. Des. 2015, 82, 326–334. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J. Shear Thickening Fluid/Cork Composites Against Blunt Impacts in Football Shin Guards Applications. In Shear Thickening Fluid: Case Studies in Engineering, Gürgen, S., Ed. Springer International Publishing: Cham, Switzerland, 2023; 10.1007/978-3-031-35521-9_4pp. 41-61.
- Montenegro, M.; Campo-Deaño, L.; Galindo-Rosales, F.J. Formulating, assessing and using Shear Thickening Fluids for cork helmet liners. Compos. Struct. 2023, 327, 117707. [Google Scholar] [CrossRef]
- Campo Deaño, L.; Galindo Rosales, F. Composite Layer Material for Dampening External Load, Obtaining Process, and Uses Thereof. U.S. Patent 10443678B2, 15 October 2019. [Google Scholar]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- Bian, X.; Litvinov, S.; Ellero, M.; Wagner, N.J. Hydrodynamic shear thickening of particulate suspension under confinement. J. Non-Newton. Fluid Mech. 2014, 213, 39–49. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Oliveira, M.S.N.; Alves, M.A. Optimized cross-slot microdevices for homogeneous extension. RSC Adv. 2014, 4, 7799–7804. [Google Scholar] [CrossRef]
- Haward, S.J.; Oliveira, M.S.N.; Alves, M.A.; McKinley, G.H. Optimized Cross-Slot Flow Geometry for Microfluidic Extensional Rheometry. Phys. Rev. Lett. 2012, 109, 128301. [Google Scholar] [CrossRef]
- Ejlebjerg Jensen, K.; Szabo, P.; Okkels, F. Topology optimization of viscoelastic rectifiers. Appl. Phys. Lett. 2012, 100, 234102. [Google Scholar] [CrossRef]
- Sousa, P.C.; Pinho, F.T.; Oliveira, M.S.N.; Alves, M.A. Efficient microfluidic rectifiers for viscoelastic fluid flow. J. Non-Newton. Fluid Mech. 2010, 165, 652–671. [Google Scholar] [CrossRef]
- Sousa, P.C.; Pinho, F.T.; Oliveira, M.S.N.; Alves, M.A. High performance microfluidic rectifiers for viscoelastic fluid flow. RSC Adv. 2012, 2, 920–929. [Google Scholar] [CrossRef]
- Parras, L.; Galindo-Rosales, F.J. Modelling the fluid-flow inside a microchannel under impact loads. J. Fluids Struct. 2020, 97, 103069. [Google Scholar] [CrossRef]
- Munson, B.R.; Young, D.F.; Okiishi, T.; Huebsch, W.W. Fundamentals of fluid mechanics. In Differential Analysis of Fluid Flow, Ch. 6, 6th ed.; 2009; pp. 307–308.
- Durst, F.; Ray, S.; Ünsal, B.; Bayoumi, O.A. The Development Lengths of Laminar Pipe and Channel Flows. J. Fluids Eng. 2005, 127, 1154–1160. [Google Scholar] [CrossRef]
- Ferreira, G.; Sucena, A.; Ferrás, L.L.; Pinho, F.T.; Afonso, A.M. Hydrodynamic Entrance Length for Laminar Flow in Microchannels with Rectangular Cross Section. Fluids 2021, 6, 240. [Google Scholar] [CrossRef]
- Bertoco, J.; Leiva, R.T.; Ferrás, L.L.; Afonso, A.M.; Castelo, A. Development Length of Fluids Modelled by the gPTT Constitutive Differential Equation. Appl. Sci. 2021, 11, 10352. [Google Scholar] [CrossRef]
- Gupta, R. On developing laminar non-Newtonian flow in pipes and channels. Nonlinear Anal. Real World Appl. 2001, 2, 171–193. [Google Scholar] [CrossRef]
- Chebbi, R. Laminar flow of power-law fluids in the entrance region of a pipe. Chem. Eng. Sci. 2002, 57, 4435–4443. [Google Scholar] [CrossRef]
- Poole, R.; Ridley, B. Development-Length Requirements for Fully Developed Laminar Pipe Flow of Inelastic Non-Newtonian Liquids. J. Fluids Eng. Trans. Asme J. Fluid. Eng. 2007, 129, 1281–1287. [Google Scholar] [CrossRef]
- Fernandes, C.; Ferrás, L.L.; Araujo, M.S.; Nóbrega, J.M. Development length in planar channel flows of inelastic non-Newtonian fluids. J. Non-Newton. Fluid Mech. 2018, 255, 13–18. [Google Scholar] [CrossRef]
- Lambride, C.; Syrakos, A.; Georgiou, G.C. Entrance length estimates for flows of power-law fluids in pipes and channels. J. Non-Newton. Fluid Mech. 2023, 317, 105056. [Google Scholar] [CrossRef]
- Morrison, F.A.; Morrison, A.P.C.E.F.A. Understanding Rheology; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Galindo-Rosales, F.J.; Rubio-Hernández, F.J.; Sevilla, A. An apparent viscosity function for shear thickening fluids. J. Non-Newton. Fluid Mech. 2011, 166, 321–325. [Google Scholar] [CrossRef]
- Khandavalli, S.; Lee, J.A.; Pasquali, M.; Rothstein, J.P. The effect of shear-thickening on liquid transfer from an idealized gravure cell. J. Non-Newton. Fluid Mech. 2015, 221, 55–65. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Rubio-Hernández, F.J.; Sevilla, A.; Ewoldt, R.H. How Dr. Malcom M. Cross may have tackled the development of “An apparent viscosity function for shear thickening fluids”. J. Non-Newton. Fluid Mech. 2011, 166, 1421–1424. [Google Scholar] [CrossRef]
- ANSYS. Ansys® Fluent Theory Guide, Release 2019 R1; ANSYS: Canonsburg, PA, USA, 2019. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Çengel, Y.A.; Cimbala, J.M. Fluid Mechanics Fundamentals and Applications; McGraw-Hill Higher Education: Boston, MA, USA, 2006. [Google Scholar]
- Li, H.; Li, Y.; Huang, B.; Xu, T. Flow Characteristics of the Entrance Region with Roughness Effect within Rectangular Microchannels. Micromachines 2020, 11, 30. [Google Scholar] [CrossRef]
- Metzner, A.B.; Reed, J.C. Flow of non-newtonian fluids—Correlation of the laminar, transition, and turbulent-flow regions. AIChE J. 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Ortega-Casanova, J.; Jimenez-Canet, M.; Galindo-Rosales, F.J. Numerical study of the heat and momentum transfer between a flat plate and an impinging jet of power law fluids. Int. J. Heat Mass Transf. 2019, 141, 102–111. [Google Scholar] [CrossRef]
- Schuller, T.; Fanzio, P.; Galindo-Rosales, F.J. Analysis of the importance of shear-induced elastic stresses in material extrusion. Addit. Manuf. 2022, 57, 102952. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.j.; Rubio-Hernández, F.j. Numerical Simulation in Steady Flow of Non-Newtonian Fluids in Pipes with Circular Cross-Section. In Numerical Simulations; Lutz, A., Ed.; IntechOpen: Rijeka, Croatia, 2010. [Google Scholar]
- Tesla, N. Valvular. Conduit. Patent U.S. 1329559A, 3 February 1920. [Google Scholar]
- Ejlebjerg Jensen, K.; Szabo, P.; Okkels, F.; Alves, M.A. Experimental characterisation of a novel viscoelastic rectifier design. Biomicrofluidics 2012, 6, 044112. [Google Scholar] [CrossRef] [PubMed]
- Mehboudi, A.; Yeom, J. A passive Stokes flow rectifier for Newtonian fluids. Sci. Rep. 2021, 11, 10182. [Google Scholar] [CrossRef] [PubMed]
- Galindo-Rosales, F.J.; Rubio-Hernàndez, F.J. Static and dynamic yield stresses of Aerosil® 200 suspension in polypropylene glycol. App Rheol. 2010, 20, 22787. [Google Scholar]
- Galindo-Rosales, F.J.; Campo-Deaño, L.; Sousa, P.C.; Ribeiro, V.M.; Oliveira, M.S.N.; Alves, M.A.; Pinho, F.T. Viscoelastic instabilities in micro-scale flows. Exp. Therm. Fluid Sci. 2014, 59, 128–139. [Google Scholar] [CrossRef]


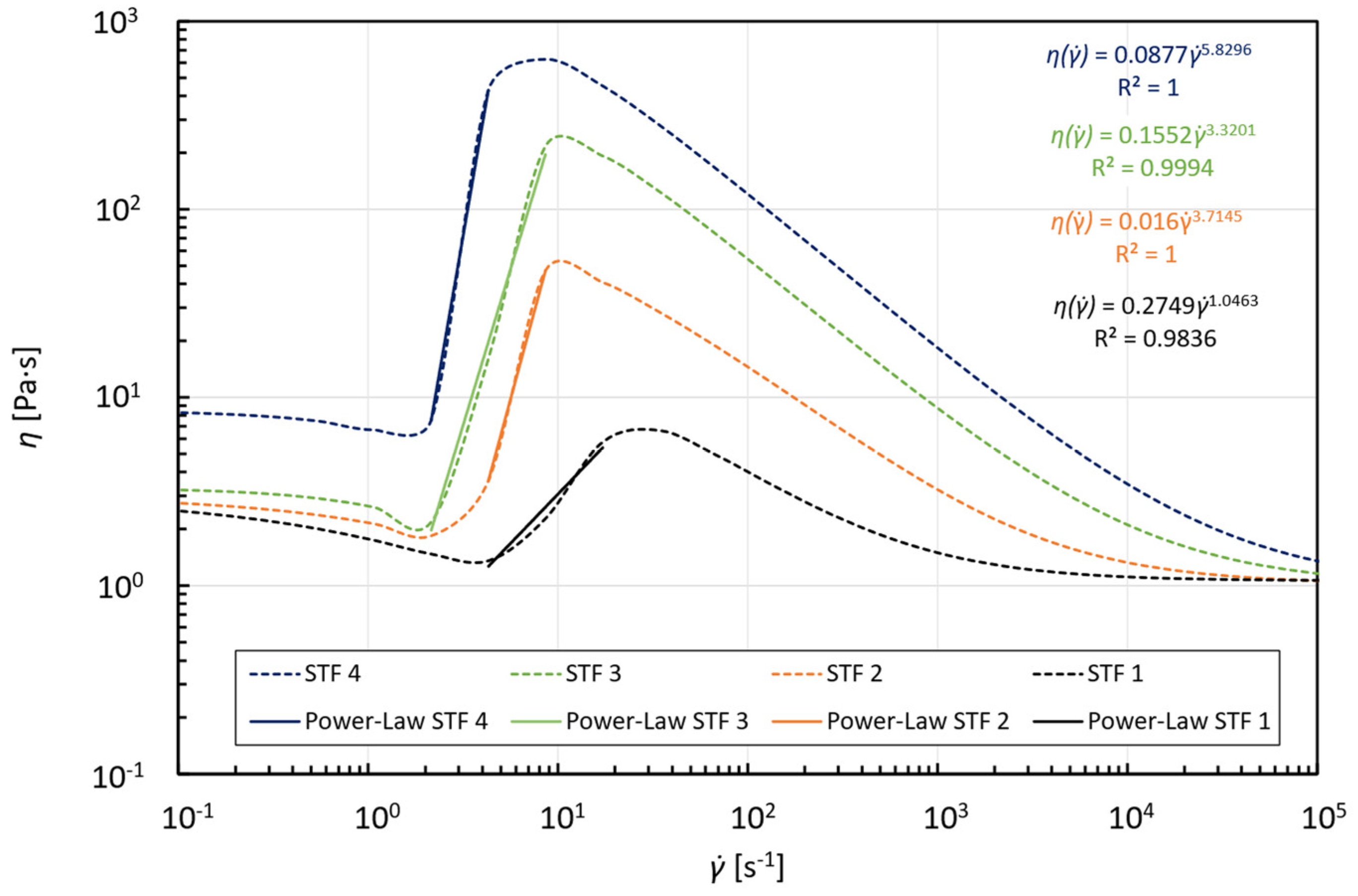
| Silica [wt%] | [Pa∙s] | [Pa∙s] | [ms] | [ms] | |||||
|---|---|---|---|---|---|---|---|---|---|
| 7.5 | 3.0 | 1.0 | 0.5 | 0.01 | 100 | 3.3 | −2.0 | 62 | 16 |
| 10 | 3.0 | 1.0 | 0.6 | 0.11 | 100 | 10 | −3.0 | 180 | 48 |
| 15 | 3.3 | 1.0 | 1.0 | 0.15 | 300 | 11 | −0.9 | 200 | 300 |
| 20 | 8.5 | 1.0 | 1.0 | 0.15 | 300 | 11 | −0.9 | 300 | 260 |
| Mesh | Divisions | Divisions | Number of Elements |
|---|---|---|---|
| 1 | 2000 | 100 | 200,000 |
| 2 | 1000 | 100 | 100,000 |
| 3 | 1000 | 50 | 50,000 |
| = 0.1 | = 0.2 | = 0.5 | = 1 | = 2 | |
|---|---|---|---|---|---|
| 200,000, 100,000, 50,000 | |||||
| 1.30 | |||||
| 1.14 | |||||
| 1.1224 | 1.3358 | 1.7682 | 1.8866 | 1.8863 | |
| 1.1436 | 1.3900 | 1.8402 | 1.8893 | 1.8906 | |
| 1.1444 | 1.3922 | 1.8425 | 1.8886 | 1.88891 | |
| 7.70 | 7.38 | 7.96 | 3.92 | 2.74 | |
| 1.1191 | 1.3264 | 1.7577 | 1.8851 | 1.8821 | |
| 1.9% | 4.1% | 4.1% | 0.1% | 0.2% | |
| 0.3% | 0.7% | 0.6% | 0.1% | 0.2% | |
| 0.4% | 0.9% | 0.7% | 0.1% | 0.3% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montenegro, M.; Galindo-Rosales, F.J. On the Complex Flow Dynamics of Shear Thickening Fluids Entry Flows. Micromachines 2024, 15, 1281. https://doi.org/10.3390/mi15111281
Montenegro M, Galindo-Rosales FJ. On the Complex Flow Dynamics of Shear Thickening Fluids Entry Flows. Micromachines. 2024; 15(11):1281. https://doi.org/10.3390/mi15111281
Chicago/Turabian StyleMontenegro, Miguel, and Francisco J. Galindo-Rosales. 2024. "On the Complex Flow Dynamics of Shear Thickening Fluids Entry Flows" Micromachines 15, no. 11: 1281. https://doi.org/10.3390/mi15111281
APA StyleMontenegro, M., & Galindo-Rosales, F. J. (2024). On the Complex Flow Dynamics of Shear Thickening Fluids Entry Flows. Micromachines, 15(11), 1281. https://doi.org/10.3390/mi15111281







