Multi-Frame Vibration MEMS Gyroscope Temperature Compensation Based on Combined GWO-VMD-TCN-LSTM Algorithm
Abstract
1. Introduction
2. Multi-Frame Vibration MEMS Gyroscope
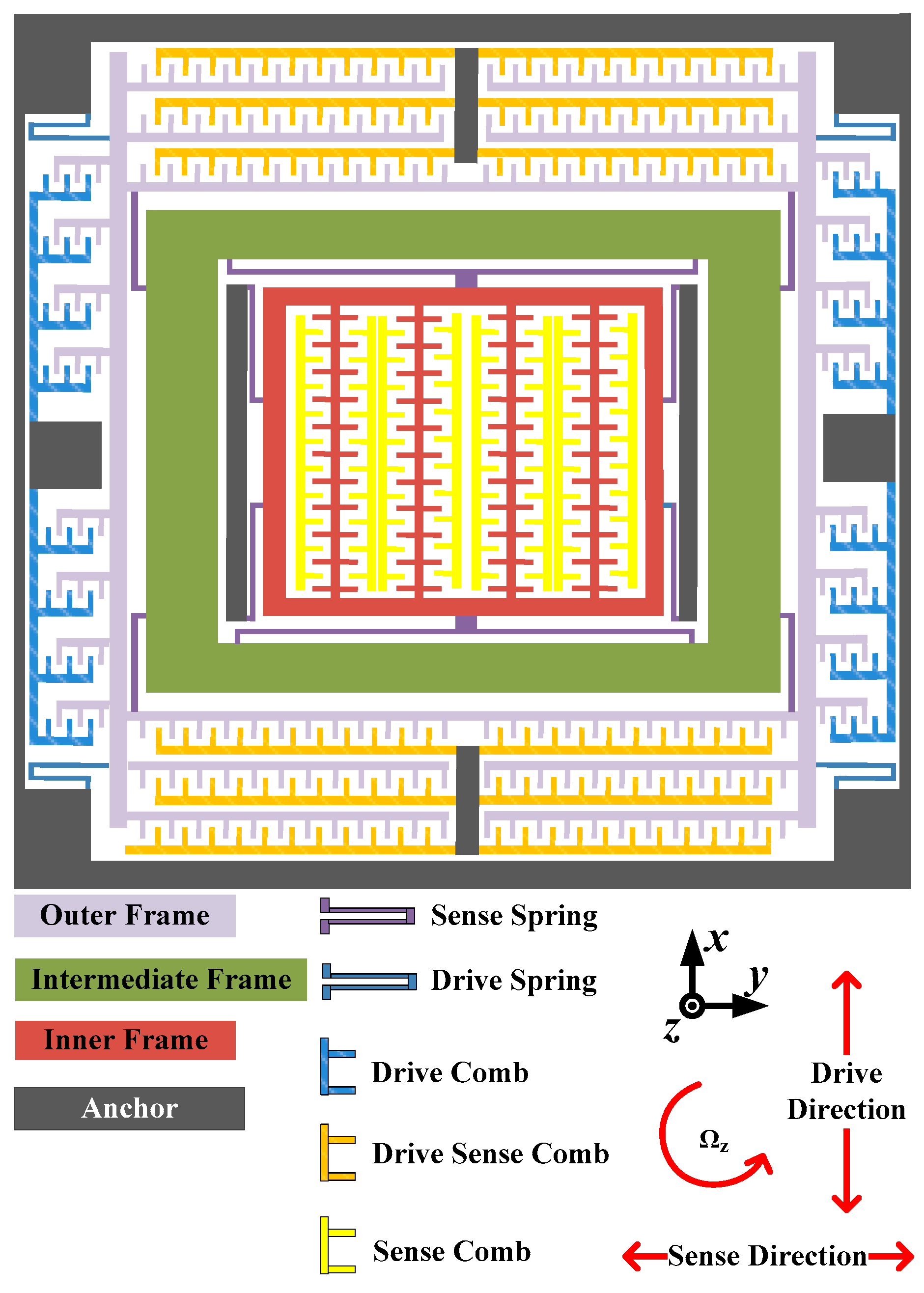
2.1. DMFVMG Structure Design and Working Principle
- The outer frame is actuated by electrostatic forces, causing it to move along the X-axis;
- The intermediate frame is propelled along the X-axis by the impetus of the outer frame, aligning with the initial segment;
- When a specific angular velocity is applied around the Z-axis, the middle frame undergoes elliptical motion in the x-o-y plane due to the combined effects of the driving force and Coriolis force;
- The inner frame and detection comb vibrate in the y-axis direction, with the amplitude of vibration being proportional to the input angular rate.
2.2. DMFVMG Structure Mode Simulation
2.3. Work of DMFVMG
2.4. Temperature Effects of DMFVMG
3. Algorithms and Models
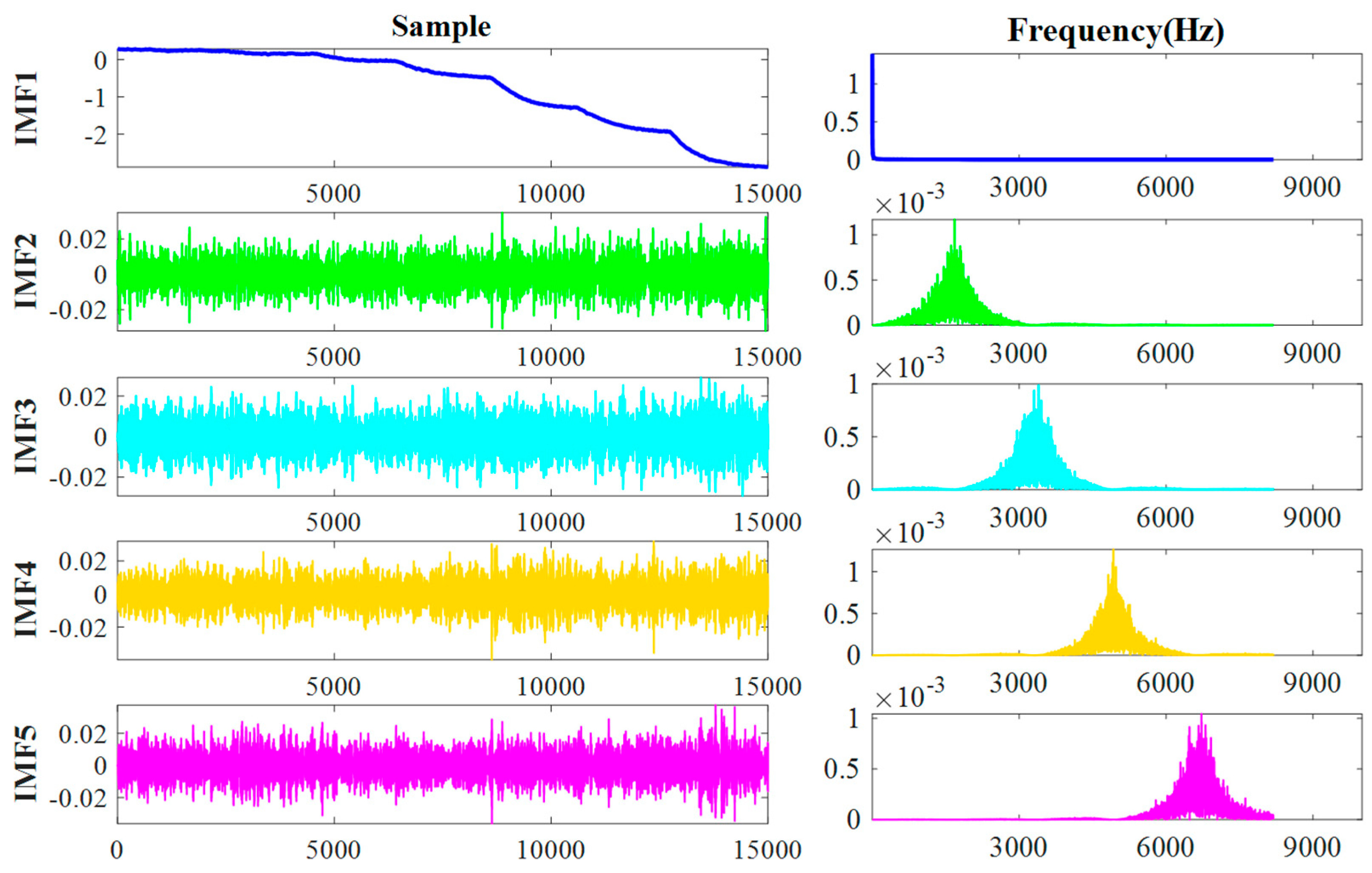
3.1. Variational Mode Decomposition (VMD)
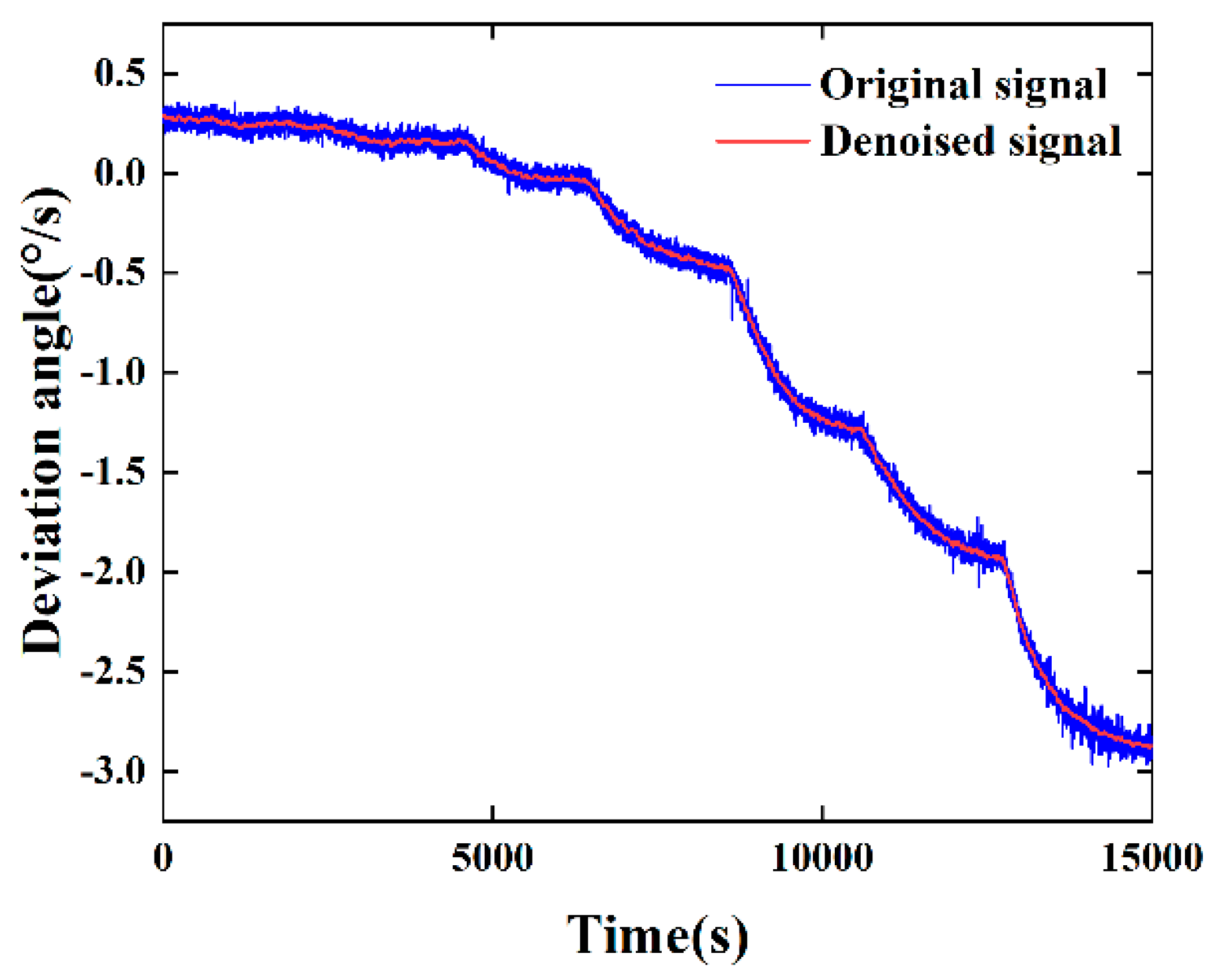
3.2. Grey Wolf Optimization Variational Mode Decomposition (GWO-VMD) Algorithm’s Digital Signal Denoising
- In the α-tier wolf pack, the leader in the population is responsible for leading the entire wolf pack in hunting the prey, i.e., the optimal solution in the optimized algorithm;
- In the β-tier wolf pack, responsible for assisting the α-layer wolf pack, the suboptimal solution is in the optimized algorithm;
- δ tier wolves follow the orders and decisions of α and β and are responsible for scouting, sentry duty, etc. Poorly adapted α and β are demoted to δ;
- ω-layer wolves update their position around α, β or δ.
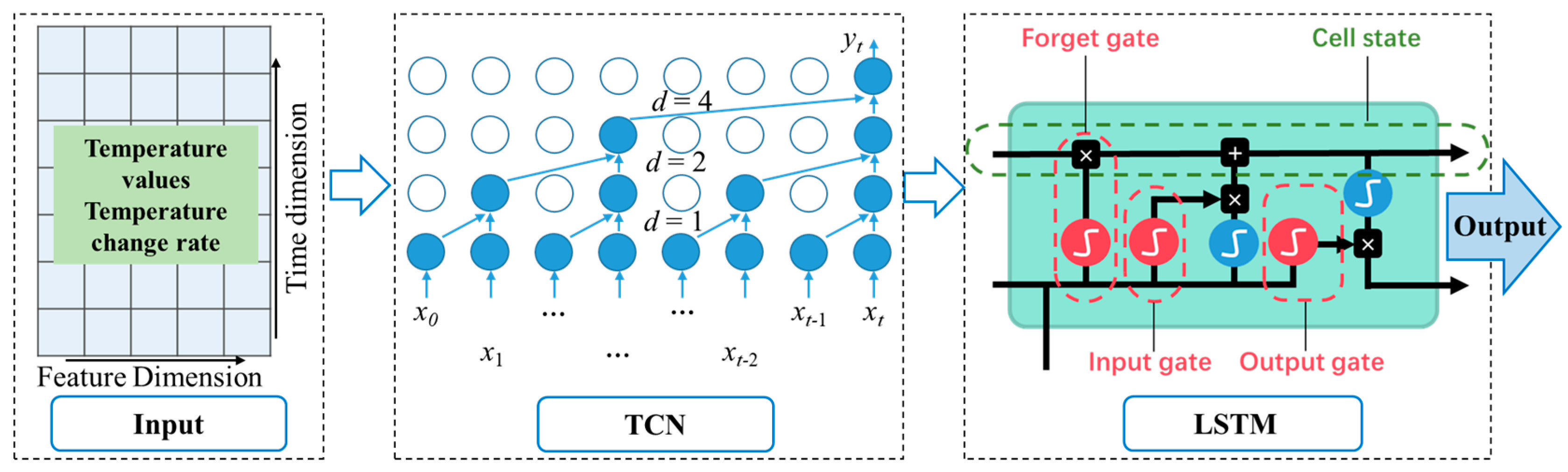
3.3. TCN-LSTM Model
- First, we used a TCN layer to extract the features from the time-series data. The TCN processed the data through a series of convolutional layers, each of which captured patterns over different time scales;
- Next, we took the output of the TCN as the input to the LSTM layer and utilized the recursive nature of the LSTM layer to capture long-term dependencies;
- When training the TCN-LSTM model, we needed to choose the appropriate network structure and hyperparameters. This included determining the number of layers and the number of units per layer for the TCN layer and the number of hidden units for the LSTM layer. We could evaluate the performance of the model under different configurations and chose the best model structure through methods such as cross-validation;
3.3.1. Temporal Convolutional Networks (TCNs)
3.3.2. Long Short-Term Memory (LSTM)
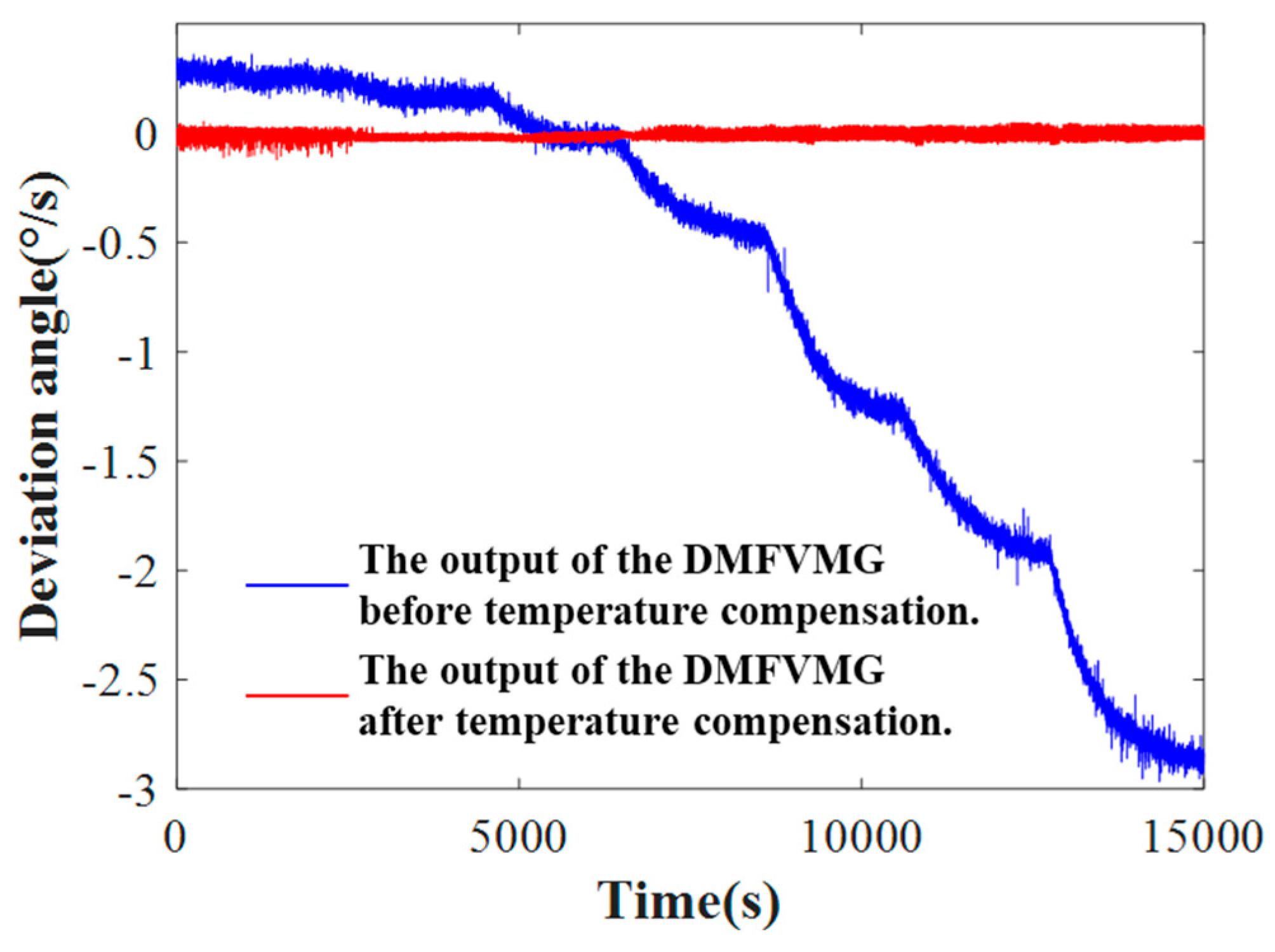
3.4. Compensation Model Based on GWO-VMD Denoising and TCN-LSTM Prediction
4. Experimental Test
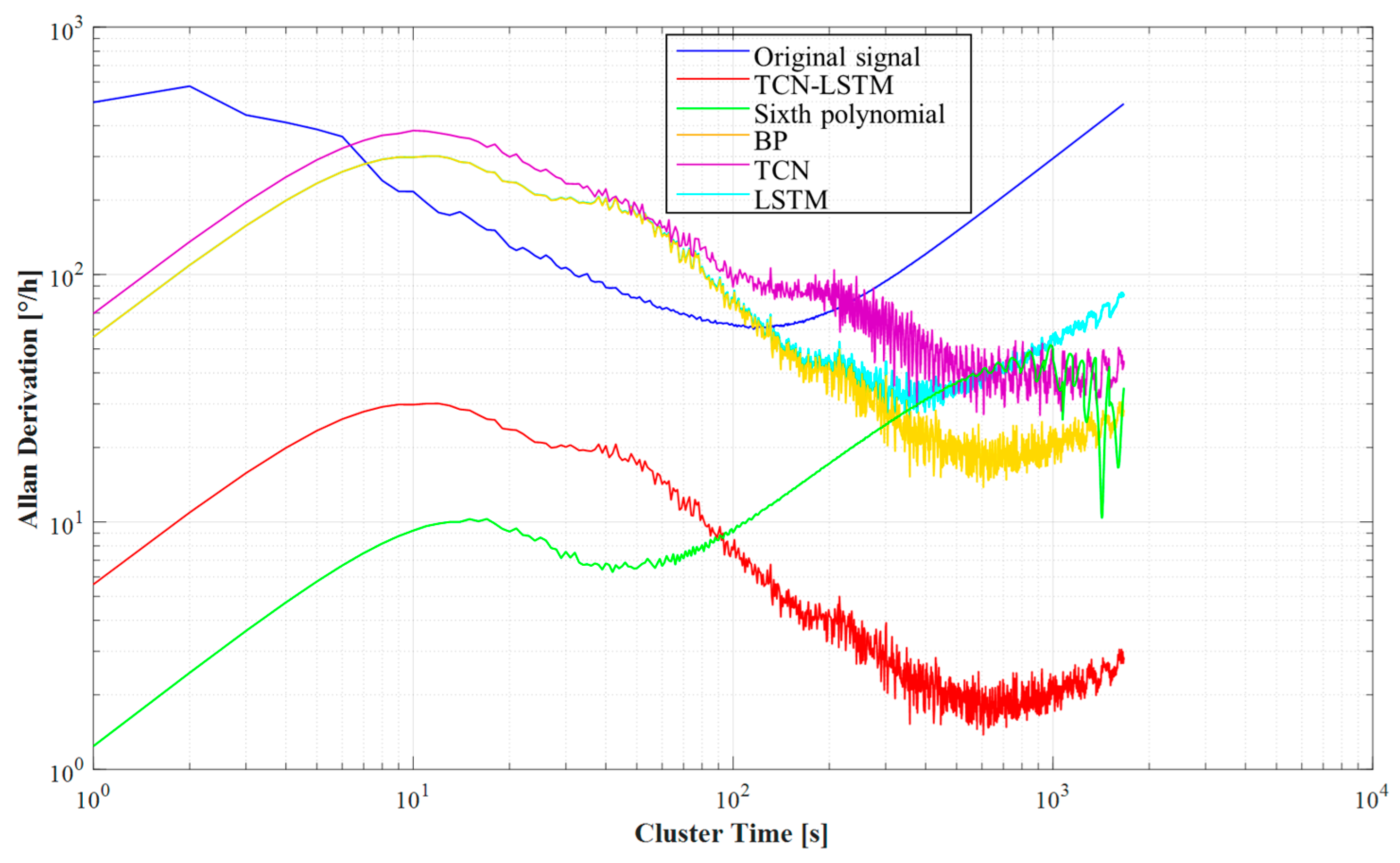
5. Experiment Analysis
5.1. Result
5.2. Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, Q.; Yang, D.; Li, J.; Chang, H. Bias Accuracy Maintenanceunder Unknown Disturbances by Multiple Homogeneous MEMS Gyroscopes Fusion. IEEE Trans. Ind. Electron. 2023, 70, 3178–3187. [Google Scholar] [CrossRef]
- Ding, X.; Ruan, Z.; Jia, J.; Huang, L.; Li, H.; Zhao, L. In-Run Mode-Matching of MEMS Gyroscopes Based on Power Symmetry of Readout Signal in Sense Mode. IEEE Sens. J. 2021, 21, 23806–23817. [Google Scholar] [CrossRef]
- Li, K.; Cui, R.; Cai, Q.; Wei, W.; Shen, C.; Tang, J.; Shi, Y.; Cao, H.; Liu, J. A Fusion Algorithm for Real-Time Temperature Compensation and Noise Suppression with a Double U-Beam Vibration Ring Gyroscope. IEEE Sens. J. 2024, 24, 7614–7624. [Google Scholar] [CrossRef]
- Zhou, Y.; Ling, B.W.K.; Mo, X.; Guo, Y.; Tian, Z. Empirical Mode Decomposition-Based Hierarchical Multiresolution Analysis for Suppressing Noise. IEEE Trans. Instrum. Meas. 2020, 69, 1833–1845. [Google Scholar] [CrossRef]
- Wang, K.; Hao, Q.; Zhang, X.; Tang, Z.; Wang, Y.; Shen, Y. Blind source extraction of acoustic emission signals for rail cracks based on ensemble empirical mode decomposition and constrained independent component analysis. Measurement 2020, 157, 107653. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Fault feature extraction of rotating machinery using a reweighted complete ensemble empirical mode decomposition with adaptive noise and demodulation analysis. Mech. Syst. Signal Process. 2020, 138, 106545. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ma, B. Fault diagnosis of reciprocating compressor using a novel ensemble empirical mode decomposition-convolutional deep belief network. Measurement 2020, 156, 107619. [Google Scholar] [CrossRef]
- Cao, H.; Zhang, Z.; Zheng, Y.; Guo, H.; Zhao, R.; Shi, Y.; Chou, X. A New Joint Denoising Algorithm for High-G Calibration of MEMS Accelerometer Based on VMD-PE-Wavelet Threshold. Shock Vib. 2021, 2021, 8855878. [Google Scholar] [CrossRef]
- Sinhashthita, W.; Jearanaitanakij, K. Improving KNN Algorithm Based on Weighted Attributes by Pearson Correlation Coefficient and PSO Fine Tuning. In Proceedings of the 2020—5th International Conference on Information Technology (InCIT), Chonburi, Thailand, 21–22 October 2020; Volume 34, pp. 27–32. [Google Scholar]
- Zhang, Z.; Zhang, J.; Zhu, X.; Ren, Y.; Yu, J.; Cao, H. MEMS Gyroscope Temperature Compensation Based on Improved Complete Ensemble Empirical Mode Decomposition and Optimized Extreme Learning Machine. Micromachines 2024, 15, 609. [Google Scholar] [CrossRef]
- Li, X.; Wang, K.; Tang, M.; Qin, J.; Wu, P.; Yang, T.; Zhang, H. Marine Drifting Trajectory Prediction Based on LSTM-DNN Algorithm. Wirel. Commun. Mob. Comput. 2022, 2022, 7099494. [Google Scholar] [CrossRef]
- Hu, C.; Cheng, F.; Ma, L.; Li, B. State of Charge Estimation for Lithium-Ion Batteries Based on TCN-LSTM Neural Networks. J. Electrochem. Soc. 2022, 169, 030544. [Google Scholar] [CrossRef]
- Cao, H.; Cai, Q.; Zhang, Y.; Shen, C.; Shi, Y.; Liu, J. Design, Fabrication, and Experiment of a Decoupled Multi-Frame Vibration MEMS Gyroscope. IEEE Sens. J. 2021, 21, 19815–19824. [Google Scholar] [CrossRef]
- Song, R.; Chen, X.; Shen, C.; Zhang, H. Modeling FOG Drift Using Back-Propagation Neural Network Optimized by Artificial Fish Swarm Algorithm. J. Sens. 2014, 2014, 276043. [Google Scholar] [CrossRef]
- Gu, H.; Liu, X.; Zhao, B.; Zhou, H. The In-Operation Drift Compensation of MEMS Gyroscope Based on Bagging-ELM and Improved CEEMDAN. IEEE Sens. J. 2019, 19, 5070–5077. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, G.; Wei, Z.; Yang, J.; Xing, D. Denoising Method of MEMS Gyroscope Based on Interval Empirical Mode Decomposition. Math. Probl. Eng. 2020, 2020, 3019152. [Google Scholar] [CrossRef]
- Cao, H.; Li, H.; Sheng, X.; Wang, S.; Yang, B.; Huang, L. A Novel Temperature Compensation Method for a MEMS Gyroscope Oriented on a Periphery Circuit. Int. J. Adv. Robot. Syst. 2013, 10, 327. [Google Scholar] [CrossRef]
- Chandradip, P.; MCCluskey, P. Simulation of the MEMS Vibratory Gyroscope through Simulink. In Proceedings of the 8th International Conference and Exhibition on Device Packaging, Fountain Hills, AZ, USA, 5–8 March 2012. [Google Scholar]
- Xia, D.; Chen, S.; Wang, S.; Li, H. Microgyroscope Temperature Effects and Compensation-Control Methods. Sensors 2009, 9, 8349–8376. [Google Scholar] [CrossRef]
- Fang, J.; Li, J.; Sheng, W. Improved temperature error model of silicon MEMS gyroscope with inside frame driving. J. Beijing Univ. Aeronaut. Astronaut. 2006, 32, 1277–1280. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Fernandes, H.S.; Sousa, S.F.; Cerqueira, N.M.F.S.A. VMD Store–A VMD Plugin to Browse, Discover, and Install VMD Extensions. J. Chem. Inf. Model. 2019, 59, 4519–4523. [Google Scholar] [CrossRef]
- Gopali, S.; Abri, F.; Siami-Namini, S.; Namin, A.S. A Comparison of TCN and LSTM Models in Detecting Anomalies in ime Series Data. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Orlando, FL, USA, 15–18 December 2021. [Google Scholar]
- Heng, L.; Hao, C.; Nan, L.C. Load forecasting method based on CEEMDAN and TCN-LSTM. PLoS ONE 2024, 19, e0300496. [Google Scholar] [CrossRef]
- Liu, M.; Sun, X.; Wang, Q.; Deng, S. Short-Term Load Forecasting Using EMD with Feature Selection and TCN-Based Deep Learning Model. Energies 2022, 15, 7170. [Google Scholar] [CrossRef]
- Zhang, H.; Ge, B.; Han, B. Real-Time Motor Fault Diagnosis Based on TCN and Attention. Machines 2022, 10, 249. [Google Scholar] [CrossRef]
- Ouyang, M.; Gao, J.; Li, A.; Zhang, X.; Shen, C.; Cao, H. Micromechanical gyroscope temperature compensation based on combined LSTM-SVM-DBN algorithm. Sens. Actuators A Phys. 2024, 369, 115128. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Lin, T.; Li, X.; Wang, T. Characterization of a fiber optic gyroscope in a measurement while drilling system with the dynamic Allan variance. Measurement 2015, 75, 263–272. [Google Scholar] [CrossRef]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. Performance characterization of a new temperature-robust gain-bandwidth improved MEMS gyroscope operated in air. Sens. Actuators A Phys. 2008, 155, 16–22. [Google Scholar] [CrossRef]
- Xu, L.; Li, W.; Zhang, B.; Zhu, Y.; Lang, C. Fault Diagnosis of Mine Truck Hub Drive System Based on LMD Multi-Component Sample Entropy Fusion and LS-SVM. Actuators 2023, 12, 468. [Google Scholar] [CrossRef]
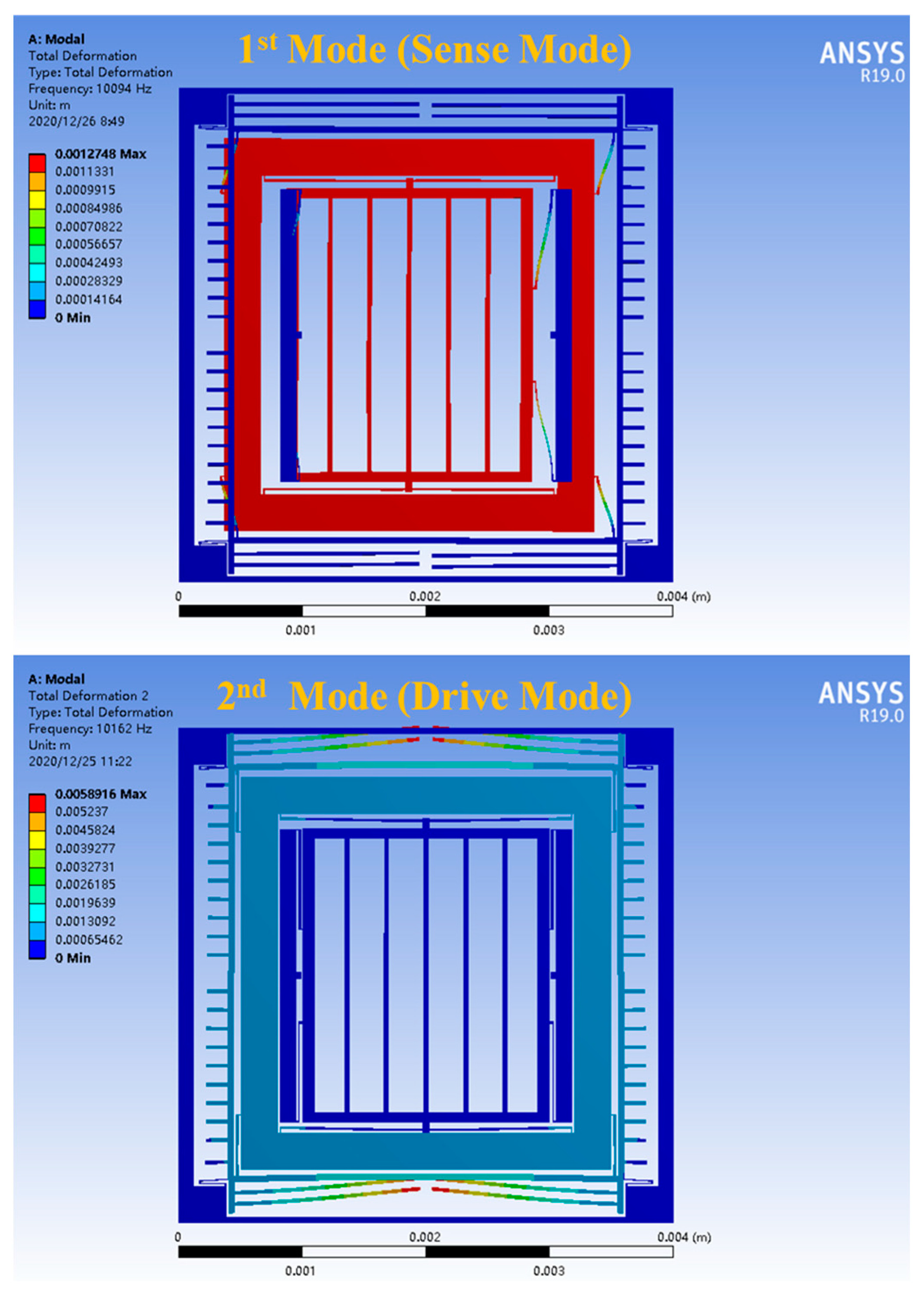




| Mode Order | Resonant Frequency Value (Hz) | Remarks |
|---|---|---|
| 1 | 10,094 | Sense Mode |
| 2 | 10,162 | Drive Mode |
| 3 | 14,986 | z-axis vibration |
| 4 | 15,661 | Comb frame movement |
| 5 | 15,811 | Structure rotating around z-axis |
| 6 | 16,181 | Comb frame movement |
| 7 | 18,234 | Comb frame movement |
| 8 | 18,242 | Comb frame movement |
| 9 | 18,251 | Comb frame movement |
| 10 | 18,254 | Comb frame movement |
| Model | Mean Absolute Error (MAE) | Mean Absolute Percentage Error (MAPE) | Root Mean Square Error (RMSE) |
|---|---|---|---|
| LSTM | 0.0669 | 1.6561 | 0.1132 |
| TCN | 0.1293 | 0.8360 | 0.1854 |
| BP | 0.1597 | 1.4782 | 0.1977 |
| Sixth polynomial | 0.0567 | 0.7894 | 0.0859 |
| TCN-LSTM | 0.023 | 0.4391 | 0.0421 |
| Model | ARRW (°/h/√Hz) | Zero-Bias Instability (°/h) |
|---|---|---|
| Original signal | 102.929 | 63.70 |
| LSTM | 39.2343 | 27.96 |
| TCN | 25.2652 | 26.99 |
| BP | 22.6733 | 13.79 |
| Sixth polynomial | 19.7748 | 6.27 |
| TCN-LSTM | 17.6903 | 1.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Cui, K.; An, D.; Wang, X.; Cao, H. Multi-Frame Vibration MEMS Gyroscope Temperature Compensation Based on Combined GWO-VMD-TCN-LSTM Algorithm. Micromachines 2024, 15, 1379. https://doi.org/10.3390/mi15111379
Li A, Cui K, An D, Wang X, Cao H. Multi-Frame Vibration MEMS Gyroscope Temperature Compensation Based on Combined GWO-VMD-TCN-LSTM Algorithm. Micromachines. 2024; 15(11):1379. https://doi.org/10.3390/mi15111379
Chicago/Turabian StyleLi, Ao, Ke Cui, Daren An, Xiaoyi Wang, and Huiliang Cao. 2024. "Multi-Frame Vibration MEMS Gyroscope Temperature Compensation Based on Combined GWO-VMD-TCN-LSTM Algorithm" Micromachines 15, no. 11: 1379. https://doi.org/10.3390/mi15111379
APA StyleLi, A., Cui, K., An, D., Wang, X., & Cao, H. (2024). Multi-Frame Vibration MEMS Gyroscope Temperature Compensation Based on Combined GWO-VMD-TCN-LSTM Algorithm. Micromachines, 15(11), 1379. https://doi.org/10.3390/mi15111379








