Suspended Slot Membrane Waveguide Based on Germanium-on-Silicon-on-Insulator at λ = 4.23 µm for CO2 Monitoring
Abstract
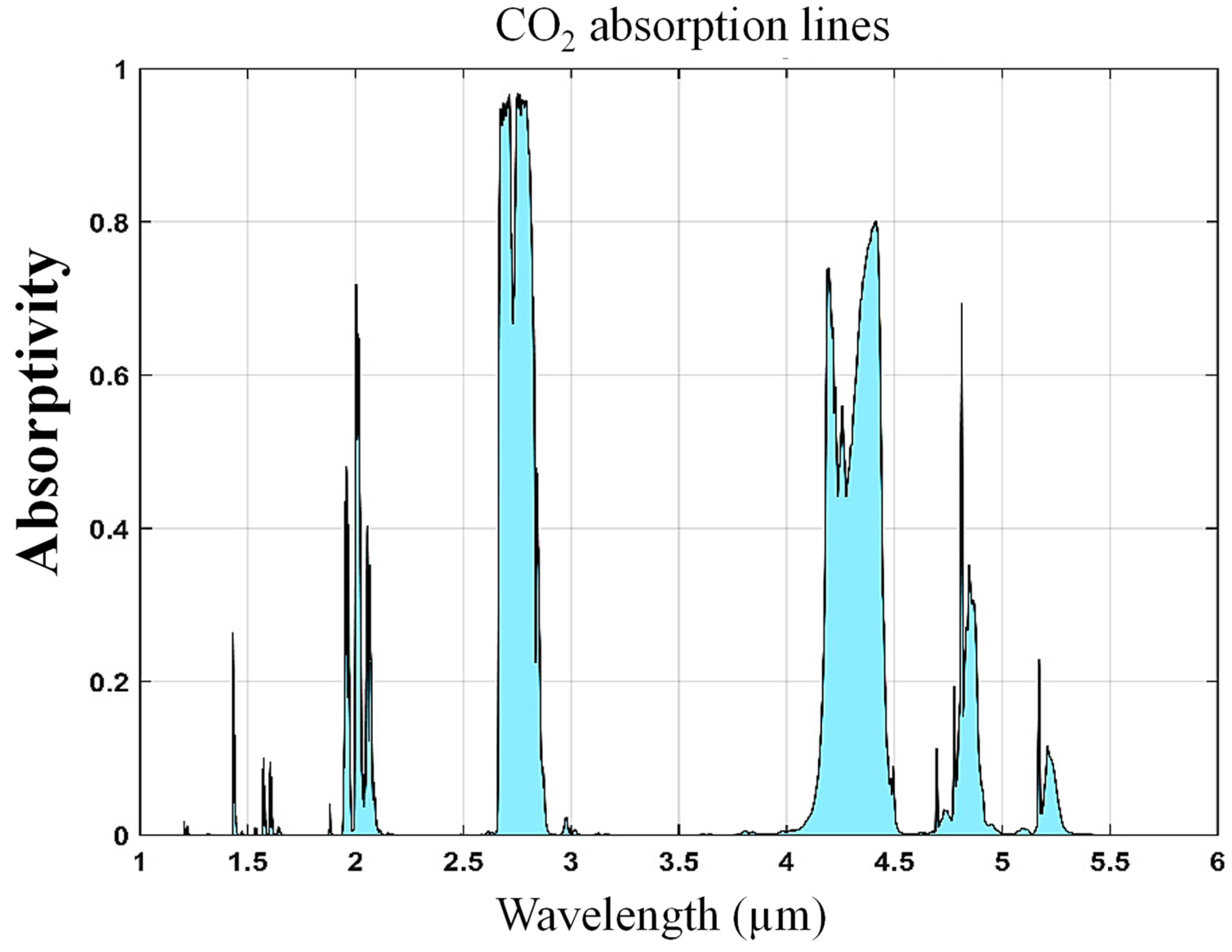
:1. Introduction
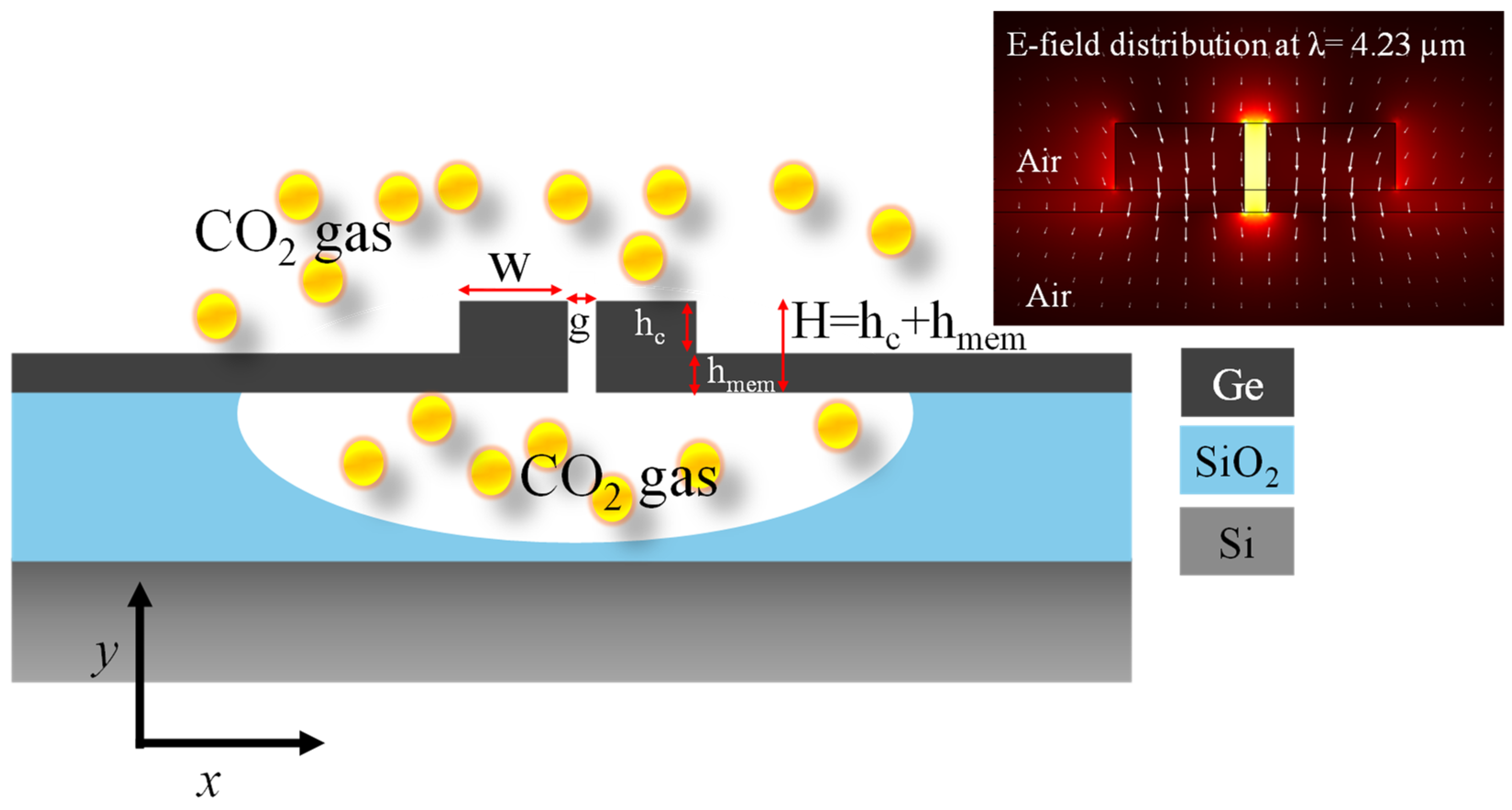
2. Device Design and Numerical Model
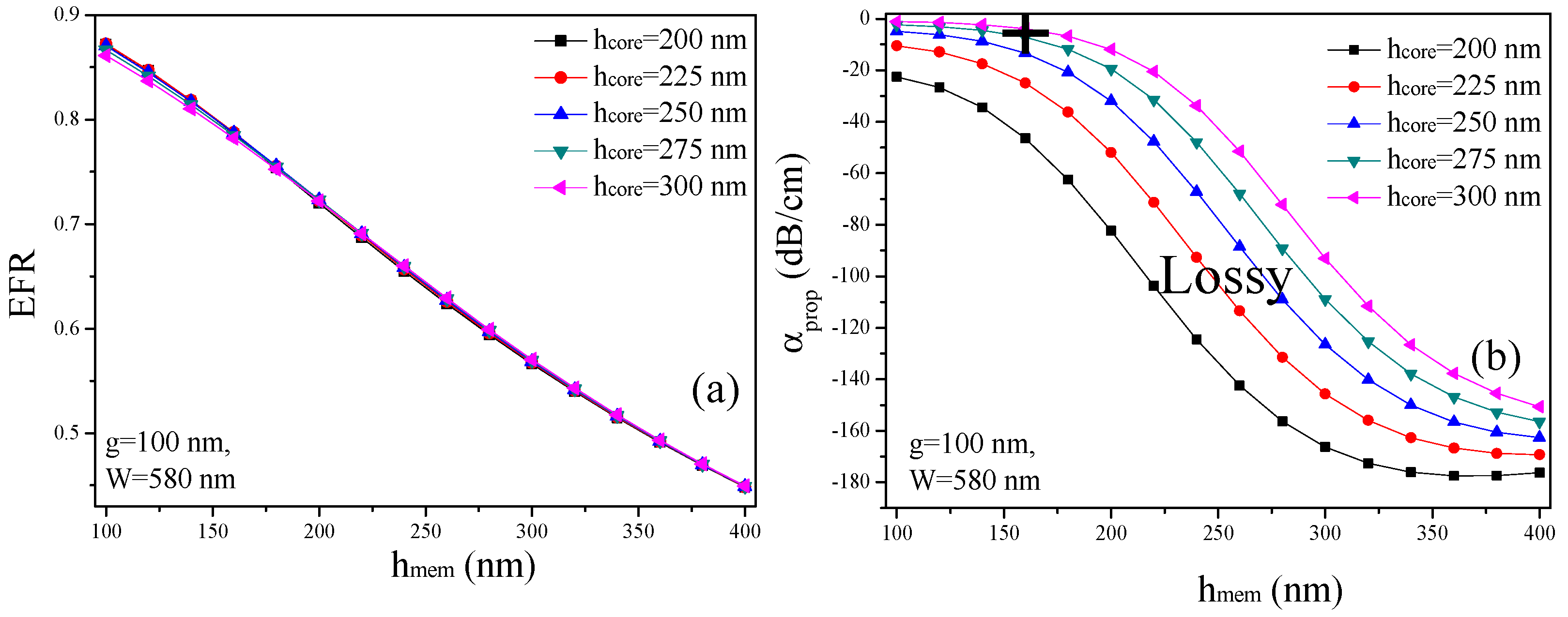
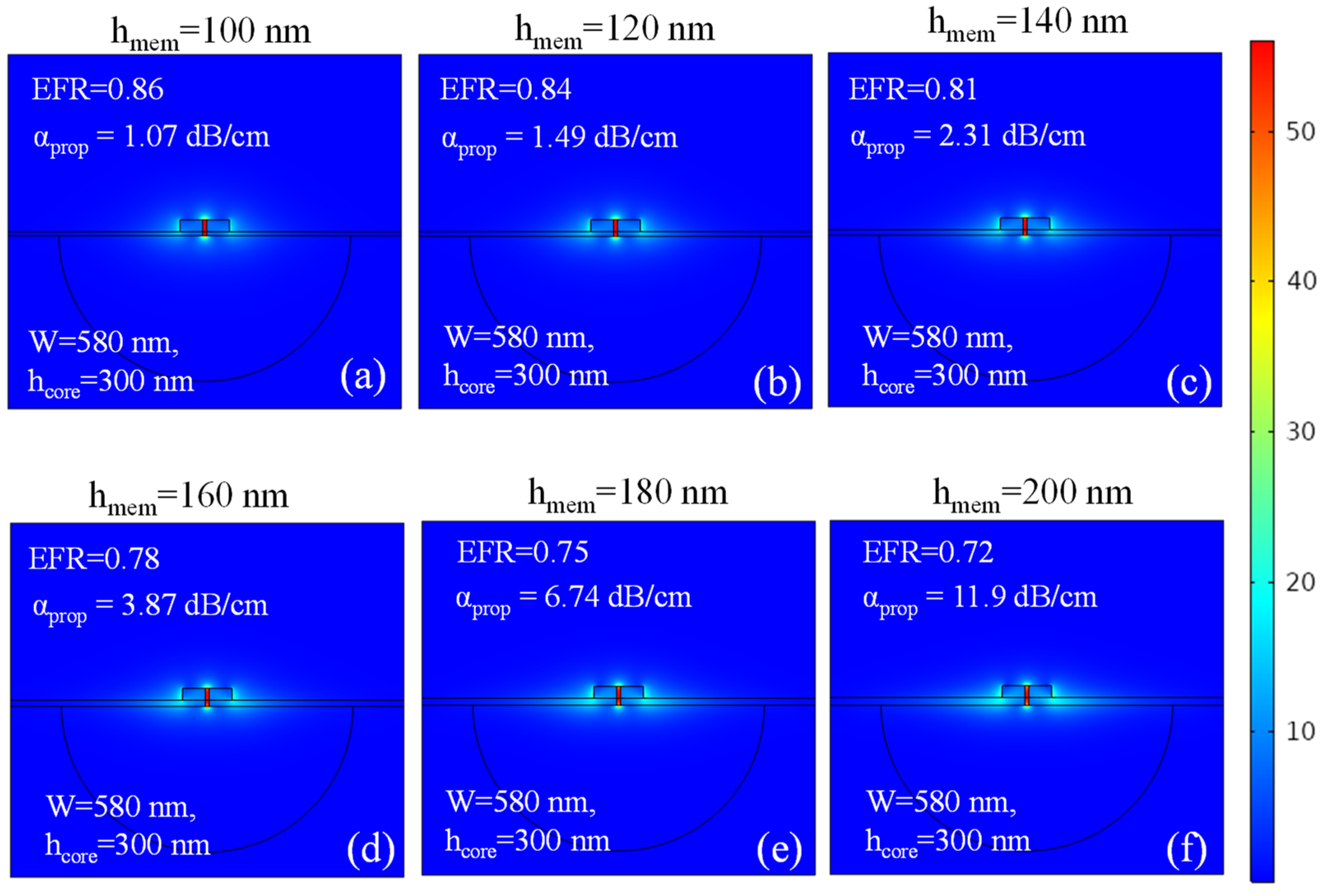
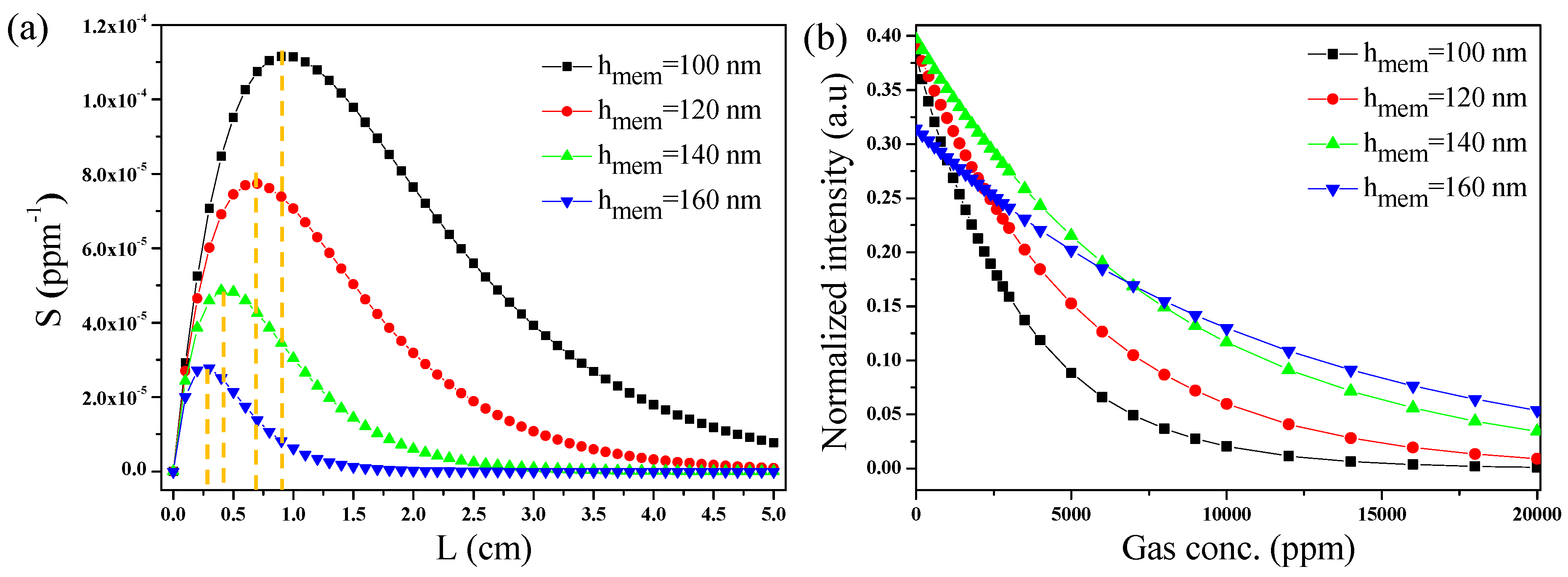
3. Evanescent Field Ratio and αprop of SSMW
4. Discussion
5. CO2 Gas Sensing
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harivelo, R.Z.M.; Harifidy, R.Z. A Review of Environmental Protection and Sustainable Development in Madagascar. J 2022, 5, 512–531. [Google Scholar] [CrossRef]
- Wu, L.; Qing, C.; Jin, S. Environmental Protection and Sustainable Development of Enterprises in China: The Moderating Role of Media Attention. Front. Environ. Sci. 2022, 10, 966479. [Google Scholar] [CrossRef]
- Wentworth, A. As Climate Disasters Grow, Early Warning Systems Become Essential. Available online: https://www.climatechangenews.com/2023/12/08/as-climate-disasters-grow-early-warning-systems-become-essential/ (accessed on 24 August 2024).
- Dai, D.; Zhou, B.; Zhao, S.; Li, K.; Liu, Y. Research on Industrial Carbon Emission Prediction and Resistance Analysis Based on CEI-EGM-RM Method: A Case Study of Bengbu. Sci. Rep. 2023, 13, 14528. [Google Scholar] [CrossRef] [PubMed]
- Permentier, K.; Vercammen, S.; Soetaert, S.; Schellemans, C. Carbon Dioxide Poisoning: A Literature Review of an Often Forgotten Cause of Intoxication in the Emergency Department. Int. J. Emerg. Med. 2017, 10, 14. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, T.A.; Kler, J.S.; Hernke, M.T.; Braun, R.K.; Meyer, K.C.; Funk, W.E. Direct Human Health Risks of Increased Atmospheric Carbon Dioxide. Nat. Sustain. 2019, 2, 691–701. [Google Scholar] [CrossRef]
- Duarte, C.M.; Jaremko, Ł.; Jaremko, M. Hypothesis: Potentially Systemic Impacts of Elevated CO2 on the Human Proteome and Health. Front. Public Health 2020, 8, 543322. [Google Scholar] [CrossRef]
- Eldesouki, M.H.; Rashed, A.E.; El-Moneim, A.A. A Comprehensive Overview of Carbon Dioxide, Including Emission Sources, Capture Technologies, and the Conversion into Value-Added Products. Clean Technol. Environ. Policy 2023, 25, 3131–3148. [Google Scholar] [CrossRef]
- Baldacci, A.; Malathy Devi, V.; Chen, D.-W.; Narahari Rao, K.; Fridovich, B. Absorption Spectrum of Carbon Dioxide at 4.3 Μm. J. Mol. Spectrosc. 1978, 70, 143–159. [Google Scholar] [CrossRef]
- Wei, P.-S.; Hsieh, Y.-C.; Chiu, H.-H.; Yen, D.-L.; Lee, C.; Tsai, Y.-C.; Ting, T.-C. Absorption Coefficient of Carbon Dioxide across Atmospheric Troposphere Layer. Heliyon 2018, 4, e00785. [Google Scholar] [CrossRef]
- Ottonello-Briano, F.; Errando-Herranz, C.; Rödjegård, H.; Martin, H.; Sohlström, H.; Gylfason, K.B. Carbon Dioxide Absorption Spectroscopy with a Mid-Infrared Silicon Photonic Waveguide. Opt. Lett. OL 2020, 45, 109–112. [Google Scholar] [CrossRef]
- Romaniello, V.; Spinetti, C.; Silvestri, M.; Buongiorno, M.F. A Sensitivity Study of the 4.8 Μm Carbon Dioxide Absorption Band in the MWIR Spectral Range. Remote Sens. 2020, 12, 172. [Google Scholar] [CrossRef]
- Nedeljkovic, M.; Penades, J.S.; Mittal, V.; Murugan, G.S.; Khokhar, A.Z.; Littlejohns, C.; Carpenter, L.G.; Gawith, C.B.E.; Wilkinson, J.S.; Mashanovich, G.Z. Germanium-on-Silicon Waveguides Operating at Mid-Infrared Wavelengths up to 8.5 Μm. Opt. Express OE 2017, 25, 27431–27441. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.; Shim, J.; Geum, D.-M.; Kim, S. Experimental Demonstration of Germanium-on-Silicon Slot Waveguides at Mid-Infrared Wavelength. IEEE Photonics J. 2022, 14, 1–9. [Google Scholar] [CrossRef]
- Yeh, P.-L.; Wu, B.-R.; Peng, Y.-W.; Wu, C.-W.; Jheng, Y.-T.; Lee, K.H.; Chen, Q.; Tan, C.S.; Chang, G.-E. Defect-Engineered Electrically-Injected Germanium-on-Insulator Waveguide Light Emitters at Telecom Wavelengths. Adv. Electron. Mater. 2023, 9, 2300288. [Google Scholar] [CrossRef]
- Kozak, D.A.; Tyndall, N.F.; Pruessner, M.W.; Rabinovich, W.S.; Stievater, T.H. Germanium-on-Silicon Waveguides for Long-Wave Integrated Photonics: Ring Resonance and Thermo-Optics. Opt. Express OE 2021, 29, 15443–15451. [Google Scholar] [CrossRef]
- Li, W.; Anantha, P.; Bao, S.; Lee, K.H.; Guo, X.; Hu, T.; Zhang, L.; Wang, H.; Soref, R.; Tan, C.S. Germanium-on-Silicon Nitride Waveguides for Mid-Infrared Integrated Photonics. Appl. Phys. Lett. 2016, 109, 241101. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazanskiy, N.L.; Khonina, S.N.; Voronkov, G.S.; Grakhova, E.P.; Kutluyarov, R.V. A Review on Photonic Sensing Technologies: Status and Outlook. Biosensors 2023, 13, 568. [Google Scholar] [CrossRef]
- Butt, M.A.; Mateos, X.; Piramidowicz, R. Photonics Sensors: A Perspective on Current Advancements, Emerging Challenges, and Potential Solutions (Invited). Phys. Lett. A 2024, 516, 129633. [Google Scholar] [CrossRef]
- Butt, M.A.; Piramidowicz, R. Integrated Photonic Sensors for the Detection of Toxic Gasses—A Review. Chemosensors 2024, 12, 143. [Google Scholar] [CrossRef]
- Butt, M.A.; Voronkov, G.S.; Grakhova, E.P.; Kutluyarov, R.V.; Kazanskiy, N.L.; Khonina, S.N. Environmental Monitoring: A Comprehensive Review on Optical Waveguide and Fiber-Based Sensors. Biosensors 2022, 12, 1038. [Google Scholar] [CrossRef]
- Anjana, N.S.; Amarnath, A.; Harindranathan Nair, M.V. Toxic Hazards of Ammonia Release and Population Vulnerability Assessment Using Geographical Information System. J. Environ. Manag. 2018, 210, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Degtyarev, S.A.; Khonina, S.N.; Kazanskiy, N.L. An Evanescent Field Absorption Gas Sensor at Mid-IR 3.39 Μm Wavelength. J. Mod. Opt. 2017, 64, 1892–1897. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Polarization-Insensitive Hybrid Plasmonic Waveguide Design for Evanescent Field Absorption Gas Sensor. Photonic Sens. 2021, 11, 279–290. [Google Scholar] [CrossRef]
- Butt, M.A. Analyzing the Evanescent Field Ratio of Ridge Waveguide Based on Different Material Platforms for Sensing Applications. J. Opt. 2024, 26, 095803. [Google Scholar] [CrossRef]
- Joshi, K.; Meena, B.L.; Gehlot, K. Performance of Silicon-on-Insulator and Silicon-on-Sapphire Based Evanescent Field Gas Sensor Operating at 2.86 Μm. AIP Conf. Proc. 2023, 2768, 020023. [Google Scholar] [CrossRef]
- Tang, X.; Li, Y.; Chen, F.; Yang, W. Gas Concentration and Refractive Index Sensor Based on Plasmonic Induced Absorption in Metal-Insulator-Metal Waveguide Coupled with Arc Resonators Structure. Phys. Scr. 2024, 99, 065561. [Google Scholar] [CrossRef]
- Wamg, G.; Shi, Q.; Chen, F.; Yu, Y. Gas Sensor Based on Multiple Fano Resonances in Metal-Insulator-Metal Waveguide Resonator System. J. Optoelectron. Adv. Mater. 2022, 24, 323–331. [Google Scholar]
- Khonina, S.N.; Kazanskiy, N.L.; Butt, M.A.; Kaźmierczak, A.; Piramidowicz, R. Plasmonic Sensor Based on Metal-Insulator-Metal Waveguide Square Ring Cavity Filled with Functional Material for the Detection of CO2 Gas. Opt. Express OE 2021, 29, 16584–16594. [Google Scholar] [CrossRef]
- Stewart, G.; Jin, W.; Culshaw, B. Prospects for Fibre-Optic Evanescent-Field Gas Sensors Using Absorption in the near-Infrared. Sens. Actuators B Chem. 1997, 38, 42–47. [Google Scholar] [CrossRef]
- Vlk, M.; Datta, A.; Alberti, S.; Yallew, H.D.; Mittal, V.; Murugan, G.S.; Jágerská, J. Extraordinary Evanescent Field Confinement Waveguide Sensor for Mid-Infrared Trace Gas Spectroscopy. Light Sci. Appl. 2021, 10, 26. [Google Scholar] [CrossRef]
- Ranacher, C.; Consani, C.; Hedenig, U.; Grille, T.; Lavchiev, V.; Jakoby, B. A Photonic Silicon Waveguide Gas Sensor Using Evanescent-Wave Absorption. In Proceedings of the 2016 IEEE Sensors, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Song, Y.; Li, B.; Zhang, H.; Li, M.; Li, Q.; He, J.-J. Silicon Waveguide Sensors for Carbon Dioxide Gas Sensing in the Mid-Infrared Region. Photonics 2023, 10, 120. [Google Scholar] [CrossRef]
- Butt, M.A.; Piramidowicz, R. Standard Slot Waveguide and Double Hybrid Plasmonic Waveguide Configurations for Enhanced Evanescent Field Absorption Methane Gas Sensing. Photonics Lett. Pol. 2022, 14, 10–12. [Google Scholar] [CrossRef]
- Ranacher, C.; Consani, C.; Vollert, N.; Tortschanoff, A.; Bergmeister, M.; Grille, T.; Jakoby, B. Characterization of Evanescent Field Gas Sensor Structures Based on Silicon Photonics. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Butt, M.A.; Kazansky, N.L. SOI Suspended Membrane Waveguide at 3.39 Μm for Gas Sensing Application. Photonics Lett. Pol. 2020, 12, 67–69. [Google Scholar] [CrossRef]
- Zhou, W.; Cheng, Z.; Wu, X.; Zhu, B.; Sun, X.; Tsang, H.K. Fully Suspended Slot Waveguides for High Refractive Index Sensitivity. Opt. Lett. OL 2017, 42, 1245–1248. [Google Scholar] [CrossRef]
- Zhou, W.; Cheng, Z.; Wu, X.; Sun, X.; Tsang, H.K. Fully Suspended Slot Waveguide Platform. J. Appl. Phys. 2018, 123, 063103. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Butt, M.A.; Khonina, S.N. Silicon Photonic Devices Realized on Refractive Index Engineered Subwavelength Grating Waveguides-A Review. Opt. Laser Technol. 2021, 138, 106863. [Google Scholar] [CrossRef]
- Gehl, M.; Kindel, W.; Karl, N.; Orozco, A.; Musick, K.; Trotter, D.; Dallo, C.; Starbuck, A.; Leenheer, A.; DeRose, C.; et al. Characterization of Suspended Membrane Waveguides towards a Photonic Atom Trap Integrated Platform. Opt. Express OE 2021, 29, 13129–13140. [Google Scholar] [CrossRef]
- Bian, D.; Lei, X.; Chen, S. Dispersion Characteristics of Nanometer-Scaled Silicon Nitride Suspended Membrane Waveguides. J. Semicond. 2016, 37, 114007. [Google Scholar] [CrossRef]
- Comprehensive Material Library with over 15,000 Materials. Available online: https://www.comsol.com/material-library (accessed on 23 August 2024).
- Hoang, T.; Duhamel, D.; Foret, G. Wave Finite Element Method for Waveguides and Periodic Structures Subjected to Arbitrary Loads. Finite Elem. Anal. Des. 2020, 179, 103437. [Google Scholar] [CrossRef]
- Koshiba, M. Optical Waveguide Theory by the Finite Element Method. IEICE Trans. Electron. 2014, E97C, 625–635. [Google Scholar] [CrossRef]
- Butt, M.A. Dielectric Waveguide-Based Sensors with Enhanced Evanescent Field: Unveiling the Dynamic Interaction with the Ambient Medium for Biosensing and Gas-Sensing Applications—A Review. Photonics 2024, 11, 198. [Google Scholar] [CrossRef]
- Qiao, Q.; Sun, H.; Liu, X.; Dong, B.; Xia, J.; Lee, C.; Zhou, G. Suspended Silicon Waveguide with Sub-Wavelength Grating Cladding for Optical MEMS in Mid-Infrared. Micromachines 2021, 12, 1311. [Google Scholar] [CrossRef] [PubMed]
- Rothman, L.S.; Jacquemart, D.; Barbe, A.; Chris Benner, D.; Birk, M.; Brown, L.R.; Carleer, M.R.; Chackerian, C.; Chance, K.; Coudert, L.H.; et al. The HITRAN 2004 Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2005, 96, 139–204. [Google Scholar] [CrossRef]
- Hill, C.; Gordon, I.E.; Kochanov, R.V.; Barrett, L.; Wilzewski, J.S.; Rothman, L.S. HITRANOnline: An Online Interface and the Flexible Representation of Spectroscopic Data in the HITRAN Database. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 4–14. [Google Scholar] [CrossRef]


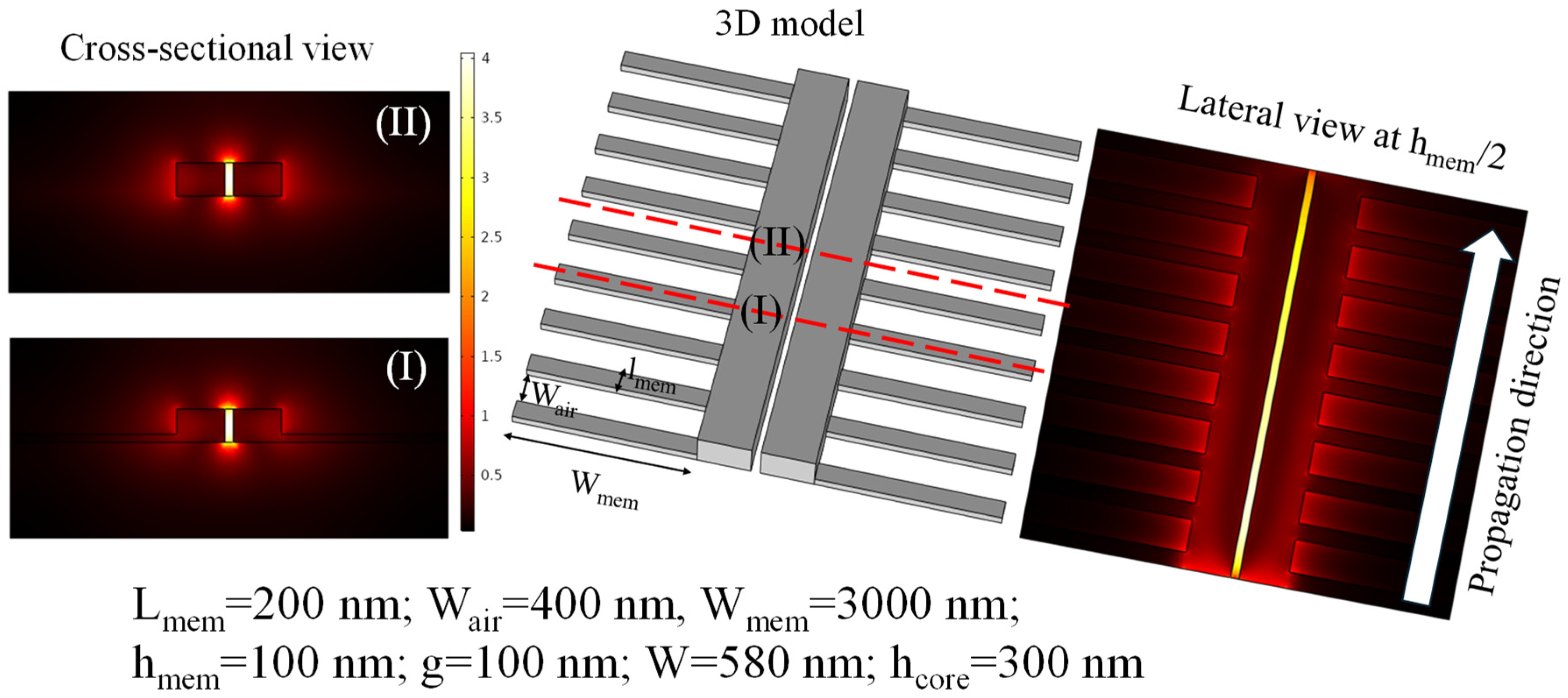
| Variable | Expression | Range (nm) |
|---|---|---|
| W | Width of the waveguide rail | 400–800 |
| g | Nanogap | 100–200 |
| hmem | Thickness of the membrane | 100–400 |
| hcore | Thickness of the waveguide core | 200–300 |
| H | Total height (hc + hmem) | 300–700 |
| g = 100 nm | |||
|---|---|---|---|
| hmem (nm) | EFR | αprop (dB/cm) | Remarks |
| 100 | 0.86 | 1.07 | Highly desirable |
| 120 | 0.83 | 1.49 | Highly desirable |
| 140 | 0.81 | 2.31 | Highly desirable |
| 160 | 0.78 | 3.86 | Desirable |
| 180 | 0.75 | 6.74 | Least desirable |
| 200 | 0.72 | 11.88 | Lossy |
| hmem (nm) | Lopt (cm) | Sensitivity (ppm−1) |
|---|---|---|
| 100 | 0.9 | 1.12 × 10−4 |
| 120 | 0.6 | 7.69 × 10−5 |
| 140 | 0.4 | 4.85 × 10−5 |
| 160 | 0.3 | 2.77 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, M.A.; Piramidowicz, R. Suspended Slot Membrane Waveguide Based on Germanium-on-Silicon-on-Insulator at λ = 4.23 µm for CO2 Monitoring. Micromachines 2024, 15, 1434. https://doi.org/10.3390/mi15121434
Butt MA, Piramidowicz R. Suspended Slot Membrane Waveguide Based on Germanium-on-Silicon-on-Insulator at λ = 4.23 µm for CO2 Monitoring. Micromachines. 2024; 15(12):1434. https://doi.org/10.3390/mi15121434
Chicago/Turabian StyleButt, Muhammad A., and Ryszard Piramidowicz. 2024. "Suspended Slot Membrane Waveguide Based on Germanium-on-Silicon-on-Insulator at λ = 4.23 µm for CO2 Monitoring" Micromachines 15, no. 12: 1434. https://doi.org/10.3390/mi15121434
APA StyleButt, M. A., & Piramidowicz, R. (2024). Suspended Slot Membrane Waveguide Based on Germanium-on-Silicon-on-Insulator at λ = 4.23 µm for CO2 Monitoring. Micromachines, 15(12), 1434. https://doi.org/10.3390/mi15121434







