Cooling Performance Prediction of Particle-Based Radiative Cooling Film Considering Particle Size Distribution
Abstract
:1. Introduction
2. Methodology
2.1. Prediction Process for Cooling Performance
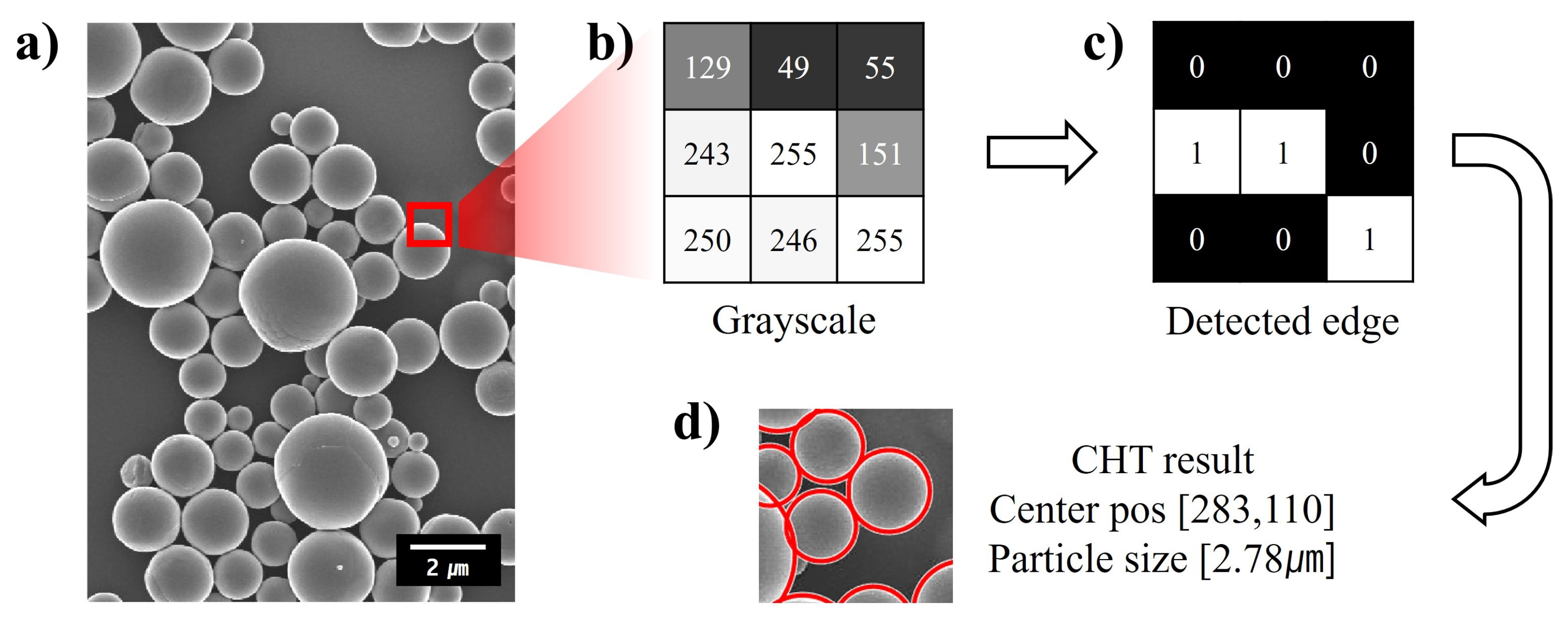
2.2. Size Measurement of Micro-Nanoparticles
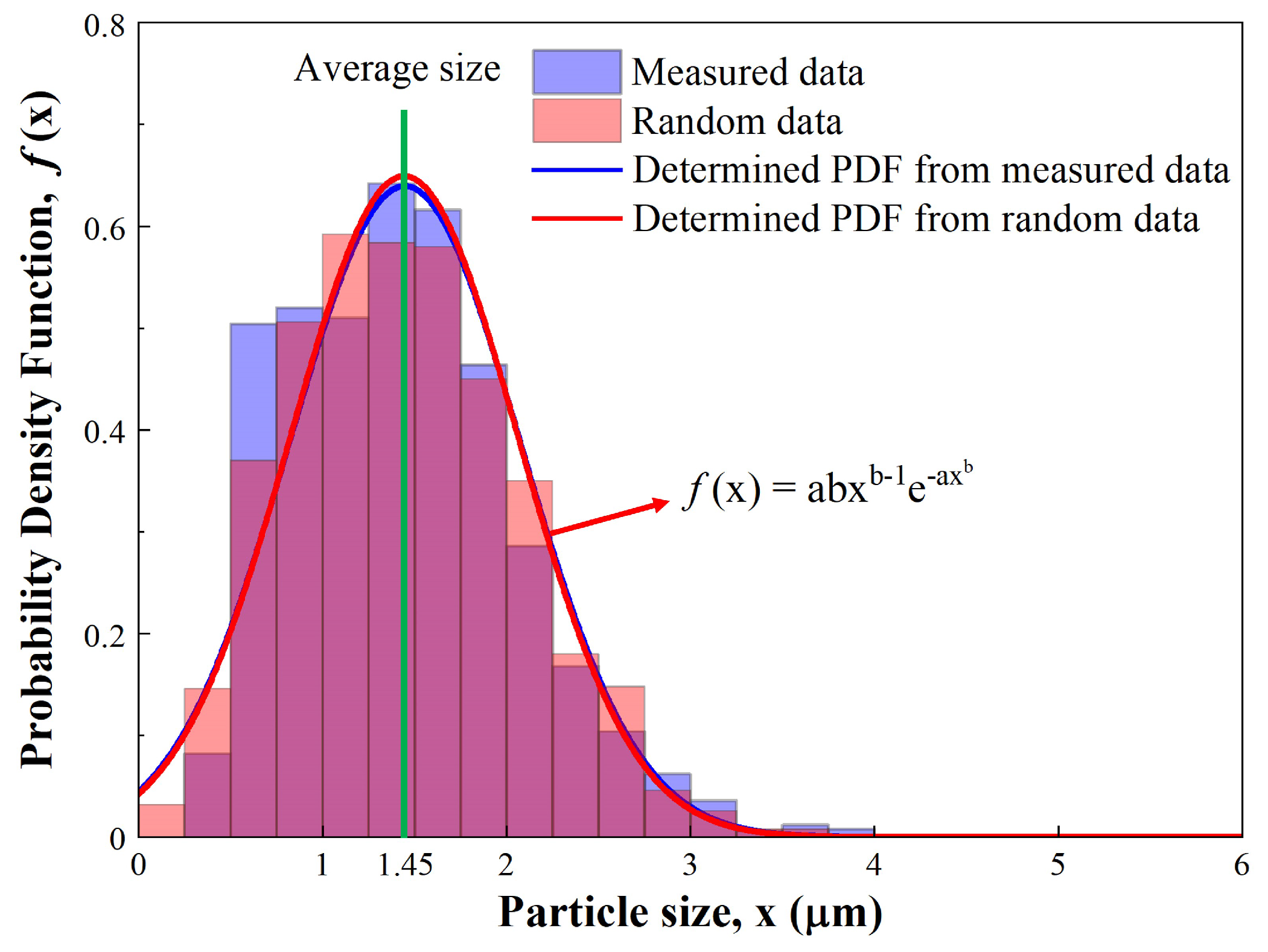
2.3. Regression Analysis
2.4. Prediction of Cooling Performance
3. Results
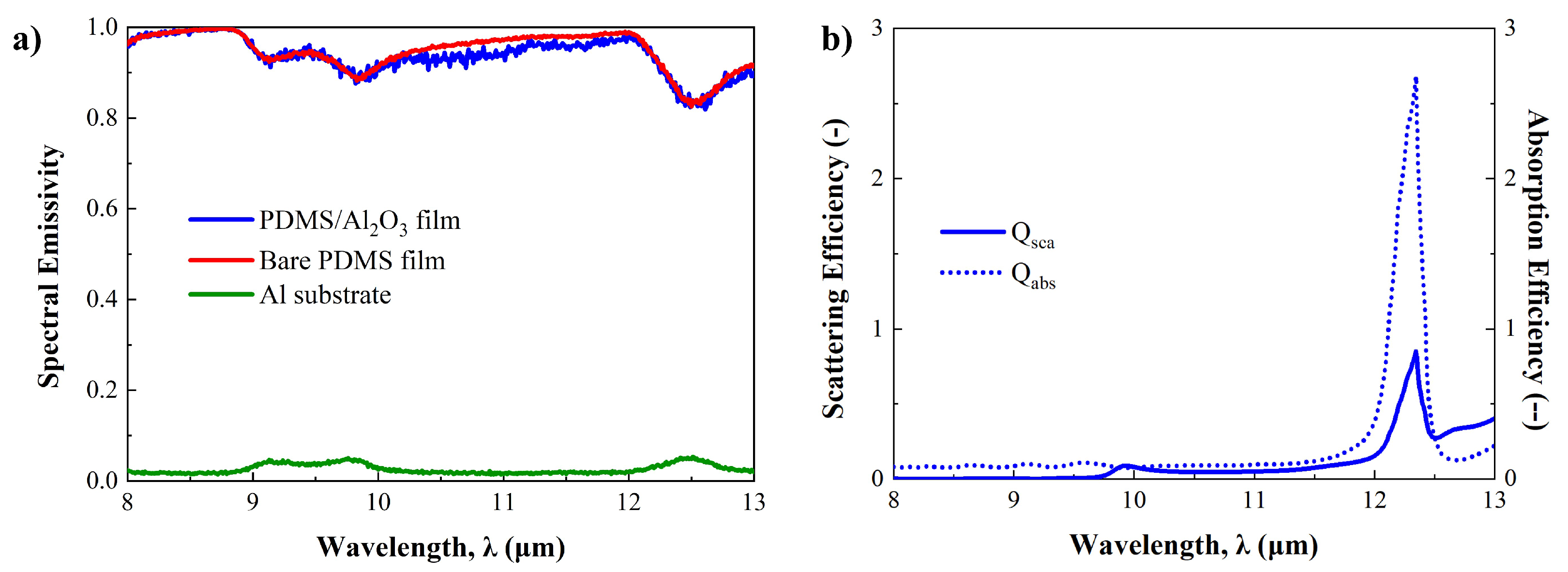
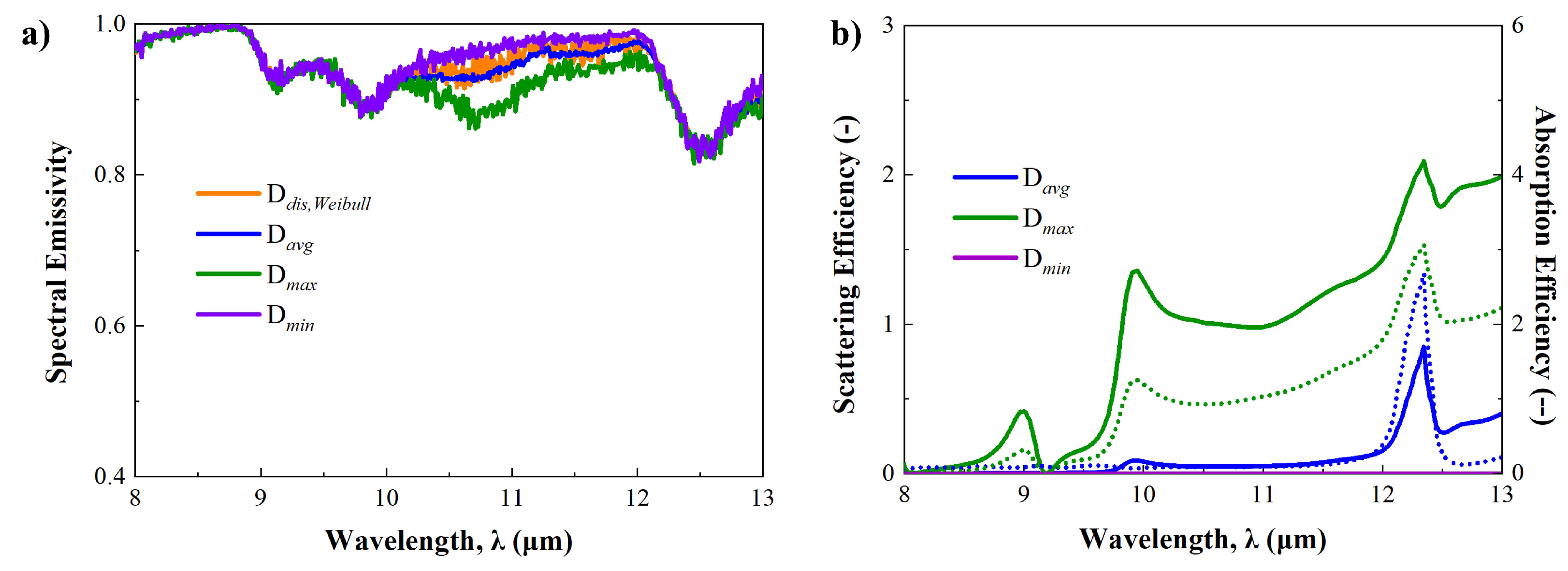
3.1. Effects of Micro-Nanoparticles on Radiative Properties
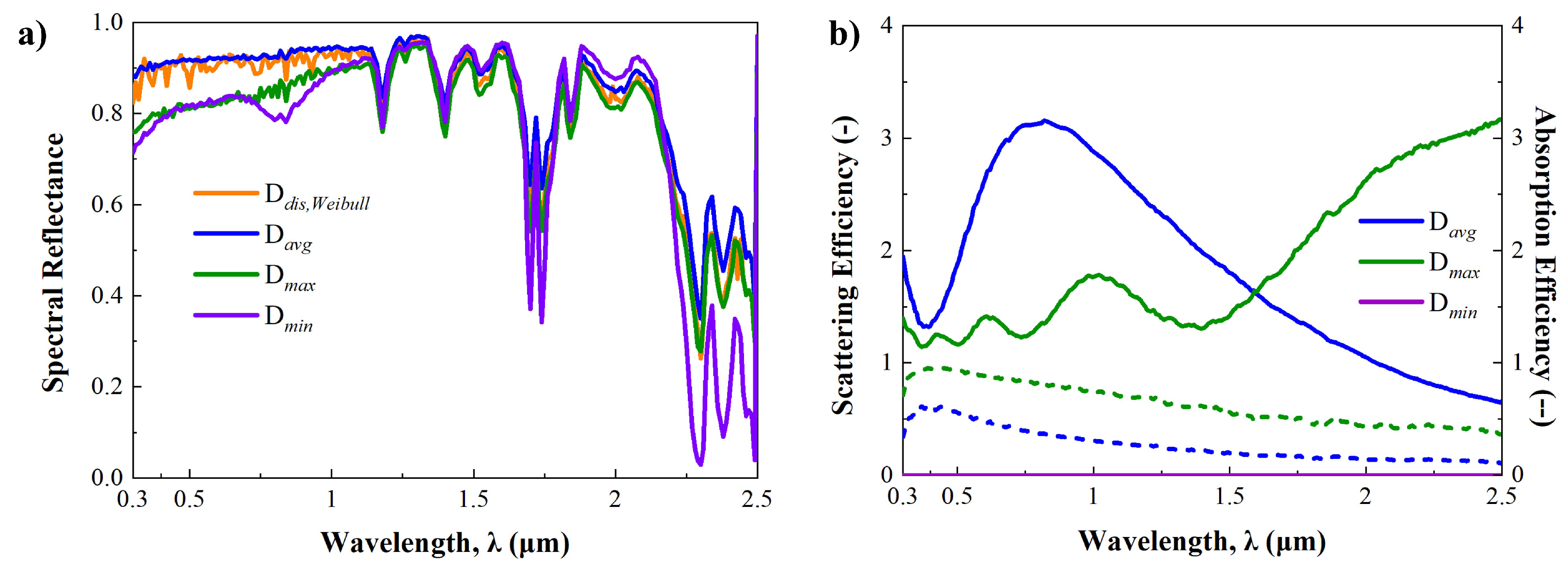
3.2. Effects of Particle Size Distribution on Radiative Properties
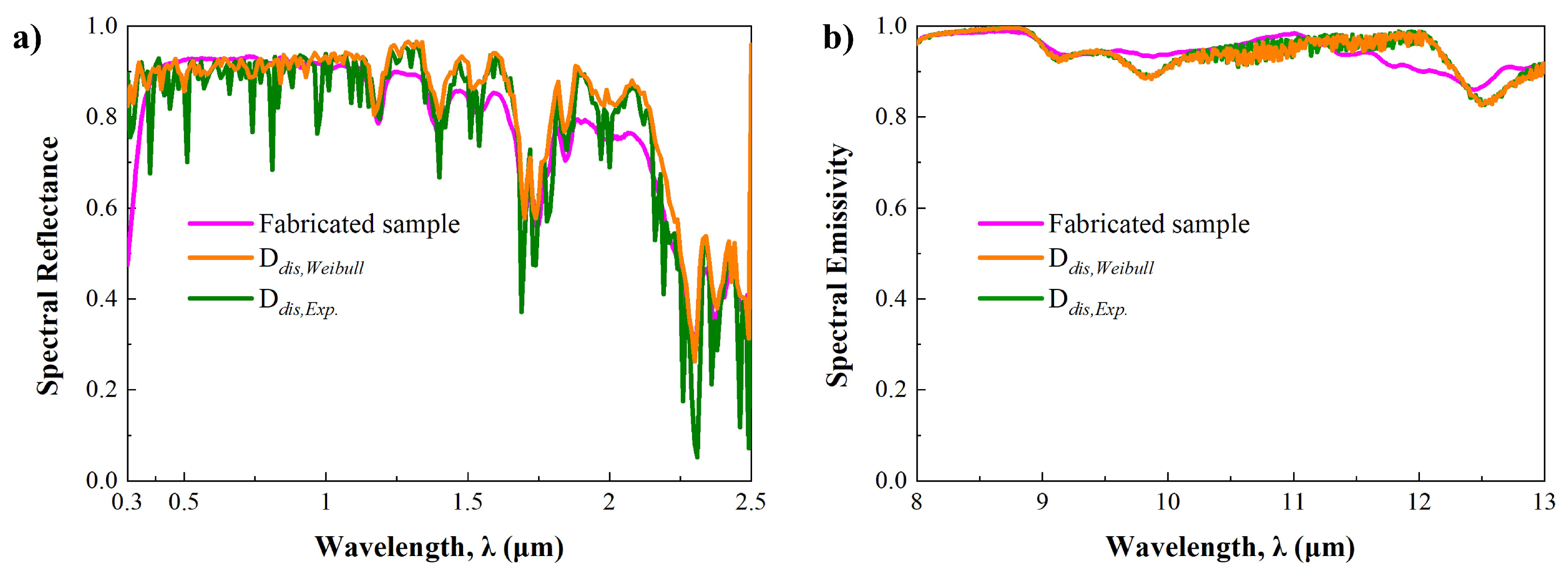
3.3. Validation of the Prediction Method on Radiative Properties of Pbrc
3.4. Cooling Performance Prediction Considering Particle Size Distribution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, X.; Chan, J.; Chen, C. Review of radiative cooling materials: Performance evaluation and design approaches. Nano Energy 2021, 88, 106259. [Google Scholar] [CrossRef]
- Chae, D.; Kim, M.; Jung, P.H.; Son, S.; Seo, J.; Liu, Y.; Lee, B.J.; Lee, H. Spectrally selective inorganic-based multilayer emitter for daytime radiative cooling. ACS Appl. Mater. Interfaces 2020, 12, 8073–8081. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, D.; Fang, C.; He, P.; Ye, Y.H. A multilayer emitter close to ideal solar reflectance for efficient daytime radiative cooling. Polymers 2019, 11, 1203. [Google Scholar] [CrossRef]
- Jing, W.; Zhang, S.; Zhang, W.; Chen, Z.; Zhang, C.; Wu, D.; Gao, Y.; Zhu, H. Scalable and flexible electrospun film for daytime subambient radiative cooling. ACS Appl. Mater. Interfaces 2021, 13, 29558–29566. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tan, X.; Qi, G.; Yang, X.; Hu, D.; Fyffe, P.; Chen, X. Effective radiative cooling with ZrO2/PDMS reflective coating. Sol. Energy Mater. Sol. Cells 2021, 229, 111129. [Google Scholar] [CrossRef]
- Wang, T.; Wu, Y.; Shi, L.; Hu, X.; Chen, M.; Wu, L. A structural polymer for highly efficient all-day passive radiative cooling. Nat. Commun. 2021, 12, 365. [Google Scholar] [CrossRef]
- Zhai, Y.; Ma, Y.; David, S.N.; Zhao, D.; Lou, R.; Tan, G.; Yang, R.; Yin, X. Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling. Science 2017, 355, 1062–1066. [Google Scholar] [CrossRef]
- Li, X.; Peoples, J.; Yao, P.; Ruan, X. Ultrawhite BaSO4 paints and films for remarkable daytime subambient radiative cooling. ACS Appl. Mater. Interfaces 2021, 13, 21733–21739. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Ruan, X. Nanoparticle embedded double-layer coating for daytime radiative cooling. Int. J. Heat Mass Transf. 2017, 104, 890–896. [Google Scholar] [CrossRef]
- Chae, D.; Son, S.; Lim, H.; Jung, P.H.; Ha, J.; Lee, H. Scalable and paint-format microparticle–polymer composite enabling high-performance daytime radiative cooling. Mater. Today Phys. 2021, 18, 100389. [Google Scholar] [CrossRef]
- Lin, S.; Ai, L.; Zhang, J.; Bu, T.; Li, H.; Huang, F.; Zhang, J.; Lu, Y.; Song, W. Silver ants-inspired flexible photonic architectures with improved transparency and heat radiation for photovoltaic devices. Sol. Energy Mater. Sol. Cells 2019, 203, 110135. [Google Scholar] [CrossRef]
- Yuan, Q.; Jiang, J.; Li, Y.; Xu, C.; Cheng, Y.; Jiang, L.; Zhu, Z.; Qin, Z.; Wang, H.; Wang, J.; et al. The compatible method of designing the transparent ultra-broadband radar absorber with low infrared emissivity. Infrared Phys. Technol. 2022, 123, 104114. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Y.; Qiu, J.; Cao, J.; Zou, Y.; Wang, S.; Ouyang, J.; Jia, D.; Zhou, Y. A visibly transparent radiative cooling film with self-cleaning function produced by solution processing. J. Mater. Res. Technol. 2021, 90, 76–84. [Google Scholar] [CrossRef]
- Xu, H.; Chen, X.; Ouyang, S.; Kako, T.; Ye, J. Size-dependent Mie’s scattering effect on TiO2 spheres for the superior photoactivity of H2 evolution. J. Phys. Chem. C 2012, 116, 3833–3839. [Google Scholar] [CrossRef]
- Tsai, M.C.; Tsai, T.L.; Shieh, D.B.; Chiu, H.T.; Lee, C.Y. Detecting HER2 on cancer cells by TiO2 spheres Mie scattering. Anal. Chem. 2009, 81, 7590–7596. [Google Scholar] [CrossRef] [PubMed]
- Nentwich, A. Production of Nanoparticles and Nanomaterials. 2011. Available online: http://epub.oeaw.ac.at/ita/nanotrust-dossiers/dossier006en.pdf (accessed on 5 February 2024).
- Brouwer, D. Exposure to manufactured nanoparticles in different workplaces. Toxicology 2010, 269, 120–127. [Google Scholar] [CrossRef]
- Thakkar, K.N.; Mhatre, S.S.; Parikh, R.Y. Biological synthesis of metallic nanoparticles. Nanomed. Nanotechnol. Biol. Med. 2010, 6, 257–262. [Google Scholar] [CrossRef]
- Fuqiang, W.; Hao, W.; Dayang, G.; Ziming, C.; Lanxin, M. Radiative transfer analysis of semitransparent medium with particles having non-uniform size distribution by differential-integration method. Int. J. Heat Mass Transf. 2019, 130, 342–355. [Google Scholar] [CrossRef]
- Peoples, J.; Li, X.; Lv, Y.; Qiu, J.; Huang, Z.; Ruan, X. A strategy of hierarchical particle sizes in nanoparticle composite for enhancing solar reflection. Int. J. Heat Mass Transf. 2019, 131, 487–494. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, F.; Wang, H.; Liang, H.; Ma, L. Effect of embedded polydisperse glass microspheres on radiative cooling of a coating. Int. J. Therm. Sci. 2019, 140, 358–367. [Google Scholar] [CrossRef]
- Wen, B.; Aydin, A.; Duzgoren-Aydin, N.S. A comparative study of particle size analyses by sieve-hydrometer and laser diffraction methods. Geotech. Test. J. 2002, 25, 434–442. [Google Scholar]
- Cheetham, M.D.; Keene, A.F.; Bush, R.T.; Sullivan, L.A.; Erskine, W.D. A comparison of grain-size analysis methods for sand-dominated fluvial sediments. Sedimentology 2008, 55, 1905–1913. [Google Scholar] [CrossRef]
- Pearson, R.A.; Yee, A.F. Influence of particle size and particle size distribution on toughening mechanisms in rubber-modified epoxies. J. Mater. Sci. 1991, 26, 3828–3844. [Google Scholar] [CrossRef]
- Ferro, V.; Mirabile, S. Comparing particle size distribution analysis by sedimentation and laser diffraction method. J. Agric. Eng. 2009, 40, 35–43. [Google Scholar] [CrossRef]
- Quilaqueo, M.; Gim-Krumm, M.; Ruby-Figueroa, R.; Troncoso, E.; Estay, H. Determination of size distribution of precipitation aggregates using non-invasive microscopy and semiautomated image processing and analysis. Minerals 2019, 9, 724. [Google Scholar] [CrossRef]
- Ma, Z.; Merkus, H.G.; de Smet, J.G.; Heffels, C.; Scarlett, B. New developments in particle characterization by laser diffraction: Size and shape. Powder Technol. 2000, 111, 66–78. [Google Scholar] [CrossRef]
- Goodall, W.R.; Scales, P.J. An overview of the advantages and disadvantages of the determination of gold mineralogy by automated mineralogy. Miner. Eng. 2007, 20, 506–517. [Google Scholar] [CrossRef]
- Jung, J.; Yoon, S.; Kim, B.; Kim, J.B. Development of High-Performance Flexible Radiative Cooling Film Using PDMS/TiO2 Microparticles. Micromachines 2023, 14, 2223. [Google Scholar] [CrossRef] [PubMed]
- Vincent, O.R.; Folorunso, O. A descriptive algorithm for sobel image edge detection. In Proceedings of the Informing Science & IT Education Conference (InSITE), Macon, GA, USA, 12–15 June 2009; Volume 40, pp. 97–107. [Google Scholar]
- Luo, L.; Xu, D.; Zhang, Z.; Zhang, J.; Qu, W. A fast and robust circle detection method using perpendicular bisector of chords. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 2856–2860. [Google Scholar]
- Chernov, N.; Lesort, C. Least squares fitting of circles. J. Math. Imaging Vis. 2005, 23, 239–252. [Google Scholar] [CrossRef]
- Ayala-Ramirez, V.; Garcia-Capulin, C.H.; Perez-Garcia, A.; Sanchez-Yanez, R.E. Circle detection on images using genetic algorithms. Pattern Recognit. Lett. 2006, 27, 652–657. [Google Scholar] [CrossRef]
- Atherton, T.J.; Kerbyson, D.J. Size invariant circle detection. Image Vis. Comput. 1999, 17, 795–803. [Google Scholar] [CrossRef]
- Dunbar, C.A.; Hickey, A.J. Evaluation of probability density functions to approximate particle size distributions of representative pharmaceutical aerosols. J. Aerosol Sci. 2000, 31, 813–831. [Google Scholar] [CrossRef]
- Al-Thyabat, S.; Miles, N. An improved estimation of size distribution from particle profile measurements. Powder Technol. 2006, 166, 152–160. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Mandelbrot, B.B. A case against the lognormal distribution. In Fractals and Scaling in Finance: Discontinuity, Concentration, Risk. Selecta Volume E; Springer: New York, NY, USA, 1997; pp. 252–269. [Google Scholar]
- Rana, R.; Singhal, R. Chi-square test and its application in hypothesis testing. J. Pract. Cardiovasc. Sci. 2015, 1, 69–71. [Google Scholar]
- Santos-Neto, M.; Cysneiros, F.J.A.; Leiva, V.; Barros, M. Reparameterized Birnbaum-Saunders regression models with varying precision. Electron. J. Statist. 2016, 10, 2825–2855. [Google Scholar] [CrossRef]
- Tanaka, H.; Ishibuchi, H.; Yoshikawa, S. Exponential possibility regression analysis. Fuzzy Sets Syst. 1995, 69, 305–318. [Google Scholar] [CrossRef]
- Calabrese, R.; Osmetti, S.A. Modelling small and medium enterprise loan defaults as rare events: The generalized extreme value regression model. J. Appl. Stat. 2013, 40, 1172–1188. [Google Scholar] [CrossRef]
- Hambuckers, J.; Groll, A.; Kneib, T. Understanding the economic determinants of the severity of operational losses: A regularized generalized Pareto regression approach. J. Appl. Econom. 2018, 33, 898–935. [Google Scholar] [CrossRef]
- Pescim, R.R.; Ortega, E.M.; Cordeiro, G.M.; Demtrio, C.G.; Hamedani, G. The log-beta generalized half-normal regression model. J. Stat. Theory Appl. 2013, 12, 330–347. [Google Scholar] [CrossRef]
- Lukman, A.F.; Algamal, Z.Y.; Kibria, B.G.; Ayinde, K. The KL estimator for the inverse Gaussian regression model. Concurr. Comput. Pract. Exp. 2021, 33, e6222. [Google Scholar] [CrossRef]
- Faradmal, J.; Soltanian, A.R.; Roshanaei, G.; Khodabakhshi, R.; Kasaeian, A. Comparison of the performance of log-logistic regression and artificial neural networks for predicting breast cancer relapse. Asian Pac. J. Cancer Prev. APJCP 2014, 15, 5883–5888. [Google Scholar] [CrossRef] [PubMed]
- Speed, T.; Yu, B. Model selection and prediction: Normal regression. Ann. Inst. Stat. Math. 1993, 45, 35–54. [Google Scholar] [CrossRef]
- Palm, B.G.; Bayer, F.M.; Cintra, R.J.; Pettersson, M.I.; Machado, R. Rayleigh regression model for ground type detection in SAR imagery. IEEE Geosci. Remote Sens. 2019, 16, 1660–1664. [Google Scholar] [CrossRef]
- Sahu, S.K.; Dey, D.K.; Aslanidou, H.; Sinha, D. A Weibull regression model with gamma frailties for multivariate survival data. Lifetime Data Anal. 1997, 3, 123–137. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Chen, M.; Pang, D.; Chen, X.; Yan, H.; Yang, Y. Passive daytime radiative cooling: Fundamentals, material designs, and applications. EcoMat 2022, 4, e12153. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, K.; Ye, P.; Niu, Z.; Song, G. Effect of electronic and phonon properties on polar dielectric embedded polymer-based radiative cooling materials. Sol. Energy Mater. Sol. Cells 2023, 260, 112473. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ma, H.; Wang, L.; Dou, S.; Zhao, H.; Huang, M.; Xu, Z.; Zhang, X.; Xu, X.; Zhang, A.; Yue, H.; et al. Flexible daytime radiative cooling enhanced by enabling three-phase composites with scattering interfaces between silica microspheres and hierarchical porous coatings. ACS Appl. Mater. Interfaces 2021, 13, 19282–19290. [Google Scholar] [CrossRef]
- Lu, X.; Xu, P.; Wang, H.; Yang, T.; Hou, J. Cooling potential and applications prospects of passive radiative cooling in buildings: The current state-of-the-art. Renew. Sustain. Energy Rev. 2016, 65, 1079–1097. [Google Scholar] [CrossRef]
- Raman, A.P.; Anoma, M.A.; Zhu, L.; Rephaeli, E.; Fan, S. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 2014, 515, 540–544. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo-Fernandez, J.; Yang, H.; Schertel, L.; Whitworth, G.L.; Garcia, P.D.; Vignolini, S.; Sotomayor-Torres, C.M. Highly-scattering cellulose-based films for radiative cooling. Adv. Sci 2022, 9, 2104758. [Google Scholar] [CrossRef]
- Liu, Y.; Son, S.; Chae, D.; Jung, P.H.; Lee, H. Acrylic membrane doped with Al2O3 nanoparticle resonators for zero-energy consuming radiative cooling. Sol. Energy Mater Sol. Cells 2020, 213, 110561. [Google Scholar] [CrossRef]




| Distribution Type | |
|---|---|
| Birnbaum–Saunders | 97.2 |
| Exponential | 1362.2 |
| Extreme Value | 333.7 |
| Generalized Pareto | 850.5 |
| Half Normal | 691.7 |
| Inverse Gaussian | 105.6 |
| LogLogistic | 129.2 |
| Lognormal | 101.1 |
| Normal | 84.3 |
| Rayleigh | 92.3 |
| Weibull | 29.8 |
| Case | Particle Size |
|---|---|
| Ddis,Weibull | f(x) = |
| Ddis,Exp. | f(x) = 1.44 |
| Davg | 1.447 m |
| Dmax | 4.856 m |
| Dmin | 0.006 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, J.; Jung, J.; Rho, J.; Kim, J.B. Cooling Performance Prediction of Particle-Based Radiative Cooling Film Considering Particle Size Distribution. Micromachines 2024, 15, 292. https://doi.org/10.3390/mi15030292
Lim J, Jung J, Rho J, Kim JB. Cooling Performance Prediction of Particle-Based Radiative Cooling Film Considering Particle Size Distribution. Micromachines. 2024; 15(3):292. https://doi.org/10.3390/mi15030292
Chicago/Turabian StyleLim, Jaehyun, Junbo Jung, Jinsung Rho, and Joong Bae Kim. 2024. "Cooling Performance Prediction of Particle-Based Radiative Cooling Film Considering Particle Size Distribution" Micromachines 15, no. 3: 292. https://doi.org/10.3390/mi15030292
APA StyleLim, J., Jung, J., Rho, J., & Kim, J. B. (2024). Cooling Performance Prediction of Particle-Based Radiative Cooling Film Considering Particle Size Distribution. Micromachines, 15(3), 292. https://doi.org/10.3390/mi15030292







