Behind the Non-Uniform Breakup of Bubble Slug in Y-Shaped Microchannel: Dynamics and Mechanisms
Abstract
:1. Introduction
2. Methodology
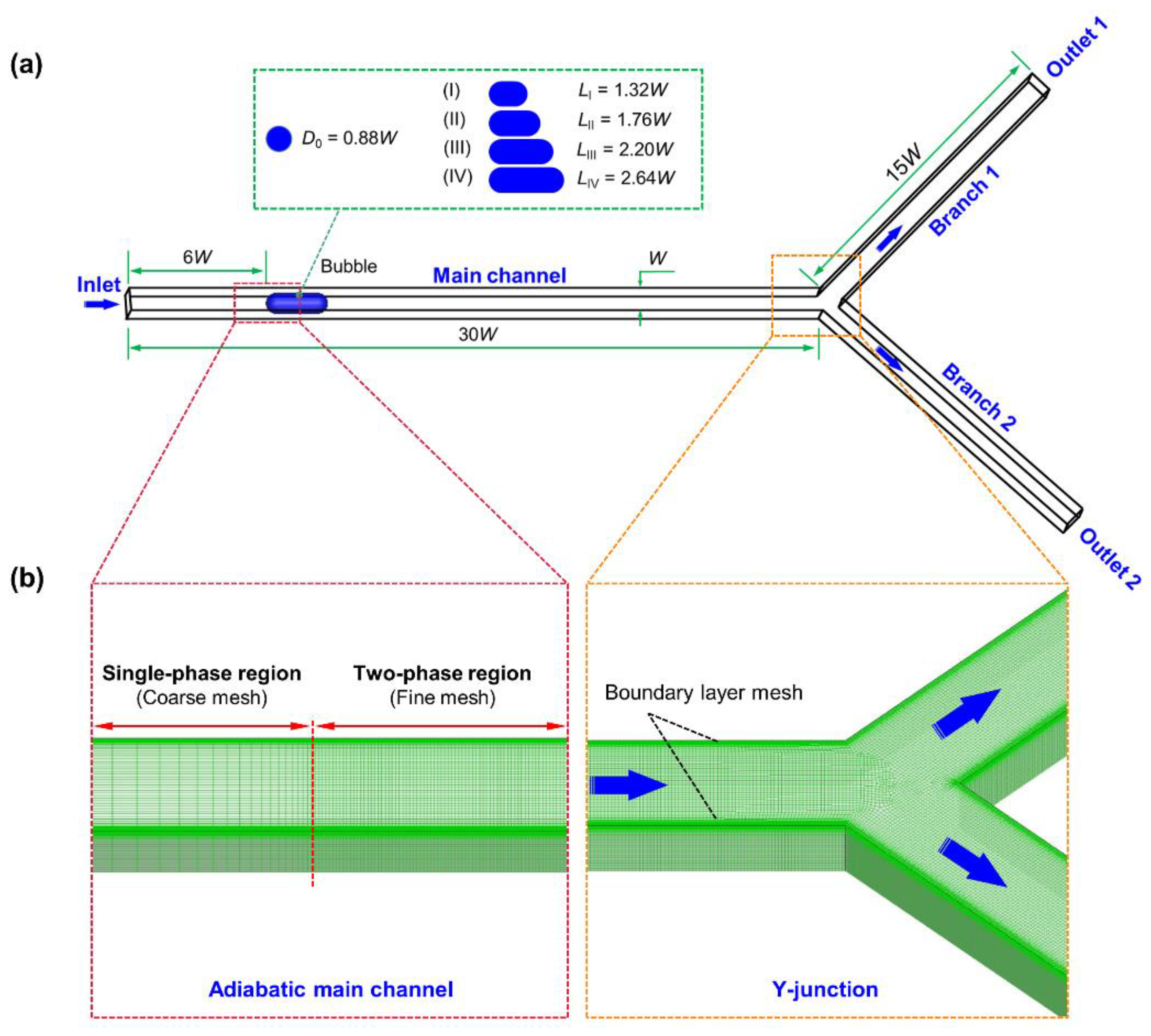
2.1. Problem Statement
2.2. Model and Implementation
2.3. Validation
3. Results and Discussion
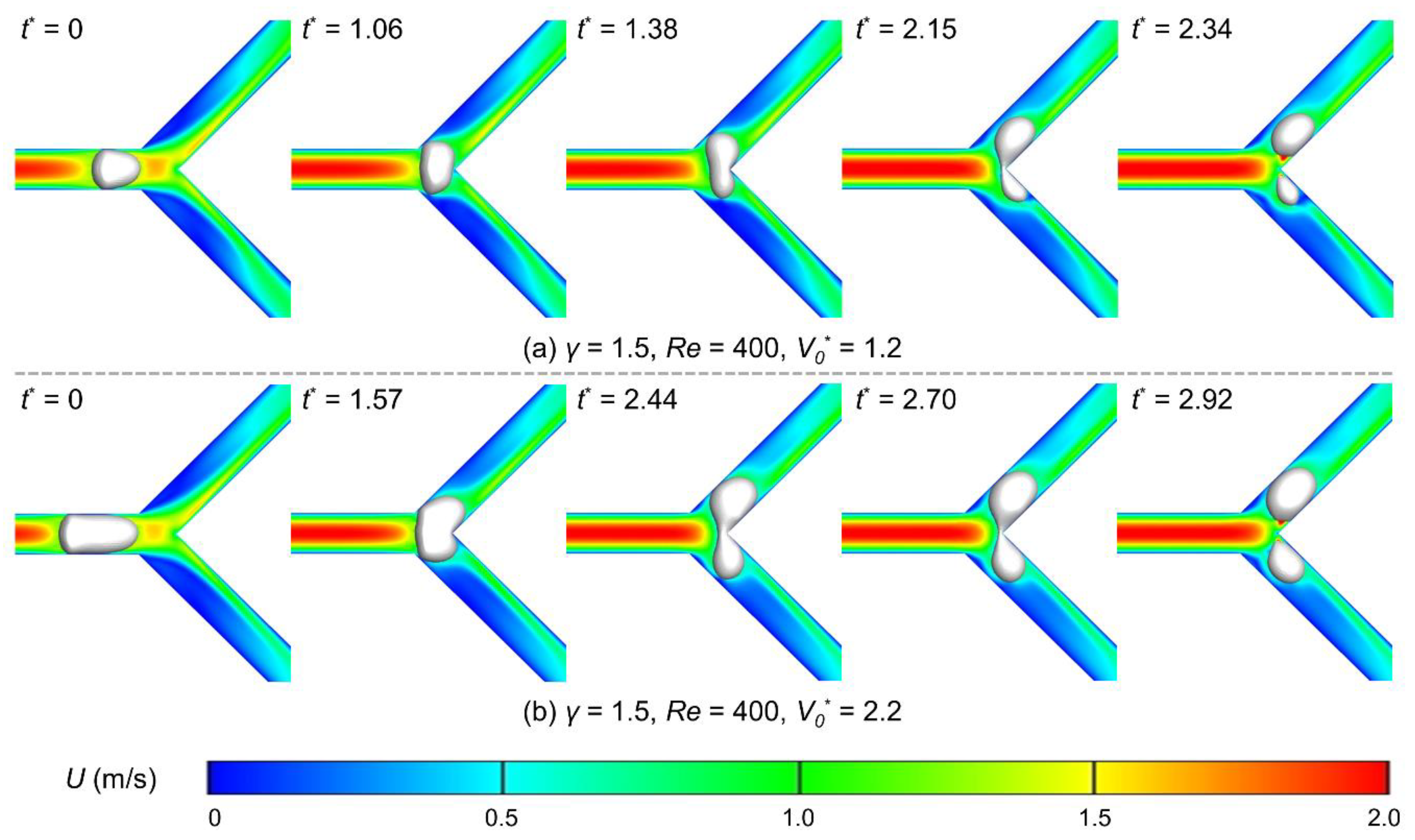
3.1. Non-Uniform Breakup Patterns of the Bubble
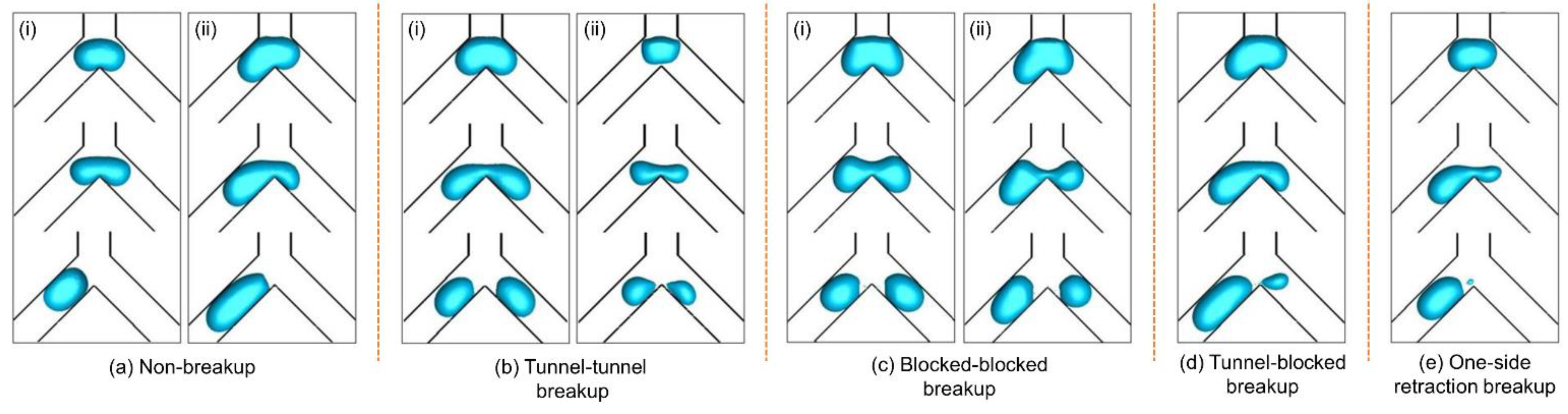
- (a)
- Non-breakup. As the bubble arrives at the Y-junction, it first slows down and slightly penetrates the junction, then flows into one of the branches under a random disturbance (Figure 3a(i)). If the flow ratio is large enough, the bubble may also directly enter the high-flow-rate branch without breakup (Figure 3a(ii)).
- (b)
- Tunnel–tunnel breakup. Under a synergy effect of squeezing force, shearing force, and the sharp corner of the Y-junction, the bubble can continue to deform and finally break up [2]. A tunnel–tunnel breakup pattern depicts that both bubble-laden flows in the two branches show a tunnel style after the initial bubble breaks up at the bifurcation. The breakup can be either symmetrical (Figure 3b(i)) or asymmetrical (Figure 3b(ii)).
- (c)
- (d)
- Tunnel–blocked breakup. Tunnel flow in one branch channel and blocked flow in the other (Figure 3d).
- (e)
- One-side retraction breakup. When the flow ratio is relatively large, a daughter bubble about to separate from the initial bubble may be retracted back into the initial bubble due to the surface tension, during which a satellite bubble is generated. The main and satellite bubbles will enter the high-flow-rate branch (Figure 3e).
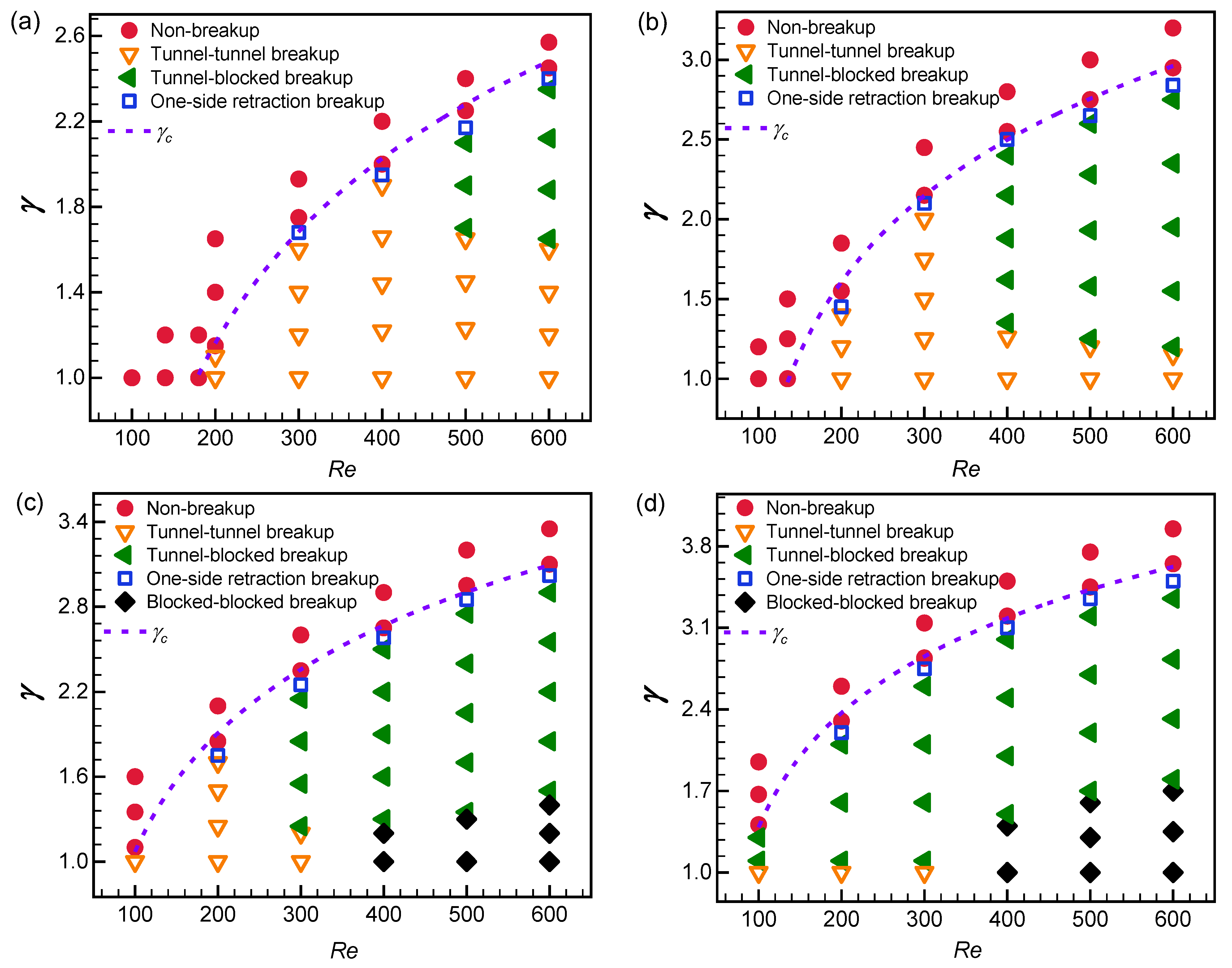
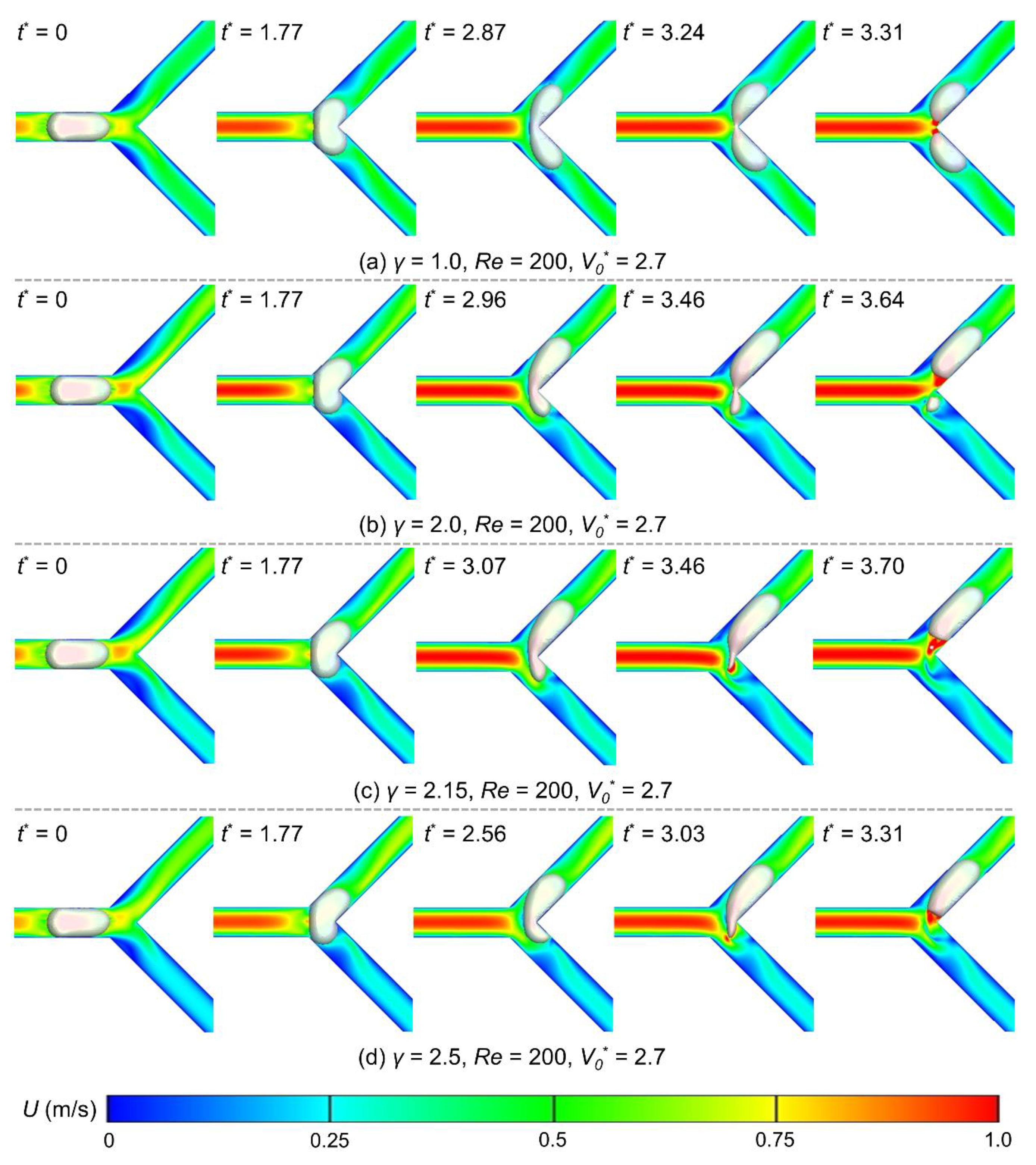
3.2. Effects of Flow Ratio, Reynolds Number, and Bubble Volume on Breakup Dynamics
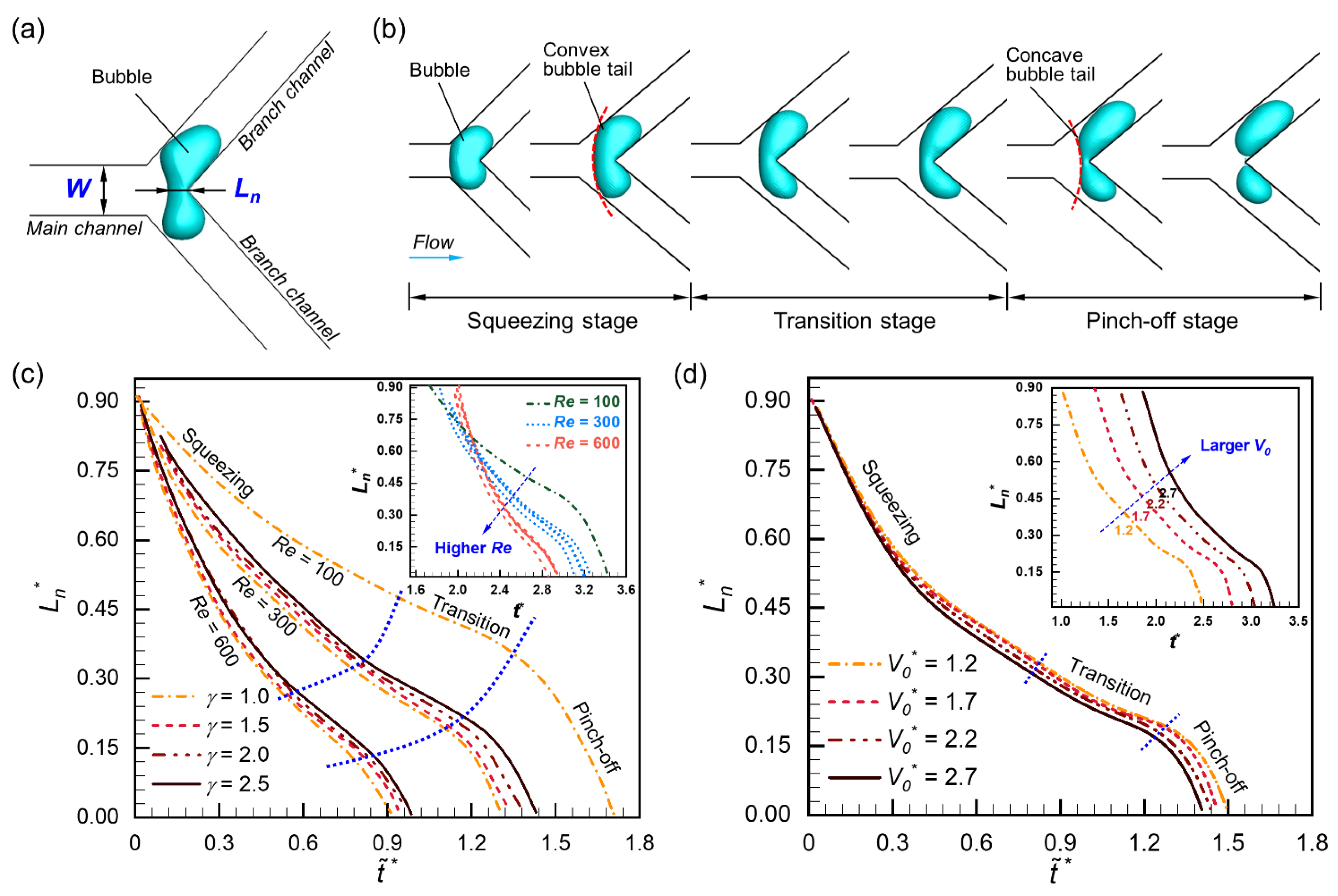
3.3. Bubble Neck Dynamics
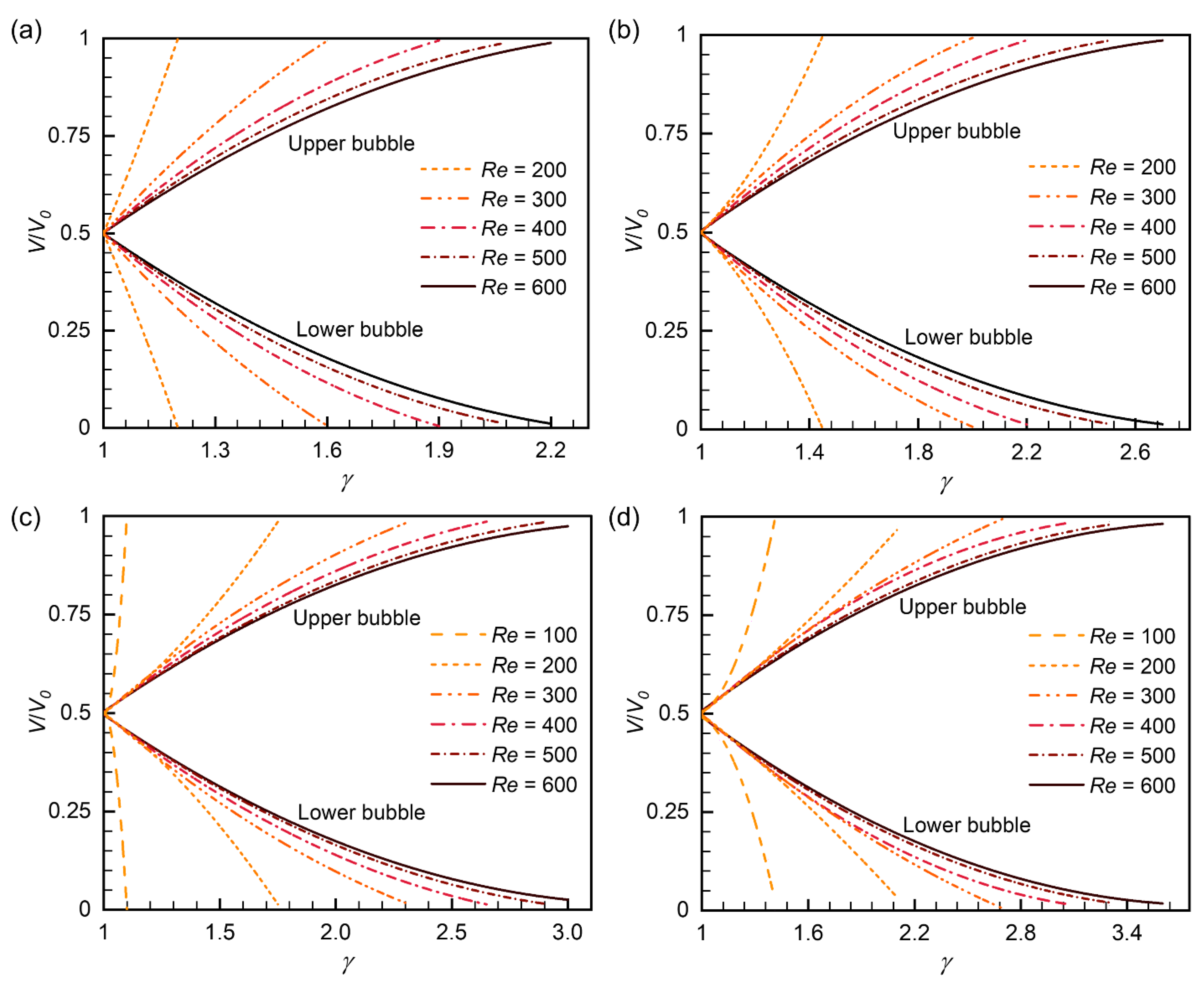
3.4. Volume Distribution after Breakup
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Li, G.; Li, Y.; Chen, Y.; Li, J.; Chen, H. Flow field around bubbles on formation of air embolism in small vessels. Proc. Natl. Acad. Sci. USA 2021, 118, e2025406118. [Google Scholar] [CrossRef] [PubMed]
- Fei, Y.; Zhu, C.; Fu, T.; Gao, X.; Ma, Y. The breakup dynamics of bubbles stabilized by nanoparticles in a microfluidic Y-junction. Chem. Eng. Sci. 2021, 245, 116867. [Google Scholar] [CrossRef]
- Arzhavitina, A.; Steckel, H. Foams for pharmaceutical and cosmetic application. Int. J. Pharm. 2010, 394, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Eisner, M.D.; Wildmoser, H.; Windhab, E.J. Air cell microstructuring in a high viscous ice cream matrix. Colloids Surf. A 2005, 263, 390–399. [Google Scholar] [CrossRef]
- Rashid, M.T.; Ahmad, N.; Swati, R.F.; Khan, M.B. Flow Boiling of Liquid n-Heptane in Microtube with Various Fuel Flow Rate: Experimental and Numerical Study. Micromachines 2023, 14, 1760. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Zhang, L.; Yang, Y.; Niu, X.; Zeng, Z.; Shu, B. Flow Pattern Study and Pressure Drop Prediction of Two-Phase Boiling Process in Different Surface Wettability Microchannel. Micromachines 2023, 14, 958. [Google Scholar] [CrossRef] [PubMed]
- Anna, S.L. Droplets and Bubbles in Microfluidic Devices. Annu. Rev. Fluid Mech. 2016, 48, 285–309. [Google Scholar] [CrossRef]
- Fu, T.; Ma, Y. Bubble formation and breakup dynamics in microfluidic devices: A review. Chem. Eng. Sci. 2015, 135, 343–372. [Google Scholar] [CrossRef]
- Nagargoje, M.S.; Gupta, R. Experimental investigations on the bubble dynamics in a symmetric bifurcating channel. Int. J. Multiph. Flow 2023, 159, 104318. [Google Scholar] [CrossRef]
- Fursenko, R.V.; Chudnovskii, V.M.; Minaev, S.S.; Okajima, J. Mechanism of high velocity jet formation after a gas bubble collapse near the micro fiber immersed in a liquid. Int. J. Heat Mass Transf. 2020, 163, 120420. [Google Scholar] [CrossRef]
- Liu, H.; Tian, T.; Kang, R. A probability model for predicting the bubble size distribution in fully developed bubble flow in vertical pipes. Int. Commun. Heat Mass Transf. 2021, 120, 105015. [Google Scholar] [CrossRef]
- Hoang, D.A.; Portela, L.M.; Kleijn, C.R.; Kreutzer, M.T.; van Steijn, V. Dynamics of droplet breakup in a T-junction. J. Fluid Mech. 2013, 717, R4. [Google Scholar] [CrossRef]
- Yu, W.; Liu, X.; Li, B.; Chen, Y. Experiment and prediction of droplet formation in microfluidic cross-junctions with different bifurcation angles. Int. J. Multiph. Flow 2022, 149, 103973. [Google Scholar] [CrossRef]
- Cerdeira, A.T.S.; Campos, J.; Miranda, J.M.; Araujo, J.D.P. Review on Microbubbles and Microdroplets Flowing through Microfluidic Geometrical Elements. Micromachines 2020, 11, 201. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Koh, K.S.; Yew, M.; Chin, J.K.; Chan, Y.; Yan, Y. Droplet breakup dynamics in bi-layer bifurcating microchannel. Micromachines 2018, 9, 57. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Li, H.; Wang, K.; Qiu, T. Accelerating intelligent microfluidic image processing with transfer deep learning: A microchannel droplet/bubble breakup case study. Sep. Purif. Technol. 2023, 315, 123703. [Google Scholar] [CrossRef]
- Chu, P.; Finch, J.; Bournival, G.; Ata, S.; Hamlett, C.; Pugh, R.J. A review of bubble break-up. Adv. Colloid Interface Sci. 2019, 270, 108–122. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Peng, H.; Zhu, M.; Wu, L.; Jia, C.; Zhou, H.; Zhao, J. A Facile Strategy for Visualizing and Modulating Droplet-Based Microfluidics. Micromachines 2019, 10, 291. [Google Scholar] [CrossRef] [PubMed]
- Fu, T.; Ma, Y.; Funfschilling, D.; Li, H.Z. Dynamics of bubble breakup in a microfluidic T-junction divergence. Chem. Eng. Sci. 2011, 66, 4184–4195. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Yu, W.; Deng, Z.; Chen, Y. Bubble breakup in a microfluidic T-junction. Sci. Bull. 2016, 61, 811–824. [Google Scholar] [CrossRef]
- Lu, Y.; Fu, T.; Zhu, C.; Ma, Y.; Li, H.Z. Dynamics of bubble breakup at a T junction. Phys. Rev. E 2016, 93, 022802. [Google Scholar] [CrossRef] [PubMed]
- Dai, C.; Fang, S.; Wu, Y.; Wu, X.; Zhao, M.; Zou, C.; Li, H.; Zhou, H.; Zhang, K. Experimental study of bubble breakup process in non-Newtonian fluid in 3-D pore-throat microchannels. Colloids Surf. A 2017, 535, 130–138. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, C.; Fu, T.; Qiu, T.; Ma, Y. Critical condition for bubble breakup in a microfluidic flow-focusing junction. Chem. Eng. Sci. 2017, 164, 178–187. [Google Scholar] [CrossRef]
- Magnini, M.; Municchi, F.; El Mellas, I.; Icardi, M. Liquid film distribution around long gas bubbles propagating in rectangular capillaries. Int. J. Multiph. Flow 2022, 148, 103939. [Google Scholar] [CrossRef]
- Pan, Z.; Weibel, J.A.; Garimella, S.V. A saturated-interface-volume phase change model for simulating flow boiling. Int. J. Heat Mass Transf. 2016, 93, 945–956. [Google Scholar] [CrossRef]
- Sun, D.-L.; Xu, J.-L.; Wang, L. Development of a vapor–liquid phase change model for volume-of-fluid method in FLUENT. Int. Commun. Heat Mass Transf. 2012, 39, 1101–1106. [Google Scholar] [CrossRef]
- Endaylalu, S.A.; Tien, W.H. A Numerical Investigation of the Mixing Performance in a Y-Junction Microchannel Induced by Acoustic Streaming. Micromachines 2022, 13, 338. [Google Scholar] [CrossRef] [PubMed]
- Chiriac, E.; Avram, M.; Balan, C. Investigation of Multiphase Flow in a Trifurcation Microchannel—A Benchmark Problem. Micromachines 2022, 13, 974. [Google Scholar] [CrossRef] [PubMed]
- Lou, Q.; Li, T.; Yang, M. Numerical simulation of the bubble dynamics in a bifurcated micro-channel using the lattice Boltzmann method. J. Appl. Phys. 2019, 126, 034301. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, X.; Li, Q.; Wu, L. Numerical Study of Bubble Breakup in Fractal Tree-Shaped Microchannels. Int. J. Mol. Sci. 2019, 20, 5516. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Zhang, G.; Tian, M. The bubble breakup process and behavior in T-type microchannels. Phys. Fluids 2023, 35, 013319. [Google Scholar] [CrossRef]
- Chen, X.; Zielinski, R.; Ghadiali, S.N. Computational Analysis of Microbubble Flows in Bifurcating Airways: Role of Gravity, Inertia, and Surface Tension. J. Biomech. Eng. 2014, 136, 101007. [Google Scholar] [CrossRef]
- Qamar, A.; Warnez, M.; Valassis, D.T.; Guetzko, M.E.; Bull, J.L. Small-bubble transport and splitting dynamics in a symmetric bifurcation. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1182–1194. [Google Scholar] [CrossRef] [PubMed]
- Linstrom, P.J.; Mallard, W.G. The NIST Chemistry WebBook: A chemical data resource on the internet. J. Chem. Eng. Data 2001, 46, 1059–1063. [Google Scholar] [CrossRef]
- Pan, Z.; Weibel, J.A.; Garimella, S.V. Spurious current suppression in VOF-CSF simulation of slug flow through small channels. Numer. Heat Tr. A-Appl. 2014, 67, 1–12. [Google Scholar] [CrossRef]
- Wang, C.; Tian, M.; Zhang, J.; Zhang, G.; Zhang, Y. Numerical study on pressure drop and heat transfer characteristics of gas-liquid Taylor flow in a microchannel based on FFR method. Int. Commun. Heat Mass Transf. 2020, 117, 104802. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Magnini, M.; Pulvirenti, B.; Thome, J.R. Numerical investigation of hydrodynamics and heat transfer of elongated bubbles during flow boiling in a microchannel. Int. J. Heat Mass Transf. 2013, 59, 451–471. [Google Scholar] [CrossRef]
- Ghosh, K.; Lopez-Pamies, O. Elastomers filled with liquid inclusions: Theory, numerical implementation, and some basic results. J. Mech. Phys. Solids 2022, 166, 104930. [Google Scholar] [CrossRef]
- Guo, H.; Jiang, P.; Peng, W.; Zhu, Y. Large eddy simulation of highly compressible film cooling in transonic crossflow. Int. J. Heat Mass Transf. 2023, 202, 123765. [Google Scholar] [CrossRef]
- Jatau, T.; Bello-Ochende, T. Heat transfer and flow pattern map development of R134A in a U-bend tube for flow boiling evaporation. Int. Commun. Heat Mass Transf. 2021, 128, 105629. [Google Scholar] [CrossRef]
- Xu, Z.; Fu, T.; Zhu, C.; Jiang, S.; Ma, Y.; Wang, K.; Luo, G. Dynamics of partially obstructed breakup of bubbles in microfluidic Y-junctions. Electrophoresis 2019, 40, 376–387. [Google Scholar]
- Jullien, M.-C.; Ching, M.-J.T.M.; Cohen, C.; Menetrier, L.; Tabeling, P. Droplet breakup in microfluidic T-junctions at small capillary numbers. Phys. Fluids 2009, 21, 072001. [Google Scholar] [CrossRef]


| Physical Properties | Water | Air |
|---|---|---|
| Density, ρ (kg/m3) | 998.2 | 1.205 |
| Viscosity, μ (Pa·s) | 1.005 × 10−3 | 1.81 × 10−5 |
| Surface tension, σ (N/m) | 0.07275 | / |
| Cell Number | 499,890 | 1,003,170 | 1,586,530 | 2,401,453 | ||||
|---|---|---|---|---|---|---|---|---|
| Re | 100 | 600 | 100 | 600 | 100 | 600 | 100 | 600 |
| Bubble length | 2.122 | 2.563 | 2.196 (r.v.) † | 2.595 (r.v.) † | 2.187 | 2.589 | 2.190 | 2.592 |
| |Deviation| | 3.37% | 1.23% | / | / | 0.41% | 0.23% | 0.27% | 0.12% |
| Fitting Parameter | V0* = 1.2 | V0* = 1.7 | V0* = 2.2 | V0* = 2.7 |
|---|---|---|---|---|
| c1 | 0.019 | 0.036 | 0.038 | 0.067 |
| c2 | −0.561 | −2.177 | −0.911 | −2.691 |
| V0* | Parameter | Re | |||||
|---|---|---|---|---|---|---|---|
| 100 | 200 | 300 | 400 | 500 | 600 | ||
| 1.2 | a | \ | 1.38 | −0.37 | −0.30 | −0.25 | −0.21 |
| b | \ | −0.54 | 1.78 | 1.42 | 1.22 | 1.08 | |
| c | \ | −0.34 | −0.91 | −0.62 | −0.47 | 0.37 | |
| 1.7 | a | \ | 1.01 | −0.20 | −0.16 | −0.14 | −0.12 |
| b | \ | −1.35 | 1.09 | 0.91 | 0.81 | 0.73 | |
| c | \ | 0.85 | −0.39 | −0.25 | −0.17 | −0.10 | |
| 2.2 | a | 50.01 | 0.30 | −0.11 | −0.10 | −0.09 | −0.09 |
| b | −99.94 | −0.17 | 0.72 | 0.66 | 0.59 | 0.58 | |
| c | 50.43 | 0.37 | −0.12 | −0.06 | −0.004 | 0.01 | |
| 2.7 | a | 2.36 | 0.06 | −0.06 | −0.08 | −0.06 | −0.06 |
| b | −4.50 | 0.22 | 0.49 | 0.55 | 0.47 | 0.45 | |
| c | 2.65 | 0.22 | 0.06 | 0.03 | 0.10 | 0.12 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Liu, J.; Yu, J.; Pan, W.; Yan, Z.; Pan, Z. Behind the Non-Uniform Breakup of Bubble Slug in Y-Shaped Microchannel: Dynamics and Mechanisms. Micromachines 2024, 15, 695. https://doi.org/10.3390/mi15060695
Huang H, Liu J, Yu J, Pan W, Yan Z, Pan Z. Behind the Non-Uniform Breakup of Bubble Slug in Y-Shaped Microchannel: Dynamics and Mechanisms. Micromachines. 2024; 15(6):695. https://doi.org/10.3390/mi15060695
Chicago/Turabian StyleHuang, Haoxiang, Jiazheng Liu, Jialing Yu, Wentao Pan, Zhe Yan, and Zhenhai Pan. 2024. "Behind the Non-Uniform Breakup of Bubble Slug in Y-Shaped Microchannel: Dynamics and Mechanisms" Micromachines 15, no. 6: 695. https://doi.org/10.3390/mi15060695
APA StyleHuang, H., Liu, J., Yu, J., Pan, W., Yan, Z., & Pan, Z. (2024). Behind the Non-Uniform Breakup of Bubble Slug in Y-Shaped Microchannel: Dynamics and Mechanisms. Micromachines, 15(6), 695. https://doi.org/10.3390/mi15060695




