Modeling and Experimental Study of Vibration Energy Harvester with Triple-Frequency-Up Voltage Output by Vibration Mode Switching
Abstract
1. Introduction
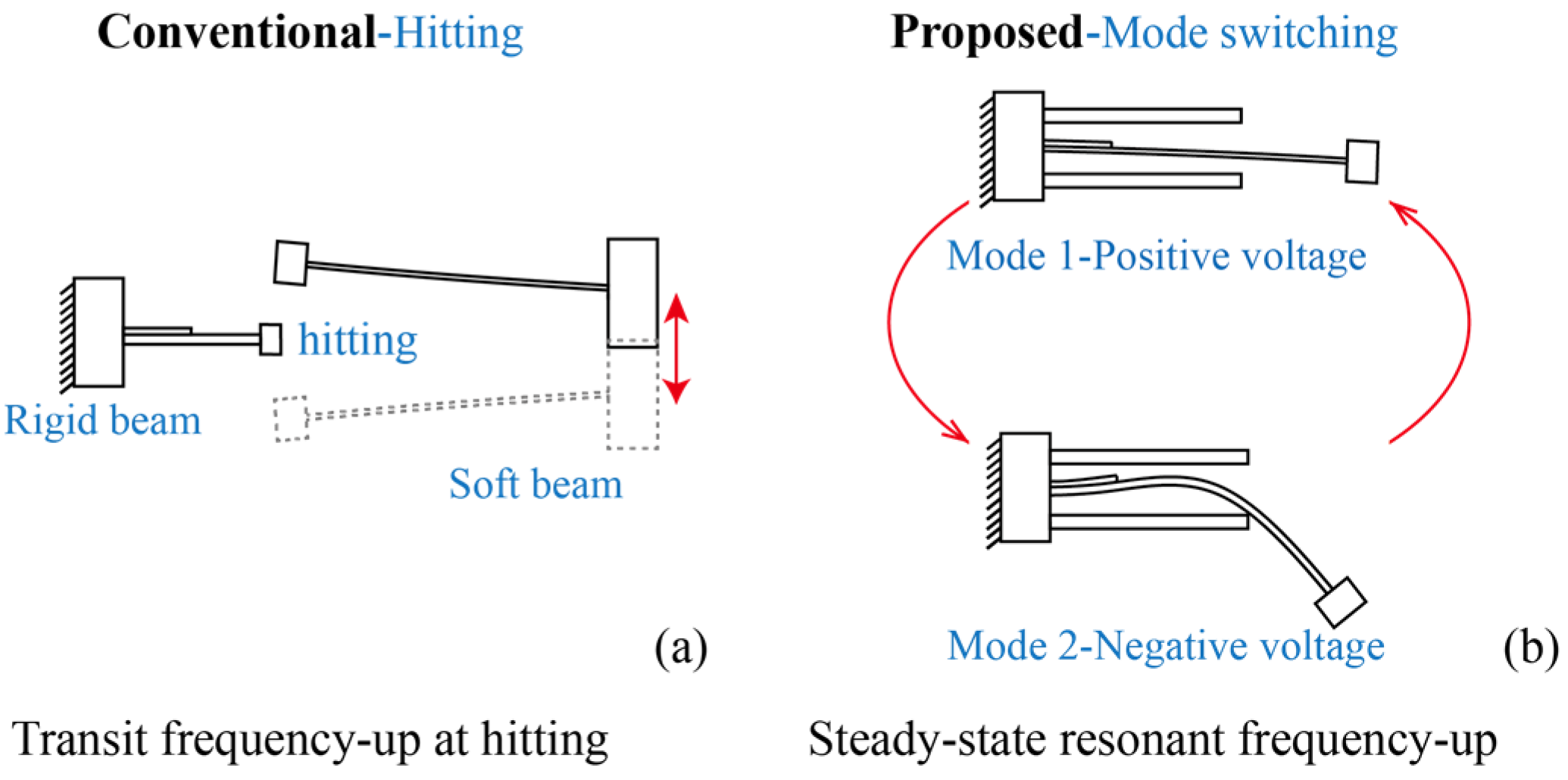
2. System Configuration and Operational Principle
3. Modeling of Vibration Modes
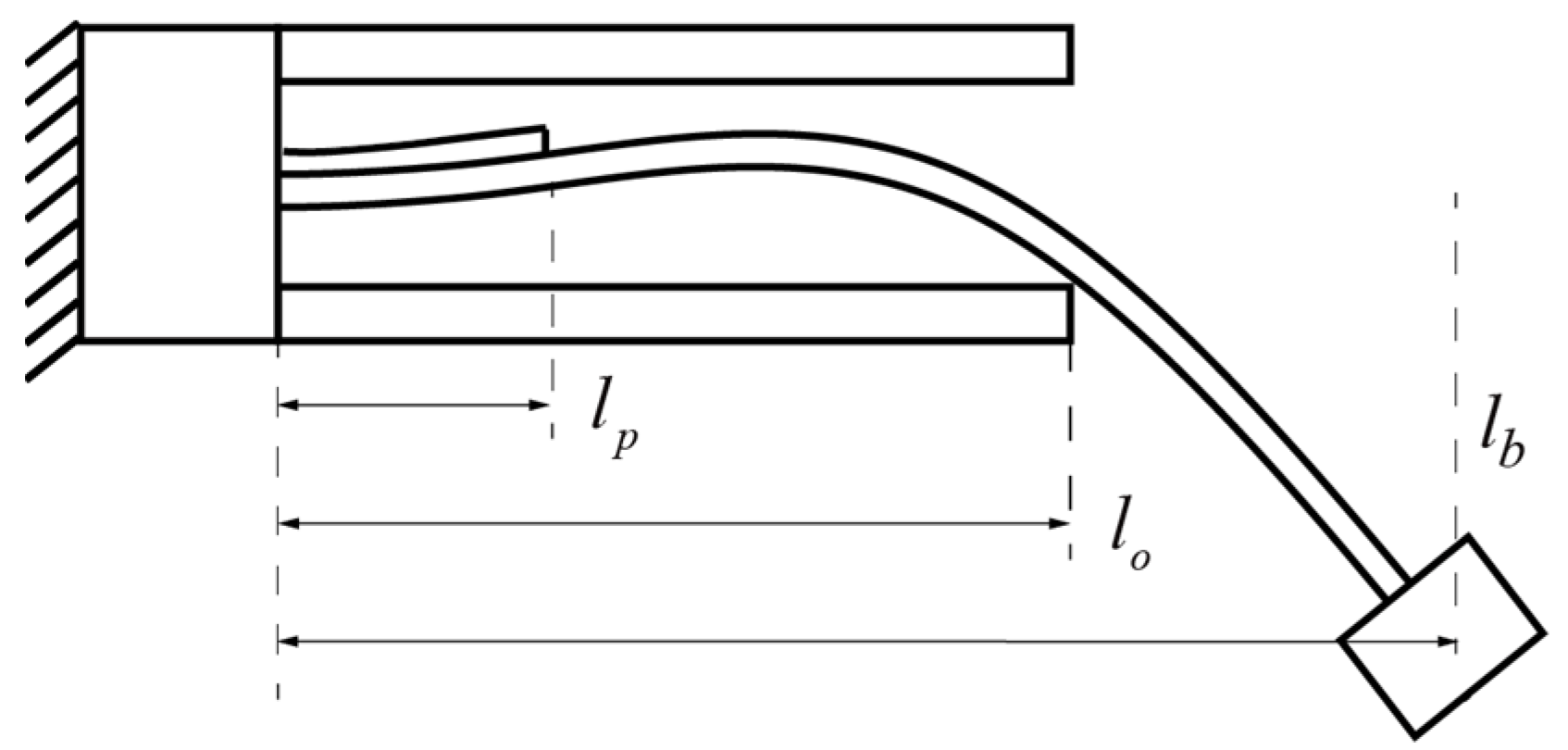
3.1. Theoretical Modeling of Vibration Mode
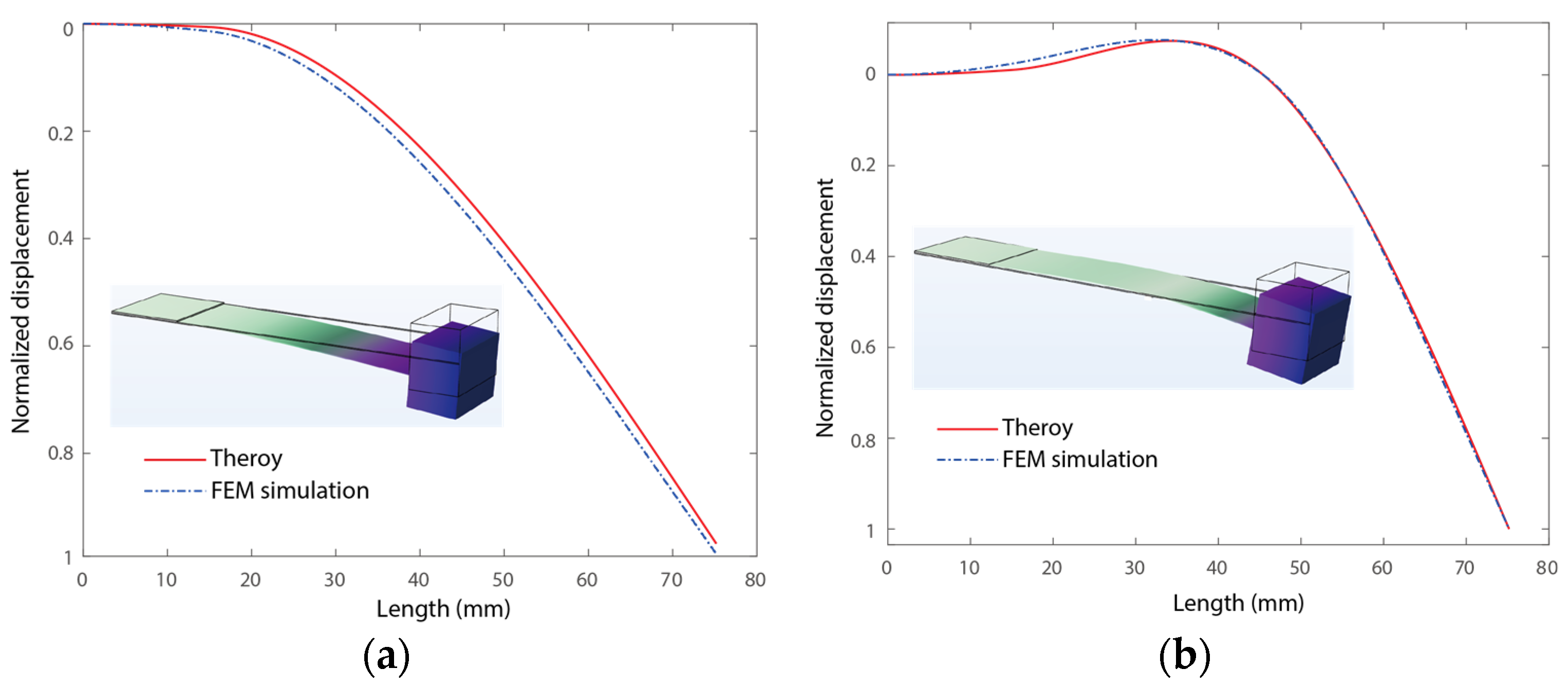
3.2. Vibration Mode Analysis
4. Experimental Studies and Discussions
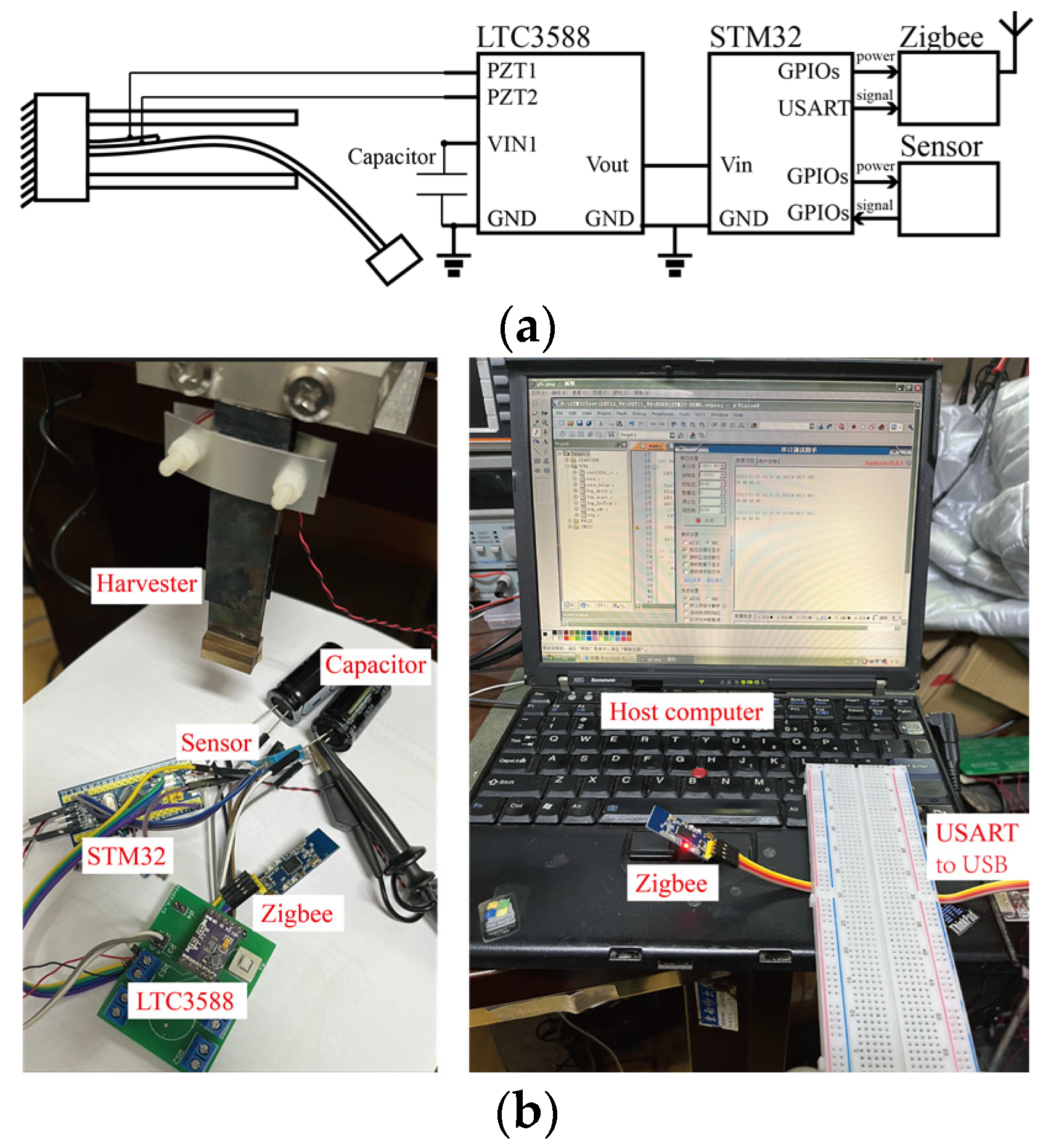
4.1. Experimental Set-Up
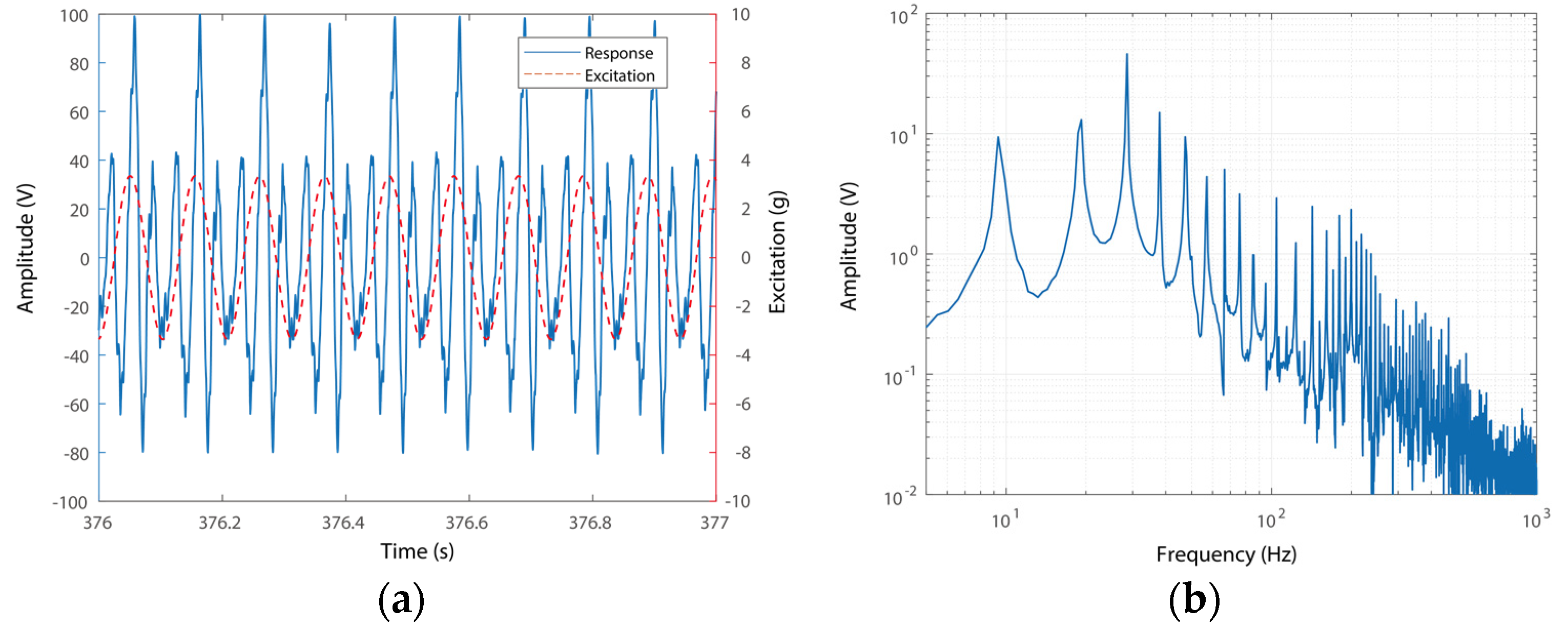
4.2. Triple Frequency Up-Conversion
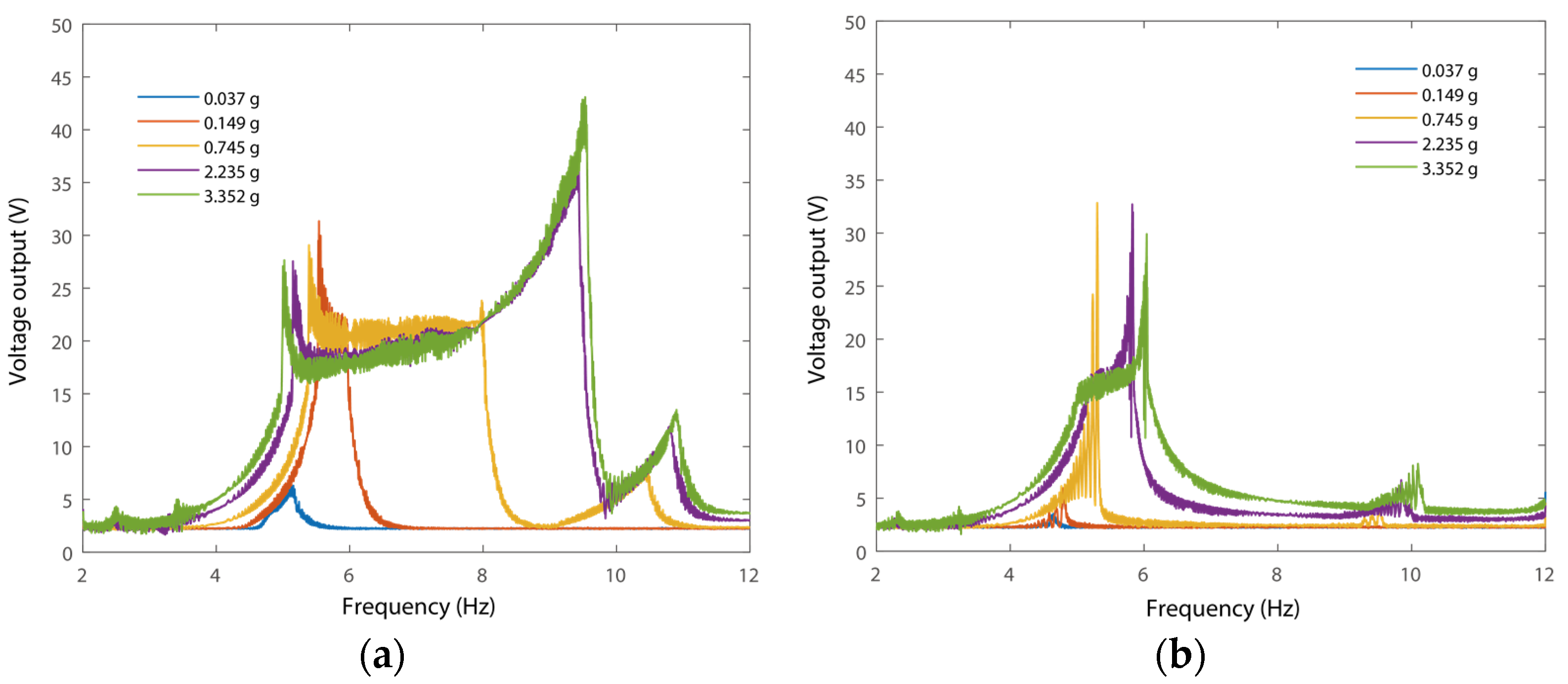
4.3. Frequency Responses
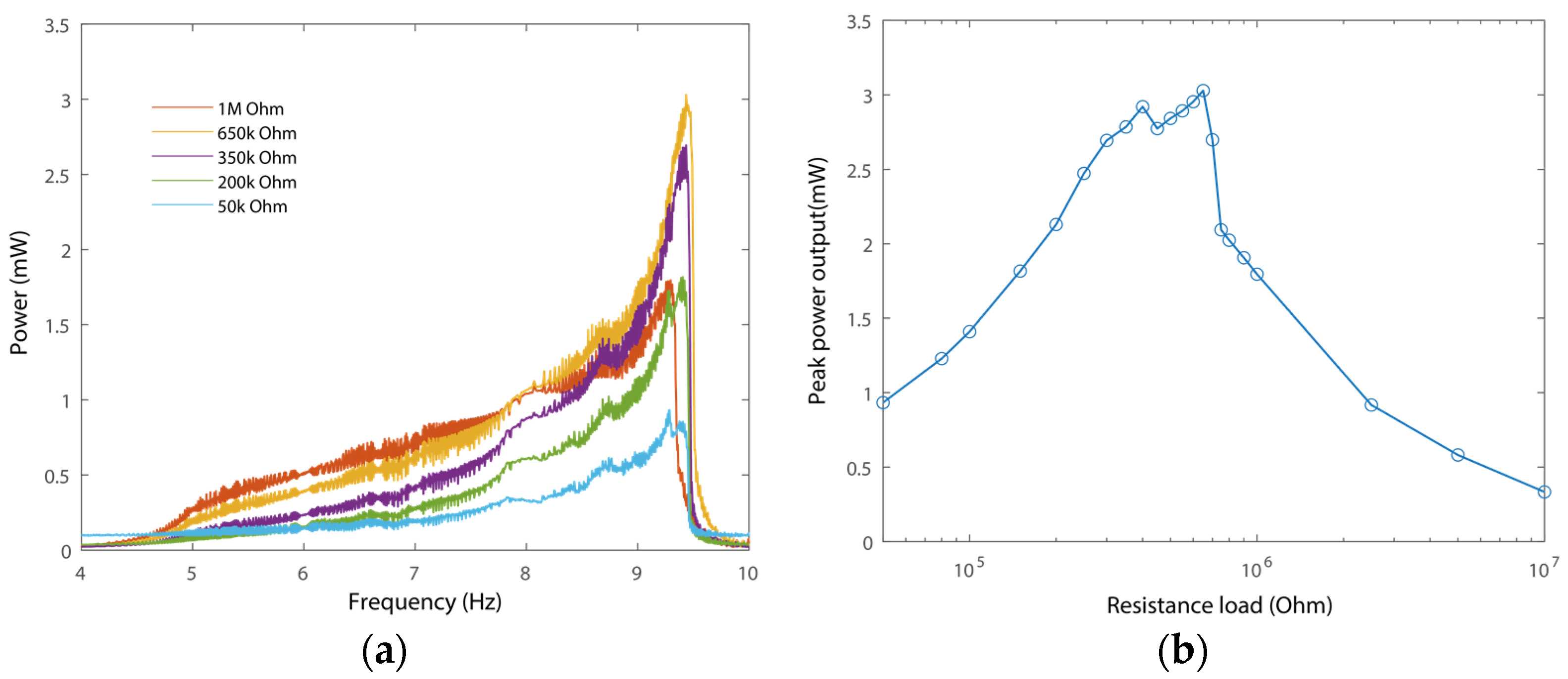
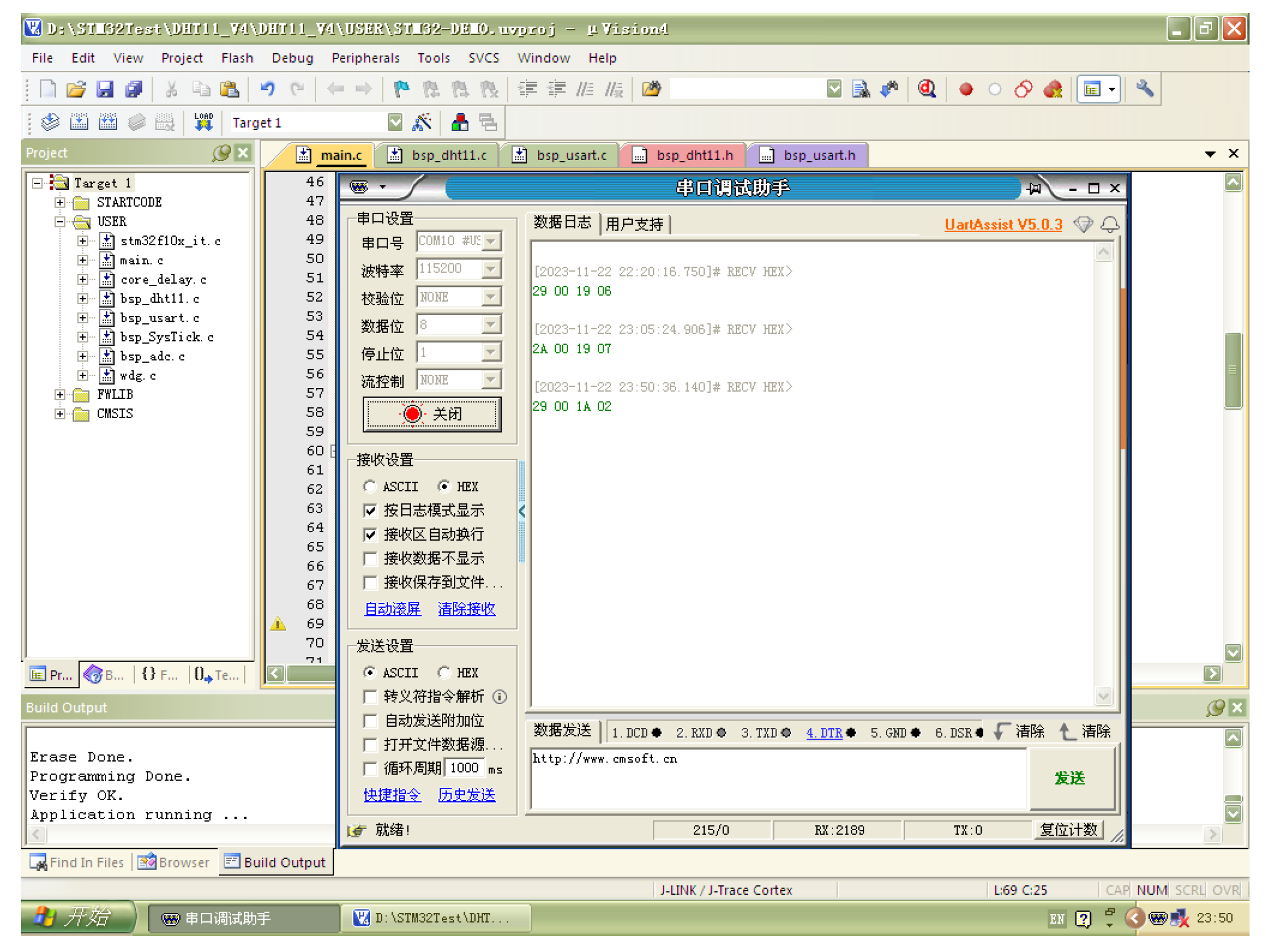
4.4. Case Study of Self-Powered Sensor
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, H.S.; Kim, J.H.; Kim, J. A Review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2018, 96, 1457–1486. [Google Scholar] [CrossRef]
- Paradiso, J.A.; Starner, T. Energy scavenging for mobile and wireless electronics. IEEE Pervas Comput. 2005, 4, 18–27. [Google Scholar] [CrossRef]
- Priya, S. Advances in energy harvesting using low profile piezoelectric transducers. J. Electroceram. 2007, 19, 165–182. [Google Scholar] [CrossRef]
- Roundy, S.; Leland, E.S.; Baker, J.; Carleton, E.; Reilly, E.; Lai, E.; Otis, B.; Rabaey, J.M.; Wright, P.K.; Sundararajan, V. Improving power output for vibration-based energy scavengers. IEEE Pervasive Comput. 2005, 4, 28–36. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Mater. Struct. 2009, 18, 025009. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Toward Broadband Vibration-based Energy Harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1867–1897. [Google Scholar] [CrossRef]
- Challa, V.R.; Prasad, M.G.; Shi, Y.; Fisher, F.T. A vibration energy harvesting device with bidirectional resonance frequency tunability. Smart Mater. Struct. 2008, 17, 015035. [Google Scholar] [CrossRef]
- Al-Ashtari, W.; Hunstig, M.; Hemsel, T.; Sextro, W. Frequency tuning of piezoelectric energy harvesters by magnetic force. Smart Mater. Struct. 2012, 21, 035019. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X. Nonlinear vibration energy harvesting with adjustable stiffness, damping and inertia. Nonlinear Dyn. 2017, 88, 79–95. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.K.; Kobayashi, T.; Tay, C.J.; Quan, C.G. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers. Smart Mater. Struct. 2012, 21, 035005. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y. A nonlinear piezoelectric energy harvester with magnetic oscillator. Appl. Phys. Lett. 2012, 101, 094102. [Google Scholar] [CrossRef]
- Xu, J.W.; Liu, Y.B.; Shao, W.W.; Feng, Z. Optimization of a right-angle piezoelectric cantilever using auxiliary beams with different stiffness levels for vibration energy harvesting. Smart Mater. Struct. 2012, 21, 065017. [Google Scholar] [CrossRef]
- Xu, J.W.; Shao, W.W.; Kong, F.R.; Feng, Z.H. Right-angle piezoelectric cantilever with improved energy harvesting efficiency. Appl. Phys. Lett. 2010, 96, 152904. [Google Scholar] [CrossRef]
- Shao, W.W.; Feng, Z.H.; Xu, J.W.; Pan, C.L.; Liu, Y.B. Radiator heightens power density of piezoelectric transformers. Electron. Lett. 2010, 46, 1662–1663. [Google Scholar] [CrossRef]
- Lan, C.; Qin, W. Enhancing ability of harvesting energy from random vibration by decreasing the potential barrier of bistable harvester. Mech. Syst. Signal Process. 2017, 85, 71–81. [Google Scholar] [CrossRef]
- Cottone, F.; Vocca, H.; Gammaitoni, L. Nonlinear energy harvesting. Phys. Rev. Lett. 2009, 102, 080601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Qin, W.; Zhou, Z.; Zhu, P.; Du, Q. Piezomagnetoelastic energy harvesting from bridge vibrations using bi-stable characteristics. Energy 2023, 263, 125859. [Google Scholar] [CrossRef]
- Lai, Z.; Xu, J.; Fang, S.; Qiao, Z.; Wang, S.; Wang, C.; Huang, Z.; Zhou, S. Energy harvesting from a hybrid piezo-dielectric vibration energy harvester with a self-priming circuit. Energy 2023, 273, 127205. [Google Scholar] [CrossRef]
- Stanton, S.C.; McGehee, C.C.; Mann, B.P. Nonlinear dynamics for broadband energy harvesting: Investigation of a bistable piezoelectric inertial generator. Physica D 2010, 239, 640–653. [Google Scholar] [CrossRef]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Masana, R.; Daqaq, M.F. Relative performance of a vibratory energy harvester in mono- and bi-stable potential. J. Sound Vib. 2011, 330, 6036–6052. [Google Scholar] [CrossRef]
- Leadenham, S.; Erturk, A. Nonlinear M-shaped broadband piezoelectric energy harvester for very low base accelerations: Primary and secondary resonances. Smart Mater. Struct. 2015, 24, 055021. [Google Scholar] [CrossRef]
- Kim, P.; Seok, J. Dynamic and energetic characteristics of a tri-stable magnetopiezoelastic energy harvester. Mech. Mach. Theory 2015, 94, 41–63. [Google Scholar] [CrossRef]
- Shao, N.; Chen, Z.; Wang, X.; Zhang, C.; Xu, J.; Xu, X.; Yan, R. Modeling and analysis of magnetically coupled piezoelectric dual-beam with an annular potential energy function for broadband vibration energy harvesting. Nonlinear Dyn. 2023, 111, 11911–11937. [Google Scholar] [CrossRef]
- Shao, N.; Yang, H.; Huang, Z.; Xu, J.; Xu, X.; Yan, R. Improving energy harvesting by nonlinear dualbeam energy harvester with an annular potential energy function. Smart Mater. Struct. 2023, 32, 015018. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.; Liu, S.; Wang, W.; Lin, J. Impact-induced high-energy orbits of nonlinear energy harvesters. Appl. Phys. Lett. 2015, 106, 093901. [Google Scholar] [CrossRef]
- Zhou, Z.; Qin, W.; Du, W.; Zhu, P.; Liu, Q. Improving energy harvesting from random excitation by nonlinear flexible bi-stable energy harvester with a variable potential energy function Mech. Syst. Signal Process. 2019, 115, 162–172. [Google Scholar] [CrossRef]
- Xu, J.; Tang, J. Multi-directional vibration energy harvesting by internal resonance. Appl. Phys. Lett. 2015, 107, 21. [Google Scholar] [CrossRef]
- Xu, J.; Tang, J. Modeling and analysis of piezoelectric cantilever-pendulum system for multi-directional energy harvesting. J. Intell. Mater. Syst. Struct. 2017, 28, 323–338. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, W. Internal resonance energy harvesting. J. Appl. Mech. 2015, 28, 031004. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, L. Investigation on the characteristics of a novel internal resonance galloping oscillator for concurrent aeroelastic and base vibratory energy harvesting. Mech. Syst. Signal Process. 2022, 173, 109022. [Google Scholar] [CrossRef]
- Xiong, L.; Tang, L.; Mace, B.R. A comprehensive study of 2:1 internal-resonance-based piezoelectric vibration energy harvesting. Nonlinear Dyn. 2018, 91, 1817–1834. [Google Scholar] [CrossRef]
- Shahruz, S.M. Design of mechanical band-pass filters for energy scavenging. J. Sound Vib. 2006, 292, 987–998. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y. Development of a broadband nonlinear two-degree-of-freedom piezoelectric energy harvester. J. Intell. Mater. Syst. Struct. 2014, 25, 1875–1889. [Google Scholar] [CrossRef]
- Kulah, H.; Najafi, K. Energy Scavenging from Low-Frequency Vibrations by Using Frequency Up-Conversion for Wireless Sensor Applications. IEEE Sens. J. 2008, 8, 261–268. [Google Scholar] [CrossRef]
- Fu, H.; Yeatman, E.M. Rotational energy harvesting using bi-stability and frequency-up converting for low-power sensing applications: Theoretical modeling and experimental validation. Mech. Syst. Signal Process. 2019, 125, 229–244. [Google Scholar] [CrossRef]
- Haroun, A.; Yamada, I.; Warisawa, S. Study of electromagnetic vibration energy harvesting with free/impact motion for low frequency operation. J. Sound Vib. 2015, 349, 389–402. [Google Scholar] [CrossRef]
- Cook-Chennault, K.A.; Thambi, N.; Sastry, A.M. Powering MEMS portable devices–a review of non-regenerative and regenerative power supply systems with special emphasis on piezoelectric energy harvesting systems. Smart Mater. Struct. 2008, 17, 043001. [Google Scholar] [CrossRef]
- Williams, C.B.; Yates, R.B. Analysis of micro-electric generator for microsystems. Sens. Actuators A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Renaud, M.; Fiorini, P.; Schaijk, R.; Hoof, C. Harvesting energy from the motion of human limbs: The design and analysis of an impact based piezoelectric generator. Smart Mater. Struct. 2009, 18, 035001. [Google Scholar] [CrossRef]
- Maamer, B.; El-Bab, A.M.F.; Tounsi, F. Impact-driven frequency-up converter based on high flexibility quasi-concertina spring for vibration energy harvesting. Energy Convers. Manag. 2022, 274, 116460. [Google Scholar] [CrossRef]
- Sun, R.; Zhou, S.; Cheng, L. Ultra-low frequency vibration energy harvesting: Mechanisms, enhancement techniques, and scaling laws. Energy Convers. Manag. 2023, 276, 116585. [Google Scholar] [CrossRef]
- Ashraf, K.; Khir, M.H.M.; Dennis, J.O.; Baharudin, Z. A wideband, frequency up-converting bounded vibration energy harvester for a low-frequency environment. Smart Mater. Struct. 2013, 22, 049601. [Google Scholar] [CrossRef]
- Halim, M.A.; Park, J.Y. Theoretical modeling and analysis of mechanical impact driven and frequency up-converted piezoelectric energy harvester for low-frequency and wide-bandwidth operation. Sens. Actuators A Phys. 2014, 208, 56–65. [Google Scholar] [CrossRef]
- Hasani, M.; Khazaee, M.; Huber, J.; Rosendahl, L.; Rezania, A. Design and analytical evaluation of an impact-based four-point bending configuration for piezoelectric energy harvesting. Appl. Energy 2023, 347, 121461. [Google Scholar] [CrossRef]
- Xu, J.; Li, S.; Tang, J. Customized Shaping of Vibration Modes by Acoustic Metamaterial Synthesis. Smart Mater. Struct. 2018, 27, 045001. [Google Scholar] [CrossRef]
- Rahman, M.; Sohel Rana, S.M.; Salauddin Md Maharjan, P.; Bhatta, T.; Kim, H.; Cho, H.; Park, J. A highly miniaturized freestanding kinetic-impact-based non-resonant hybridized electromagnetic-triboelectric nanogenerator for human induced vibrations harvesting. Appl. Energy 2020, 279, 115799. [Google Scholar] [CrossRef]
- Xu, J.; Xia, D.; Lai, Z.; Chen, G.; Dai, W.; Wang, J.; Yang, H. Experimental Study of Vibration Modes Switching based Triple Frequency-up Converting Energy Harvesting with Pre-biased Displacement. Smart Mater. Struct. 2024, 33, 045035. [Google Scholar] [CrossRef]







| Refs. | Mechanism | Volume | Power | Continuous Frequency Up-Conversion |
|---|---|---|---|---|
| [42] | Impact-based | 14 cm3 | 600 μW /42.8 μW cm−3 | No |
| [45] | Impact-based | 27.38 cm3 | 2.68 mW /65.74 μW cm−3 | No |
| [46] | Impact-based | 18.9 cm3 | 734 μW /38.8 μW cm−3 | No |
| This work | Vibration mode switching | 6.01 cm3 | 3.03 mW /504.16 μW cm−3 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Liu, Z.; Dai, W.; Zhang, R.; Ge, J. Modeling and Experimental Study of Vibration Energy Harvester with Triple-Frequency-Up Voltage Output by Vibration Mode Switching. Micromachines 2024, 15, 1013. https://doi.org/10.3390/mi15081013
Xu J, Liu Z, Dai W, Zhang R, Ge J. Modeling and Experimental Study of Vibration Energy Harvester with Triple-Frequency-Up Voltage Output by Vibration Mode Switching. Micromachines. 2024; 15(8):1013. https://doi.org/10.3390/mi15081013
Chicago/Turabian StyleXu, Jiawen, Zhikang Liu, Wenxing Dai, Ru Zhang, and Jianjun Ge. 2024. "Modeling and Experimental Study of Vibration Energy Harvester with Triple-Frequency-Up Voltage Output by Vibration Mode Switching" Micromachines 15, no. 8: 1013. https://doi.org/10.3390/mi15081013
APA StyleXu, J., Liu, Z., Dai, W., Zhang, R., & Ge, J. (2024). Modeling and Experimental Study of Vibration Energy Harvester with Triple-Frequency-Up Voltage Output by Vibration Mode Switching. Micromachines, 15(8), 1013. https://doi.org/10.3390/mi15081013






