Online Handwriting Recognition Method with a Non-Inertial Reference Frame Based on the Measurement of Linear Accelerations and Differential Geometry: An Alternative to Quaternions
Abstract
:1. Introduction
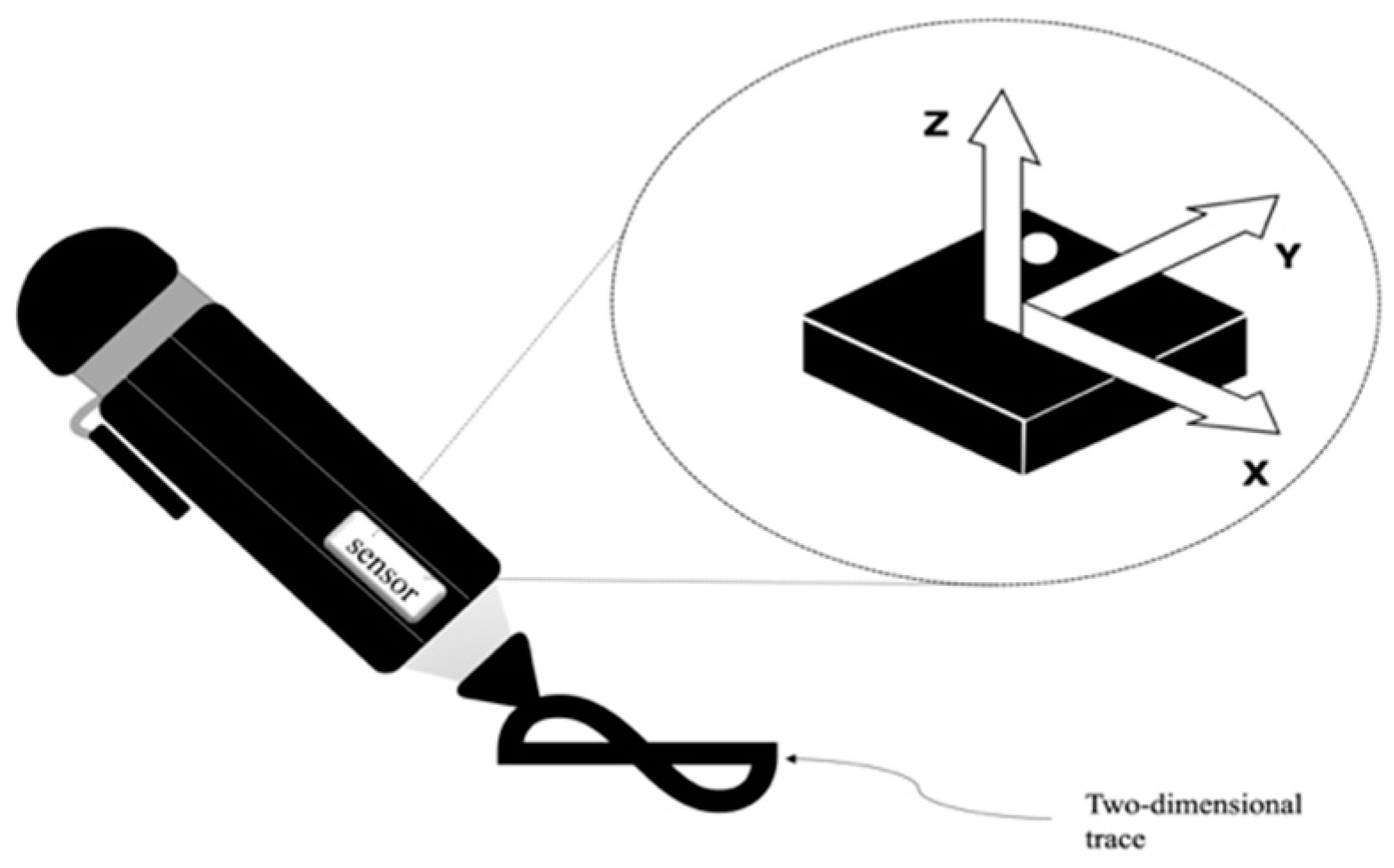
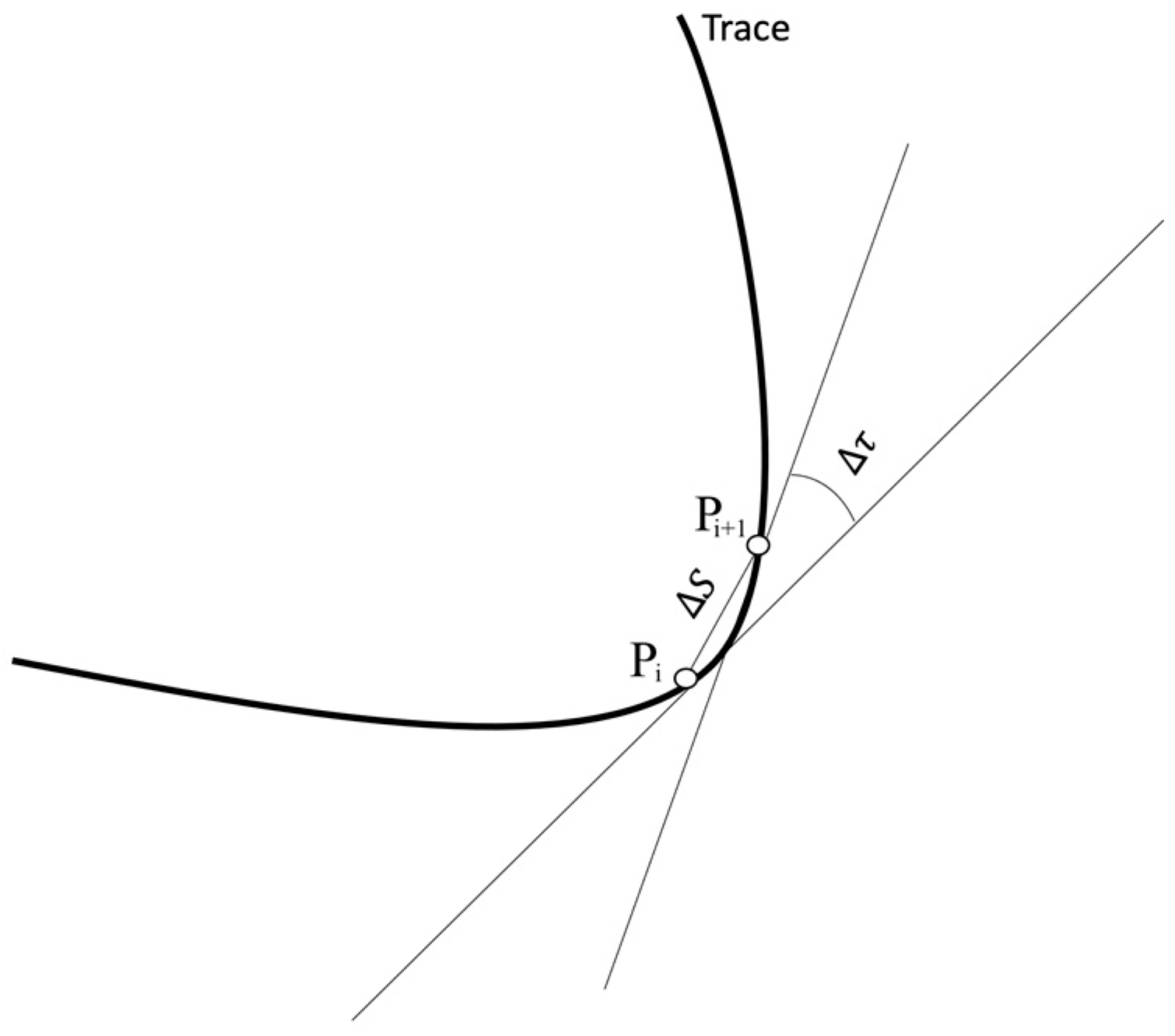
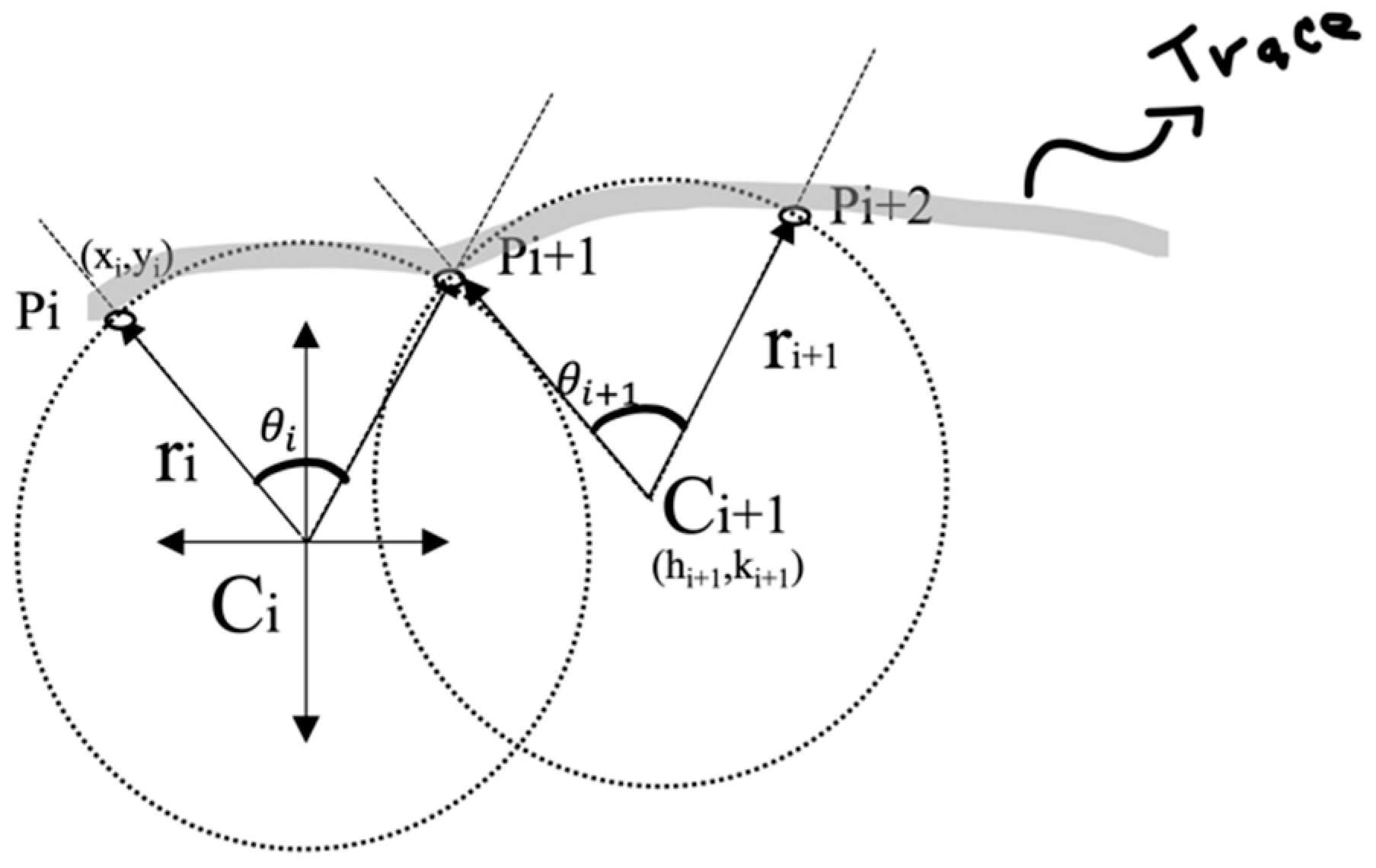
2. Materials and Methods
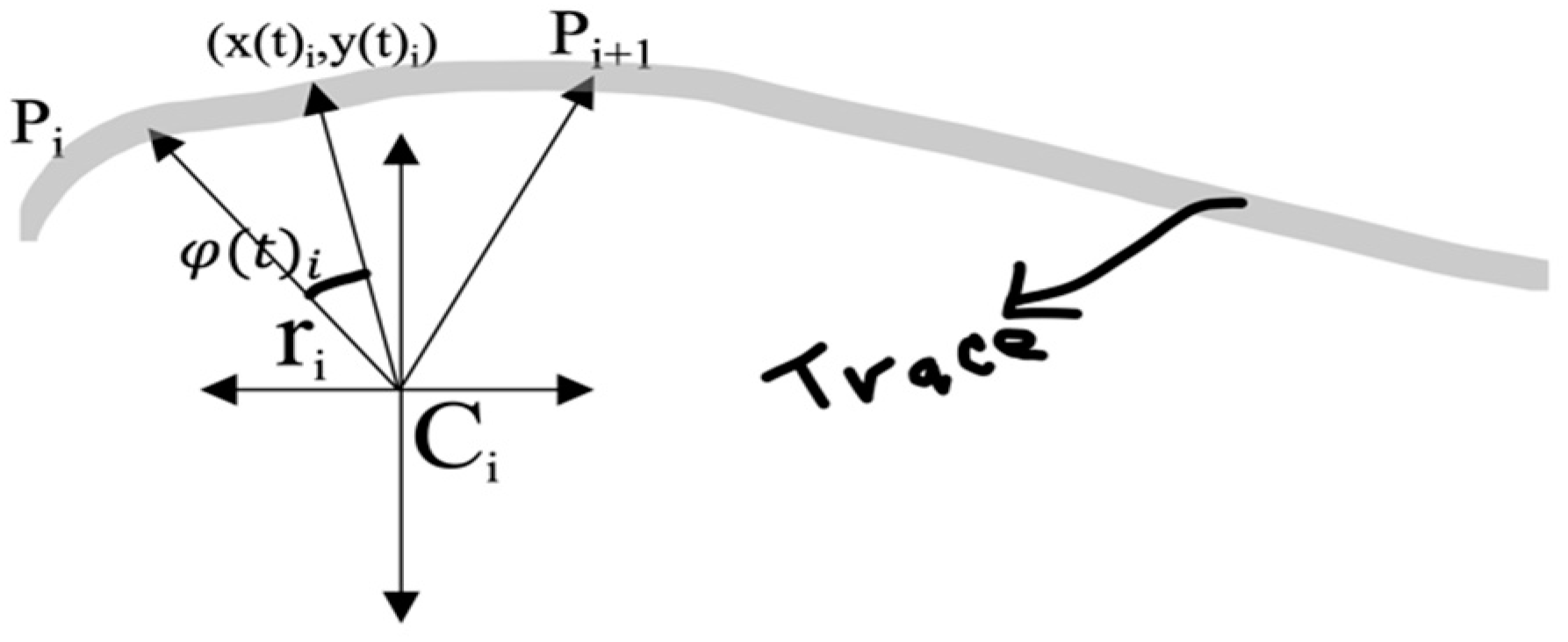
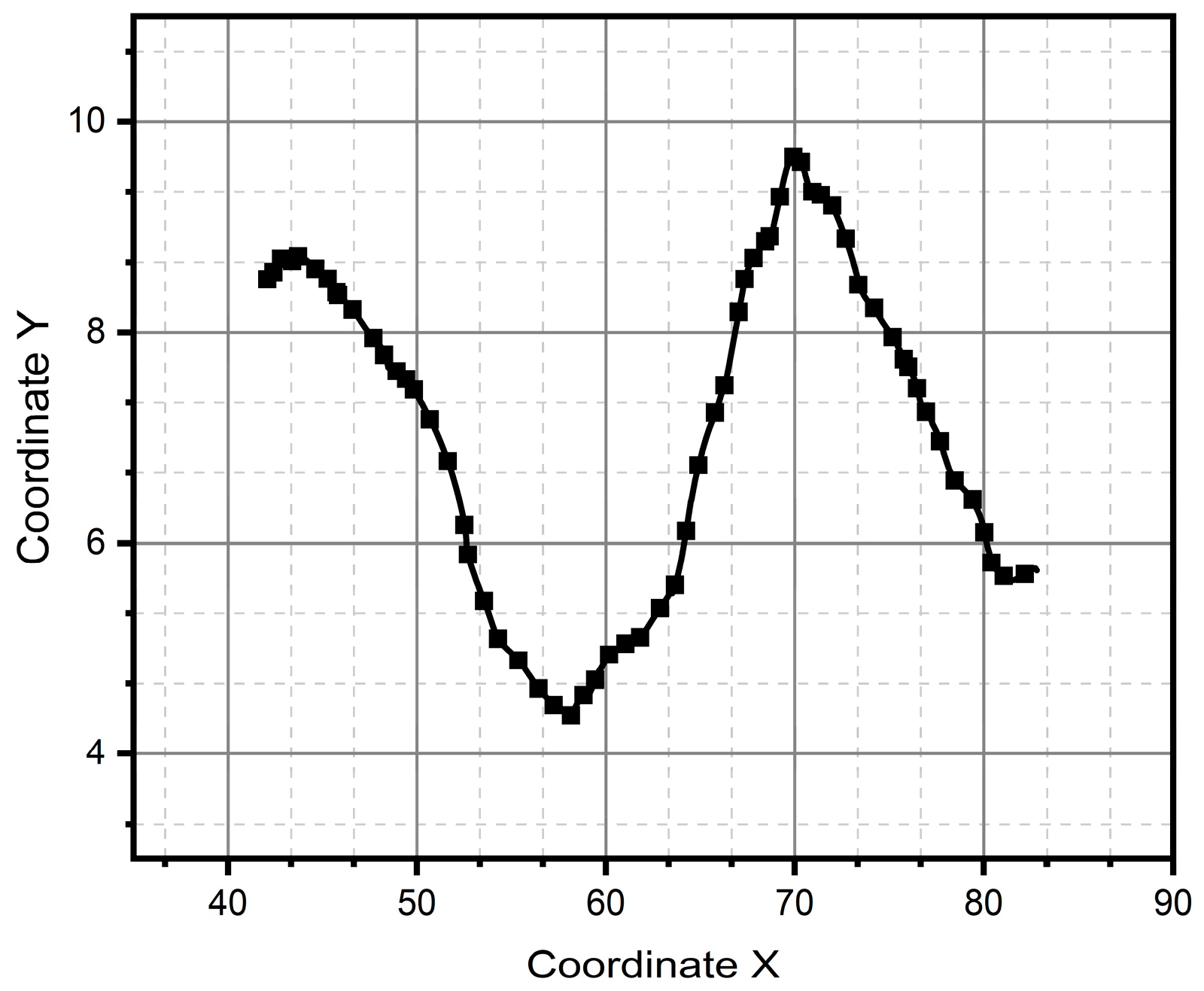
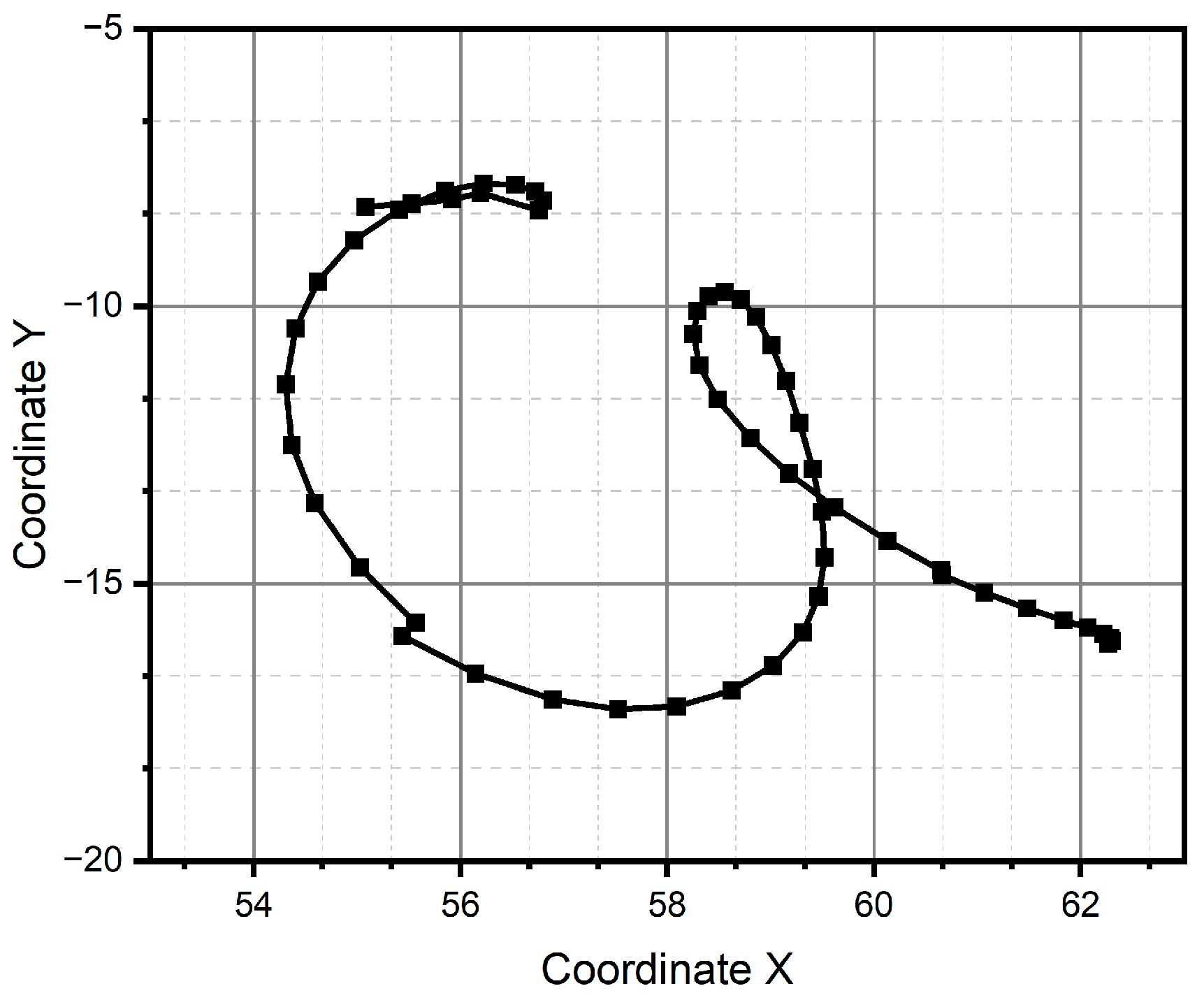
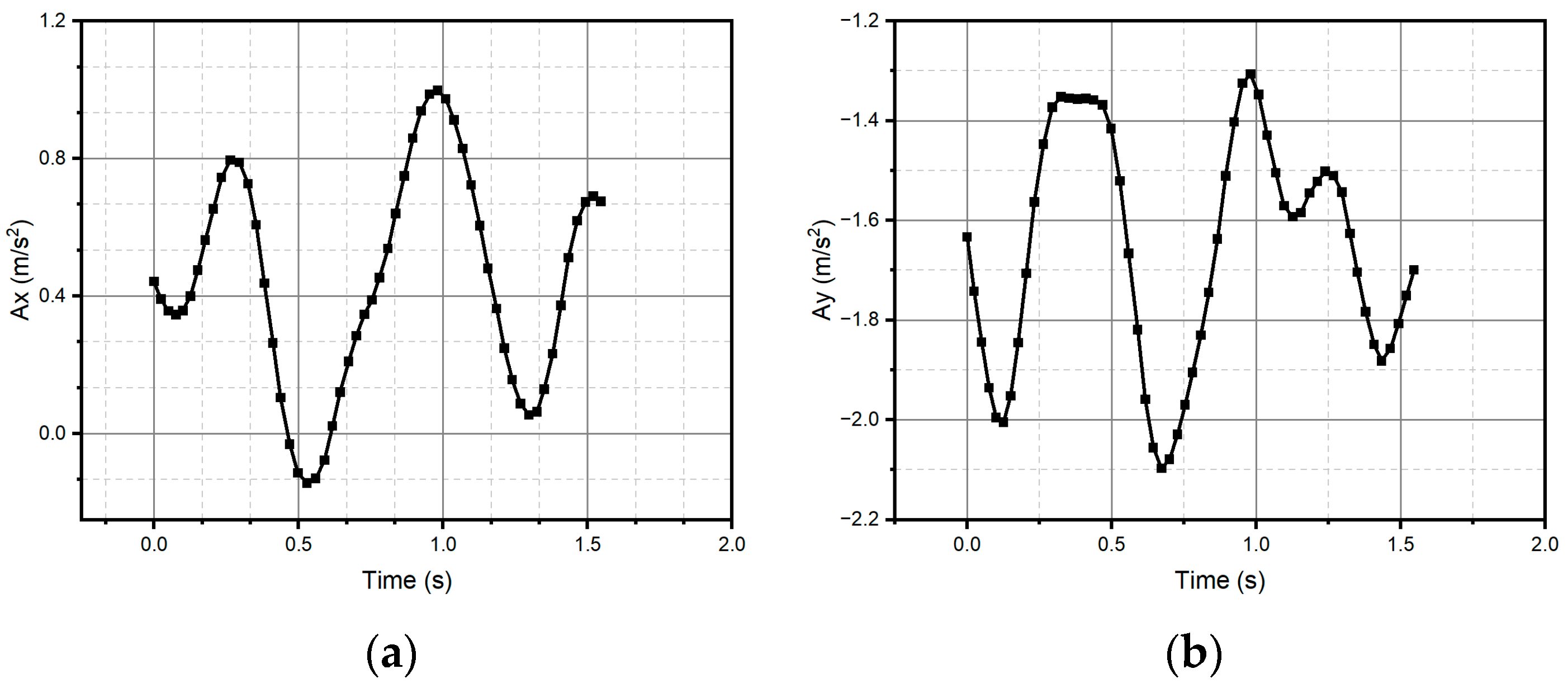
3. Results
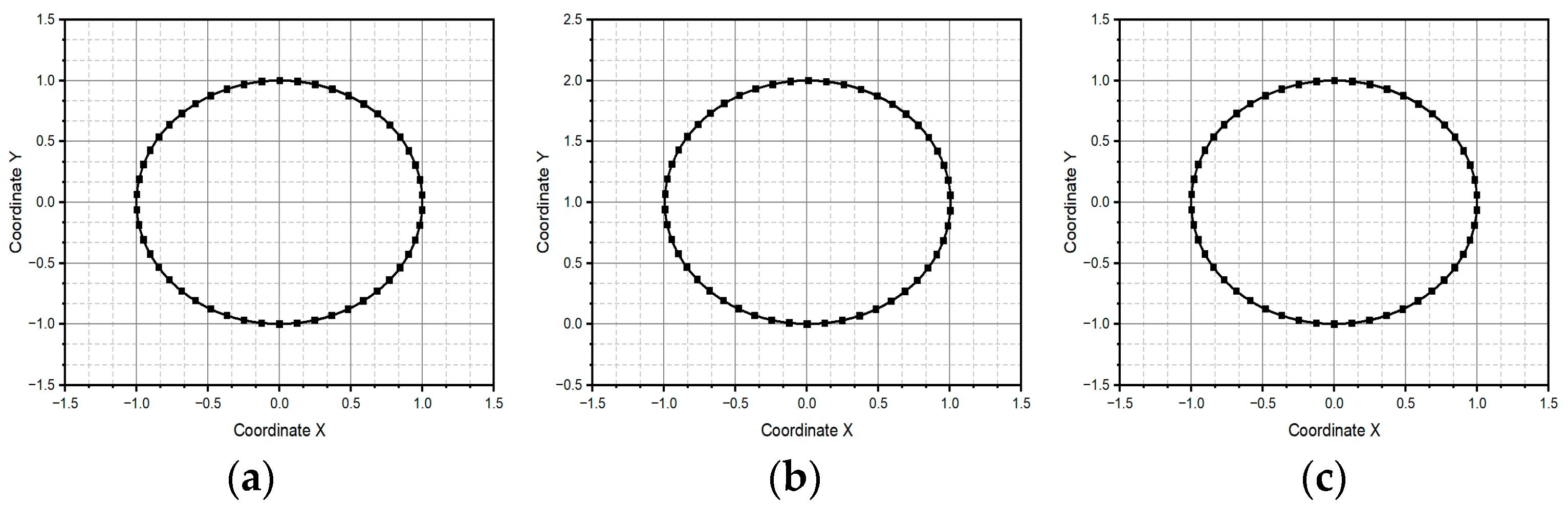
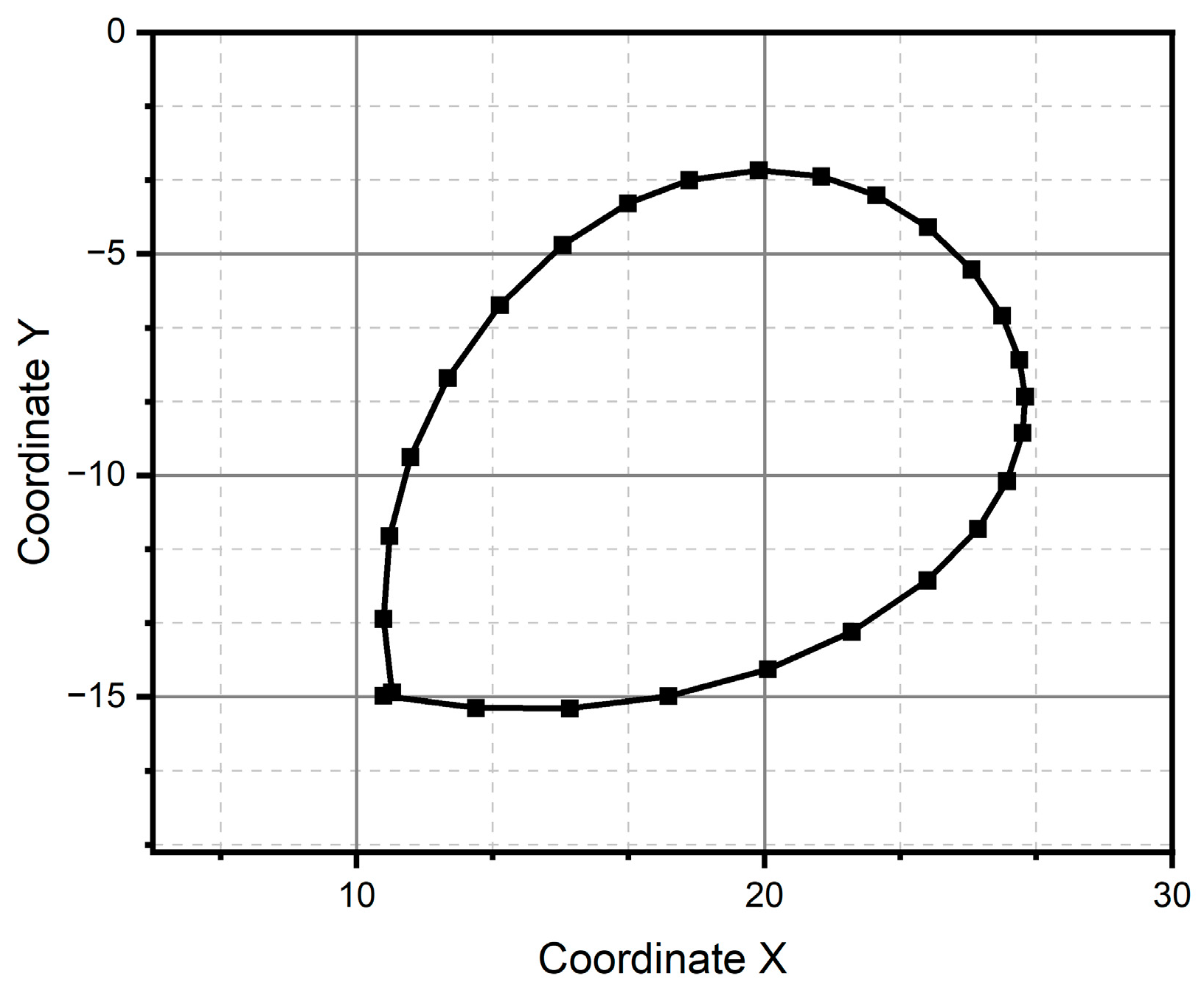
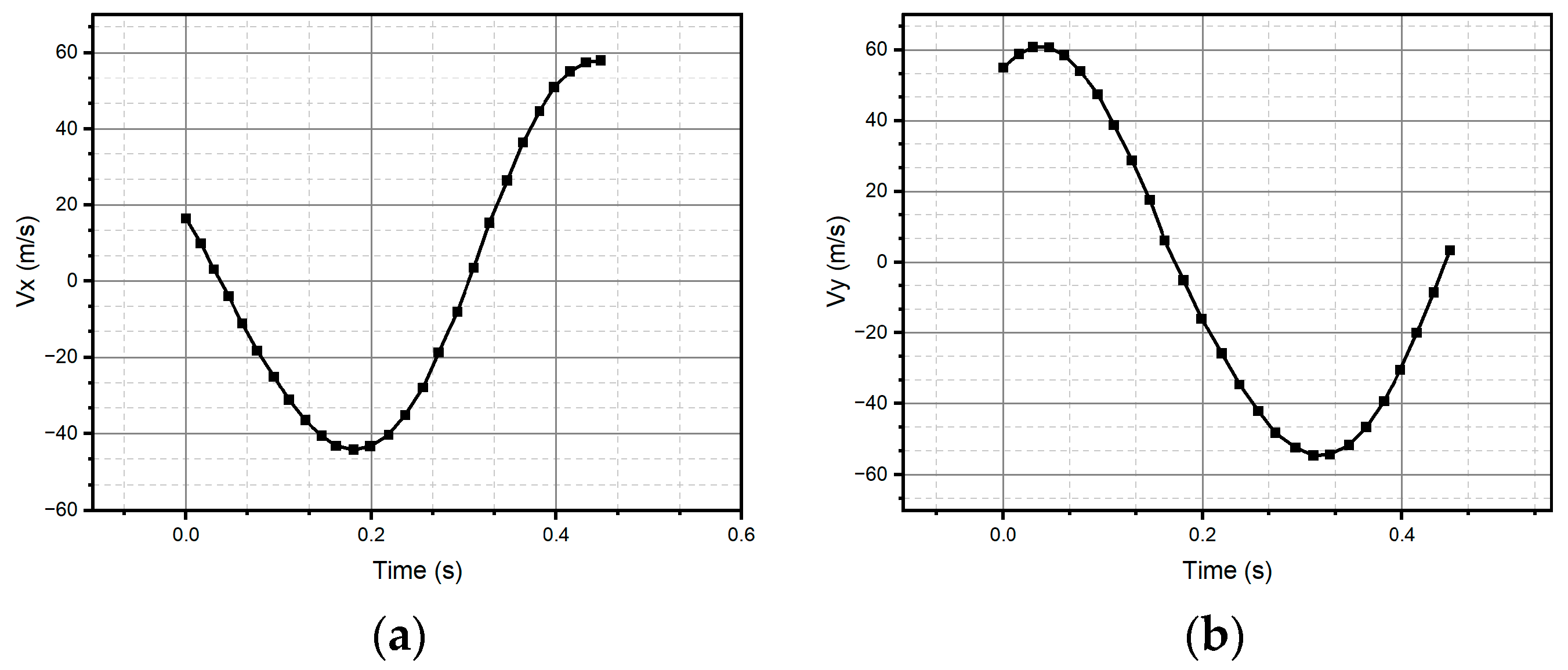
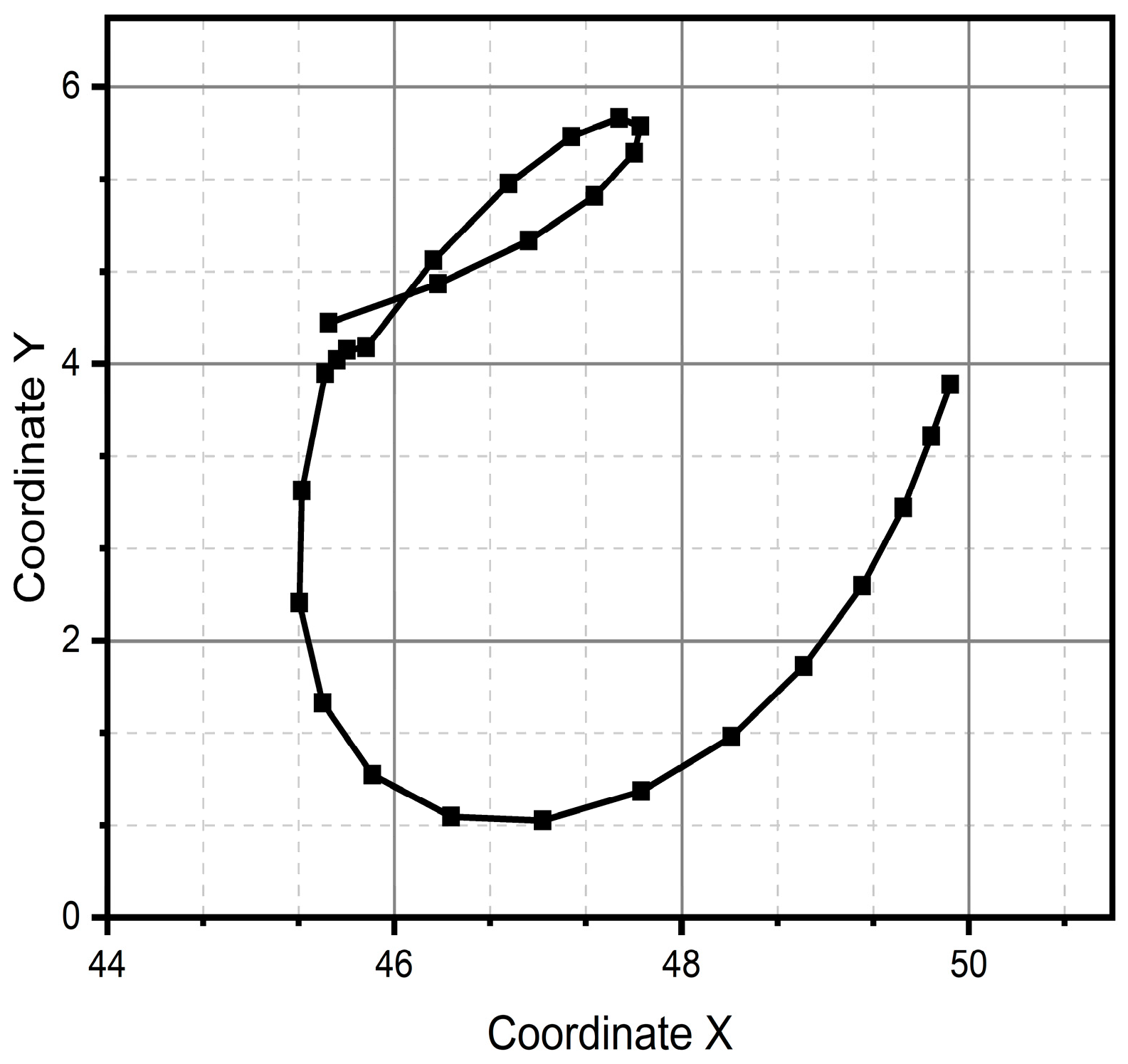
3.1. Simulation
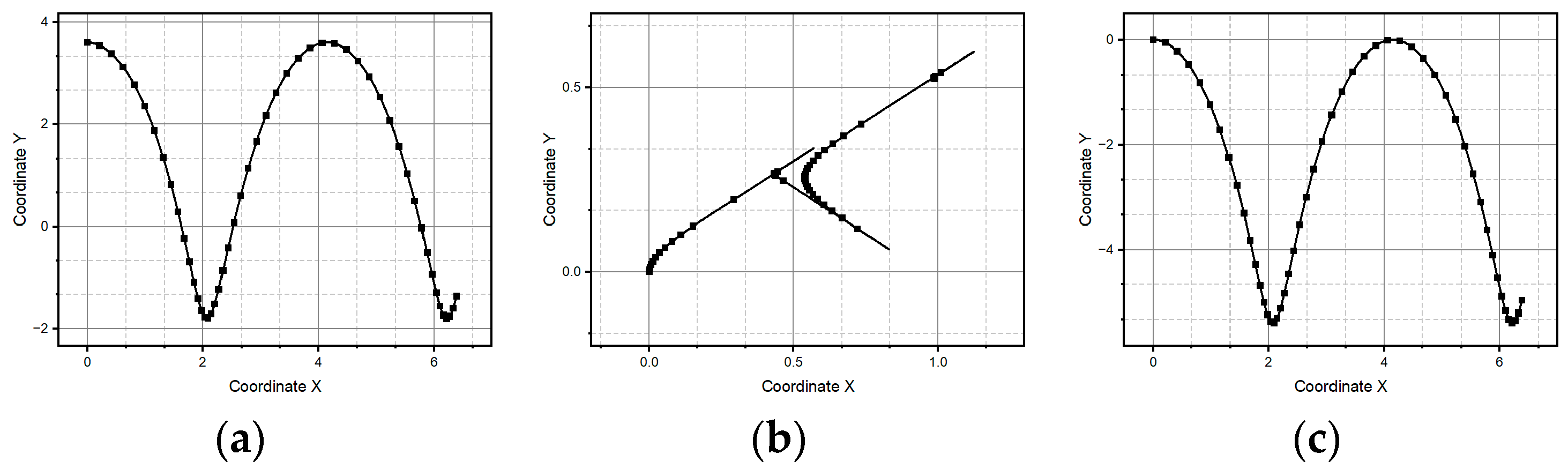


3.2. Experimental Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bu, Y.; Xie, L.; Yin, Y.; Wang, C.; Ning, J.; Cao, J.; Lu, S. Handwriting-Assistant: Reconstructing Continuous Strokes with Millimeter-level Accuracy via Attachable Inertial Sensors. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2021, 5, 146–170. [Google Scholar]
- Zhao, B.; Tao, J.; Yang, M.; Tian, Z.; Fan, C.; Bai, Y. Deep imitator: Handwriting calligraphy imitation via deep attention networks. Pettern Recognit. 2020, 104, 107080. [Google Scholar]
- Gao, X.; Zhou, C.; Chao, F.; Yang, L.; Lin, C.M.; Xu, T.; Shang, C.; Shen, Q. A data-driven robotic Chinese calligraphy system using convolutional auto-encoder and differential evolution. Knowl.-Based Syst. 2019, 182, 104802. [Google Scholar]
- Phang, S.K.; Lai, S.; Wang, F.; Lan, M.; Chen, B.M. Systems design and implementation with jerk-optimized trajectory generation for UAV calligraphy. Mechatronics 2015, 30, 65–75. [Google Scholar]
- Choudhury, H.; Prasanna, S.M. Representation of online handwriting using multi-component sinusoidal model. Pattern Recognit. 2019, 91, 200–215. [Google Scholar]
- Ltaief, M.; Bezine, H.; Alimi, A.M. A Spiking Neural Network Model with Fuzzy Learning Rate Application for Complex Handwriting Movements Generation. In International Conference on Hybrid Intelligent Systems, Proceedings of the 16th International Conference on Hybrid Intelligent Systems (HIS 2016), Marrakech, Morocco, 21–23 November 2016; Springer: Cham, Switzerland, 2017; Volume 552. [Google Scholar]
- Qian, Z.; Huang, K.; Wang, Q.-F.; Xiao, J.; Zhang, R. Generative adversarial classifier for handwriting characters super-resolution. Pattern Recognit. 2020, 107, 107453. [Google Scholar]
- Al-Omari, F.A.; Al-Jarrah, O. Handwritten Indian numerals recognition system using probabilistic neural networks. Adv. Eng. Inform. 2004, 18, 9–16. [Google Scholar]
- Fadl, S.; Hosny, K.M.; Hammad, M. Automatic fake document identification and localization using DE-Net and color-based features of foreign inks. J. Vis. Commun. Image Represent. 2023, 92, 103801. [Google Scholar]
- Nicole, D.C.; Giuseppe, D.G.; Claudio, D.S.; Francesco, F.; Angelo, M.; Antonio, P. Diagnosing Alzheimer’s disease from on-line handwriting: A novel dataset and performance benchmarking. Eng. Appl. Artif. Intell. 2022, 111, 104822. [Google Scholar] [CrossRef]
- Erdogmus, P.; Kabakus, A.T. The promise of convolutional neural networks for the early diagnosis of the Alzheimer’s disease. Eng. Appl. Artif. Intell. 2023, 123, 106254. [Google Scholar] [CrossRef]
- Masaki, M. Electronic Pen, Handwriting Output System and Control State Detection Method. Patent JP2004199591A, 15 July 2004. Available online: https://patents.google.com/patent/JP2004199591A/ja (accessed on 4 March 2024).
- Zhang, L.; Shang, H.; Lin, Y. A Novel Distribution for Representation of 6D Pose Uncertainty. Micromachines 2022, 13, 126. [Google Scholar] [CrossRef]
- Liu, M.; Cai, Y.; Zhang, L.; Wang, Y. Attitude Estimation Algorithm of Portable Mobile Robot Based on Complementary Filter. Micromachines 2021, 12, 1373. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xu, X.; Luo, Y.; Wang, G.; Yang, Y. Hypercomplex context guided interaction modeling for scene graph generation. Pattern Recognit. 2023, 141, 109634. [Google Scholar] [CrossRef]
- Song, T.; Xin, L.; Gao, C.; Zhang, T.; Huang, Y. Quaternionic extended local binary pattern with adaptive structural pyramid pooling for color image representation. Pattern Recognit. 2021, 115, 107891. [Google Scholar] [CrossRef]
- Shao, Z.; Shu, H.; Wu, J.; Chen, B.; Coatrieux, J.L. Quaternion Bessel–Fourier moments and their invariant descriptors for object reconstruction and recognition. Pattern Recognit. 2014, 47, 603–611. [Google Scholar] [CrossRef]
- Pan, L.; Deng, Y.; Cheong, K.H. Quaternion model of Pythagorean fuzzy sets and its distance measure. Expert Syst. Appl. 2023, 213, 119222. [Google Scholar] [CrossRef]
- Świtoński, A.; Josiński, H.; Michalczuk, A.; Wojciechowski, K. Quaternion statistics applied to the classification of motion capture data. Expert Syst. Appl. 2021, 164, 113813. [Google Scholar] [CrossRef]
- Wang, R.; Feng, Q. Weighted Convolution for Quaternion Linear Canonical Cosine Transform and Its Application. Axioms 2024, 13, 402. [Google Scholar] [CrossRef]
- Liu, X.; Shi, T.; Zhang, Y. Solution to Several Split Quaternion Matrix Equations. Mathematics 2024, 12, 1707. [Google Scholar] [CrossRef]
- Jang, J.; Ban, Y.; Lee, K. Dual-Modality Cross-Interaction-Based Hybrid Full-Frame Video Stabilization. Appl. Sci. 2024, 14, 4290. [Google Scholar] [CrossRef]
- Zheng, J.; Zhu, J.; Xi, H. Short-term energy consumption prediction of electric vehicle charging station using attentional feature engineering and multi-sequence stacked Gated Recurrent Unit. Comput. Electr. Eng. 2023, 108, 108694. [Google Scholar]
- Oprea, S.-V.; Bâra, A. Machine learning classification algorithms and anomaly detection in conventional meters and Tunisian electricity consumption large datasets. Comput. Electr. Eng. 2021, 94, 107329. [Google Scholar]
- Manzari, O.N.; Kashiani, H.; Dehkordi, H.A.; Shokouhi, S.B. Robust transformer with locality inductive bias and feature normalization. Eng. Sci. Technol. Int. J. 2023, 38, 101320. [Google Scholar]



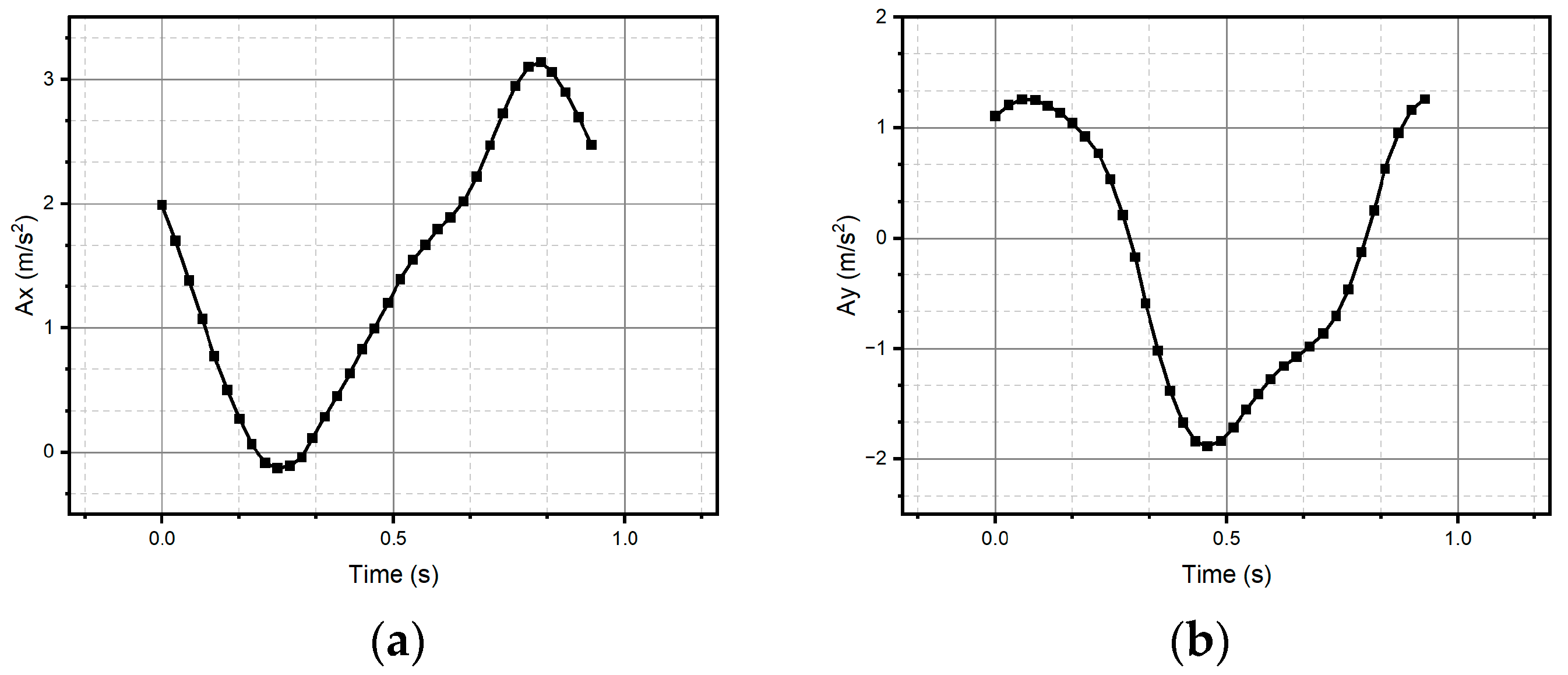


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abarca Jiménez, G.S.; Muñoz Garnica, C.C.; Reyes Barranca, M.A.; Mares Carreño, J.; Vega Blanco, M.V.; Gutiérrez Galicia, F. Online Handwriting Recognition Method with a Non-Inertial Reference Frame Based on the Measurement of Linear Accelerations and Differential Geometry: An Alternative to Quaternions. Micromachines 2024, 15, 1053. https://doi.org/10.3390/mi15081053
Abarca Jiménez GS, Muñoz Garnica CC, Reyes Barranca MA, Mares Carreño J, Vega Blanco MV, Gutiérrez Galicia F. Online Handwriting Recognition Method with a Non-Inertial Reference Frame Based on the Measurement of Linear Accelerations and Differential Geometry: An Alternative to Quaternions. Micromachines. 2024; 15(8):1053. https://doi.org/10.3390/mi15081053
Chicago/Turabian StyleAbarca Jiménez, Griselda Stephany, Carmen Caritina Muñoz Garnica, Mario Alfredo Reyes Barranca, Jesús Mares Carreño, Manuel Vladimir Vega Blanco, and Francisco Gutiérrez Galicia. 2024. "Online Handwriting Recognition Method with a Non-Inertial Reference Frame Based on the Measurement of Linear Accelerations and Differential Geometry: An Alternative to Quaternions" Micromachines 15, no. 8: 1053. https://doi.org/10.3390/mi15081053
APA StyleAbarca Jiménez, G. S., Muñoz Garnica, C. C., Reyes Barranca, M. A., Mares Carreño, J., Vega Blanco, M. V., & Gutiérrez Galicia, F. (2024). Online Handwriting Recognition Method with a Non-Inertial Reference Frame Based on the Measurement of Linear Accelerations and Differential Geometry: An Alternative to Quaternions. Micromachines, 15(8), 1053. https://doi.org/10.3390/mi15081053






