Development of Highly Sensitive and Thermostable Microelectromechanical System Pressure Sensor Based on Array-Type Aluminum–Silicon Hybrid Structures
Abstract
:1. Introduction
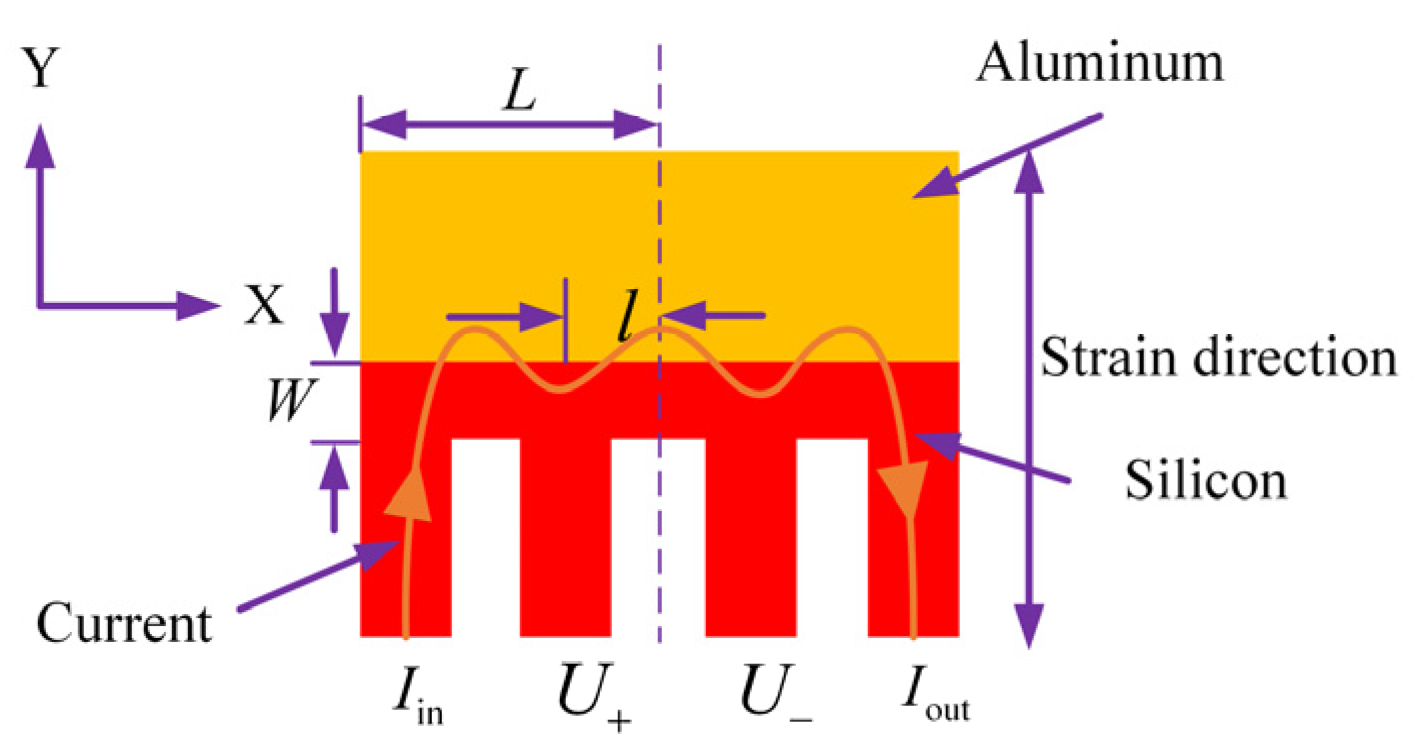
2. Principle of Hybrid Structure
3. Realization of Array-Type Sensor
3.1. Structure Design of the Array-Type Sensor
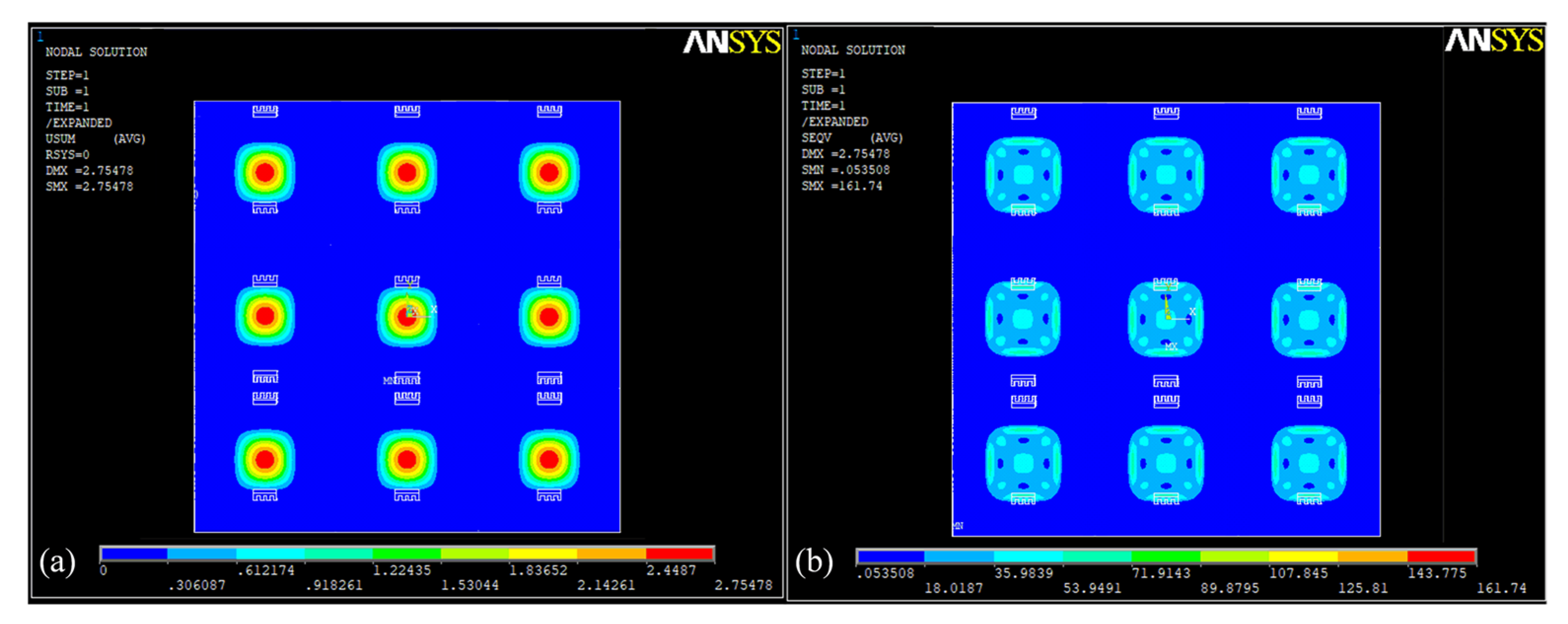
3.2. Finite Element Analysis
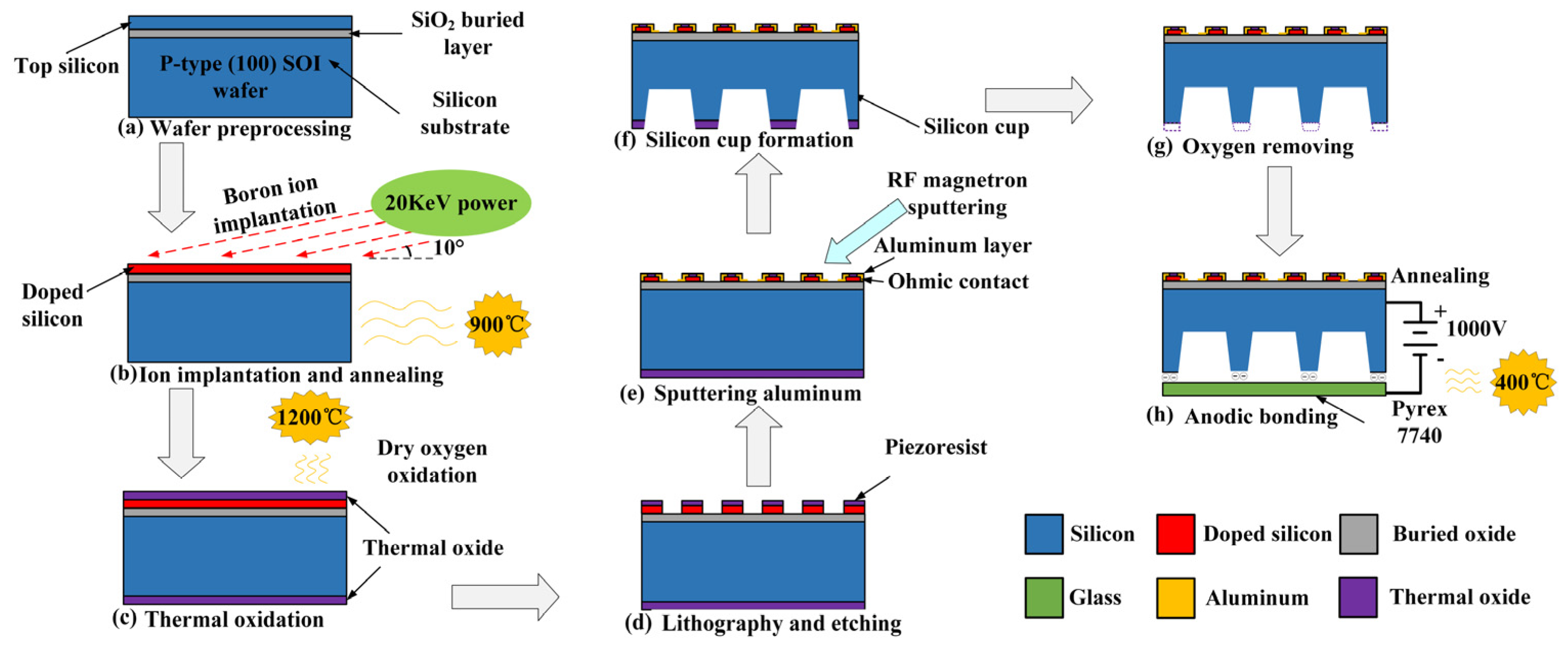
3.3. Process Flow and Packing Design
4. Experiment Results and Discussion
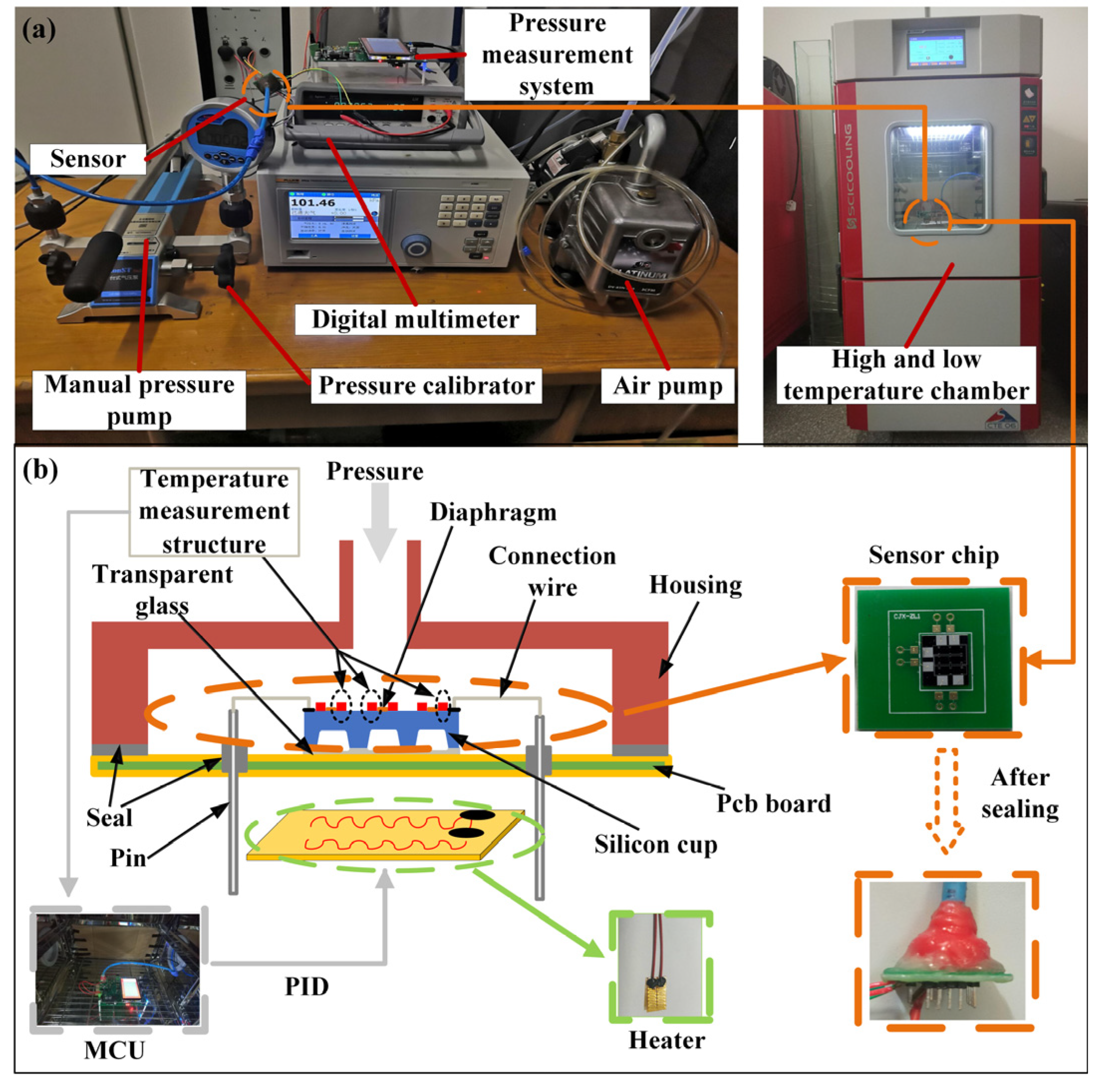
4.1. Platform Construction
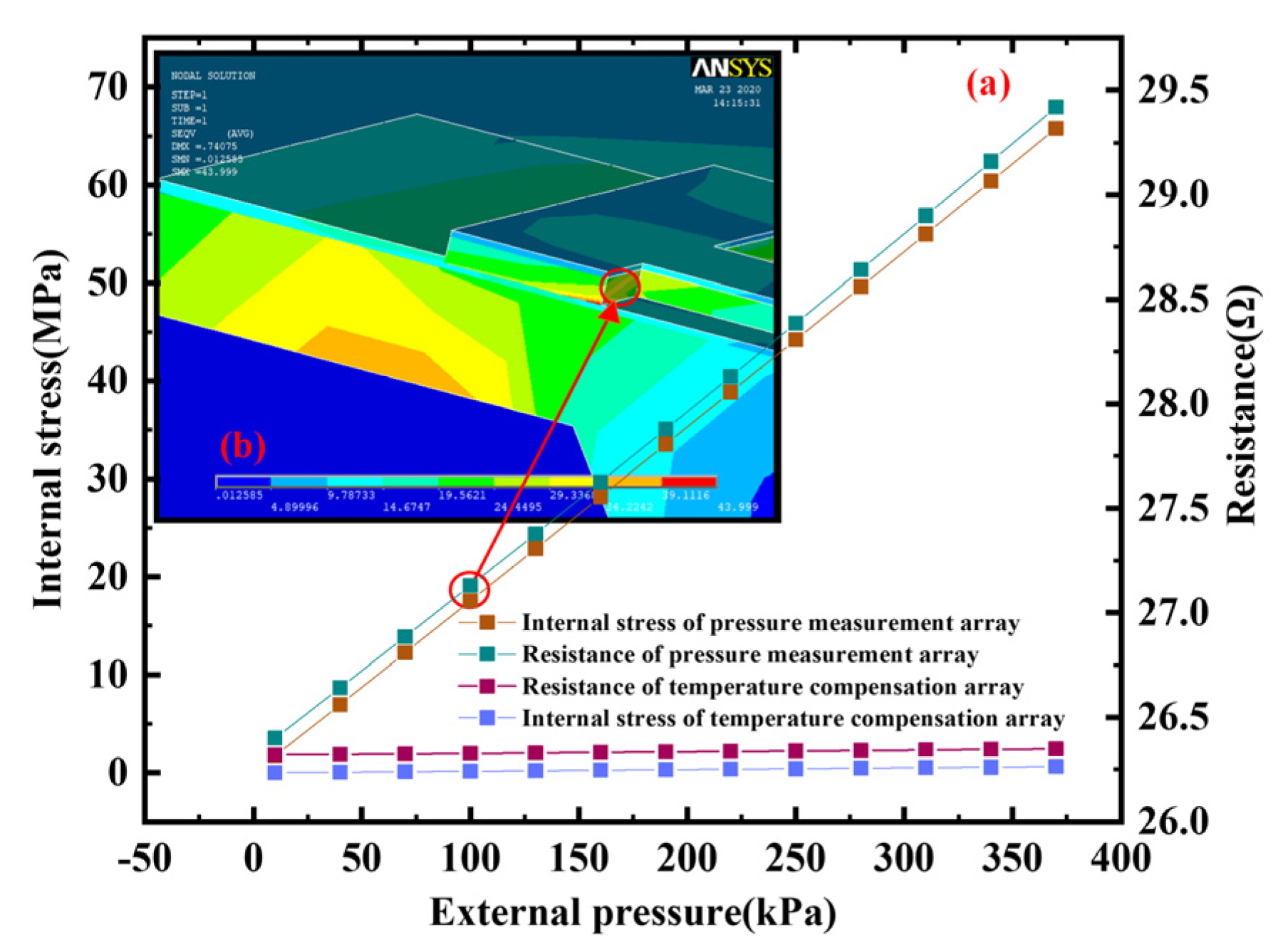
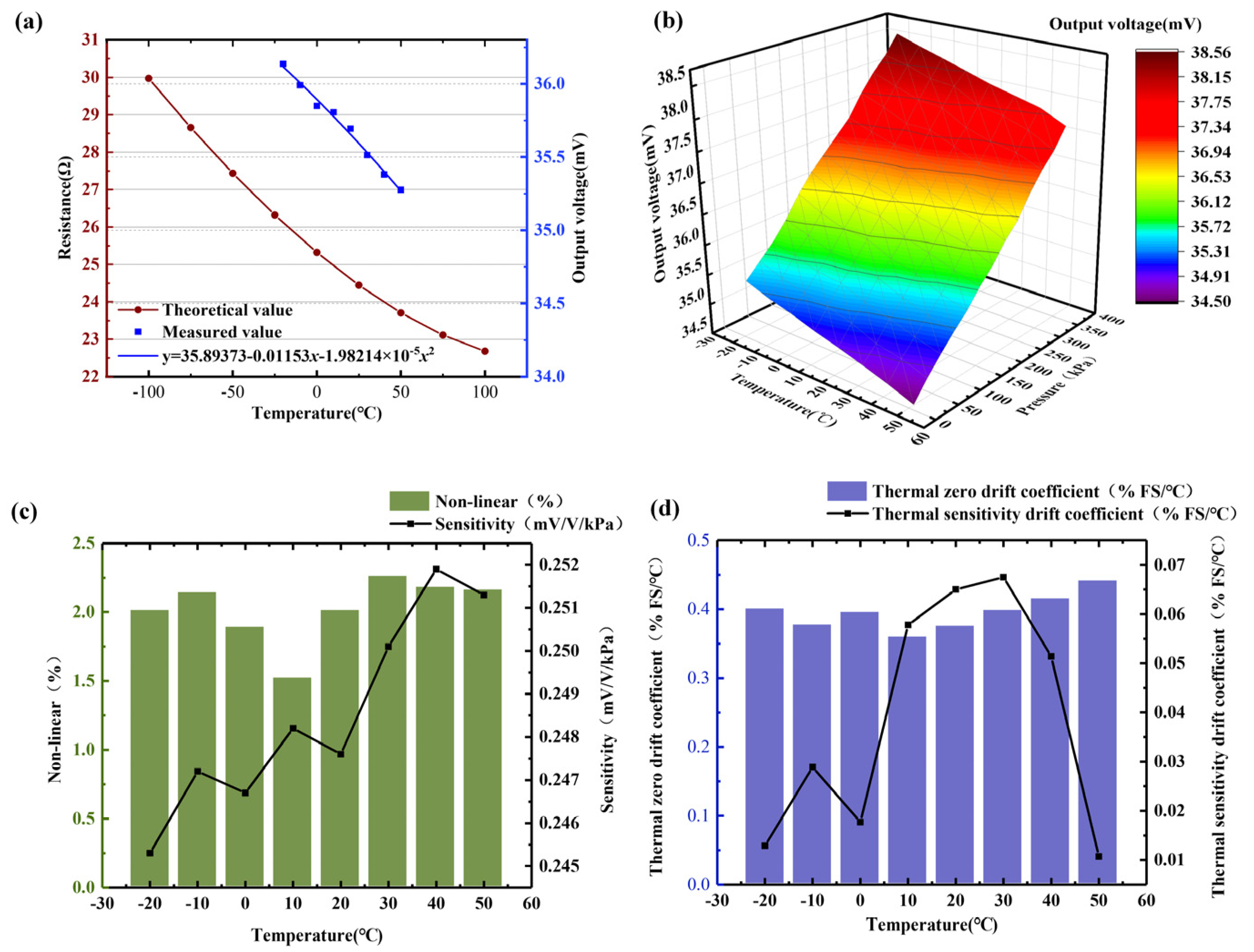
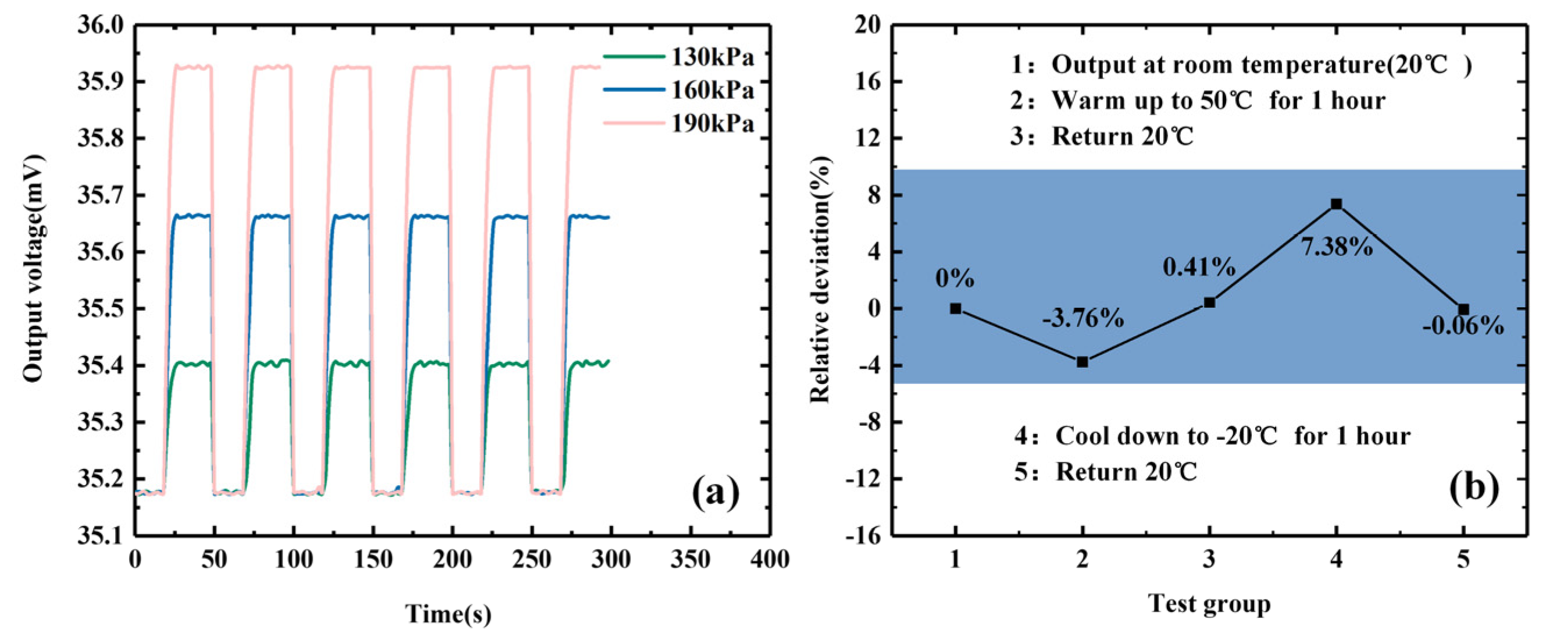
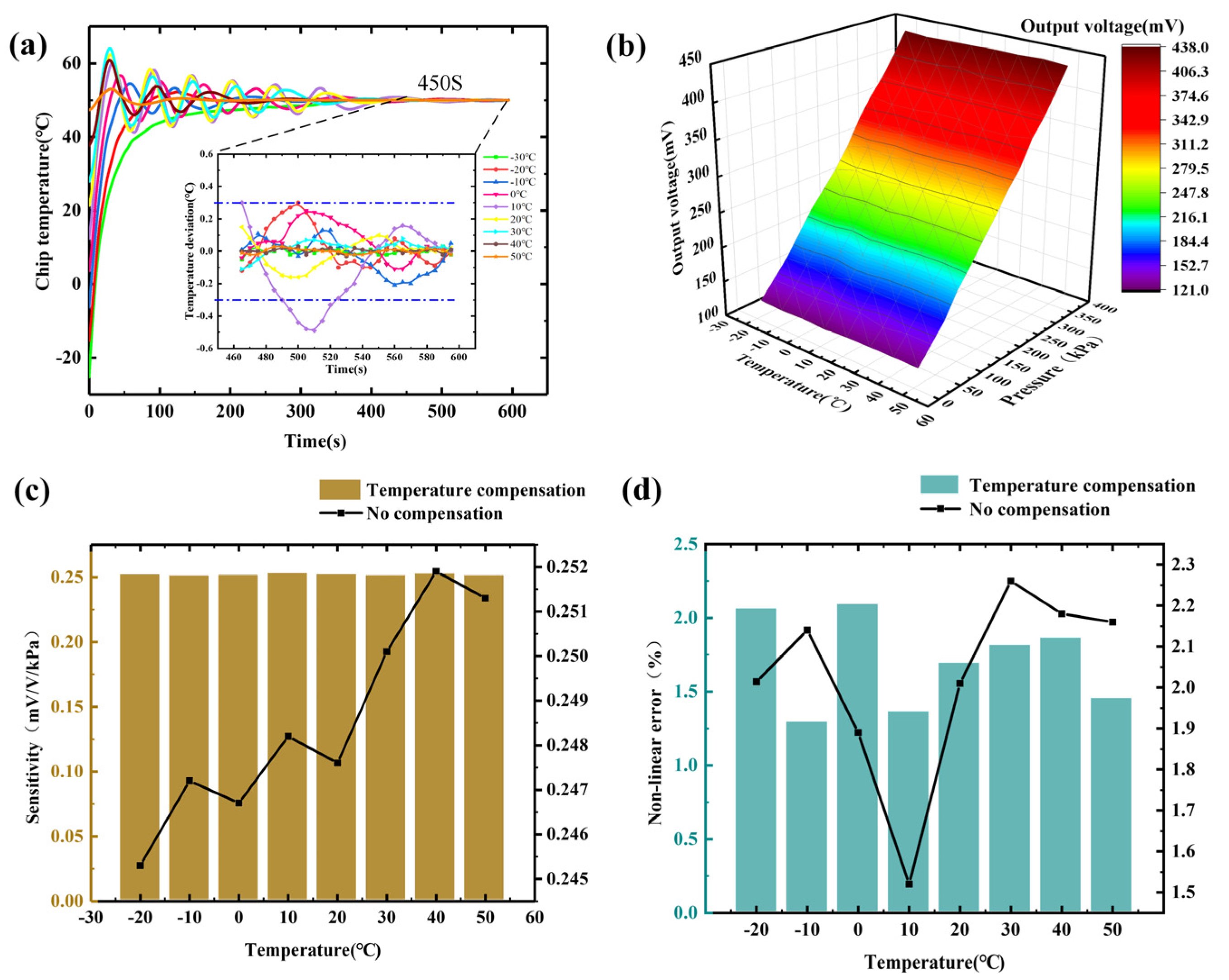
4.2. Test Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sindhanaiselvi, D.; Shanmuganantham, T. Performance analysis of embossed diaphragm based MEMS piezo resistive pressure sensor for flood level measurement. Mater. Today Proc. 2018, 5, 21363–21372. [Google Scholar] [CrossRef]
- Devi, R.; Gill, S.S.; Singh, B. Quantitative analysis of MEMS piezoresistive squared diaphragm pressure sensor for biomedical applications. Meas. Sens. 2022, 24, 100522. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, J.; Li, M.; Ge, Y.; Wang, T.; Shan, P.; Mao, X. Design, fabrication and implementation of an array-type MEMS piezoresistive intelligent pressure sensor system. Micromachines 2018, 9, 104. [Google Scholar] [CrossRef] [PubMed]
- Basov, M.; Prigodskiy, D.M. Investigation of high-sensitivity piezoresistive pressure sensors at ultra-low differential pressures. IEEE Sens. J. 2020, 20, 7646–7652. [Google Scholar] [CrossRef]
- Rajavelu, M.; Sivakumar, D.; Daniel, R.J.; Sumangala, K. Perforated diaphragms employed piezoresistive MEMS pressure sensor for sensitivity enhancement in gas flow measurement. Flow Meas. Instrum. 2014, 35, 63–75. [Google Scholar] [CrossRef]
- Song, J.W.; Lee, J.S.; An, J.E.; Park, C.G. Design of a MEMS piezoresistive differential pressure sensor with small thermal hysteresis for air data modules. Rev. Sci. Instrum. 2015, 86, 065003. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Xie, X.; Li, M.; Mao, X. Development of MEMS composite sensor with temperature compensation for tire pressure monitoring system. J. Micromech. Microeng. 2021, 31, 125015. [Google Scholar] [CrossRef]
- Kumar, S.S.; Pant, B.D. Polysilicon thin film piezoresistive pressure microsensor: Design, fabrication and characterization. Microsyst. Technol. 2015, 21, 1949–1958. [Google Scholar] [CrossRef]
- Bosseboeuf, A.; Allain, P.E.; Parrain, F.; Roux, X.L.; Isac, N.; Jacob, S.; Poizat, A.; Coste, P.; Maaroufi, S.; Walther, A. Thermal and electromechanical characterization of top-down fabricated p-type silicon nanowires. Adv. Nat. Sci. Nanosci. Nanotechnol. 2015, 6, 025001. [Google Scholar] [CrossRef]
- Zhang, S.; Lou, L.; Gu, Y. Development of silicon nanowire-based NEMS absolute pressure sensor through surface micromachining. IEEE Electron Device Lett. 2017, 38, 653–656. [Google Scholar] [CrossRef]
- Zang, X.N.; Zhou, Q.; Chang, J.; Liu, Y.; Lin, L. Graphene and carbon nanotube (CNT) in MEMS/NEMS applications. Microelectron. Eng. 2015, 132, 192–206. [Google Scholar] [CrossRef]
- Devi, R.; Gill, S.S. A squared bossed diaphragm piezoresistive pressure sensor based on CNTs for low pressure range with enhanced sensitivity. Microsyst. Technol. 2021, 27, 3225–3233. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Lou, L.; Tsang, W.M.; Sawada, R.S.; Kwong, D.L.; Lee, C.K. Annularly grooved diaphragm pressure sensor with embedded silicon nanowires for low pressure application. J. Microelectromech. Syst. 2014, 23, 1396–1407. [Google Scholar] [CrossRef]
- Soon, B.W.; Neuzil, P.; Wong, C.C.; Reboud, J.; Feng, H.H.; Lee, C.K. Ultrasensitive nanowire pressure sensor makes its debut. Procedia Eng. 2010, 5, 1127–1130. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Y.; Wang, L. Application of femtosecond laser micromachining in silicon carbide deep etching for fabricating sensitive diaphragm of high temperature pressure sensor. Sens. Actuators A Phys. 2020, 309, 112017. [Google Scholar] [CrossRef]
- Helgason, R.; Campigotto, A.; Lai, Y.J. The development of a pressure sensor using a technique for patterning silver nanowires on 3-dimensional curved PDMS membranes. J. Micromech. Microeng. 2020, 30, 095013. [Google Scholar] [CrossRef]
- Basov, M. Pressure Sensor with Novel Electrical Circuit Utilizing Bipolar Junction Transistor. In Proceedings of the 2021 IEEE Sensors, Sydney, Australia, 31 October–3 November 2021; pp. 1–4. [Google Scholar]
- Hafez, N.; Haas, S.; Loebel, K.-U.; Reuter, D.; Ramsbeck, M.; Schramm, M.; Horstmann, J.T.; Otto, T. Characterisation of MOS Transistors as an Electromechanical Transducer for Stress. Phys. Status Solidi (a) 2019, 216, 1700680. [Google Scholar] [CrossRef]
- Rowe, A.C.H.; Donoso-Barrera, A.; Renner, C.; Arscott, S. Giant room-temperature piezoresistance in a metal-silicon hybrid structure. Phys. Rev. Lett. 2008, 100, 145501. [Google Scholar] [CrossRef]
- Ngo, H.-D.; Tekin, T.; Vu, T.-C.; Fritz, M.; Kurniawan, W.; Mukhopadhyay, B.; Kolitsch, A.; Schiffer, M.; Lang, K.-D. MEMS sensor with giant piezoresistive effect using metall-semiconductor hybrid structure. In Proceedings of the 2011 IEEE 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 1018–1021. [Google Scholar]
- Xie, X.; Zhang, J.; Li, M.; Liu, Q.; Mao, X. Design and fabrication of temperature-insensitive MEMS pressure sensor utilizing aluminum-silicon hybrid structures. IEEE Sens. J. 2020, 21, 5861–5870. [Google Scholar] [CrossRef]
- Yellapantula, K.; Devaraj, H.; Assadian, M.; Stuart, L.; Lo, C.Y.; Gan, W.C.; Aw, K. Soft and flexible sensor array using carbon black pillars for object recognition via pressure mapping. Measurement 2020, 159, 107781. [Google Scholar] [CrossRef]
- Ghosh, R.; Song, M.; Park, J.B.; Tchoe, Y.; Guha, P.; Lee, W.; Lim, Y.; Kim, B.; Kim, S.-W.; Kim, M. Fabrication of piezoresistive Si nanorod-based pressure sensor arrays: A promising candidate for portable breath monitoring devices. Nano Energy 2021, 80, 105537. [Google Scholar] [CrossRef]
- Chang, S.-P.; Lee, J.-B.; Allen, M.G. Robust capacitive pressure sensor array. Sens. Actuators A Phys. 2002, 101, 231–238. [Google Scholar] [CrossRef]
- Jeong, Y.-J.; Park, J.-H.; Lee, D.-W. Pressure level sensor using a conductive diaphragm and microswitch arrays. Sens. Actuators A Phys. 2014, 218, 154–161. [Google Scholar] [CrossRef]
- Zhao, Z.X.; Shin, M.; Gallman, J.M.; White, R.D. A microfabricated shear sensor array on a chip with pressure gradient calibration. Sens. Actuators A Phys. 2014, 205, 133–142. [Google Scholar] [CrossRef]
- Bhat, K.N. Silicon micromachined pressure sensors. J. Indian Inst. Sci. 2007, 87, 115. [Google Scholar]
- Sahay, R.; Jindal, S.K. Design and analysis of a MEMS pressure sensor with a bossed membrane and ancillary bi-functional frog arm structure for low pressure measurement. J. Comput. Electron. 2021, 20, 1012–1019. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, D. Structured diaphragm with a centre boss and four peninsulas for high sensitivity and high linearity pressure sensors. Mirco Nano Lett. 2014, 9, 460–463. [Google Scholar] [CrossRef]
- Zhao, L.; Xu, T.; Hebibul, R.; Jiang, Z.; Ding, J.; Peng, N.; Guo, X.; Xu, Y.; Wang, H.; Zhao, Y. A bossed diaphragm piezoresistive pressure sensor with a peninsula–island structure for the ultra-low-pressure range with high sensitivity. Meas. Sci. Technol. 2016, 27, 124012. [Google Scholar] [CrossRef]
- Basov, M.; Prigodskiy, D. Development of high-sensitivity piezoresistive pressure sensors for −0.5...+0.5 kPa. J. Micromech. Microeng. 2020, 30, 105006. [Google Scholar] [CrossRef]
- Tran, A.V.; Zhang, X.; Zhu, B. The Development of a New Piezoresistive Pressure Sensor for Low Pressures. IEEE Trans. Ind. Electron. 2017, 65, 6487–6496. [Google Scholar] [CrossRef]
- Yao, Z.; Liang, T.; Jia, P.; Hong, Y.; Qi, L.; Lei, C.; Zhang, B.; Li, W.; Zhang, D.; Xiong, J. Passive resistor temperature compensation for a high-temperature piezoresistive pressure sensor. Sensors 2016, 16, 1142. [Google Scholar] [CrossRef]
- Zhou, G.; Zhao, Y.; Guo, F. A Temperature Compensation System for Silicon Pressure Sensor Based on Neural Networks. In Proceedings of the 2014 IEEE 9th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS), Waikiki Beach, HI, USA, 13–16 April 2014; pp. 467–470. [Google Scholar]
- Du, L.; Zhao, Z.; Fang, Z.; Feng, Y.; Yan, J. Thermodynamic control of MEMS meteorology pressure sensing element in low-temperature application down to −45° C. IET Sci. Meas. Technol. 2017, 11, 907–913. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, D.; Hall, N.A. On-diaphragm thermistor for high-temperature dynamic pressure sensors. IEEE Sens. J. 2019, 20, 2287–2293. [Google Scholar] [CrossRef]
- Mohammed, O.K.; Amr, A.B.; Lou, E.; Walied, A.M. Development of doped silicon multi-element stress sensor rosette with temperature compensation. IEEE Sens. J. 2019, 20, 1176–1183. [Google Scholar]
- Hansen, O.; Reck, K.; Thomsen, E.V. Giant geometrically amplified piezoresistance in metal-semiconductor hybrid resistors. J. Appl. Phys. 2008, 104, 114510. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Xiao, Y.; Zhang, J.; Liu, Q.; Jiang, X.; Hua, W. Development of Highly Sensitive and Thermostable Microelectromechanical System Pressure Sensor Based on Array-Type Aluminum–Silicon Hybrid Structures. Micromachines 2024, 15, 1065. https://doi.org/10.3390/mi15091065
Li M, Xiao Y, Zhang J, Liu Q, Jiang X, Hua W. Development of Highly Sensitive and Thermostable Microelectromechanical System Pressure Sensor Based on Array-Type Aluminum–Silicon Hybrid Structures. Micromachines. 2024; 15(9):1065. https://doi.org/10.3390/mi15091065
Chicago/Turabian StyleLi, Min, Yang Xiao, Jiahong Zhang, Qingquan Liu, Xianglong Jiang, and Wenhao Hua. 2024. "Development of Highly Sensitive and Thermostable Microelectromechanical System Pressure Sensor Based on Array-Type Aluminum–Silicon Hybrid Structures" Micromachines 15, no. 9: 1065. https://doi.org/10.3390/mi15091065
APA StyleLi, M., Xiao, Y., Zhang, J., Liu, Q., Jiang, X., & Hua, W. (2024). Development of Highly Sensitive and Thermostable Microelectromechanical System Pressure Sensor Based on Array-Type Aluminum–Silicon Hybrid Structures. Micromachines, 15(9), 1065. https://doi.org/10.3390/mi15091065





