Research on Adaptive Closed-Loop Control of Microelectromechanical System Gyroscopes under Temperature Disturbance
Abstract
:1. Introduction
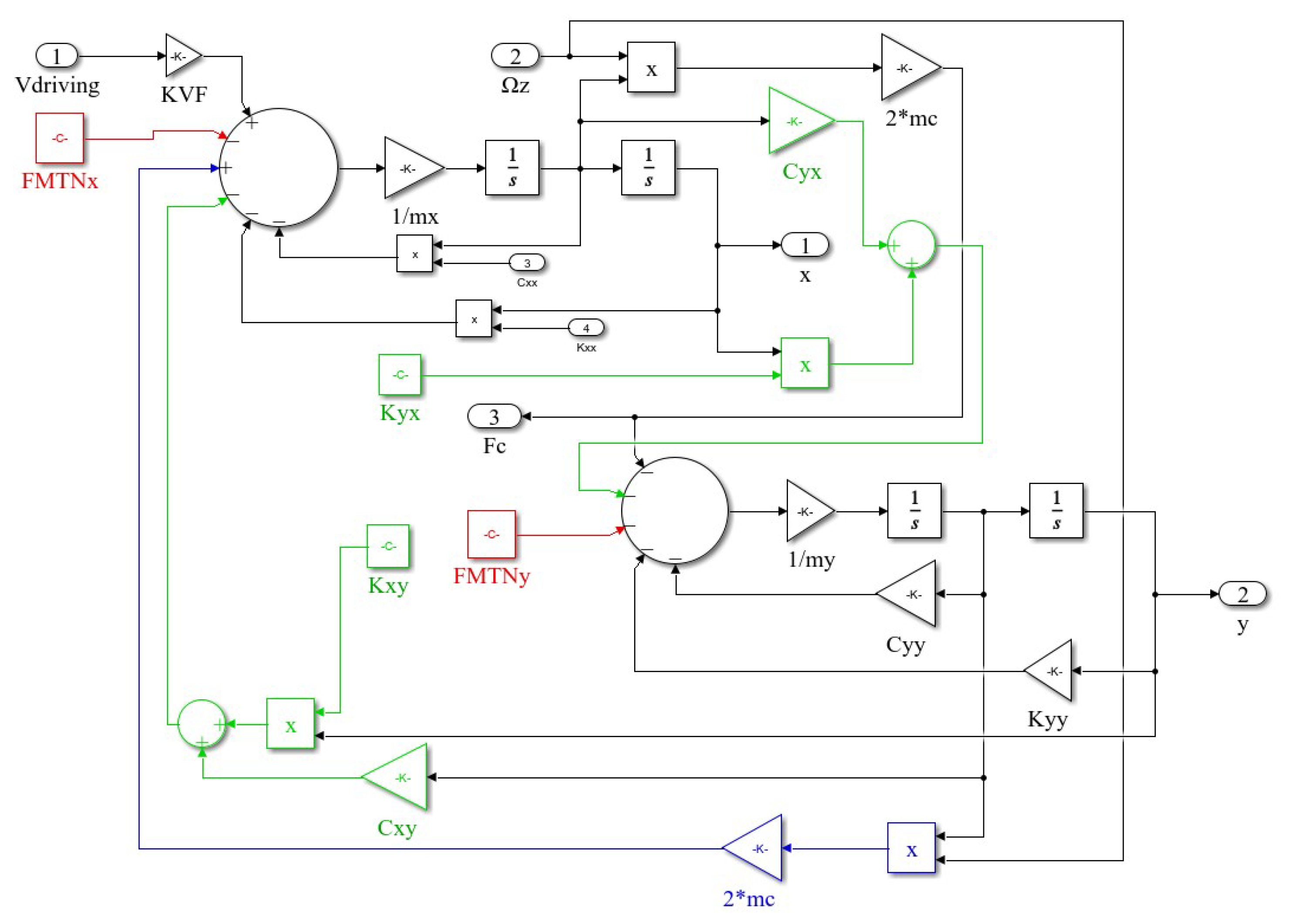
2. Simulation Model of MEMS Gyroscope
2.1. Structure of MEMS Gyroscope
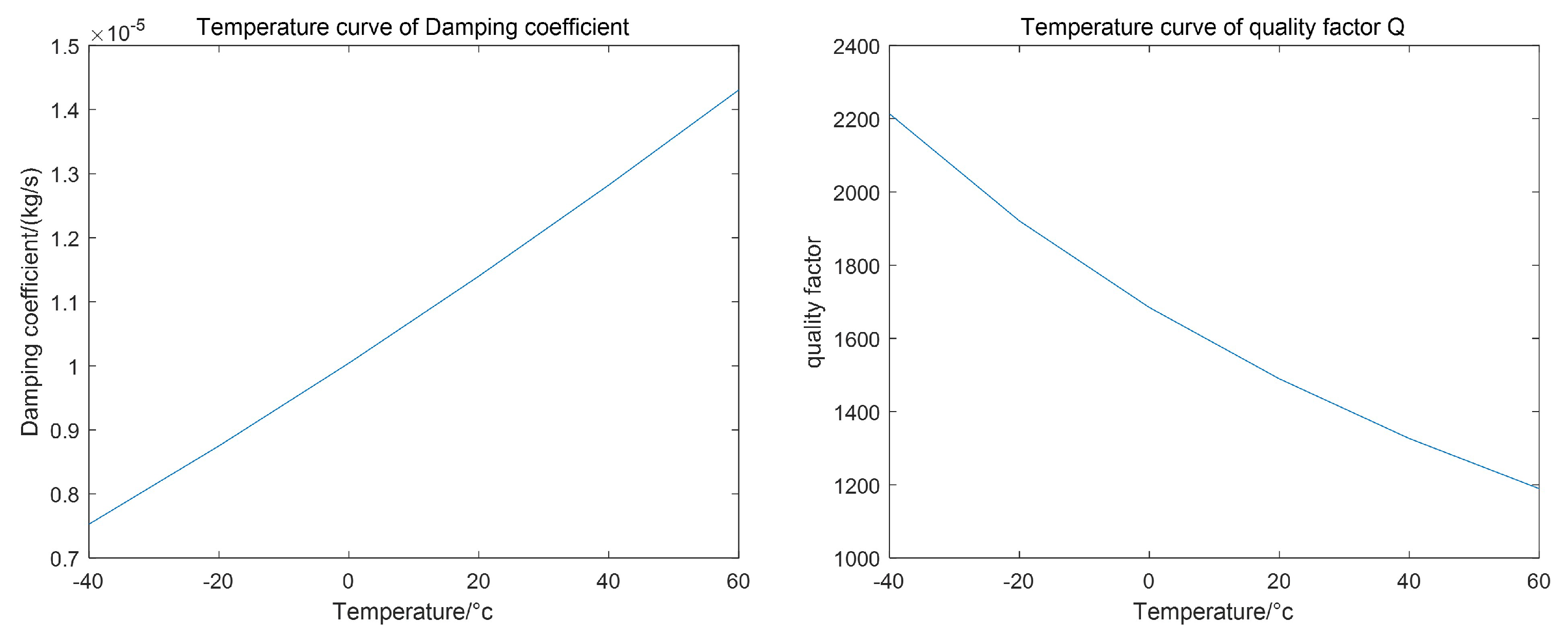
2.2. Relevant Parameters of MEMS Gyroscopes under Temperature Disturbances
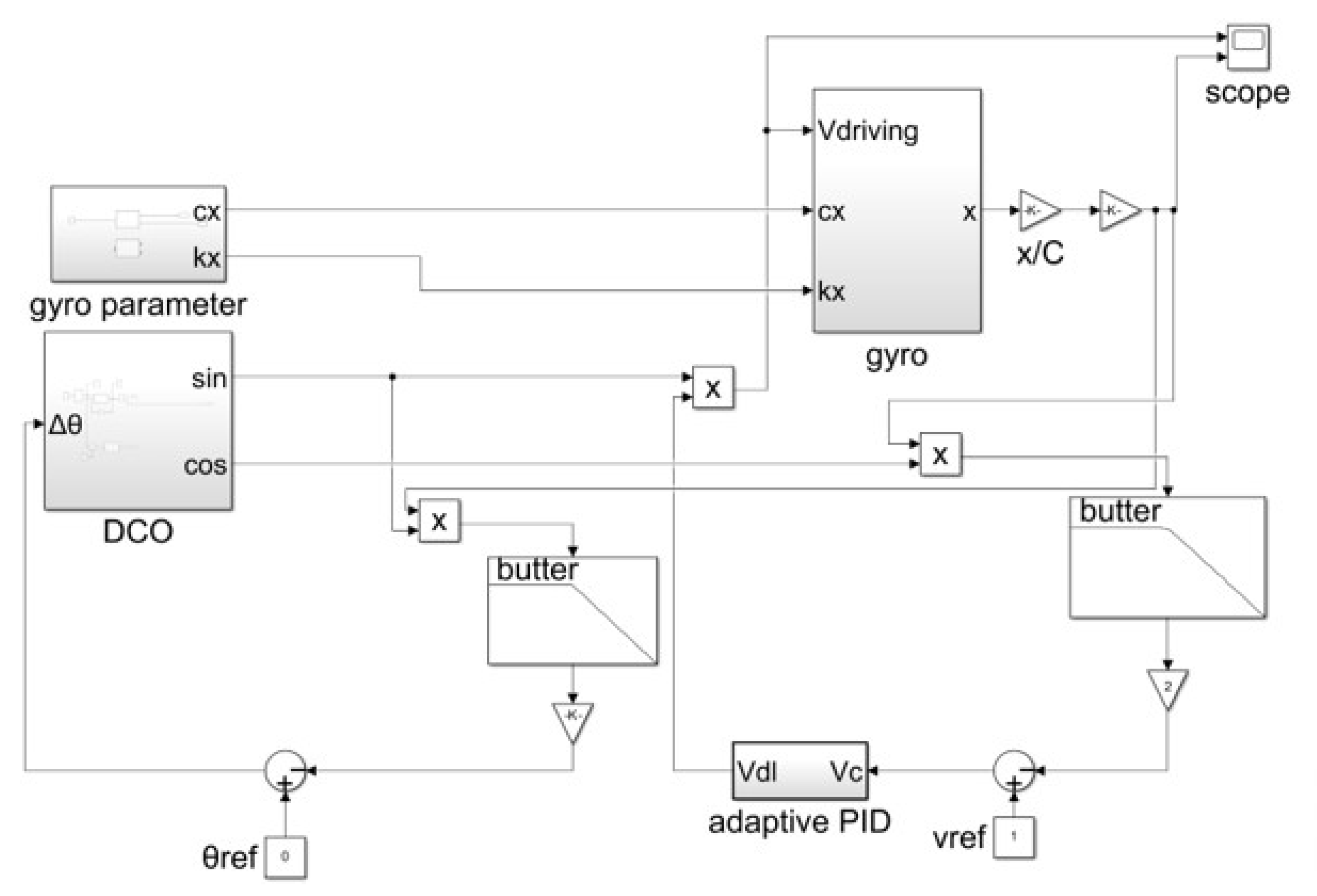
3. MEMS Gyroscope Closed-Loop Drive Control System
3.1. MEMS Gyroscope Closed-Loop Drive Control System
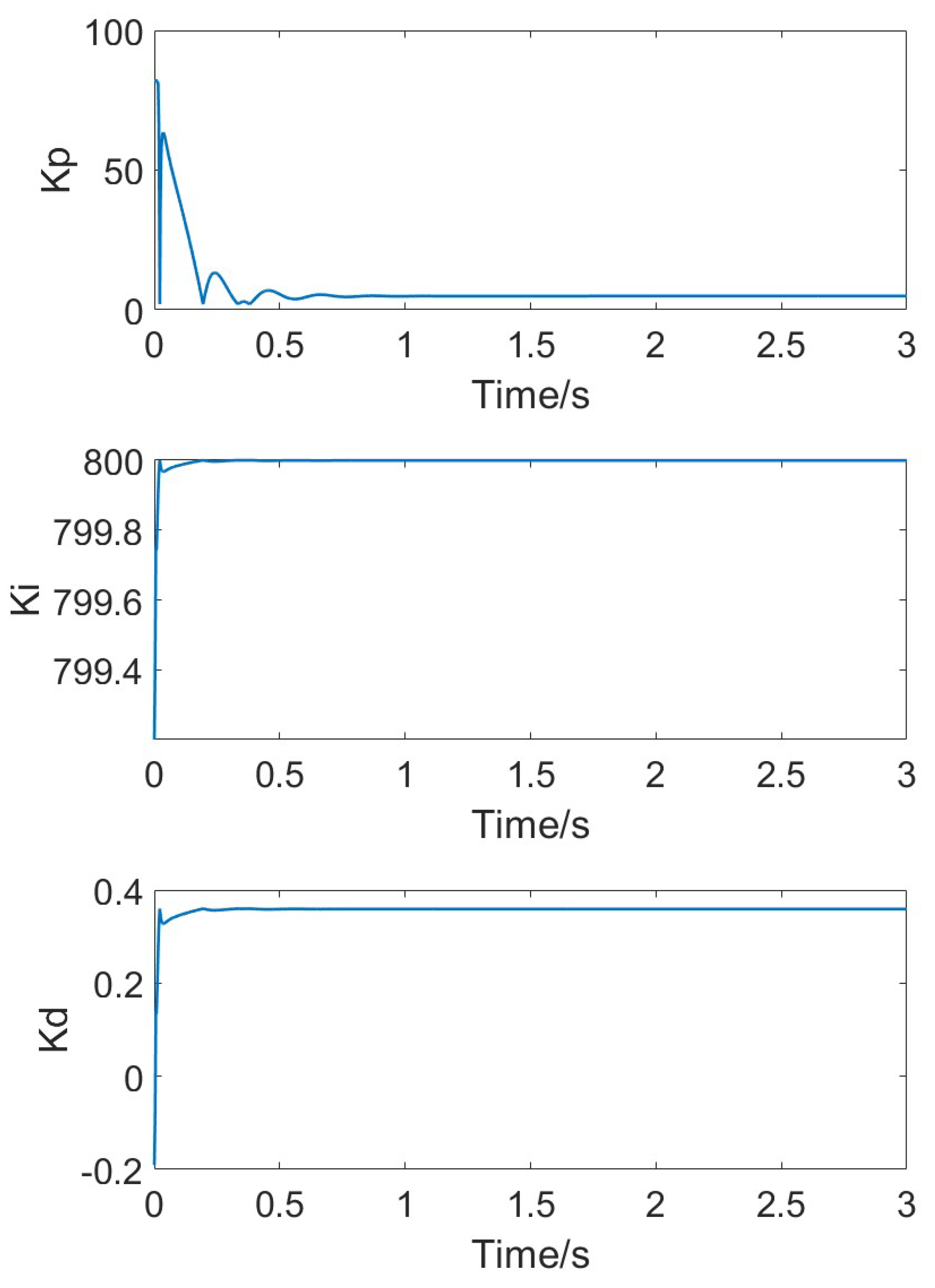
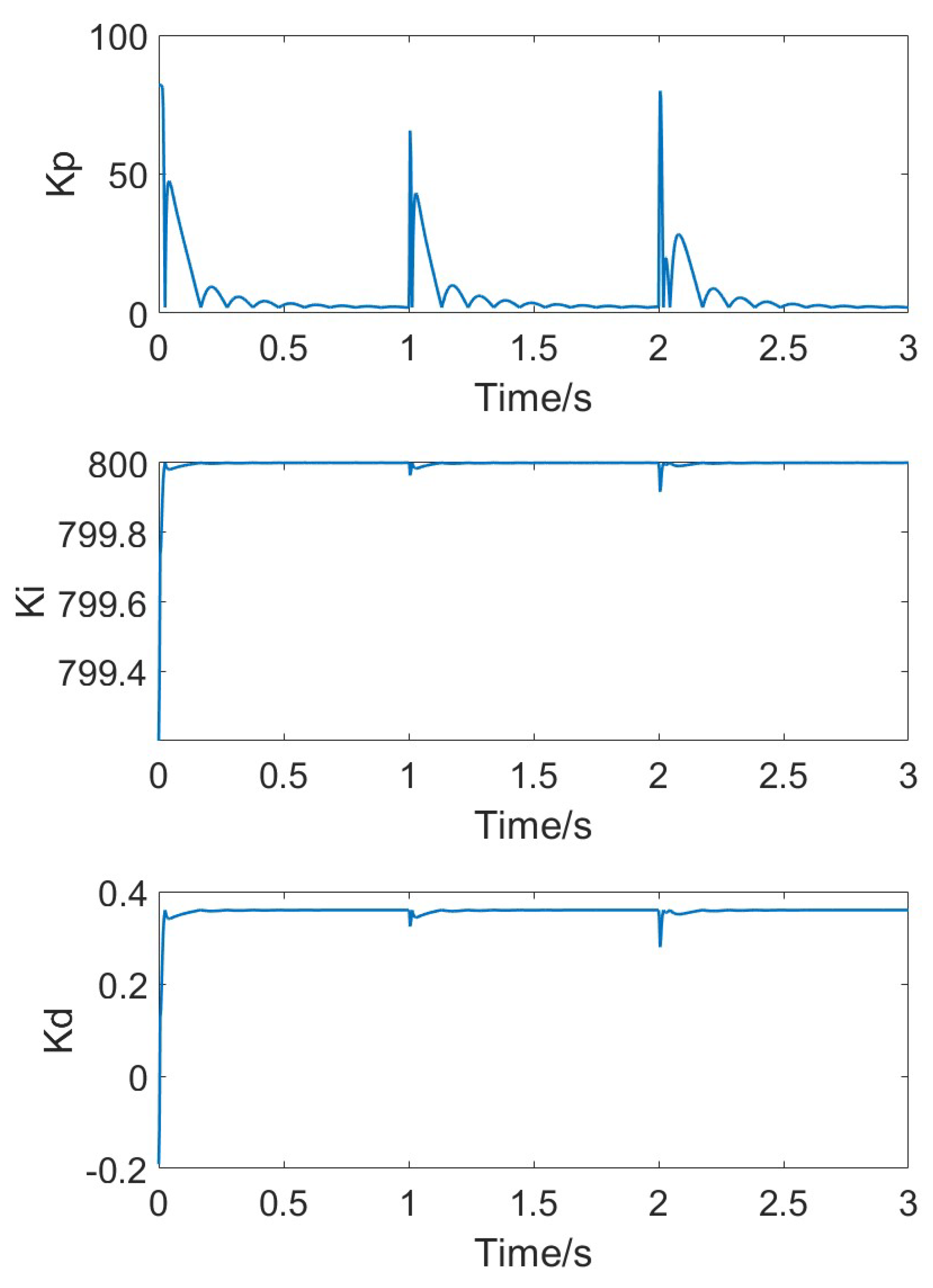
3.2. Adaptive PID Controller
3.3. Simulink Model of MEMS Gyroscope Closed-Loop Drive Control System
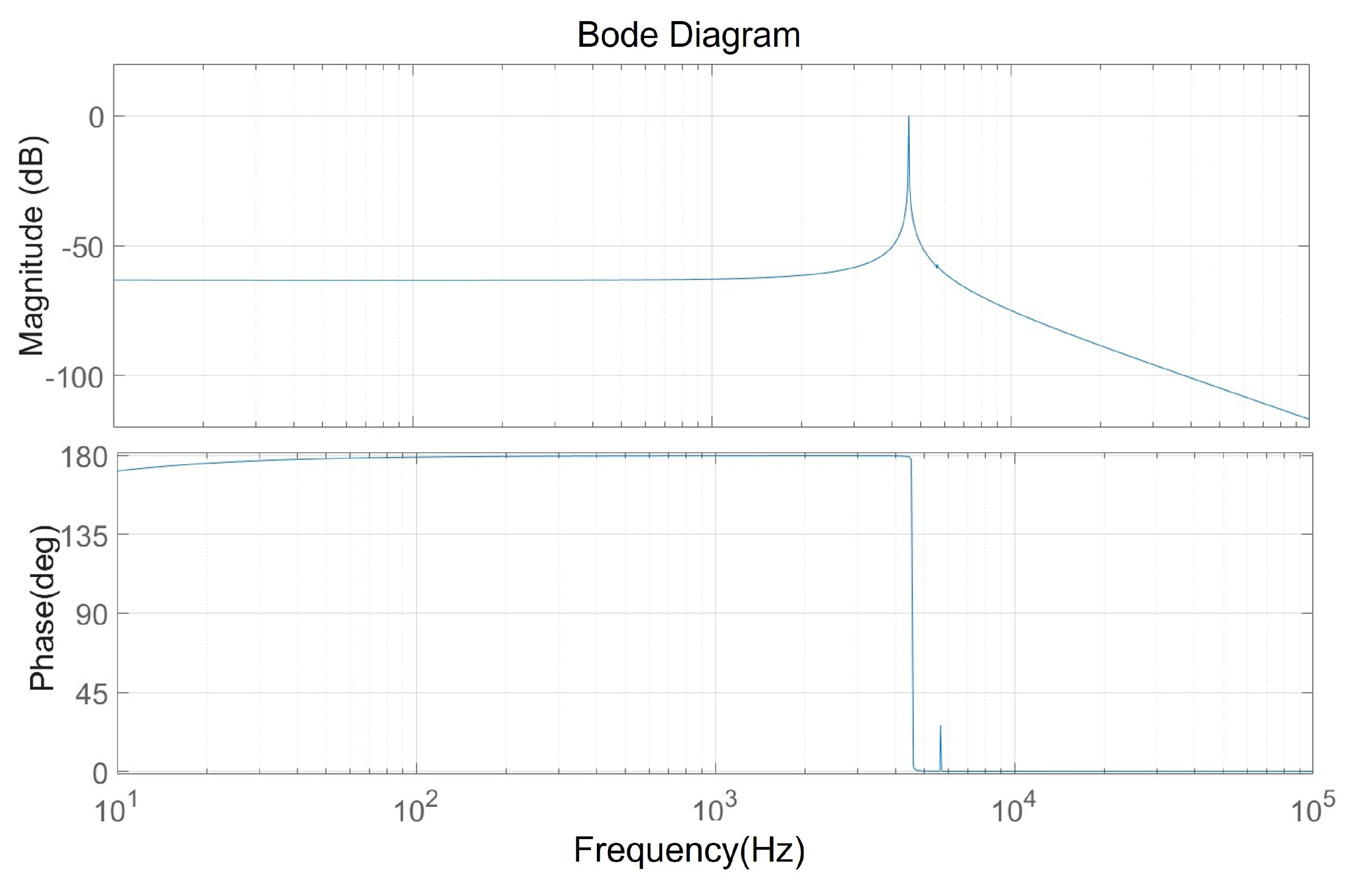
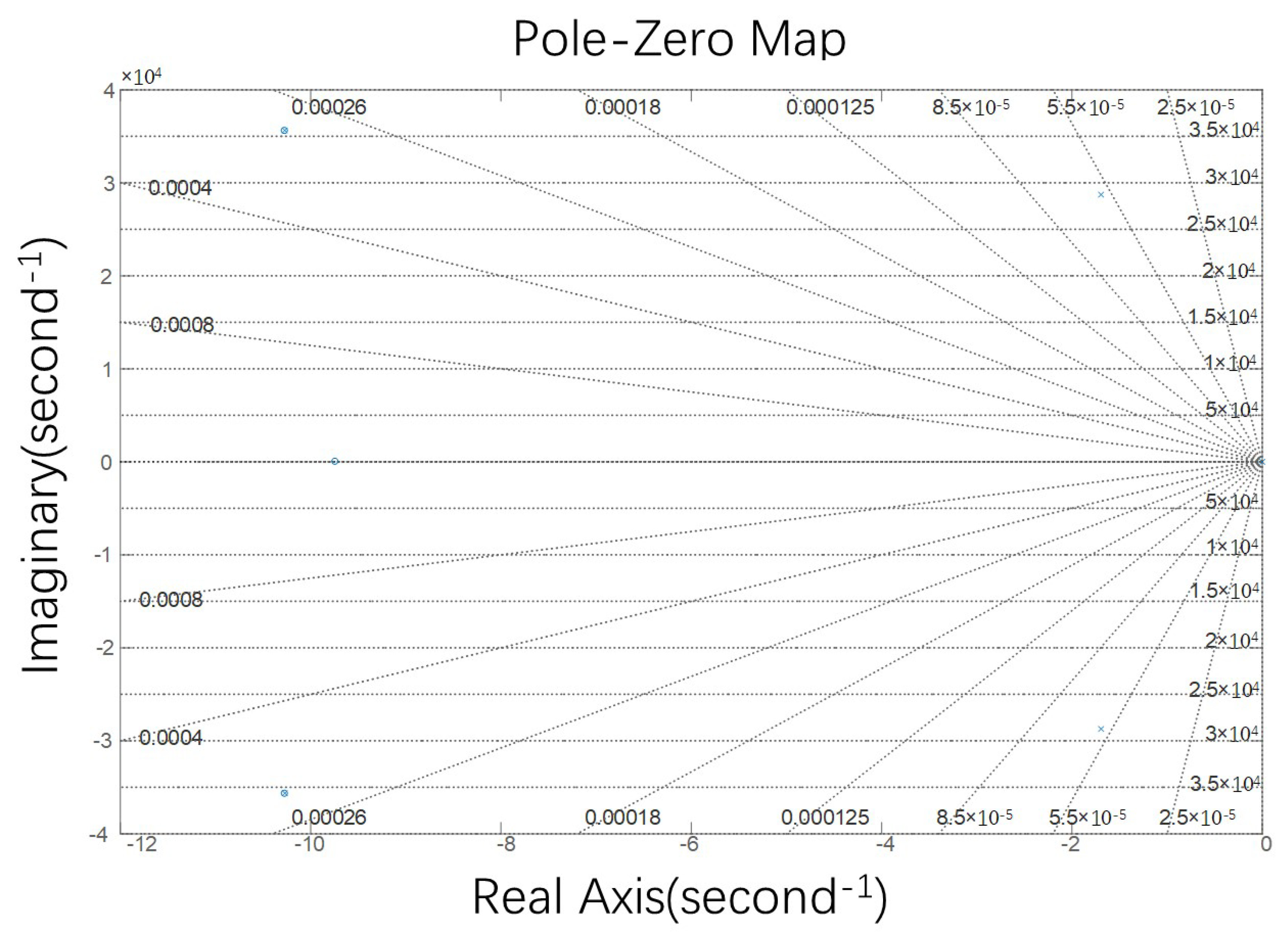
3.4. The Stability of the Drive Loop
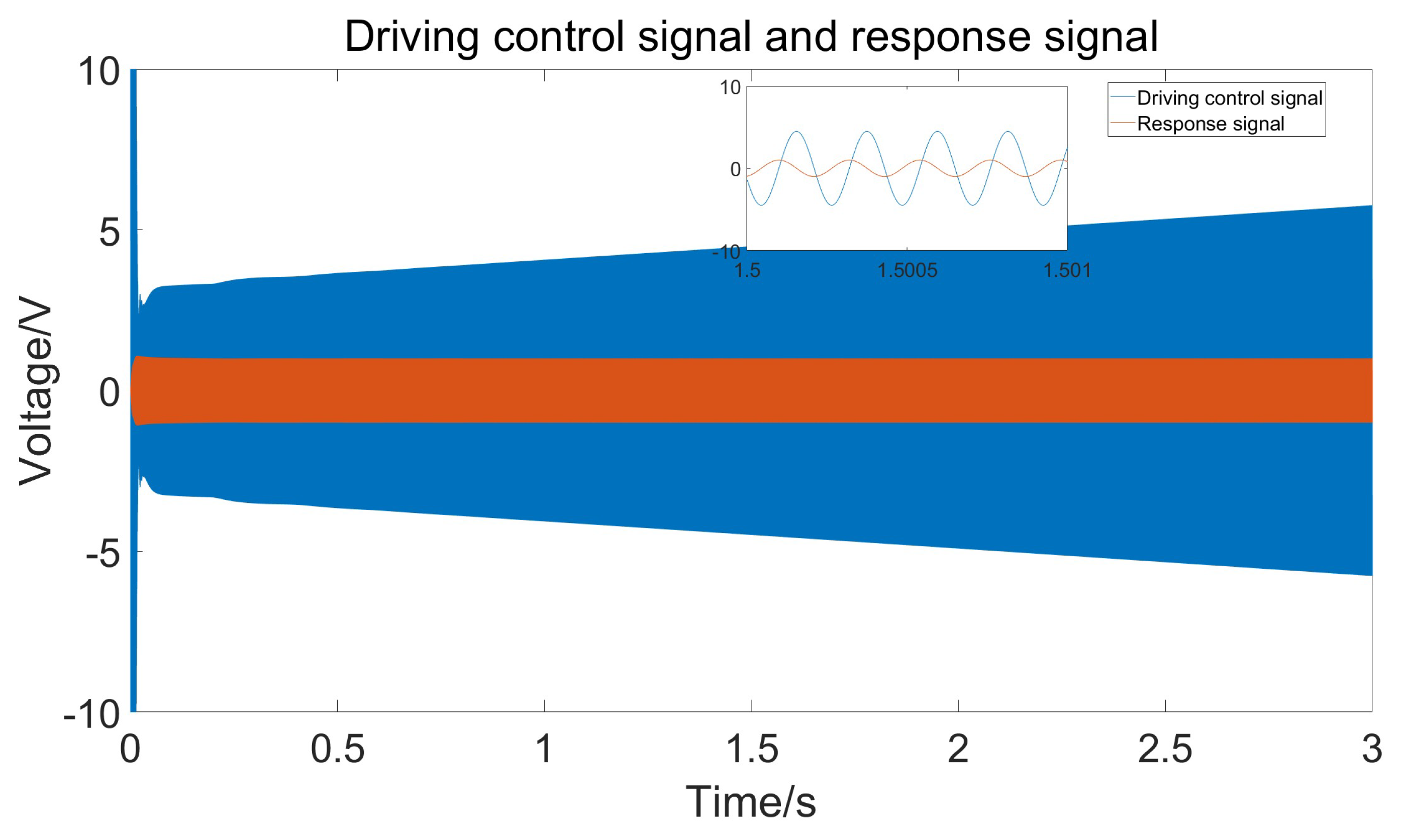
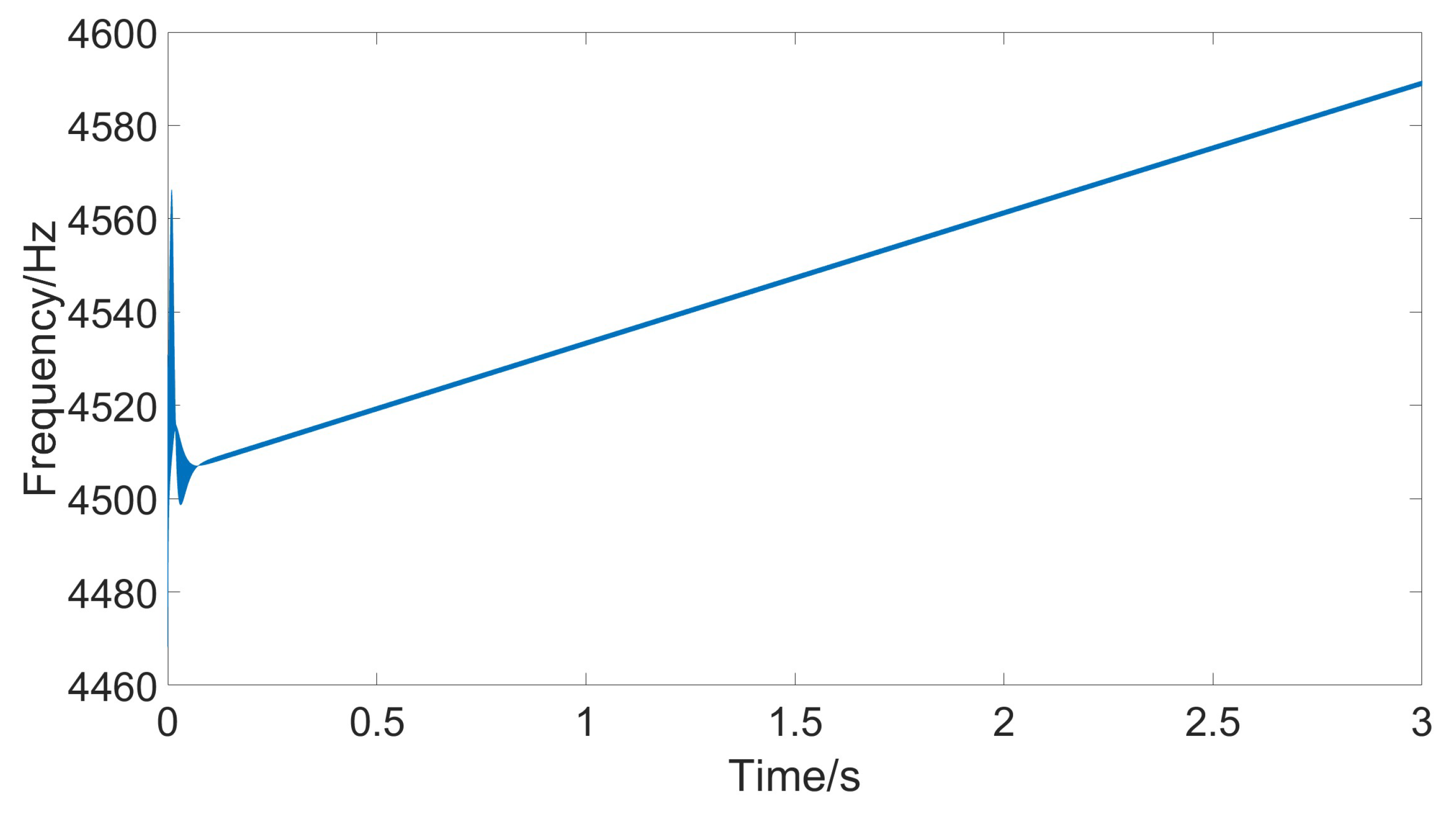
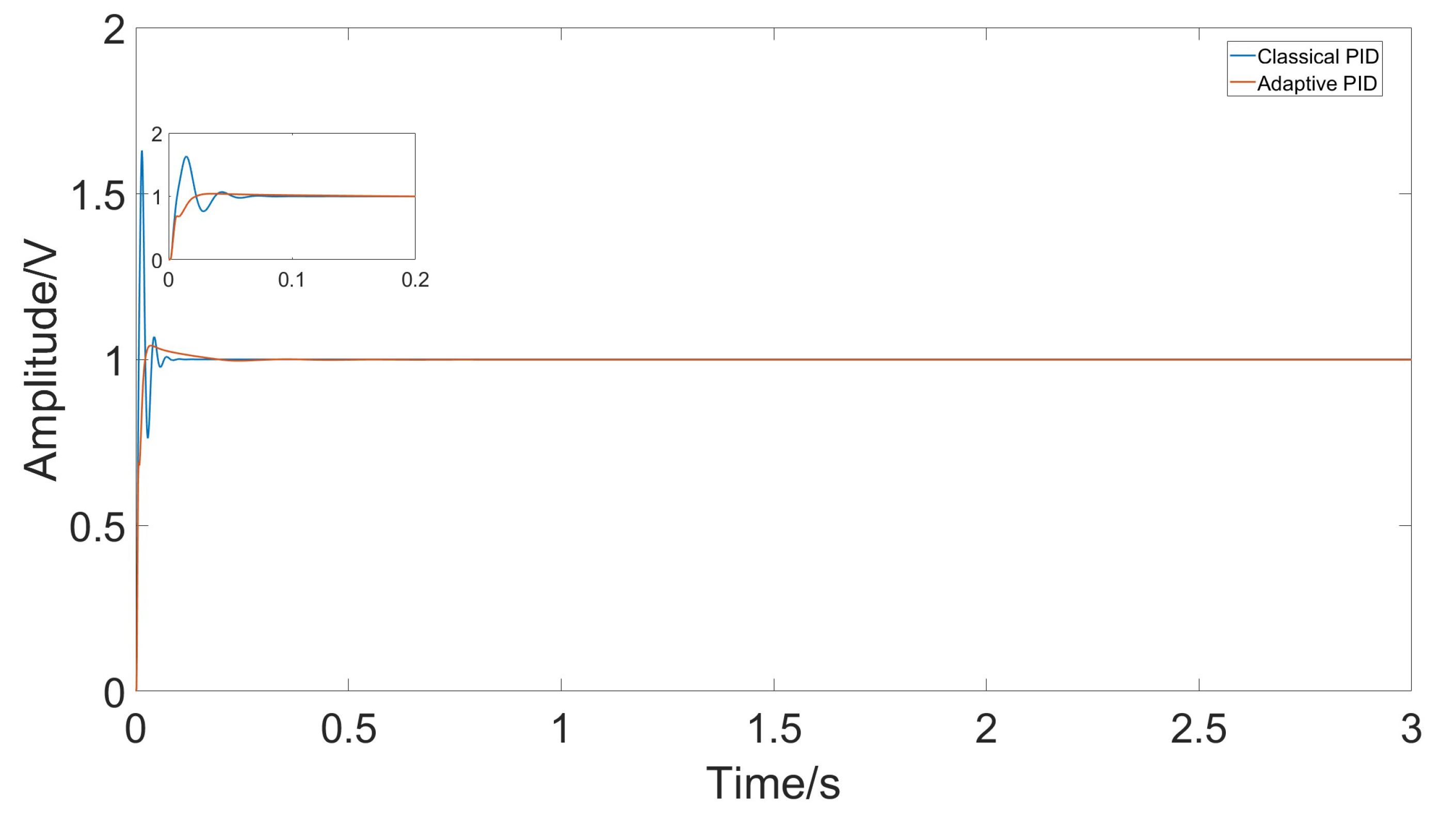
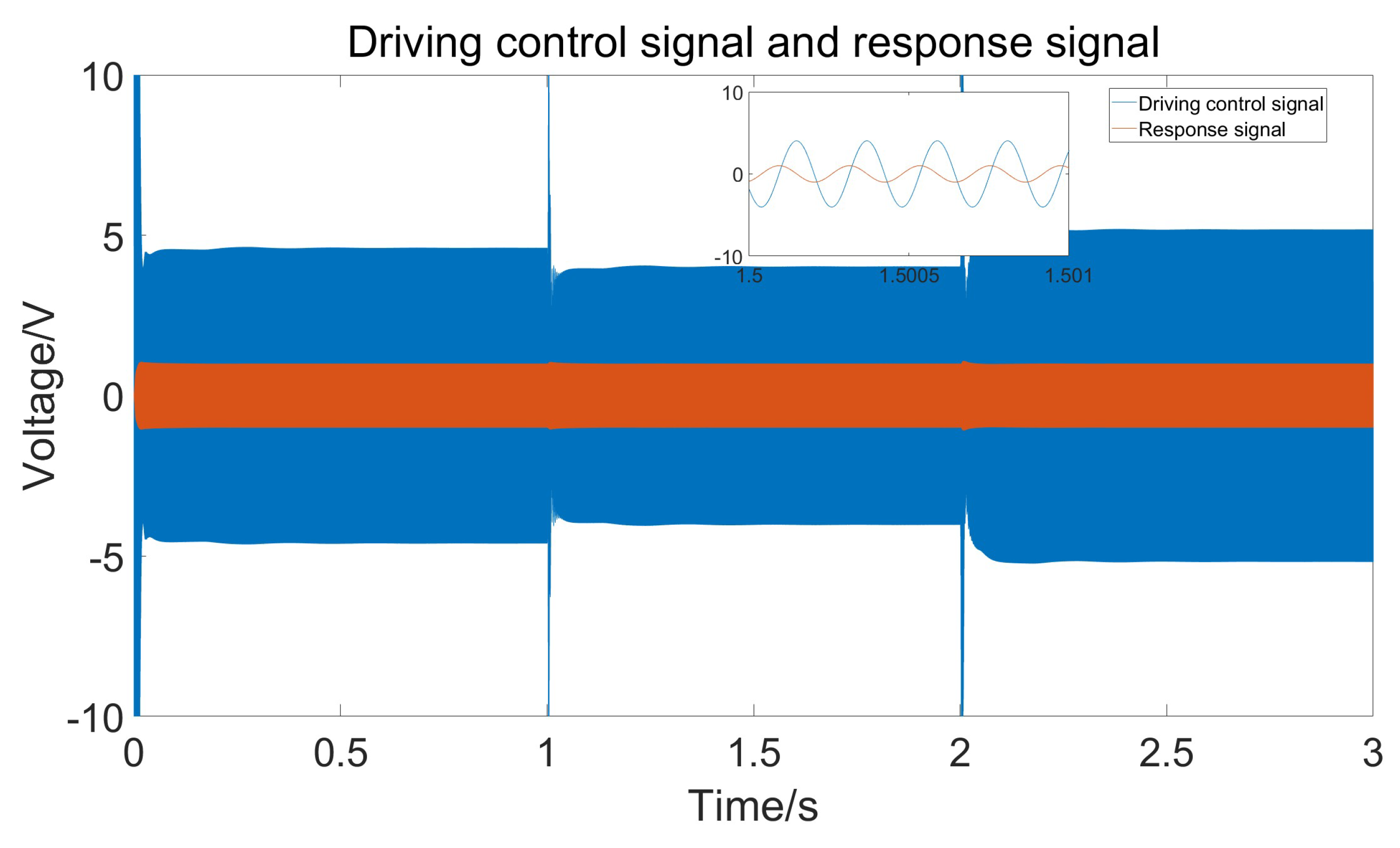
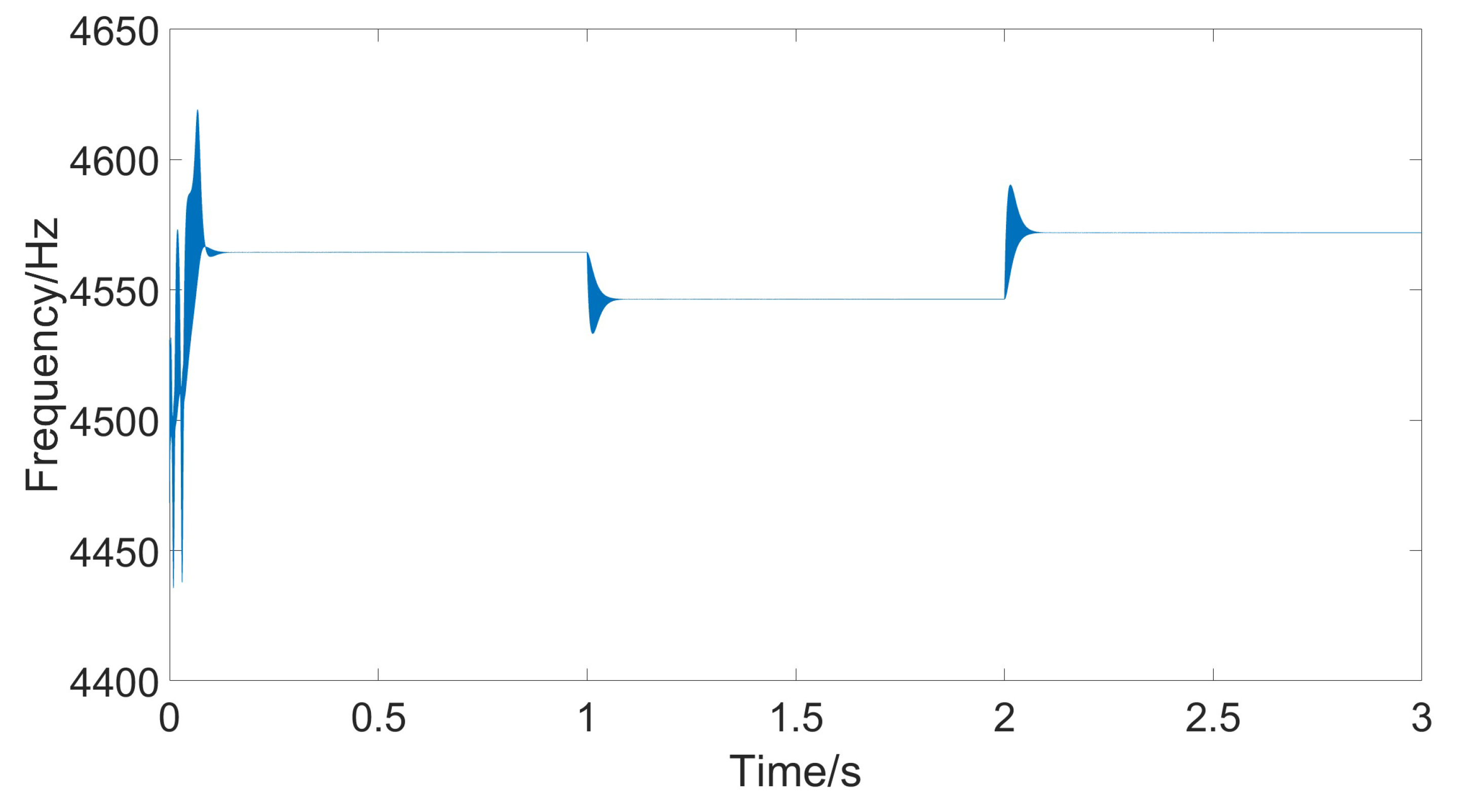
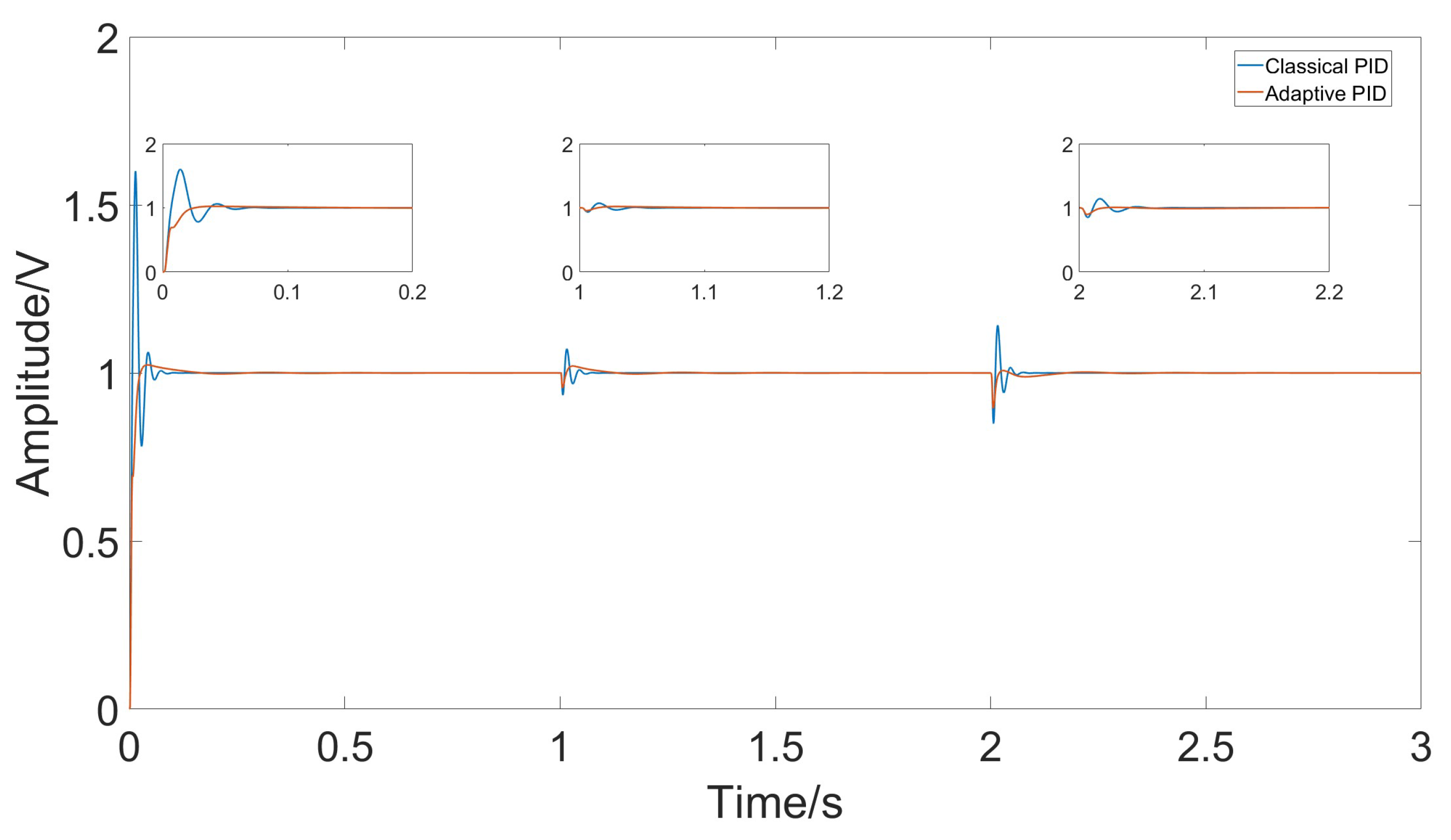
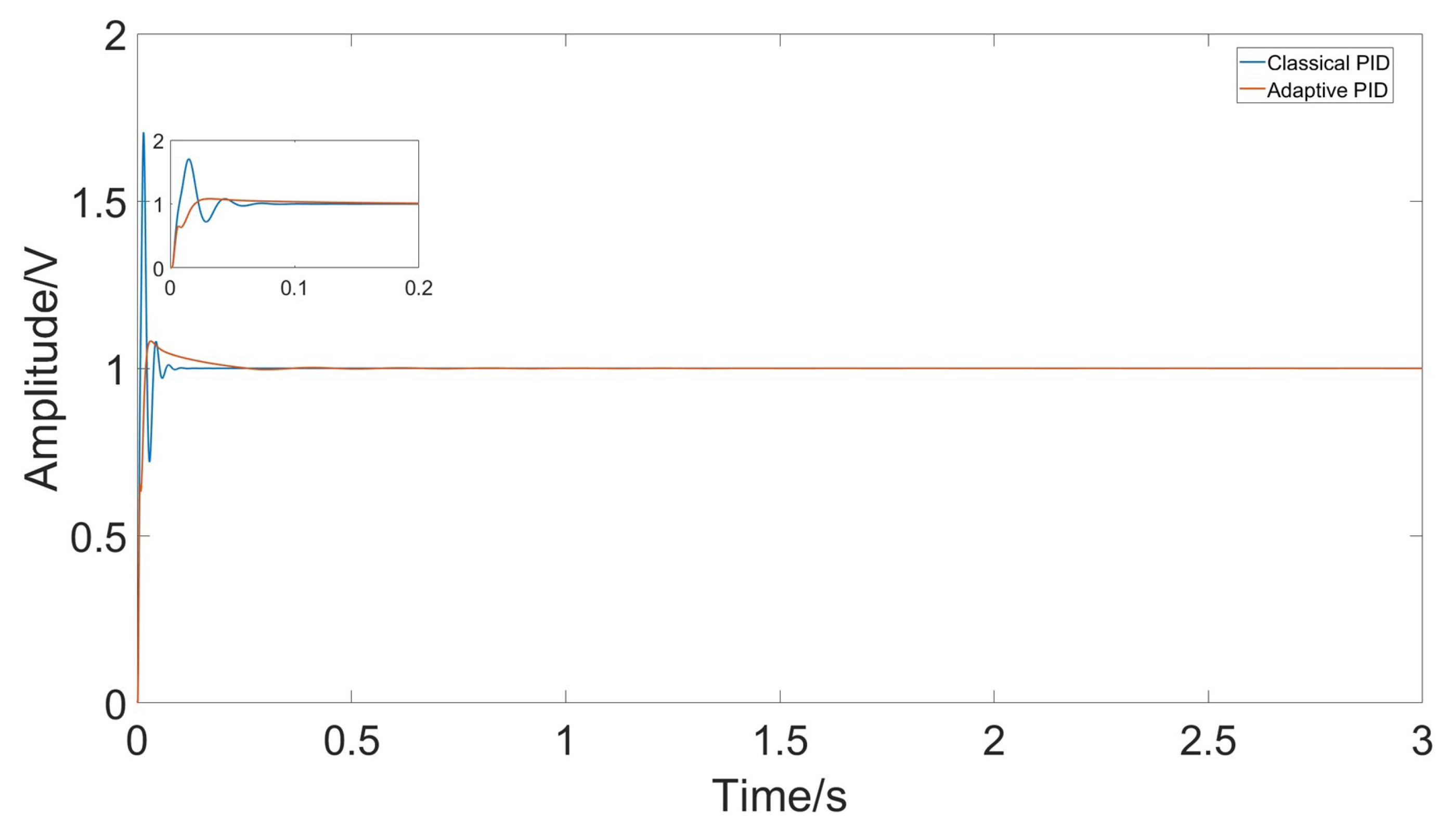
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MEMS | Microelectromechanical System |
| PID | Proportion Integration Differentiation |
| PLL | Phase-locked Loops |
| AGC | Automatic Gain Control |
References
- Huang, W.; Yan, X.; Zhang, S.; Li, Z.; Hassan, J.N.A.; Chen, D.; Wen, G.; Chen, K.; Deng, G.; Huang, Y. MEMS and MOEMS Gyroscopes: A Review. Photonic Sens. 2023, 13, 230419. [Google Scholar] [CrossRef]
- Ren, X.; Zhou, X.; Yu, S.; Wu, X.; Xiao, D. Frequency-Modulated MEMS Gyroscopes: A Review. IEEE Sens. J. 2021, 21, 26426–26446. [Google Scholar] [CrossRef]
- Mohammadi, Z.; Salarieh, H. Investigating the effects of quadrature error in parametrically and harmonically excited MEMS rate gyroscopes. Measurement 2016, 87, 152–175. [Google Scholar] [CrossRef]
- Geen, J.A. Very low cost gyroscopes. IEEE Sens. 2005, 1, 537–540. [Google Scholar]
- Cui, M.; Huang, Y.; Wang, W.; Cao, H. MEMS Gyroscope Temperature Compensation Based on Drive Mode Vibration Characteristic Control. Micromachines 2019, 10, 248. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Tan, C.-W.; Kim, H.; Hong, S.K. Oscillation Control Algorithms for Resonant Sensors with Applications to Vibratory Gyroscopes. Sensors 2009, 9, 5952–5967. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, W.; Yin, L.; Fu, Q.; Zhang, Y. Design of the digital interface circuit system for MEMS gyroscope. Mod. Phys. Lett. B 2022, 36, 2250127. [Google Scholar] [CrossRef]
- Liu, Y.; He, C.; Liu, D.; Yang, Z.; Yan, G. Digital Closed-loop Driver Design of Micromechanical Gyroscopes Based on Coordinated Rotation Digital Computer Algorithm. In Proceedings of the 8th Annual IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Suzhou, China, 7–10 April 2013. [Google Scholar]
- Cao, H.; Zhang, Y.; Shen, C.; Liu, Y.; Wang, X. Temperature Energy Influence Compensation for MEMS Vibration Gyroscope Based on RBF NN-GA-KF Method. Shock Vib. 2018, 2018, 2830686.1–2830686.10. [Google Scholar] [CrossRef]
- Wang, T.; Zhong, S.; Luo, H.; Kuang, N. Drift Error Calibration Method Based on Multi-MEMS Gyroscope Data Fusion. Int. J. Precis. Eng. Manuf. 2023, 24, 1835–1844. [Google Scholar] [CrossRef]
- Lian, J.; Li, J.; Xu, L. The Effect of Displacement Constraints on the Failure of MEMS Tuning Fork Gyroscopes under Shock Impact. Micromachines 2019, 10, 343. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.; Li, Y.; Tang, Y.; Li, J.; Xu, L. Analysis of the vulnerability of MEMS tuning fork gyroscope during the gun launch. Microelectron. Reliab. 2020, 107, 113619. [Google Scholar] [CrossRef]
- Cao, H.L. Research and Experiment on the Technology of Elelctrostatic Compensation and Control of Silicon Micro-Machined Gyroscope. Ph.D. Thesis, Southeast University, Nanjing, China, 2014. [Google Scholar]
- Cao, H.L.; Li, H.S. Investigation of a vacuum packaged MEMS gyroscope architecture’s temperature robustness. Int. J. Appl. Electromagn. Mech. 2013, 41, 495–506. [Google Scholar] [CrossRef]
- Li, Z.; Cui, Y.; Gu, Y.; Wang, G.; Yang, J.; Chen, K.; Cao, H. Temperature Drift Compensation for Four-Mass Vibration MEMS Gyroscope Based on EMD and Hybrid Filtering Fusion Method. Micromachines 2023, 14, 971. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Ayazi, F. A Review of Eigenmode and Frequency Control in Piezoelectric MEMS Resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2023, 70, 1172–1188. [Google Scholar] [CrossRef] [PubMed]
- Qi, B.; Cheng, J.; Wang, Z.; Jiang, C.; Jia, C. A Novel Temperature Drift Error Estimation Model for Capacitive MEMS Gyros Using Thermal Stress Deformation Analysis. Micromachines 2024, 15, 324. [Google Scholar] [CrossRef] [PubMed]
- Fan, B.; Guo, S.; Cheng, M.; Yu, L.; Zhou, M.; Hu, W.; Zheng, F.; Bu, F.; Xu, D. Frequency Symmetry Comparison of Cobweb-Like Disk Resonator Gyroscope With Ring-Like Disk Resonator Gyroscope. IEEE Electron Device Lett. 2019, 40, 1515–1518. [Google Scholar] [CrossRef]
- Clark, W.A. Micromachined Vibratory Rate Gyroscopes. Ph.D. Thesis, University of California, Berkeley, Berkeley, CA, USA, 1997. [Google Scholar]
- Ismail, A.; George, B.; Elmallah, A.; Mokhtar, A.; Abdelazim, M.; Elmala, M.; Elshennawy, A.; Omar, A.; Saeed, M.; Mosta, I.; et al. A high performance MEMS based digital-output gyroscope. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013. [Google Scholar]
- Liu, D.; Lu, N.N.; Cui, J.; Lin, L.T.; Ding, H.T.; Yang, Z.C.; Hao, Y.L.; Yan, G. Digital closed-loop control based on adaptive filter for drive mode of a MEMS gyroscope. IEEE Sens. 2010, 1722–1726. [Google Scholar] [CrossRef]
- Tan, B.; Wang, D.; Yu, K. Variable-structure PID control in forging manipulator. J. Xi’an Technol. Univ. 2009, 29, 466–470. [Google Scholar]






| Parameters | Unit | Value or Expression |
|---|---|---|
| kg | ||
| N/m/s | T | |
| N/m | T | |
| / | N/m/s | |
| / | N/m | |
| N | ||
| N | ||
| N/V | ||
| F/m | ||
| F/V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Li, J.; Yang, J.; Xu, L. Research on Adaptive Closed-Loop Control of Microelectromechanical System Gyroscopes under Temperature Disturbance. Micromachines 2024, 15, 1102. https://doi.org/10.3390/mi15091102
Yang K, Li J, Yang J, Xu L. Research on Adaptive Closed-Loop Control of Microelectromechanical System Gyroscopes under Temperature Disturbance. Micromachines. 2024; 15(9):1102. https://doi.org/10.3390/mi15091102
Chicago/Turabian StyleYang, Ke, Jianhua Li, Jiajie Yang, and Lixin Xu. 2024. "Research on Adaptive Closed-Loop Control of Microelectromechanical System Gyroscopes under Temperature Disturbance" Micromachines 15, no. 9: 1102. https://doi.org/10.3390/mi15091102






