Continuous High-Precision Positioning in Smartphones by FGO-Based Fusion of GNSS–PPK and PDR
Abstract
:1. Introduction
2. Methodology
2.1. PDR
2.2. GNSS
- is the pseudorange from satellite i;
- c is the speed of light;
- and are the receiver and satellite clock biases, respectively;
- represents satellite orbit errors;
- and are the ionospheric and tropospheric delays;
- encompasses various noise sources and multipath errors.
- Clock offsets: the receiver’s clock is less accurate compared with the atomic clocks on GNSS satellites, leading to timing errors.
- Ephemeris errors: inaccuracies in the satellite’s transmitted position.
- Ionospheric and tropospheric delays: signal propagation is affected by the Earth’s atmosphere, causing delays.
- Multipath and NLOS (non-line-of-sight): signals reflecting off surfaces before reaching the receiver, leading to errors in the measured pseudorange.
- is the carrier phase measurement;
- is the carrier wavelength;
- is the integer ambiguity (number of whole carrier wavelengths between the satellite and the receiver);
- Other terms are similar to those in the pseudorange equation, with representing the measurement noise specific to carrier phase.
- Ambiguity resolution: PPK involves resolving the integer ambiguity , which is crucial for achieving high precision. This often requires a reference station (a nearby base station) with known coordinates to help resolve these ambiguities.
- Error corrections: PPK applies corrections for ionospheric and tropospheric delays, satellite clock errors, and ephemeris errors. These corrections are typically derived from precise models or additional reference stations.
2.3. PDR Fusion with GNSS–SPP and PPK with KF in Smartphones
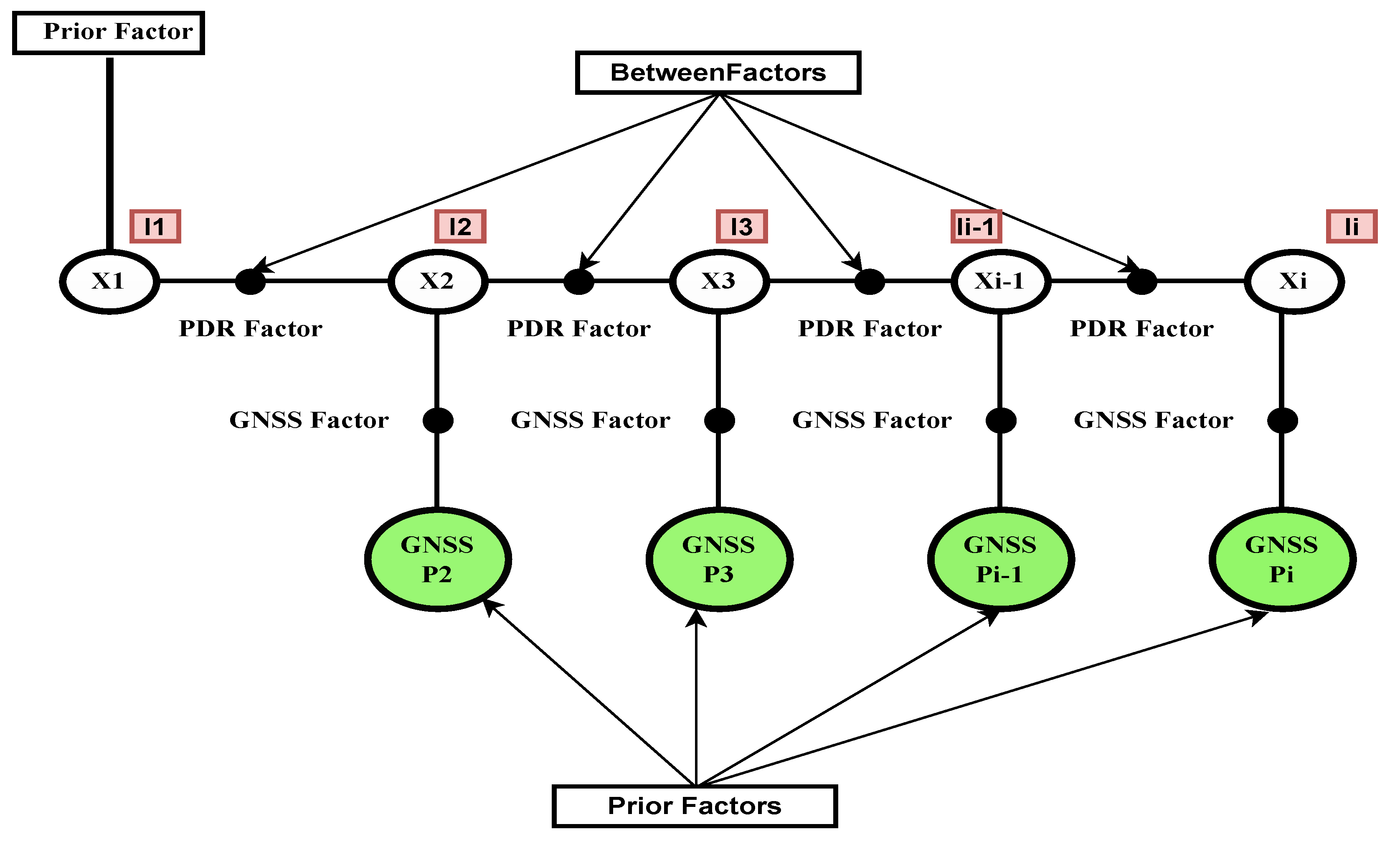
2.4. PDR Fusion with GNSS–SPP and GNSS–PPK with FGO in Smartphones
3. Experimental Evaluation
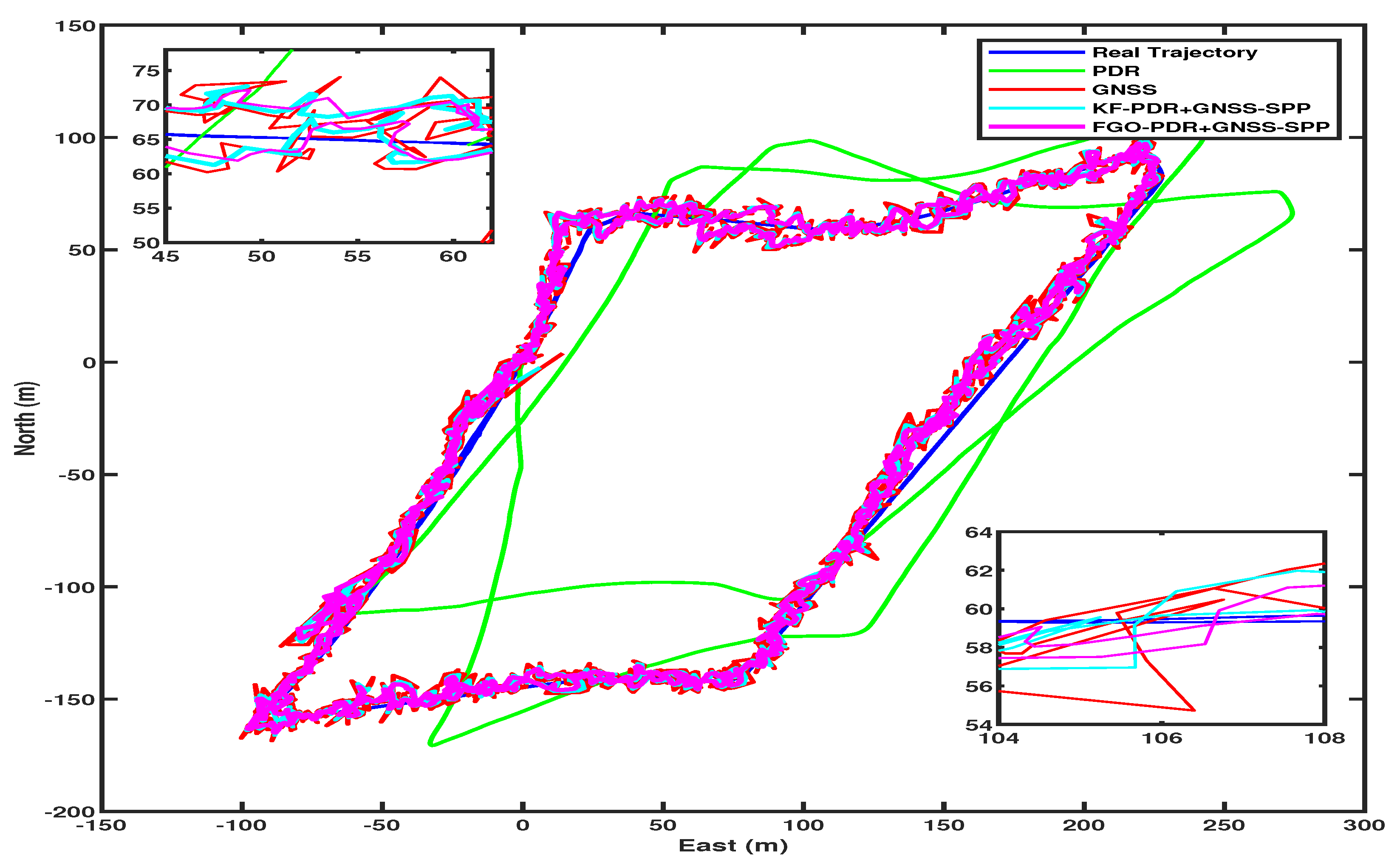
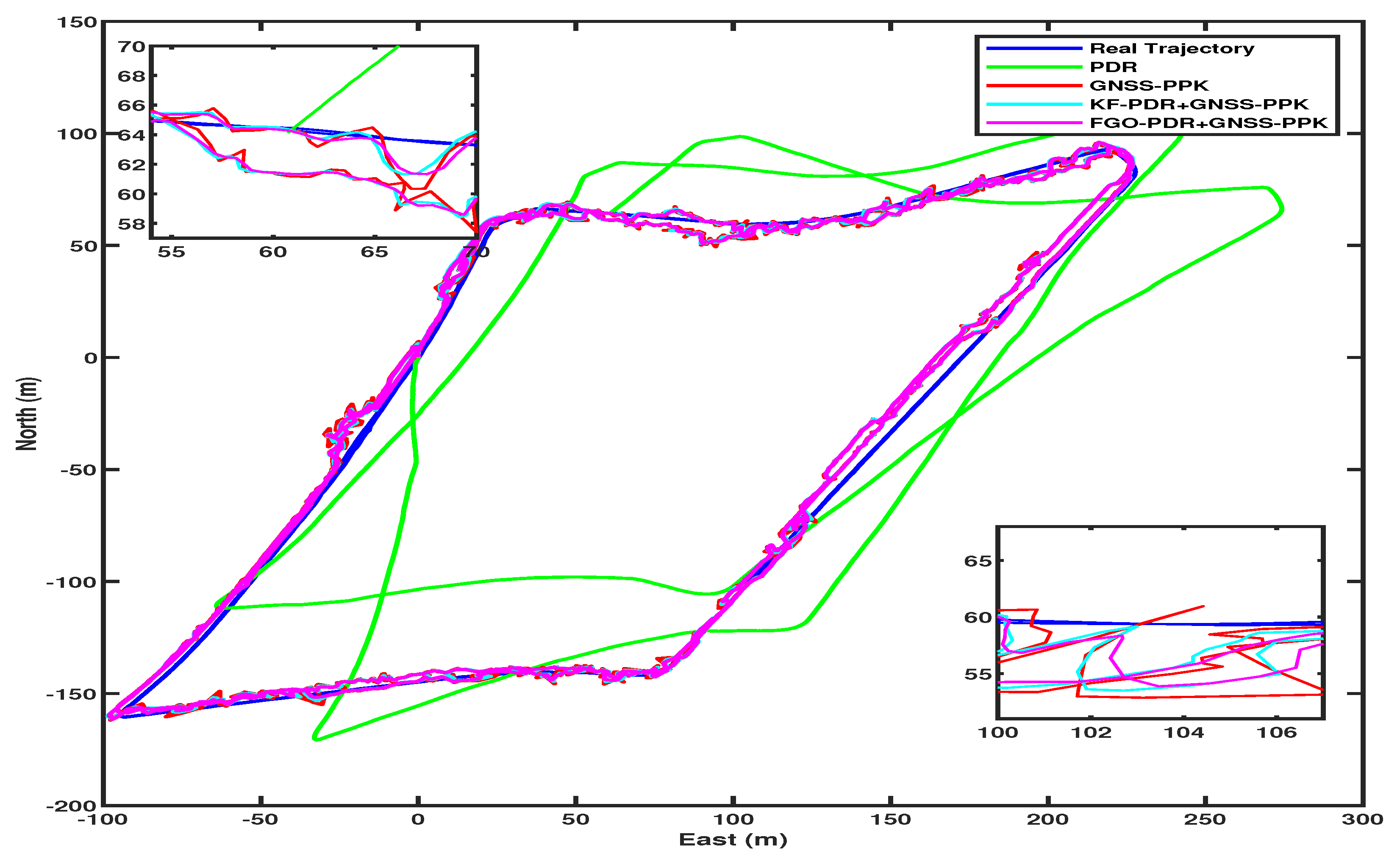
3.1. Experimental Description
3.2. Results
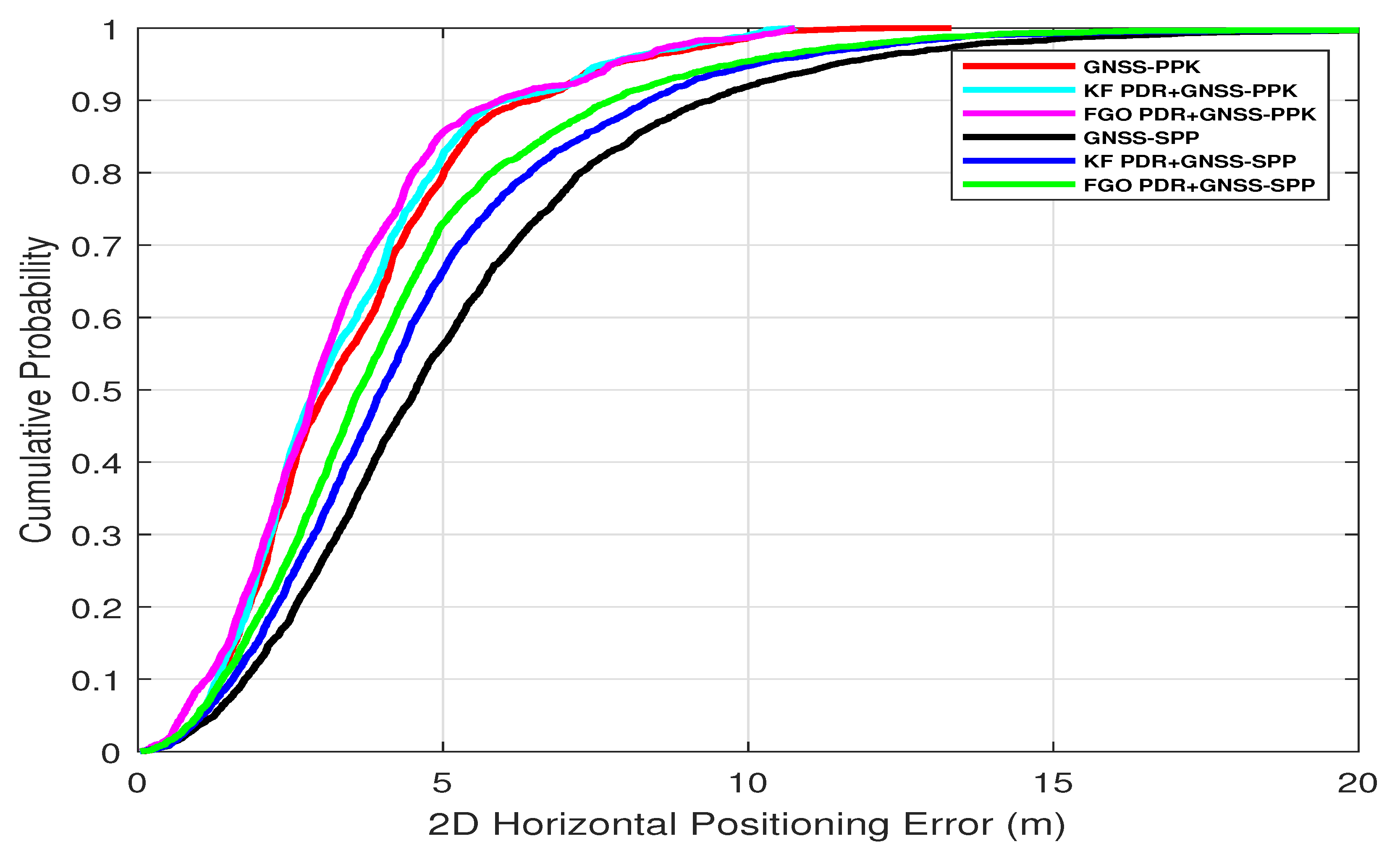
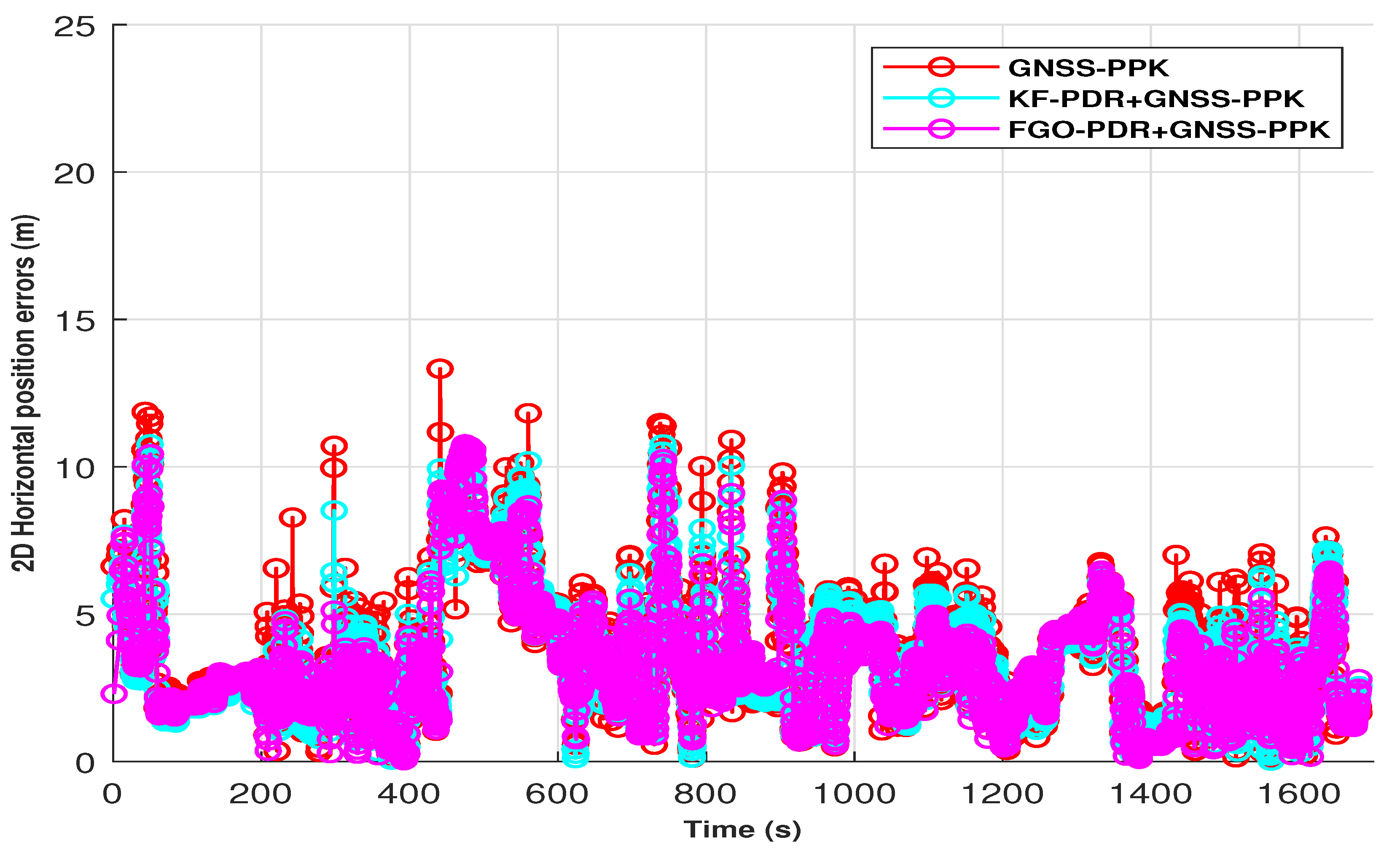
3.2.1. Position Error
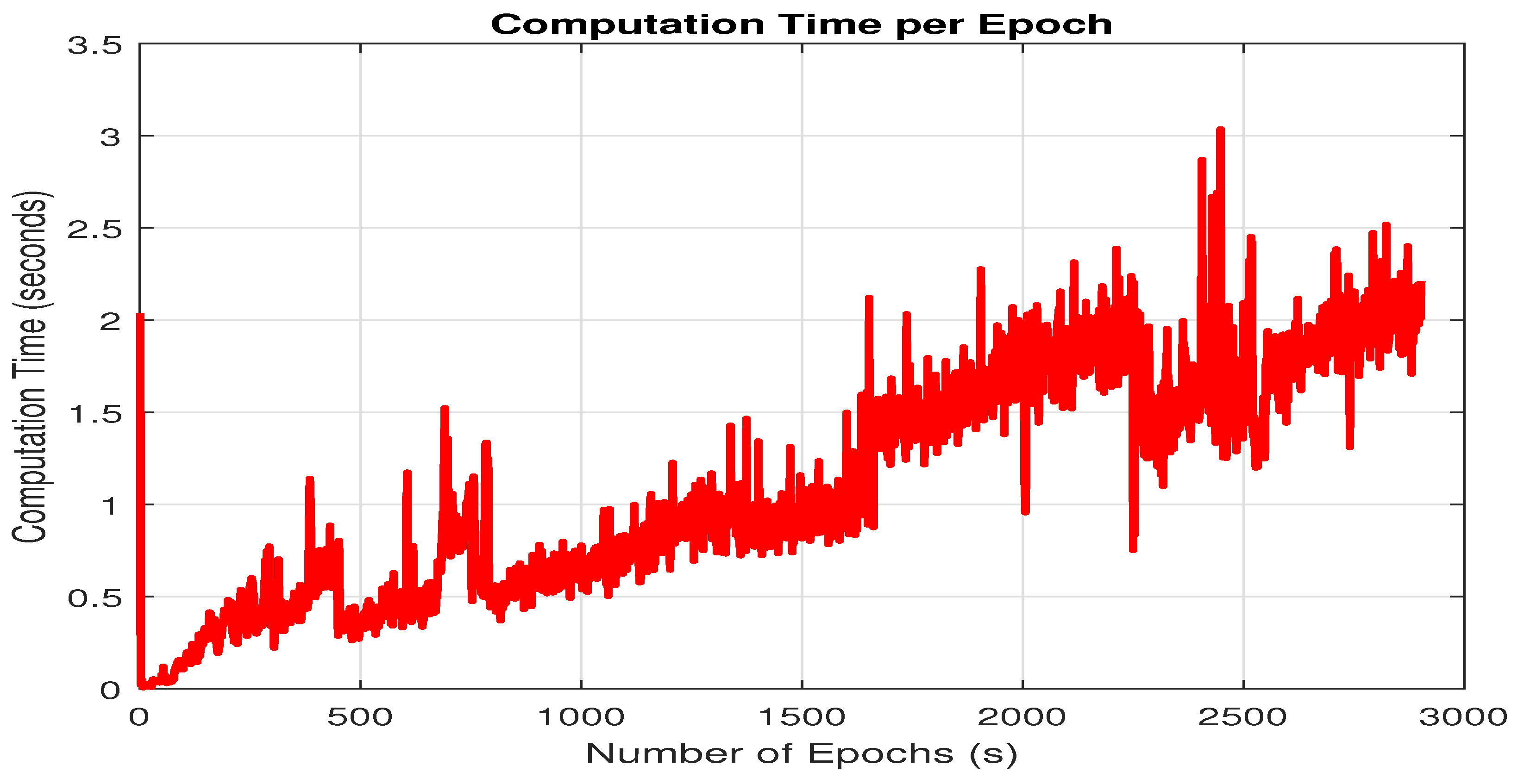
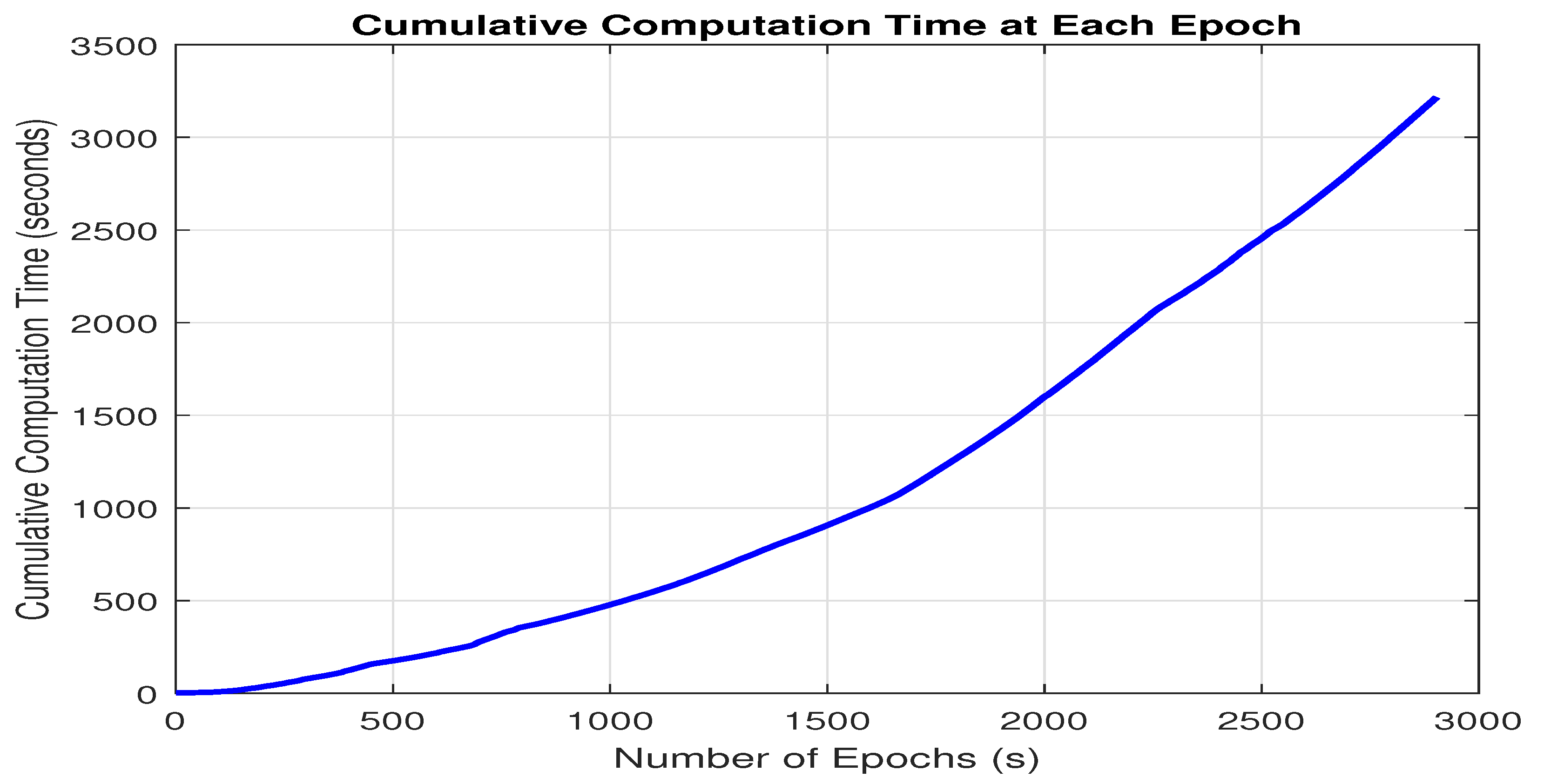
3.2.2. Computational Load
3.3. Discussion
4. Conclusions and Future Work
- (1)
- It is essential to explore the balance between computational load and the performance of FGO–PDR/GNSS systems. Implementing a sliding window for optimization could be a promising approach to reduce computational demands while preserving the system’s performance.
- (2)
- We want to assess our fusion architecture’s performance using more datasets in a variety of complex environments, including real-time smartphone locations and deep urban canyons, using sliding window-based FGO to maintain a healthy balance between computational complexity and accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FGO | Factor Graph Optimization |
| GNSS | Global Navigation Satellite Systems |
| IMU | Inertial Measurement Unit |
| KF | Kalman Filter |
| NLOS | Non-Line-of-Sight |
| PNT | Positioning Navigation and Timing |
| PDR | Pedestrian Dead Reckoning |
| SPP | Single-Point Positioning |
| PPK | Post-Processing Kinematics |
References
- Paziewski, J. Recent advances and perspectives for positioning and applications with smartphone GNSS observations. Meas. Sci. Technol. 2020, 31, 091001. [Google Scholar] [CrossRef]
- Weng, D.; Chen, W.; Ji, S.; Wang, J. Intelligent Urban Positioning Using Smartphone-Based GNSS and Pedestrian Network. IEEE Internet Things J. 2024, 11, 22537–22549. [Google Scholar] [CrossRef]
- Banville, S.; Van Diggelen, F. Precise positioning using raw GPS measurements from Android smartphones. GPS World 2016, 27, 43–48. [Google Scholar]
- Specht, C.; Szot, T.; Dąbrowski, P.; Specht, M. Testing GNSS receiver accuracy in Samsung Galaxy series mobile phones at a sports stadium. Meas. Sci. Technol. 2020, 31, 064006. [Google Scholar] [CrossRef]
- Yun, J.; Lim, C.; Park, B. Inherent limitations of Smartphone GNSS Positioning and effective methods to increase the accuracy utilizing dual-frequency measurements. Sensors 2022, 22, 9879. [Google Scholar] [CrossRef]
- Karaim, M.; Elsheikh, M.; Noureldin, A.; Rustamov, R. GNSS error sources. Multifunct. Oper. Appl. GPS 2018, 32, 137–144. [Google Scholar]
- Burke, J. DARPA positioning, navigation, and timing (PNT) technology and their impacts on GPS users. In Proceedings of the 23rd Meeting Space-Based Positioning, Navigation, and Timing (PNT) Advisory Board, Alexandria, VA, USA, 6–7 June 2019. [Google Scholar]
- Zhuang, Y.; Sun, X.; Li, Y.; Huai, J.; Hua, L.; Yang, X.; Cao, X.; Zhang, P.; Cao, Y.; Qi, L.; et al. Multi-sensor integrated navigation/positioning systems using data fusion: From analytics-based to learning-based approaches. Inf. Fusion 2023, 95, 62–90. [Google Scholar] [CrossRef]
- Elmezayen, A.; Elsheikh, M.; Iqbal, U.; Noureldin, A. Examining the Capabilities of Smartphone-Based High Precision Positioning in Challenging Suburban Environments. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022; pp. 2329–2338. [Google Scholar]
- Kuang, J.; Niu, X.; Chen, X. Robust pedestrian dead reckoning based on MEMS-IMU for smartphones. Sensors 2018, 18, 1391. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Liu, Z.; Xia, Q.; Chen, C.; Hyyppa, J. A Probabilistic Method-Based Smartphone GNSS Fault Detection and Exclusion System Utilizing PDR Step Length. Remote Sens. 2023, 15, 4993. [Google Scholar] [CrossRef]
- Zhu, F.; Tao, X.; Liu, W.; Shi, X.; Wang, F.; Zhang, X. Walker: Continuous and precise navigation by fusing GNSS and MEMS in smartphone chipsets for pedestrians. Remote Sens. 2019, 11, 139. [Google Scholar] [CrossRef]
- Zhang, R.; Mi, J.; Li, J.; Wang, Q. A Continuous PDR and GNSS Fusing Algorithm for Smartphone Positioning. Remote Sens. 2022, 14, 5171. [Google Scholar] [CrossRef]
- Yan, W.; Zhang, Q.; Wang, L.; Mao, Y.; Wang, A.; Zhao, C. A modified kalman filter for integrating the different rate data of gyros and accelerometers retrieved from android smartphones in the GNSS/IMU coupled navigation. Sensors 2020, 20, 5208. [Google Scholar] [CrossRef]
- Li, W.; Cui, X.; Lu, M. A robust graph optimization realization of tightly coupled GNSS/INS integrated navigation system for urban vehicles. Tsinghua Sci. Technol. 2018, 23, 724–732. [Google Scholar] [CrossRef]
- Wen, W.; Bai, X.; Kan, Y.C.; Hsu, L.T. Tightly coupled GNSS/INS integration via factor graph and aided by fish-eye camera. IEEE Trans. Veh. Technol. 2019, 68, 10651–10662. [Google Scholar] [CrossRef]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L.T. Comparison of extended Kalman filter and factor graph optimization for GNSS/INS integrated navigation system. arXiv 2020, arXiv:2004.10572. [Google Scholar]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L.T. Factor graph optimization for GNSS/INS integration: A comparison with the extended Kalman filter. NAVIGATION J. Inst. Navig. 2021, 68, 315–331. [Google Scholar] [CrossRef]
- Wen, W.; Kan, Y.C.; Hsu, L.T. Performance comparison of GNSS/INS integrations based on EKF and factor graph optimization. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3019–3032. [Google Scholar]
- Li, Q.; Zhang, L.; Wang, X. Loosely coupled GNSS/INS integration based on factor graph and aided by ARIMA model. IEEE Sens. J. 2021, 21, 24379–24387. [Google Scholar] [CrossRef]
- Xin, S.; Wang, X.; Zhang, J.; Zhou, K.; Chen, Y. A Comparative Study of Factor Graph Optimization-Based and Extended Kalman Filter-Based PPP-B2b/INS Integrated Navigation. Remote Sens. 2023, 15, 5144. [Google Scholar] [CrossRef]
- Boguspayev, N.; Akhmedov, D.; Raskaliyev, A.; Kim, A.; Sukhenko, A. A Comprehensive Review of GNSS/INS Integration Techniques for Land and Air Vehicle Applications. Appl. Sci. 2023, 13, 4819. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Jia, J.; Sun, H.; Wang, T.; Hyyppa, J. Implementation and performance analysis of the PDR/GNSS integration on a smartphone. GPS Solut. 2022, 26, 81. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Chen, S.; Meng, Q.; Bo, Y.; Hyyppa, J. Cooperative Smartphone GNSS/PDR for Pedestrian Navigation. IEEE Trans. Circuits Syst. II Express Briefs 2022, 70, 2301–2305. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Jia, J.; Sun, H.; Wang, T.; Hyyppä, J. Smartphone PDR/GNSS Integration via Factor Graph Optimization for Pedestrian Navigation. IEEE Trans. Instrum. Meas. 2022, 71, 8504112. [Google Scholar] [CrossRef]
- Hussain, A.; Díez, L.E. Comparison of FGO and KF for PDR-GNSS Fusion on Smartphone for Diverse Pedestrian Movements. In Proceedings of the 2023 13th International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nuremberg, Germany, 25–28 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Magsi, A.H.; Díez, L.E. Comparison of FGO and KF for PDR-GNSS Fusion under Different PDR Errors. IEEE Trans. Instrum. Meas. 2024, 73, 8506312. [Google Scholar] [CrossRef]
- Weinberg, H. Using the ADXL202 in pedometer and personal navigation applications. Analog Devices AN-602 Appl. Note 2002, 2, 1–6. [Google Scholar]
- Li, G.; Geng, J. Characteristics of raw multi-GNSS measurement error from Google Android smart devices. GPS Solut. 2019, 23, 90. [Google Scholar] [CrossRef]
- Fu, G.M.; Khider, M.; Van Diggelen, F. Android raw GNSS measurement datasets for precise positioning. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2020), Online, 22–25 September 2020; pp. 1925–1937. [Google Scholar]
- Lachapelle, G.; Gratton, P.; Horrelt, J.; Lemieux, E.; Broumandan, A. Evaluation of a low cost hand held unit with GNSS raw data capability and comparison with an android smartphone. Sensors 2018, 18, 4185. [Google Scholar] [CrossRef]
- Jiménez-Martínez, M.J.; Farjas-Abadia, M.; Quesada-Olmo, N. An approach to improving GNSS positioning accuracy using several GNSS devices. Remote Sens. 2021, 13, 1149. [Google Scholar] [CrossRef]
- Paziewski, J.; Pugliano, G.; Robustelli, U. Performance assessment of GNSS single point positioning with recent smartphones. In Proceedings of the IMEKO TC-19 International Workshop on Metrology for the Sea, Naples, Italy, 5–7 October 2020; pp. 5–7. [Google Scholar]
- Everett, T.; Taylor, T.; Lee, D.K.; Akos, D.M. Optimizing the use of RTKLIB for smartphone-based GNSS measurements. Sensors 2022, 22, 3825. [Google Scholar] [CrossRef]
- Darugna, F.; Wübbena, J.; Ito, A.; Wübbena, T.; Wübbena, G.; Schmitz, M. RTK and PPP-RTK using smartphones: From short-baseline to long-baseline applications. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 3932–3945. [Google Scholar]
- Dellaert, F. Factor Graphs and GTSAM: A Hands-On Introduction; Technical Report; Georgia Institute of Technology: Atlanta, GA, USA, 2012. [Google Scholar]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems; Department of Civil and Environmental Engineering Duke University: Durham, NC, USA, 2019; Volume 19. [Google Scholar]
- GNSSLogger. 2016. Available online: https://github.com/google/gps-measurement-tools (accessed on 15 May 2024).
- Takasu, T. RTKLIB: An Open Source Program Package for GNSS Positioning. Version 2.4.3. 2023. Available online: https://www.rtklib.com (accessed on 15 May 2024).
- Zangenehnejad, F.; Gao, Y. GNSS smartphones positioning: Advances, challenges, opportunities, and future perspectives. Satell. Navig. 2021, 2, 1–23. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, M.; Zhou, C.; Zhang, P. Precise point positioning using dual-frequency GNSS observations on smartphone. Sensors 2019, 19, 2189. [Google Scholar] [CrossRef]
- Glaner, M.F.; Weber, R. Breaking the one-meter accuracy level with smartphone GNSS data. Eng. Proc. 2023, 54, 16. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Development of the low-cost RTK-GPS receiver with an open source program package RTKLIB. In Proceedings of the International Symposium on GPS/GNSS, Seogwipo-si, Republic of Korea, 4–6 November 2009; Volume 1, pp. 1–6. [Google Scholar]



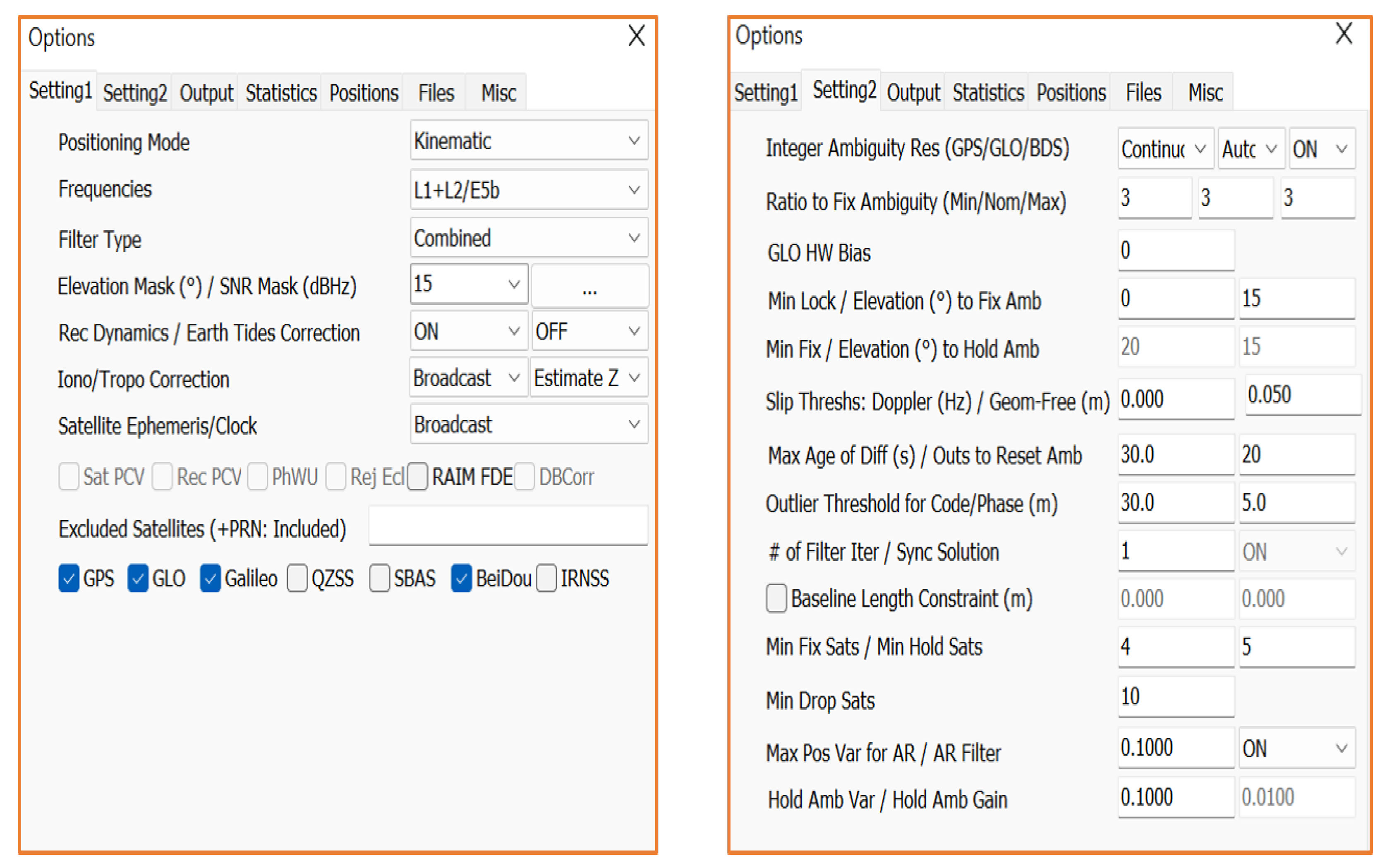


| Positioning Mode | Kinematic |
| Filter Type | Combined |
| GNSS Constellations | Disable QZSS, IRNSS, and SBAS |
| Ionospheric Correction | Broadcast |
| Tropospheric Correction | Estimate ZTD |
| Satellite Clock | Broadcast |
| Integer AR | Continuous for GPS |
| Approach | GNSS Processing Techniques | % FGO Mean Improvement over GNSS and KF | |||||
|---|---|---|---|---|---|---|---|
| PPK | SPP | ||||||
| Mean Error | Median Error | STD | Mean Error | Median Error | STD | ||
| GNSS (only) | 3.56 m | 3.11 m | 2.10 m | 5.23 m | 4.55 m | 3.56 m | 7.28% (PPK) and 18.5% (SPP) |
| KF–PDR+GNSS | 3.44 m | 2.92 m | 2.04 m | 4.60 m | 4.00 m | 3.16 m | 4.36% (PPK) and 7.60% (SPP) |
| FGO–PDR+GNSS | 3.29 m | 2.88 m | 2.03 m | 4.25 m | 3.62 m | 3.02 m | as compared with SPP 22.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magsi, A.H.; Díez, L.E.; Knauth, S. Continuous High-Precision Positioning in Smartphones by FGO-Based Fusion of GNSS–PPK and PDR. Micromachines 2024, 15, 1141. https://doi.org/10.3390/mi15091141
Magsi AH, Díez LE, Knauth S. Continuous High-Precision Positioning in Smartphones by FGO-Based Fusion of GNSS–PPK and PDR. Micromachines. 2024; 15(9):1141. https://doi.org/10.3390/mi15091141
Chicago/Turabian StyleMagsi, Amjad Hussain, Luis Enrique Díez, and Stefan Knauth. 2024. "Continuous High-Precision Positioning in Smartphones by FGO-Based Fusion of GNSS–PPK and PDR" Micromachines 15, no. 9: 1141. https://doi.org/10.3390/mi15091141
APA StyleMagsi, A. H., Díez, L. E., & Knauth, S. (2024). Continuous High-Precision Positioning in Smartphones by FGO-Based Fusion of GNSS–PPK and PDR. Micromachines, 15(9), 1141. https://doi.org/10.3390/mi15091141








