Theoretical and Experimental Investigation on a Novel Cavitation-Assisted Abrasive Flow Polishing Method
Abstract
:1. Introduction
2. Materials and Methods
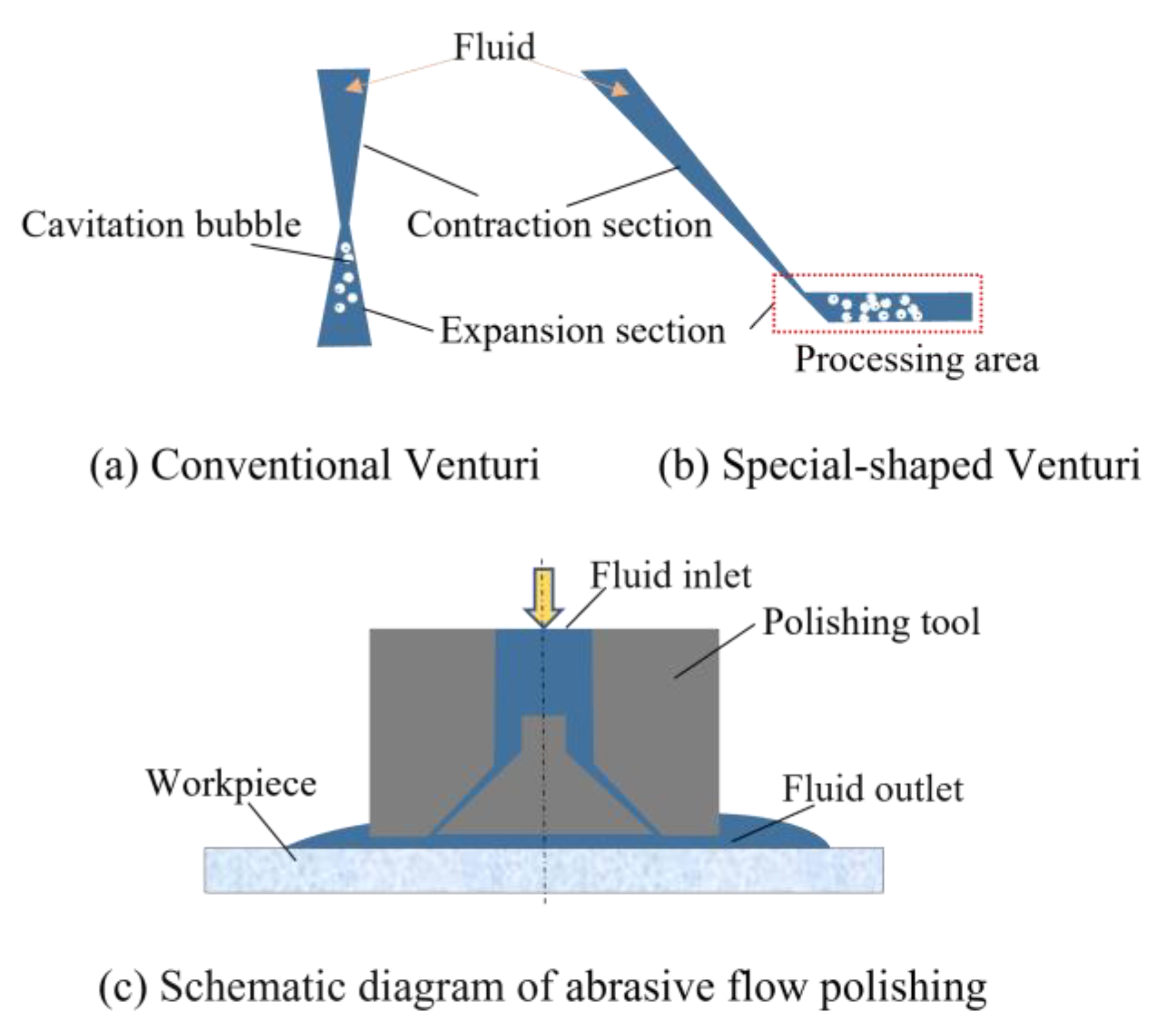
2.1. Venturi Tube Analysis
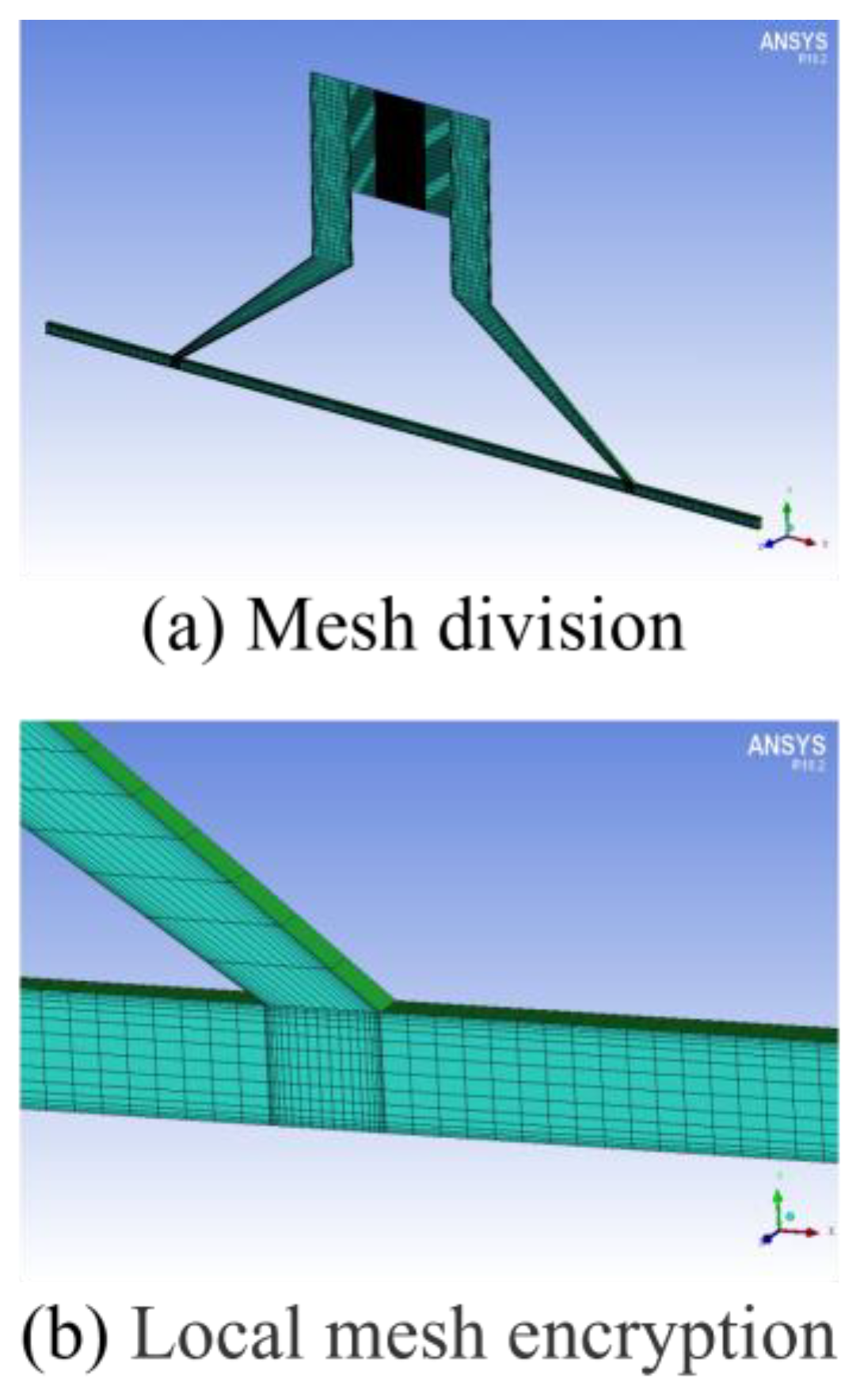
2.2. Numerial Simulation Method for the Special-Shaped Venturi Cavitaiton Abrasive Flow Polishing Tools
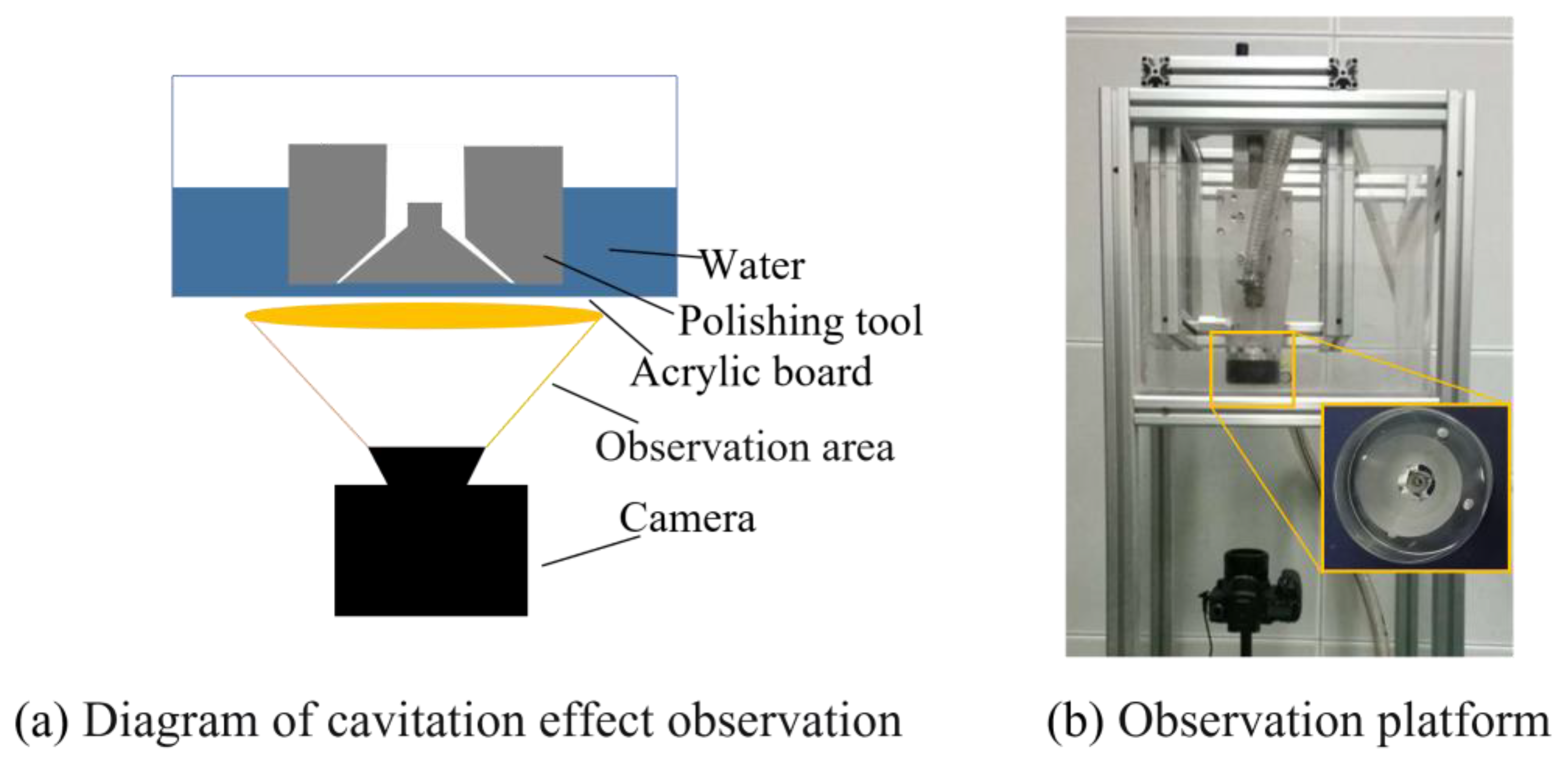
2.3. Cavitation-Assisted Abrasive Flow Polishing Experiment
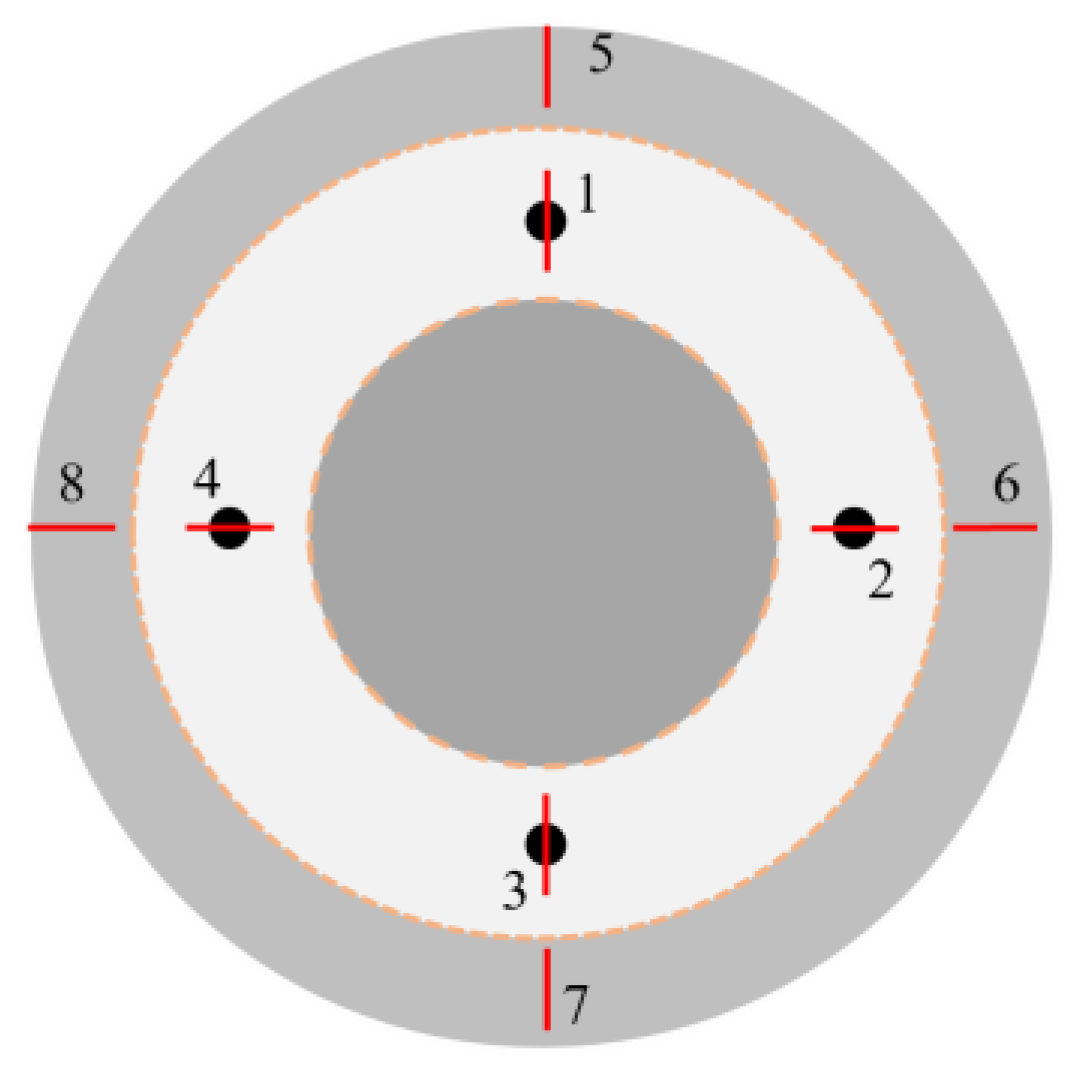
2.4. Measuring Methodology
3. Results and Discussion
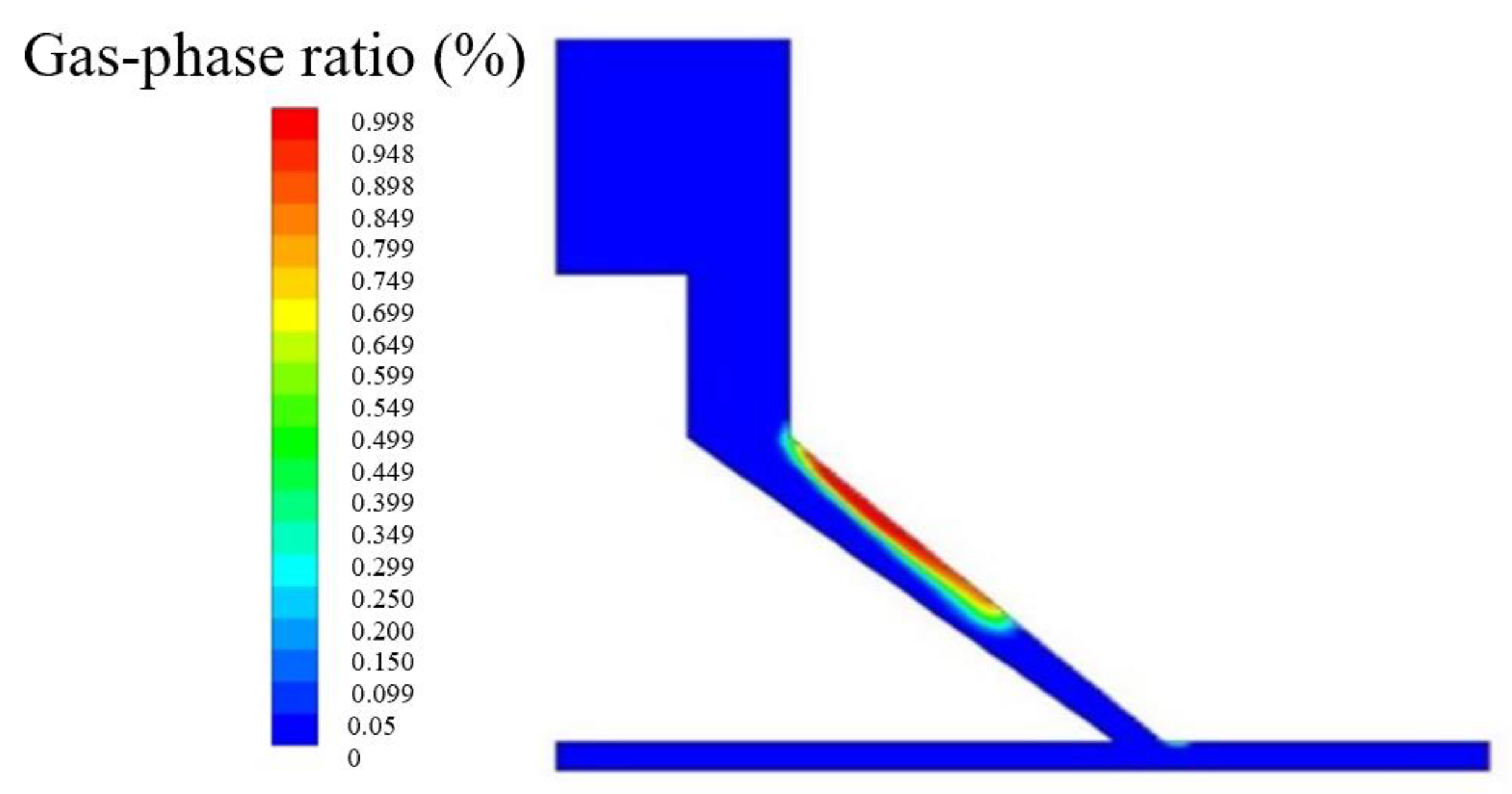
3.1. Numerical Simulation Analysis
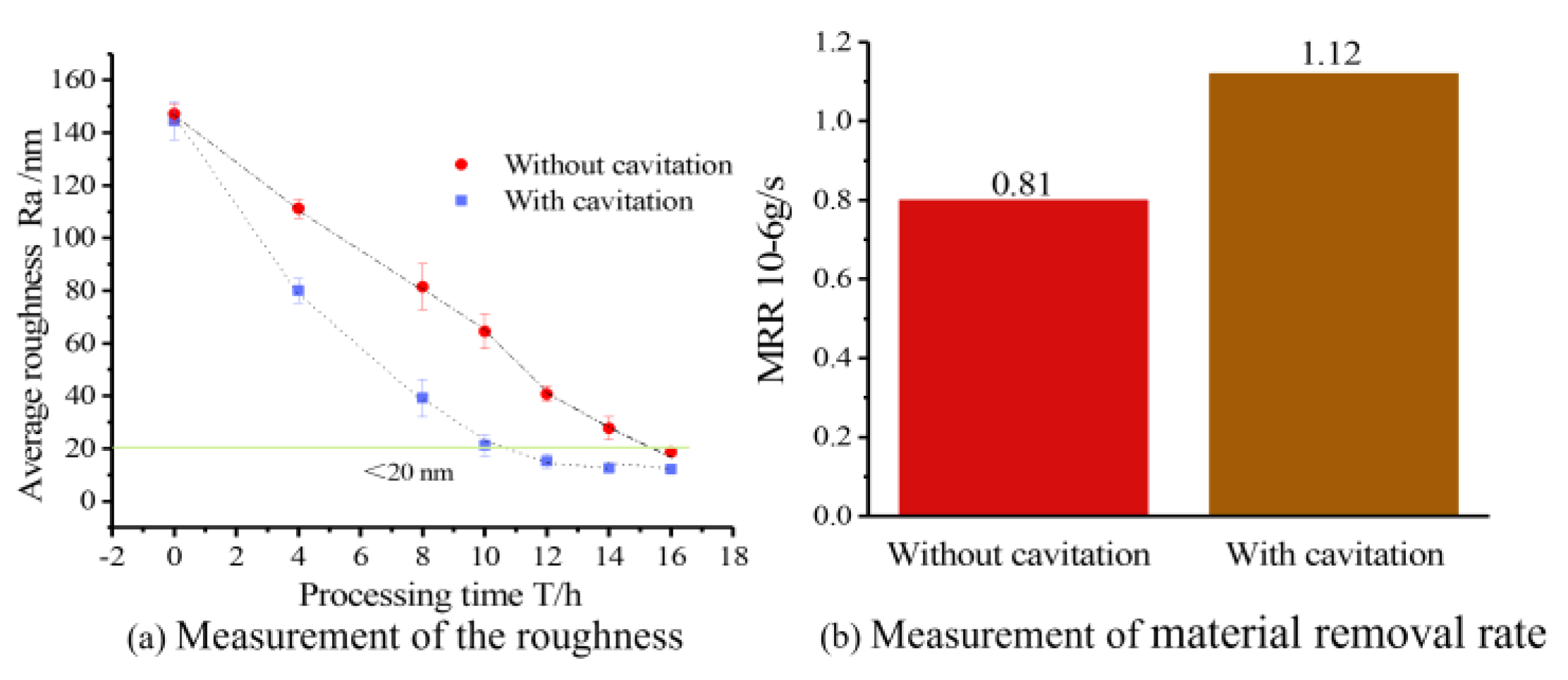
3.2. Experimental Analysis
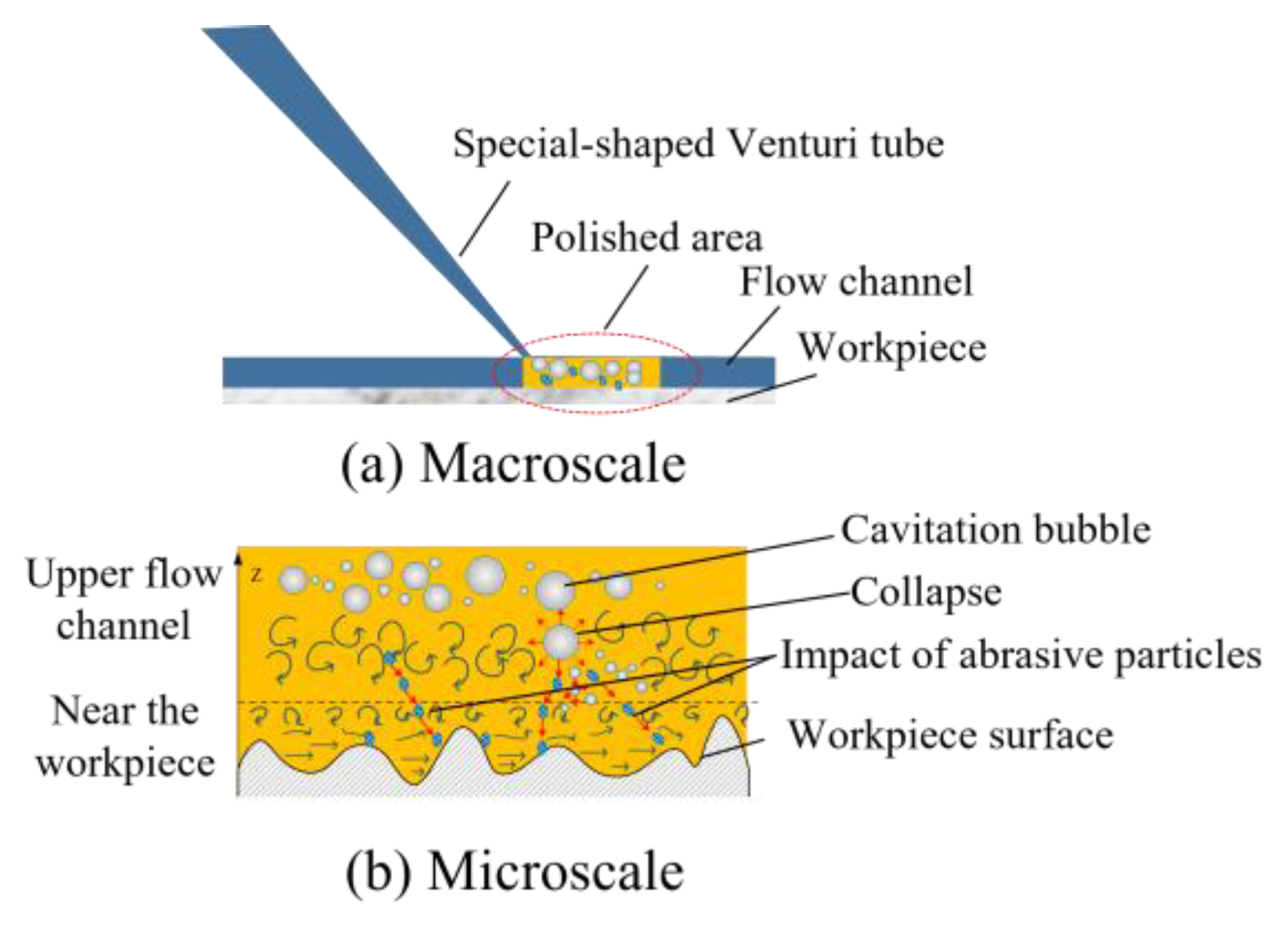
- Water flow directly propels abrasive particles, causing them to erode the workpiece.
- Due to the structure of the special-shaped Venturi tube, cavitation bubbles are generated and located higher up in the flow channel. The cavitation bubbles do not collapse directly near the workpiece surface, causing extensive cavitation erosion on the workpiece. The micro-jets generated by the collapse of the cavitation bubbles change the direction of the abrasive movement as the abrasive particles pass over the flow channel; thereby, the mechanism significantly amplifies the material removal rate, rendering cavitation-assisted abrasive erosion markedly more efficient than its traditional counterpart.
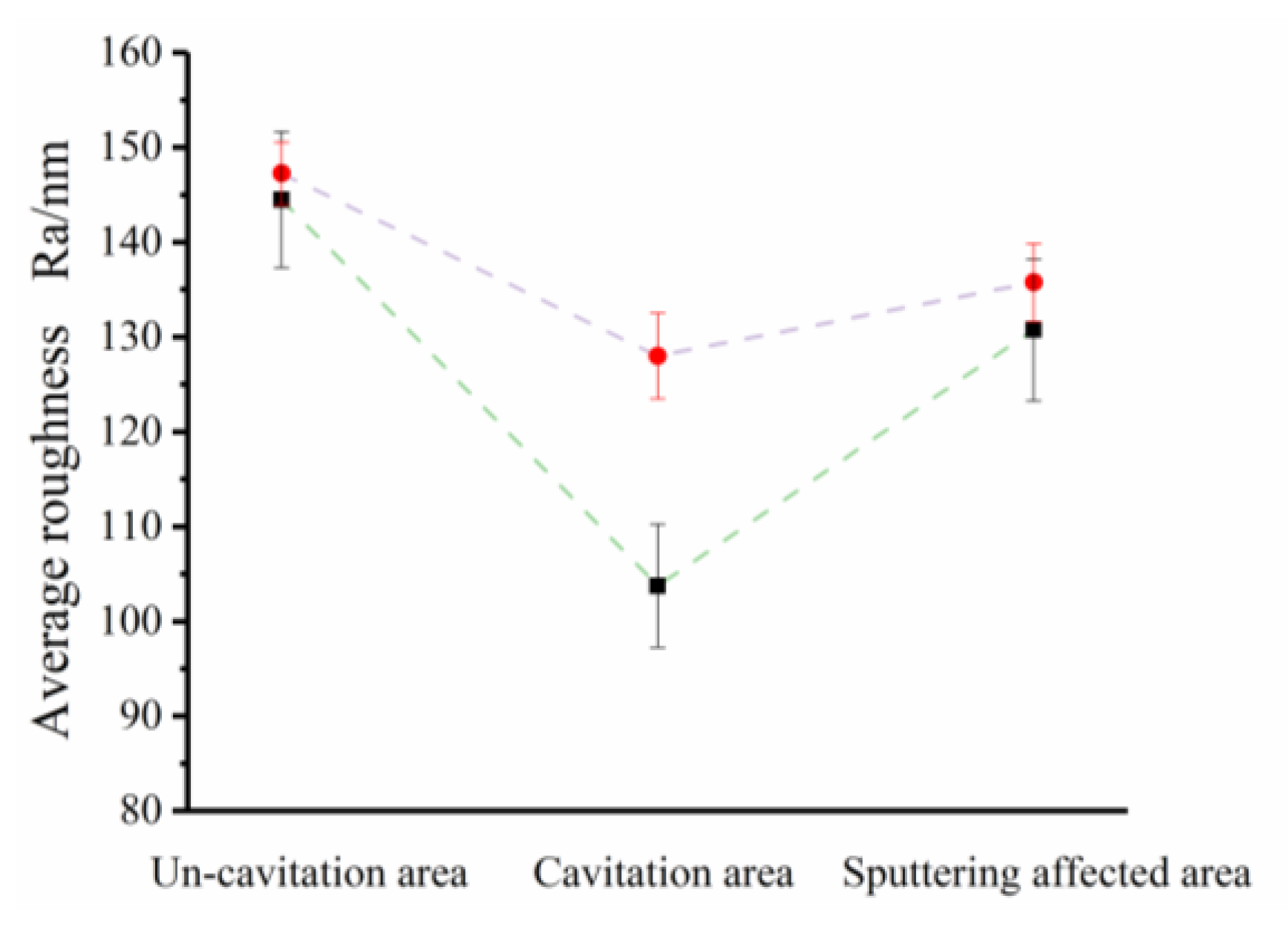
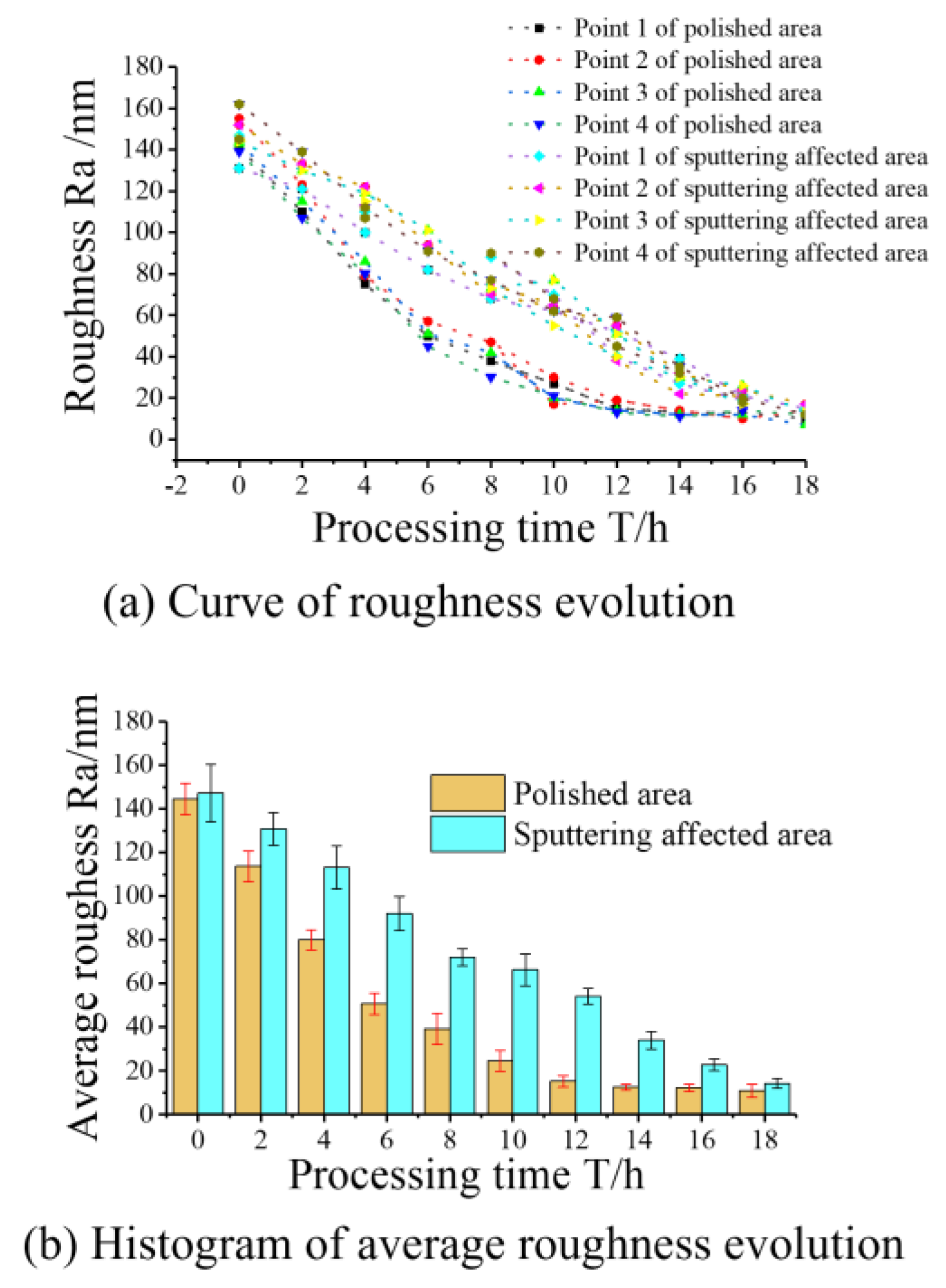
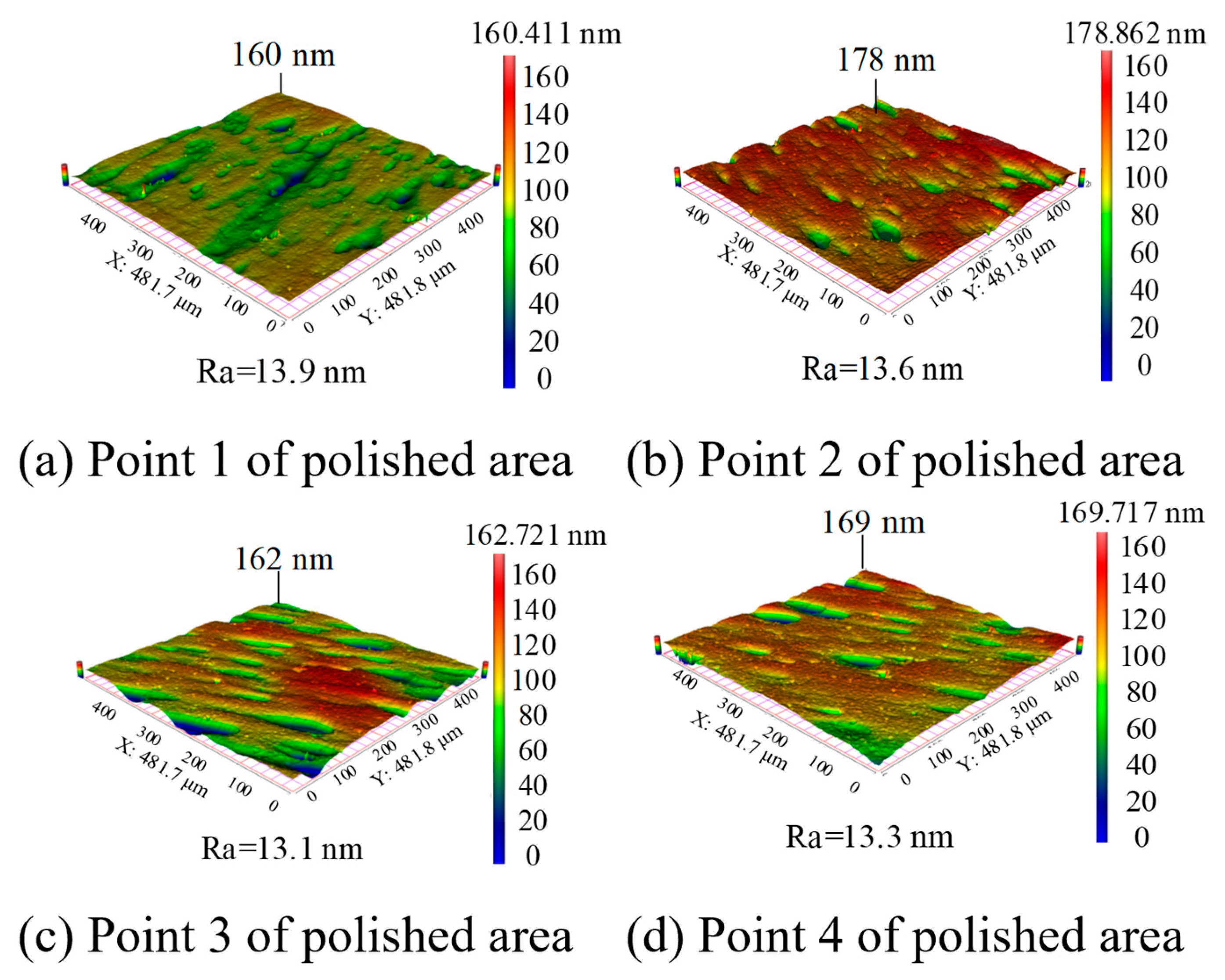
3.3. Surface Topography Changing after Processing
4. Conclusions
- Orthogonal test-based numerical simulation was employed to refine the Venturi tube’s structure, specifically tailored for the polishing of flat workpieces. When the angle is 55°, the size is 0.9 mm, and the size is 1.4 mm in the special-shaped Venturi structure, apparent cavitation phenomena can be generated in the machining area, and the cavitation area can account for ~70% of the processing region, which is ~5.8% different from the simulation;
- Silicon wafer processing experiments conducted using the cavitation-assisted abrasive flow polishing system confirmed that the cavitation effect, facilitated by the special-shaped Venturi design, significantly aids the abrasive flow polishing process. This innovation has resulted in a roughly 60% enhancement in processing efficiency compared to traditional methods while maintaining equivalent surface quality standards.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, P.; Cheung, C.F.; Wang, C.; Zhao, C. Novel hybrid robot and its processes for precision polishing of freeform surfaces. Precis. Eng. 2020, 64, 53–62. [Google Scholar] [CrossRef]
- Wen, J.; Yao, H.; Li, H.; You, B. Research on the Hobbing Processing Method of Marine Beveloid Gear. Machines 2024, 12, 35. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J.; Zhang, J.; Hartmaier, A. Atomistic investigation of machinability of monocrystalline 3C–SiC in elliptical vibration-assisted diamond cutting. Ceram. Int. 2021, 47, 2358–2366. [Google Scholar] [CrossRef]
- Kim, W.B.; Lee, S.J.; Kim, Y.J.; Lee, E.S. The electromechanical principle of electrorheological fluid-assisted polishing. Int. J. Mach. Tools Manuf. 2003, 43, 81–88. [Google Scholar] [CrossRef]
- Singh, M.; Singh, A.K. Magnetorheological finishing of variable diametric external surface of the tapered cylindrical workpieces for functionality improvement. J. Manuf. Process. 2021, 61, 153–172. [Google Scholar] [CrossRef]
- Beaucamp, A.T.H.; Nagai, K.; Hirayama, T.; Okada, M.; Suzuki, H.; Namba, Y. Elucidation of material removal mechanism in float polishing. Precis. Eng. 2022, 73, 423–434. [Google Scholar] [CrossRef]
- Li, P.; Wang, Y.; Li, L.; Gong, Y.; Zhou, J.; Lu, J. Ablation oxidation and surface quality during laser polishing of TA15 aviation titanium alloy. J. Mater. Res. Technol. 2023, 23, 6101–6114. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, E.; Qi, H.; Ji, S.; Chen, Z. A novel polishing method for single-crystal silicon using the cavitation rotary abrasive flow. Precis. Eng. 2020, 61, 72–81. [Google Scholar] [CrossRef]
- Manoj, M.; Jinu, G.R.; Muthuramalingam, T. Multi Response Optimization of AWJM Process Parameters on Machining TiB2 Particles Reinforced Al7075 Composite Using Taguchi-DEAR Methodology. Silicon 2018, 10, 2287–2293. [Google Scholar] [CrossRef]
- Muthuramalingam, T.; Vasanth, S.; Vinothkumar, P.; Geethapriyan, T.; Rabik, M.M. Multi Criteria Decision Making of Abrasive Flow Oriented Process Parameters in Abrasive Water Jet Machining Using Taguchi-DEAR Methodology. Silicon 2018, 10, 2015–2021. [Google Scholar] [CrossRef]
- Karkalos, N.E.; Karmiris-Obratański, P.; Kudelski, R.; Markopoulos, A.P. Experimental study on the sustainability assessment of AWJ machining of Ti-6Al-4V using glass beads abrasive particles. Sustainability 2021, 13, 8917. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, Z.; Qi, Z.; Cai, D.; Cheng, Z.; Qi, H. CFD-based study of the abrasive flow characteristics within constrained flow passage in polishing of complex titanium alloy surfaces. Powder. Technol. 2018, 333, 209–218. [Google Scholar] [CrossRef]
- Ge, J.; Zhou, H.; Li, C.; Li, Z.; Qian, P.; Li, C.; Chen, C. Soft abrasive flow polishing method and optimization research on the constrained space. Int. J. Adv. Manuf. Technol. 2022, 118, 1673–1688. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, V.; Kumar, A.; Yadav, H.N.S.; Das, M. CFD analysis of MR fluid applied for finishing of gear in MRAFF process. Mater. Today Proc. 2021, 1, 45. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Kumar, A.S.; Jin, M. Experimental and theoretical study of internal finishing by a novel magnetically driven polishing tool. Int. J. Mach. Tools Manuf. 2020, 153, 103552. [Google Scholar] [CrossRef]
- Fan, C.; Liu, K.; Chen, Y.; Xue, Y.; Zhao, J.; Khudoley, A. A new modelling method of material removal profile for electrorheological polishing with a mini annular integrated electrode. J. Mater. Process. Technol. 2022, 305, 117589. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, B.; Xie, Y.; Ji, R.; Li, Y.; Mao, W. Control mechanism of particle flow in the weak liquid metal flow field on non-uniform curvature surface based on lippmann model. Front. Mater. 2022, 9, 895263. [Google Scholar] [CrossRef]
- Van Wijngaarden, L. Mechanics of collapsing cavitation bubbles. Ultrason. Sonochem. 2016, 29, 524–527. [Google Scholar] [CrossRef]
- Chen, F.; Wang, H.; Yin, S.; Huang, S.; Tang, Q.; Luo, H. Cavitation water-suction polishing of metallic materials under negative-pressure effect. J. Mater. Process. Technol. 2019, 273, 116257. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Wu, J.; Li, L.; Tan, D. Machinability evolution of gas–liquid-solid three-phase rotary abrasive flow finishing. Int. J. Adv. Manuf. Technol. 2023, 14, 2145–2164. [Google Scholar] [CrossRef]
- Ge, J.; Ren, Y.; Xu, X.; Li, C.; Li, Z.; Xiang, W. Numerical and experimental study on the ultrasonic-assisted soft abrasive flow polishing characteristics. Int. J. Adv. Manuf. Technol. 2021, 112, 3215–3233. [Google Scholar] [CrossRef]
- Ge, J.; Li, C.; Gao, Z.; Ren, Y.; Xu, X.; Li, C. Softness abrasive flow polishing method using constrained boundary vibration. Powder Technol. 2021, 382, 173–187. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Radius R1 (mm) | 10 |
| Radius R2 (mm) | 40 |
| Inlet width LA (mm) | 4.4 |
| Initial pressure P (MPa) | 0.5 |
| Parameters | (∠) | (mm) | (mm) |
|---|---|---|---|
| Level 1 | 25 | 0.8 | 1 |
| Level 2 | 35 | 0.9 | 1.1 |
| Level 3 | 45 | 1.0 | 1.2 |
| Level 4 | 55 | 1.1 | 1.3 |
| Level 5 | 65 | 1.2 | 1.4 |
| Parameters | Details |
|---|---|
| Workpiece | Silicon wafer |
| Abrasive | Type: silicon carbide (SiC) |
| Particle size: 4000# | |
| Mass ratio: 10% | |
| Base fluid | Type: deionized water; temperature: 25 °C |
| I nitial pressure | 0.5 MPa |
| Parameters | (∠) | (mm) | (mm) | ) |
|---|---|---|---|---|
| 1 | 25 | 0.8 | 1 | 2.21% |
| 2 | 25 | 0.9 | 1.1 | 2.77% |
| 3 | 25 | 1.0 | 1.2 | 1.47% |
| 4 | 25 | 1.1 | 1.3 | 0% |
| 5 | 25 | 1.2 | 1.4 | 66.16% |
| 6 | 35 | 0.8 | 1.1 | 35.35% |
| 7 | 35 | 0.9 | 1.2 | 26.67% |
| 8 | 35 | 1 | 1.3 | 15.40% |
| 9 | 35 | 1.1 | 1.4 | 65.68% |
| 10 | 35 | 1.2 | 1 | 53.73% |
| 11 | 45 | 0.8 | 1.2 | 28.98% |
| 12 | 45 | 0.9 | 1.3 | 30.69% |
| 13 | 45 | 1.0 | 1.4 | 67.57% |
| 14 | 45 | 1.1 | 1 | 70.67% |
| 15 | 45 | 1.2 | 1.1 | 73.65% |
| 16 | 55 | 0.8 | 1.3 | 29.62% |
| 17 | 55 | 0.9 | 1.4 | 75.80% |
| 18 | 55 | 1.0 | 1 | 68.65% |
| 19 | 55 | 1.1 | 1.1 | 62.65% |
| 20 | 55 | 1.2 | 1.3 | 60.57% |
| 21 | 65 | 0.8 | 1.4 | 14.60% |
| 22 | 65 | 0.9 | 1 | 7.62% |
| 23 | 65 | 1.0 | 1.1 | 4.72% |
| 24 | 65 | 1.1 | 1.2 | 2.47% |
| 25 | 65 | 1.2 | 1.3 | 2.22% |
| (∠) | (mm) | (mm) | |
|---|---|---|---|
| Level 1 | 72.61 | 110.78 | 202.88 |
| Level 2 | 196.84 | 143.55 | 179.16 |
| Level 3 | 271.56 | 157.81 | 120.16 |
| Level 4 | 297.29 | 201.47 | 77.93 |
| Level 5 | 31.63 | 206.33 | 189.85 |
| R | 869.93 | 819.94 | 769.98 |
| Condition | Group | M | SD | T | df | p | Cohen’s d |
|---|---|---|---|---|---|---|---|
| Uncavitated area | Before polishing | 147.25 | 3.30 | 1.29 | 3 | 0.29 | 0.50 |
| After polishing | 144.50 | 7.19 | |||||
| Cavitated area | Before polishing | 128.00 | 4.55 | 8.56 | 3 | 0.003 | 3.99 |
| After polishing | 108.75 | 5.06 | |||||
| Sputtering-affected area | Before polishing | 135.75 | 4.11 | 1.33 | 3 | 0.28 | 0.83 |
| After polishing | 130.75 | 7.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Dong, X.; Zhu, L.; Zhou, Z. Theoretical and Experimental Investigation on a Novel Cavitation-Assisted Abrasive Flow Polishing Method. Micromachines 2024, 15, 1142. https://doi.org/10.3390/mi15091142
Wang J, Dong X, Zhu L, Zhou Z. Theoretical and Experimental Investigation on a Novel Cavitation-Assisted Abrasive Flow Polishing Method. Micromachines. 2024; 15(9):1142. https://doi.org/10.3390/mi15091142
Chicago/Turabian StyleWang, Jiayu, Xiaoxing Dong, Lijun Zhu, and Zhenfeng Zhou. 2024. "Theoretical and Experimental Investigation on a Novel Cavitation-Assisted Abrasive Flow Polishing Method" Micromachines 15, no. 9: 1142. https://doi.org/10.3390/mi15091142
APA StyleWang, J., Dong, X., Zhu, L., & Zhou, Z. (2024). Theoretical and Experimental Investigation on a Novel Cavitation-Assisted Abrasive Flow Polishing Method. Micromachines, 15(9), 1142. https://doi.org/10.3390/mi15091142






